一维无限深势阱 (2)
一维无限深势阱 (2)

论文题目:一维无限深势阱简述制作人:刘子毅(应用物理(1))学号:09510113一维无限深势阱一、引言Hu = Eu,,2222Eu Vu dxu d m =+- (1) 在图中Ⅰ区,-a/2<x<a/2,式中的V=0;在图中Ⅱ区,x<-a/2和x>a/2, V=∞. 现在解Ⅰ区情况的方程,V=0,(1)式成为.2,22222mEk u k u mE dx u d =-=-= 设axe u =,那么u a u n2=,代入上式,u k u a 22-= ik a ±=所以ikx ikx Be Ae u -++=kx D kx C u sin cos += (2)(2)式是Ⅰ区的通解。
2、一维无限深阱电子的基态222222282n mdh n md E n == π n=1、2、3…… 无量纲处理:以波尔半径2200m e a ε=里德伯20242ε me R y =分别为长度和能量单位能量可化为21d E π3、数值模拟当n=1时,1E 和d 的一组数值用计算机编程模拟如下: 设d 从0.3 3.0 include ‹stdio.h › include ‹math.h ›main() { double e,d,c; int i; c=3.14,d=0.3; for(i=0;i ‹10;i++) { e=c/(d*d); printf(“%lf ”,&e); d=d+0.3;} }d 的取值利用画图软件描绘出横坐标为d ,纵坐标为E 的曲线 设d 从0.3 3.0,能量化简为:21dE π=模拟如下:。
高二物理竞赛课件一维无限深势阱

满足归一化条件,另外
z
和
1 me
z
z
还要满足边界条件.
有限深势阱能带
有限
无限
有效质量
En k
E n,0
2k 2 2m 0
2
m
2 0
nn
un0 k p un0 2 En0 En0
E n,0
2k 2
2
1
m
0
m 022k2
nn
un0
k
p
un0
En0 En0
2
E n,0
2k 2 2me
2 2
z
1
me z z
nz
zV
z nz
z
Enz
nz
z,
波函数形式为
B expz,z lz 2
nz
Acoskz, lz A sinkz, lz
B exp z
2
2
,
z z z
lz
lz lz 2
2 2
其中 k
2meI Enz 2
,
2meII V0 Enz 2
,
nz z
一维无限深势阱
一维无限深势阱
E nz
2 2 2me ,hLz2
nz2 ,nz
1,2,3,
有限深真实势阱,仅存在着几个束缚态,
E nz nz2, 系数变小,能级降低.这是由于
势垒降低,电子产生贯穿(Δx↑→ Δ p↓
→ p↓).当 lz 0,Enz (发散)电子 态接近于势垒中的布洛赫态.
.
1
me1m0 Nhomakorabeam 022k2
nn
un0 k p un0 En0 En0
16-3一维势阱和势垒问题解读
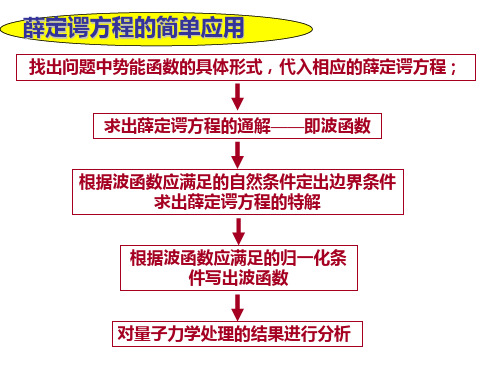
x a
a x
第k激发态(n=k+1)有k个节点。
(2)一维无限深势阱 的粒子位置概率密度 分布
1
2
n 1
0 2 2 n 2 a
2
x
0 无数峰:量子 经典均匀分布 0
a a n 1,x 处,几率最大 0 3 2 b n ,峰数 ,当n 时,
4
U0
II
III
o
a
x
而在微观粒子的情形,却会发生反射。
ቤተ መጻሕፍቲ ባይዱ
(2)E<U0 从解薛定谔方程的结果来看,在 势垒内部存在波函数2。即在势垒内 部找出粒子的概率不为零,同时,在 x>a区域也存在波函数,所以粒子还 I 可能穿过势垒进入x>a区域。
V
V0
II
III
o
a
x
粒子在总能量E小于势垒高度时仍能贯穿势垒的 现象称为隧道效应。
式中 A和α是待定常数,由边界条件和归一化条 件确定。
( x) A sin( kx )
从物理上考虑,粒子不可能透过阱壁,因而按照波 函数的统计诠释,要求在阱壁上和阱外波函数为0。 考虑波函数在阱壁上等于零的情况,即
(0) 0, (a) 0
————边界条件
(0) 0
这说明:并非任何 E值所对应的波函数都能满足一维 无限深方势阱所要求的边界条件,只有当能量取上式 给出的那些分立的值 En(体系的能量本征值)时, 相应的波函数才是物理上有意义的,即本问题中体系 的能量是量子化的,亦即体系的能谱是分立的。
2
2
2 2 2
( x) A sin kx
nx n ( x) A sin( ) a
2无限深势阱

(odd function)
l =1 时, = /2,e Acos kx
是偶函数
(even function)
l 为其他整数值时,给出相同结果
(可能差正负号,但不影响| |2 )
由 o (a / 2) Asin(ka / 2) 0
ka n , n 2,4,6,
一维无限深方形势阱中的波函数与能量
U(x)
U(x)
U=U0
U=U0
U→∞
U→∞
E
极
U=0 限
0
x
金属
a
E
U=0
a /2 0 a /2 x
无限深方势阱 (potential well)
x a / 2 U( x) , 0
x
a / 2 U(x)
0 ,Hˆ
2 2m
d2 d x2
a
所以有能量本征函数:
on
a sin n x 2a
en
a n cos x
2a
0
xa 2
x a 2
(2)全部波函数
考虑振动因子有
n
(
x,
t
)
n
(
x)
e
i
Ent
“能量本征波函数”,“能量本征态”
(3)概率密度:|n( x, t) |2 |n( x) |2
无限深方势阱中的粒子
定态薛定谔方程
[
2
2
U (r )] (r )
E (r )
2m
从数学上来讲:E 不论为何值该方程都有解 从物理上来讲: E只有取某些特定值,该方
量子力学一维势阱

III
(x)
2
2
(U
E )
III
(x)
0
xa
方程可 简化为:
d2
dx
2
I
2 I
0
d2
dx
2
II
2 II
0
d2
dx
2
III
2 III
0
U(x)
I
II
-a 0
III a
U(x)
I
II
-a 0
III
a
1 单值,成立; 2 有限:
当x - ∞ , ψ 有限条件要求
C2=0。
d2
(x)
2
2
[U ( x)
E ]
(x)
0
β2
势V(x)分为三个区域, 用 I 、II 和 III 表达, 其上旳波函数分别为 ψI(x),ψII(x) 和 ψIII (x)。则方程为:
d2
dx 2
I
(x)
2
2
(U
E )
I
(x)
0
x a
d2 dx 2
II
(x)
2
2
E
II
(x)
0
a xa
d2
dx 2
(r , t) (r , t)
称波函数具有偶宇称;
(r , t) (r , t)
称波函数具有奇宇称;
(3)假如在空间反射下,
(r , t) (r , t)
则波函数没有拟定旳宇称
(四)讨论
一维无限深 势阱中粒子 旳状态
(1)n = 1, 基态,
0
n
1
n
sin
2.6 一微无限深势阱

由归一化条件
a
0
( x, t ) dx ( x) dx
0
2
a
2
可得 A 2 a
a
0
n A sin x dx 1 a
2
0 x 0, x a n ( x) n 1,2, n 2 a sin a x 0 x a
2mE k 2
a a
m n m n m n 1 sin x sin x cos x cos x a a 2 a a
可得 若
a 2
a
0
m n dx 0
mn
2
a 1 n 2n 2 A sin xdx A 1 cos x dx 0 0 2 a a 1 A2 a 2
x
所以,系数A必须为零,则Байду номын сангаас由于
e x
x
当
Be e
x
x0
0
所以,系数B必须为零,则
d ( x) E ( x) 阱内 2 2m dx
2
令
k 2mE
2
2
2
d ( x) 2 k ( x) 0 2 dx
其通解为 ( x) Asin kx
a
| ( x) | dx 1
2
1 , a
(与n无关)
最后,波函数是:
1 n n (x) sin ( x a ). 2a a
A和 为待定常数
根据波函数的连续、单值的条件有
(0) 0 0
sin ka 0
0
16-3 一维势阱和势垒问题
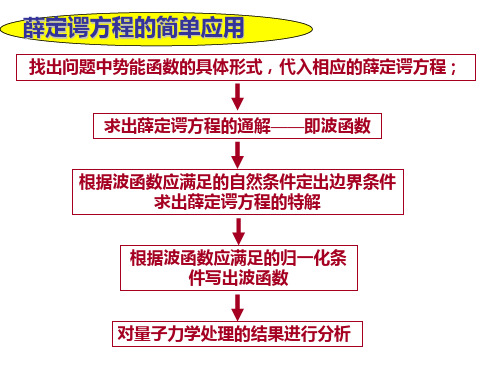
ψ(x) = Asinkx
nπx ψn(x) = Asin ( ) a
ka = nπ , n = 1,2,3,......
(0< x < a) n =12,3 , ,...
与能量本征值E 与能量本征值 n相对应的本征波函数ψn (x)为:
利用归一化条件
∫
2
ψn(x) dx = ∫ ψn(x) dx =1 0 −∞
ψ2 =0
理由:因为势壁无限高 所以粒子不能穿透势壁 理由 因为势壁无限高,所以粒子不能穿透势壁 故势 因为势壁无限高 所以粒子不能穿透势壁,故势 阱外的 波函数为零
定态薛定谔方程为
d ψ 2µ E + 2 ψ =0 2 dx ℏ
2
E是粒子的总能量,E > 0,令 是粒子的总能量, 是粒子的总能量 , 定态薛定谔方程变为
ℏ
V
U0
0≤ x≤a
I II III
O a
x
ℏ
d2ψ1(x) 2 + k ψ1(x) = 0, x ≤0 2 dx 三个区间的薛定 2 谔方程简化为: 谔方程简化为: d ψ 2 ( x) − γ 2ψ ( x) = 0, 0≤ x≤a 2 2 dx d 2ψ3 (x) 2 + k ψ3 (x) = 0, x≥a 2 dx
一维无限深方势阱的数学表达形式 :
U (x ) =
0
(0 < x < a )
∞ ( x ≤ 0 及x ≥ a )
一维无限深方势阱的图形表达形式 : ∞
U(x)
∞ 粒子只能在宽为 a 的两个无 限高势壁间运动, 限高势壁间运动,这种势称为 一维无限深方势阱。
0
a
x
因为系统的势能与时间无关, 因为系统的势能与时间无关,因此这是一个定 态问题,可以用定态薛定谔方程进行求解。 态问题,可以用定态薛定谔方程进行求解。
一维无限深势阱ppt课件

n个节点。
四.几率分布:
在经典力学中,在ξ到ξ+dξ之间的区域内找到质点的 11
几率ω (ξ) dξ与质点在此区域内逗留的时间dt成
比例:
( )d dt
T
T是振动周期。因此有
( )
T
1
d
dt
1 vt
即几率密度与质点的速度成反比。对于经典的线性谐振子,ξ= a sin(ωt+δ ) ,在ξ点的速度为
J
i
2
[
i
d dx
* i
* i
d dx
i
]
k1
|
A |2
JD
k1
| c |2 ,
JR
k1
|
A |2
16
透射系数与反射系数为:
D
JD J
(k12
4k12k22 k22 )2 sin 2 k2a 4k12k22
R
JR J
(k12
(k12 k22 )2 sin 2 k2a k22 )2 sin 2 k2a 4k12k22
13
如果将此问题推广到三维,显然它是散射问题。
二、方势垒的穿透 (1)E>U0 的情况:
薛定谔方程为
d 2
dx 2
2
2
(E
U
0
)
0
令 k1 2E / 2
则其解为
k2 2 (E U 0 ) / 2
1 Aeik1x Ae ik1x
x0
2 Beik2x Beik2x 0 x a
3 Ceik1x C e ik1x
数为:
2 2[U ( x)E ]dx
D D0e
贯穿势垒U(x)的透射系数应等于贯穿所有这些方形势垒的透射 系数之积,即
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
论文题目:一维无限深势阱简述
制作人:刘子毅(应用物理(1))
学号:09510113
一维无限深势阱
一、引言
Hu = Eu,
,2222Eu Vu dx
u d m =+- (1) 在图中Ⅰ区,-a/2<x<a/2,式中的V=0;在图中Ⅱ区,x<-a/2和x>a/2, V=∞. 现在解Ⅰ区情况的方程,V=0,(1)式成为
.2,22
2
22
mE
k u k u mE dx u d =-=-= 设ax
e u =,那么u a u n
2
=,代入上式,
u k u a 22-= ik a ±=
所以
ikx ikx Be Ae u -++=
kx D kx C u sin cos += (2)
(2)式是Ⅰ区的通解。
2、一维无限深阱电子的基态
2
2
22
22
282n md
h n md E n == π n=1、2、3…… 无量纲处理:以波尔半径2
2
00m e a ε=
里德伯2024
2ε me R y =分别为长度和能量单位
能量可化为2
1
d E π
3、数值模拟
当n=1时,1E 和d 的一组数值用计算机编程模拟如下: 设d 从0.3 3.0 include ‹stdio.h › include ‹math.h ›
main() { double e,d,c; int i; c=3.14,d=0.3; for(i=0;i ‹10;i++) { e=c/(d*d); printf(“%lf ”,&e); d=d+0.3;} }
d 的取值利用画图软件描绘出横坐标为d ,纵坐标为E 的曲线 设d 从0.3 3.0,能量化简为:2
1d
E π
=
模拟如下:。
