立体几何专题练习(全国通用)
全国通用2020_2022三年高考数学真题分项汇编专题06立体几何解答题文(含答案)

高考数学真题分项汇编专题:06 立体几何(解答题)(文科专用)1.【2022年全国甲卷】小明同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图所示:底面ABCD是边长为8(单位:cm)的正方形,△EAB,△FBC,△GCD,△HDA均为正三角形,且它们所在的平面都与平面ABCD垂直.(1)证明:EF//平面ABCD;(2)求该包装盒的容积(不计包装盒材料的厚度).【答案】(1)证明见解析;√3.(2)6403【解析】【分析】(1)分别取AB,BC的中点M,N,连接MN,由平面知识可知EM⊥AB,FN⊥BC,EM=FN,依题从而可证EM⊥平面ABCD,FN⊥平面ABCD,根据线面垂直的性质定理可知EM//FN,即可知四边形EMNF为平行四边形,于是EF//MN,最后根据线面平行的判定定理即可证出;(2)再分别取AD,DC中点K,L,由(1)知,该几何体的体积等于长方体KMNL−EFGH的体积加上四棱锥B−MNFE体积的4倍,即可解出.(1)如图所示:,分别取AB,BC 的中点M,N ,连接MN ,因为△EAB,△FBC 为全等的正三角形,所以EM ⊥AB,FN ⊥BC ,EM =FN ,又平面EAB ⊥平面ABCD ,平面EAB ∩平面ABCD =AB ,EM ⊂平面EAB ,所以EM ⊥平面ABCD ,同理可得FN ⊥平面ABCD ,根据线面垂直的性质定理可知EM//FN ,而EM =FN ,所以四边形EMNF 为平行四边形,所以EF//MN ,又EF ⊄平面ABCD ,MN ⊂平面ABCD ,所以EF//平面ABCD . (2)如图所示:,分别取AD,DC 中点K,L ,由(1)知,EF//MN 且EF =MN ,同理有,HE//KM,HE =KM ,HG//KL,HG =KL ,GF//LN,GF =LN ,由平面知识可知,BD ⊥MN ,MN ⊥MK ,KM =MN =NL =LK ,所以该几何体的体积等于长方体KMNL −EFGH 的体积加上四棱锥B −MNFE 体积的4倍.因为MN =NL =LK =KM =4√2,EM =8sin60∘=4√3,点B 到平面MNFE 的距离即为点B 到直线MN 的距离d ,d =2√2,所以该几何体的体积V =(4√2)2×4√3+4×13×4√2×4√3×2√2=128√3+2563√3=6403√3.2.【2022年全国乙卷】如图,四面体ABCD 中,AD ⊥CD,AD =CD,∠ADB =∠BDC ,E 为AC的中点.(1)证明:平面BED⊥平面ACD;(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求三棱锥F−ABC 的体积.【答案】(1)证明详见解析(2)√34【解析】【分析】(1)通过证明AC⊥平面BED来证得平面BED⊥平面ACD.(2)首先判断出三角形AFC的面积最小时F点的位置,然后求得F到平面ABC的距离,从而求得三棱锥F−ABC的体积.(1)由于AD=CD,E是AC的中点,所以AC⊥DE.由于{AD=CD BD=BD∠ADB=∠CDB,所以△ADB≅△CDB,所以AB=CB,故AC⊥BD,由于DE∩BD=D,DE,BD⊂平面BED,所以AC⊥平面BED,由于AC⊂平面ACD,所以平面BED⊥平面ACD.(2)依题意AB=BD=BC=2,∠ACB=60°,三角形ABC是等边三角形,所以AC=2,AE=CE=1,BE=√3,由于AD=CD,AD⊥CD,所以三角形ACD是等腰直角三角形,所以DE=1. DE2+BE2=BD2,所以DE⊥BE,由于AC∩BE=E,AC,BE⊂平面ABC,所以DE⊥平面ABC.由于△ADB≅△CDB,所以∠FBA=∠FBC,由于{BF =BF∠FBA =∠FBC AB =CB ,所以△FBA ≅△FBC ,所以AF =CF ,所以EF ⊥AC ,由于S △AFC =12⋅AC ⋅EF ,所以当EF 最短时,三角形AFC 的面积最小值. 过E 作EF ⊥BD ,垂足为F ,在Rt △BED 中,12⋅BE ⋅DE =12⋅BD ⋅EF ,解得EF =√32,所以DF =√12−(√32)2=12,BF =2−DF =32,所以BF BD =34.过F 作FH ⊥BE ,垂足为H ,则FH//DE ,所以FH ⊥平面ABC ,且FHDE =BFBD =34, 所以FH =34,所以V F−ABC =13⋅S △ABC ⋅FH =13×12×2×√3×34=√34.3.【2021年甲卷文科】已知直三棱柱111ABC A B C -中,侧面11AA B B 为正方形,2AB BC ==,E ,F 分别为AC 和1CC 的中点,11BF A B ⊥.(1)求三棱锥F EBC -的体积;(2)已知D 为棱11A B 上的点,证明:BF DE ⊥. 【答案】(1)13;(2)证明见解析.【解析】 【分析】(1)先证明ABC 为等腰直角三角形,然后利用体积公式可得三棱锥的体积;(2)将所给的几何体进行补形,从而把线线垂直的问题转化为证明线面垂直,然后再由线面垂直可得题中的结论. 【详解】(1)由于11BF A B ⊥,11//AB A B ,所以AB BF ⊥, 又AB ⊥BB 1,1BB BF B ⋂=,故AB ⊥平面11BCC B , 则AB BC ⊥,ABC 为等腰直角三角形, 111221222BCE ABC S S ⎛⎫==⨯⨯⨯= ⎪⎝⎭△△,11111333F EBC BCE V S CF -=⨯⨯=⨯⨯=△. (2)由(1)的结论可将几何体补形为一个棱长为2的正方体1111ABCM A B C M -,如图所示,取棱,AM BC 的中点,H G ,连结11,,A H HG GB ,正方形11BCC B 中,,G F 为中点,则1BF B G ⊥, 又111111,BF A B A B B G B ⊥=,故BF ⊥平面11A B GH ,而DE ⊂平面11A B GH , 从而BF ⊥DE . 【点睛】求三棱锥的体积时要注意三棱锥的每个面都可以作为底面,例如三棱锥的三条侧棱两两垂直,我们就选择其中的一个侧面作为底面,另一条侧棱作为高来求体积.对于空间中垂直关系(线线、线面、面面)的证明经常进行等价转化.4.【2021年乙卷文科】如图,四棱锥P ABCD -的底面是矩形,PD ⊥底面ABCD ,M 为BC 的中点,且PB AM ⊥.(1)证明:平面PAM ⊥平面PBD ;(2)若1PD DC ==,求四棱锥P ABCD -的体积.【答案】(1)证明见解析;(2 【解析】 【分析】(1)由PD ⊥底面ABCD 可得PD AM ⊥,又PB AM ⊥,由线面垂直的判定定理可得AM ⊥平面PBD ,再根据面面垂直的判定定理即可证出平面PAM ⊥平面PBD ;(2)由(1)可知,AM BD ⊥,由平面知识可知,~DAB ABM ,由相似比可求出AD ,再根据四棱锥P ABCD -的体积公式即可求出. 【详解】(1)因为PD ⊥底面ABCD ,AM ⊂平面ABCD , 所以PD AM ⊥, 又PB AM ⊥,PBPD P =,所以AM ⊥平面PBD , 而AM ⊂平面PAM , 所以平面PAM ⊥平面PBD . (2)[方法一]:相似三角形法 由(1)可知AM BD ⊥. 于是∽ABD BMA ,故=AD ABAB BM.因为1,,12===BM BC AD BC AB ,所以2112BC =,即BC =故四棱锥P ABCD -的体积13=⋅⋅=V AB BC PD . [方法二]:平面直角坐标系垂直垂直法由(2)知⊥AM DB ,所以1⋅=-AM BD k k . 建立如图所示的平面直角坐标系,设2(0)BC a a =>.因为1DC =,所以(0,0)A ,(1,0)B ,(0,2)D a ,()1,M a . 从而2020(2)211001--⋅=⨯=⨯-=-=---AM BD a a k k a a a .所以2a =,即DA =. [方法三]【最优解】:空间直角坐标系法 建立如图所示的空间直角坐标系D xyz -,设||=DA t ,所以(0,0,0)D ,(0,1,0)C ,(0,0,1)P ,(,0,0)A t ,(,1,0)B t . 所以,1,02t M ⎛⎫ ⎪⎝⎭,(,1,1)PB t =-,,1,02t AM ⎛⎫=- ⎪⎝⎭.所以2110(1)1022t t PB AM t ⎛⎫⋅=⋅-+⨯+⨯-=-+= ⎪⎝⎭.所以t ,即||=DA . [方法四]:空间向量法由PB AM ⊥,得0PB AM ⋅=. 所以()0++⋅=PD DA AB AM . 即0⋅+⋅+⋅=PD AM DA AM AB AM .又PD ⊥底面ABCD ,AM 在平面ABCD 内, 因此PD AM ⊥,所以0⋅=PD AM . 所以0⋅+⋅=DA AM AB AM ,由于四边形ABCD 是矩形,根据数量积的几何意义,得221||||02-+=DA AB ,即21||102-+=BC .所以||2BC =,即BC =. 【整体点评】(2)方法一利用相似三角形求出求出矩形的另一个边长,从而求得该四棱锥的体积; 方法二构建平面直角坐标系,利用直线垂直的条件得到矩形的另一个边长,从而求得该四棱锥的体积;方法三直接利用空间直角坐标系和空间向量的垂直的坐标运算求得矩形的另一个边长,为最常用的通性通法,为最优解;方法四利用空间向量转化求得矩形的另一边长.5.【2020年新课标1卷文科】如图,D 为圆锥的顶点,O 是圆锥底面的圆心,ABC 是底面的内接正三角形,P 为DO 上一点,∠APC =90°.(1)证明:平面PAB ⊥平面PAC ;(2)设DO ,求三棱锥P −ABC 的体积.【答案】(1)证明见解析;(2【解析】 【分析】(1)根据已知可得PA PB PC ==,进而有PAC △≌PBC ,可得90APC BPC ∠=∠=,即PB PC ⊥,从而证得PC ⊥平面PAB ,即可证得结论;(2)将已知条件转化为母线l 和底面半径r 的关系,进而求出底面半径,由正弦定理,求出正三角形ABC 边长,在等腰直角三角形APC 中求出AP ,在Rt APO 中,求出PO ,即可求出结论.【详解】(1)连接,,OA OB OC ,D 为圆锥顶点,O 为底面圆心,OD ∴⊥平面ABC ,P 在DO 上,,OA OB OC PA PB PC ==∴==,ABC 是圆内接正三角形,AC BC ∴=,PAC △≌PBC ,90APC BPC ∴∠=∠=︒,即,PB PC PA PC ⊥⊥,,PA PB P PC =∴⊥平面,PAB PC ⊂平面PAC ,∴平面PAB ⊥平面PAC ;(2)设圆锥的母线为l ,底面半径为r ,圆锥的侧面积为,rl rl π==2222OD l r =-=,解得1,r l ==2sin 603AC r ==在等腰直角三角形APC 中,AP ==在Rt PAO 中,PO ===∴三棱锥P ABC -的体积为11333P ABC ABC V PO S -=⋅==△【点睛】本题考查空间线、面位置关系,证明平面与平面垂直,求锥体的体积,注意空间垂直间的相互转化,考查逻辑推理、直观想象、数学计算能力,属于中档题.6.【2020年新课标2卷文科】如图,已知三棱柱ABC –A 1B 1C 1的底面是正三角形,侧面BB 1C 1C 是矩形,M ,N 分别为BC ,B 1C 1的中点,P 为AM 上一点.过B 1C 1和P 的平面交AB 于E ,交AC 于F .(1)证明:AA 1//MN ,且平面A 1AMN ⊥平面EB 1C 1F ;(2)设O 为△A 1B 1C 1的中心,若AO =AB =6,AO //平面EB 1C 1F ,且∠MPN =π3,求四棱锥B –EB 1C 1F 的体积.【答案】(1)证明见解析;(2)24. 【解析】 【分析】(1)由,M N 分别为BC ,11B C 的中点,1//MN CC ,根据条件可得11//AA BB ,可证1MN AA //,要证平面11EB C F ⊥平面1A AMN ,只需证明EF ⊥平面1A AMN 即可;(2)根据已知条件求得11EB C F S 四边形和M 到PN 的距离,根据椎体体积公式,即可求得11B EB C F V -. 【详解】 (1),M N 分别为BC ,11B C 的中点,1//MN BB ∴又11//AA BB 1//MN AA ∴在等边ABC 中,M 为BC 中点,则BC AM ⊥ 又侧面11BB C C 为矩形, 1BC BB ∴⊥1//MN BBMN BC ⊥由MN AM M ⋂=,,MN AM ⊂平面1A AMN ∴BC ⊥平面1A AMN又11//B C BC ,且11B C ⊄平面ABC ,BC ⊂平面ABC ,11//B C ∴平面ABC又11B C ⊂平面11EB C F ,且平面11EB C F ⋂平面ABC EF =11//B C EF ∴//EF BC ∴又BC ⊥平面1A AMN∴EF ⊥平面1A AMNEF ⊂平面11EB C F∴平面11EB C F ⊥平面1A AMN(2)过M 作PN 垂线,交点为H ,画出图形,如图//AO 平面11EB C FAO ⊂平面1A AMN ,平面1A AMN ⋂平面11EB C F NP =//AO NP ∴ 又//NO AP∴6AO NP ==O 为111A B C △的中心.∴1111sin 606sin 6033ON AC =︒=⨯⨯︒=故:ON AP ==3AM AP ==平面11EB C F ⊥平面1A AMN ,平面11EB C F ⋂平面1A AMN NP =,MH ⊂平面1A AMN∴MH ⊥平面11EB C F 又在等边ABC 中EFAPBC AM =即2AP BCEF AM ⋅===由(1)知,四边形11EB C F 为梯形∴四边形11EB C F 的面积为:111126=62422EB C F EF B C S NP ++=⋅⨯=四边形 111113B EBC F EB C F V S h -∴=⋅四边形,h 为M 到PN 的距离sin 603MH =︒=, ∴1243243V =⨯⨯=. 【点睛】本题主要考查了证明线线平行和面面垂直,及其求四棱锥的体积,解题关键是掌握面面垂直转为求证线面垂直的证法和棱锥的体积公式,考查了分析能力和空间想象能力,属于中档题.7.【2020年新课标3卷文科】如图,在长方体1111ABCD A B C D -中,点E ,F 分别在棱1DD ,1BB 上,且12DE ED =,12BF FB =.证明:(1)当AB BC =时,EF AC ⊥;(2)点1C 在平面AEF 内.【答案】(1)证明见解析;(2)证明见解析.【解析】【分析】(1)根据正方形性质得AC BD ⊥,根据长方体性质得1AC BB ⊥,进而可证AC ⊥平面11BB D D ,即得结果;(2)只需证明1//EC AF 即可,在1CC 上取点M 使得12CM MC =,再通过平行四边形性质进行证明即可.【详解】(1)因为长方体1111ABCD A B C D -,所以1BB ⊥平面ABCD ∴1AC BB ⊥,因为长方体1111,ABCD A B C D AB BC -=,所以四边形ABCD 为正方形AC BD ∴⊥ 因为11,BB BD B BB BD =⊂、平面11BB D D ,因此AC ⊥平面11BB D D ,因为EF ⊂平面11BB D D ,所以AC EF ⊥;(2)在1CC 上取点M 使得12CM MC =,连,DM MF ,因为111112,//,=D E ED DD CC DD CC =,所以11,//,ED MC ED MC =所以四边形1DMC E 为平行四边形,1//DM EC ∴因为//,=,MF DA MF DA 所以M F A D 、、、四点共面,所以四边形MFAD 为平行四边形, 1//,//DM AF EC AF ∴∴,所以1E C A F 、、、四点共面,因此1C 在平面AEF 内【点睛】本题考查线面垂直判定定理、线线平行判定,考查基本分析论证能力,属中档题.。
“立体几何”大题的常考题型探究(课件)2023年高考数学二轮复习(全国通用)

因为 ,所以 .由已知得 ,故 .又 ,所以 .因为 , , , , ,所以 .
提分秘籍 体积问题考查的本质就是点面距离,解题关键是抓住以下几种方法:
(1)等体积法(仅限三棱锥)转换顶点;
(2)顶点不变,延展或缩小底面,如四棱锥的高即同顶点的三棱锥的高,点 到平面 的距离可看作点 到平面 的距离;
设 ,则 , , .设平面 的法向量为 ,则 即
令 ,则 ,∴平面 的一个法向量为 , .∵直线的方向向量与平面的法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值,∴直线 与平面 所成角的正弦值等于, ,当且仅当 时取等号.
∴直线 与平面 所成角的正弦值的最大值为 .(法二:定义法)如图2, 平面 , , 平面 .
大题攻略03 平面与平面所成的角
例3 (2021年全国甲卷)已知直三棱柱 中,侧面 为正方形, , , 分别为 和 的中点, 为棱 上的点, .
(1)证明: .(2)当 为何值时,平面 与平面 所成的二面角的正弦值最小?
▶审题微“点”
切入点
(1)常规方法是几何法,不过用几何法较为复杂,根据题目条件建系是最优解法;(2)建系是常规方法,也是最优法
▶审题微“点”
切入点
(1)关键是在平面 内找一条直线与 平行,根据线面平行的判定定理即可证明;(2)将包装盒分割成几个规则的锥体和柱体求解
障碍点
(1)在平面 内找直线与 平行;(2)将不规则的几何体分割或补形成几个规则的几何体
隐蔽点
(1)平面 内与 平行的直线;(2)包装盒的高
[解析] (1)如图1所示,分别取 , 的中点 , ,连接 ,因为 , 为全等的正三角形,所以 , , .
六年级下册数学试题-小升初能力训练:几何综合——立体几何(解析版)全国通用
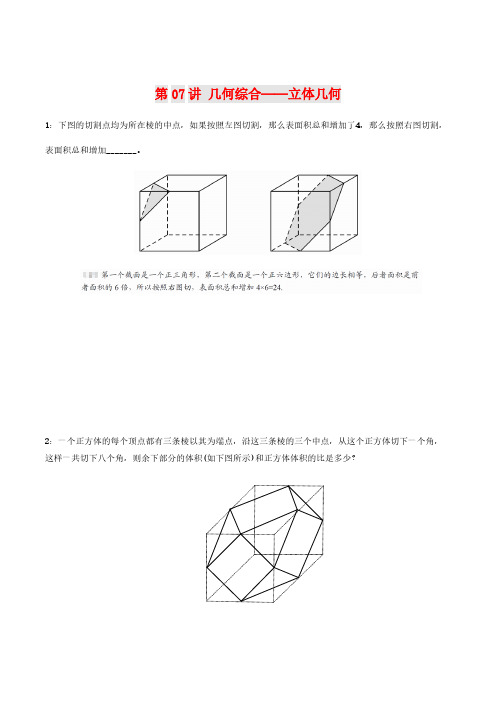
第07讲几何综合——立体几何1:下图的切割点均为所在棱的中点,如果按照左图切割,那么表面积总和增加了4,那么按照右图切割,表面积总和增加_______。
2:一个正方体的每个顶点都有三条棱以其为端点,沿这三条棱的三个中点,从这个正方体切下一个角,这样一共切下八个角,则余下部分的体积(如下图所示)和正方体体积的比是多少?假设正方体的边长为1,那么每个切去的角(三棱锥)的体积为,211111322248⎛⎫⨯⨯⨯= ⎪⎝⎭所以八个角一共切去的体积,所以余下的体积是正方体体积的,118486⨯=15166-=即余下部分的体积与正方体体积的比为.5:63:如图,原正方体的棱长为12厘米,沿图中的线将正方体切掉正面的部分,求剩下不规则立体图形的体积.倾斜于上下底面的切面,把正方体一分为二.被切掉的部分的图形和剩下的部分图形关于正方形的中心是对称的.33122864(cm )÷=4:如图,正方体的棱长为,连接正方体其中六条棱的中点形成一个正六边形,而连接其中三个顶点6cm 形成一个正三角形.正方体夹在六边形与三角形之间的立体图形有 个面,它的体积是.3cm乙9乙从图中可以看出,夹在六边形与三角形之间的立体图形有2个底面和6个侧面(六边形的每一条边对应一个侧面),所以共有个面,8由于正方体是关于它的中心成中心对称的,而根据正六边形和正三角形的连法,如果从正方体中去掉以这个正三角形为底面的三棱锥以及与它相对的三棱锥后,剩下的部分正好被六边形分成2个同样的立体图形,这就是所要求的立体图形.所以所要求的立体图形的体积是:.3111666266672(cm )232⎡⎤⎛⎫⨯⨯⨯-⨯⨯⨯⨯⨯= ⎪⎢⎥⎝⎭⎣⎦5:如图,有一个棱长为2厘米的正方体。
从正方体的上面正中间下挖一个棱长为1厘米的正方体小洞;接着在小洞的底面正中间再向下挖一个棱长为厘米的小洞;第三个小洞的挖法与前面两个相同,棱长为12厘米,最后得到的额例题图形的表面积是多少平方厘米?146:如图,把正方体用两个与它的底面平行的平面切开,分成三个长方体,这三个长方体的表面积比是3:4:5时,用最简单的整数比表示这三个长方体的体积比:::。
立体几何专项训练

立体几何专项训练1.如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D−AF−E与二面角C−BE−F都是60°.(Ⅰ)证明:平面ABEF⊥平面EFDC;(Ⅱ)求二面角E−BC−A的余弦值.2.如图,在四棱锥P−ABCD中,AB//CD,且∠BAP=∠CDP=90°.(1)证明:平面PAB⊥平面PAD;(2)若PA=PD=AB=DC,∠APD=90°,求二面角A−PB−C的余弦值.3.如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC折起,使点C到达点P的位置,且PF⊥BF.(1)证明:平面PEF⊥平面ABFD;(2)求DP与平面ABFD所成角的正弦值.4.如图,直四棱柱ABCD−A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN//平面C1DE;(2)求二面角A−MA1−N的正弦值.5.如图,D为圆锥的顶点,O是圆锥底面的圆心,AE为底面直径,AE=AD.△ABC是底面的内接正三角形,P为DO上DO.一点,PO=√66(1)证明:PA⊥平面PBC;(2)求二面角B−PC−E的余弦值6.如图,四棱锥P−ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.(1)证明:l⊥平面PDC;(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.7.如图,在三棱锥A−BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.(1)证明:OA⊥CD;(2)若△OCD是边长为1的等边三角形,点E在棱AD上,DE=2EA,且二面角E−BC−D的大小为45°,求三棱锥A−BCD的体积.8.如图,直三棱柱ABC−A1B1C1的体积为4,△A1BC的面积为2√2.(1)求A到平面A1BC的距离;(2)设D为A1C的中点,AA1=AB,平面A1BC⊥平面ABB1A1,求二面角A−BD−C的正弦值.。
立体几何100题

立体几何100 题1. 如图,三角形中,,是边长为l 的正方形,平面底面,若分别是的中点.(1)求证:底面;(2)求几何体的体积.2.在三棱锥P ABC 中,PAC 和PBC 是边长为 2 的等边三角形,AB 2 ,O,D分别是AB, PB 的中点.(1)求证:OD / / 平面PAC ;(2)求证: OP 平面ABC ;(3)求三棱锥 D ABC 的体积.3.如图,在直三棱柱ABC A1B1C1 中,0BAC 90 ,AB AC 2 ,点M , N 分别为A1C1, AB1 的中点.(1)证明:MN / / 平面BBC C ;1 1(2)若CM MN ,求三棱锥M NAC 的体积..4.如图,在三棱柱中,平面,点是与的交点,点在线段上,平面.(1)求证:;(2)若, 求点到平面的距离.5 .如图,四棱锥P A B C中,底面ABCD 是直角梯形,1AB BC, AD / /BC, AB BC AD ,PAD 是正三角形, E 是PD 的中点.2(1)求证:AD PC ;(2)判定CE 是否平行于平面PAB ,请说明理由.6.如图,在四棱锥S ABCD 中,侧面SAD 底面ABCD ,SA SD ,AD / /BC ,AD 2BC 2CD ,M ,N 分别为AD ,SD的中点.(1)求证:SB/ / 平面CMN ;(2)求证:BD 平面SCM .7.如图,在矩形中,,平面,分别为的中点,点是上一个动点.(1) 当是中点时,求证: 平面平面;(2) 当时,求的值.8.如图,在正三棱柱A1B1C1 ABC 中,点D, E 分别是A1C,AB 的中点.求证:ED ∥平面B BC C1 1若A B 2BB 求证:A1B⊥平面B1CE.19.如图,在长方体ABCD A1B1C1D1 中,AB 2, AD 1, A1A 1.(1)证明直线B C 平行于平面D1AC ;1(2)求直线B C 到平面D1AC 的距离.110.如图所示,菱形ABCD 与正三角形BCE 所在平面互相垂直,FD 平面ABCD ,且AB ,FD 3 .2(1)求证:EF / / 平面ABCD ;(2)若C BA ,求几何体EFABCD 的体积.311.在直三棱柱ABC-A1B1C1 中,AB=AC,E 是BC的中点,求证:(Ⅰ)平面AB1E⊥平面B1BCC1;(Ⅱ)A1C// 平面AB1E.12.如图,在三棱柱中,平面,,,点为的中点.(1)证明:平面;(2)求三棱锥的体积.13.如图,在多面体中,四边形是正方形,在等腰梯形中,,,,为中点,平面平面.(1)证明:;(2)求三棱锥的体积.14.已知三棱锥,,,为的中点,平面,,,是中点,与所成的角为,且.(1)求证:;(2)求三棱锥的体积.15.在四棱锥中,平面平面,,是等边三角形,已知,,.(1)设是上一点,求证:平面平面.(2)求四棱锥的体积.16.如图,在四棱锥P ABCD中,PA底面A B C D,底面A B C D为菱形,ABC,PA PB1,E为PC的中点60.(1)求证:PA / / 平面BDE ;(2)求三棱锥P BDE 的体积.17.如图,在直三棱柱(侧棱与底面垂直的棱柱)ABC A1B1C1 中,点G 是AC 的中点.(1)求证:B1C / / 平面A1BG ;(2)若A B BC ,AC 2 AA1 ,求证:AC1 A1B.18.如图所示,四棱锥S ABCD 中,平面SAD 平面ABCD ,SA AD ,AD / /BC ,4SA BC AB 2 AD 4 .3(1)证明:在线段SC 上存在一点 E ,使得ED / / 平面SAB;(2)若AB AC ,在(1)的条件下,求三棱锥S AED 的体积.19.(本小题共12 分)如图,边长为 3 的正方形ABCD 所在平面与等腰直角三角形ABE 所在平面互相垂直,AE AB ,且EM 2MD ,AB 3AN .(Ⅰ)求证:MN / / 平面BEC ;(Ⅱ)求三棱锥 E BMC 的体积.20.如图,在四棱锥中,底面是边长为2的正方形,分别为的中点,平面底面.(1)求证:平面;(2)若,求三棱锥的体积.21.在直三棱柱ABC-A1B1C1中,AB=AC,E是BC的中点,求证:(Ⅰ)平面AB1E⊥平面B1BCC1;(Ⅱ)A1C//平面AB1E.22.如图1,四边形ABCD为等腰梯形,AB2,AD DC CB1,将ADC沿AC 折起,使得平面ADC平面ABC,E为AB的中点,连接DE,DB.(1)求证:BC AD;(2)求E到平面BCD的距离.23.如图,四棱锥中,底面为菱形,平面,为的中点.(Ⅰ)证明:平面;(Ⅱ)设,求三棱锥的体积.24.如图,在多面体中,四边形是正方形,在等腰梯形中,,,,为中点,平面平面.(1) 证明:;(2) 求三棱锥的体积.25.如图1,在矩形中,,,是的中点,将沿折起,得到如图 2 所示的四棱锥,其中平面平面.(1)证明:平面;(2)设为的中点,在线段上是否存在一点,使得平面,若存在,求出的值;若不存在,请说明理由.26.如图,在四棱锥P ABCD 中,ABC ACD 90 ,BAC CAD 60 ,PA 平面ABCD ,PA 2, AB 1. 设M ,N分别为PD, AD 的中点.(1)求证:平面CMN ∥平面PAB ;(2)求三棱锥P ABM 的体积.27.如图所示,在长方体ABCD A1B1C1D1中,底面ABCD是边长为1的正方形,AA12,P为棱B B上的一个动点.1(1)求三棱锥C PAA的体积;1(2)当A P PC取得最小值时,求证:1PD平面PAC.128.在三棱柱ABC A1B1C1中,已知侧棱CC1底面ABC,M为BC的中点,AC AB3,BC2,CC2.1(1)证明:B C平面AMC1;(2)求点A1到平面AMC1的距离.129.五边形ANB1C1C是由一个梯形ANB1B与一个矩形BB1C1C组成的,如图甲所示,B为AC的中点,A C CC12AN8.先沿着虚线BB1将五边形ANB1C1C折成直二面角A BB C,如图乙所示.1(Ⅰ)求证:平面BNC平面C B N;(Ⅱ)求图乙中的多面体的体积.1130.如图1,AFA1中,FA FA1,AA18,CF2,点B,C,D为线段AA1的四等分点,线段BE,CF,DG互相平行,现沿BE,CF,DG折叠得到图2所示的几何体,此几何体的底面ABCD为正方形.(1)证明:A,E,F,G四点共面;(2)求四棱锥B AEFG的体积.31.如图,三棱锥P ABC中,PC平面ABC,F,G,H分别是PC,AC,BC的中点,I是线段FG上的任意一点,PC AB2BC2,过点F作平行于底面ABC的平面DEF交AP于点D,交BP于点E.(1)求证:HI//平面ABD;(2)若AC BC,求点E到平面FGH的距离.32.如图,已知正方体的棱长为3,分别是棱、上的点,且.(1)证明:四点共面;(2)求几何体的体积.33 .如图,在四棱柱ABCD A1B1C1D1 中,已知平面AA1C1C 平面A B C D,且AB BC CA 3,AD CD 1.(1)求证:BD AA1 ;(2)若E 为棱BC 的中点,求证:AE / / 平面DCC1D1 .34.如图,在三棱柱ABC A1B1C1 中,底面ABC 是等边三角形,且AA1 平面ABC , D 为AB 的中点,( Ⅰ) 求证:直线B C1 / / 平面A1CD ;( Ⅱ) 若A B BB1 2,E 是B B1 的中点,求三棱锥A1 CDE 的体积;35.如图,将菱形沿对角线折叠,分别过,作所在平面的垂线,,垂足分别为,,四边形为菱形,且.(1)求证:平面;(2)若,求该几何体的体积.36.如图,在四棱锥P ABCD中,AD CD,PC平面ABCD.1PC AD CD AB2,AB//DC,2(1)求证:BC平面PAC;(2)若M为线段PA的中点,且过C,D,M三点的平面与线段PB交于点N,确定点N的位置,说明理由;并求三棱锥A CMN的高.37.如图,在四棱锥O ABCD中,底面ABCD是边长为2的正方形,侧棱OB底面ABCD,且侧棱OB的长是2,点E,F,G分别是AB,OD,BC的中点.(Ⅰ)证明:OD平面EFG;(Ⅱ)求三棱锥O EFG的体积.38.如图,多面体ABCDEF中,AD//BC,AB AD,FA平面ABCD,FA//DE,且AB AD AF2BC2DE2.(Ⅰ)M为线段EF中点,求证:CM//平面ABF;(Ⅱ)求多面体ABCDEF的体积.39.在如图所示的几何体中,四边形BB1C1C是矩形,BB1平面ABC,A1B1//AB,AB2A1B1,E是AC的中点.(1)求证:A1E//平面BB1C1C;(2)若AC BC,A B2BB,求证平面BEA1平面AA1C1.140.如图,四边形ABCD为梯形,AB CD,PD平面A B C D,BAD ADC90,DC2AB2a,DA3a,E为BC中点.(1)求证:平面PBC平面PDE;(2)线段PC上是否存在一点F,使PA平面BDF?若有,请找出具体位置,并进行证明:若无,请分析说明理由.41.已知四棱锥S ABCD中,底面ABCD是边长为2的菱形,BAD60,SA SD5,SB7,点E是棱AD的中点,点F在棱SC上,且S FSC,SA//平面BEF.(Ⅰ)求实数的值;(Ⅱ)求三棱锥F EBC的体积.42.在三棱柱ABC-A1B1C1中,AB=BC=CA=A1=A2,侧棱AA1⊥平面ABC,且D,E分别是棱A1B1,AA1的中点,点F在棱AB上,且AF=14 AB。
立体几何专题

立体几何专题1. (北京文) (18) (本小题 14 分)如图,在四棱锥 P-ABCD 中,底面 ABCD 为矩形, 平面 PAD⊥平面 ABCD , PA⊥ PD , PA=PD , E , F 分别为 AD , PB 的中点.( Ⅰ ) 求证: PE ⊥BC ; (Ⅱ)求证:平面 PAB ⊥平面 PCD ; (Ⅲ) 求证: EF∥平面 PCD.2. (北京理) (16) (本小题 14 分)如图, 在三棱柱 ABC- A 1B 1C 1 中, CC 1 」平面 ABC , D , E , F , G 分别为 AA 1,AC , A 1C 1,BB 1 的中点, AB=BC= 5, AC= AA 1 =2.( Ⅰ ) 求证: AC⊥平面 BEF ; ( Ⅱ ) 求二面角B-CD-C 1 的余弦值; (Ⅲ) 证明: 直线 FG 与平面 BCD 相交.3. (江苏) (15) (本小题满分 14 分)在平行六面体ABCD 一 A B C D 中,AA = AB, AB 」B C .求证: (1) AB∥平面A B C; (2) 平面ABB A 」平面A BC.4. (浙江) (19) (本题满分 15 分)如图,已知多面体 ABCA1B1C1,A1A, B1B, C1C均垂直于平面 ABC,∠ABC=120°, A1A=4, C1C=1, AB=BC=B1B=2.(Ⅰ)证明:AB1 ⊥平面A1B1C1;(Ⅱ)求直线 AC1 与平面 ABB1 所成的角的正弦值.1 1 1 1 1 1 1 1 1 1 1 1 1第 2 页共 10 页5. (天津文) (17)(本小题满分 13 分)如图,在四面体 ABCD 中,△ABC 是等边三角形,平面 ABC⊥平面 ABD,点 M 为棱AB 的中点, AB=2, AD= 2 3 ,∠BAD=90°.( Ⅰ )求证:AD⊥BC;( Ⅱ ) 求异面直线 BC 与 MD 所成角的余弦值;(Ⅲ)求直线 CD 与平面 ABD 所成角的正弦值.6. (天津理) (17)(本小题满分 13 分)如图,AD∥BC 且 AD=2BC,AD 」CD , EG∥AD且 EG=AD,CD∥FG 且 CD=2FG,DG 」平面ABCD, DA=DC=DG=2.(I)若 M 为 CF 的中点, N 为 EG 的中点,求证:MN∥平面CDE;(II)求二面角E BC F 的正弦值;(III)若点 P 在线段 DG 上,且直线 BP 与平面 ADGE 所成的角为60°,求线段 DP 的长.7. (全国卷一文)(18)(12 分)如图, 在平行四边形 ABCM 中, AB = AC = 3, ∠ACM = 90, 以 AC 为折痕 将△ ACM 折起,使点 M 到达点 D 的位置,且 AB⊥DA. (1)证明:平面 ACD ⊥平面 ABC ;(2) Q 为线段 AD 上一点, P 在线段 BC 上, 且 BP = DQ = DA , 求三棱锥3Q ABP 的体积.8. (全国卷一理)(18)(12 分)如图, 四边形 ABCD 为正方形, E, F 分别为 AD, BC 的中点, 以 DF 为折 痕把 △DFC 折起,使点 C 到达点 P 的位置,且 PF 」BF . (1)证明:平面 PEF 」平面 ABFD ; (2)求 DP 与平面 ABFD 所成角的正弦值 .29. (全国卷二文)( 19) (12 分)如图,在三棱锥P ABC 中,AB = BC = 2 2,PA = PB = PC = AC = 4,O为AC 的中点.(1)证明:PO 」平面ABC;(2)若点M 在棱 BC 上,且MC = 2MB,求点C 到平面POM 的距离.10. (全国卷二理)(20)(12分)如图,在三棱锥P ABC 中,AB = BC = 2 2,PA = PB = PC = AC = 4,O 为AC 的中点.(1)证明:PO 」平面ABC;(2) 若点M 在棱BC 上,且二面角M PA C 为30,求PC 与平面 PAM 所成角的正弦值.POA CMB11. (全国卷三文)(19)(12分)如图,矩形ABCD所在平面与半圆弧 CD 所在平面垂直,M 是CD 上异于C, D 的点.(1)证明:平面AMD⊥平面BMC;(2)在线段AM 上是否存在点 P ,使得MC∥平面PBD ?说明理由.12. (全国卷三理)(19)(12分)如图,边长为 2 的正方形ABCD所在的平面与半圆弧CD 所在平面垂直,M 是CD 上异于C, D 的点.(1)证明:平面 AMD⊥平面BMC;(2) 当三棱锥M ABC 体积最大时,求面 MAB 与面MCD所成二面角的正弦值.13. (12 分)如图,四棱锥 P-ABCD 中,侧面 PAD 为等比三角形且垂直于底面 ABCD,1AB = BC = AD, 三BAD = 三ABC = 90o , E 是 PD 的中点.2(1) 证明:直线CE/ / 平面 PAB(2) 点 M 在棱 PC 上,且直线 BM 与底面 ABCD 所成锐角为45o ,求二面角 M-AB-D 的余弦值14. (12 分)如图,在四棱锥 P-ABCD 中, AB//CD,且三BAP = 三CDP = 90(1)证明:平面 PAB⊥平面PAD;(2)若 PA=PD=AB=DC, 三APD = 90 ,求二面角 A-PB-C 的余弦值.15. (12 分)如图,四面体 ABCD 中,△ABC 是正三角形,△ACD 是直角三角形,∠ABD= ∠CBD,AB=BD.(1) 证明:平面ACD⊥平面 ABC;(2) 过 AC 的平面交 BD 于点 E,若平面 AEC 把四面体 ABCD 分成体积相等的两部分,求二面角 D –AE –C 的余弦值.16.如图,在四棱锥 P-ABCD 中,底面 ABCD 为正方形,平面PAD⊥平面 ABCD,点 M在线段 PB 上, PD//平面 MAC, PA=PD= 6, AB=4.(I)求证: M 为 PB 的中点;(II)求二面角 B-PD-A 的大小;(III)求直线 MC 与平面 BDP 所成角的正弦值.17.如图,在三棱锥 P-ABC 中,PA⊥底面 ABC,三BAC = 90o .点 D, E, N 分别为棱PA, PC, BC 的中点, M 是线段 AD 的中点, PA=AC=4, AB=2.(Ⅰ)求证: MN∥平面BDE;(Ⅱ)求二面角 C-EM-N 的正弦值;7(Ⅲ) 已知点 H 在棱 PA 上,且直线 NH 与直线 BE 所成角的余弦值为,求线段 AH21的长.18.如图,几何体是圆柱的一部分,它是由矩形为旋转轴旋转得到的,是的中点.(Ⅰ)设是(Ⅱ)当上的一点,且,求的大小;,,求二面角的大小.(及其内部) 以边所在直线19. (本题满分 15 分)如图,已知四棱 P–ABCD,△PAD 是以 AD 为斜边的等腰直角三角形,BC∥AD,D⊥AD, PC=AD=2DC=2CB, E 为 PD 的中点.(Ⅰ)证明:CE∥平面PAB;(Ⅱ)求直线CE 与平面PBC 所成角的正弦值.。
【2023高考必备】2013-2022十年全国高考数学真题分类(全国通用):立体几何选填题(解析版)

3 3
时等号成立,故选:C
【题目栏目】立体几何\球的问题\球的其它问题 【题目来源】2022 年全国乙卷理科·第 9 题
5.(2022 年全国乙卷理科·第 7 题) 在正方体 ABCD A1B1C1D1 中,E,F 分别为 A B , B C 的中点,则
()
A.平面 B1 E F 平面 BD D1
乙圆锥的高 h2
l2
1 l2 9
22 3
l
,所以 V甲 V乙
1 3
r12
h1
1 3
r2
2
h2
4l2 5 l 93 1l2 2 2 l 93
10 .
故选:C.
【题目栏目】立体几何\空间几何体的结构特征及其直观图、三视图\空间几何体的展开图问题 【题目来源】2022 年全国甲卷理科·第 9 题
2.(2022 年全国甲卷理科·第 7 题) 在长方体 ABCD A1B1C1D1 中,已知 B1D 与平面 ABCD 和平面 AA1B1B 所成
2013-2022 十年全国高考数学真题分类汇编
专题 16 立体几何选填题
一、选择题 1.(2022 年全国甲卷理科·第 9 题) 甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为 2π ,侧面积
分别为
S甲
和
S乙
,体积分别为 V甲
和 V乙
.若
S甲 S乙
=2
,则
V甲 V乙
=
(
)
A. 5 【答案】C
tan BAE c 2 ,所以 BAE 30 ,B 错误; a2
对于 C, AC a2 b2 3c , CB1 b2 c2 2c , AC CB1 ,C 错误;
对于
立体几何专项练习及答案
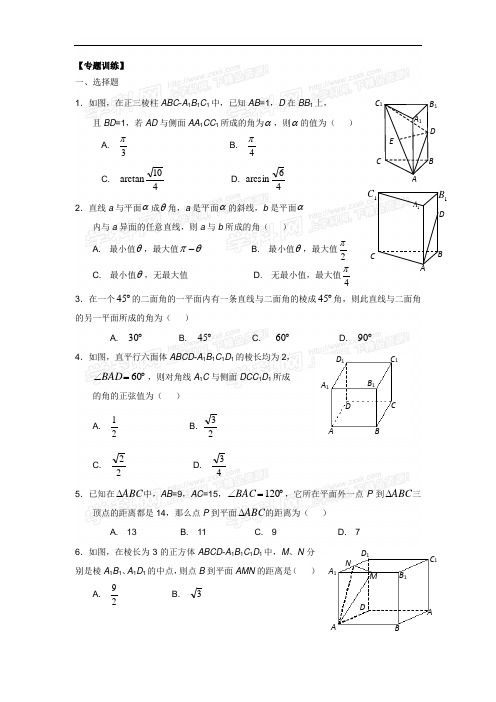
【专题训练】 一、选择题1.如图,在正三棱柱ABC -A 1B 1C 1中,已知AB =1,D 在BB 1上,且BD =1,若AD 与侧面AA 1CC 1所成的角为α,则α的值为( ) A.3π B. 4πC. 410arctanD. 46arcsin2.直线a 与平面α成θ角,a 是平面α的斜线,b 是平面α内与a 异面的任意直线,则a 与b 所成的角( )A. 最小值θ,最大值θπ-B. 最小值θ,最大值2πC. 最小值θ,无最大值D. 无最小值,最大值4π3.在一个︒45的二面角的一平面内有一条直线与二面角的棱成︒45角,则此直线与二面角的另一平面所成的角为( )A. ︒30B. ︒45C. ︒60D. ︒904.如图,直平行六面体ABCD -A 1B 1C 1D 1的棱长均为2,︒=∠60BAD ,则对角线A 1C 与侧面DCC 1D 1所成的角的正弦值为( )A.21 B. 23 C.22 D. 435.已知在ABC ∆中,AB =9,AC =15,︒=∠120BAC ,它所在平面外一点P 到ABC ∆三顶点的距离都是14,那么点P 到平面ABC ∆的距离为( )A. 13B. 11C. 9D. 76.如图,在棱长为3的正方体ABCD -A 1B 1C 1D 1中,M 、N 分别是棱A 1B 1、A 1D 1的中点,则点B 到平面AMN 的距离是( )A.29B. 3BAC DD 1 C 1B 1A 1CBA1A1B 1C DADBAD 1 C 1B 1A 1M NB CDE A 1B 1C 1C.556 D. 2 7.将︒=∠60QMN ,边长MN =a 的菱形MNPQ 沿对角线NQ 折成︒60的二面角,则MP 与NQ 间的距离等于( )A.a 23 B. a 43 C. a 46 D.a 438.二面角βα--l 的平面角为︒120,在α内,l AB ⊥于B ,AB =2,在β内,l CD ⊥于D ,CD =3,BD =1, M 是棱l 上的一个动点,则AM +CM 的最小值为( )A. 52B. 22C.26 D. 629.空间四点A 、B 、C 、D 中,每两点所连线段的长都等于a , 动点P 在线段AB 上, 动点Q 在线段CD 上,则P 与Q 的最短距离为( )A.a 21 B. a 22 C. a 23D.a 10.在一个正四棱锥,它的底面边长与侧棱长均为a ,现有一张正方形包装纸将其完全包住(不能裁剪纸,但可以折叠),那么包装纸的最小边长应为( )A. a )62(+B.a 262+ C. a )31(+ D. a 231+ 11.已知长方体ABCD -A 1B 1C 1D 1中,A 1A =AB =2,若棱AB 上存在点P ,使PC P D ⊥1,则棱AD 的长的取值范围是 ( )A. (]1,0B. (]2,0C. (]2,0D. (]2,112.将正方形ABCD 沿对角线AC 折起,使点D 在平面ABC 外,则DB 与平面ABC 所成的角一定不等于( )A. ︒30B. ︒45C. ︒60D. ︒90二、填空题1.如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,E 是A 1B 1的中点,则下列四个命题:DCBAED 1A 1C 1B 1① E 到平面ABC 1D 1的距离是21; ② 直线BC 与平面ABC 1D 1所成角等于︒45;③ 空间四边形ABCD 1在正方体六个面内的射影围成面积最小值为21; ④ BE 与CD 1所成的角为1010arcsin2.如图,在四棱柱ABCD ---A 1B 1C 1D 1中,P 是A 1C 1上的动点,E 为CD 上的动点,四边形ABCD 满 足___________时,体积AEB P V -恒为定值(写上你认为正确的一个答案即可)3.边长为1的等边三角形ABC 中,沿BC 边高线AD折起,使得折后二面角B -AD -C 为60°,则点A 到 BC 的距离为_________,点D 到平面ABC 的距离 为__________.4.在水平横梁上A 、B 两点处各挂长为50cm 的细绳,AM 、BN 、AB 的长度为60cm ,在MN 处挂长为60cm 的木条,MN 平行于横梁,木条的中点为O ,若木条 绕过O 的铅垂线旋转60°,则木条比原来升高了 _________.5.多面体上,位于同一条棱两端的顶点称为相邻的.如图正方体的一个顶点A 在α平面内.其余顶点在α的同侧,正方体上与顶点A 相邻的三个顶点到α的距离分别是1、2和4. P 是正方体其余四个顶点中的一个,则P 到平面α的距离可能是: ①3;②4;③5;④6;⑤7. 以上结论正确的为 . (写出所有正确结论的编号..) 6. 如图,棱长为1m 的正方体密封容器的三个面上有三个锈蚀的小孔(不计小孔直径)O 1、O 2、O 3它们分别是所在面的中心.如果恰当放置容器,容器存水的最大容积是_______m 3.∙O 1 ∙O 2∙O 3ABDCPEA 1D 1C 1B 1三、解答题1.在正三棱柱ABC—A1B1C1中,底面边长为a,D为BC为中点,M在BB1上,且BM=13B1M,又CM⊥AC1;(1)求证:CM⊥C1D;(2)求AA1的长.2.如图,在四棱锥P-ABCD中,底面是矩形且AD=2,AB=PA=2,PA⊥底面ABCD,E是AD的中点,F在PC上.(1) 求F在何处时,EF⊥平面PBC;(2) 在(1)的条件下,EF是不是PC与AD的公垂线段.若是,求出公垂线段的长度;若不是,说明理由;(3) 在(1)的条件下,求直线BD与平面BEF所成的角.3.如图,四棱锥S—ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SB=3.(1)求证BC SC;(2)求面ASD与面BSC所成二面角的大小;(3)设棱SA的中点为M,求异面直线DM与SB所成角的大小.4.在直角梯形ABCD 中,∠D=∠BAD=90︒,AD=DC=21AB=a,(如图一)将△ADC 沿AC 折起,使D 到D '.记面AC D '为α,面ABC 为β.面BC D '为γ.(1)若二面角α-AC -β为直二面角(如图二),求二面角β-BC -γ的大小; (2)若二面角α-AC -β为60︒(如图三),求三棱锥D '-ABC 的体积.5.如图,已知正方形ABCD 和矩形ACEF 所在的平面互相垂直,AB =2,AF =1,M 是线段EF 的中点.(1)求证AM //平面BDE ; (2)求二面角A -DF -B 的大小;(3)试在线段AC 上确定一点P ,使得PF 与BC 所成的角是60︒.【参考答案】 一.选择题1.D 提示:AD 在面ACC 1A 1上的射影应在AC 与A 1C 1中点的连线上,令射影为E ,则∠EAD 为所求的角.在Rt △EAD 中,.46223sin .2,23===∠∴==AD DE EAD AD DE .46arcsin=∠∴EAD 2.B 提示:由最小角定理知,最小角为θ,又异面直线所成角的范围为⎥⎦⎤⎝⎛2,0π,∴最大角为2π. 3.A 提示:由最小角定理知,此直线与另一面所成的角应小于等于它与交线所成的角,故排除C 、D ,又此二面角为45°,则此直线与另一平面所成的角只能小于它与交线所成的角,故选A.4.D 提示:由题意,A 1在面DCC 1D 1上的射影应在C 1D 1延长线E 上,且D 1E =1,则∠A 1CE 为所求角,在Rt △AA 1C 中,.43sin ,3,411112211==∠∴==+=C A E A CE A E A AC AA C A 5.D 提示:由P 到△ABC 三个顶点的距离都是14,知P 在底面ABC 的射影是△ABC 的外心,所以PO 为所求.由余弦定理得:BC =21.由3142321120sin 2==︒=BC R 得外接圆半径为37,即37=OB ,在Rt △POB 中,.722=-=BO PB PO6.D 提示:由题图得AMB AMN AMB N AMN B S S h V V ∆∆--⋅⋅=⋅⋅∴=233131. 212333 2.22AMB AMN AMNS h S S ∆∆∆⨯⨯∴===⋅ 7.B 提示:连结MP 、NQ 交于O ,由四边形MNPQ 是菱形得MP ⊥NQ 于O ,将MNQ 折起后易得MO ⊥QN ,OP ⊥QN ,所以∠MOP =60°,且QN ⊥面MOP ,过O 作OH ⊥MP ,所以OH ⊥QN ,从而OH 为异面直线MP 、QN 的公垂线,经计算得.43a OH =8.C 提示:把α半平面展到半平面β内,此时,连结AC 与棱的交点为M ,这时AM +CM 取最小值等于AC . (AM +CM )min =.26)32(12=++9.B 提示:P 、Q 的最短距离即为异面直线AB 与CD 间的距离,当P 为AB 的中点,Q 为CD 的中点时符合题意.10.B 提示:将正棱锥展开,设正方形边长为m ,则262,32+=∴+=m a a m 11.A 提示:∴⊥∴⊥,,1PC DP PC P D 在长方形ABCD 中AB 边存在P ,作PC DP ⊥,又因为AB =2,由对称性可知,P 为AB 的中点时,AD 最大为1,(]1,0∈∴AD 故选A. 12.D 提示:若BD 与平面ABC 所成的角为︒90,则A BC A BD 平面平面⊥,取AC 的中点O ,则AC DO AC BD ⊥⊥,且BO =DO ,BO BD 与∴不垂直,故BD 与平面ABC 所成的角一定不等于︒90. 二.填空题1.②③④ 提示:对于①,由ABE C ABC E V V --=11得ABE ABC S S h ∆∆⨯⨯=⋅⋅131311,221==∴∆∆ABC ABE S S h ,①错.对于②连CB 1交BC 1于O ,则O 为C 在面ABC 1D 1上的射影,︒=∠∴45CBO 为所成的线面角,②正确.作图易知③正确,对于④连A 1B ,则BE A 1∠为所成的角,解BE A 1∆得1010sin 1=∠BE A ,④正确. 2.AB ∥CD 提示:ABE P AEB P S h V ∆-⋅⋅=31,要使体积为定值,则ABE S ∆为定值,与E 点位置无关,则AB ∥CD 3.1015,415 提示:作BC DE ⊥与E ,易知BCD AD 平面⊥,从而BC AE ⊥,︒=∠60BDC 又由21==DC BD ,得,,又2343==AD DE 41522=+=∴AD DE AE ,由可解的点到平面的距离为1015.4.10cm 提示:MO =NO =30cm ,过O 作''M N 与旋转前的MN 平行且相等,所以旋转后AB 与平面N O M ''的距离为40305022=-,故升高了50-40=10cm. 5.①③④⑤. 6.65. 三、解答题1.(1)证明:在正三棱柱ABC —A 1B 1C 1中,D 为BC 中点,则AD ⊥面BCC 1B 1,从而AD ⊥MC又∵CM ⊥AC 1,则MC 和平面ADC 1内两相交直线AD ,AC 1均垂直∴MC ⊥面ADC 1,于是MC ⊥DC 1. (2)解:在矩形BB 1C 1C 中,由CM ⊥DC 1 知△DCC 1∽△BMC ,设BB 1=h,则BM=14h ∴14h:a=,22ah h a =:求得 从而所求AA 12a2.解:(Ⅰ)以A 为坐标原点,以射线AD 、AB 、AP 分别为x 轴、y 轴、z 轴建立空间直角坐标系,则p (0,0,2),A (0,0,0),B (0,2,0),C (2,2,0),D (2,0,0),E (1,0,0)∵F 在PC 上,∴可令,PC PF λ=设F (x ,y ,z ) ()()()z ,y ,x EF ,,,PC ,,,BC 1222002-=-==∵EF ⊥平面PBC ,∴0=∙PC EF 且0=∙BC EF ,又PC PF λ=, 可得22121====z y ,x ,λ故F 为PC 的中点.(Ⅱ)由(Ⅰ)可知:EF ⊥PC ,且EF ⊥BC 即EF ⊥AD ∴EF 是PC 与AD 的公垂线段,其长为|EF |=1(Ⅲ)由(Ⅰ)可知()222-=,PC 即为平面BEF 的一个法向量而()022,,BD -=设BD 与平面BEF 所成角θ,则:sin θ=cos 63=∙∙=∙PC BD PC BD PC BD∴θ=arc sin63.故BD 与平面BEF 所成角为arc sin 63 3.(1)证法一:如图,∵底面ABCD 是正方形, ∴BC ⊥DC . ∵SD ⊥底面ABCD ,∴DC 是SC 在平面ABCD 上的射影, 由三垂线定理得BC ⊥SC .证法二:如图1,∵底面ABCD 是正方形, ∴BC ⊥DC .∵SD ⊥底面ABCD ,∴SD ⊥BC ,又DC ∩SD=D ,∴BC ⊥平面SDC ,∴BC ⊥SC . (2)解:如图2,过点S 作直线,//AD l l ∴在面ASD 上, ∵底面ABCD 为正方形,l BC AD l ∴∴,////在面BSC 上,l ∴为面ASD 与面BSC 的交线.l ∴,,,,SC l SD l SC BC AD SD ⊥⊥∴⊥⊥∴∠CSD 为面ASD 与面BSC 所成二面角的平面角.∵23SAD=1.∴045.CSD ∠=(3)解1:如图2,∵SD=AD=1,∠SDA=90°, ∴△SDA 是等腰直角三角形.又M 是斜边SA 的中点,∴DM ⊥SA .∵BA ⊥AD ,BA ⊥SD ,AD ∩SD=D ,∴BA ⊥面ASD ,SA 是SB 在面ASD 上的射影.由三垂线定理得DM ⊥SB . ∴异面直线DM 与SB 所成的角为90°.解2:如图3,取AB 中点P ,连结MP ,DP .在△ABS 中,由中位线定理得 MP//SB ,DMP ∠∴是异面直线DM 与SB 所成的角.2321==SB MP ,又,25)21(1,222=+==DP DM∴在△DMP 中,有DP 2=MP 2+DM 2,︒=∠∴90DMP ∴异面直线DM 与SB 所成的角为90°.4. 解:(1)在直角梯形ABCD 中, 由已知∆DAC 为等腰直角三角形, ∴ 45,2=∠=CAB a AC , 过C 作CH ⊥AB ,由AB=2a ,可推得 AC=BC=.2a ∴ AC ⊥BC .取 AC 的中点E ,连结E D ', 则 E D '⊥AC 又 ∵ 二面角β--AC a 为直二面角,∴ E D '⊥β 又 ∵ ⊂BC 平面β ∴ BC ⊥E D ' ∴ BC ⊥a ,而a C D ⊂', ∴ BC ⊥C D ' ∴ CA D '∠为二面角γβ--BC 的平面角.图1图2图3由于 45='∠CA D , ∴二面角γβ--BC 为 45.(2)取AC 的中点E ,连结E D ',再过D '作β⊥'O D ,垂足为O ,连结OE . ∵ AC ⊥E D ', ∴ AC ⊥OE ∴ EO D '∠为二面角β--AC a 的平面角, ∴ EO D '∠ 60=. 在OE D Rt '∆中,a AC E D 2221==',∴O D S V ABC ABC D '⋅=∆-'31O D BC AC '⋅⋅⨯=2131a a a 462261⨯⨯⨯=.1263a =5.解法一: (1)记AC 与BD 的交点为O,连接OE, ∵O 、M 分别是AC 、EF 的中点,ACEF是矩形,∴四边形AOEM 是平行四边形,∴AM ∥OE .∵⊂OE 平面BDE , ⊄AM 平面BDE ,∴AM ∥平面BDE .(2)在平面AFD 中过A 作AS ⊥DF 于S ,连结BS ,∵AB ⊥AF , AB ⊥AD , ,A AF AD = ∴AB ⊥平面ADF ,∴AS 是BS 在平面ADF 上的射影,由三垂线定理得BS ⊥DF .∴∠BSA 是二面角A —DF —B 的平面角.在Rt ΔASB 中,,2,36==AB AS∴,60,3tan ︒=∠=∠ASB ASB ∴二面角A —DF —B 的大小为60º.(3)设CP=t (0≤t ≤2),作PQ ⊥AB 于Q ,则PQ ∥AD ,∵PQ ⊥AB ,PQ ⊥AF ,A AF AB = ,∴PQ ⊥平面ABF ,QF ⊂平面ABF ,∴PQ ⊥QF .在Rt ΔPQF 中,∠FPQ=60º,PF=2PQ . ∵ΔPAQ 为等腰直角三角形,∴).2(22t PQ -=又∵ΔPAF 为直角三角形,∴1)2(2+-=t PF ,∴).2(2221)2(2t t -⋅=+-所以t=1或t=3(舍去),即点P 是AC 的中点.解法二: (1)建立如图所示的空间直角坐标系. 设N BD AC = ,连接NE , 则点N 、E 的坐标分别是()0,22,22、(0,0,1), ∴)1,22,22(--=, 又点A 、M 的坐标分别是)0,2,2(,()1,22,22∴ =()1,22,22--∴AM NE =且NE 与AM 不共线,∴NE ∥AM .又∵⊂NE 平面BDE , ⊄AM 平面BDE ,∴AM ∥平面BDF .(2)∵AF ⊥AB ,AB ⊥AD ,AF ,A AD = ∴AB ⊥平面ADF . ∴)0,0,2(-=为平面DAF 的法向量. ∵⋅=()1,22,22--·)0,2,2(-=0, ∴⋅=()1,22,22--·)0,2,2(=0得DB NE ⊥,NF NE ⋅,∴NE 为平面BDF 的法向量.∴cos<>⋅NE AB =21∴AB 与NE 的夹角是60º.即所求二面角A —DF —B 的大小是60º.(3)设P(t,t,0)(0≤t ≤2)得PF ),1,2,2(t t --=∴BC =(2,0,0) 又∵PF 和BC 所成的角是60º.∴21)2()2(2)2(60cos 22⋅+-+-⋅-=︒t t t 解得22=t 或223=t (舍去),即点P 是AC 的中点.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何专题练习1、如图,网格纸上的小正方形边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )A. 8+43B. 8+23C. 4+43D. 4+232、某几何体的三视图如图所示,则该几何体的表面积等于 ( )A. 822+B. 1122+C. 1422+D. 15 3、某几何体的三视图如图2所示,则该几何体的体积A. B. C. D.4、一个几何体的三视图如图所示,则这个几何体的体积为( ) A.32316+33π B. 16833π+ C.32363π+ D. 836π+ 5、已知某几何体的三视图如图所示,则该几何体的体积为( )A. 2πB. 3πC. 5πD. 7π6、如图所示,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则此几何体的体积为()A. B. 2 C. 4 D.7、已知某几何体的三视图如图所示,则该几何体的体积等于( )A. B. 18 C. 20 D. 248、如图是某几何体的三视图,其中俯视图为等边三角形,正视图为等腰直角三角形,若该几何体的各个顶点都在同一个球面上,则这个球的体积与该几何体的体积的比为()A. 73πB.289πC.1479πD.43π9、如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的外接球的表面积是A. B. C. D.10、某多面体的三视图如图所示,则该多面体的体积为()A. B. C. D.11、如图,直四棱柱ABCD –A 1B 1C 1D 1中,AB//CD ,AD⊥AB,AB=2,AD=,AA 1=3,E 为CD 上一点,DE=1,EC=3. (1)证明:BE ⊥平面BB 1C 1C; (2)求点B 1到平面EA 1C 1的距离.12、已知四棱锥P ABCD -的底面ABCD 是菱形,60BAD ∠=,又PD ⊥平面ABCD ,点E 是棱AD 的中点,F 在棱PC 上.(1)证明:平面BEF ⊥平面PAD .(2)试探究F 在棱PC 何处时使得//PA 平面BEF .13、如图,在直三棱柱111ABC A B C -中,底面ABC 是等边三角形,D 为BC 的中点. (Ⅰ)求证1A C ∥平面1ADB ;(Ⅱ)若12AB AA ==,求三棱锥11A ADB -的体积.14、如图,四棱锥S ABCD -的底面为平行四边形, DA DS =, DA DS ⊥, 2AB BS SA BD ====.(1)求证:平面ASD ⊥平面ABS ; (2)求四棱锥S ABCD -的体积.15、如图,四棱锥V ABCD -中,底面ABCD 是边长为2的正方形,其它四个侧面都是侧棱长为5的等腰三角形,E 为AB 的中点.(1)在侧棱VC 上找一点F ,使BF ∥平面VDE ,并证明你的结论; (2)在(1)的条件下求三棱锥E BDF -的体积.16、如图所示,在直三棱柱ABC -A 1B 1C 1中,AC =3,BC =4,AB =5,AA 1=4,点D 是AB 的中点.(1)求证:AC 1∥平面CDB 1;(2)求异面直线AC 1与B 1C 所成角的余弦值.17、如图所示,在三棱锥A BOC -中,OA ⊥底面BOC ,030OAB OAC ∠=∠=,2AB AC ==,2BC =,动点D 在线段AB 上.()1求证:平面COD ⊥平面AOB ;()2当OD AB ⊥时,求三棱锥C OBD -的体积.18、已知正方体1111ABCD A B C D -,O 是底ABCD 对角线的交点. 求证:(1)C 1O ∥面11AB D ;(2)面BDC 1∥面11AB D .19、如图,在四棱锥P ABCD -中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,2PD DC ==,E 是PC 的中点.(Ⅰ)证明://PA 平面EDB ; (Ⅱ)求三棱锥A BDP -的体积.参考答案1、【答案】A2、【答案】B3、【答案】C4、【答案】D5、【答案】B6、【答案】A7、【答案】D8、【答案】C9、【答案】D10、【答案】C11、【答案】(1)详见解析;(2).(1)过B作CD的垂线交CD于F,则,在试题分析:和利用勾股定理证明,再证明,即可证明;(2)先求得的面积,设点B1到平面的距离为d,用表示,列式计算即可.试题解析:(1)过B作CD的垂线交CD于F,则在在,故由(2),同理,因此.设点B1到平面的距离为d,则,从而考点:椎体体积公式、点到面的距离、线面垂直的判定.12、【答案】(1)证明见解析;(2)当12PF FC =::时,//PA 平面BEF 试题分析:(1)要证明面面垂直可先证线面垂直,由题意PD ABCD PD EB EB ABCD ⊥⎫⇒⊥⎬⊂⎭平面平面,又底面ABCD 是60A ∠=的菱形,且点E 是棱AD的中点,所以EB AD ⊥,又PD AD D ⋂=,所以BE ⊥平面PAD ,即可证得平面BEF ⊥平面PAD .(2)当12PF FC =::时,//PA 平面BEF ,证明如下:连接AC 交BE 于G ,连接GF .因为底面ABCD 是菱形,且点E 是棱AD 的中点,所以AEG ∆∽CBG ∆且::12AG GC AE BC ==:,又:12PF FC =:,所以//FG AP ,根据线线平行可得线面平行. 试题解析:(1)证明:PD ABCD PD EB EB ABCD ⊥⎫⇒⊥⎬⊂⎭平面平面,又底面ABCD 是60A ∠=的菱形,且点E 是棱AD 的中点,所以EB AD ⊥, 又PD AD D ⋂=,所以BE ⊥平面PAD .BE PAD BE BEF ⊥⎫⇒⎬⊂⎭平面平面平面BEF ⊥平面PAD .(2)解:当12PF FC =::时,//PA 平面BEF ,证明如下: 连接AC 交BE 于G ,连接GF .因为底面ABCD 是菱形,且点E 是棱AD 的中点,所以AEG ∆∽CBG ∆且::12AG GC AE BC ==:, 又:12PF FC =:,所以//FG AP ,////FG APFG BEF PA AP BEF ⎫⎪⊂⇒⎬⎪⊄⎭平面平面平面BEF . 13、【答案】3试题分析:(Ⅰ)连1A B 交1AB 于E ,则E 为1A B 的中点,连结ED ,由三角形中位线的性质可得DE ∥1A C ,根据线面平行的判定定理可得结论成立.(Ⅱ)根据等积法求解,即由1111A ADB C ADB B ADC V V V ---==可得体积的值.试题解析:(Ⅰ)连1A B 交1AB 于E ,则E 为1A B 的中点,连结ED .∵D 为BC 的中点,DE ∴∥1A C ,又DE ⊂平面1ADB ,1A C ⊄平面1ADB ,1A C ∴∥平面1ADB .(Ⅱ)1A C ∥平面1ADB ,1111A ADB C ADB B ADC V V V ---∴==211113322332ADC S B B ∆⎛⎫=⋅=⨯⨯= ⎪ ⎪⎝⎭, 即三棱锥11A ADB -314、【答案】(1)证明见解析;2315、【答案】(1)见解析(2)3E BDF V -=试题分析:(1)F 为VC 的中点,取CD 的中点为H ,由三角形中位线性质得线线平行,再由线线平行证得面面平行,即得线面平行(2)因为V ABCD -为正四棱锥,所以可求V 到底面距离,即得F 到底面距离,再根据等体积法得E BDF F BDE V V --=,最后代入锥体体积公式即可 试题解析:(1)F 为VC 的中点. 取CD 的中点为H ,连BH HF 、 ABCD 为正方形,E 为AB 的中点BE ∴平行且等于DH ,BH DE ∴平行又FH VD 平行∴平面BHF VDE 平行平面BF ∴平行平面VDE .(2)F 为VC 的中点,ABCD 14BDESS =正方形 18E BDF F BDE V ABCD V V V ---∴==V ABCD -为正四棱锥V ∴在平面ABCD 的射影为AC 的中点O 5,2,3VA AO VO ==∴=21432333v ABCD V -∴=⋅⋅=36E BDF V -∴=. 16、【答案】(1)见解析;(2)225. 试题分析:(1)设CB 1与C 1B 的交点为E ,连接DE ,由三角形中位线定理可证得DE ∥AC 1,从而可得AC 1∥平面CDB 1。
(2)由DE ∥AC 1可得∠CED 为AC 1与B 1C 所成的角(或其补角),在CDE ∆中,可得55,,2222ED CD CE ===,解三角形得225cos CED ∠=,即为所求。
试题解析:(1)证明:设CB 1与C 1B 的交点为E ,连接DE ,∵四边形BCC 1B 1为正方形, ∴E 是BC 1的中点, 又D 是AB 的中点, ∴DE ∥AC 1。
又DE ⊂平面CDB 1,AC 1⊄平面CDB 1, ∴AC 1∥平面CDB 1. (2)解:∵DE ∥AC 1,∴∠CED 为AC 1与B 1C 所成的角(或其补角). 在△CED 中,1115151,,2222222ED AC CD AB CE CB ======, ∴12222552CE cos CED DE ∠===。
∴异面直线AC 1与B 1C 所成角的余弦值为225。
17、【答案】(1)见解析(2)324试题分析:(1)由OA ⊥底面BOC ,可知AO OC ⊥,AO OB ⊥,由勾股定理,得1OC OB ==,再由2BC =,可得OC OB ⊥,又OC OA ⊥,可证平面COD ⊥平面AOB 。
(2)OAB 中由面积相等,求得32OD =及12BD =,由三棱锥的体积公式C OBD V -1=OC 3OBD S ⋅求得体积。
试题解析:()1证明:∵OA ⊥底面BOC ,∴AO OC ⊥,AO OB ⊥.∵030OAB OAC ∠=∠=,2AB AC ==,∴1OC OB ==.又2BC =OC OB ⊥,又OC AO ⊥AO OB O ⋂=∴OC ⊥平面AOB .∵OC ⊂平面COD .∴平面COD ⊥平面AOB .()2解:∵OD AB ⊥,∴1BD =13,22BD OD ==.∴1111322C OBD V -=⨯⨯= 18、试题解析:(1)连结11A C ,设11111A C B D O ⋂=连结1AO,1111ABCD A B C D -是正方体11A ACC ∴是平行四边形11A C AC ∴且11A C AC =又1,O O 分别是11,A C AC 的中点,11O C AO ∴且11O C AO =11AOC O ∴是平行四边形111,C O AO AO ∴⊂面11AB D ,1C O ⊄面11AB D∴1C O 面11AB D(2)证明:////''''''AB DC D C ABC D AB DC D C ⎫⇒⎬==⎭是平行四边形 '//'''''''BC AD BC AB D AD AB D ⇒⎫⎪⊄⎬⎪⊂⎭平面平面'//'''//'''''BC AB D C D AB D BC C D C ⇒⎫⎪⎬⎪⋂=⎭平面同理,平面⇒平面'//C DB 平面''AB D .点睛:本题主要考查了平面与平面之间的位置关系,考查学生的空间想象能力、运算能力和推理论证能力,属于中档题.要证面面平行,主要考虑的方向是,一个平面经过另一个平面的两条平行线,且这两条线相交,或垂直一条直线的两个平面;要证线面平行,只需证一条线与平面内的线平行.19、【答案】(Ⅰ)证明见解析;(Ⅱ)34. 试题解析:(Ⅰ)连接AC 交BD 于O ,连接OE ,∴ABCD 是正方形,∵O 是AC 中点,又E 是PC 中点,∴//OE PA ,又∵PA ⊄平面BDE ,OE ⊂平面BDE ,∴//PA 平面EDB . (Ⅱ)1122423323A BDP P ABD ABD V V S PD --∆⨯===⨯⨯=. 【考点】(1)直线与平面平行的判定;(2)几何体的体积.【方法点睛】本题考查了线面平行的证明及三棱锥的体积计算,利用线线平行证明线面平行是证明线面平行的基本方法.在线面平行的证明中最常见的证法:1、利用三角形的中位线;2、构造平行四边形;3、利用面面平行;在求三棱锥的体积中,关键是找到顶点到底面的距离,利用等体积转换,求出其体积.在该题中应用1、利用三角形的中位线;以及ABD P BDP A V V --=.。
