玻尔氢原子理论简介
合集下载
8.4.2 玻尔的氢原子理论
8 02h3c
(
1 k2
1 n2
)
3
RH
me4
8 02h3c
1 097373107 m1
2
布 拉 开 系
-0.85eV
-1.5eV
-3.39eV
从其它能级到同一能级的跃
迁属于同一谱线系。
n1
-13.6eV
玻尔的氢原子理论
二、玻尔理论意义与局限性
1、玻尔的贡献
玻尔关于“定态” 和“能级跃迁决定谱线 频率”的假设是两个重要的基本概念，在量子 力学理论中占有重要的地位。
则发射或吸收光子的频率为：
kn
En Ek h
称为 玻尔的频率条件
玻尔的氢原子理论
Ek
玻尔的氢原子理论
2、氢原子轨道半径的计算
由量子化条件及牛顿定律：
mvr
e2
4p 0 r 2
n
h
2mpv2,
r
角动量量子化
,库仑力=向心力
rn
n2
0h2 p me2
1 2
mvn
2
e2
8p 0rn
n=4 v
m n=3
在这些轨道上运动的电子 不辐射（或吸收）能量而处于 稳定状态，称为定态。
相应的轨道称为定态轨道 与定态相应的能量（能级） 分别为 ： E1，E2 ，E3 …
E1 < E2 < E3 < …
玻尔的氢原子理论
E1 E2 E3
玻尔的氢原子理论
一、玻尔的氢原子理论
1、玻尔的氢原子理论 2)角动量量子化条件假设
1）正确地指出原子能级的存在（原子能量量子化）. 2）正确地指出定态和角动量量子化的概念. 3）正确的解释了氢原子及类氢离子（单电子）光谱.
(
1 k2
1 n2
)
3
RH
me4
8 02h3c
1 097373107 m1
2
布 拉 开 系
-0.85eV
-1.5eV
-3.39eV
从其它能级到同一能级的跃
迁属于同一谱线系。
n1
-13.6eV
玻尔的氢原子理论
二、玻尔理论意义与局限性
1、玻尔的贡献
玻尔关于“定态” 和“能级跃迁决定谱线 频率”的假设是两个重要的基本概念，在量子 力学理论中占有重要的地位。
则发射或吸收光子的频率为：
kn
En Ek h
称为 玻尔的频率条件
玻尔的氢原子理论
Ek
玻尔的氢原子理论
2、氢原子轨道半径的计算
由量子化条件及牛顿定律：
mvr
e2
4p 0 r 2
n
h
2mpv2,
r
角动量量子化
,库仑力=向心力
rn
n2
0h2 p me2
1 2
mvn
2
e2
8p 0rn
n=4 v
m n=3
在这些轨道上运动的电子 不辐射（或吸收）能量而处于 稳定状态，称为定态。
相应的轨道称为定态轨道 与定态相应的能量（能级） 分别为 ： E1，E2 ，E3 …
E1 < E2 < E3 < …
玻尔的氢原子理论
E1 E2 E3
玻尔的氢原子理论
一、玻尔的氢原子理论
1、玻尔的氢原子理论 2)角动量量子化条件假设
1）正确地指出原子能级的存在（原子能量量子化）. 2）正确地指出定态和角动量量子化的概念. 3）正确的解释了氢原子及类氢离子（单电子）光谱.
玻尔的氢原子理论
玻尔的氢原⼦理论§4. 玻尔的氢原⼦理论⼀玻尔(1885-1962)丹麦物理学家尼尔斯·玻尔，⽣于丹麦哥本哈根的⼀个富裕知识分⼦家庭，⽗亲是哥本哈根⼤学⽣理学教授。
1903年进⼊哥本哈根⼤学数学和⾃然科学系，⼤学⼆年级时他热中于研究⽔的表⾯张⼒问题，并在丹麦皇家科学院的有奖征⽂中容获⾦质奖章，1909年获硕⼠学位，1911年以论⽂《⾦属电⼦论的研究》获博⼠学位。
1911年9⽉，他到英国剑桥卡⽂迪什实验室进修，据说他第⼀次与导师J.J.汤姆孙见⾯时，就把他论⽂中批评汤姆孙的段落当⾯指出，使导师很不⾼兴，因⽽给以冷遇。
1912年3⽉转到了曼彻斯特随卢瑟福⼯作，这成了他⼀⽣的重要转折点。
玻尔在卢瑟福实验室⼯作期间（约4个⽉），正值卢瑟福发表有核原⼦理论，并组织对这⼀理论进⾏检验。
玻尔参加了α粒⼦散射实验⼯作，因此清楚这⼀理论所⾯临的困难。
但玻尔坚信卢瑟福有核原⼦模型的正确性，认为“只有量⼦假说是摆脱困难的唯⼀出路”。
1913年提出著名的玻尔原⼦理论。
1916年任哥本哈根⼤学教授，1921年起⼀直领导着该校为他建⽴的理论物理研究所，直到去世。
玻尔于1916年、1927年分别提出对应原理和互补原理，1936年提出原⼦核的液滴核模型，1939年创⽴核裂变理论，预⾔铀的⾃⾝裂变。
曾参加第⼀颗原⼦弹的制造。
1922年因对原⼦结构和原⼦辐射的研究⽽获得诺贝尔物理学奖。
⼆玻尔的氢原⼦理论1．汉森的拜访1912年7⽉回到哥本哈根，1913年初，玻尔的好友、光谱学家汉森(H.M.Hansen)在拜访玻尔时问到原⼦结构和光谱学中的谱线有什么关系？并向玻尔详细介绍了巴尔末的发现，以及谁也⽆法对巴尔末公式作出解释。
2．斯塔克的启⽰1913年2⽉玻尔注意到德国物理学家斯塔克(J.Stark)在《原⼦动⼒学原理》⼀书中的⼀段话：“⼀个光谱的全部谱线是由单独⼀个电⼦造成的，是在这个电⼦从⼀个（⼏乎）完全分离的状态逐次向势能最⼩的状态跃迁过程中辐射出来的。
玻尔的氢原子理论
玻尔的氢原子理论
为此,J.汤姆孙在1904年提出了原子结构的枣糕式模型.该模型认 为，原子可以看作一个球体，原子的正电荷和质量均匀分布在球内， 电子则一颗一颗地镶嵌其中.1909年，J.汤姆孙的学生卢瑟福为了验证 原子结构的枣糕式模型，完成了著名的α粒子散射实验.实验发现α粒 子在轰击金箔时，绝大多数α粒子都穿透金箔，方向也几乎不变，但 是大约有1/8 000的α粒子会发生大角度偏转，即被反弹回来.这样的 实验结果是枣糕式模型根本无法解释的，因为如果说金箔中的金原子 都是枣糕式的结构，那么整个金箔上各点的性质应该近乎均匀，α粒 子轰击上去，要么全部透射过去，要么全部反弹回来，而不可能是一 些穿透过去，一些反弹回来.
玻尔的氢原子理论
二、 原子结构模型
1897年，J.汤姆孙发现了电子.在此之前，原 子被认为是物质结构的最小单元，是不可分的，可 是电子的发现却表明原子中包含带负电的电子.那 么，原子中必然还有带正电的部分，这就说明原子 是可分的，是有内部结构的.执着的科学家就会继 续追问：原子的内部结构是什么样的？简洁的里德 伯光谱公式是不是氢原子内部结构的外在表现？
玻尔的氢原子理论
三、 玻尔的三点基本假设
为了解决原子结构有核模型的稳定性和氢原子光谱的分 立性问题，玻尔提出以下三个假设：
（1）定态假设.原子中的电子绕着原子核做圆周运动， 但是只能沿着一系列特定的轨道运动，而不能够任意转动， 当电子在这些轨道运动时，不向外辐射电磁波，原子系统处 于稳定状态，具有一定的能量.不同的轨道，具有不同的能 量，按照从小到大的顺序记为E1、E2、E3等.
玻尔的氢原子理论
可是这个模型却遭到很多物理学家的质疑.因为按照当时的物 理理论（包括经典力学、经典电磁理论及热力学统计物理），这 样一个模型是根本不可能的，原因有以下两个：
16.4玻尔氢原子理论
h L=m r =n v = nh 2π n 叫做量子数。 h = h 2π 叫做约化普朗克常数。 叫做量子数 量子数。 叫做约化普朗克常数 约化普朗克常数。
2. 氢原子轨道和能量
{
v 1 e m = r 4 πε0 r2 L = nh
2
2
r
r v
得到第 n 个定态的轨道半径和 氢原子能量分别为： 氢原子能量分别为：
16.4 玻尔氢原子理论
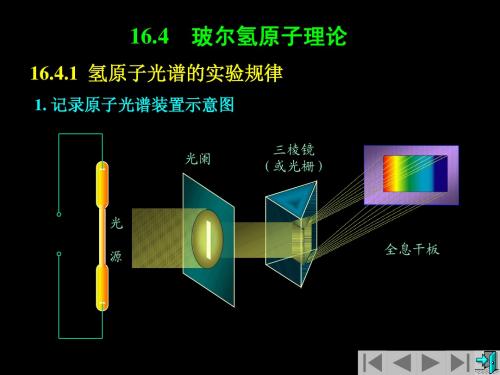
16.4.1 氢原子光谱的实验规律 氢原子光谱的实验规律
1. 记录原子光谱装置示意图
三棱镜 （或光栅）
光阑
光 全息干板 源
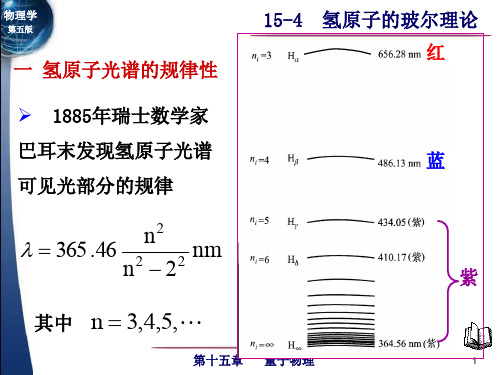
2. 氢原子光谱 关于氢原子光谱的研究，可追溯到十九世纪中叶。 关于氢原子光谱的研究，可追溯到十九世纪中叶。瑞典物 原子光谱的研究 理学家埃格斯特朗（ 理学家埃格斯特朗（1814～1874）首先在气体放电的光谱中 ～ ） 发现了氢 后来他又发现了氢 发现了氢原子光谱的 Hα 线，后来他又发现了氢原子光谱在可 见光波段的其它三条谱线，并且精确地测量了它们的波长。 见光波段的其它三条谱线，并且精确地测量了它们的波长。
计算氢原子巴耳末系的最短波长和最长波长。 例 计算氢原子巴耳末系的最短波长和最长波长。 解 最长波长是 E3 E2 能级的跃迁产生的： 能级的跃迁产生的：
1
λmax
1 1 5 7 = R( 2 − 2 ) = 1.097 ×10 × 2 3 36
λmax = 6563A
最短波长即线系限波长： 最短波长即线系限波长： 即线系限波长
rn = n2 (
) = n2r 1 2 πme
ε0h2
(n = 1,2,3,L )
E1 1 me4 En = − 2 ( 2 2 ) = 2 n 8ε0 h n
氢原子的玻尔理论
电子在原子中可以在一些特定的圆轨道上运动 而不辐射电磁波，这时，原子处于稳定状态，简称 定态.
与定态相应的能量 分别为 E1，E2… ， E1 < E2< E3
是对经典概念的修改！
E1+ E3
第十五章 量子物理
24
物理学
第五版 (2)量子化条件
15-4 氢原子的玻尔理论
引入角动量量子化的概念 L mvr n h 2π
第十五章 量子物理
2
物理学
第五版
紫外 可见光
红外
15-4 氢原子的玻尔理论
莱曼系
1
R(112
1 n2
)
,
巴尔末系
1
R(
1 22
1 n2
)
,
n 2,3, n 3,4,
帕邢系
1
R(312
1 n2
),
n 4,5,
布拉开系
1
R(
1 42
1 n2
)
,
玻尔理论对氢原子光谱的解释
En
me4
8
2 0
h
2
1 n2
h Ei E f
1c Nhomakorabea
me4
8
2 0
h3c
(
1 n2f
1 ni2
)
,
ni n f
里德伯常量
R
me4
8 02 h3c
1.0973731107
氢原子的玻尔理论
③氢原子的能级 ( energy level ) E1 基态 ( ground state ) E2 ， E3 ，… ，激发态 ( excited ) ④由玻尔假设可导出广义巴尔末公式
hν = En- Ek /8ε 1/λ = ν /c = me4/8ε0h3c(1/k2 - 1/n2 ) 1/λ = R (1/k2 - 1/n2 ) , n > k
小结
1.玻尔假设 1.玻尔假设 ①定态假设 跃迁假设 ②跃迁假设 hν = En- Ek 2.德布罗意 德布罗意假设 2.德布罗意假设 λ = h / mv ; E = hν
h 1 1 λ= =h • mv 2qm U
电子的德布罗意波长： 电子的德布罗意波长： 德布罗意波长
λ e = 1.23 •
1 U
(nm)
3.电子衍射
二、电子显微镜
■光学显微镜能分辨的两点间最小距离： 光学显微镜能分辨的两点间最小距离：
λ越小，Z越小，则分辨本领越高。 越小， 越小，则分辨本领越高。 ■但可见光波长较大，即光学显微镜分辨 但可见光波长较大， 本领有限。 本领有限。 ■电子显微镜可提高分辨本领 利用电子射线代替照射光
λ = h / p = h / mv ν =E / h
（德布罗意公式） 德布罗意公式 公式）
2.德布罗意波长 德布罗意波长
设带电粒子的电量：q ，质量：m ，速度： 质量： 速度： 设带电粒子的电量： v ，加速它的电压：U 。则粒子获得的动 加速它的电压： 能为： 能为： 1 2qU 2 mv = qU 则 v = m 2 带电粒子的德布罗意波长： 德布罗意波长 带电粒子的德布罗意波长：
hν = En- Ek
辐射或吸收光子的频率： 辐射或吸收光子的频率： ν =（En- Ek）/ h
波尔的氢原子理论
5
2 卢瑟福的核式模型
卢瑟福1871年8月13日出生在 新西兰，1894年大学毕业，1895年 到 英 国 剑 桥 大 学 学 习 ， 成 为 J.J. 汤 姆孙的研究生。1908年卢瑟福荣获 诺贝尔化学奖，同年在曼切斯特大 学任教，继续指导他的学生进行 粒子散射的实验研究。
卢瑟福的α粒子散射验证了核式模型。
19-1 波尔的氢原子理论
量子物理起源于对原子物理的研究，人们从高能粒子的 散射实验和原子光谱中获得原子内部信息。
3
4
一 玻尔理论的实验基础
1 汤姆逊葡萄干面包模型
1903年，汤姆孙提出原子结构模 型：原子里面带正电的部分均匀地 分布在整个原子球体中，而带负电 的电子镶嵌在带正电的球体之中。 带正电的球体与带负电的电子二者 电量相等，故原子不显电性。
5 6 普芳德（Pfund）系
区域 紫外 可见 可见 红外 红外
此后又发现碱金属也有类似的规律。
日期 1906年 1880年 1908年 1922年 1924年
3 里兹并合原理
~ T(m α) T(n β)
R
光谱项 ： T(m) (m )2
R
T (n) (n )2 10
三 经典电磁理论遇到的困难
6
粒子散射
4 2
H
e
,
q 2e, 原子量为4，m 7500me
粒子束射向金箔：
-
(1) 多数 0
+
（2）少数 较大
1 / 8000被反射，
（3）极少数 ，反弹
大部分透过。
7
1911年，卢瑟福提出原子的 “有核结构模型”
原子的核式模型
原子由原子核和核外电子 构成，原子核带正电荷，占据 整个原子的极小一部分空间， 而电子带负电，绕着原子核转 动，如同行星绕太阳转动一样。
2 卢瑟福的核式模型
卢瑟福1871年8月13日出生在 新西兰，1894年大学毕业，1895年 到 英 国 剑 桥 大 学 学 习 ， 成 为 J.J. 汤 姆孙的研究生。1908年卢瑟福荣获 诺贝尔化学奖，同年在曼切斯特大 学任教，继续指导他的学生进行 粒子散射的实验研究。
卢瑟福的α粒子散射验证了核式模型。
19-1 波尔的氢原子理论
量子物理起源于对原子物理的研究，人们从高能粒子的 散射实验和原子光谱中获得原子内部信息。
3
4
一 玻尔理论的实验基础
1 汤姆逊葡萄干面包模型
1903年，汤姆孙提出原子结构模 型：原子里面带正电的部分均匀地 分布在整个原子球体中，而带负电 的电子镶嵌在带正电的球体之中。 带正电的球体与带负电的电子二者 电量相等，故原子不显电性。
5 6 普芳德（Pfund）系
区域 紫外 可见 可见 红外 红外
此后又发现碱金属也有类似的规律。
日期 1906年 1880年 1908年 1922年 1924年
3 里兹并合原理
~ T(m α) T(n β)
R
光谱项 ： T(m) (m )2
R
T (n) (n )2 10
三 经典电磁理论遇到的困难
6
粒子散射
4 2
H
e
,
q 2e, 原子量为4，m 7500me
粒子束射向金箔：
-
(1) 多数 0
+
（2）少数 较大
1 / 8000被反射，
（3）极少数 ，反弹
大部分透过。
7
1911年，卢瑟福提出原子的 “有核结构模型”
原子的核式模型
原子由原子核和核外电子 构成，原子核带正电荷，占据 整个原子的极小一部分空间， 而电子带负电，绕着原子核转 动，如同行星绕太阳转动一样。
玻尔的氢原子理论
~ T( k ) T( n ) T( k )
R R ,T ( n ) 2 称为光谱项 2 k n
从氢原子光谱规律可以看出：
1、光谱是线状的，谱线对应一定的位置，不因观 察方式不同而改变顺序；
2、谱线间有一定的关系，各系可用一个公式表示， 不同线系有共同的光谱项； 3、每一谱线的可以用两光谱项之差表示；
2、频率假设
原子从一较大能量En的定态向另一较低能量Ek的定 态跃迁时，辐射一个光子
h En Ek
跃迁频率条件
原子从较低能量Ek的定态向较大能量En的定态 跃迁时，吸收一个光子 3、轨道角动量量子化假设
h Ln 2
轨道量子化条件
n为正整数，称为量子数
基本假设应用于氢原子：
(1)轨道半径量子化
由图可知，可见光的谱线为 n=4和n=3跃迁到n=2的两条
1 1 ~ 42 R( 2 2 ) 2 4 1 1 1.097 107 ( ) 4 16 0.21 107 m 1
n4 n3 n2 n1
42
o 1 ~ 4861 A 42
1 1 ~ 32 R( 2 2 ) 2 3
2 h rn n 2 ( 0 2 ) me
1 me4 En 2 ( 2 2 ) n 8 0 h
基态能级
(n 1, 2,3, )
E1 13.58 eV
激发态能级 En E1 13.58 eV n2 n2 氢原子的电离能
E电离 E E1 13.58 eV
二、玻尔氢原子理论 原子的核式结构的缺陷：
无法解释原子的稳定性 无法解释原子光谱的不连续性 玻尔原子理论的三个基本假设： 1、定态假设
原子系统存在一系列不连续的能量状态，处于这些状态
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
v
| Ek En |
En
h
3. 角动量量子化假设
轨道角动量 Lmvrnhn 2π
n1,2,3...
h 2
约化普朗克常数
r
v
4. 氢原子轨道半径和能量的计算
1）半径
向心力是库仑力
mv2 r
1
4π 0
e2 r2
Lmvrnhn
2π
由上两式得, 第 n 个定态的轨道半径为
rnn2(πm 0h2 2)e n2r1 n1 ,2,3,
(3) k = 2 (n = 3, 4, 5, … ) 谱线系 —— 赖曼系 （1908年）
k = 1 (n = 2, 3, 4, … ) 谱线系 —— 巴耳末系（1880年）
为什么光谱会是分立的呢？
爱因斯坦1905年提出光量子的 概念后，不受名人重视，甚至 到1913年德国最著名的四位物 理学家(包括普朗克)还把爱因斯 坦的光量子概念说成是“迷失 了方向”。可是，当时年仅28 岁的玻尔，却创造性地把量子 概念用到了当时人们持怀疑的 卢瑟福原子结构模型，解释了 近30年的光谱之谜。
意义
1.成功的把氢原子结构和光谱线结构联系起来, 从理论上说 明了氢原子和类氢原子的光谱线结构。
2. 揭示了微观体系的量子化规律，为建立量子力学奠定了 基础。
缺陷
1.不能处理复杂原子的问题
2. 完全没涉及谱线的强度、宽度等特征
3. 以经典理论为基础, 是半经典半量子的理论。 对于电子绕核的运动，用经典理论处理； 对于电子轨道半径，则用量子条件处理。
o
玻尔半径 r1 0.529A
2）能量
r2=4r1 r2=9r1
En
1mv2 1 e2
2
4π0 rn
1mv2 1 e2
2
8π0 rn
-13.6 eV
En n12(8m 02h4e2)nE21
En ( eV) 0
-1.51 -3.39
En
E1 n2
光频
nk
En
Ek h
n= 6 n= 5 n= 4
n= 3
n= 2
氢 原 子 能 级 图
-13.6
n= 1
莱曼系 巴耳末系 帕邢系 布拉开系
波数(波长的倒数)
~nk
1
nk
nk
c
h1c(En Ek) hE1c(k12 n12)
RH理论(k12 n12)
n rn En 0
EEn1En 0
故可知当n很大时谱线趋于连续
由前面推导计算得到 R H 理 1 论 .03 91 7 7 1 7 3 m 0 1
此次实验测得
R H 实 验 1 .09 07 1 5 1 6 7m 0 1
考虑到此次测量是在空气中完成的，由： 1
R测量 n(212 n12)R理论 /n
所以经过修正
R HR 测 量 n1.097 3 13 70 m 4 1 6
可以看到此时理论值与实验值在实验误差范围内符合 的很好
玻尔理论的意义和缺陷
玻尔
氢原子理论简介
－－氢氘光谱实验原理之一
郭松 pb03203164棱镜谱仪氢 放 电 管光 2~3 kV
源
光阑
三棱镜 （或光栅）
全息干板
记录氢原子光谱原理示意图
光栅摄谱仪
氢原子的巴耳末线系照片 (1) 分立线状光谱
(2)谱线的波数可表示为
~1RH(k12n12)
氢光谱的里德伯常量 R H 1 .03 91 7 1 7 3 m 0 1
里德伯 - 里兹并合原则 (1896年)
普朗克量子假设 （1900年）
卢瑟福原子的有核模型 （1911年）
玻尔氢原子理论 (1913年）
玻尔氢原子理论
1. 定态假设
稳 • 电子作圆周运动
定 状
• 不辐射电磁波
态 • 这些定态的能量不连续
2. 跃迁假设
原子从一个定态跃迁到另一定态， E k
会发射或吸收一个光子，频率
同位素移位
在谱线上，同位素对应的谱线会发生移位， 称同位素移位。移位大小与核质量有关：核 质量越轻，移位效应越大，因此氢具有最大 的同位素移位。
谢谢大家！
参考资料：《量子力学教程》 《近代物理学》 互联网