振动理论练习题
振动理论练习题
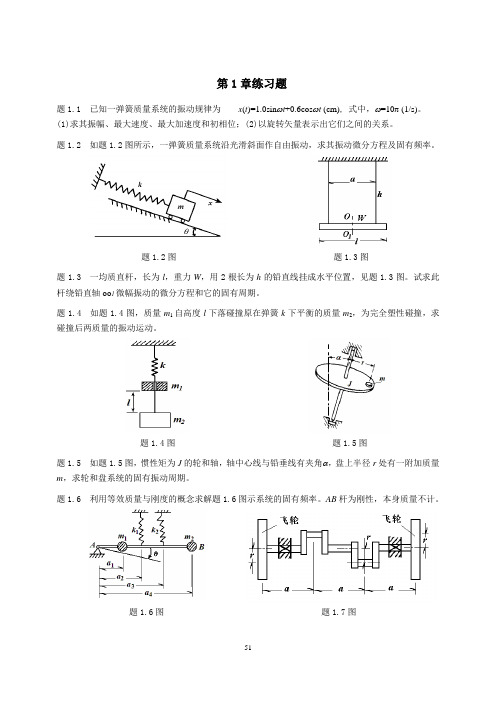
第1章练习题题1.1 已知一弹簧质量系统的振动规律为x(t)=1.0sinωt+0.6cosωt (cm), 式中，ω=10π (1/s)。
(1)求其振幅、最大速度、最大加速度和初相位；(2)以旋转矢量表示出它们之间的关系。
题1.2 如题1.2图所示，一弹簧质量系统沿光滑斜面作自由振动，求其振动微分方程及固有频率。
题1.2图题1.3图题1.3 一均质直杆，长为l，重力W，用2根长为h的铅直线挂成水平位置，见题1.3图。
试求此杆绕铅直轴oo1微幅振动的微分方程和它的固有周期。
题1.4 如题1.4图，质量m1自高度l下落碰撞原在弹簧k下平衡的质量m2，为完全塑性碰撞，求碰撞后两质量的振动运动。
题1.4图题1.5图题1.5 如题1.5图，惯性矩为J的轮和轴，轴中心线与铅垂线有夹角α，盘上半径r处有一附加质量m，求轮和盘系统的固有振动周期。
题1.6 利用等效质量与刚度的概念求解题1.6图示系统的固有频率。
AB杆为刚性，本身质量不计。
题1.6图题1.7图题1.7 两缸发动机的曲轴臂及飞轮如题1.7图所示，曲轴相当于在半径r 处有偏心质量m e ，为平衡这一质量将平衡配重放在飞轮上，设所在位置同样距轴心r ，求平衡配重所需质量。
题1.8 用衰减振动法测定某系统的阻尼系数时，测得在40周内振幅由0.268mm 减少到0.14mm 。
求此系统的相对阻尼系数ζ。
题1.9 某洗衣机滚筒部分重14kN ，用四个弹簧对称支承，每个弹簧的刚度为k =80N ／mm 。
(1)试计算此系统的临界阻尼系数c c ；(2)这个系统装有四个阻尼缓冲器，每个阻尼系数c =1.8N ·s ／mm 。
试问此系统自由振动时经过多少时间后，振幅衰减到10％?(3)衰减振动的周期是多少?与不安装缓冲器时的振动周期作比较。
题1.10 如题1.10图,展开周期半正弦函数F (t )成傅里叶级数，求出所示弹簧质量系统在该F (t ) 作用下的响应。
振动考试题(带答案)
振动考试试卷一、选择题：（30分）在正确的答案后面打对号。
1、以下那些因素会引发轴承使用寿命达不到设计要求？（1）润滑不良（2）不对中（3）过载（4）转动惯量不平衡（5）轴承座松动（6）转速过低2、最简单的周期振动称为：（1）简谐振动（2）阻尼震动（3）共振3、振动三要素包括：振幅、（）和（）（1）时间（2）频率（3）相位4、简谐振动公式：F=kx，k反映了系统的：（1）刚度（2）挠度（3）硬度5、振动问题都可以简化为一个含有基本参数m（）、c（阻尼）、k（刚度）的系统模型。
（1）m（质量）（2）T（惯量）（3）F（外力）6、以下三种振动传感器哪一种响应最快？（1）位移型（2）速度型（3）加速度型7、两种分析振动的基本频谱是时域谱和（）（1）质量谱（2）频域谱（3）色谱8、不平衡震动的特点是：（1）通常水平方向的振幅大于垂直方向的幅值、振幅随转速增加而增加、振动主要发生在1倍频（2）通常垂直方向的振幅大于水平方向的幅值、振幅随转速增加而增加、振动主要发生在1倍频（3）通常水平方向的振幅大于垂直方向的幅值、振幅随转速增加而减少、振动主要发生在1倍频9、不平衡分为：静不平衡、（）、动不平衡（1）奇不平衡（2）偶不平衡（3）简谐不平衡10、不对中类型：平行不对中，（），综合不对中。
（1）角度不对中（2）垂直不对中（3）距离不对中二、问答题（20分）提高转速能否区分不对中和不平衡振动？为什么？答：能，区分不对中和不平衡的一个方法是提高机器的转速。
如果是不平衡，振幅的增加会与速度的平方成正比；反之，不对中引起的振动却不会随速度发生变化。
三、频域谱分析题（30分）1、判断以下频域谱，哪个是转子不平衡、哪个是轴弯曲、哪个是轴承座松动？频谱1判断为（转子不平衡）频谱2判断为（轴弯曲）频谱3判断为（轴承座松动）四、时域谱分析题（20分）以下时域谱中，哪个是轴承外滚道损伤？哪个是内滚道损伤？判断为（外滚道损伤）判断为（内滚道损伤）。
第9章振动之练习题及参考答案
1、 一质点沿x 轴作简谐振动，振动方程为 )312cos(1042π+π⨯=-t x (SI)．从t = 0时刻起，到质点位置在x = -2 cm 处，且向x 轴正方向运动的最短时间间隔为(A)s 81(B)s 61 (C)s 41 (D)s 31 (E)s 21 ［ ］2、一物体作简谐振动，振动方程为)41cos(π+=t A x ω．在 t = T /4（T 为周期）时刻，物体的加速度为 (A) 2221ωA -． (B)2221ωA ．(C) 2321ωA -． (D) 2321ωA ．3、一个质点作简谐振动，振幅为A ，在起始时刻质点的位移为A 21，且向x 轴的正方向运动，代表此简谐振动的旋转矢量图为［ ］4、一弹簧振子作简谐振动，总能量为E 1，如果简谐振动振幅增加为原来的两倍，重物的质量增为原来的四倍，则它的总能量E 2变为(A) E 1/4． (B) E 1/2．(C) 2E 1． (D) 4 E 1 ． ［ ］5、一质点沿x 轴作简谐振动，振动范围的中心点为x 轴的原点．已知周期为T ，振幅为A ．(1) 若t = 0时质点过x = 0处且朝x 轴正方向运动，则振动方程为x =_____________________________．(2) 若t = 0时质点处于A x 21=处且向x 轴负方向运动，则振动方程为x =_____________________________．(A (B ) (C )(D -x6、一简谐振动的旋转矢量图如图所示，振幅矢量长2 cm ，则该简谐振动的初相为____________．振动方程为____________________________．7、一质点在x 轴上作简谐振动，选取该质点向右运动通过A 点时作为计时起点( t = 0 )，经过2秒后质点第一次经过B 点，再经过2秒后质点第二次经过B 点，若已知该质点在A 、B 两点具有相同的速率，且AB = 10 cm 求：(1) 质点的振动方程；(2) 质点在A 点处的速率．8、一弹簧振子沿x 轴作简谐振动（弹簧为原长时振动物体的位置取作x 轴原点）．已知振动物体最大位移为x m = 0.4 m 最大恢复力为F m = 0.8 N ，最大速度为v m = 0.8π m/s ，又知t = 0的初位移为+0.2 m ，且初速度与所选x 轴方向相反．(1) 求振动能量；(2) 求此振动的表达式．9、质量m = 10 g 的小球与轻弹簧组成的振动系统，按)318cos(5.0π+π=t x 的规律作自由振动，式中t 以秒作单位，x 以厘米为单位，求(1) 振动的角频率、周期、振幅和初相； (2) 振动的速度、加速度的数值表达式； (3) 振动的能量E ； (4) 平均动能和平均势能．10、一简谐振动的振动曲线如图所示．求振动方程．参考答案1、E2、B3、B4、Dt-5、)212cos(π-πTt A ， )312c o s (π+πTt A6、 π/4 ， )4/c o s (1022π+π⨯=-t x (SI)7、解：由旋转矢量图和 |v A | = |v B | 可知 T /2 = 4秒， ∴ T = 8 s ， ν = (1/8) s -1，ω = 2πν = (π /4) s -1(1) 以AB 的中点为坐标原点，x 轴指向右方． t = 0时， 5-=x cm φcos A = t = 2 s 时， 5=x cm φφωsin )2cos(A A -=+=由上二式解得 tg φ = 1 因为在A 点质点的速度大于零，所以φ = -3π/4或5π/4（如图）25c o s /==φx A cm∴ 振动方程 )434c o s (10252π-π⨯=-t x (SI) (2) 速率)434s i n (41025d d 2π-π⨯π-==-t t xv (SI)当t = 0 时，质点在A 点221093.3)43sin(10425d d --⨯=π-⨯π-==tx v m/s 8、解：(1) 由题意 kA F m =，m x A =，m m x F k /=． 16.021212===m m m x F kx E J(2) π===2mm m x Av v ω rad /s由 t = 0， φc o s0A x ==0.2 m ， 0sin 0<-=φωA v 可得 π=31φ则振动方程为)312c o s (4.0π+π=t x9、解：(1) A = 0.5 cm ；ω = 8π s -1；T = 2π/ω = (1/4) s ；φ = π/3(2) )318s i n (1042π+π⨯π-==-t xv (SI))318cos(103222π+π⨯π-==-t xa (SI)(3) 2222121Am kAE E E P K ω==+==7.90×10-5 J(4) 平均动能 ⎰=TK tm T E 02d 21)/1(v⎰π+π⨯π-=-Tt t m T 0222d )318(s i n )104(21)/1(= 3.95×10-5 J =E2110、解：(1) 设振动方程为 )c o s (φω+=t A x由曲线可知 A = 10 cm , t = 0，φcos 1050=-=x ，0sin 100<-=φωv 解上面两式，可得 φ = 2π/3由图可知质点由位移为 x 0 = -5 cm 和v 0 < 0的状态到x = 0和 v > 0的状态所需时间t = 2 s ，代入振动方程得 )3/22c o s (100π+=ω (SI) 则有2/33/22π=π+ω，∴ ω = 5 π/12 故所求振动方程为 )3/212/5cos(1.0π+π=t x (SI)。
物理振动试题及答案高中
物理振动试题及答案高中一、单项选择题（每题3分，共30分）1. 简谐运动的振动图象中，质点的振动周期与振幅无关，与下列哪个因素有关？（）A. 振动的位移B. 振动的速度C. 振动的频率D. 振动的加速度答案：C2. 弹簧振子做简谐运动时，若振幅不变，周期减小，则下列哪个量增大？（）A. 弹簧的劲度系数B. 振子的质量C. 振子的动能D. 振子的势能答案：A3. 两个简谐运动的合成，其合成振动的频率与下列哪个因素有关？（）A. 两个简谐运动的振幅B. 两个简谐运动的周期C. 两个简谐运动的相位差D. 两个简谐运动的频率答案：D4. 两个简谐运动的合成，其合成振动的振幅与下列哪个因素有关？（）A. 两个简谐运动的振幅B. 两个简谐运动的周期C. 两个简谐运动的相位差D. 两个简谐运动的频率答案：A5. 阻尼振动的振幅随时间减小，其振动周期与下列哪个因素有关？（）A. 振幅B. 振动的速度C. 振动的频率D. 振动的加速度答案：C6. 受迫振动的频率与下列哪个因素有关？（）A. 振子的固有频率B. 驱动力的频率C. 振子的振幅D. 振子的加速度答案：B7. 共振现象发生时，振子的振幅与下列哪个因素有关？（）A. 振子的固有频率B. 驱动力的频率C. 振子的振幅D. 振子的加速度答案：B8. 波的传播速度与下列哪个因素有关？（）A. 波的频率B. 波的振幅C. 波的周期D. 介质的性质答案：D9. 波的干涉现象中，两列波的相位差与下列哪个因素有关？（）A. 波的频率B. 波的振幅C. 波的周期D. 波的传播速度答案：A10. 波的衍射现象中，波的传播方向与下列哪个因素有关？（）A. 波的频率B. 波的振幅C. 波的周期D. 障碍物的大小答案：D二、多项选择题（每题4分，共20分）11. 简谐运动的特点包括（）。
A. 周期性B. 振动图象为正弦曲线C. 振动速度随时间均匀变化D. 振动加速度随时间均匀变化答案：AB12. 两个简谐运动的合成，下列哪些因素会影响合成振动的频率？（）A. 两个简谐运动的振幅B. 两个简谐运动的周期C. 两个简谐运动的相位差D. 两个简谐运动的频率答案：BD13. 阻尼振动的特点包括（）。
物理振动试题及答案解析
物理振动试题及答案解析1. 简谐运动的振动周期与哪些因素有关？答案：简谐运动的振动周期与振子的质量以及弹簧的劲度系数有关，与振幅无关。
2. 什么是阻尼振动？其振动周期与自由振动相比有何不同？答案：阻尼振动是指在振动过程中受到阻力作用的振动。
与自由振动相比，阻尼振动的振动周期会变长。
3. 简述单摆的周期公式。
答案：单摆的周期公式为 \( T = 2\pi \sqrt{\frac{L}{g}} \)，其中 \( T \) 是周期，\( L \) 是摆长，\( g \) 是重力加速度。
4. 什么是共振现象？请举例说明。
答案：共振现象是指当驱动力的频率接近或等于系统的固有频率时，系统振幅急剧增大的现象。
例如，当行人在桥上行走时，如果步频与桥的固有频率接近，可能会引起桥梁的共振，导致桥梁剧烈振动甚至断裂。
5. 请解释为什么在声波传播中，频率越高的声波传播距离越短？答案：频率越高的声波波长越短，波长越短的声波在传播过程中更容易受到空气分子的散射作用，因此传播距离较短。
6. 什么是多普勒效应？请用物理公式表达。
答案：多普勒效应是指当波源和观察者相对运动时，观察者接收到的波频率与波源发出的频率不同的现象。
多普勒效应的公式为 \( f'= \frac{f(u + v)}{u + v \cos \theta} \)，其中 \( f' \) 是观察者接收到的频率，\( f \) 是波源发出的频率，\( u \) 是波源的速度，\( v \) 是观察者的速度，\( \theta \) 是波源和观察者之间的夹角。
7. 请解释为什么在弹簧振子的振动过程中，振幅会逐渐减小？答案：在弹簧振子的振动过程中，振幅逐渐减小是因为存在阻力作用，如空气阻力或摩擦阻力，这些阻力会消耗振子的机械能，导致振幅减小。
8. 什么是机械波？请列举三种常见的机械波。
答案：机械波是指需要介质传播的波，其传播过程中介质的质点并不随波迁移，而是在平衡位置附近做振动。
振动理论习题答案
《振动力学》——习题第二章 单自由度系统的自由振动2-1 如图2-1 所示，重物1W 悬挂在刚度为k 的弹簧上并处于静止平衡位置，另一重物2W 从高度为h 处自由下落到1W 上且无弹跳。
试求2W 下降的最大距离和两物体碰撞后的运动规律。
解：222221v gW h W =，gh v 22=动量守恒：122122v gW W v g W +=，gh W W W v 221212+=平衡位置：11kx W =，kW x 11=1221kx W W =+，kW W x 2112+=故：kW x x x 21120=-= ()2121W W kgg W W k n +=+=ω故：tv t x txt x x n nn n nn ωωωωωωsin cos sin cos 12000+-=+-=xx 0x 1x 12平衡位置2-2 一均质等直杆，长为l ，重量为w ，用两根长h 的相同的铅垂线悬挂成水平位置，如图2-2所示。
试写出此杆绕通过重心的铅垂轴做微摆动的振动微分方程，并求出振动固有周期。
解：给杆一个微转角2a＝h 2F ＝mg由动量矩定理：ah a mg a mg Fa M ml I M I 822cos sin 12122-=-≈⋅-====αθαθ其中12cossin ≈≈θααh l ga p ha mg ml n 22222304121==⋅+θθ g h a l ga h l p T n 3π23π2π222===2-3 一半圆薄壁筒，平均半径为R , 置于粗糙平面上做微幅摆动，如图2-3所示。
试求其摆动的固有频率。
图2-3 图2-42-4 如图2-4 所示，一质量m连接在一刚性杆上，杆的质量忽略不计，试求下列情况系统作垂直振动的固有频率：（1）振动过程中杆被约束保持水平位置；（2）杆可以在铅垂平面内微幅转动；（3）比较上述两种情况中哪种的固有频率较高，并说明理由。
图T 2-9 答案图T 2-9解：（1）保持水平位置：m kk n 21+=ω（2）微幅转动：mglllF2112+=mgl1l2xx2xx'mglll2121+=k2k1ml1l2()()()()()()()()()mgk k l l k l k l mgk k l l k l l k l l l k l mg k k l l k l k l l l l k l l mg l mgk l l l k l l l l l l k l l mg l l l l x x k F x x x 2122122212121221221121212221212211211121212122211211121221112111 ++=+-++=+-⋅+++=⎥⎦⎤⎢⎣⎡+-++++=+-+='+=故：()22212121221k l k l k k l l k e++=mk en =ω 2-5 试求图2-5所示系统中均质刚性杆AB 在A 点的等效质量。
振动习题答案
振动习题答案振动习题答案振动是物体在固定轴线附近做往复运动的现象。
它在我们的日常生活中随处可见，比如钟摆的摆动、弹簧的振动等等。
振动习题是学习振动理论的重要一环，通过解答习题可以加深对振动原理的理解和应用。
下面是一些常见的振动习题及其答案，希望对大家的学习有所帮助。
1. 一个质点沿直线做简谐振动，振幅为2cm，周期为4s，求该质点的速度和加速度。
解答：简谐振动的速度和加速度与位置的关系可以通过振动的位移方程得到。
位移方程为：x = A * sin(ωt + φ)，其中A为振幅，ω为角频率，t为时间，φ为初相位。
根据周期和角频率的关系，可知ω = 2π / T，其中T为周期。
根据题目中的数据，振幅A = 2cm，周期T = 4s。
代入上述公式可得ω = 2π /4 = π / 2。
因此，位移方程可写为：x = 2 * sin(π/2 * t + φ)。
速度v = dx / dt，加速度a = dv / dt。
对位移方程求一次导数得到速度和加速度的表达式：v = d(2 * sin(π/2 * t + φ)) / dt = 2 * (π/2) * cos(π/2 * t + φ) = π * cos(π/2 * t + φ)，a = d(π * cos(π/2 * t + φ)) / dt = - (π/2)^2 * sin(π/2 * t + φ) = - (π^2 / 4) *sin(π/2 * t + φ)。
2. 一个弹簧的振动周期为2s，振幅为5cm，求该弹簧的角频率和振动频率。
解答：角频率ω = 2π / T，振动频率f = 1 / T，其中T为周期。
根据题目中的数据，周期T = 2s。
代入上述公式可得角频率ω = 2π / 2 = π，振动频率f = 1 / 2 = 0.5Hz。
3. 一个质点的振动方程为x = 3sin(2πt + π/4)，求该质点的振幅、周期、角频率、初相位、速度和加速度。
机械振动考试题和答案
机械振动考试题和答案一、单项选择题（每题2分，共20分）1. 简谐运动的振动周期与振幅无关，与（）有关。
A. 质量B. 频率C. 弹簧常数D. 初始条件答案：C2. 阻尼振动中，振幅逐渐减小的原因是（）。
A. 系统内部摩擦B. 外部阻力C. 系统内部摩擦和外部阻力D. 系统内部摩擦或外部阻力答案：C3. 两个简谐运动合成时，合成运动的频率等于（）。
A. 两个简谐运动频率之和B. 两个简谐运动频率之差C. 两个简谐运动频率中较大的一个D. 两个简谐运动频率中较小的一个答案：D4. 受迫振动的频率与（）有关。
A. 驱动力频率B. 系统固有频率C. 驱动力大小D. 系统阻尼系数答案：A5. 阻尼振动中，阻尼系数越大，振动周期（）。
A. 越大B. 越小C. 不变D. 无法确定答案：B6. 受迫振动中，当驱动力频率接近系统固有频率时，会发生（）。
A. 共振B. 反共振C. 振动增强D. 振动减弱答案：A7. 简谐运动的振动周期与（）成正比。
B. 频率C. 弹簧常数D. 质量的平方根答案：D8. 阻尼振动中，阻尼系数越小，振动周期（）。
A. 越大B. 越小C. 不变D. 无法确定答案：C9. 受迫振动中，当驱动力频率等于系统固有频率时，振动的振幅（）。
A. 最小C. 不变D. 无法确定答案：B10. 简谐运动的振动周期与（）无关。
A. 质量B. 频率C. 弹簧常数D. 初始条件答案：D二、多项选择题（每题3分，共15分）11. 简谐运动的振动周期与以下哪些因素有关？（）A. 质量C. 弹簧常数D. 初始条件答案：AC12. 阻尼振动中，振幅逐渐减小的原因包括（）。
A. 系统内部摩擦B. 外部阻力C. 系统内部摩擦和外部阻力D. 系统内部摩擦或外部阻力答案：CD13. 两个简谐运动合成时，合成运动的频率等于以下哪些选项？（）A. 两个简谐运动频率之和B. 两个简谐运动频率之差C. 两个简谐运动频率中较大的一个D. 两个简谐运动频率中较小的一个答案：BD14. 受迫振动的频率与以下哪些因素有关？（）A. 驱动力频率B. 系统固有频率C. 驱动力大小D. 系统阻尼系数答案：AB15. 阻尼振动中，阻尼系数越大，振动周期的变化情况是（）。
振动学基础---练习题
振动学基础---练习题一、选择1、物体做简谐运动时，下列叙述中正确的是 [ ]（A ）在平衡位置加速度最大； （B ）在平衡位置速度最小； （C ）在运动路径两端加速度最大； （D ）在运动路径两端加速度最小。
2、作简谐运动的单摆，在最大角位移向平衡位置运动过程中 [ ]（A ）动能减少，势能增加； (B) 动能增加，势能减少；（C ）动能增加，势能增加； (D) 动能减少，势能减少。
3、弹簧振子沿直线作简谐振动，当振子连续两次经过相同位置时，以下说法正确的是（A ）加速度不同，动能相同； [ ] （B ）动能相同，动量相同； （C ）回复力相同，弹性势能相同； （D ）位移、速度和加速度都相同。
4、一弹簧振子，当0t =时，物体处在/2x A =（A 为振幅）处且向负方向运动，则它的初相为[ ]（A ）π3； （B ）π6； （C ）-π3； （D ）-π6。
5、把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度θ ，然后由静止放手任其振动，从放手时开始计时。
若用余弦函数表示其运动方程，则该单摆振动的初相为 [ ](A) π ； (B) π/2 ； (C) 0 ； (D) θ 。
6、一质点作简谐振动，周期为T 。
当它由平衡位置向x 轴正方向运动时，从二分之一最大位移处到最大位移处这段路程所需要的时间为 [ ](A) T /12 ； (B) T /8 ； (C) T /6 ； (D) T /4 7、一质点沿x 轴作简谐振动，振动方程为 10.04cos(2)3x t ππ=+（SI ），从t = 0时刻起，到质点位置在x = -0.02 m 处，且向x 轴正方向运动的最短时间间隔为 [ ](A)s 81； (B) s 61； (C) s 41； (D) s 21。
8、一弹簧振子，物体的质量为m ，弹簧的劲度系数为k ，该振子作振幅为A 的简谐振动。
当物体通过平衡位置且向规定的正方向运动时开始计时。
大学机械振动考试题目及答案
大学机械振动考试题目及答案一、选择题（每题2分，共10分）1. 在简谐振动中，振幅与振动的能量关系是（）。
A. 无关B. 成正比C. 成反比D. 振幅越大，能量越小答案：B2. 下列哪个不是机械振动系统的自由度？（）。
A. 转动B. 平动C. 振动D. 形变答案：C3. 一个单自由度系统在受到初始条件激励后，其振动形式是（）。
A. 简谐振动B. 阻尼振动C. 受迫振动D. 自由振动答案：D4. 在阻尼振动中，如果阻尼系数增加，振动的振幅将（）。
A. 增加B. 不变C. 减小D. 先增加后减小答案：C5. 对于一个二自由度振动系统，其振动模态数量是（）。
A. 1B. 2C. 3D. 4答案：B二、填空题（每题2分，共10分）6. 一个物体做自由振动时，其频率称为______。
答案：固有频率7. 当外力的频率与系统的固有频率相等时，系统发生的振动称为______。
答案：共振8. 阻尼力与速度成正比的阻尼称为______阻尼。
答案：线性9. 振动系统的动态响应可以通过______分析法求解。
答案：傅里叶10. 在转子动力学中，临界转速是指转子发生______振动的转速。
答案：自激三、简答题（每题5分，共20分）11. 简述什么是简谐振动，并说明其运动方程的形式。
答案：简谐振动是一种周期性的振动，其加速度与位移成正比，且方向相反。
在数学上，简谐振动的运动方程可以表示为：x(t) = A * cos(ωt + φ)其中，A 是振幅，ω 是角频率，t 是时间，φ 是初相位。
12. 解释什么是阻尼振动，并说明其特点。
答案：阻尼振动是指在振动系统中存在能量耗散，导致振幅随时间逐渐减小的振动。
其特点包括振幅逐渐衰减，振动频率可能会随着振幅的减小而发生变化，且阻尼力通常与振动速度成正比。
13. 描述什么是受迫振动，并给出其稳态响应的条件。
答案：受迫振动是指系统在周期性外力作用下的振动。
当外力的频率接近系统的固有频率时，系统将发生共振，此时振幅会显著增大。
(完整版)振动力学试题
1.转动惯量为J 的圆盘由三段抗扭刚度分别为1k 、2k 和3k 的轴约束，如图所示。
求系统的固有频率。
解：系统的动能为 221•=θJ T2k 和3k 相当于串联，则 32θθθ+= 3322θθk k =联立以上两式得 θθ3232k k k +=θθ3223k k k +=系统的势能为 ()[]223322221323232121212121θθθθk k k k k k k k k k U +++=++=利用θωθn =•和U T =可得 ()()3232132n k k J k k k k k +++=ω2.面积为S ，质量为m 的薄板连接于弹簧下端，在粘性流体中振动，如图所示。
作用于薄板的阻尼力为νμS F d 2=，S 2为薄板总面积，ν为速度。
若测得薄板无阻尼自由振动的周期为0T ，在粘性流体中自由振动的周期为d T 。
求系数μ。
解：平面在液体中上下振动时：02=++•••kx x S x m μ dn d n T T m k πξωωπω2-1,220====kS m S m S n n 222,22μξωμξξωμ==⇒= kS k 222--1μξ=2020220-2-22T T T ST mk S k T T T T d dd πμμ=⇒=3.如图所示均匀刚性杆质量为1m ，求系统的频率方程。
解：先求刚度矩阵。
令0x 1,==θ得：22212111a k b k a a k b b k k +=⋅+⋅=b k 221-k =令1,0==x θ得：a k k 212-=222-k k =则刚度矩阵为：⎥⎦⎤⎢⎣⎡+=2222221--k ak a k a k b k K再求质量矩阵。
令0,1==••••x θ ，得：0,31212111==m a m m令1,0==••••x θ，得：22212,0m m m ==则质量矩阵为： ⎥⎥⎦⎤⎢⎢⎣⎡=2210031m a m M故频率方程为： 0-2=M K ω4.在图所示系统中，已知m 和k 。
高考机械振动试题及答案
高考机械振动试题及答案1. 单摆的周期公式为T=2π√(L/g)，其中L为摆长，g为重力加速度。
若单摆的摆长增加到原来的2倍，其周期将变为原来的多少倍？答案：周期将变为原来的√2倍。
2. 弹簧振子的振动周期公式为T=2π√(m/k)，其中m为振子质量，k为弹簧劲度系数。
若弹簧振子的质量增加到原来的2倍，而弹簧劲度系数不变，其振动周期将如何变化？答案：振动周期将增加到原来的√2倍。
3. 简谐运动中，振幅A、角频率ω和周期T之间的关系为T=2π/ω。
若振幅增加到原来的2倍，角频率不变，周期将如何变化？答案：周期不变。
4. 阻尼振动中，振幅随时间指数衰减，其振幅公式为A(t)=A0e^(-γt)，其中A0为初始振幅，γ为阻尼系数，t为时间。
若阻尼系数增加到原来的2倍，初始振幅不变，振幅衰减速度将如何变化？答案：振幅衰减速度将加快。
5. 受迫振动中，振子的振动频率等于驱动力的频率。
若驱动力的频率增加到原来的2倍，振子的振动频率将如何变化？答案：振子的振动频率将增加到原来的2倍。
6. 共振现象发生在驱动力频率等于振子的固有频率时。
若振子的固有频率增加到原来的2倍，而驱动力的频率不变，是否还会出现共振现象？答案：不会出现共振现象，因为驱动力频率与振子固有频率不再相等。
7. 波的干涉中，两列波的相位差为Δφ=2π(Δx)/λ，其中Δx为两列波的波程差，λ为波长。
若波程差增加到原来的2倍，波长不变，相位差将如何变化？答案：相位差将增加到原来的2倍。
8. 波的衍射中，当波遇到障碍物时，会发生弯曲传播。
若障碍物的尺寸增加到原来的2倍，波长不变，衍射现象将如何变化？答案：衍射现象将减弱，因为波长与障碍物尺寸的比值变小。
9. 波的多普勒效应中，观察者与波源相对运动时，观察到的波频率会发生变化。
若波源向观察者靠近，速度增加到原来的2倍，波长不变，观察到的波频率将如何变化？答案：观察到的波频率将增加。
10. 波的反射中，当波遇到边界时会发生反射。
物理机械振动考试题及答案
物理机械振动考试题及答案一、单项选择题（每题3分，共30分）1. 简谐运动的振动周期与振幅无关，与以下哪个因素有关？A. 质量B. 弹簧常数C. 初始位移D. 初始速度答案：B2. 阻尼振动中，振幅逐渐减小的原因是：A. 摩擦力B. 重力C. 弹力D. 空气阻力答案：A3. 以下哪个量描述了简谐运动的振动快慢？A. 振幅B. 周期C. 频率D. 相位答案：C4. 两个简谐运动的合成，以下哪个条件可以产生拍现象？A. 频率相同B. 频率不同C. 振幅相同D. 相位相反答案：B5. 以下哪个量是矢量？A. 位移B. 速度C. 加速度D. 以上都是答案：D6. 单摆的周期与以下哪个因素无关？A. 摆长B. 摆球质量C. 重力加速度D. 摆角答案：B7. 以下哪个量描述了简谐运动的能量？A. 振幅C. 频率D. 相位答案：A8. 以下哪个因素会影响单摆的周期？A. 摆长B. 摆球质量C. 摆角D. 重力加速度答案：A9. 阻尼振动中，振幅减小到原来的1/e时，经过的时间为：A. 1/2TB. TC. 2T答案：C10. 以下哪个现象不是简谐运动？A. 弹簧振子B. 单摆C. 弹簧振子的振幅逐渐减小D. 单摆的振幅逐渐减小答案：C二、填空题（每题4分，共20分）11. 简谐运动的周期公式为：T = 2π√(____/k)，其中m为质量，k为弹簧常数。
答案：m12. 单摆的周期公式为：T = 2π√(L/g)，其中L为摆长，g为重力加速度。
答案：L13. 阻尼振动的振幅公式为：A(t) = A0 * e^(-γt)，其中A0为初始振幅，γ为阻尼系数，t为时间。
答案：A014. 简谐运动的频率公式为：f = 1/T，其中T为周期。
答案：1/T15. 简谐运动的相位公式为：φ = ωt + φ0，其中ω为角频率，t 为时间，φ0为初始相位。
答案：ωt + φ0三、计算题（每题10分，共50分）16. 一个质量为2kg的物体，通过弹簧连接在墙上，弹簧的弹簧常数为100N/m。
振动理论-习题
《振动力学》——习题单自由度系统的自由振动2-1 如图2-1 所示，重物1W 悬挂在刚度为k 的弹簧上并处于静止平衡位置，另一重物2W 从高度为h 处自由下落到1W 上且无弹跳。
试求2W 下降的最大距离和两物体碰撞后 的运动规律。
图2-1 图2-2 2-2 一均质等直杆，长为l ，重量为w ，用两根长h 的相同的铅垂线悬挂成水平位置， 如图2-2所示。
试写出此杆绕通过重心的铅垂轴做微摆动的振动微分方程，并求 出振动固有周期。
2-3 一半圆薄壁筒，平均半径为R , 置于粗糙平面上做微幅摆动，如图2-3所示。
试求 其摆动的固有频率。
图2-3 图2-4 2-4 如图2-4 所示，一质量m 连接在一刚性杆上，杆的质量忽略不计，试求下列情况 系统作垂直振动的固有频率：（1）振动过程中杆被约束保持水平位置；（2）杆可以在铅垂平面内微幅转动；（3）比较上述两种情况中哪种的固有频率较高，并说明理由。
2-5 试求图2-5所示系统中均质刚性杆AB 在A 点的等效质量。
已知杆的质量为m ，A 端弹簧的刚度为k 。
并问铰链支座C 放在何处时使系统的固有频率最高？图2-5 图2-6 2-6 在图2-6所示的系统中，四个弹簧均未受力。
已知m =50kg ，19800N m k =，234900N m k k ==，419600N m k =。
试问：（1）若将支撑缓慢撤去，质量块将下落多少距离？（2）若将支撑突然撤去，质量块又将下落多少距离？2-7 图2-7所示系统，质量为m 2的均质圆盘在水平面上作无滑动的滚动，鼓轮绕轴的转动惯量为I ，忽略绳子的弹性、质量及各轴承间的摩擦力。
试求此系统的固有频 率。
图2-72-8 如图2-8所示的系统中，钢杆质量不计，建立系统的运动微分方程，并求临界阻尼系数及阻尼固有频率。
图2-8 图2-9 2-9 图2-9所示的系统中，m ＝1kg ，k ＝224N/m ，c ＝48N.s/m ，l 1＝l ＝0.49m ，l 2＝l /2，l 3＝l /4，不计钢杆质量。
(完整版)大学物理振动习题含答案
一、选择题：1．3001：把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度θ ，然后由静止放手任其振动，从放手时开始计时。
若用余弦函数表示其运动方程，则该单摆振动的初相为(A) π (B) π/2 (C) 0 (D) θ ［ ］2．3002：两个质点各自作简谐振动，它们的振幅相同、周期相同。
第一个质点的振动方程为x 1 = A cos(ωt + α)。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处。
则第二个质点的振动方程为：(A))π21cos(2++=αωt A x (B) )π21cos(2-+=αωt A x (C))π23cos(2-+=αωt A x (D) )cos(2π++=αωt A x ［ ］3．3007：一质量为m 的物体挂在劲度系数为k 的轻弹簧下面，振动角频率为ω。
若把此弹簧分割成二等份，将物体m 挂在分割后的一根弹簧上，则振动角频率是(A) 2 ω (B) ω2 (C) 2/ω (D) ω /2 ［ ］4．3396：一质点作简谐振动。
其运动速度与时间的曲线如图所示。
若质点的振动规律用余弦函数描述，则其初相应为 (A) π/6 (B) 5π/6 (C) -5π/6 (D) -π/6 (E) -2π/3 ［ ］5．3552：一个弹簧振子和一个单摆（只考虑小幅度摆动），在地面上的固有振动周期分别为T 1和T 2。
将它们拿到月球上去，相应的周期分别为1T '和2T '。
则有(A) 11T T >'且22T T >' (B) 11T T <'且22T T <'(C) 11T T ='且22T T =' (D) 11T T ='且22T T >' ［ ］ 6．5178：一质点沿x 轴作简谐振动，振动方程为)312cos(1042π+π⨯=-t x (SI)。
物理振动试题及答案
物理振动试题及答案一、选择题（每题4分，共20分）1. 简谐运动中，振幅、周期和频率之间的关系是：A. 振幅和周期成正比B. 振幅和周期成反比C. 振幅和频率成正比D. 振幅和频率成反比答案：D2. 以下哪个选项描述的是阻尼振动？A. 振幅逐渐减小的振动B. 振幅逐渐增大的振动C. 振幅保持不变的振动D. 周期逐渐减小的振动答案：A3. 两个简谐运动的合运动，其频率分别为f1和f2，当f1和f2满足什么条件时，合运动是周期性的？A. f1 = f2B. f1 ≠ f2C. f1 = 2f2D. f1 = 3f2答案：A4. 波在传播过程中，以下哪个物理量是不变的？A. 波长B. 频率C. 波速D. 振幅答案：B5. 波的干涉现象中，以下哪个条件是必须满足的？A. 两列波的频率相同B. 两列波的振幅相同C. 两列波的传播方向相同D. 两列波的相位差恒定答案：A二、填空题（每题4分，共20分）1. 简谐运动的振动方程可以表示为：x = A * sin(ωt + φ)，其中A代表______，ω代表______，φ代表______。
答案：振幅；角频率；初相位2. 波的传播速度v、波长λ和频率f之间的关系是：v = ______ * ______。
答案：λ；f3. 波的干涉现象中，当两列波的相位差为2π的整数倍时，会发生______干涉。
答案：构造性4. 波的衍射现象是指波能够绕过______继续传播的现象。
答案：障碍物5. 多普勒效应描述的是波源和观察者之间存在相对运动时，观察者接收到的波的______发生变化的现象。
答案：频率三、计算题（每题10分，共40分）1. 一个质量为m的质点做简谐运动，其振动方程为x = A * cos(ωt)，其中A = 0.1m，ω = 2π rad/s。
求该质点在t = 0.5s时的位移和速度。
答案：位移：x = 0.1 * cos(2π * 0.5) = -0.05m速度：v = -Aω * sin(ωt) = -0.1 * 2π * sin(2π * 0.5) = 0 m/s2. 一列波的波长为λ，波速为v，求该波的频率f。
物理振动试题及答案
物理振动试题及答案一、选择题（每题2分，共20分）1. 简谐振动的周期与振幅的关系是：A. 振幅越大，周期越长B. 振幅越大，周期越短C. 周期与振幅无关D. 振幅越大，周期越不稳定答案：C2. 阻尼振动的振幅会：A. 逐渐增大B. 逐渐减小C. 保持不变D. 先增大后减小答案：B3. 单摆的周期与摆长的关系是：A. 摆长越长，周期越长B. 摆长越长，周期越短C. 摆长与周期无关D. 摆长越长，周期先长后短答案：A4. 以下哪种振动是等幅振动：A. 阻尼振动B. 受迫振动C. 简谐振动D. 非线性振动答案：C5. 波的传播速度与介质的关系是：A. 介质越硬，波速越快B. 介质越软，波速越快C. 波速与介质无关D. 介质越软，波速越慢答案：A6. 波的干涉现象中，两列波的相位关系是：A. 总是相同的B. 总是相反的C. 总是相差180度D. 可以是任意的答案：A7. 波的衍射现象发生的条件是：A. 波长与障碍物尺寸相近B. 波长远大于障碍物尺寸C. 波长远小于障碍物尺寸D. 波速与障碍物无关答案：A8. 声波的频率与音调的关系是：A. 频率越高，音调越低B. 频率越高，音调越高C. 频率与音调无关D. 频率越低，音调越高答案：B9. 光的干涉现象中，两列光波的相位关系是：A. 总是相同的B. 总是相反的C. 总是相差180度D. 可以是任意的答案：A10. 光的衍射现象中，光波通过小孔后：A. 波长变长B. 波长变短C. 波长不变D. 波长变宽答案：C二、填空题（每题2分，共20分）1. 简谐振动的周期公式为 T = _______。
答案：2π√(L/g)2. 单摆的周期公式为 T = _______。
答案：2π√(L/g)3. 阻尼振动的振幅随时间的变化关系可以表示为 A(t) = A0 * e^(-γt)，其中γ是 _______。
答案：阻尼系数4. 波的干涉条件是两列波的频率 _______。
物理振动试题及答案高中
物理振动试题及答案高中一、选择题（每题3分，共30分）1. 简谐运动的周期与振幅无关，与下列哪个因素有关？A. 质量B. 弹簧常数C. 振幅D. 初始条件答案：B2. 单摆的周期公式为T=2π√(L/g)，其中g代表什么？A. 重力加速度B. 质量C. 摆长D. 振幅答案：A3. 阻尼振动中，振幅逐渐减小的原因是？A. 能量守恒B. 能量转化C. 能量耗散D. 能量积累答案：C4. 以下哪个选项不是简谐运动的特征？A. 周期性B. 能量守恒C. 振幅不变D. 速度变化答案：D5. 弦乐器的音调高低与弦的什么因素有关？A. 长度B. 粗细C. 松紧D. 材料答案：A6. 波的干涉现象中，两个波的相位差为π，则它们是？A. 相长干涉B. 相消干涉C. 相位相同D. 相位相反答案：B7. 波的衍射现象发生在波遇到障碍物时，以下哪个条件最容易发生衍射？A. 障碍物尺寸远大于波长B. 障碍物尺寸远小于波长C. 障碍物尺寸等于波长D. 障碍物尺寸与波长无关答案：B8. 波的反射现象中，反射角等于入射角，这适用于以下哪种波？A. 声波B. 光波C. 电磁波D. 所有波答案：D9. 多普勒效应描述的是声波源和观察者相对运动时，观察者接收到的频率变化，以下哪个选项不是多普勒效应的条件？A. 声波源和观察者之间有相对运动B. 声波源和观察者之间距离不变C. 声波源和观察者之间距离变化D. 声波源和观察者之间速度变化答案：B10. 根据光的干涉原理，以下哪种情况不能形成干涉图样？A. 两束相干光波B. 两束非相干光波C. 两束相位差恒定的光波D. 两束频率相同的光波答案：B二、填空题（每题2分，共20分）1. 简谐运动的周期公式为T=2π√(m/k)，其中k表示______。
答案：弹簧常数2. 单摆的周期公式中，L表示______。
答案：摆长3. 阻尼振动的振幅随时间的变化规律是______。
答案：指数衰减4. 弦乐器的音调高低与弦的______有关。
物理机械振动考试题及答案
物理机械振动考试题及答案一、选择题1. 简谐振动的频率与振幅无关，这是由什么决定的？A. 振子的质量B. 振子的弹性系数C. 振子的阻尼D. 振子的初始条件答案：B2. 在阻尼振动中，振幅随时间如何变化？A. 保持不变B. 逐渐减小C. 逐渐增大D. 先增大后减小答案：B3. 以下哪个不是简谐振动的特点？A. 周期性B. 振幅不变C. 频率恒定D. 振子质量不变答案：D4. 什么是共振现象？A. 振子的振动频率等于系统固有频率时的现象B. 振子的振幅达到最大时的现象C. 振子的振动频率等于外部驱动频率时的现象D. 振子的振动频率等于外部阻尼频率时的现象答案：A5. 以下哪个公式描述了简谐振动的位移？A. \( x = A \sin(\omega t + \phi) \)B. \( x = A \cos(\omega t + \phi) \)C. \( x = A \tan(\omega t + \phi) \)D. \( x = A \sec(\omega t + \phi) \)答案：B二、填空题6. 一个物体在水平面上做简谐振动，其振动周期 \( T \) 与振动频率 \( f \) 的关系是 \[ T = \frac{1}{f} \]。
7. 阻尼振动中，振幅随时间的衰减速度与振子的________成正比。
8. 共振现象中，振子的振动频率等于系统的________频率。
9. 简谐振动的位移公式中，\( \omega \) 表示________，\( \phi \) 表示________。
10. 阻尼振动的振幅随时间的衰减可以表示为 \( A(t) = A_0 e^{-\alpha t} \)，其中 \( \alpha \) 表示________。
三、简答题11. 简述什么是阻尼振动，并说明其振幅随时间的变化趋势。
答案：阻尼振动是指在振动过程中，由于存在阻力（如空气阻力、摩擦力等），振子的振动能量逐渐减小，导致振幅逐渐减小的振动。
《振动力学》习题集(含答案)
《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。
求系统的固有频率。
图E1.1解： 系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。
求系统的固有频率。
图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得： ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。
求系统的固有频率。
图E1.3解： 系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第1章练习题
题1.1 已知一弹簧质量系统的振动规律为x(t)=1.0sinωt+0.6cosωt (cm), 式中，ω=10π (1/s)。
(1)求其振幅、最大速度、最大加速度和初相位；(2)以旋转矢量表示出它们之间的关系。
题1.2 如题1.2图所示，一弹簧质量系统沿光滑斜面作自由振动，求其振动微分方程及固有频率。
题1.2图题1.3图
题1.3 一均质直杆，长为l，重力W，用2根长为h的铅直线挂成水平位置，见题1.3图。
试求此杆绕铅直轴oo1微幅振动的微分方程和它的固有周期。
题1.4 如题1.4图，质量m1自高度l下落碰撞原在弹簧k下平衡的质量m2，为完全塑性碰撞，求碰撞后两质量的振动运动。
题1.4图题1.5图
题1.5 如题1.5图，惯性矩为J的轮和轴，轴中心线与铅垂线有夹角α，盘上半径r处有一附加质量m，求轮和盘系统的固有振动周期。
题1.6 利用等效质量与刚度的概念求解题1.6图示系统的固有频率。
AB杆为刚性，本身质量不计。
题1.6图题1.7图
题1.7 两缸发动机的曲轴臂及飞轮如题1.7图所示，曲轴相当于在半径r 处有偏心质量m e ，为平衡这一质量将平衡配重放在飞轮上，设所在位置同样距轴心r ，求平衡配重所需质量。
题1.8 用衰减振动法测定某系统的阻尼系数时，测得在40周内振幅由0.268mm 减少到0.14mm 。
求此系统的相对阻尼系数ζ。
题1.9 某洗衣机滚筒部分重14kN ，用四个弹簧对称支承，每个弹簧的刚度为k =80N ／mm 。
(1)试计算此系统的临界阻尼系数c c ；(2)这个系统装有四个阻尼缓冲器，每个阻尼系数c =1.8N ·s ／mm 。
试问此系统自由振动时经过多少时间后，振幅衰减到10％?(3)衰减振动的周期是多少?与不安装缓冲器时的振动周期作比较。
题1.10 如题1.10图,展开周期半正弦函数F (t )成傅里叶级数，求出所示弹簧质量系统在该F (t ) 作用下的响应。
题1.10图
题1.11图
题1.11 求题1.11图所示初始时静止的弹簧质量系统在力F (t )=F o e -bt 作用下的瞬态响应。
题1.12 试求在t =0时，有冲量F 作用下，有阻尼弹簧质量系统的瞬态响应峰值x m 及其出现时间t m 。
题1.13 弹簧质量系统30o
光滑斜面降落，如题1.13图所示。
自弹簧开始接触底面到离开为止，求所需的时间为多少?
题1.13图
题1.14图
题1.14 无阻尼单自由度质量弹簧m-k 系统，受题1.14图所示力的作用， 记x s =F 0/k ，m k n /2
=ω，
求证，在t < t 0 内，有 )sin (1
)(0
t t t x t x n n n s ωωω-= 在t > t 0内， 有
)(cos ]sin )([sin 1
)(000
t t t t t t x t x n n n n s -+--=ωωωω。
题1.15 如题1.15图,为车辆行驶通过曲线路面模型，设道路曲面方程为：)2cos 1(x l
a y s π
-=，求： 1）车辆通过曲线路面时的振动；2）车辆通过曲线路面后的振动。
题1.15图
题1.16图
题1.16 如题1.16图，质量m 1，m 2被无质量弦牵引，求所示质量的微幅振动微分方程和固有频率，分别给各阶模态形状，设张力T 不变。
题1.17 求如题1.17图所示系统的固有频率，分别给出n ＝l ，n =2时的模态形状。
题1.17图
题1.18图
题1.18 求如题1.18图所示扭转系统在扭转刚度k 1＝k 2,转动惯量J 1＝2J 2时的固有频率和正则模态。
题1.19 在题1.18中，若k 1=0，02≠k 则成为2自由度退化系统，具有一个零固有频率和一个非零固有频率，求其正则模态。
讨论此系统对应的移动位移运动的弹簧质量M -K 系统的形式。
求证当使用φ=θ1-θ2为坐标时，系统可被看成单自由度系统。
题1.20 设n 自由度无阻尼系统自由运动方程为 0Kx x M =+
，设它的n 个固有频率ωi (i =1,2,…, n )互不相同，求证系统模态向量ϕi (i =1,2,…, n )对质量矩阵M 和刚度矩阵K 的正交性，即证明
⎩
⎨⎧≠==j i j i m i j
T i 0M φφ，⎩⎨⎧≠==j i j i k i j T
i 0K φφ, i , j =1, 2, 3, … , n 。
题1.21 如题1.21图，为滑块＋单摆系统，设x (t )= a sin ωt ，其中m k =ω。
求： （1）单摆的最大摆角；（2）系统的固有频率。
题1.21图
题1.22图
题1.22 如题1.22图，其中2/3km c =，m 1=m 2=m ，m 1上受阶跃力F 1，求零初始条件下系统响应。
题1.23 如题1.23图，各质量上的激励力F 1=F 2=F 3=F sin ωt ，其中ω=1.25m k /，各阶模态阻尼比为ζ1=ζ2=ζ3=0.01，求各质量的稳态响应。
题1.23图
题1.24图
题1.24 如题1.24图所示简支梁，三等分处各有质量m 1＝m 2=m ，各质量下有阻尼器，阻尼系数为C 1=C 2=300m k ,其中k 0=486EJ /l 3，EJ 为梁的抗弯刚度，l 为梁长度，设梁的质量不计。
求： （1）各阶相对阻尼系数ζ1，ζ2；（2）质量m 1上受到一单位脉冲力δ(t )作用，m 1，m 2的运动规律。
题1.25 设一等直杆在左端自由，右端固定，求它的纵向振动的表达式。
题1.26 求如题1.26图所示的阶梯杆的纵向振动的特征方程，有ρ1=ρ2=ρ。
提示：杆的连续条件是当x 1＝l 1, x 2＝0时，u 1＝u 2，EA 1
11x u ∂∂＝EA 22
2x u
∂∂。
题 1.26 图
题 1.27 图
题1.27 如题1.27图所示，长为l 的等直圆杆以等角速度ω转动。
某瞬时左端突然固定，求杆扭转振动的响应。
题1.28 一根重的柔性钢索，长度为l ，单位长度的质量为ρ，上端悬挂，在平面内作自由振动，如题1.28图所示，试推导钢索横向运动微方程，并证明可分离成两个常微分方程。
题1.28 图
题 1.29 图
题1.29 如题1.29图所示，等截面悬臂梁的自由端有一弹性支承，其刚度系数为k ，求特征方程和主振型的正交性条件。
题1.30 一等截面梁，x ＝0端自由，x ＝l 端简支，若简支端有横向运动y l (t )=Y l sin ωt ，证明简支端与
自由端的振幅比为0cos sin sin l Y sh l l ch l l Y sh l l
ββββββ-=
-,其中EJ A ρωβ24
=。
题1.31 如题1.31图所示，一根矩形截面杆一端固定一端自由，其长度为l ，厚度为b ，横截面积A 按直线规律变化：A (x )＝A 0(1+x /l )，其中A 0为自由端的截面积，试用里兹法运用模态截断的思路求杆纵向振动的第1，2阶固有频率。
设
第1，2阶振形函数为：2211)(l x x -=φ , 33
21)(l
x x -=φ。
题1.32 随机过程X [t ]的样本函数为：)sin )sin )(2211φωφω+++=t a t a t x 21((，式中a 1，a 2，ω1，
ω2是常数，φ1，φ2为统计独立的在[0，2π]上均匀分布的随机变量，求自相关函数R xx (τ)。
题1.33 某平稳随机过程的自相关函数为：162cos 25)(4+=-τπττ
f e R xx ，求其均值μx ，方差2x ε，
功率谱密度函数S xx (f )和单边谱密度函数G xx (f )。
题1.34 已知某振动系统的输入为力，输出为位移，系统位移响应的y (t )的自功率谱为：
)(4)()(2
2022
220
∞<<-∞+-=
ωωωςωωωa
S yy ，求响应y (t )的自相关函数和均方值。
题1.35 系统示意图如题1.22图，设F 1 (t )为均值为零的白噪声，其自功率谱密度函数为S FF (ω)，求稳态情况下响应的自功率谱密度函数，互功率谱密度函数及各响应的均方值。
题1.36 如题1.36图，系统由主系统（m 1，k 1）和副系统（m 2，C 2，k 2）组成，设作用在m 1上的F 1(t )为零均值白噪声，试以响应y 1(t )的均方值最小为条件确定副系统的m 2，C 2，k 2。
题1.37 设线性系统随机运动方程为
)(t W KX X C X
=++ 其中： ⎥⎦
⎤⎢⎣⎡--=5.1119C ; C K 100=。
W (t )为平稳白噪声激励向量，有 E [W (t )]=0，E [W (t )W T (t +τ)]=I δ(t )，I 为单位矩阵，用实模态分析法求响应的相关函数矩阵R XX (t )。
题1.31图
题1.36图。