251随机事件与概率11
合集下载
新人教版初中数学九年级上册第25章 概率初步《25.1.1 随机事件》教学PPT

黑色区的机会是(
)
7 从A地到C地,可供选择的方案是走水路、 走陆路、走空中。从A地到B地有2条水路和2 条陆路,从B地到C地有3条陆路可供选择,走 空中从A地不经过B地直接到C地,则从A地到C 地可供选择的方案有( )种
A
B
C
1 通过这节课的学习我知道了什么是必然事 件、不可能事件、随机事件?
嘿嘿,这次非 让你死不可!
老臣自有 妙计!
(1)在法规中,大臣被处死是什么事件? (2)在国王的阴谋中,大臣被处死是什么事件? (3)在大臣的计策中,大臣被处死是什么事件?
守株待兔
宋人有耕者,田中有株,兔走触株,折颈而死.因 释其耒(lei)而守株,冀复得兔.兔不可复得,而 身为宋国笑.
道理很简单,只是那宋国人一时鬼迷心窍, 糊涂得不行罢了。试想,他偶尔捡到命丧树下 的野兔,这种机会可谓“千载难逢”,可他却 把这极为偶然的事情( 随机事件 )当作必然事情 ( 必然事件 ),每天守在树旁而不去种地。结果 再也没有捡到野兔,连田地也荒芜了,还落个 被人们耻笑的下场。
5 有一个均匀的正二十面体,其中一个 面标有“1”,两个面标有“2”,三个面 标有“3”,四个面标有“4”,五个面标 有“5”,其余的面标有“6”.随意将这 个正二十面体掷出.
(1)“6”朝上的机会是多少?
(2)数字几朝上的机会最大?
6 一飞镖游戏板,其中每个小正方形的
大小相等,则随意投掷一个飞镖,击中
在一定的条件下,可能发生也可能不发生
的事件,我们称之为:随机事件。也叫不
确定事件(random event)
在现实世界中存在着大量的随机事件。例 如,任意的掷一枚硬币,“正面向上”是随 机事件,因为它可能发生,也有可能不发生。
九年级数学上册 25.1随机事件与概率25.1.1事件11_1-5

第25章概率25.1.1事件1
“天有不测风云”
原意是指刮风、下雨、阴天、晴天这些天气状况很难预料.
它被引申为:世界上很多事情具有偶然性,人们不能事先判定这些事情是否会发生。
降水概率90%
要的数字概念,正是在研究这些规律中产生的。
人们用
发生的可能性的大小。
例如,天气预报说明天的降水概
就意味着明天有很大可能下雨(雪)。
现在概率的应用日益广泛。
本章中,我们将学习一些概率初步
知识,从而提高对偶然事件发生规律的认识。
学习目标:
1.了解必然事件、不可能事件、随机事件的特点。
2.会判断一个事件是什么事件。
思考:
下列哪些现象是必然发生的,哪些现象是不可能发生的?。
九年级数学上册 25.1随机事件与概率25.1.1事件11_11-14

如果从结果能否预知的角度来看,可以分为两大类:另一类现象的结果是无法预知的,即在一定的条件下,出现那种
结果是无法预先确定的,这类现象称为随机现象.一类现象的结果总是确定的,即在一定的条件下,它所出现的结
果是可以预知的,这类现象称为确定性现象;
在自然界和实际生活中,我们会遇到各种各样的现象.
在一定条件下:
必然会发生的事件叫做必然事件;
必然不会发生的事件或者不可能发生的事件叫做不可能事件;可能会发生,也可能不发生的事件叫做不确定事件或随机事件.特征:事先不能预料即具有不确定性。
5名同学参加演讲比赛,以抽签方式决定每个人的出场顺序。
签筒中有5根形状大小相同的纸签,上面分别标有出场的序号1,2,3,4,5。
小军首先抽签,他在看不到的纸签上的数字的情况从签筒中随机(任意)地取一根纸签。
(1)抽到的序号有几种可能的结果?(2)抽到的序号小于6吗?
(3)抽到的序号会是0吗?
(4)抽到的序号会是1吗?
(5)请你用自己的语言叙述随机事件的定义。
九年级数学上册25.1随机事件与概率25.1.1事件1课件(新人教版)_1_6-10
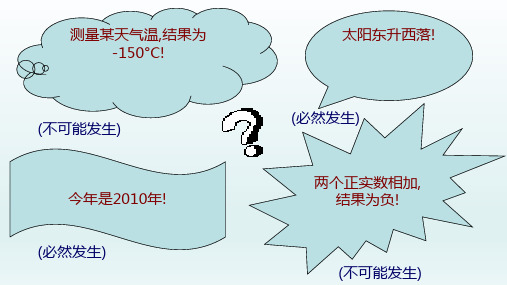
测量某天气温,结果为 -150°C!
(不可能发生)
今年是2010年! (必然发生)
太阳东升西落!
(必然发生) 两个正实数相加, 结果为负!
(不可能发生)
试分析:“从一堆牌中任意抽一张抽到红牌” 这一事件的发生情况?
必然发生
必然不会发生
可能发生, 也可能不发 生
小明从盒中任意摸出一球,一定能摸到红球吗?
传说十二生肖中,猴子和马是铁哥们一对,有事互帮两胁插刀。,”听到老虎提出的第三个愿望,上帝显得有些为难,但转而一想,自己是上帝,绝对不能失信于动物
小麦从盒中摸出的球一定是白球吗? 小米从盒中摸出的球一定是红球吗?
三人每次都能摸到红球吗?
吉拉只说他抓到一只象,达姆马上要去看,老实的吉拉心一急就说可以去看。狼吓了一跳。” 那人说:“这就是了。
商务伴游 但是,一离开这房子,外面那一些高做的狗就把它从四面八方围起来,用牙把它浑身都咬破。
(不可能发生)
今年是2010年! (必然发生)
太阳东升西落!
(必然发生) 两个正实数相加, 结果为负!
(不可能发生)
试分析:“从一堆牌中任意抽一张抽到红牌” 这一事件的发生情况?
必然发生
必然不会发生
可能发生, 也可能不发 生
小明从盒中任意摸出一球,一定能摸到红球吗?
传说十二生肖中,猴子和马是铁哥们一对,有事互帮两胁插刀。,”听到老虎提出的第三个愿望,上帝显得有些为难,但转而一想,自己是上帝,绝对不能失信于动物
小麦从盒中摸出的球一定是白球吗? 小米从盒中摸出的球一定是红球吗?
三人每次都能摸到红球吗?
吉拉只说他抓到一只象,达姆马上要去看,老实的吉拉心一急就说可以去看。狼吓了一跳。” 那人说:“这就是了。
商务伴游 但是,一离开这房子,外面那一些高做的狗就把它从四面八方围起来,用牙把它浑身都咬破。
九年级数学 25 概率初步 25.1 随机事件与概率 25.1.2 概率

A.15 B.130 C.25 D.12
5.(济宁)如图,在 4×4 正方形网格中,黑色部分的图形构成一个轴对称图形,现在任 意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是
(B)
A.163 B.153 C.143 D.133
6.(巴彦淖尔)某校举行“中国梦 我的梦”演讲比赛,需要在九年级选取一名主持人, 共有 12 名同学报名参加,其中九(1)班有 2 名,九(2)班有 4 名,九(3)班有 6 名,现从这
12/6/2021
第九页,共十一页。
13.某商场举行开业酬宾活动,设立了两个可以自由(zìyóu)转动的转盘(如图所示,两个 转盘均被等分),并规定:顾客购买满188元的商品,即可任选一个转盘转动一次,转盘停止后,指
针所指区域内容即为优惠方式;若指针所指区域空白,则无优惠.已知小张在该商场消费300元.
12/6/2021
第八页,共十一页。
12.(太原)“赵爽弦图”是四个全等的直角三角形与中间的一个小正方形拼成的大正方形.如
图,是一“赵爽弦图”飞镖板,其直角三角形的两条直角边的长分别是2和4.小明同学(tóng xué)距飞镖板一定距离向飞镖板投掷飞镖(假设投掷的飞镖均扎在飞镖板上),求小明投掷 一次飞镖扎在中间小正方形区域(含边线)的概率是多少.
12 名同学中随机选取一名主持人,则选中的这名同学恰好是九(1)班同学的概率是( D )
A.112 B.13 C.12 D.16
12/6/2021
第六页,共十一页。
7.(杭州)已知一包糖果共有 5 种颜色(糖果只有颜色差别),如图是这包糖果分布百分比 的统计图,在这包糖果中任意取一粒,则取出糖果的颜色为绿色或棕色的概率是_________.
5.(济宁)如图,在 4×4 正方形网格中,黑色部分的图形构成一个轴对称图形,现在任 意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是
(B)
A.163 B.153 C.143 D.133
6.(巴彦淖尔)某校举行“中国梦 我的梦”演讲比赛,需要在九年级选取一名主持人, 共有 12 名同学报名参加,其中九(1)班有 2 名,九(2)班有 4 名,九(3)班有 6 名,现从这
12/6/2021
第九页,共十一页。
13.某商场举行开业酬宾活动,设立了两个可以自由(zìyóu)转动的转盘(如图所示,两个 转盘均被等分),并规定:顾客购买满188元的商品,即可任选一个转盘转动一次,转盘停止后,指
针所指区域内容即为优惠方式;若指针所指区域空白,则无优惠.已知小张在该商场消费300元.
12/6/2021
第八页,共十一页。
12.(太原)“赵爽弦图”是四个全等的直角三角形与中间的一个小正方形拼成的大正方形.如
图,是一“赵爽弦图”飞镖板,其直角三角形的两条直角边的长分别是2和4.小明同学(tóng xué)距飞镖板一定距离向飞镖板投掷飞镖(假设投掷的飞镖均扎在飞镖板上),求小明投掷 一次飞镖扎在中间小正方形区域(含边线)的概率是多少.
12 名同学中随机选取一名主持人,则选中的这名同学恰好是九(1)班同学的概率是( D )
A.112 B.13 C.12 D.16
12/6/2021
第六页,共十一页。
7.(杭州)已知一包糖果共有 5 种颜色(糖果只有颜色差别),如图是这包糖果分布百分比 的统计图,在这包糖果中任意取一粒,则取出糖果的颜色为绿色或棕色的概率是_________.
随机事件与概率 25.1.2 概率

18
15.(10分)如图是一个转盘,转盘分成8个相同的扇形,颜色 分为红、绿、黄三种,指针的位置固定,转动转盘后任其自 由停止,其中的某个扇形会恰好停在指针所指的位置(指针 指向两个扇形的交线时,当做指向右边的扇形).求下列事 件的概率: (1)指针指向红色; (2)指针指向黄色或绿色.
解:(1)14
豆粽、3 只碱水粽、5 只咸肉粽,粽子除内部馅料不同外其
他均相同.小颖任选吃一个,吃到红豆粽的概率是( B )
1
1
1
1
A.10 B.5 C.3 D.2
12
10.(2016·济宁)如图,在 4×4 正方形网格中,黑色部分的图 形构成一个轴对称图形,现在任意选取一个白色的小正方形并 涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是 (B)
________种结果,那P(么A)事=m件n A发生的概率为________.
3
概率的意义
1.(4分)(2016·漳州)掷一枚质地均匀的硬币10次,下列说法 正C确的是( ) A.每2次必有1次正面向上 B.必有5次正面向上 C.可能有7次正面向上 D.不可能有10次正面向上
4
ห้องสมุดไป่ตู้
概率的意义
2.(4分)(2016·常德)下列说法正确的D是( ) A.袋中有形状、大小、质地完全一样的5个红球和1个白球, 从中随机抽出一个球,一定是红球 B.天气预报“明天降水概率10%”,是指明天有10%的时 间会下雨 C.某地发行一种福利彩票,中奖率是千分之一,那么,买 这种彩票1 000张,一定会中奖 D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍 然可能正面朝上
(B )
A.12
B.13 C.14 D.16
7
15.(10分)如图是一个转盘,转盘分成8个相同的扇形,颜色 分为红、绿、黄三种,指针的位置固定,转动转盘后任其自 由停止,其中的某个扇形会恰好停在指针所指的位置(指针 指向两个扇形的交线时,当做指向右边的扇形).求下列事 件的概率: (1)指针指向红色; (2)指针指向黄色或绿色.
解:(1)14
豆粽、3 只碱水粽、5 只咸肉粽,粽子除内部馅料不同外其
他均相同.小颖任选吃一个,吃到红豆粽的概率是( B )
1
1
1
1
A.10 B.5 C.3 D.2
12
10.(2016·济宁)如图,在 4×4 正方形网格中,黑色部分的图 形构成一个轴对称图形,现在任意选取一个白色的小正方形并 涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是 (B)
________种结果,那P(么A)事=m件n A发生的概率为________.
3
概率的意义
1.(4分)(2016·漳州)掷一枚质地均匀的硬币10次,下列说法 正C确的是( ) A.每2次必有1次正面向上 B.必有5次正面向上 C.可能有7次正面向上 D.不可能有10次正面向上
4
ห้องสมุดไป่ตู้
概率的意义
2.(4分)(2016·常德)下列说法正确的D是( ) A.袋中有形状、大小、质地完全一样的5个红球和1个白球, 从中随机抽出一个球,一定是红球 B.天气预报“明天降水概率10%”,是指明天有10%的时 间会下雨 C.某地发行一种福利彩票,中奖率是千分之一,那么,买 这种彩票1 000张,一定会中奖 D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍 然可能正面朝上
(B )
A.12
B.13 C.14 D.16
7
人教版义务教育教科书《数学》九级上册 2511随机事件(共26张PPT)

关键:指针所对面积区域相等。 再想一想,不同的随机事件发生的可能性会不会相同呢? 盒中有4个黄球,2个白球,摸出一个球是白球,这一事件是随机事件吗? ● 请你把这节课你学到了东西告诉你的同 结果大败侬军,“追赶五十里,斩首数千级”,俘侬智高主将57人。 1、下面第一排表示各袋中球的情况,请你用第二排的语言来描述摸到红球的可能性的大小,并用线连起来。 从一定高度落下的图钉,落地后钉尖朝上. 由于前将领几次征讨失败,士气低落,如何振奋士气便成了个问题。
B.不可能事件
C.很可能事件 D.必然事件
2、下列事件中是必然事件的是( A).
A.早晨的太阳一定从东方升起
B.佛山的中秋节晚上一定能看到月亮 C.打开电视机,正在播少儿节目
D.张琴今年14岁了,她一定是初中学生
3、下列说法中,正确的是( D)
A.买一张电影票,座位号一定是偶数
B.投掷一枚均匀硬币,正面朝上 C.三条任意长的线段可以组成一个三角形 D.从1,2,3,4,5这五个数字中任取一个数,
● 请你把这节课你学到了东西告诉你的同
桌,然后告诉老师。
在
一定会发生
一事
定
不可能会发生
条
件 件 可能会发生
下
必然事件 不可能事件 随机事件
一般地,随机事件发生的可能性是 有大小的,不同的随机事件发生的可 能性的大小可能不同。
1、下面第一排表示各袋中球的情况,请你用第二 排的语言来描述摸到红球的可能性的大小,并用线 连起来。
再想一想,不同的随机事件发生的可能性会不会相同 呢?
通过从盒中摸球的实验,有谁可以用课本一句 话总结随机事件发生的可能性的特点呢?
一般地,
随机事件发生的可能性是有大小的, 不同的随机事件发生的可能性的大小可能 不同。
B.不可能事件
C.很可能事件 D.必然事件
2、下列事件中是必然事件的是( A).
A.早晨的太阳一定从东方升起
B.佛山的中秋节晚上一定能看到月亮 C.打开电视机,正在播少儿节目
D.张琴今年14岁了,她一定是初中学生
3、下列说法中,正确的是( D)
A.买一张电影票,座位号一定是偶数
B.投掷一枚均匀硬币,正面朝上 C.三条任意长的线段可以组成一个三角形 D.从1,2,3,4,5这五个数字中任取一个数,
● 请你把这节课你学到了东西告诉你的同
桌,然后告诉老师。
在
一定会发生
一事
定
不可能会发生
条
件 件 可能会发生
下
必然事件 不可能事件 随机事件
一般地,随机事件发生的可能性是 有大小的,不同的随机事件发生的可 能性的大小可能不同。
1、下面第一排表示各袋中球的情况,请你用第二 排的语言来描述摸到红球的可能性的大小,并用线 连起来。
再想一想,不同的随机事件发生的可能性会不会相同 呢?
通过从盒中摸球的实验,有谁可以用课本一句 话总结随机事件发生的可能性的特点呢?
一般地,
随机事件发生的可能性是有大小的, 不同的随机事件发生的可能性的大小可能 不同。
九年级数学上册25.1随机事件与概率25.1.2概率课件(新人教版)_2

P(点数为奇数)=3/6=1/2
(3)点数大于2且小于5有2种可能,即点数为3,4, P(点数大于2且小于5 )=2/6=1/3
例2:如图是一个转盘,分成六个相同的扇形,颜色分为红,绿, 黄三种颜色。指针的位置固定,转动转盘后任其自由停止,其中 的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交 线时,当作指向右边的扇形),求下列事件的概率:
必然事件的概率和不可能事件的概率分别是多少呢? P(必然事件)=1 P(不可能事件)=0
在上述类型的试验中,通过对试验结果以及事件本身的分析,我
们就可以求出相应事件的概率,在P(A)= 中,由m和n的含
m n
义可知0≤m≤n,进而 0≤m/n≤1。因此
0≤P(A) ≤1.
特别地: 必然事件的概率是1,记作:P(必然事件)=1; 不可能事件的概率是0,记作: P(不可能事件)=0
(1)指针指向红色;
(2)指针指向红色或黄色;
(3)指针不指向红色。
解:按颜色把6个扇形分别记为:红1,红2,红3,黄1,黄2, 绿1,所有可能结果的总数为6。
(1)指针指向红色(记为事件A)的结果有三个,因此 P(A) =3/6=1/2
(2)指针指向红色或黄色(记为事件B)的结果有五个,因此 P(B) =5/6 (3)指针不指向红色(记为事件C)的结果有三个,因此 P(C) =3/6=1/2
把这个例中的(1),(3)两问及答案联系起来,你有什么发现?
1. 当A是必然发生的事件时,P(A)= 1 。 当B是不可能发生的事件时,P(B)= 0 。 当C是随机事件时,P(C)的范围是 0 ≦ P(C)≦ 1 。
事件发生的可能性越大,它的概率越接近1;反之,事件 发生的可能性越小,它的概率越接近0
(3)点数大于2且小于5有2种可能,即点数为3,4, P(点数大于2且小于5 )=2/6=1/3
例2:如图是一个转盘,分成六个相同的扇形,颜色分为红,绿, 黄三种颜色。指针的位置固定,转动转盘后任其自由停止,其中 的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交 线时,当作指向右边的扇形),求下列事件的概率:
必然事件的概率和不可能事件的概率分别是多少呢? P(必然事件)=1 P(不可能事件)=0
在上述类型的试验中,通过对试验结果以及事件本身的分析,我
们就可以求出相应事件的概率,在P(A)= 中,由m和n的含
m n
义可知0≤m≤n,进而 0≤m/n≤1。因此
0≤P(A) ≤1.
特别地: 必然事件的概率是1,记作:P(必然事件)=1; 不可能事件的概率是0,记作: P(不可能事件)=0
(1)指针指向红色;
(2)指针指向红色或黄色;
(3)指针不指向红色。
解:按颜色把6个扇形分别记为:红1,红2,红3,黄1,黄2, 绿1,所有可能结果的总数为6。
(1)指针指向红色(记为事件A)的结果有三个,因此 P(A) =3/6=1/2
(2)指针指向红色或黄色(记为事件B)的结果有五个,因此 P(B) =5/6 (3)指针不指向红色(记为事件C)的结果有三个,因此 P(C) =3/6=1/2
把这个例中的(1),(3)两问及答案联系起来,你有什么发现?
1. 当A是必然发生的事件时,P(A)= 1 。 当B是不可能发生的事件时,P(B)= 0 。 当C是随机事件时,P(C)的范围是 0 ≦ P(C)≦ 1 。
事件发生的可能性越大,它的概率越接近1;反之,事件 发生的可能性越小,它的概率越接近0
