二项式分布列与数学期望
北京市海淀区2023-2024学年高二下学期期末数学试卷(含答案)

北京市海淀区2023-2024学年高二下学期期末考试数学试卷本试卷共6页,共两部分。
19道题,共100分。
考试时长90分钟。
试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
考试结束后,请将答题卡交回。
第一部分(选择题共40分)一、选择题共10小题,每小题4分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.5(1)x -的展开式中,所有二项式的系数和为A.0B.52C.1D.622.已知函数sin (),cos xf x x=则(0)f '的值为A.0B.1C.1- D.π3.若等比数列{}n a 的前n 项和21n n S =-,则公比q =A.12B.12-C.2D.2-4.下列函数中,在区间[]1,0-上的平均变化率最大的时A.2y x = B.3y x = C.12xy ⎛⎫= ⎪⎝⎭D.2xy =5.将分别写有2,0,2,4的四章卡片,按一定次序排成一行组成一个四位数(首位不为0),则组成的不同四位数的个数为A.9B.12C.18D.246.小明投篮3次,每次投中的概率为0.8,且每次投篮互不影响,若投中一次的2分,没投中得0分,总得分为X ,则A.() 2.4E X = B.() 4.8E X = C.()0.48D X = D.()0.96D X =7.已知一批产品中,A 项指标合格的比例为80%,B 项指标合格的比例为90%,A 、B 两项指标都合格的比例为60%,从这批产品中随机抽取一个产品,若A 项指标合格,则该产品的B 项指标也合格的概率是A.37B.23C.34D.568.已知等差数列n a 的前n 项和为n S ,若10a <、则“n S 有最大值”是“公差0d <”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件9.设函数()()ln 1sin f x x a x =-+.若()()0f x f ≤在()1,1-上恒成立,则A.0a =B.1a ≥C.01a <≤ D.1a =10.在经济学中,将产品销量为x 件时的总收益称为收益函数,记为()R x ,相应地把()R x '称为边际收益函数,它可以帮助企业决定最优的生产或销售水平.假设一个企业的边际收益函数()1000R x x '=-(注:经济学中涉及的函数有时是离散型函数,但仍将其看成连续函数来分析).给出下列三个结论:①当销量为1000件时,总收益最大;②若销量为800件时,总收益为T ,则当销量增加400件时,总收益仍为T ;③当销量从500件增加到501件时,总收益改变量的近似值为500.其中正确结论的个数为A.0B.1C.2D.3第二部分(非选择题共60分)二、填空题共5小题,每小题4分,共20分。
贵州省遵义市凤冈二中2024届高三下学期第一次模拟考试(数学试题理)试题

贵州省遵义市凤冈二中2024届高三下学期第一次模拟考试(数学试题理)试题考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。
选择题必须用2B 铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知向量0,2a ,()23,b x =,且a 与b 的夹角为3π,则x =( )A .-2B .2C .1D .-12.已知盒中有3个红球,3个黄球,3个白球,且每种颜色的三个球均按A ,B ,C 编号,现从中摸出3个球(除颜色与编号外球没有区别),则恰好不同时包含字母A ,B ,C 的概率为( ) A .1721B .1928C .79D .23283.做抛掷一枚骰子的试验,当出现1点或2点时,就说这次试验成功,假设骰子是质地均匀的.则在3次这样的试验中成功次数X 的期望为( ) A .B .C .1D .24.已知函数()2ln 2,03,02x x x x f x x x x ->⎧⎪=⎨+≤⎪⎩的图像上有且仅有四个不同的点关于直线1y =-的对称点在 1y kx =-的图像上,则实数k 的取值范围是( ) A .1,12⎛⎫⎪⎝⎭B .13,24⎛⎫ ⎪⎝⎭C .1,13⎛⎫ ⎪⎝⎭D .1,22⎛⎫ ⎪⎝⎭5.函数2()1cos 1xf x x e ⎛⎫=-⎪+⎝⎭图象的大致形状是( ) A . B .C .D .6.中国古代用算筹来进行记数,算筹的摆放形式有纵横两种形式(如图所示),表示一个多位数时,像阿拉伯记数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,其中个位、百位、方位……用纵式表示,十位、千位、十万位……用横式表示,则56846可用算筹表示为( )A .B .C .D .7.已知集合{}2230A x x x =--≤{}2B x x =<,则A B =( )A .()1,3B .(]1,3C .[)1,2-D .()1,2-8.35(1)(2)x y --的展开式中,满足2m n +=的m nx y 的系数之和为( )A .640B .416C .406D .236-9.一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积为( )A 3B .36C .33D .23310.将函数()sin 2f x x =的图象向左平移02πϕϕ⎛⎫≤≤ ⎪⎝⎭个单位长度,得到的函数为偶函数,则ϕ的值为( ) A .12π B .6π C .3π D .4π11.已知(),A A A x y 是圆心为坐标原点O ,半径为1的圆上的任意一点,将射线OA 绕点O 逆时针旋转23π到OB 交圆于点(),B B B x y ,则2AB yy +的最大值为( )A .3B .2C .3D .512.我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,用现代式子表示即为:在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,则ABC ∆的面积222221()42a b c S ab ⎡⎤⎛⎫+-⎢⎥=- ⎪⎢⎥⎝⎭⎣⎦.根据此公式,若()cos 3cos 0a B b c A ++=,且2222a b c --=,则ABC ∆的面积为( )A .2B .22C .6D .23二、填空题:本题共4小题,每小题5分,共20分。
【高考数学】利用二项式分布思想高考数学“秒杀”概率中的数学期望

二项分布:在 n 次独立重复试验中,用 X 表示事件 A 发生的次数,设每次试验中事件 A 发生的
概率为 p,则称随机变量 X 服从二项分布.记为: X ~ B(n, p) .
很明显,二项分布需满足的条件为:独立性、重复性、试验的结果只有两个.
反观上题,我们再细细的分析一下:若记“担任领导岗位的男员工人数”为 ,相当于在领导岗
终的期望仍可以将三个两点分布的期望相加得到,即:EX
1
1
2
(三个两点分布的期望之和).
223
通过上述两种解法的对比,我们可以进一步深入理解二项分布的概念,从而达到了一个新的层次.
问题启示:上述两则案例告诉我们,二项分布的期望等价于若干个两点分布的期望之和,或者等
价于若干个二项分布的期望之和,故我们可以将类似于上述案例中求期望的方法延伸到一般化,即:
球.现从甲、乙两个盒内各任取 2 个球.假设每个球被取到的可能性相同,设 为取出的 4 个球中红球
的个数,则 E =______
参考解析: (一)、常规解法:
0
1
2
3
1
4
13
1
P
10
10
30
15
E 22 15
(二)、按“秒杀”思路分析:
记“从甲盒中取出红球的个数”为 1 ,“从乙盒中取出红球的个数”为 2
E(X1 X2 ... Xn ) E(X1) E(X2) ... E(Xn ) ;
注:其中 X 1、X 2 ...X n 都服从于两点分布或服从于二项分布.
读者不妨再用两种解法做一下练习 2. 练习 2:已知甲盒内有大小相同的 2 个红球和 3 个黑球,乙盒内有大小相同的 1 个红球和 2 个黑
北师大版高中数学选择性必修第一册 第六章 4.1 二项分布
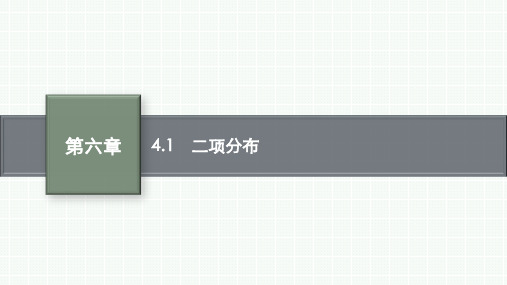
变式训练3某种种子每粒发芽的概率为0.9,现播种了1 000粒,对于没有发芽
的种子,每坑需再补种2粒,每个坑至多补种一次,补种的种子数记为X,则X
的数学期望为(
)
A.100 B.200 C.300 D.400
答案 B
解析 由题意可设,不发芽的种子数为Y,Y服从二项分布,即Y~B(1 000,0.1),所
Dξ=10×
课堂篇 探究学习
探究一
n重伯努利试验的概率
例1(1)某射手射击一次,击中目标的概率是0.9,他连续射击三次,且他每次
射击相互之间没有影响,有下列结论:
①他三次都击中目标的概率是0.93;
②他恰好在第三次击中目标的概率是0.9;
③他恰好2次击中目标的概率是2×0.92×0.1;
④他恰好2次未击中目标的概率是3×0.9×0.12.
∴P(AB+)=P(A)P(B)+P()P()
1 1
1
1 1
=2 × 2+(1-2)×(1-2)=2.
1 4-k
1
1 k
(2)随机变量 ξ 的可能取值为 0,1,2,3,4,且 ξ~B(4,2).∴P(ξ=k)=C4 (2) (1-2)
1 4
=C4 (2) (k=0,1,2,3,4).
k=0,1,2,3,4,
25
P(η=5)=P(5 个均为绿灯)=(3) .
故η的分布列为
η
0
1
2
3
4
5
P
1
3
2
9
4
27
8
81
16
243
32
243
反思感悟 1.本例属于二项分布,当X服从二项分布时,应弄清X~B(n,p)中的
2021-2022学年重庆市名校联盟高二下学期5月联考数学试题(解析版)

2021-2022学年重庆市名校联盟高二下学期5月联考数学试题一、单选题1.已知两个正态密度函数()()()2221,1,22πx i i i i x e x i μσϕσ--=∈=R 的图象如图所示,则( )A .12μμ<,12σσ<B .12μμ>,12σσ<C .12μμ<,12σσ>D .12μμ>,12σσ>【答案】A【分析】正态曲线关于直线x μ=对称,且μ越大图象越靠右,所以1ϕ图象的均值比2ϕ图象的均值小,又由σ越小图象越“瘦高”,得到正确的结果. 【详解】正态曲线关于直线x μ=对称,且在x μ=2πσ 由题图易得12μμ<,因为()1x ϕ的图象更“瘦高”,()2x ϕ的图象更“矮胖”,则12σσ<. 故选:A.2.甲、乙、丙、丁四位同学各自对,x y 两变量的线性相关性做试验,分别求得样本相关系数r ,如下表:甲 乙 丙 丁r0.20 0.95- 0.12- 0.85则试验结果中,x y 两变量有更强线性相关性的是( )A .甲 B .乙C .丙D .丁【答案】B【分析】由相关系数的绝对值的大小判断.【详解】由已知,乙的相关系数的绝对值为0.95r =,是四人中最大的,因此乙同学有更强的相关性. 故选:B .3.6(12)x +的展开式中2x 的系数为( ) A .15 B .60 C .120 D .240【答案】B【分析】根据二项展开式通项公式计算.【详解】()166C 2C 2rr rr r r T x x +==⨯, 所以2x 的系数是226C 260⨯=.故选:B .4.从5名男同学和4名女同学中任选2名同学,在选到的都是同性别同学的条件下,都是男同学的概率是( ) A .13B .514C .1013 D .58【答案】D【分析】根据已知条件及古典概型公式,结合条件概率的计算公式即可求解. 【详解】设“任选2名同学,都是男同学”的事件为A , 设“任选2名同学,都是同性别同学”的事件为B ,所以()2529C 10C 45P AB ==,()225429C C 16C 45P B +==, 所以在选到的都是同性别同学的条件下,都是男同学的概率为()()()1054516845P AB P A B P B ===.故选:D.5.下表是某饮料专卖店一天卖出奶茶的杯数y 与当天气温x (单位:C )的对比表,已知表中数据计算得到y 关于x 的线性回归方程为ˆˆ27ybx =+,则据此模型预计35C 时卖出奶茶的杯数为( ) CA .4B .5C .6D .7【答案】C【分析】先求得ˆb的值,再据此模型计算出35C 时卖出奶茶的杯数. 【详解】由题可知1(510152025)155x =++++=,1(2620161414)185y =++++=,由ˆ181527b=+,可得3ˆ5b =-, 则3ˆ352765y=-⨯+= 则据此模型预计35C 时卖出奶茶的杯数为6. 故选:C6.函数()33f x x x =-在区间()m,2上有最小值,则m 的取值范围是( )A .()2,1-B .[)2,1-C .()2,1--D .(]1,1-【答案】B【分析】根据f (x )的导数求f (x )的单调性和极值,作出f (x )简图,数形结合即可求m 的范围.【详解】()()()233311f x x x x ==+'--,易知()f x 在(),1-∞-,()1,+∞单调递增,在()1,1-单调递减, 又()22f -=-,()12f -=,12f ,()2f x =,故f (x )图像如图:函数()33f x x x =-在区间()m,2上有最小值,则由图可知21m -≤<.故选:B.7.由1,2,3,4,5组成的没有重复数字的五位数,从中任意抽取一个,则其恰好为“前3个数字保持递减,后3个数字保持递增”(如五位数“43125”,前3个数字“431”保持递减,后3个数字“125”保持递增)的概率是( ) A .120B .112C .110 D .16【答案】A【分析】首先根据已知条件“定位”中间数字,其次在剩余的四个数字中任取两个数字,放置在首或末位,则其余数字排列方式唯一确定.最后由古典概型计算公式即可得解【详解】由1,2,3,4,5组成的没有重复数字的五位数共55A 120=个,前3个数字保持递减,后3个数字保持递增,说明中间数字为1;在剩余的四个数字中任取两个数字,按照递减顺序,仅有一种排列方式放置在首两位(或末两位),则剩余两位数字排列方式唯一确定,放置在最后两位(或首两位).24C ?16=因此“前3个数字保持递减,后3个数字保持递增”的五位数有24C 6=个,所以所求的概率6112020P ==. 故选:A .8.已知()()21ln f x x a x =-+在1,4⎛⎫+∞ ⎪⎝⎭上恰有两个极值点1x ,2x ,且12x x <,则()12f x x 的取值范围为( ) A .13,ln 22⎛⎫-- ⎪⎝⎭B .1ln 2,12⎛⎫- ⎪⎝⎭C .1,ln 22⎛⎫-∞- ⎪⎝⎭D .13ln 2,ln 224⎛⎫-- ⎪⎝⎭【答案】D【分析】由题意得导函数在区间1,4⎛⎫+∞ ⎪⎝⎭有两个零点,根据二次函数的性质可得3182a <<,由根与系数的关系可得121212x x a x x +=⎧⎪⎨=⎪⎩以及21324x <<,求出()12f x x 的表达式,将1x 用2x 表示,表示为关于2x 的函数,利用导数与单调性的关系即可求出结果.【详解】由题意得()()222220a x x af x x x x x-+'=-+=>,令()0f x '=,得2220x x a -+=,由题意知2220x x a -+=在1,4⎛⎫+∞ ⎪⎝⎭上有两个根1x ,2x ,∴20,1122044480a a a >⎧⎪⎪⎛⎫⨯-⨯+>⎨ ⎪⎝⎭⎪⎪∆=->⎩,得3182a <<.由根与系数的关系得121212x x a x x +=⎧⎪⎨=⎪⎩,由求根公式得1,2x ==, ∵12x x <,∴2x =,∵3182a <<,∴21324x <<.则()()()()2211121212222221ln 2ln 21ln 1f x x a x x x x x x x x x x x -++===+--()()222213121ln 1124x x x x ⎛⎫=-+--+<< ⎪⎝⎭,令21t x =-,则1142t <<. 设()112ln 142g t t t t t ⎛⎫=-++<< ⎪⎝⎭,则()12ln g t t '=+,易知()g t '在11,42⎛⎫⎪⎝⎭上单调递增,∴()12ln 12ln 2ln 04eg t t '=+<-=<,∴当1142t <<时,函数()g t 为减函数, ∴()11132ln 1ln 24444g t <-+⨯+=-,且()11112ln ln 1ln 22222g t >-+⨯+=-,∴()1213ln 2,ln 224f x x ⎛⎫∈-- ⎪⎝⎭, 故选:D .【点睛】关键点点睛:(1)根据极值点的概念,结合根据系数的关系和二次函数的性质得到参数a 的取值范围,以及1x 与2x 之间的关系;(2)将题意转化为关于2x 的函数,构造出21t x =-,利用导数判断单调性.二、多选题9.已知随机变量,X Y 满足8X Y +=,若()10,0.6X B ,则下列选项正确的有( )A .()6E x =B .()6E Y =C .() 2.4=D XD .() 2.4D Y =【答案】ACD【分析】根据已知条件及二项分布的期望与方差公式,结合期望与方差的线性公式即可求解.【详解】因为()10,0.6XB ,所以()100.66E x =⨯=,故A 正确;所以()()100.610.6 2.4D X =⨯⨯-=,故C 正确; 又因为8X Y +=,所以8Y X =-,所以()()()88862E Y E X E X =-=-=-=,故B 不正确; 所以()()()()2811 2.4 2.4D Y D X D X =-=-=⨯=,故D 正确. 故选:ACD.10.已知(2)n a b +的展开式中第6项的二项式系数最大,则n 的值可以为( ) A .8 B .9 C .10 D .11【答案】BCD【分析】利用二次项系数的性质即可求解.【详解】因为(2)n a b +的展开式中第6项的二项式系数5C n 最大,则n 的值可以为9或10或11.当9n =时,(2)n a b +的展开式共有10项,其中第5项与第6项的二项式系数相等且最大,满足题意,当10n =时,(2)n a b +的展开式共有11项,只有第6项的二项式系数最大,满足题意, 当11n =时,(2)n a b +的展开式共有12项,其中第6项与第7项的二项式系数相等且最大,满足题意, 故选:BCD.11.从7名男生和5名女生中选4人参加夏令营,规定男、女生至少各有1人参加,则不同的选法种数应为( ) A .1127510C C C B .312213757575C C C C C C ++ C .4441275C C C -- D .()112112756464C C C C C C ++【答案】BC【分析】可以用两种方法求解:①分三类:3男1女,2男2女,1男3女;②用任选4人的方法数减去全部为男生或全部为女生的方法种数.据此几何判断求解.【详解】(1)分三类:3男1女,2男2女,1男3女,∴男、女生至少各有1人参加的选法种数为312213757575C C C C C C ++.(2)任选4人的方法种数为412C ,其中全部为男生或全部为女生的方法种数为4475C C +,所以男、女生至少各有1人参加的选法种数为4441275C C C --. 故选:BC .12.记()f x 的导函数为()f x ',若()()()2f x xf x f x x '<<-对任意的正数都成立,则下列不等式中成立的有( ) A .()1122f f ⎛⎫< ⎪⎝⎭B .()()1122f f < C .()11412f f ⎛⎫<- ⎪⎝⎭D .()()111242f f <+ 【答案】BC【分析】对于AB ,构造函数()()f x F x x=,求导,借助单调性比较大小即可;对于CD ,构造函数()2()=f x xh x x -,求导,借助单调性比较大小即可. 【详解】解:因为()()f x f x x <',所以()()0f x x f x '->,则()()()()2=0f x f x x f x F x x x ''-⎡⎤'=>⎢⎥⎣⎦,所以()()f x F x x =在()0,x ∈+∞单调递增,所以()112F F ⎛⎫> ⎪⎝⎭,即()112112f f ⎛⎫⎪⎝⎭>,所以()1122f f⎛⎫> ⎪⎝⎭,故A 错误;同理()()21F F >,即()()2121f f >,所以()()1122f f <,故B 正确;因为()()2xf x f x x '<-,所以()()20xf x f x x '-+<,构造函数()2()=f x xh x x -,则()()()232()==0f x x xf x f x xh x x x ''--+⎡⎤'<⎢⎥⎣⎦,所以()2()=f x x h x x -在()0,x ∈+∞单调递减,所以1(1)()2h h <,即()111f -112214f ⎛⎫-⎪⎝⎭<,化简得()11412f f ⎛⎫<- ⎪⎝⎭,故C 正确;同理(2)(1)h h <,即()224f -()111f -<,化简得()()111242f f >+,故D 错误.故选:BC.三、填空题13.已知2()1f x x =-,则12f ⎛⎫'= ⎪⎝⎭__________.【答案】1【分析】求出导函数,直接代入.【详解】因为2()1f x x =-,所以()2f x x '=,所以12f ⎛⎫'= ⎪⎝⎭1.故答案为:114.已知随机变量X 服从正态分布()2,N μσ,若()260.6P X <<=,()60.2P X ≥=,则μ=______. 【答案】4【分析】先求出()2P X ≤的概率,然后根据正态分布的特征求解即可. 【详解】解:由题意得:∵()()()()2162610.60.20.26P X P X P X P X ≤=-≥-<<=--==≥ ∴2与6关于x μ=对称 ∴4μ=. 故答案为:415.若方程:12348x x x x +++=,则方程的正整数解的个数为___________. 【答案】35【分析】将问题转化为将8个相同的小球装入4个不同的盒子中,每个盒子中至少有1个小球,采用隔板法求解即可.【详解】解:原问题相当于将8个相同的小球装入4个不同的盒子中,每个盒子中至少有1个小球,采用隔板法,将8个小球排成一排,在其中的7个空位上插入3个隔板即可,故共有37765C 35321⨯⨯==⨯⨯种.故答案为:35.16.已知函数()ln f x x m =-与()273g x x x =-+的图象在区间[]1,3上存在关于x 轴对称的点,则m 的取值范围为___________. 【答案】35ln32,ln 24⎡⎤-+⎢⎥⎣⎦【分析】()f x 与()g x 的图象在区间[]1,3上存在关于x 轴对称的点,即方程()()0f x g x -=在区间[]1,3内有解,即方程27ln 3m x x x =-+在区间[]1,3有解,所以构造函数()[]27ln 1,3,3h x x x x x =-+∈,利用导数的知识点求出()h x 的值域即可求出答案【详解】函数()ln f x x m =-与()273g x x x =-+的图象在区间[]1,3上存在关于x 轴对称的点,即方程27ln 03x x x m -+-=在区间[]1,3内有解, 所以方程27ln 3m x x x =-+在区间[]1,3有解. 令()[]27ln 1,3,3h x x x x x =-+∈, 所以()()()23123176732333x x x x h x x x x x+--++'=-+==-令()0h x '=,解得13x =-或32x =所以当[]1,3x ∈时,()h x ',()h x 随x 的变化情况如下表:由上表可知()413h =,()43ln 323h =-<,又335ln 224h ⎛⎫=+ ⎪⎝⎭,所以当[]1,3x ∈时,()h x ∈35ln 32,ln 24⎡⎤-+⎢⎥⎣⎦,故m 的取值范围是35ln 32,ln 24⎡⎤-+⎢⎥⎣⎦.故答案为:35ln32,ln 24⎡⎤-+⎢⎥⎣⎦四、解答题17.(1)若282828x x C C -=,求x 的值;(2)求3334510C C C +++的值.【答案】(1)8或12;(2)329.【分析】(1)根据组合数的定义及组合数的性质1即可求解; (2)根据组合数的定义及组合数的性质2即可求解;【详解】(1)由282828x x C C -=,得282828N 28x x x x x +⎧⎪⎪⎨≤-≤∈-=⎪⎪⎩或282828N 2828x x x x x +≤-≤∈-=-⎧⎪⎪⎨⎪⎪⎩,解得8x =或12x =;实数x 的值为8或12.(2)由组合数的性质知,333333451045410444C C C C C C C C =++++++-+44344446643413355101140C C C C C C C 329C C C =-=++-=-+++=+.所以3334510C C C +++的值为329.18.袋中有6个白球、3个黑球,从中随机地连续抽取2次,每次取1个球. (1)若每次抽取后都放回,设取到黑球的次数为X ,求X 的分布列和期望; (2)若每次抽取后都不放回,设取到黑球的个数为Y ,求Y 的分布列和期望. 【答案】(1)分布列答案见解析,数学期望:23(2)分布列答案见解析,数学期望:23【分析】(1)根据题意X 满足二项分布,建立二项分布模型,得到X 的可能取值,利用二项分布计算概率,列出分布列即可;(2)根据题意可得Y 满足超几何分布,得出Y 的可能取值,分别计算其概率,列出分布列即可求得.【详解】(1)由题意,每次抽取后都放回,取得黑球的次数X 的可能取值为0,1,2, 其中每次抽取到黑球的概率均为13,所以2次取球可以看成2次的独立重复试验,则12,3X B ⎛⎫~ ⎪⎝⎭,可得:()02021140C 1339P X ⎛⎫⎛⎫==⨯-= ⎪⎪⎝⎭⎝⎭, ()121141C 1339P X ⎛⎫==⨯⨯-= ⎪⎝⎭, ()2221112C 1339P X ⎛⎫⎛⎫==⨯-= ⎪⎪⎝⎭⎝⎭, 所以随机变量X 的分布列为:23E X; (2)若每次抽取后都不放回,取到黑球的个数Y 的可能取值为0,1,2,可得()()()21126633222999C C C C 5110,1,2C 12C 2C 12P Y P Y P Y =========,所以随机变量Y 的分别列为:()152********12E Y =⨯+⨯+⨯=. 19.已知函数()31443f x x x =-+.(1)求函数()f x 的单调区间;(2)若直线y a =与()f x 的图像有三个不同的交点,求实数a 的范围. 【答案】(1)增区间:((),2),2,∞∞--+;减区间:(2,2)- (2)428,33⎛⎫- ⎪⎝⎭【分析】(1)对函数求导,解导函数大于零得增区间,解导函数小于零得减区间;(2)根据()f x 单调性、极值画出函数()31443f x x x =-+的图像,结合图像,根据直线y a =与()f x 的图像有三个不同的交点,可求得实数a 的范围.【详解】(1)因为()31443f x x x =-+,所以()24=(2)(2)f x x x x '=-+-,由()0f x '>,解得2x >或2x <-,所以()f x 的增区间为(,2)-∞-,()2,+∞ 由()0f x '<,解得22x -<<,所以()f x 的减区间为(2,2)-, 综上,()f x 的增区间为(,2)-∞-,()2,+∞,减区间为(2,2)-; (2)由(1)知,当2x =-,函数取得极大值28(2)3f -=,当2x =,函数取得极小值4(2)3f =-,根据函数单调性,极值情况,其图像大致如图所示,结合图像知42833a -<<. 20.在二项式12nx x ⎛ ⎝的展开式中,______.给出下列条件:①若展开式前三项的二项式系数的和等于46; ②所有奇数项的二项式系数的和为256.试在上面两个条件中选择一个补充在上面的横线上,并解答下列问题: (1)求展开式中二项式系数最大的项; (2)求展开式的常数项;(3)求展开式中项的系数最大的项. 【答案】(1)356316T x -=,326638T x -= (2)7212T =(3)7212T =【解析】(1)选择①:01246n n n C C C ++=,即()11462n n n -++=, 即2900n n +-=,即()()1090n n +-=,解得9n =或10n =-(舍去).选择②:024...256n n n C C C +++=,即12256n -=,解得9n =.展开式中二项式系数最大的项为第5项和第6项,5452359163216T C x x x --⎛⎫== ⎪⎝⎭,45354226916328T C x x x --⎛⎫== ⎪⎝⎭.(2)展开式的通项为()93189922199122kk k k k k k k T C xx C x-----+⎛⎫== ⎪⎝⎭,令31802k -=,得6k =,所以展开式中常数项为第7项,常数项为63792122T C -=⨯=; (3)由展开式的通项为()93189922199122kk k k kk k k T C xx C x-----+⎛⎫== ⎪⎝⎭,假设第1k +项系数最大,则910199981992222k k k k k k k k C C C C -----+⎧≥⎨≥⎩,解得172033k ≤≤,且0,1,,9k =,所以6k =,即系数最大项为7212T =. 21.第24届冬季奥林匹克运动会( The XXIVO lympic WinterGames ),即2022年北京冬季奥运会,是由中国举办的国际性奥林匹克赛事,于2022年2月4日开幕,2月20日闭幕.2022年北京冬季奥运会共设7个大项,15个分项,109个小项.北京赛区承办所有的冰上项目,延庆赛区承办雪车、雪橇及高山滑雪项目,张家口赛区承办除雪车、雪橇、高山滑雪之外的所有雪上项目.为调查学生对冬季奥运会项目的了解情况,某中学进行了一次抽样调查,统计得到以下22⨯列联表.(1)先完成22⨯列联表,并依据0.005α=的独立性检验,分析该校学生对冬季奥运会项目了解情况与性别是否有关;(2)①为弄清学生不了解冬季奥运会项目的原因,按照性别采用分层抽样的方法,从样本中不了解冬季奥运会项目的学生中随机抽取5人,再从这5人中抽取3人进行面对面交流,求“男、女生至少各抽到一名”的概率;②用样本估计总体,若再从该校全体学生中随机抽取40人,记其中对冬季奥运会项目了解的人数为X ,求X 的数学期望.附表:附:()()()()22()n ad bc a b c d a c b d χ-=++++ 【答案】(1)列联表答案见解析,该校学生对冬季奥运会项目了解情况与性别有关 (2)①910;②25【分析】(1)根据公式可求计算2χ的值,根据临界值表可得相应结论.(2)①根据古典概型的概率公式结合组合计数方法可求“男、女生至少各抽到一名”的概率;②根据二项分布的期望公式可求X 的数学期望.【详解】(1)零假设0H :该校学生对冬季奥运会项目了解情况与性别无关(独立),根据所给数据得220.005400(1409011060)9.67.879250150200200x χ⨯-⨯==>=⨯⨯⨯, 并依据0.005α=的独立性检验,零假设0H 不成立,即该校学生对冬季奥运会项目了解情况与性别有关,该推断犯错误的概率不超过0.005. (2)①采用分层抽样的方法,从样本中不了解冬季奥运会项目的学生中随机抽取5人,由题可得不了解冬季奥运会项目的学生中男女比例为2:3,故这5人中包含3名女生,2名男生,再从这5人中抽取3人进行面对面交流,则“男、女生至少各抽到一名”的概率为3335C 1911C 1010-=-=; ②由题意得学生了解冬季奥运会项目的概率为25054008=,可知540,8XB ⎛⎫ ⎪⎝⎭,故()540258E X =⨯=.22.已知函数()x 2e 24f x mx mx =--,其中R m ∈.(1)若函数()f x 在[)1,+∞单调递增,求m 的取值范围; (2)已知函数()f x 存在两个极值点(1210x x -<<<),当211351x x +≤≤+时,求12x x +的取值范围.【答案】(1)e 8m ≤;(2)3ln 52ln 32,2]2[--.【分析】(1)求出函数的导数,由题意转化为不等式恒成立,分离参数,构造函数利用导数求最小值即可; (2)根据所给极值点得出21211e1x x x x -+=+,换元后可得12(1)ln 2,1t tx x t ++=--构造函数,利用导数研究函数单调性,由单调性求范围即可. 【详解】(1)()2e 24x f x mx mx =--,()e 44x f x mx m '∴=--,函数()f x 在[)1,+∞单调递增,()e 440x f x mx m '∴=--≥在[)1,+∞上恒成立, 即e 41xm x ≤+在[)1,+∞上恒成立,令e ()1x h x x =+,则[)1,x ∞∈+时,2e ()0(1)x x h x x '=>+, 所以e ()1xh x x =+在[)1,x ∞∈+时,单调递增,所以min e ()(1)2h x h ==,所以e42m ≤,即e 8m ≤.(2)因为函数()f x 存在两个极值点(1210x x -<<<),所以1212e 440e 440x x mx m mx m ⎧--=⎨--=⎩,可得21211e 1x x x x -+=+,令2111x t x +=+,则[]3,5t ∈,所以111e ,tx x t t -+-=取对数可得111ln ,tx x t t -+-=12ln ln 1,111t t t x x t t ∴+=+=--,12(1)ln 2,1t tx x t ++=-- 令(1)ln ()21t tm t t +=--,则212ln ()(1)t t t m t t --'=-, 令1()2ln n t t t t =--,则22221(1)()10t n t t t t -'=-+=>, 所以()n t 在[)1,t ∈+∞上单调递增,因为(1)0n =,所以()0n t >在[]3,5t ∈恒成立,所以()0m t '>在[]3,5t ∈恒成立,所以(1)ln ()21t tm t t +=--在[]3,5t ∈上单调递增, 所以(3)()(5)m m t m ≤≤,即3ln 52ln 32()22m t -≤≤-, 即 123ln 52ln 32,2]2[x x ∈-+- 【点睛】关键点点睛:本题第二问解题的关键在于先根据极值点的定义得出21211e 1x x x x -+=+,进而换元2111x t x +=+,求出12(1)ln 2,1t t x x t ++=--构造函数,利用导数研究函数的单调性,由单调性求出12x x +的范围.。
二项式

排列组合二项式定理及概率高考复习建议本章知识结构一、排列与组合1.正确理解概念公式,明确五个2。
①两个原理关键是做一件事指的是什么?弄清是分类还是分步。
②两个定义 关键是弄清需要考虑顺序还是不需考虑顺序。
③两组公式 关键是根据题目特点合理选用。
④两个约定: 0n C =1 ,0!=1⑤两个性质:m n C = m n n C -,m n C +1m n C -=m 1n C + (m ≤n,m,n ∈N *)2.对排列组合知识的认识(1)问题实质:数数 (2)数数的方法⎧⎨⎩分类计数分步计数(3)题目模式:1234N M M M M =⨯+⨯(4)重点:⎧⎪⎨⎪⎩两个原理两个定义两个公式(5)难点:应用3.解题步骤;分类→ 分步→判断4. 解决问题的思维程序;做一件什么事?怎样才算把事情做完?用不用分类?怎样分类?例1.从6名男生和4名女生中,选出3名代表,要求至少包含1名女生则不同的选法有多少种?例2. 9名翻译中,6个懂英语,4个懂日语,从中选拔5人参加外事活动,要求其中3人担任英语翻译,2人担任日语翻译,选拔的方法有多少种?5.要善于退,足够地退,退到最简单而不失重要性的地方是解决数学问题的诀窍 例3(05北京理)北京《财富》全球论坛期间,某高校有14名志愿者参加接待工作.若每天排早、中、晚三班,每班4人,每人每天最多值一班,则开幕式当天不同的排班种数为(A )(A )124414128C C C (B )124414128C A A (C )12441412833C C C A(D )12443141283C C C A6.掌握基本题型 (1)投信问题例: ①三封信投入到5个邮筒,有多少种投法? ②由{a,b,c,d}到{e,f}的映射共有多少个?(2)“在与不在”的问题例: 3位男生,5位女生坐在一排照相,共有多少种坐法?①甲、乙两人必须在两端,有多少种坐法?②甲不在排头乙不在排尾,有多少种坐法?(3)“邻与不邻”问题例1:3位男生,5位女生坐在一排照相①三位男生必须坐在一起,有多少种坐法? ②甲、乙相隔一人,有多少种坐法?例2 :3位男生5位女生坐在一排照相,三位男生中任意两人不能相邻,有多少种坐法? 例3: 4位男生,4位女生相间站队,有多少种站法? 例4: 4位男生,5位女生相间站队,有多少种站法?(4) “含与不含”问题例1: 100件产品中,正品97件,次品3件,现从中取出5件检验, (1)取出的5件全是正品的取法有___________种; (2)取出的5件中恰好有2次品的取法有___________种; (3)取出的5件中至少有2次品的取法有___________种. (5)顺序一定问题例: 3位男生,5位女生坐在一排照相①甲、乙、丙三人顺序一定,有多少种坐法?②甲、乙相邻且甲在乙的左边,有多少种坐法?⑹分组问题(注意有序均分和无序均分的区别) 例1: 把4人分成两组①两组人数分别为1、3,有多少种分法? ②平均分成第一、第二两组,有多少种分法? ③平均分成两组,有多少种分法?例2: 把6本不同的书①平均分给3人,有多少种分配方案? ②平均分成3堆,有多少种分配方案?③分给甲、乙、丙三人,甲3本,乙2本,丙1本,有多少种分配方案? ④分给三人,其中一人得3本,一人得2本,一人得1本,有多少种分配方案? ⑤分成三堆,其中一堆3本,一堆2本,一堆1本,有多少种分配方案? ⑥分成三堆,其中一堆4本,其余两堆各1本,有多少种分配方案?二、二项式定理1.(a+b)n =0n C a n +1n C a n-1 b+2n C a n-2b 2 +…+r n C a n-r b r +…+n n C b n特点:①展开式共有n+1项.②在每一项中, a 、b 的位置不能颠倒,a,b 的指数和为n 且b 的指数与组合数的上标相同.③二项式系数的上标从0增加到n,a 的指数从n 减少到0,b 的指数从0增加到n.性质:①二项式展开式中,与首尾两端等距离的两项的二项式系数相等. ②二项式展开式的二项式系数在中间位置取得最大值③0n C +1n C +2n C +…+n n C =2n (n ∈N); 0n 2C +2n 2C +4n 2C +…+n2n 2C =22n-1 (n ∈N) 1n 2C +3n 2C +5n 2C +…+1n 2n2C -=22n-1 (n ∈N) 通项公式: T r+1 = r n C an-rb r2.高考类型题(1)利用通项公式解题例1:求61)x①常数项 ②32x 项的系数 ③各项系数的和 ④写出所有的无理项 (2)根据恒等式意义解题例2:设9290129(13)x a a x a x a x -=++++①求0a =②求0129a a a a ++++ = ③求0129||||||||a a a a ++++ =(3)和二项式定理有关的问题例1在25(32)x x ++的展开式中x 的系数为( )A 、160 B 、240 C 、360 D 、800 例2:求(1+x)3+(1+x)4+(1+x)5+…+(1+x)n+2展开式中的含x 2的项的系数.(4)利用二项式的性质化简例1填空①0n C +2n C +4n C +…+n n C = ②18C +28C +38C +…+88C =③19C +39C +59C +…+99C = ④210242322C C C C ++++ =三、概率(一)求随机事件概率的基本方法1.随机试验法2.结果分析法(根据试验中各结果出现的等可能性求概率)(1)掌握等可能事件的概率计算公式P (A )=m/n(2)掌握概率计算的三个步骤:用字母表示事件;求m 、n ;计算P (A )。
二项分布-高二数学同步精讲课件(人教A版2019选择性必修第三册)

复习引入
前面我们学习了离散型随机变量的有关知识,本节将利用这些知识研究两类重
要的概率模型——二项分布和超几何分布.
在实际问题中,有许多随机试验与掷硬币试验具有相同的特征,它们只包含两
个可能结果.例如,检验一件产品结果为合格或不合格,飞碟射击时中靶或脱靶,医
学检验结果为阳性或阴性等.我们把只包含两个可能结果的试验叫做伯努利试验.
互平行但相互错开的圆柱形小木钉,小木钉之间留有适当的空隙
作为通道,前面挡有一块玻璃.将小球从顶端放入,小球下落的
过程中,每次碰到小木钉后都等可能地向左或向右落下,最后落
入底部的格子中.格子从左到右分别编号为0,1,2,…,10,用
表示小球最后落入格子的号码,求的分布列.
解:设 =“向右下落”,则ҧ =“向左下落”,且
斥,每个结果都是3个相互独立事件的积.由概率的加法公式和乘法公式得:
新知探索
( = 0) = (1 2 3 ) = 0.23 ,
( = 1) = (1 2 3 ) + (1 2 3 ) + (1 2 3 ) = 3 × 0.8 × 0.22 ,
( = 2) = (1 2 3 ) + (1 2 3 ) + (1 2 3 ) = 3 × 0.82 × 0.2,
( = 3) = 2 . 均值和方差分别为
() = 0 × (1 − )2 +1 × 2(1 − ) + 2 × 2 = 2.
() = 02 × (1 − )2 +12 × 2(1 − ) + 22 × 2 − (2)2 = 2(1 − ).
新知探索
一般地,可以证明:如果~(,),那么() = ,() = (1 − ).
(理科)专题训练(二项式定理、分布列、期望与方差)

高三数学(理科)专题训练(1)-----概率、二项式定理、分布列、数学期望1.如果一条直线与一个平面平行,那么称此直线与平面构成一个“平面线面组”.在一个长方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“平行线面组”的个数是()A.60 B.48 C.36D.242..甲、乙两人进行象棋比赛,甲获胜的概率是0.4,两人下成和棋的概率是0.2,则甲不输的概率是()A.0.6B.0.8C.0.2D.0.43.在第3、6、16路公共汽车的一个停靠站(假定这个车站只能停靠一辆公共汽车),有一位乘客需在5分钟之内乘上公共汽车赶到厂里,他可乘3路或6路公共汽车到厂里,已知3路车、6路车在5分钟之内到此车站的概率分别为0.20和0.60,则该乘客在5分钟内能乘上所需要的车的概率为()A.0.20 B.0.60 C.0.80D.0.124.掷一颗质地均匀的骰子,观察所得的点数a,设事件A:a=3;事件B:a=4;事件C:a为奇数,则下列结论正确的是() A.A与B为互斥事件B.A与B为对立事件C.A与C为对立事件D.A与C为互斥事件5.某家庭电话在家里有人时,打进电话响第一声被接的概率为0.1,响第二声时被接的概率为0.3,响第三声时被接的概率为0.4,响第四声时被接的概率为0.1,那么电话在响前4声内被接的概率是()A.0.622 B.0.9 C.0.659 8 D.0.002 87.袋中装有3个白球,4个黑球,从中任取3个球,则①恰有1个白球和全是白球;②至少有1个白球和全是黑球;③至少有1个白球和至少有2个白球;④至少有1个白球和至少有1个黑球.在上述事件中,是对立事件的为()A.①B.②C.③D.④7.已知(x+ax)6(a>0)的展开式中常数项为240,则(x+a)(x-2a)2的展开式中x2项的系数为________.8.已知a=π2(sin2x2-12)d x,则(ax+12ax)9的展开式中,关于x的一次项的系数为________.9.自“钓鱼岛事件”以来,中日关系日趋紧张并不断升级.为了积极响应“保钓行动”,某学校举办了一场“保钓知识大赛”,共分两组.其中甲组得满分的有1个女生和3个男生,乙组得满分的有2个女生和4个男生.现从得满分的同学中,每组各任选2个同学,作为“保钓行动代言人”.(1)求选出的4个同学中恰有1个女生的概率;(2)设X为选出的4个同学中女生的个数,求X的分布列和数学期望.高三数学(理科)专题训练(2)-----概率、二项式定理、分布列、数学期望1.随机变量X 的分布列如下:其中a ,b ,c 成等差数列,则P (|X |=1)=( ) A.16B.13C.12D.23.2.设随机变量ξ的概率分布列为P (ξ=i )=i a )43(i,i =1,2,3,则a 的值是( )A.64111B.64101C.2764D.37643.设随机变量X 的概率分布列如下表所示:F (x )=P (X ≤x ),则当x 的取值范围是[1,2)时,F (x )=( )A.13B.16C.12D.564.一个篮球运动员投篮一次得3分的概率为a ,得2分的概率为b ,不得分的概率为c ,且a 、b 、c ∈(0,1),已知他投篮一次得分的数学期望为1(不计其他得分情况),则ab 的最大值为________.5..已知⎝⎛⎭⎪⎫x +13x n 的展开式的二项式系数之和比(a +b )2n 的展开式的系数之和小240,求⎝ ⎛⎭⎪⎫x +13x n的展开式中系数最大的项.6.(2014·北京)把5件不同产品摆成一排,若产品A 与产品B 相邻,且产品A 与产品C 不相邻,则不同的摆法有________种.7.离散型随机变量X 的概率分布规律为P (X =n )=ann +1(n =1,2,3,4),其中a 是常数,则P ()12<X <52=______.8.已知随机变量ξ只能取三个值:x 1,x 2,x 3,其概率依次成等差数列,则公差d 的取值范围是________.9.(河南省信阳市2015届高中毕业班第二次调研检测数学理试题19).某高中随机抽取部分高一学生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].(Ⅰ)求直方图中x 的值;(Ⅱ)如果上学路上所需时间不少于1小时的学生可申请在学校住宿,若招生1200名,请估计新生中有多少名学生可以申请住宿; (Ⅲ)从学校的高一学生中任选4名学生,这4名学生中上学路上所需时间少于20分钟的人数记为X,求X的分布列和数学期望.(以直方图中的频率作为概率)X -1 0 1 PabcX 0 1 2 Pa1316【参考答案】高三数学(理科)专题训练-----概率、二项式定理、分布列、数学期望(1)1.【答案】B【解析】长方体的6个表面构成的“平行线面组”有6×6=36个,另含4个顶点的6个面(非表面)构成的“平行线面组”有6×2=12个,共36+12=48个,故选B.2.【答案】A【解析】甲获胜的概率是0.4,两人下成和棋的概率是0.2,所以甲不输的概率为0.4+0.2=0.6.故选A.3.【答案】C【解析】由互斥事件的概率加法公式可得,该乘客在5分钟内能乘上所需的车的概率为0.20+0.60=0.80.故选C.4.【答案】A【解析】依题意,事件A与B不可能同时发生,故A与B是互斥事件,但A与B不是对立事件,显然,A与C既不是对立事件也不是互斥事件.故选A.5.【答案】B【解析】根据互斥事件的概率加法公式,电话在响前4声内被接的概率=电话响第一声被接的概率+响第二声时被接的概率+响第三声时被接的概率+响第四声时被接的概率,故电话在响前4声内被接的概率是0.1+0.3+0.4+0.1=0.9,故选B.6.【答案】B【解析】从7个球中任取3个球的所有可能为:1个白球2个黑球;2个白球1个黑球;3个白球;3个黑球.故①中的两事件互斥,但不对立;②中的两事件对立;③中的两事件中不互斥;④中的两事件不互斥,故选B.7.【答案】-6【解析】(x+ax)6的二项展开式的通项T r+1=C r6x6-r(ax)r=C r6362rax-,令6-3r2=0,得r=4,则其常数项为C46a4=15a4=240,则a4=16,由a>0,故a=2.又(x+a)(x-2a)2的展开式中,x2项为-3ax2,故x2项的系数为(-3)×2=-6.8.【答案】-6316【解析】a=π2⎰(sin2x2-12)d x=π20⎰(1-cos x2-12)d x=π20⎰(-cos x2)d x=-12sin xπ20|=-12.此时二项展开式的通项为T r+1=C r 9(-12x )9-r (-1x )r =C r 9(-12)9-r (-1)r x 9-2r ,令9-2r =1,得r =4,所以关于x 的一次项的系数为C 49(-12)9-4(-1)4=-6316. 9.【解析】(1)设“从甲组内选出的2个同学均是男生;从乙组内选出的2个同学中,1个是男生,1个是女生”为事件A ,“从乙组内选出的2个同学均是男生;从甲组内选出的2个同学中1个是男生,1个是女生”为事件B ,由于事件A ,B 互斥,且P (A )=C 23C 12C 14C 24C 26=415,P (B )=C 13C 24C 24C 26=15.所以选出的4个同学中恰有1个女生的概率为P (A +B )=P (A )+P (B )=415+15=715. (2)由条件知X 的所有可能值为0,1,2,3.;P (X =0)=C 23C 24C 24C 26=15,P (X =1)=C 23C 12C 14+C 13C 24C 24C 26=715,P (X =3)=C 13C 24C 26=130,P (X =2)=1-15-715-130=310.[来源所以X 的分布列为 所以X 的数学期望为E (X )=0×15+1×715+2×310+3×130=76.高三数学(理科)专题训练-----概率、二项式定理、分布列、数学期望(2)1.【答案】D 【解析】因为a ,b ,c 成等差数列,所以2b =a +c .又a +b +c =1,得b =13,所以P (|X |=1)=a +c =23.故选D2.【答案】A 【解析】1=P (ξ=1)+P (ξ=2)+P (ξ=3)=a ⎣⎡⎦⎤34+()342+()343,解得a =64111,选A. 3.【答案】D 【解析】∵a +13+16=1,∴a =12.[来源:学_科_网]∵x ∈[1,2),∴F (x )=P (X ≤x )=12+13=56.选D.4.【答案】124 【解析】由已知3a +2b +0×c =1,∴3a +2b =1,∴ab =16·3a ·2b ≤163a +2b24=124,当且仅当a =16,b =14时等号成立. 5.【解析】由题意,得2n =22n -240,∴22n -2n -240=0,即(2n -16)(2n +15)=0.又∵2n +15>0,∴2n -16=0.∴n =4.∴⎝⎛⎭⎪⎫x +13x n =⎝⎛⎭⎪⎫x +13x 4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二项式分布列与数学期望
二项式分布列(BinomialDistribution)是概率论中一种常见的概率分布。
它可以用来描述可以重复的试验的结果,且每次试验的结果只有两种可能:成功和失败。
该分布非常常用,在数学、统计学、投资学和金融学等领域都被广泛使用。
二项式分布列是由概率论家Jacob Bernoulli创立的,后来又有概率论家Pierre-Simon Laplace进一步完善。
与其他概率分布一样,二项式分布亦有属于自己的数学期望。
关于二项式分布的数学期望,它可以表示为:
数学期望,简称期望,是概率论中重要的概念。
它可以用来度量随机变量的长期期望值。
数学期望计算的结果取决于概率的变化,因此对于每一个可能的变量,都会得出一个固定的数学期望。
二项式分布期望可以用来解决众多实际问题,非常实用。
例如,给定一个具有特定概率的投掷正面朝上的硬币,我们就可以用二项式分布来估算其中可能发生的正面朝上的次数。
同时,二项式分布数学期望也可以用来评估投资者的投资组合的收益潜力,评估和估算投资者的投资组合所处的风险水平,以及确定建立有效的投资组合的最佳组合。
最后,二项式分布数学期望也可以用来评估大型企业或组织的财务活动,例如预测收入总额和盈利能力,以及估计组织的财务风险水平。
总之,二项式分布数学期望在解决实际问题方面发挥了重要作用,
因此它经常被应用于各个领域。
从概率论到企业或组织的财务管理,都会用到二项式分布数学期望特定的应用程序。
