薛定谔方程及其解法
高中奥赛---薛定谔方程及其求解方法94页PPT

36、如果我们国家的法律中只有某种 神灵, 而不是 殚精竭 虑将神 灵揉进 宪法, 总体上 来说, 法律就 会更好 。—— 马克·吐 温 37、纲纪废弃之日,便是暴政兴起之 时。— —威·皮 物特
38、若是没有公众舆论的支持,法律 是丝毫 没有力 量的。 ——菲 力普斯 39、一个判例造出另一个判例,它们 迅速累 聚,进 而变成 法律。 ——朱 尼厄斯
40、人类法律,事物有规律,这是不 容忽视 的。— —爱献 生
谢谢!
51、 天 下 之 事 常成 于困约 ,而败 于奢靡 。——陆 游 52、 生 命 不 等 于是呼 吸,生 命是活 动。——卢 梭
53、 伟 大 的 事 业,需 要决心 ,能力 ,组织 和责任 感。 ——易 卜 生 54、 唯 书 籍 不 朽。——乔 特
55、 为 中 华 之 崛起而 读书
薛定谔方程组及其解法

薛定谔方程组及其解法薛定谔方程组(Schrodinger Equation)是量子力学的基础方程之一,描述了量子系统的波动性质和粒子运动的规律。
在量子力学发展的过程中,人们通过不断地尝试和探索,发现了各种各样的解法,使得该方程的应用范围越来越广,成为了现代物理学的重要工具之一。
1. 薛定谔方程组及其含义薛定谔方程组最初是由奥地利物理学家薛定谔(Erwin Schrodinger)于1926年提出的,他通过研究光谱现象,认为物理系统的运动可以用波函数来描述。
而波函数则可以通过一个方程来求解,这个方程就是薛定谔方程组。
薛定谔方程组描述了微观粒子的运动规律和波动性质,用于计算微观尺度下的物理量,如粒子的位置、速度、动量、能量等。
方程中的波函数可以归一化,即保证粒子存在的概率为1。
因此,波函数可以被解释为一个粒子的存在概率密度。
2. 薛定谔方程组的解法薛定谔方程组的解法主要基于两种方法:定态微扰理论和变分法。
定态微扰理论是通过在原方程中加入微小扰动项,逐步展开波函数的级数,来求得精确的解。
而变分法则通过尝试不同的波函数形式来寻找最优解,从而得到薛定谔方程组的解。
此外,还有一些基于计算机算法的数值解法应用于薛定谔方程组,如有限元方法、有限差分法和网格方法等。
3. 应用范围和意义薛定谔方程组的应用范围非常广泛,涉及到各种物理现象和工程问题。
在纳米技术领域,薛定谔方程组可以用于描述纳米材料的电子结构和催化反应的机理,从而辅助设计新型材料和开发高效催化剂。
在化学领域,薛定谔方程组可以用于计算化学反应的机理和产物的构成,帮助人们预测化学反应过程和控制反应的产物。
在固态物理学中,薛定谔方程组可以用来解释材料的电、光、热、声等性质,帮助人们研发新型的半导体材料和纳米电子器件。
总之,薛定谔方程组在物理学、化学、材料学等领域有着广泛的应用和重要的意义,对推动人类社会的发展发挥着重要的作用。
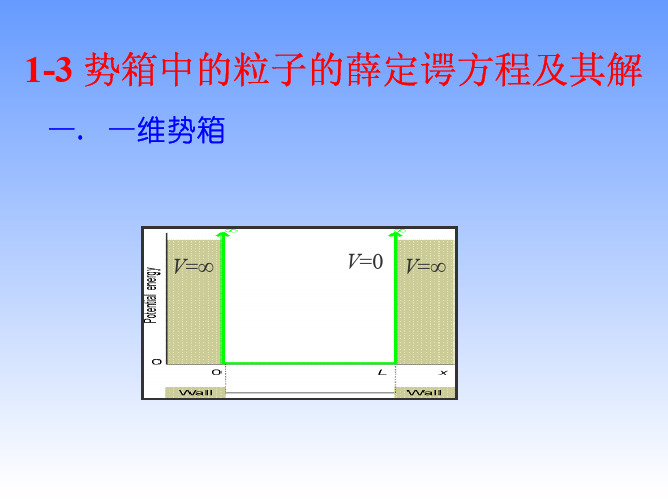
势箱中的粒子的薛定谔方程及其解
三.量子力学处理问题的一般方法
1. 2. 3. 写出体系的哈密顿算符[H](主要是势能算符); 写出Sch.方程; 解Sch.方程.解Sch.方程和通常解微分方程差不 多,解Sch.方程时,把 Ψ 当作未知函数E 作为参 数看待. 4. 由所得Ψi就可知道体系的几率分布以及体系的其 它物理性质.
1 4
第一章习题 6 7 9 11 12 18 21
�
1 2 X (x) 1 2Y ( y) 1 2 Z (z) 8π 2 m + + = 2 (Ex + Ey + Ez ) 2 2 2 X (x) x Y ( y) y Z (z) z h
因为x,y,z是三个变数,要满足上式,必须下列三式同时成立
d 2 X ( x) 8π 2 mE x + X ( x) = 0 2 2 dx h 2 8π 2 mE y d Y ( y) + Y ( y) = 0 2 2 dy h
长,宽,高分别为a,b,c 的三维势箱,Sch.方程为
2 2 2 [ 2 ( 2 + 2 + 2 ) + V ( x, y, z )]ψ ( x, y, z ) = Eψ ( x, y, z ) y 8π m x z h2
设
Ψ(x,y,z)=X(x)Y(y)Z(z) E = E x + Ey + E z 8π 2 m 代入Sch.方程,并以X(x)Y(y)Z(z)除之,两边乘 2 h
通式 R2N-(CH=CH-)rCH=NR2+
E h[(r + 3) 2 (r + 2) 2 ] h(2r + 5) = = ν= 2 h 8ml 8ml 2
8ml 2 c 3.30l 2 3.30(248r + 565) 2 = = λ = c/ν = pm h(2r + 5) 2r + 5 2r + 5
高级中学奥赛-薛定谔方程及其求解方法

狄拉克(Paul Adrien Maurice Dirac,1902-1984)
英国理论物理学家。1925年,他作为一名 研究生便提出了非对易代数理论,而成为 量子力学的创立者之一。第二年提出全同 粒子的费米-狄拉克统计方法。1928年提出 了电子的相对论性运动方程,奠定了相对 论性量子力学的基础,并由此预言了正负 电子偶的湮没与产生,导致承认反物质的 存在,使人们对物质世界的认识更加深入。 他还有许多创见(如磁单极子等)都是当 代物理学中的基本问题。由于他对量子力 学所作的贡献,他与薛定谔共同获得1933 年诺贝尔物理学奖金。
[
2
2
U (r )] (r )
E (r )
2
E为一常数
i df (t) Ef (t) dt
df (t) f (t)
i
Edt
解出:
f
(t
)
Ce
i
Et
(r ,
t
)
(r )e
i
Et
――定态波函数
1.定态中E不随时间变化,粒子有确定的能量
2.定态中粒子的几率密度不随时间变化
(r ,
t
)
*
(r ,
爱因斯坦觉察到德布罗意物质波思 想的重大意义,誉之为“揭开一幅大幕 的一角”。
德布罗意假设
一个质量为m的实物粒子以速率v 运动时,即具有以能量E
和动量P所描述的粒子性,也具有以频率n和波长l所描述的
波动性。 德布罗意波,也叫物质波。
E hn
P= h
l
(p
h
n
k )
l
德布罗意 公式
l= h
例1. 计算下列运动物质的德布罗意波长
(1) 质量100g, v = 10m·s1运动的小球。
解定态薛定谔方程的一般方法

( n
L
)2
n
sin
n
L
x
(x,t)
an
n
exp(
i
Ent)
由归一化条件: *dx 1 L*dx
0
及正交完备性:
n*
ndx
(n
n)
故:
a
* n
an
1,粒子处于某一 n的概率为:a*nan
n
北京邮电大学理学院 原子物理
解得T T0eiEt 并将常数T0归到所含常数中,得 (r, t) (r)eiEt
得出定态薛定谔方程为
(11) (12)
[ 2 2 u(r)] E
2m
(13)
并注意到,由(12)式几率密度 * *与时间无关。
北京邮电大学理学院 原子物理
V
有
E
V0
方势垒为:u
(
x)
0, V0
,
x x1, x x2 (1) x1 x x2
限 高 势 垒
0
X1 X2
x
当入射粒子从 x x1 的地方向右入射,如其入射能量 E
低于 V0 时,按照经典力学观点,粒子不可能穿过势垒,将全
部返回。但是量子力学将给出完全不同的结果。从一维定态薛
求其特解,把波函数写为 (r, t) (r)T (t)得
i dT 1 [ 2 2 u(r)] T dt 2m
于是有分离常数E使(9)式得 i dT E T dt
北京邮电大学理学院 原子物理
(8)
(9) (10)
§3.1 薛定谔方程
和 1 [ 2 2 u(r)] E 2m
薛定谔方程及其解法

关于薛定谔方程一. 定义及重要性薛定谔方程(Schrdinger equation )是由奥地利物理学家薛定谔提出的量子力学中的一个基本方程,也是量子力学的一个基本假定,其正确性只能靠实验来检验.是将物质波的概念和波动方程相结合建立的二阶偏微分方程,可描述微观粒子的运动,每个微观系统都有一个相应的薛定谔方程式,通过解方程可得到波函数的具体形式以及对应的能量,从而了解微观系统的性质。
薛定谔方程是量子力学最基本的方程,亦是量子力学的一个基本假定,它的正确性只能靠实验来检验.二. 表达式三. 定态方程()()222V r E r m ηψψ+⎡⎤-∇=⎢⎥⎣⎦所谓势场,就是粒子在其中会有势能的场,比如电场就是一个带电粒子的势场;所谓定态,就是假设波函数不随时间变化。
其中,E 是粒子本身的能量;v(x ,y ,z )是描述势场的函数,假设不随时间变化。
2222222z y x ∂∂∂∂∂∂++=∇可化为d 0)(222=-+ψψv E h m dx薛定谔方程的解法一. 初值解法;欧拉法,龙格库塔法二. 边值解法;差分法,打靶法,有限元法龙格库塔法(对欧拉法的完善)给定初值问题).()()((3)),(),()( ,,(2))(),( 3112122111021h O t y t y hk y h t f k y t f k k c k c h y y y c c a y b t a y t f dt dyi i i i i i i i =-⎪⎪⎩⎪⎪⎨⎧++==++==⎪⎩⎪⎨⎧=≤≤=++的局部截断误差使以下数值解法的值及确定常数ββαβα.))(,(,,(3) )()(2)()( ,))(,())(,())(,()( ))(,()( )()(2)()()( )( 3213211处的函数值分别表示相应函数在点其中得代入上式将处展成幂级数在首先将i i y t y t i i y t i i i i i i t y t f f f h O ff f h hf t y t y t y t f t y t f t y t f t y t y t f t y h O t y h t y h t y t y t t y '++++=+'=''='+''+'+=+++.)(21 1 ,,021,01 ),()()())(21()1()( ,)( 3221212213113222111的计算公式局部截断误差为可得到但只有两个方程,因此方程组有三个未知数,满足条件即常数当且仅当要使局部截断误差得下假设在局部截断误差的前提h O c c c c c c c c h O y t y h O ff f c h f c c h y t y t y y i i y t i i i i ==+=-=-+=-++-+-+-=-=++++ββββ有限元方法有限元的概念早在几个世纪前就已产生并得到了应用,例如用多边形(有限个直线单元)逼近圆来求得圆的周长,但作为一种方法而被提出,则是最近的事。
量子力学中的薛定谔方程及其求解

量子力学中的薛定谔方程及其求解量子力学是研究微观粒子行为的重要理论,其核心是薛定谔方程。
薛定谔方程描述了量子体系中粒子的波函数以及随时间演化的规律。
本文将介绍薛定谔方程的基本原理,并讨论一些常见的求解方法。
一、薛定谔方程的基本原理薛定谔方程是波动方程,描述了量子体系中粒子的行为。
它的一般形式为:iħ∂ψ/∂t = Hψ其中,i是虚数单位,ħ是约化普朗克常数,ψ是粒子的波函数,t 是时间,H是哈密顿算符。
薛定谔方程的左边代表了波函数随时间变化的导数,右边代表了粒子在量子力学描述下的总能量。
通过求解这个方程,我们可以得到波函数的时间演化规律,从而揭示粒子的行为。
二、薛定谔方程的求解方法求解薛定谔方程是量子力学中的关键问题,涉及到很多数学方法和物理概念。
下面介绍几种常见的求解方法。
1. 一维自由粒子的求解方法对于一维自由粒子,其哈密顿算符可以简化为动能算符,即H = -ħ^2/2m * ∂^2/∂x^2。
将这个算符代入薛定谔方程,可以得到一维自由粒子的薛定谔方程为:iħ∂ψ/∂t = -ħ^2/2m * ∂^2ψ/∂x^2这是一个简单的偏微分方程,可以通过分离变量法求解。
假设波函数可以分解为时间部分和空间部分的乘积,即ψ(x, t) = φ(x) * χ(t),代入薛定谔方程后可以分离变量,得到两个独立的常微分方程。
分别求解这两个方程,再将它们的解合并,即可得到一维自由粒子的波函数。
2. 一维势阱的求解方法一维势阱是限制粒子运动在有限空间内的一种势场。
在势阱中,波函数的形式将受到势场的影响。
求解一维势阱的薛定谔方程需要考虑势场对波函数的贡献。
对于势阱中的波函数,只有在势阱内部才能存在。
在势阱内部,薛定谔方程的形式与自由粒子类似,但是边界条件会影响波函数的形式。
边界条件一般为波函数在势阱边界处连续且导数连续。
通过求解这个边界问题,可以得到一维势阱中的波函数。
3. 二维和三维量子体系的求解方法对于二维和三维的量子体系,薛定谔方程将变为偏微分方程。
薛定谔方程的含义和求解方法

薛定谔方程的含义和求解方法薛定谔方程是量子力学中的基本方程之一,描述了微观粒子(如电子)的行为。
本文将介绍薛定谔方程的含义及其求解方法。
一、薛定谔方程的含义薛定谔方程是由奥地利物理学家薛定谔于1926年提出的,用来描述微观粒子的运动和性质。
该方程是一个偏微分方程,包含粒子的波函数(Ψ)和哈密顿量(H)。
薛定谔方程的一般形式为:iℏ∂Ψ/∂t = HΨ其中,i是虚数单位,ℏ是约化普朗克常数,t是时间。
Ψ是粒子的波函数,H是系统的哈密顿量。
薛定谔方程描述了一个量子系统的演化过程。
通过对波函数的求解,我们可以得到粒子在不同位置和时间的概率分布,从而理解其行为和性质。
二、薛定谔方程的求解方法薛定谔方程是一个高度复杂的偏微分方程,一般情况下无法通过解析方法求解。
但可以通过一些近似方法和数值方法来求解。
1. 解析方法对于简单的系统,可以通过解析方法求解薛定谔方程。
例如,对于自由粒子,可以得到平面波的解。
对于一维谐振子,可以得到谐振子波函数的解。
然而,对于复杂的系统,如多电子体系或相互作用体系,解析方法往往不适用。
因此,需要使用近似方法和数值方法来求解。
2. 近似方法常用的近似方法包括变分法、微扰法和量子力学近似等。
变分法通过选取适当的波函数的形式和参数,使得波函数的能量最小化。
微扰法将系统的哈密顿量分解为一个已知的部分和一个微扰项,通过级数展开的方式求解波函数。
3. 数值方法数值方法是求解薛定谔方程的重要手段之一。
常用的数值方法包括有限差分法、有限元法和动态变分法等。
这些方法通过将波函数和哈密顿量离散化,将偏微分方程转化为一组代数方程,然后通过迭代求解来得到波函数的数值解。
数值方法的优点是适用于各种复杂系统,并且可以提供较高的精度。
但需要注意选择合适的离散化方法和参数,以及控制误差和收敛性。
总之,薛定谔方程是研究微观粒子的基本工具之一,可以描述粒子的运动和性质。
通过适当的求解方法,我们可以获得粒子的波函数,从而深入理解量子力学中的各种现象和行为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于薛定谔方程
一. 定义及重要性
薛定谔方程(Schrdinger equation )是由奥地利物理
学家薛定谔提出的量子力学中的一个基本方程,也是量子力学的一个基本假定,其正确性只能靠实验来检验。
是将物质波的概念和波动方程相结合建立的二阶偏微分方程,可描述微观粒子的运动,每个微观系统都有一个相应的薛定谔方程式,通过解方程可得到波函数的具体形式以及对应的能量,从而了解微观系统的性质。
薛定谔方程是量子力学最基本的方程,亦是量子力学的一个基本假定,它的正确性只能靠实验来检验。
二. 表达式
三. 定态方程
()()2
22V r E r m ηψψ+⎡⎤-∇=⎢⎥⎣⎦
所谓势场,就是粒子在其中会有势能的场,比如电场就是一个带电粒子的势场;所谓定态,就是假设波函数不随时间变化。
其中,E 是粒子本身的能量;v(x ,y ,z)是描述势场的函数,假设不随时间变化。
2
2
22222z y x ∂∂
∂∂∂∂++=∇
可化为d 0)(222=-+ψψ
v E h m dx
薛定谔方程的解法
一. 初值解法;欧拉法,龙格库塔法
二. 边值解法;差分法,打靶法,有限元法
龙格库塔法(对欧拉法的完善)
给定初值问题
).()()((3)
)
,()
,()
( ,,(2)
)()
,( 3112122111021h O t y t y hk y h t f k y t f k k c k c h y y y c c a y b t a y t f dt dy
i i i i i i i i =-⎪⎪⎩⎪⎪⎨⎧++==++==⎪⎩⎪⎨⎧
=≤≤=++的局部截断误差使以下数值解法
的值及确定常数ββα
βα
.))(,(,,(3) )()(2
)()( ,))(,())(,())(,()( ))
(,()( )()(2
)()()( )( 32
132
11处的函数值分别表示相应函数在点其中得
代入上式将
处展成幂级数
在首先将i i y t y t i i y t i i i i i i t y t f f f h O ff f h hf t y t y t y t f t y t f t y t f t y t y t f t y h O t y h t y h t y t y t t y '++++=+'=''='+''+'+=+++.
)(2
1 1 ,,02
1,01 ),()()())(2
1()1()( ,)( 322121221311322
2111的计算公式局部截断误差为可得到但只有两个方程,因此方程组有三个未知数,满足条件
即常数当且仅当要使局部截断误差得
下假设在局部截断误差的前提h O c c c c c c c c h O y t y h O ff f c h f c c h y t y t y y i i y t i i i i ==+=-=-+=-++-+-+-=-=++++ββββ
有限元方法
有限元的概念早在几个世纪前就已产生并得到了应用,例如用多边形(有限个直线单元)逼近圆来求得圆的周长,但作为一种方法而被提出,则是最近的事。
有限元法最初被称为矩阵近似方法,应用于航空器的结构强度计算,并由于其方便性、实用性和有效性而引起从事力学研
究的科学家的浓厚兴趣。
经过短短数十年的努力,随着计算机技术的快速发展和普及,有限元方法迅速从结构工程强度分析计算扩展到几乎所有的科学技术领域,成为一种丰富多彩、应用广泛并且实用高效的数值分析方法。
有限元方法与其他求解边值问题近似方法的根本区别在于它的近似性仅限于相对小的子域中。
有限元分析的基本概念是用较简单的问题代替复杂问题后再求解。
它将求解域看成是由许多称为有限元的小的互连子域组成,对每一单元假定一个合适的(较简单的)近似解,然后推导求解这个域总的满足条件,从而得到问题的解。
这个解不是准确解,而是近似解,因为实际问题被较简单的问题所代替。
不同于求解(往往是困难的)满足整个定义域边界条件的函数的Rayleigh Ritz法,有限元法将函数定义在简单几何形状(如二维问题中的三角形或任意四边形)的单元域上(分片函数),且不考虑整个定义域的复杂边界条件,这是有限元法优于其他近似方法的原因之一。
