折半查找法例题
利用数组进行数据查找_折半查找法_C语言程序

↑low↑mid↑high
第三步:上一步中,所找数80比mid指示的100小,可知新的查找区间为[56 80],low不变,mid与high的值作相应修改。mid指示的数为56,还要继续查找。
-12 0 6 16 23 [ 56 80 ] 100 110 115
scanf("%d",&n);
while(low<=high)
{mid=(low+high)/2;
if (n= =a[mid]) {found=1;break;}/*找到,结束循环*/
else if (n>a[mid]) low=mid+1;
else high=mid-1;
}
if (found==1) printf("The index of %d is %d",n,mid);
例7.10假设在数组a中的数据是按由小到大顺序排列的:
-12 0 6 16 23 56 80 100 110 115,从键盘上输入一个数,判定该数是否在数组中,若在,输出所在序号;若不在,输出相应信息。
查找过程如下:
第一步:设low、mid和high三个变量,分别指示数列中的起始元素、中间元素与最后一个元素位置,其初始值为low=0,high=9,mid=4,判断mid指示的数是否为所求,mid指示的数是23,不是要找的80,须继续进行查找。
选定这批数中居中间位置的一个数与所查数比较看是否为所找之数若不是利用数据的有序性可以决定所找的数是在选定数之前还是在之后从而很快可以将查找范围缩小一半
适应情况:在一批有序数据中查找某数
基本思想:选定这批数中居中间位置的一个数与所查数比较,看是否为所找之数,若不是,利用数据的有序性,可以决定所找的数是在选定数之前还是在之后,从而很快可以将查找范围缩小一半。以同样的方法在选定的区域中进行查找,每次都会将查找范围缩小一半,从而较快地找到目的数
折半查找——精选推荐

折半查找⼀.题⽬要求·题⽬输⼊n(n<100)个有序正数,请⽤折半查找算法,查找x在其中的位置。
·测试输⼊:5 1,2,3,4,5 2输出:2注:测试集合中,x数⼀定在正数数组中。
即不⽤处理错误逻辑。
⼆.题⽬分析输⼊的第⼀个数是数的个数,第⼆组数是⼀组有序的数,即不需要⾃⼰排序,第三个数则是要查找的数。
折半查找,也称⼆分查找,即利⽤⼆分法进⾏查找。
在某些情况下相⽐于顺序查找,使⽤折半查找算法的效率更⾼。
但是该算法的使⽤的前提是静态查找表中的数据必须是有序的。
三.代码实现#include <stdio.h>int main() {int n, i;int series[100];int t;int right, left, middle;//输⼊scanf_s("%d", &n);for (i = 0; i < n; i++) {scanf_s("%d,", &series[i]);}scanf_s("%d", &t);//初始化left = 0;right = n - 1;middle = (n - 1) / 2;//⼆分法查找while (series[middle] != t) {if (series[middle] < t) right = middle;else left = middle;middle = (left + right) / 2;}printf("%d", middle);return 0;}好吧,上⾯的代码还是运⾏不了(似曾相识)。
调试的时候发现数组元素的输⼊没有成功,但是没有找到错误的原因。
然后我在⽹上找到了⼩刘同学分享的代码。
我这⾥也展⽰⼀下他的源码。
#include <stdio.h>int main(){int num[100];int a,b,flag,i=0;scanf("%d",&a);for(i=0;i<a;i++){scanf("%d,",&num[i]);}scanf("%d",&b);int left=0,right=a-1;while(left<=right){flag = (left+right)/2;if(b==num[flag]){printf("%d",flag+1);break;}if(num[flag] > b)right = flag-1;else if(num[flag] < b)left = flag+1;}}我对⽐了⼀下,除了⼆分查找的实现部分,前⾯的不~TM~是⼀样的吗。
折半查找法
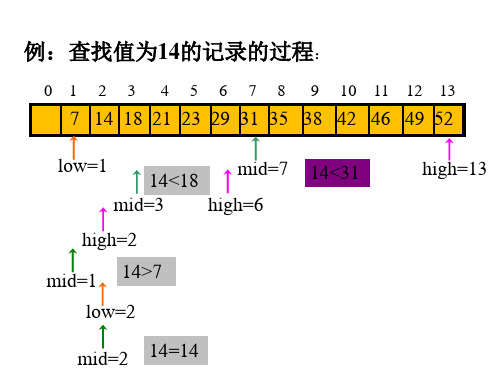
0 1 2 3 4 5 6 7 8 9 10 11 12 13
7 14 18 21 23 29 31 35 38 42 46 49 52
low=1 14<18 mid=7 14<31 mid=3 high=6
high=2 mid=1 14>7
low=2
mid=2 14=14
return BinSearch2(r, low, mid-1, k); else if (k>r[mid])
return BinSearch2(r, mid+1, high, k); else return mid; } }
折半查找判定树
判定树:折半查找的过程可以用二叉树来描述,树
中的每个结点对应有序表中的一个记录,结点的值为 该记录在表中的位置。通常称这个描述折半查找过程
的二叉树为折半查找判定树,简称判定树。
判定树的构造方法
⑴ 当n=0时,折半查找判定树为空;
⑵ 当n>0时,折半查找判定树的根结点是有序表中序 号为mid=(n+1)/2的记录,根结点的左子树是与有序 表r[1] ~ r[mid-1]相对应的折半查找判定树,根结点的 右子树是与r[mid+1] ~ r[n]相对应的折半查找判定树。
else return mid; } return 0; }
折半查找——递归算法
int BinSearch2(int r[ ], int low, int high, int k) //数组r[1] ~ r[n]存放查找集合 {
if (low>high) return 0; else {
mid=(low+high)/2; if (k<r[mid])
折半查找_数据结构(C语言版)_[共3页]
![折半查找_数据结构(C语言版)_[共3页]](https://img.taocdn.com/s3/m/c92549ae168884868662d611.png)
if(ST.R[i].key==key) return i; //从后往前找return 0;}//Search _Seq 算法7.1在查找过程中每步都要检测整个表是否查找完毕,即每步都要有循环变量是否满足条件i >=1的检测。
改进这个程序,可以免去这个检测过程。
改进方法是查找之前先对ST.R[0]的关键字赋值key ,在此,ST.R[0]起到了监视哨的作用,如算法7.2所示。
算法7.2 设置监视哨的顺序查找【算法描述】int Search _Seq(SSTable ST,KeyType key){//在顺序表ST 中顺序查找其关键字等于key 的数据元素。
若找到,则函数值为//该元素在表中的位置,否则为0ST.R[0].key=key; //“哨兵”for(i=ST.length;ST.R[i].key!=key;--i); //从后往前找retutn i;}//Search _Seq 【算法分析】算法7.2仅是一个程序设计技巧上的改进,即通过设置监视哨,免去查找过程中每一步都要检测整个表是否查找完毕。
然而实践证明,这个改进能使顺序查找在ST.length ≥1000时,进行一次查找所需的平均时间几乎减少一半。
当然,监视哨也可设在高下标处。
算法7.2和算法7.1的时间复杂度一样,在第2章已经做过分析,即 1112n i n ASL i n =+==∑ 算法7.2的时间复杂度为O (n )。
顺序查找的优点是:算法简单,对表结构无任何要求,既适用于顺序结构,也适用于链式结构,无论记录是否按关键字有序均可应用。
其缺点是:平均查找长度较大,查找效率较低,所以当n 很大时,不宜采用顺序查找。
7.2.2 折半查找折半查找(Binary Search )也称二分查找,它是一种效率较高的查找方法。
但是,折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
在下面及后续的讨论中,均假设有序表是递增有序的。
折半查找例题

折半查找(Binary Search)是一种高效的查找算法,适用于已排序的数组。
其基本思想是每次将待查找的元素与数组中间元素进行比较,根据比较结果缩小查找范围,直到找到目标元素或查找范围为空。
下面是一个折半查找的例题:假设有一个已排序的整数数组`arr = [1, 3, 5, 7, 9]`,请编写一个折半查找算法,查找元素`target = 5`在数组中的位置。
解析:1. 初始化左指针`left`和右指针`right`,分别指向数组的第一个元素和最后一个元素。
2. 当`left <= right`时,执行以下操作:a. 计算中间位置`mid = (left + right) // 2`。
b. 如果`arr[mid] == target`,则返回`mid`。
c. 如果`arr[mid] < target`,则将左指针`left`更新为`mid + 1`。
d. 如果`arr[mid] > target`,则将右指针`right`更新为`mid - 1`。
3. 如果遍历完数组仍未找到目标元素,则返回-1表示未找到。
代码实现(Python):```pythondef binary_search(arr, target):left, right = 0, len(arr) - 1while left <= right:mid = (left + right) // 2if arr[mid] == target:return midelif arr[mid] < target:left = mid + 1else:right = mid - 1return -1arr = [1, 3, 5, 7, 9]target = 5result = binary_search(arr, target)print(result) # 输出:2```。
折半查找算法(Python版)

折半查找算法(Python版)⽬录介绍⼆分查找也称折半查找(Binary Search),它是⼀种效率较⾼的查找⽅法。
但是,折半查找要求线性表必须采⽤顺序存储结构,⽽且表中元素按关键字有序排列。
前提必须待查找的序列有序时间复杂度O(log2n)原理1)确定该期间的中间位置K2)将查找的值t与array[k]⽐较,若相等,查找成功返回此位置;否则确定新的查找区域,继续⼆分查找。
3)区域确定过程:若array[k]>t,由于数组有序,所以array[k,k+1,……,high]>t;故新的区间为array[low, ..., K-1];反之,若array[k]<t对应查找区间为array[k+1, ..., high]#!/usr/bin/env python# -*- coding: utf-8 -*-# @Date : 2020-07-10# @Author : 流柯# @desc : ⼆分查找算法,python版def serach(array, t):array.sort() #排序,保证列表是有序的low = 0height = len(array) - 1while low <= height:k = (low + height) // 2if array[k] < t:low = k + 1elif array[k] > t:height = k - 1else:return k #找到后返回位置return -1 #找不到返回-1array = [1, 3, 5, 7, 9, 6, 8, 0]print(serach(array, 5))End。
实现顺序查找和折半查找的算法

实现顺序查找和折半查找的算法顺序查找和折半查找(也称为二分查找)是两种常见的查找算法。
以下是它们的Python实现:1. 顺序查找:```pythondef sequential_search(list, item):pos = 0found = Falsewhile pos < len(list) and not found:if list[pos] == item:found = Trueelse:pos = pos+1return found```这个函数会检查列表中的每个元素,直到找到匹配的元素或者遍历完整个列表。
如果找到匹配的元素,函数会返回True,否则返回False。
2. 折半查找:```pythondef binary_search(list, item):low = 0high = len(list) - 1mid = 0found = Falsewhile low <= high and not found:mid = (high + low) // 2if list[mid] == item:found = Trueelif list[mid] < item:low = mid + 1else:high = mid - 1return found```这个函数使用二分查找算法,每次比较列表中间的元素和目标元素。
如果中间元素等于目标元素,函数返回True。
如果中间元素小于目标元素,函数在列表的右半部分继续查找。
如果中间元素大于目标元素,函数在列表的左半部分继续查找。
如果函数遍历完整个列表都没有找到目标元素,那么返回False。
折半查找——精选推荐

折半查找折半查找1. 算法思想2. 算法实现3. 查找判定树4. 折半查找效率折半查找的算法思想折半查找,⼜称“⼆分查找”,仅适⽤于有序的顺序表33>mid,往右查右指针到⼀个位置就-1,左指针到⼀个位置就+1low>high,查找失败折半查找的实现typedef struct{ElemType *elem;int TableLen;}SSTable;//折半查找(升序)int Binary_Search(SSTable L,ElemType key){int low = 0,high = L.TableLen-1,mid;while(low<=high){mid = (low+high)/2; //取中间位置if(L.elem[mid] == key)return mid; //查找成功则返回所在位置else if(L.elem(mid)>key)high = mid -1; //从前半部分继续查找elselow = mid +1; //从后半部分继续查找}return -1; //查找失败,返回-1}顺序表拥有随机访问的特性,链表没有查找效率复分析查找判定树的构造如果当前low和high之间有奇数个元素,则mid分隔后,左右两个部分元素个数相等如果当前low和high之间有偶数个元素,则mid分隔后,左半部分⽐右半部分少⼀个元素折半查找的判定树中,若 mid=向下取整(low+high)/2,对于任何⼀个结点,必有:右⼦树结点-左⼦树结点=0或1⾃⼰过⼀遍顺序,1个元素,2个元素,。
折半查找的判定树⼀定是平衡⼆叉树因此,元素个数为n时树⾼h=⌈log2(n+1)⌉计算完全⼆叉树也相同满⾜⼆叉排序树的定义失败节点:n+1个,等于成功结点的空链域数量知识回顾⼤部分情况下折半查找速度都⽐顺序查找快。
但是不⼀定哦从上去整,不⼀样哦,左边的⽐较多Processing math: 100%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
折半查找法例题
折半查找法,也称为二分查找法,是一种查找有序数组中特定元素的高效算法。
它通常比线性查找更快,因为它可以将搜索范围缩小一半。
下面是一个折半查找法的例题:
假设有一个有序数组:[1, 3, 5, 7, 9, 11, 13, 15, 17, 19],请使用折半查找法查找数字13的位置。
解题步骤如下:
1. 定义左右指针l和r,分别指向数组的开头和结尾。
2. 计算出中间位置mid,也就是(l + r) / 2。
3. 比较中间位置mid上的元素和目标元素13的大小关系。
4. 如果中间位置上的元素比目标元素要大,说明目标元素可能在左半边,将右指针r更新为mid - 1。
5. 如果中间位置上的元素比目标元素要小,说明目标元素可能在右半边,将左指针l更新为mid + 1。
6. 重复步骤2-5,直到找到目标元素或者左右指针相遇为止。
7. 如果左右指针相遇且相遇位置上的元素不是目标元素,则说明目标元素不在数组中。
根据上述步骤,我们可以得出结论,数字13在数组中的位置是6,也就是数组的第7个元素。
- 1 -。
