南京邮电大学 大学物理 上 13_2动生电动势和感生电动势
合集下载
大学物理之动生电动势和感生电动势

13
12.2 动生电动势和感生电动势
第12章 电磁感应
感应电动势做功,洛伦兹力不做功?
rr F ⋅V
r =(f +
r f
'
)
⋅
(vr
+
vr'
)
=
r f
⋅vr'+
fr'⋅vr
= −evBv '+ev ' Bv
Fr
r f'
−e
vrr' f
r B vr
Vr
=0
洛伦兹力做功为零。
14
12.2 动生电动势和感生电动势
=
1 2
Bθ L2
回路中的电动势
ω
εi
=
−
dΦm dt
= − 1 BL2 dθ 2 dt
= − 1 BωL2 2
方向由楞次定律确定:
A
θ
o
C
r B
方向沿 A→O AC 、CO段没有动生电动势 25
12.2 动生电动势和感生电动势
第12章 电磁感应
例:法拉第电机。设铜盘的半径为 R,角速度为ω。 求:盘上沿半径方向产生的电动势。
423) ) )求 确 确导 定 定线vrvr元和× 上BBvr的与的电夹d动lr角的势θ夹d1,ε角=θ(2vr,
×
r B
)
⋅
r dl
dl υ -a
∫ 5)由动生电动势定义求解。ε =
+
vBdl
若 6)ε动> 生0,电则动ε势的的方方向向与:dlrr 若ε < 0,则 ε 的方向与 dl
−
同向; 反向。
动生电动势,等于从起点到终点的直导线所产 生的动生电动势 。
12.2 动生电动势和感生电动势
第12章 电磁感应
感应电动势做功,洛伦兹力不做功?
rr F ⋅V
r =(f +
r f
'
)
⋅
(vr
+
vr'
)
=
r f
⋅vr'+
fr'⋅vr
= −evBv '+ev ' Bv
Fr
r f'
−e
vrr' f
r B vr
Vr
=0
洛伦兹力做功为零。
14
12.2 动生电动势和感生电动势
=
1 2
Bθ L2
回路中的电动势
ω
εi
=
−
dΦm dt
= − 1 BL2 dθ 2 dt
= − 1 BωL2 2
方向由楞次定律确定:
A
θ
o
C
r B
方向沿 A→O AC 、CO段没有动生电动势 25
12.2 动生电动势和感生电动势
第12章 电磁感应
例:法拉第电机。设铜盘的半径为 R,角速度为ω。 求:盘上沿半径方向产生的电动势。
423) ) )求 确 确导 定 定线vrvr元和× 上BBvr的与的电夹d动lr角的势θ夹d1,ε角=θ(2vr,
×
r B
)
⋅
r dl
dl υ -a
∫ 5)由动生电动势定义求解。ε =
+
vBdl
若 6)ε动> 生0,电则动ε势的的方方向向与:dlrr 若ε < 0,则 ε 的方向与 dl
−
同向; 反向。
动生电动势,等于从起点到终点的直导线所产 生的动生电动势 。
13-2动生电动势与感生电动势 - 没有幻灯片标题
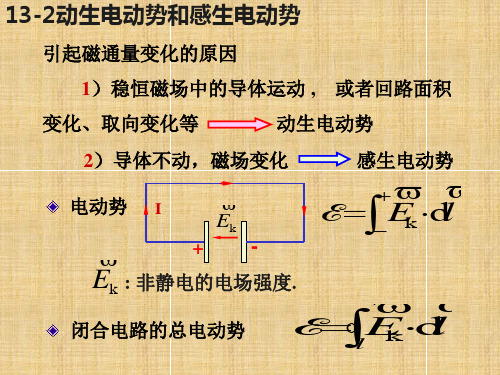
v B d r rB d r
解 d E i (v B )d r v B d r r B d r
2R2
Ei RR12rBdr
.R1 rdr
o
N
B
12B(R12 R22)
22V 6
. . M
B
Ei o'
圆盘边缘的电势高于 中心转轴的电势.
已知 R11.2m, d1.0103m, 52πrasd1
+++++++
Ei
1 2
BL2
(点
P
E i 方向 O
的电势高于点
O
P 的电势)
例2 一导线矩形框的平面与磁感强度为 B的均
匀磁场相垂直.在此矩形框上,有一质量为 m长为 l的
可移动的细导体棒 MN; 矩形框还接有一个电阻 R,
其棒值以较速之 度导v0线沿的如电图阻所值示要的大矩得形很框多运.若动,开试始求时棒,的细速导率体
Φ Bds S
LE kdlddt
B ds
S
EiLE kdl Sd d B t ds
感生电场和静电场的对比
E静 和 Ek 均对电荷有力的作用.
静电场是保守场
LE静dl 0
感生电场是非保守场 LEkdlddΦ t 0
静电场由电荷产生;感生电场是由变化的磁 场产生 .
例 4 设有一半径为R ,高度为 h 的铝圆盘, 其电导
与点 N重合即 0
则 t 时刻 t
Φ12B(R12R22)t
Ei
dΦ dt
方向与回路 MNOM绕向
相反,即盘缘的电势高于中心.
12B(R12 R22)
二 感生电动势
大学物理电磁感应定律与动生电动势

13-1 电磁感应定律
一、电磁感应现象
1、电磁感应现象的发现
•1820年,Oersted发现了电流的磁效应 •1831年11月24日,Faraday发现电磁感应现象 •1834年,Lenz在分析实验的基础上,总结出了 判断感应电流分向的法则 •1845年,Neumann借助于安培的分析,从矢势的 角度推出了电磁感应电律的数学形式。
d
dt
负号表示感应电动势 总是反抗磁通的变化
单位:1V=1Wb/s
n 0
n
B
0
2、电动势方向:
L
0, 0
与 L 反向
L
B
0, 0
与L 同向
•确定回路绕行方向;规定电动势的方向与回路的绕行方向一致时 为正。
•根据回路的绕行方向,按右手螺旋法则定出回路所包围面积的正 法线方向;在根据回路所包围面积的正法线方向,确定磁通量的 正负; •根据磁通量变化率的正负来确定感应电动势的方向。
•通过一个闭合回路所包围的面积的磁通量发生变化时,不
管这种变化是由什么原因引起的,回路中就有电流产生,
这种现象称为电磁感应现象。
•感应电流:由于通过回路中的磁通量发生变化,而在回路
中产生的电流。
•感应电动势:由于磁通量的变化而产生的电动势叫感应电
动势。
二、法拉第电磁感应定律
1、内容:
当穿过闭合回路所包围面积的磁通量发生变化时,不论这种 变化是什么原因引起的,回路中都有感应电动势产生,并且 感应电动势正比于磁通量对时间变化率的负值。
势公式
Em
i
b a
Fm e
Em
v
dl
B
b a
v
B
dl
2.动生和感生电动势

mv 其中 所以 R = eBR 电子在 E旋 作用下做加速运动,
BR 为半径R处的磁场大小,
(1)
dΦ ∫ E旋 ⋅ dl = − dt = 2πRE旋 L
1 dΦ E旋 = − 所以 2πR dt
上式为我们提供了计算 E旋 的方法, 因此
由牛顿第二定律 令, 所以,
t = 0,
d (mv ) e dΦ e = −eE旋 = ⇒ d (mv ) = dΦ dt 2πR dt 2πR
ω=
dθ dt
θ = ∫ ωdt = θ 0 + ωt = ωt ⇒ ε = NBSω sin ωt
令 ε 0 = NBSω(为电动势的峰值)⇒
ε = ε 0 sin ωt
讨论
(1) 在匀强磁场内转动的线圈中产生的电动势是随时间 作周期性变化的,周期为 2π ω 。在两个连续的半周期中, 电动势的方向相反。电动势经一次完全变化所需的时间, 叫做交流电的周期。1秒内电动势所作完全变化的次数, 叫做交流电的频率。我国的交流电频率是每秒50周(或50 赫兹,用 Hz 表示)
二. 感生电动势(又称涡旋场) 1. 涡旋电场 这时导体不动,只是磁场发生变化,这儿的非静电力 是什么呢?显然,不会是洛仑兹力。实践表明,感生电动 势完全与导体的种类和性质无关。这说明感生电动势是由 变化的磁场本身引起的。唯一的解释为:变化的磁场在其 周围也会激发出一种电场,这种电场是一种涡旋电场,其 电力线是闭合的。麦克斯韦认为:无论有没有回路存在, 只要空间的磁场发生变化,那么一定会在空间产生涡旋电 场。 表达式: 因为这种涡旋电场正是产生感应电动势的 非静电力 Fk ,即 Fk = qE旋 ,所以
(4) 导体切割磁力线时才能产生动生电动势(由上式可 以看得很清楚), 因为
大学物理动生电动势和感生电动势全篇

第十三章电磁感应
步骤:
dm
dt
b
a (v B) dl
1) 约定 右旋
2)求磁通
3)根据公式计算
1)取线元 dl ,并规定其方向
2)
写出
d
(v
B)
dl
3)确定积分范围,并积分
若结果 0,则
说明 实 与 相反
若结果 0,则
说明 实与 dl 相反
10 - 2 动生电动势和感生电动势
第十三章电磁感应
感生电场和静电场的对比
E静 和 Ek 均对电荷有力的作用.
静电场是保守场 L E静 dl 0
感生电场是非保守场
dΦ L Ek dl dt 0
静电场由电荷产生;感生电场是由变化的磁 场产生 .
10 - 2 动生电动势和感生电动势
第十三章电磁感应
例:将磁铁插入非金属环中,环内有无感
坩锅外的线圈中通交流电 电磁炉:交变磁场作用于金属锅底,产生
大量涡流
2. 电磁阻尼摆
涡电流的弊
热效应过强、温度过高, 易破坏绝缘,损耗电能,还可能造成事故
10 - 2 动生电动势和感生电动势
第十三章电磁感应
减少涡流 1、选择高阻值材料(硅钢、矽钢等) 2、多片铁芯组合
感生电场充当着产生感应电动势
的非静电力。
闭合回路中的感生电动势
L
Ek
dl
dΦ dt
10 - 2 动生电动势和感生电动势
第十三章电磁感应
闭合回路中的感生电动势
L
Ek
dl
dΦ dt
Φ SB dS
d
L Ek
dl
dt
B dS
S
S不变
动生电动势与感生电动势
0
0
0
v v
dl b
0
0
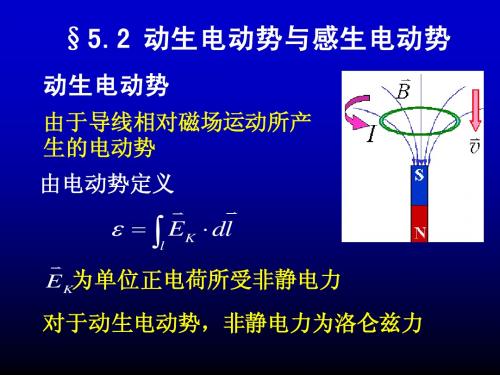
感生电动势 涡旋电场
感生电动势: 感生电动势:由于磁场随时 间变化所产生的电动势 问题: 问题:产生感应电动势的 非静电力是什么? 非静电力是什么? 麦克斯韦假设: 麦克斯韦假设: 在变化磁场的周围将产生电场, 在变化磁场的周围将产生电场,这种 电场称为感生电场 感生电场或 电场称为感生电场或涡旋电场
例3:电子感应加速器。在涡旋电场作用下, :电子感应加速器。在涡旋电场作用下, 电子可以被加速到 10-100MeV v 求:感生电场场强 已知: 已知:∂B
∂t
铁 芯 磁场 B 线圈
电 子 束
环形 真空室
S
×
× × × × ×
× × × × ×
× × × × ×
× × × × ×
r ∂B E感 = − 2 ∂t v 负号说明 E感与所设方向相反
§5.2 动生电动势与感生电动势
动生电动势
由于导线相对磁场运动所产 生的电动势 由电动势定义
v v ε = ∫ EK ⋅ dl
v EK为单位正电荷所受非静电力
对于动生电动势, 对于动生电动势,非静电力为洛仑兹力
l
洛仑兹力
v EK =
v fm
v v v fm = ev × B
e v v = v ×B
L
×
L×
R
× × × ×
× × × ×
× × × ×
× × × ×
在磁场域外( 在磁场域外(r>R) ) v v ∂B 2 ∫L E感 ⋅ dl = E感 ⋅ 2π r = − ∂t πR
R2 ∂B E感 = − 2r ∂t
× × × ×
0
0
v v
dl b
0
0
感生电动势 涡旋电场
感生电动势: 感生电动势:由于磁场随时 间变化所产生的电动势 问题: 问题:产生感应电动势的 非静电力是什么? 非静电力是什么? 麦克斯韦假设: 麦克斯韦假设: 在变化磁场的周围将产生电场, 在变化磁场的周围将产生电场,这种 电场称为感生电场 感生电场或 电场称为感生电场或涡旋电场
例3:电子感应加速器。在涡旋电场作用下, :电子感应加速器。在涡旋电场作用下, 电子可以被加速到 10-100MeV v 求:感生电场场强 已知: 已知:∂B
∂t
铁 芯 磁场 B 线圈
电 子 束
环形 真空室
S
×
× × × × ×
× × × × ×
× × × × ×
× × × × ×
r ∂B E感 = − 2 ∂t v 负号说明 E感与所设方向相反
§5.2 动生电动势与感生电动势
动生电动势
由于导线相对磁场运动所产 生的电动势 由电动势定义
v v ε = ∫ EK ⋅ dl
v EK为单位正电荷所受非静电力
对于动生电动势, 对于动生电动势,非静电力为洛仑兹力
l
洛仑兹力
v EK =
v fm
v v v fm = ev × B
e v v = v ×B
L
×
L×
R
× × × ×
× × × ×
× × × ×
× × × ×
在磁场域外( 在磁场域外(r>R) ) v v ∂B 2 ∫L E感 ⋅ dl = E感 ⋅ 2π r = − ∂t πR
R2 ∂B E感 = − 2r ∂t
× × × ×
12--2-3、动生、感生电动势共43页PPT资料
§12-3感生电动势
1、问题的提出 2、麦克斯韦假设:当空间的磁场发生变化时, 会产生一种电场。
3、感i 生电L E 场感 和d 变l 化 的 磁d d 场m 之间 t 的关S 系 B t d S
{ 感生电LE 场 感 的d 性l 质 方 程:S B t dS 0
SE感dS0
c)计( 算B )Bdl 的的大大小小、和方方向向((θ1θ)2),;再确定
d)积分计算;
+ 若 _ 则表示,εi的方向与规定的
同向 反向
例1)如图,一长为L的细铜棒在均匀磁场中以角
速度旋转,求铜棒中的动生电动势。
B
v
已知:.B.L
求: i
vl
i dl
ol
d 解 取: 一i建 dl 立( ,v 其i 速B 分 度) 割为Ld v l
vBdl
L
L
i Ld 1 iBL20 (负v号B 说明 d i0 实 l与li B 相反)d
2
例题三角2)形一线“圈A”BC长以直速导率线v 载垂有直电离流开I,长与导其线共,面求有一
处于图中位置时线圈中的感应电动势。
已知:I,a,b,c,v
求: i
I
B
c A
a
v
解(i 1):L(选v (v i B 正 B )方)向d d l Al BCA
N
棒中 i Bvl 且由 M N
棒所受安培力
FIBl B2l2v
Rl
B
I
F
v
方向沿ox轴反向 R
o
M
x
FIBl B2l2v R
棒的运动方程为
mdv B2l2v
dt
R
方向沿ox轴反向
感生电动势和动生电动势PPT教学课件
古代希腊
在古希腊早期的数学家 中,毕达哥拉斯的影响 是最大的。毕达哥拉斯 定理(即勾股定理)是毕 达哥拉斯的主要贡献该 定理对数学的发展起到 了巨大的促进作用。此 外,毕达哥拉斯在音乐、 天文、哲学方面也做出 了一定贡献,首创地圆 说,认为日、月、五星 都是球体,浮悬在太空 之中。
古代罗马
盖伦(Calen)是古罗马时 期最著名最有影响的医学 大师,他被认为是仅次于 希波克拉底的第二个医学 权威。盖伦是最著名的医 生和解剖学家。他一生专 心致力于医疗实践解剖研 究,写作和各类学术活动。
5感生电动势和动生电动势
一.感应电场与感生电动势
一个闭合电路静止于磁场中,由 于磁场强弱的变化,闭合电路内 产生了感应电动势.这种情况下, 哪一种作用扮演了非静电力的 角色?
磁场变强
英国物理学家麦克斯韦在他的电磁场理论 中指出,变化的磁场会在空间激发一种电场, 这种电场对电荷会产生力的作用如果此刻 周围空间存在闭合导体,导体中自由电荷会
克娄巴特拉七世,著名埃及女王, 凯撒之情人,安东尼之妻。只活了 39岁,却做了22年女王。她的野心 和魅力,在关键时候对罗马政治曾 产生很大影响。莎士比亚这么形容 “争强好胜的女王,你无论做什么 都是那么得体,责怪也好,笑也好, 哭也好;你的每一种情绪都充分地 力图表现得美好而动人”。
埃及女王克娄巴特拉
古代罗马
凯撒,古罗马统帅,政治家,出身 贵族,前62年与庞培、克拉苏秘密 结盟,史称"前三头同盟"。经连年 征战,凯撒获得终身独裁官、执政 官、保民官等职,兼领大将军、大 祭司长荣衔,并被尊为"祖国之父", 成为无冕之王。其代表作《高卢战 记》、《内战记》是研究古罗马军 事历史的重要文献(见凯撒的军事 思想)。凯撒的独裁统治动摇了罗 马的共和政体,激起贵族共和派的 强烈反对。前44年3月15日,他在 元老院议事厅被布鲁图、喀西约等 人阴谋刺杀。
13-2动生电动势
C A O
π OC vB cos( )dl 2
vBL sin
金属杆中的动生电动势为
v
AO OC vBL sin
其方向为由O指向C
13.2 动生电动势
例15.4: 直导线ab以v沿平行与长直载流导线的方向运 动,ab与直导线共面,且与它垂直。设直导线中的电 流强度为I,导线ab长为L,a端到直导线的距离为d, 求导线ab中的动生电动势,并判断哪端电势较高。 解法一:
R
13.2 动生电动势
安培力
F IL B
F BIL B
R
L
R
B
——安培力的方向水平向右 导体棒ab上的电流方向: 沿b→a
m gsin θ
I F
13.2 动生电动势
安培力在斜面上的分力与重力在 斜面的分力相平衡
B
R
L cos m g sin
+ _
F 洛伦兹力对应的非静电场强度 E v B k e b b 动生电动势 Ek dl (v B) dl
a a
在磁场中运动的导线ab是一个电动势源,相对 应的非静电场力是洛伦兹力。
13.2 动生电动势
当回路中只有部分导线在磁场中运动
动时,又在洛伦兹力的作 用下 u以向a 端运动 电子同时参与了向右和向 下的运动,电子的合速度
b
F
v
uv
vu
u
a
电子受到的总洛伦兹力
F e(v u ) B
总洛伦兹力与电子的合速度垂直,不对电子做功
13.2 动生电动势
π OC vB cos( )dl 2
vBL sin
金属杆中的动生电动势为
v
AO OC vBL sin
其方向为由O指向C
13.2 动生电动势
例15.4: 直导线ab以v沿平行与长直载流导线的方向运 动,ab与直导线共面,且与它垂直。设直导线中的电 流强度为I,导线ab长为L,a端到直导线的距离为d, 求导线ab中的动生电动势,并判断哪端电势较高。 解法一:
R
13.2 动生电动势
安培力
F IL B
F BIL B
R
L
R
B
——安培力的方向水平向右 导体棒ab上的电流方向: 沿b→a
m gsin θ
I F
13.2 动生电动势
安培力在斜面上的分力与重力在 斜面的分力相平衡
B
R
L cos m g sin
+ _
F 洛伦兹力对应的非静电场强度 E v B k e b b 动生电动势 Ek dl (v B) dl
a a
在磁场中运动的导线ab是一个电动势源,相对 应的非静电场力是洛伦兹力。
13.2 动生电动势
当回路中只有部分导线在磁场中运动
动时,又在洛伦兹力的作 用下 u以向a 端运动 电子同时参与了向右和向 下的运动,电子的合速度
b
F
v
uv
vu
u
a
电子受到的总洛伦兹力
F e(v u ) B
总洛伦兹力与电子的合速度垂直,不对电子做功
13.2 动生电动势
动生电动势和感生电动势
−
a
注意Biblioteka r r r ε = ∫ (v × B)⋅ dl
b a
ε 是标量, (1)ε 是标量,ε > 0 时, 的方向由 a ε 到 b ,ε < 0 时, 的方向由 b 到 a ; r r r r B 的速度, (2)v 是导体线元 dl 的速度, 是 dl 所在处的磁感应强度; 所在处的磁感应强度; r r r (3)( v × B ) ⋅ dl 中有两个夹角 α 和 β , r r r r α v 其中 v × B = vB sin α , = 0时, × B = 0 ; r r r (v × B ) ⋅ dl = vB sin α cos βdl .
vµ0 I 0.3 ln = = −4.4 × 10− 6 ( V ) 2π 0.1
指向. 电动势的方向 B 由 A 指向.
一.感生电动势:一个静止的导体回 B 感生电动势: 当它包围的磁场发生变化时, 路,当它包围的磁场发生变化时,
L
穿过它的磁通量也会发生变化, 穿过它的磁通量也会发生变化, 这时回路也会产生感应电动势。 这时回路也会产生感应电动势。 二、感生电动势产生的原因
感生电动势 r r r r dφ m d ε = ∫ E 感 ⋅ dl = − = − ∫∫ B ⋅ dS dt dt S L r r r Q E = E 静 + E感
r r ∫ E 静 ⋅ dl = 0
L
r r r ∂B r ∫ E感 ⋅ dl = − ∫∫ ∂t ⋅ dS L S
r r r ∂B r ∫ E ⋅ dl = − ∫∫ ∂t ⋅ dS L S
r u
实例: 实例:法拉第利用一半径为 R 的铜盘在均 r 中转动, 匀磁场 B 中转动,角速度为ω .求盘上沿半径 方向产生的感应电动势.解法见例1 方向产生的感应电动势.解法见例1.
a
注意Biblioteka r r r ε = ∫ (v × B)⋅ dl
b a
ε 是标量, (1)ε 是标量,ε > 0 时, 的方向由 a ε 到 b ,ε < 0 时, 的方向由 b 到 a ; r r r r B 的速度, (2)v 是导体线元 dl 的速度, 是 dl 所在处的磁感应强度; 所在处的磁感应强度; r r r (3)( v × B ) ⋅ dl 中有两个夹角 α 和 β , r r r r α v 其中 v × B = vB sin α , = 0时, × B = 0 ; r r r (v × B ) ⋅ dl = vB sin α cos βdl .
vµ0 I 0.3 ln = = −4.4 × 10− 6 ( V ) 2π 0.1
指向. 电动势的方向 B 由 A 指向.
一.感生电动势:一个静止的导体回 B 感生电动势: 当它包围的磁场发生变化时, 路,当它包围的磁场发生变化时,
L
穿过它的磁通量也会发生变化, 穿过它的磁通量也会发生变化, 这时回路也会产生感应电动势。 这时回路也会产生感应电动势。 二、感生电动势产生的原因
感生电动势 r r r r dφ m d ε = ∫ E 感 ⋅ dl = − = − ∫∫ B ⋅ dS dt dt S L r r r Q E = E 静 + E感
r r ∫ E 静 ⋅ dl = 0
L
r r r ∂B r ∫ E感 ⋅ dl = − ∫∫ ∂t ⋅ dS L S
r r r ∂B r ∫ E ⋅ dl = − ∫∫ ∂t ⋅ dS L S
r u
实例: 实例:法拉第利用一半径为 R 的铜盘在均 r 中转动, 匀磁场 B 中转动,角速度为ω .求盘上沿半径 方向产生的感应电动势.解法见例1 方向产生的感应电动势.解法见例1.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1 的均匀 磁场中,以角速度 在与磁场方向垂直的平面上绕 棒的一端转动,求铜棒两端的感应电动势. 解
一长为 L 的铜棒在磁感强度为 B
+ + + dl + + +
d Ei (v B) dl
vBdl
L
+ + + + + + + + + + + +
+ + P + + + + +
二
感生电动势 产生感生电动势的非静电场 感生电场
麦克斯韦尔假设 变化的磁场在其周围空间激 发一种电场,这个电场叫感生电场 E .
k
dΦ 闭合回路中的感生电动势 E i Ek dl L dt
Φ B ds
d L Ek dl dt SB ds S dB E i Ek dl ds L S dt
则圆环中的感生电动势的值为
r
dr
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
由计算得圆环中电流
Hale Waihona Puke kh dI rdr 2
于是圆盘中的感应电流为
r
dr
h
r
dr
kh R I dI 0 rdr 2 1 2 kR h 4
2 2 2 2
方向沿 ox轴反向
N
则
dv B l v m dt R 2 2 v dv t B l v0 v 0 mR dt
R l
B
F
v
M
o
x
计算得棒的速率随时间变化的函数关系为
v v0 e
( B 2l 2 mR ) t
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
h
R
h
r
dr
B
13 - 2 动生电动势和感生电动势
已知 求
R , h , , B , dB dt k
I
第十三章电磁感应 电磁场
r
dr
h
解 如图取一半径为 r ,宽度 为dr ,高度为 h 的圆环.
dB E i Ek dl ds L S dt dB 2 代入已知条件得 E i Sds k π r dt 1 2π r kh 又 dR rdr 所以 dI hdr 2
l
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
一 动生电动势
Fm (e)v B 平衡时 Fm Fe eEk Fm Ek v B e
动生电动势的非静电力场来源
洛伦兹力
+ + +P + + + + B ++ + + F+ + + + +
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
例 4 设有一半径为R ,高度为h 的铝圆盘, 其电导 率为 . 把圆盘放在磁感强度为 B 的均匀磁场中, 磁 场方向垂直盘面.设磁场随时间变化, 且 dB dt k 为一常量.求盘内的感应电流值.(圆盘内感应电流自 己的磁场略去不计) r dr
e
+ + + -+ + + + + + + -+ + + O+ +
Fm
+ v
+
+ + + +
E i
设杆长为
OP
Ek dl OP (v B ) dl
l
E vBdl vBl i
0
l
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
引起磁通量变化的原因
1)稳恒磁场中的导体运动 , 或者回路面积
变化、取向变化等 动生电动势 感生电动势
2)导体不动,磁场变化 电动势
I
Ek
+
Ek : 非静电的电场强度.
闭合电路的总电动势
-
E
Ek dl
E E k dl
随时间变化的函数关系. 解 如图建立坐标 棒中
第十三章电磁感应 电磁场
N N
E Blv i
且由 M
2 2
棒所受安培力
R l
B
B l v F IBl R 方向沿 ox轴反向
F
I
M
v
o
x
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
棒的运动方程为
B l v F IBl R
E vBdl i
0
B
o v + + +
Ei 方向 O P 1 2 E B L i (点 P 的电势高于点 O 的电势) 2
lBdl
0
L
+ + + + + + +
13 - 2 动生电动势和感生电动势
例2 一导线矩形框的平面与磁感强度为 B 的均 匀磁场相垂直.在此矩形框上,有一质量为 m长为 l 的 可移动的细导体棒 MN ; 矩形框还接有一个电阻 R , 其值较之导线的电阻值要大得很多.若开始时,细导体 棒以速度 v0 沿如图所示的矩形框运动,试求棒的速率
13 - 2 动生电动势和感生电动势
第十三章电磁感应 电磁场
感生电场和静电场的对比
E静 和 Ek 均对电荷有力的作用.
静电场是保守场
L
E静 dl 0
dΦ 感生电场是非保守场 L Ek dl dt 0
静电场由电荷产生;感生电场是由变化的磁 场产生 .
