线与角(习题及答案)
线与角的定义与表达(通用版)(含答案)

线与角的定义与表达(通用版)试卷简介:理解线段、射线、直线、角等基本概念,知道线段、射线、直线的区别和联系,会用符号表示线段、射线、直线、角等基本图形.掌握两个基本事实.一、单选题(共17道,每道5分)1.手电筒发射出来的光线,给我们的感觉是( )A.线段B.射线C.直线D.折线答案:B解题思路:手电筒发射出光线,给我们的感觉是手电筒是射线的端点,光的传播方向是射线的方向,因此给我们的感觉是射线.故选B.试题难度:三颗星知识点:线段、射线、直线2.下列各直线的表示方法:①直线A;②直线AB;③直线a;④直线ab,其中正确的有( )A.4个B.3个C.2个D.1个答案:C解题思路:直线可以用一个小写字母来表示,也可以用这条直线上的两个点来表示,如下图的直线可记作“直线”,也可记作“直线AB”或“直线BA”.因此②和③是正确的.故选C.试题难度:三颗星知识点:线段、射线、直线3.角是指( )A.由两条线段组成的图形B.由两条射线组成的图形C.由两条直线组成的图形D.由公共端点的两条射线组成的图形答案:D解题思路:角由两条具有公共端点的射线组成,两条射线的公共端点是这个角的顶点.故选D.试题难度:三颗星知识点:角的定义4.如图所示,下列说法正确的是( )A.直线AB和直线CD是不同的直线B.射线AC和射线BC是同一条射线C.线段AB和线段BA是同一条线段D.线段BC和线段BD是同一条线段答案:C解题思路:选项A中,点A,B,C,D在一条直线上,根据两点确定一条直线,选取其中的任意两点都可以确定这条直线,因此直线AB和直线CD是同一条直线,选项A说法错误;选项B中,射线AC是以A为端点,AC为方向的射线,射线BC是以B为端点,BC为方向的射线,射线AC和射线BC端点不同,因此是不同的射线,选项B说法错误;选项C中,线段有两个端点,没有方向,因此线段AB和线段BA是同一条线段,选项C说法正确;选项D中,线段BC的端点是B和C,线段BD的端点是B和D,因此线段BC和线段BD是不同的线段,选项D说法错误.故选C.试题难度:三颗星知识点:线段、射线、直线5.如图,下列说法正确的有( )①直线BA和直线AB是同一条直线②射线AC和射线AD是同一条射线③线段BD和线段DB是同一条线段④三条直线两两相交时,一定有三个交点A.1个B.2个C.3个D.4个答案:C解题思路:根据线段有两个端点,没有方向;射线有一个端点,有方向;直线没有端点,没有方向,可知①②③正确.三条直线两两相交时,可能交于同一点,也可能交于不同的三点,因此④说法错误,正确的有3个.故选C.试题难度:三颗星知识点:线段、射线、直线6.下列语句正确的是( )A.画直线AB=10cmB.延长直线ABC.画射线OB=3cmD.延长线段AB到点C,使BC=AB答案:D解题思路:线段不可延伸,可以度量;射线可以向一个方向延伸,不可度量;直线可以延伸,不可度量.因此只有选项D说法正确.故选D.试题难度:三颗星知识点:线段、射线、直线7.下列说法中,正确的是( )A.直线是射线长度的两倍B.线段AB是直线AB的一部分C.射线AB和射线BA是同一条射线D.直线、射线、线段中,线段最短答案:B解题思路:线段不可延伸,可以度量;射线可以向一个方向延伸,不可度量;直线可以延伸,不可度量.因此选项A和D说法错误.射线有端点和方向,射线AB和射线BA端点和方向都不同,因此不是同一条射线,选项C 说法错误.故选B.试题难度:三颗星知识点:线段、射线、直线8.下列说法中,错误的是( )A.角是由两条具有公共端点的射线组成的B.一条射线绕其端点旋转而成的图形叫做角C.大于直角的角不一定是钝角D.角的两边越长,表示的角就越大答案:D解题思路:角由两条具有公共端点的射线组成,两条射线的公共端点是这个角的顶点,角的两条边是两条射线,不可度量,与角的大小没有关系.角也可以看成是由一条射线绕着它的端点旋转而成的,因此选项A和B说法正确,选项D 说法错误;根据角的分类,大于90°而小于180°的角是钝角,等于180°的角是平角,等于360°的角是周角,因此选项C说法正确.故选D.试题难度:三颗星知识点:角的分类9.下列说法中,正确的是( )①两条射线组成的图形叫做角;②角的大小与边的长短有关;③角的两边可以一样长,也可以一长一短;④角的两边是两条射线.A.①②B.②④C.②③D.③④答案:D解题思路:角由两条具有公共端点的射线组成,两条射线的公共端点是这个角的顶点,角的两条边是两条射线,画图时可以画的长一点,也可以画的短一点,与角的大小没有关系.因此③④说法正确.故选D.试题难度:三颗星知识点:角的定义10.下列语句正确的是( )A.平角就是一条直线B.周角就是一条射线C.小于平角的角是钝角D.一周角等于四个直角答案:D解题思路:角可以看成是由一条射线绕着它的端点旋转而成的.一条射线绕它的端点旋转,当终边和始边成一条直线时,所成的角叫做平角.终边继续旋转,当它又和始边重合时,所成的角叫做周角.因此平角的特点是两条边成一条直线,但不能说平角就是一条直线;周角的特点是两条边重合成射线,但不能说周角是一条射线,因此选项A和B说法错误.小于平角的角是钝角、直角和锐角,因此选项C说法错误.一周角等于360°,一直角等于90°,因此一周角等于四个直角,因此选项D说法正确.故选D.试题难度:三颗星知识点:角的分类11.如图,下列说法错误的是( )A.∠B也可以表示为∠ABCB.∠BAC也可以表示为∠AC.∠1也可以表示为∠CD.以C为顶点且小于180°的角有3个答案:C解题思路:角有四种表示方法:①用一个大写字母(如∠A)表示,只有在顶点处只有一个角的情况下,才可用顶点处的一个字母来表示这个角;②用三个大写字母(如∠AOB)表示,其中顶点字母要写在中间,否则分不清这个字母究竟表示哪个角;③用一个希腊字母(如∠α,∠β,∠γ…)表示;④用一个数字表示(∠1,∠2…).因此选项A和B正确,选项C错误.以C为顶点且小于180°的角有:∠1,∠ACD和∠ACB,因此选项D正确.故选C.试题难度:三颗星知识点:角的表示12.如图,下列说法中正确的是( )A.∠BAC和∠DAE不是同一个角B.∠ABC和∠ACB是同一个角C.∠ADE可以用∠D来表示D.∠ABC可以用∠B来表示答案:D解题思路:角由两条具有公共端点的射线组成,两条射线的公共端点是这个角的顶点,两条射线是角的两条边.角有四种表示方法:①用一个大写字母(如∠A)表示,只有在顶点处只有一个角的情况下,才可用顶点处的一个字母来表示这个角;②用三个大写字母(如∠AOB)表示,其中顶点字母要写在中间,否则分不清这个字母究竟表示哪个角;③用一个希腊字母(如∠α,∠β,∠γ…)表示;④用一个数字表示(∠1,∠2…).因此选项D正确.故选D.试题难度:三颗星知识点:角的表示13.下面四个选项中,能用∠1,∠AOB,∠O三种方法表示同一个角的是( )A. B.C. D.答案:B解题思路:角有四种表示方法:①用一个大写字母(如∠A)表示,只有在顶点处只有一个角的情况下,才可用顶点处的一个字母来表示这个角;②用三个大写字母(如∠AOB)表示,其中顶点字母要写在中间,否则分不清这个字母究竟表示哪个角;③用一个希腊字母(如∠α,∠β,∠γ…)表示;④用一个数字表示(∠1,∠2…).故选B.试题难度:三颗星知识点:角的表示14.如图所示,下列各选项中不能表示同一个角的是( )A.∠1和∠ABFB.∠3和∠ACFC.∠α和∠BD.∠ACE和∠2答案:C解题思路:角有四种表示方法:①用一个大写字母(如∠A)表示,只有在顶点处只有一个角的情况下,才可用顶点处的一个字母来表示这个角;②用三个大写字母(如∠AOB)表示,其中顶点字母要写在中间,否则分不清这个字母究竟表示哪个角;③用一个希腊字母(如∠α,∠β,∠γ…)表示;④用一个数字表示(∠1,∠2…).故选C.试题难度:三颗星知识点:角的表示15.如图所示,由A到B有①、②、③、④四条路线,最短的线路选②的理由是( )A.因为它是直线B.两点确定一条直线C.两点间距离的定义D.两点之间,线段最短答案:D解题思路:两点之间的所有连线中,线段最短.试题难度:三颗星知识点:两点之间线段最短16.值日生每天值完日后,总是先把每一列最前和最后的课桌摆好,然后再依次摆中间的课桌,很快就能把课桌摆得整整齐齐,他们这样做的道理是( )A.两点之间线段最短B.两点之间直线最短C.两点确定一条线段D.两点确定一条直线答案:D解题思路:把每一列最前和最后的课桌看作两个点,两点确定一条直线,沿着这条直线摆放就会整整齐齐.故选D.试题难度:三颗星知识点:两点确定一条直线17.下列生活现象:①用两个钉子就可以把木条固定在墙上;②从A地到B地架设电线,总是尽可能沿着线段AB架设;③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;④把弯曲的公路改直,就能缩短路程.其中能用“两点之间,线段最短”来解释的现象有( )A.①②B.①③C.②④D.③④答案:C解题思路:①③是利用“两点确定一条直线”,②④是利用“两点之间,线段最短”.故选C.试题难度:三颗星知识点:两点之间线段最短。
数学线与角练习题

数学线与角练习题
1. 直线的斜率计算
给定两点A(2, 3)和B(5, 7),求直线AB的斜率。
2. 直线方程求解
已知直线l过点P(1, 2)且斜率为4,求直线l的方程。
3. 两条直线的交点
求直线2x - 3y + 1 = 0与直线x + y - 5 = 0的交点坐标。
4. 直线的倾斜角
若直线的斜率为-1/2,求该直线的倾斜角。
5. 角的计算
在三角形ABC中,若角A为60度,角B为45度,求角C的度数。
6. 角度的和差
计算角度120度与45度的和,以及它们之间的差。
7. 角度的倍数
若一个角的两倍加上30度等于150度,求这个角的度数。
8. 角度的补角和余角
给定一个角为75度,求它的补角和余角。
9. 正弦定理的应用
在三角形ABC中,若a=7,b=5,且角A=60度,求边c的长度。
10. 余弦定理的应用
在三角形ABC中,若a=6,b=8,c=10,求角B的余弦值。
11. 正切函数的计算
若角θ的正切值为3/4,求角θ的度数(结果保留两位小数)。
12. 正切函数的反函数
求arctan(1)的值,并将其转换为度数。
13. 角度的转换
将角度45度转换为弧度。
14. 弧度的转换
将弧度π/4转换为角度。
15. 角度的四则运算
计算(30度 + 45度) * (60度 - 20度) / 90度的结果。
线与角的题目及答案

线与角的题目及答案在初中数学中,线与角是一个不可或缺的部分,其运用广泛,涉及到许多重要概念。
对于学生来说,掌握线与角的题目和答案是非常重要的,因为这可以帮助他们更好地理解线性和角度的概念,并且有助于增强数学能力。
一、线的角度与方向问题在线性代数中,最常见的问题之一就是求两条线之间的角度。
该问题的答案可以用以下公式计算:cosθ = (a . b) / (|a | * |b|)其中,a和b分别是两条线的向量,a.b是它们的点积,|a|和|b|则是它们的长度。
这个公式可以用来计算两条线之间的夹角,然后可以将结果转换为弧度或度数。
另外,还有一个常见的问题是确定一条线相对于另一条线的方向。
该问题的答案可以使用向量叉积来解决。
具体而言,如果向量a和b之间的叉积为正,则说明向量a在向量b的左侧,如果叉积为负,则说明向量a在向量b的右侧。
二、角度与三角函数的问题许多线性问题涉及角度和三角函数,因此掌握它们的相关知识非常重要。
其中最常见的三角函数是正弦、余弦和正切。
这些函数可以用于表达一个角度的大小,也可以用于计算角度。
例如,如果我们知道一个三角形的两个角度和一侧的长度,则可以使用三角函数计算另两个边的长度。
具体而言,如果我们知道一个角的大小为θ,而该角的对边长度为a,则正弦函数、余弦函数和正切函数可以计算出这个角的相对大小:sin(θ) = a / ccos(θ) = b / ctan(θ) = a / b其中c是三角形的斜边长度。
三、向量与平面几何的问题线性问题与向量和平面几何有紧密的联系。
特别是,在三维空间中,向量可以用来表示直线和平面的位置,并且向量的叉积可以用来计算平面的面积。
例如,如果我们知道一个平面上的三个点的坐标,则可以使用向量的叉积来计算该平面的面积。
具体而言,如果我们将向量u和向量v定义为与这些点相连的向量,则该平面的面积等于向量u 和向量v的叉积的长度的一半。
总的来说,在数学中,线和角的问题是非常重要的一部分。
线与角测试题

线与角测试题1. 问题描述在几何学中,线与角是基本的概念。
掌握线与角的性质对于解决几何问题具有重要作用。
下面是一些关于线与角的测试题,希望能帮助你巩固相关知识点。
请根据每道题的要求做出正确的选择或填写答案。
2. 测试题题目一:在平面直角坐标系中,已知定点A(-3, 5),B(4, 1),C(-1, -2)。
连结AB、BC、CA,形成一个△ABC。
求△ABC内角A的度数。
题目二:在平面直角坐标系中,已知直线L1过点A(2, 4),斜率为-2。
直线L2过点B(-1, -3),与L1垂直相交。
求直线L2的方程。
题目三:已知直线L通过点A(1, -2)和B(4, 3),且过点C(3, 0)的垂直平分线也经过点A。
求直线L的方程。
题目四:已知直线L1的斜率为-1/2,过点A(-3, 4),垂直于直线L2。
直线L2过点B(1, 2)。
求直线L1和L2的交点坐标。
题目五:在平面直角坐标系中,已知角α的顶点为O(0, 0),且α的终边经过点A(-3, 4)。
求角α的度数。
题目六:已知∠ABC为直角,且AB = BC。
D为线段AC上的点,且BD垂直于AC。
若AC的长度为6,BD的长度为4,求线段AB的长度。
题目七:在三角形ABC中,∠B = 60°,AB = 6,AC = 8。
垂直平分线AD分别交BC、AB的延长线于点E和F。
求BE和CF的长度。
3. 答案及解析题目一:利用两点之间的距离公式求得AB、BC、CA的长度为√61、√26和√50。
根据余弦定理,利用向量的内积公式可以求得角A的余弦值为-0.6。
因此,角A的度数为cos^(-1)(-0.6)≈133.7°。
题目二:已知直线L1的斜率为-2,通过点A(2, 4),可以求得L1的方程为y = -2x + 8。
由于L2与L1垂直相交,所以L2的斜率为1/2。
通过点斜式,可以得到L2的方程为y - (-3) = 1/2(x - (-1)),即y = 1/2x - 5/2。
线与角的练习题

线与角的练习题线与角的练习题在数学中,线和角是基础概念,也是很多数学问题的关键要素。
通过练习题的形式,我们可以巩固对线和角的理解,培养数学思维和解决问题的能力。
本文将给出一些线与角的练习题,帮助读者更好地掌握这些概念并提升解题能力。
一、线的性质练习题1. 请画出以下线段的示意图,并标明它们的起点和终点:a) ABb) CDc) EF2. 下列线段中,哪些是相等的?a) AB和BCb) DE和EFc) GH和IJ3. 如果线段AB的长度是3cm,线段CD的长度是5cm,线段EF的长度是8cm,那么哪条线段最长?哪条线段最短?4. 如果线段AB和线段CD的长度之和等于线段EF的长度,那么线段AB和线段CD的长度分别是多少?二、角的性质练习题1. 请画出以下角的示意图,并标明它们的顶点:a) ∠ABCb) ∠DEFc) ∠GHI2. 以下哪些角是锐角?a) ∠ABCb) ∠DEFc) ∠GHI3. 以下哪些角是钝角?a) ∠ABCb) ∠DEFc) ∠GHI4. 如果∠ABC是直角,那么它的补角和余角分别是多少度?三、线与角的关系练习题1. 请画出以下线段和角的示意图,并标明它们的起点、终点和顶点:a) AB和∠ABCb) CD和∠CDEc) EF和∠EFG2. 如果∠ABC是直角,线段AB的长度是5cm,那么∠ABC的补角和余角分别是多少度?3. 如果线段AB和线段CD的长度相等,且∠ABC和∠CDE相等,那么线段AB 和线段CD之间的夹角是多少度?4. 如果线段AB和线段CD的长度之和等于线段EF的长度,且∠ABC和∠CDE 的和等于∠EFG,那么线段AB和线段CD的长度分别是多少?通过以上练习题,我们可以锻炼对线和角的认识和理解,提高解题的能力。
在解题过程中,需要注意线段的起点、终点和长度,以及角的顶点和类型(锐角、钝角、直角)。
这些练习题不仅有助于巩固基础知识,还能培养数学思维和解决问题的能力。
北师大版四年级数学上册《第二单元 线与角》测试题及答案
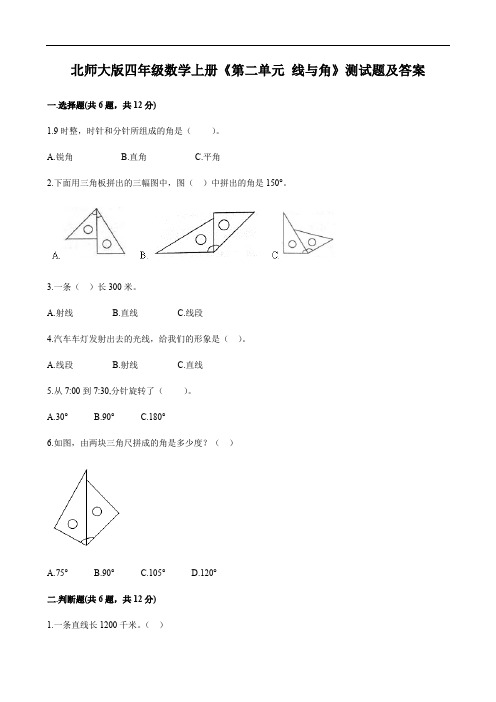
北师大版四年级数学上册《第二单元线与角》测试题及答案一.选择题(共6题,共12分)1.9时整,时针和分针所组成的角是()。
A.锐角B.直角C.平角2.下面用三角板拼出的三幅图中,图()中拼出的角是150°。
3.一条()长300米。
A.射线B.直线C.线段4.汽车车灯发射出去的光线,给我们的形象是()。
A.线段B.射线C.直线5.从7:00到7:30,分针旋转了()。
A.30°B.90°C.180°6.如图,由两块三角尺拼成的角是多少度?()A.75°B.90°C.105°D.120°二.判断题(共6题,共12分)1.一条直线长1200千米。
()2.钝角>锐角>直角。
()3.线段是直的,可以量出长度。
()4.一条射线长10厘米。
()5.手电筒和太阳射出来的光线,都可以看作是射线。
()6.用10倍的放大镜看一个20°的角,结果是200°。
()三.填空题(共6题,共27分)1.数一数,填一填。
(1)锐角是______、______、______、______(2)直角是______、______(3)钝角是______、______。
2.线段有()个端点,直线()端点,射线只有()个端点。
()可以测量长度,()和()都可以无限延伸。
()和()都是直线的一部分。
3.一个角是89度,它是______角,一个平角等于______个直角,一个周角等于______平角,一个周角等于______直角。
4.量角时,角的顶点要与量角器的______重合,角的一边要与量角器的______重合,而角的另一边所对量角器的度数就是这个角的大小。
5.量角的大小,要用_____,角的计量单位是_____,用符号_____表示。
6._____时整,时针和分针成平角;钟面上3时整,时针和分针成_____角。
四.计算题(共1题,共5分)1.量一量,算一算。
《第四单元 线和角》单元测试卷及答案
《第四单元线和角》单元测试卷及答案一、选择题(共5题,共计20分)1、度量一个角,角的一边对着量角器外圈上“180”的刻度,另一条边对着量角器内圈上“70”的刻度,这个角是()。
A.70ºB.110ºC.180º2、—条线段中间有2个点,那么一共有()条线段。
A.3B.5C.63、小学生红领巾的顶角是150°,其中的一个底角是()度.A.60B.30C.154、下面3个答案中,正确的是()A.一号羽毛比较长.B.二号羽毛比较短.C.三号羽毛最长.5、你认为下面哪一句话的表述是正确的?()A.一条线段长5厘米B.一条射线长5厘米C.一条直线长5厘米二、填空题(共8题,共计24分)6、如图中,直线有________条,射线有________条,锐角有________个,直角有________个,钝角有________个.7、线段有________个端点,射线有________个端点。
8、把平角分成两个角,其中一个角是锐角,另一个角一定是________。
9、钟面上,3 时整时,时针和分针构成________角,7 时整时,时针和分针构成________角。
10、小红用断了一截的卷尺量一根木头的长度,她从2米处开始量,最后落到7米处,这根木头________米长.11、如图,相互平行的线段有________组,如线段________和线段________;相互垂直的线段有________组,如线段________和线段________。
图中共有________个锐角,________个直角,________个钝角。
12、哪个角比直角小,将序号填在横线上。
________13、一个周角=________个平角=________个直角.三、判断题(共4题,共计8分)14、图中∠1=∠3,∠2=∠4。
()15、正北方向与西北方向的夹角是45°.()16、书边.黑板边.桌子的边都可以看成线段。
线与角练习题
线与角练习题一、选择题1. 直线AB和直线CD相交于点O,若∠AOC = 130°,则∠BOD的度数是多少?A. 130°B. 对顶角C. 50°D. 180°2. 在平面直角坐标系中,直线y = 2x + 3与x轴相交于点P,求点P 的坐标。
A. (-1, 0)B. (1, 0)C. (3, 0)D. (0, 3)3. 若直线l1的斜率为2,且通过点(1, 3),求直线l1的方程。
A. y = 2x + 1B. y = 2x - 1C. y = 2x + 3D. y = 2x - 34. 已知∠A = 40°,∠B = 60°,求∠A与∠B的和。
A. 100°B. 90°C. 120°D. 110°5. 点A(-2, 3),点B(4, -1),求线段AB的长度。
A. 3√2B. 5√2C. 6√2D. 7√2二、填空题6. 若直线AB与直线CD平行,且AB = 10cm,CD = 8cm,则AB与CD之间的距离是_______cm。
7. 已知∠α = 120°,求∠α的补角。
8. 若直线l的斜率为-3,且通过点(2, 5),求直线l的方程。
9. 已知点P(-3, 4),点Q(3, -4),求∠PQO的大小,其中O为坐标原点。
10. 若∠A = 30°,∠B = 90°,求∠A与∠B的外角。
三、简答题11. 解释什么是垂线,并给出垂线的性质。
12. 描述什么是同位角、内错角和同旁内角,并给出它们在两条平行线中的位置关系。
13. 已知直线l1和l2相交于点O,若∠AOB = 45°,求∠BOC的大小。
14. 给出一个例子,说明如何使用勾股定理来解决实际问题。
15. 解释什么是三角形的内角和定理,并证明它。
四、计算题16. 在直角三角形ABC中,∠C = 90°,AB = 13cm,AC = 5cm,求BC 的长度。
线与角练习题
线与角练习题线与角练习题数学是一门需要不断练习的学科,而线与角是数学中一个重要的概念。
在学习线与角的过程中,练习题是不可或缺的一部分。
通过练习题的解答,我们可以巩固自己对线与角的理解,提高解决问题的能力。
下面,我将给大家提供一些线与角的练习题,希望能够帮助大家更好地掌握这一知识点。
1. 请计算下列各角的度数:a) 直角的度数是多少?b) 一个角的度数是45°,请问这个角是什么类型的角?c) 两个互补角的度数分别是60°和x°,求x的值。
d) 两个补角的度数分别是120°和y°,求y的值。
2. 请判断下列各组角是否为对应角,并说明理由:a) ∠ABC与∠DEFb) ∠PQR与∠RQPc) ∠XYZ与∠ZYX3. 请判断下列各组角是否为互补角或补角,并说明理由:a) ∠MNO与∠NOPb) ∠UVW与∠XYZc) ∠ABC与∠DEF4. 请计算下列各组角的度数:a) ∠PQR与∠RQS的和的度数是多少?b) ∠ABC与∠DEF的差的度数是多少?c) ∠MNO与∠NOP的和的度数是多少?5. 请判断下列各组角是否为同位角,并说明理由:a) ∠ABC与∠DEFb) ∠PQR与∠RQSc) ∠UVW与∠XYZ6. 请计算下列各组角的度数:a) ∠ABC与∠DEF的和的度数是多少?b) ∠PQR与∠RQS的差的度数是多少?c) ∠UVW与∠XYZ的和的度数是多少?通过以上的练习题,我们可以对线与角的概念和性质进行巩固和运用。
在解答这些问题的过程中,我们需要灵活运用角的定义和性质,进行计算和推理。
这不仅有助于提高我们的数学思维能力,还能够帮助我们更好地理解和应用线与角的知识。
在解答这些练习题时,我们可以采用不同的方法和策略。
例如,在计算角的度数时,可以利用直角的定义和互补角、补角的性质进行计算。
对于判断角的类型和性质,我们可以根据角的度数和图形的特点进行推理和判断。
四年级线与角练习题
四年级线与角练习题四年级线与角练习题在四年级数学课堂上,线与角是一个重要的学习内容。
通过学习线与角的概念和性质,学生可以更好地理解几何形状和空间关系。
为了帮助同学们巩固所学的知识,下面我将给大家提供一些线与角的练习题。
练习题一:线段的长度计算1. 请计算以下线段的长度:(a) AB,其中A(-2, 3),B(4, 7);(b) CD,其中C(1, 2),D(5, 6);(c) EF,其中E(-3, -1),F(1, 3)。
2. 请计算以下线段的长度,并判断哪个线段最长:(a) GH,其中G(2, 4),H(6, 8);(b) IJ,其中I(-1, 3),J(3, -1);(c) KL,其中K(-5, 2),L(-1, -2)。
练习题二:角的性质1. 在下图中,角A和角B的度数分别是多少?(图略)2. 在下图中,角C和角D的度数分别是多少?(图略)3. 在下图中,角E和角F的度数分别是多少?(图略)练习题三:角的分类1. 根据下列描述,判断角的分类:(a) 角G的度数为90度,它是一个锐角/直角/钝角;(b) 角H的度数为180度,它是一个锐角/直角/钝角;(c) 角I的度数为45度,它是一个锐角/直角/钝角。
2. 根据下列描述,判断角的分类:(a) 角J的度数为120度,它是一个锐角/直角/钝角;(b) 角K的度数为90度,它是一个锐角/直角/钝角;(c) 角L的度数为160度,它是一个锐角/直角/钝角。
练习题四:角的度数计算1. 请计算以下角的度数:(a) 角M,其中角M的补角度数为40度;(b) 角N,其中角N的补角度数为120度;(c) 角O,其中角O的补角度数为160度。
2. 请计算以下角的度数:(a) 角P,其中角P的补角度数为60度;(b) 角Q,其中角Q的补角度数为150度;(c) 角R,其中角R的补角度数为170度。
以上是一些关于线与角的练习题,希望同学们能够通过练习加深对线与角的理解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线与角(习题)
➢ 巩固练习
1. 关于直线、射线、线段的描述正确的是( )
A.直线最长,线段最短
B.射线是直线长度的一半
C.直线没有端点,射线有一个端点,线段有两个端点
D.直线、射线及线段的长度都不确定
2. 下列说法正确的是( )
A.小于平角的角可分为锐角和钝角两类
B.两条射线组成的图形叫做角
C.射线就是直线
D.两点之间,线段最短
3. 如图,点A,B,C,D在同一直线上,那么图中共有( )条射线.
A.6 B.7
C.8 D.9
4. 给出以下四个语句:
①如果线段AB=BC,那么B是线段AC的中点;
②线段和射线都可看作直线上的一部分;
③大于直角的角是钝角;
④如图,∠ABD也可用∠B表示.
其中正确的结论有( )
A.0个 B.1个
C.2个 D.3个
5. 如图,∠AOB为平角,12AOCBOC,则∠BOC的度数是( )
A.100° B.135° C.120° D.60°
A
OCB
6. 如图,用不同的方法表示图中同一个角,并填入表格:
∠1 ∠α ∠3
∠ABC
∠E
A
BCD
DCB
A
A
B
CDE
12
3
α
β
AB①②③④⑤
第6题图 第7题图
7. 如图,从A地到B地共有五条路,为尽快到达目的地,小红应选择第_____
条路,用数学知识解释为_________________.
8. 下列说法中,正确的序号有______________.
①射线AB和射线BA是同一条射线;
②延长射线MN到C;
③延长线段MN到A,使NA=2MN;
④连接两点的线段长度叫做两点间的距离.
9. 如图,A,B,C,D,E是直线l上的五个点,则
A
BCDE
l
(1)BD=CD+_________;(2)CE=______+_______;
(3)BE=BC+______+DE;(4)BD=AD_____=BE______.
10. 如图,直线AB,CD相交于点O,∠COE是直角,∠1=57°,则∠2=___________.
11. 计算:
23°30′=________°;78.36°=_______°______′________″;
37°11′+44°49′=__________;37°11′25°35′=___________;
17°21′×5=__________;119°24′÷6=______________.
12. 时钟9点40分时,时针与分针的夹角是________度.
13. 如图,在同一平面内有四个点A,B,C,D,按照下列语句作出图形:
①作直线AB;
②作射线BD;
③连接BC;
④线段AC和线段BD相交于点O;
AO
C
D
E
1
2
B
⑤反向延长线段BC至E,使BE=BC.
D
C
B
A
➢ 思考小结
1. 请根据线段、射线、直线的性质填写下表:
线段 射线 直线
图形
端点
个数
一个
能否
延伸
否 向一个方向延伸
能否
度量
否
表示 方法 线段_____, 线段______ 或线段______. 射线_______. 直线______
或直线____.
2. 将图中的角用不同方法表示出来,并填写下表:
∠1 ∠3 ∠5
∠BCA ∠BAD
ABC
ED
1
234
5
【参考答案】
➢ 巩固练习
1. C
2. D
3. C
4. B
5. C
6.
∠1 ∠2 ∠ ∠ ∠3
∠BAE ∠ABC ∠CDE ∠AED ∠BCD
∠A ∠B ∠D ∠E ∠C
7. ③;两点之间,线段最短
8. ③④
9. (1)BC;(2)CD,DE;(3)CD;(4)AB,DE
10. 33°
11. 23.5;78,21,36;82°;11°36′;
86°45′(或86.75°);19°54′(或19.9°)
12. 50
13. 略
➢ 思考小结
1. 略
2.
∠1 ∠2 ∠3 ∠4 ∠5
∠BCE ∠BCA ∠BAC ∠BAD ∠ABC
