圆周角的定理及推论的应用

圆周角的定理及推论的应用
圆周角是数学中的一个重要概念，掌握圆周角的定理及其推论，对于解决许多几何问题非常有帮助。

本文将围绕圆周角的定理及推论的应用展开阐述。

一、圆周角的定义
圆周角是指落在圆周上的两条弧所对的角，即两个弧之间的角度量。

一般用大写字母表示圆周角，如∠ABC。

二、圆周角的定理
1、相等圆周角定理：在同一个圆周上，所对的圆周角相等。

证明：作弦AB、CD相交于点E，则∠AEB=∠CED。

由于AE、BE、CE、DE均是从一个圆心O引出的弦，故∠AEB=∠CEB，∠CED=∠BED，又因为OE=OE，故OEB≌OED，由此可得∠OEB=∠OED，即∠AEB=∠CED。

2、圆心角的定理：在同一个圆中，所对的圆心角相等。

证明：连接圆心O到AB的中垂线OH，H为AB的中点。

则OH垂直于AB，因此∠AOH、∠BOH均为直角，所以∠AOB=2∠AOH=2∠BOH。

3、正弦定理：在任意三角形ABC中，设a、b、c分别为三角形BC、AC、AB 的边长，R为外接圆半径，则有：
sinA=a/2R，sinB=b/2R，sinC=c/2R
证明：如下图所示，以AB、BC、CA为边作三角形ABC的外接圆，设圆心为O。

连接AO、BO、CO，过O点作弦AD、BE、CF，则OD=OE=OF=R，所以AOD、BOE、COF都是等边三角形。

因此，∠OAB=∠CFO、∠OBA=∠CEO、∠OBC=∠AEO、∠OCB=∠AFO。

设∠BAC=x，∠ABC=y，∠ACB=z，由三角形内角和公式得：
x+y+z=180
又由圆周角定理得：
∠BOC=2y，∠AOC=2z，∠AOB=2x
于是：
∠AOB+∠BOC+∠AOC=360
2x+2y+2z=360，
即x+y+z=180。

将sinA、sinB、sinC带入上述公式中，可得：
sinA/BC=sinB/CA=sinC/AB=1/2R
即sinA=a/2R，sinB=b/2R，sinC=c/2R。

4、余弦定理：在任意三角形ABC中，设a、b、c分别为三角形BC、AC、AB 的边长，R为外接圆半径，则有：
cosA=(b²+c²-a²)/2bc，cosB=(a²+c²-b²)/2ac，cosC=(a²+b²-c²)/2ab
证明：将ABC的外接圆的半径延长到BC、AC和AB上分别交于点D、E、F。

如下图所示：
因为DE=2RsinA、FD=2RsinB，且∠EDF=∠A+B，所以根据余弦定理得：
EF²=DE²+DF²-2DE·DFcos(∠EDF）
=4R²sin²A+4R²sin²B-4R²sinAsinBcos(∠A+B)
即：
EF²=4R²(sin²A+sin²B-2sinAsinBcosC)
因为EF²=4R²sin²C，所以：
sin²A+sin²B-2sinAsinBcosC=sin²C
整理得余弦定理：
cosC=(cosAcosB-sinAsinBcosC)/(sinC)
cosA和cosB的式子同理可得。

三、圆周角的推论
1、同弧度角定理：在同一个圆中，所对的两个弧所夹的圆周角相等。

证明：如下图所示，在同一个圆中，弧AB和弧CD都对应于同一个圆周角∠AOB。

假设∠OAB不等于∠OCD，则在三角形COD中，∠CDO+∠OCD+∠DCO=180，
因为∠CDO=∠ABC（同位角），∠DCO=∠OAB（内错角），又因为∠OAB不等于∠OCD，则∠CDO+∠DCO不等于∠AOB（外角大于内角）。

因此，三角形COD 的内角和不等于180，这与欧几里得平面公设（非退化三角形的内角和恒等于180）矛盾。

因此原命题成立，即AB和CD所对的圆周角相等。

2、相等圆心角所对的弧与相等弧所对的圆心角相等。

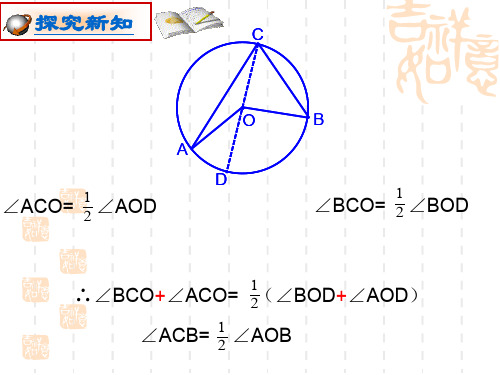
证明：如下图所示，在同一个圆中，首先连接圆心O到两个圆周角的端点A和B，然后连接O到弧AB的中点D和弧CD的中点E。

由于OA=OB，所以O为线段AD和线段BE的垂直平分线，故AD=BD，OE=CE，又因为∠DAO=∠EBO，OA=OB，OE=CE，所以∆AOD和∆BOE是全等三角形，即∠ABO=∠AOD。

同理，O为线段CD和线段EF的垂直平分线，所以∆COE 和∆DOF是全等三角形，即∠COD=∠EOF。

由于AD=BE，CD=EF，∠AOD=∠BOE，∠COD=∠EOF，所以∠ABD=∠CDE。

因此，相等圆心角所对的弧与相等弧所对的圆心角相等。

三、圆周角定理及推论的应用
圆周角定理和推论在解决很多圆的几何问题时十分有用。

下面将介绍几个应用实例：
1、已知圆上两点的位置，求圆的半径
已知圆上两点的坐标分别为（x1,y1）、（x2,y2），求圆的半径。

解答：
根据公式sinA=a/2R，可以列出下列两个方程：
sinθ= y2-y1 /(2R)
sinφ= x2-x1 /(2R)
其中θ和φ为两点到圆心的连线所对的圆周角。

将两个式子结合起来，即可得到半径R的表达式：
R=√[(x2-x1)²+(y2-y1)²]/2sin(θ+φ)/2
2、已知圆的半径和圆心到某一点的连线，求该连线所对的圆周角
已知圆的半径为R，圆心坐标为（x0，y0），某一点坐标为（x1,y1），求该点到
圆心的连线所对的圆周角。

解答：
根据余弦定理，可以算出点（x1,y1）到圆心（x0，y0）所对的圆心角的余弦值，然后用反余弦函数求出该圆心角的度数。

cos(∠O)=[(x1-x0)²+(y1-y0)²-R²]/2R(x1-x0)
使用反余弦函数求解∠O即可，即∠O=arccos(cos(∠O))。

3、已知圆的半径和一个圆上的点，求经过该点并且与该点的切线段长度为l的切点的坐标。

已知圆的半径为R，坐标为（x0，y0），过圆上一点（x1，y1）的一条切线段长度为l。

解答：
推导如下图所示。

过（x1,y1）点做切线OB，交弦CF于点E，在O点向CF作垂线AD交切线OB于点M，OD垂直于OB，且OM=R。

由圆内接四边形性质知，CF=2√(R²-CF²/4)；
由三角形BOM中，BM²+OM²=(BO+R)²，即：
BM²=R²+2R·OB+OB²；
由三角形OBD中，OD=R·√(1-CF²/4R²)，即：
DB=OB+R；
因此，OB和CF可以表示为：
OB=(DB-AB)/2
CF=AB+DB=AB+OB+R
又因为AB²+AM²=l²，AB²+BM²=R²，联立以上式子可以解得：AB=（l²-R²+2x1x0-2y1y0-2y1×y0+2）/2*(2x1-2x0)
由此，可以得到切点M的坐标：
xM=x0-Ry1/Rsinθ
yM=y0+Rx1/Rsinθ
其中θ为∠OMF的度数，可以用反正弦函数求解，即θ=arcsin(CF/2R)。

综上所述，圆周角定理及推论在几何中有着广泛的应用，几何常考题型多数与圆相关。

熟练掌握圆周角定理和推论，并能够熟练解决实际问题，是几何学习的重要一步。