Cp_Cpk_PPM_西格玛关系
Cp_Cpk_PPM_西格玛关系
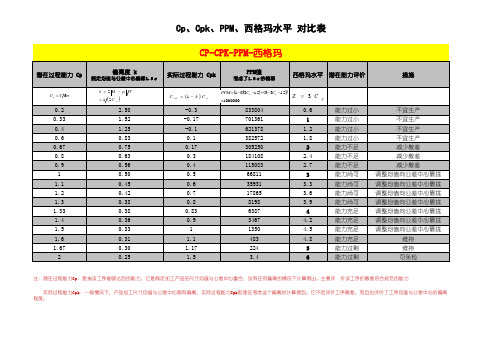
注:潜在过程能力Cp:是指该工序能够达到的能力,它是假定加工产品的尺寸均值与公差中心重合,没有任何偏离的情况下计算得出。
主要评 价该工序的散差符合规范的能力
实际过程能力Cpk:一般情况下,产品加工尺寸均值与公差中心都有偏离,实际过程能力Cpk即是在考虑这个偏离时计算得到。
它不但评价工序散差,而且也评价了工序均值与公差中心的偏离程度。
偏离度k衡量了产品加工尺寸均值与公差中心的偏离度,在上表中设定偏移量为1.5σ
PPM:上表中的PPM计算值都是考虑了尺寸均值与公差中心偏移了1.5σ距离。
如果无偏移,则PPM会少很多;如果实际偏移大于1.5σ,PPM还会高;在实际的工序能力计算中,是按照实际偏移量计算得到的。
Cp-Cpk-PPM-西格玛水平

Cp、Cpk、PPM、西格玛水平 对比表
注:潜在过程能力Cp:是指该工序能够达到的能力,它是假定加工产品的尺寸均值与公差中心重合,没有任何偏离的情况下计算得出。
主要评 价该工序的散差符合规范的能力
实际过程能力Cpk:一般情况下,产品加工尺寸均值与公差中心都有偏离,实际过程能力Cpk即是在考虑这个偏离时计算得到。
它不但评价工序散差,而且也评价了工序均值与公差中心的偏离程度。
偏离度k衡量了产品加工尺寸均值与公差中心的偏离度,在上表中设定偏移量为1.5σ
PPM:上表中的PPM计算值都是考虑了尺寸均值与公差中心偏移了1.5σ距离。
如果无偏移,则PPM会少很多;如果实际偏移大于1.5σ,PPM还会高;在实际的工序能力计算中,是按照实际偏移量计算得到的。
六西格玛之测量阶段

测量过程的主要任务是收集数据,以支持后续的分析和改善过程。
那么值得收集的数据有哪些?使用什么方式收集数据才能确保数据满足需求?拿到数据后,怎样进行整理呢?过程指标精益过程过程是将输入的东西进行处理,转化为输出。
所谓输出,即顾客需要的东西,在精益生产中,将顾客需要的东西称为价值。
例如一块手表,顾客需要它能显示时间,那么这个显示时间的功能便是价值。
而将输入原料转化为输出成本的过程,必然是增值的。
例如将手表的齿轮、时针组装到一起,便能够让其准确地显示时间,这个过程中,齿轮、时针的价值是增加的。
这一整个增加价值的过程便是价值流。
很显然,价值这个东西从来都是一个相对的概念,一块瑞士手表,其价值必然高于一块过时的儿童电子表。
手表指示时间功能的价值必然高于其星星图案的价值。
其价值的高低取决于顾客是否愿意为其买单,即顾客的需求。
在精益思想中,只有顾客需要的东西,才值得被生产,从顾客需求出发,驱使输出产生再到原料购买的过程,便是拉动。
而在整个生产中,所有不被用于产生价值,不用于生产顾客需求的过程,都是浪费。
精益的存在,便是要消除这些浪费,使过程专注于产生价值。
而我们知道,完全没有浪费的过程是不可能存在的,所以不断改善以追求完美达到极限便是精益的精神。
那么如何衡量过程的价值?如何衡量过程专注于价值生产的程度呢?过程指标与衡量衡量过程精益程度的指标有很多,以下是常用指标:WIP- 在制品在制品生产的中间产品。
由于经历了加工过程,在制品的价值或价格必然高于原材料,但通常由于下道工序还不需要用到,便只能进行库存。
变成库存的在制品便是浪费。
首先,库存本身需要仓储成本,如场地、管理费用、移入移出等。
其次,在制品在存放过程中可能出现的损坏风险。
而一旦检测出质量问题,在制品的返修和处理也会产生额外成本。
WIQ- 队列工作WIQ是上道工序已完成,正在等待下道工序加工的产品,在队列中的产品越多,说明下道工序的速度比上道工序慢,就成为过程的瓶颈,这时过程时间的不平衡便会产生浪费。
PP、PPK、CP、CPK、CM、CMK 的区别

PP、PPK、CP、CPK、CM、CMK1. Ca、Cp、Cpk的计算1) 过程准确度指数(Ca值):表示过程特性中心位置的偏移程度,越小越好Ca=(样本平均值-规格中心值)/(规格公差/2)a) 等级A:|Ca|≦12.5% 表示作业员遵守作业规范,并达规格要求b) 等级B :12.5%< |Ca|≦25% 表示必要时尽可能提升至A级c) 等级C:25%< |Ca|≦50% 表示作业员可能看错或未按标准作业,或须修改规格及作业标准。
d) 等级D:50%< |Ca| 表示应采取紧急措施,全面整改可能影响之因素,应停止生产。
2) 过程精密度能力系数(Cp值):表示过程特性分散的程度,值越大越集中。
Cp=(规格上限-规格下限)/(6×标准差)a) 合格:1.33≦Cp表示能力足够b) 警告:1.00 ≦Cp< 1.33表示能力无足够宽度,平均值稍有偏差时,不良率既会增加。
c) 不合格:Cp< 1.00表示能力不足,有不合格品,须全数筛选,并设法缩小变异或整改规格公差。
3) 过程综合能力系数(Cpk值):同时考虑“偏移”程度及“分散程度Cpk=(1-Ca) ×Cpa) 此系数为过程评价用系数,用于过程改善b) 客户指定Cpk值时,欲达到此Cpk值,可先探讨Ca及Cp值:“准确度”“精密度”是否有适当能力c) 一般客户是指定值多数为≧1.33;Cpk值≧3.00时,表示过程能力已经足够了,继续维持即可;若想进一步改善,应考虑成本效益。
Cp=(Usl-Lsl)/6δCpku=(Ucl-Xbar)/3δ Cpkl=(Xbar-Lsl)/3δCpk=min(Cpku : Cpkl)2、首先我们先说明Pp、Cp两者的定义及公式Cp(Capability Indies of Process):稳定过程的能力指数,定义为容差宽度除以过程能力,不考虑过程有无偏移,一般表达式为:Cpk,Ca,Cp三者的关系:Cpk = Cp×(1-┃Ca┃),Cpk是Ca及Cp两者的中和反应,Ca反应的是位置关系(集中趋势),Cp反应的是散布关系(离散趋势)Pp(Performance Indies of Process):过程性能指数,定义为不考虑过程有无偏移时,容差范围除以过程性能,一般表达式为:(该指数仅用来与Cp及Cpk对比,或/和Cp、Cpk一起去度量和确认一段时间内改进的优先次序)CPU:稳定过程的上限能力指数,定义为容差范围上限除以实际过程分布宽度上限,一般表达式为:CPL:稳定过程的下限能力指数,定义为容差范围下限除以实际过程分布宽度下限,一般表达式为:3、现在我们来阐述Cpk、Ppk的含义Cpk:这是考虑到过程中心的能力(修正)指数,定义为CPU与CPL的最小值。
关于Cp、Cpk、Ppk

关于Cp、Cpk、Cpm、Cpmk、Pp、Ppk什么是过程能力?过程能力是指加工方面满足加工质量的能力。
此种能力表现在过程稳定的程度,σ越小,过程能力越稳定,|M-μ|的值越小,表示过程能力的偏差越小,99.73%的质量特性散布区间在[μ-3σ,μ+3σ]。
过程能力指数Cp、CpkCp是表征过程固有的波动状态,即技术水平。
它是在过程的平均值μ与目标值M重合的情形,过程处于统计控制状态时(非分析状态),过程能力指数Cp可用下式表示:Cp=(USL-LSL)/6σ=T/6σCp与不良品率的关系Cp P1.0 0.27%1.33 0.007%1.5 6.8PPm2.0 2.0PPb实际过程中,平均值与目标志重合的情形非常少,因此引入了偏移度的概念,即过程平均值与目标值的偏离过程K=2|M-μ|/TCp-Cpk=|M-μ|/3σCpk与不良品率的关系Cpk P(%)1.0 0.13~0.271.1 0.05~0.101.2 0.02~0.031.3 48.1~96.2PPM1.4 13.4~26.7PPM过程能力指数Cpm、Cpmk过程能力指数是根据田口玄一关于质量损失函数而设计出来的。
将目标值与均值的偏差也考虑进来,因为有实际的改进意义Cpm=(USL-LSL)/6SQRT((σp)2+(|M-μ|)2)Cpm<Cp,这是因为考虑了过程平均值与目标值发生偏差的结果过程能力指数Cpmk是考虑过程能力与平均值偏离目标值的综合结果,因此又叫综合过程能力指数Cpmk=Cpk/SQRT(1+((|M-μ|)/σ)2)过程绩效指数Pp、Ppk过程Pp=(USL-LSL)/6σ总Ppk=min((USL-u)/3σ总,(u-LSL)/3σ总)Cpk——过程能力指数CPK= Min[ (USL- Mu)/3s, (Mu - LSL)/3s]Cpk应用讲义1. Cpk的中文定义为:制程能力指数,是某个工程或制程水准的量化反应,也是工程评估的一类指标。
不良率与西格玛(σ)水平的关系

不良率与西格玛(σ)水平的关系制程能力指标Cp或Cpk之值在产品或制程特性分布为正态且在管制状态下时,通过正态分布的概率计算,可以换算为该产品或制程特性的良率或不良率,同时也可以几个Sigma来对照。
现以产品或制程特性中心没偏移目标值、中心偏移目标值1.5σ及中心偏移目标值T/8分别说明,因为有质量专家认为,对于Sigma水平较小时,偏移的幅度应相对的小,才较合理,因此提出偏移目标值T/8的考虑,在分析前,先定义以下几个符号:●X:个别产品或制程特性值●USL:规格上限●LSL:规格下限●m:目标值或规格中心,一般为(USL+LSL)/2●T=USL-LSL:规格界限宽度●μ:产品或制程特性中心或平均数●σ:产品或制程特性标准差1、产品或制程特性中心没偏移目标值(即Ca=0),即μ=m=(USL+LSL)/2Sigma 水平=±kσ;即 T = USL - LSL = 2 kσCp=规格界限宽度/ 6σ=T / 6σ=(USL - LSL)/ 6σ=2 kσ/ 6σ=k / 3=Cpk不良率= P [ | X | > kσ] = P [ | Z |> k ]=标准常态分布右尾概率×2良率=( 1-不良率)Sigma水平(±kσ)Cpk/ Cp良率%PPM不良率2σ0.6795.45%45,6003σ 1.0099.73%2,7004σ 1.3399.9937%635σ 1.6799.999943%0.576σ 2.0099.9999998%0.0022、产品或制程特性中心偏移目标值1.5σ,即μ=(USL+LSL)/2 ± 1.5σSigma 水平=±kσ;即 T=USL-LSL= 2 kσ●产品或制程特性中心大于目标值1.5σC PU=(USL - μ)/3σ=(kσ- 1.5σ)/ 3σ=( k-1.5 ) / 3C PL=(μ- LSL) / 3σ= ( kσ+ 1.5σ) / 3σ= (k+1.5) /3Cpk = MIN{CPU,CPL}=(k-1.5)/3不良率=P [ X > USL ] + P [ X < LSL ] = P [ Z > 3 x CPU ] +P[ Z > 3 x CPL ]=P [ Z > ( k -1.5 ) ] + P [ Z > ( k + 1.5 )]良率=( 1- 不良率)●产品或制程特性中心小于目标值1.5σCPU=(USL-μ) / 3σ=(kσ+ 1.5 σ)/ 3σ=(k+1.5) /3CPL=(μ-LSL) / 3σ=(kσ+ 1.5 σ)/ 3σ=(k-1.5) /3Cpk= MIN{CPU,CPL}=(k-1.5) /3不良率= P [ X > USL ] + P [ X < LSL ]=P[ Z > 3 x CPU ] + P[ Z > 3 x CPL ]= P[ Z > ( k + 1.5 )] + P[Z > 3 x ( k - 1.5 ) ]良率=( 1-不良率)Sigma水平Cpk Cp良率%PPM不良率2σ0.670.1769.13%308,770 3σ 1.000.5093.32%66,811 4σ 1.330.8399.379%6,2105σ 1.67 1.1799.99767%2336σ 2.00 1.5099.99966% 3.4 3、产品或制程特性中心偏移目标值T/8,即μ=(USL+LSL)/2 + - T / 8Sigma 水平= + - kσ;即T=USL-LSL= 2kσ●产品或制程特性中心大于目标值T/8=2kσ/ 8=(k / 4)σCPU=(USL-μ)/ 3σ=(kσ-( k / 4)σ)/ 3σ=3k/12CPL=(μ-LSL)/3σ=(kσ+( k / 4)σ)/ 3σ=5k/12Cpk= MIN{CPU,CPL}=3k/12不良率=P [ X > USL ] + P [ X < LSL]=P[ Z > 3 x CPU ] + P[ Z > 3x CPL ]=P[ Z > 3k / 12 )] + P[ Z > P [ Z > 5k /12 ]良率=( 1- 不良率)●产品或制程特性中心小于目标值T/8=2kσ/ 8=( k / 4)σCPU=(USL-μ)/ 3σ=(kσ+ (k / 4)σ) / 3σ= 5k/12CPL=(μ-LSL)/ 3σ=(kσ- (k / 4)σ) / 3σ= 3k/12。
CP、CPK、PP、PPK的定义与关系
CP、CPK、PP、PPK的定义与关系CP、CPK、PP、PPK的定义与关系CP、CPK、PP、PPK的定义与关系最近常看见论坛里面有些关于CP、CPK、PP、PPK定义的帖子,其实论坛里面都解释的很清楚了,只需要大家认真找找。
我整理了一部分,传上来,希望以后不要没认真找就随便发没多少价值帖子。
1、基本定义:σST :短期差异,σST = Rbar/d2σLT :长期差异,σLT =(这里本来是一个图片,可惜粘不上来)ε :分布中心u与规范中心M的偏移,ε=∣u - M∣K :分布中心u与规范中心M的偏移度,K=ε/2T = 2ε/T2、定义:CP :无偏移短期过程能力指数(或无偏移固有过程能力指数)CP = T/6σ≈T/6σSTCPK:有偏移短期过程能力指数(或有偏移固有过程能力指数)CPK=(1-K)CP≈(T-2ε)/6σSTPP :无偏移长期过程能力指数(或无偏移实绩过程能力指数)PP = T/6σ≈(TU-TL)/6σLTPPU:无偏移上单侧长期过程能力指数(或无偏移上单侧实绩过程能力指数)PPU=(TU-u)/3σ≈(TU-Xbar)/3σSTPPL:无偏移上单侧长期过程能力指数(或无偏移上单侧实绩过程能力指数)PPL=(u-TL)/3σ≈(Xbar- TL)/3σSTPPK:有偏移长期过程能力指数(或有偏移实绩过程能力指数)PPK=Min(PPU,PPL)3、比较与关系无偏移情况的CP表示过程加工的一致性,即“质量能力”,CP越大,则质量特性值的分布越“苗条”,质量能力越强;而有偏移情况的CPK表示过程中心u与规范中心M的偏移情况下的过程能力指数,CPK越大,则二者偏移越小,也即过程分布中心对规范中心越“瞄准”,是过程的“质量能力”与“管理能力”二者综合的结果。
故CP与CPK二者的着重点不同,需要同时加以考虑。
类似的,PP与PPK也需要联合应用。
对于同一个过程而言,通常,长期标准差的估计值σLT大于短期标准差的估计值σST。
CPK及6西格玛精品资料
Cp≤0.67 工序能力严重不足,产品质量水平很低,不合格品率高。
●措施:
(1)必须立即分析原因,采取措施 ,提高工序能力; (2)为了保证产品的出厂质量,应通过全数检查; (3)若更改设计、放宽规格要求 不致影响产品质量或从经济性考虑更为合理时, 也可以用更改设计的方法予以解决,但要慎重处理。
(2)在保证产品质量和提高经济效益的前提下更改设计,加严规格要求; (3)合并或减少工序也是常用的方法之一。
制程能力的评价与处置
1.67≥Cp>1.33
对精密加工而言,工序能力适宜;对一般加工来说工序能力仍比较充裕有一定贮备 。 ●措施:
(1) (2)非关键工序可放宽检验; (3)工序控制的抽样间隔可适当放宽。
CPK培训教材
龍元 2014/01/15
CPK(Process Capability index)
一般我们讲CPK时是指“制程能力指数研究” 英文是:Process Capability Analysis
LSL
USL
制程能力研究包含以下两方面:
• 离散型与连续型数据能力研究 • 短期能力研究与长期能力研究
=Cp(1-/Ca/)
Ca等级评定及处理原则
等級
Ca值
處理原則
A
|Ca|<12.5% 作業員遵守作業標準操作並達到規格之要求,需繼續保持.
B
12.5%<|Ca|<25% 有必要盡可能將其改進為A級
C
25%<|Ca|<50% 作業員可能看錯規格不按作業標準操作或檢討規格及作業標準.
CPK、Sigma和PPM的换算关系
过程能力指数(Cp和Cpk)表示的是过程在稳定(即没有特殊原因干扰产出品的特性或者说是在可控(under control)的)状态下能使其产出品达到可接受标准的程度的指标。
按照常识,Cpk越高越好,产品的不良率也越低。
SQE在PPAP审核时,要求供应商提交的过程能力报告,关键特性的Cpk大于1.33,此时供应商内部的百万分之不良率PPM为63。
拓展到Cpk=1.0,Cpk=1.67的PPM如下:在不考虑偏移的情况下:Cpk=1.33 对应4σ 水平其PPM=63.3;Cpk=1.67 对应5σ 水平其PPM=0.570;Cpk=2.0 对应6σ 水平其PPM=0.0020;那么,这个值是怎么来的,其他Cpk对应的PPM数值是多少?过程能力指数Cp或Cpk在产品或制程特性分布为正态且在稳定状态下时,通过正态分布的概率计算,可以换算为该产品或制程特性的良率或不良率,同时也可以几个Sigma来对照。
CPK是过程能力,西格玛水平是管理水平,PPM是管理结果。
下文将以产品或制程特性中心没偏移目标值和中心偏移目标值1.5σ说明。
我们从正态分布讲起。
若随机变量X服从一个数学期望为μ、方差为σ2的正态分布,记为N(μ,σ2)。
其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。
当μ = 0,σ = 1时的正态分布是标准正态分布。
若随机变量X,服从一个位置参数为μ、尺度参数为σ的概率分布,其概率密度函数为:当μ=0,σ=1时,正态分布就成为标准正态分布。
我们对其积分,也就是求面积,所得值为1。
(每个质量人追求的100.00%合格)接下来,我们谈一下什么是西格玛水平。
西格玛水平Sigma Level:过程能力的一种衡量指标,将过程分布的平均值、标准偏差与质量特性的目标值、规格线结合起来。
西格玛水平越高,过程满足质量要求的能力就越强,反之,西格玛水平越低,过程满足质量要求的能力就越低。
我们可以简单的理解为规格线与目标值间的距离最少能容纳k个标准偏差σ,当k = 3时,我们称之为3西格玛水平,上下规格极限之差为6σ。
西格玛、cp_cpk在设计中的应用
PPM与CP的关系
CP
0.00 0.06 0.11 0.17 0.22 0.28
一、西格玛、CP/CPK基础知识
规格界限宽度 ±Kδ
3.33 3.50 3.66 3.83 4.00 4.16
(制程中心没有偏移)
CP
1.11 1.17 1.22 1.28 1.33 1.39
规格界限宽度 ±Kδ
0.00034% (PPM:3.4)
1.67
2.0
5ơ
6ơ
二、CP/CPK在设计中的应用案例
2、案例二、与顾客协商变更规格
A、问题点:
完成品SPEC: 4.70±0.15
CELL: 4.25±0.20 DESAY PACK: 0.50±0.10
即4.85max
即 4.45max 即0.60max
Frequency
0.33
0.39 0.44 0.50 0.56 0.61 0.67 0.72 0.78 0.83 0.89
1.00
1.17 1.33 1.50 1.67 1.83 2.00 2.17 2.33 2.50 2.67
317310.508
243345.009 182422.439 133614.403 95580.705 66753.015 45500.264 30260.280 19630.658 12419.331 7660.761
五、最优化设计
建立设计参量的目标函数Y=f(x)和参量矩阵,通
过计算机寻找最优解。首先要确定产品的重要特性,
多视角分析市场和潜在顾客的影响;其次进行达成 这些特性的产品要素分析,确定重要品质特性的设 计中心值与最大误差,进行早期产品的试验或仿真 试验,解决设计中存在的问题,确保CP≥2(CPK ≥1.5)的要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
注:潜在过程能力Cp:是指该工序能够达到的能力,它是假定加工产品的尺寸均值与公差中心重合,没有任何偏离的情况下计算得出。
主要评 价该工序的散差符合规范的能力
实际过程能力Cpk:一般情况下,产品加工尺寸均值与公差中心都有偏离,实际过程能力Cpk即是在考虑这个偏离时计算得到。
它不但评价工序散差,而且也评价了工序均值与公差中心的偏离程度。
偏离度k衡量了产品加工尺寸均值与公差中心的偏离度,在上表中设定偏移量为1.5σ
PPM:上表中的PPM计算值都是考虑了尺寸均值与公差中心偏移了1.5σ距离。
如果无偏移,则PPM会少很多;如果实际偏移大于1.5σ,PPM还会高;在实际的工序能力计算中,是按照实际偏移量计算得到的。
