高一上期末数学复习---常用逻辑用语
高一数学逻辑用语知识点

高一数学逻辑用语知识点
以下是 8 条关于高一数学逻辑用语知识点:
1. 命题呀,就像我们说出的一句话,可以判断真假呢!比如“今天天气真好!”这就是一个命题。
2. 全称量词,嘿,那可不得了!像“所有的同学都很努力”,这里的“所有”就是全称量词。
3. 特称量词也很有趣哦,“存在一个数是奇数”,这里的“存在”就是啦。
4. 且命题呀,就像是同时要满足两个条件,好比“既要学习好,又要品德好”。
5. 或命题呢,就像有多个选择,“或者选文科,或者选理科”。
6. 否定命题,不就是把原来的说法否定一下嘛,“这个苹果不是红的”。
7. 充分条件和必要条件,这不就像要去一个地方,坐火车是充分条件,有车票是必要条件。
8. 等价命题就像是双胞胎一样,它们表达的意思几乎一样,比如“2+3=5”和“5=2+3”。
我觉得这些逻辑用语知识点就像是一把打开数学大门的钥匙,让我们能更好地理解和探索数学的奥秘呀!。
高一数学中的常用逻辑用语有哪些

高一数学中的常用逻辑用语有哪些在高一数学的学习中,逻辑用语就像是搭建数学大厦的基石,它们帮助我们更准确、清晰地表达数学概念和进行推理。
接下来,让我们一起深入了解一下高一数学中常见的逻辑用语。
一、命题命题是能够判断真假的陈述句。
比如“2 是偶数”,这是一个真命题;而“1 + 1 =3”,则是一个假命题。
命题通常用小写字母 p、q、r 等来表示。
理解命题的关键在于明确其陈述的内容是否能够明确地判断出真假。
二、充分条件与必要条件这是高一数学中非常重要的逻辑概念。
如果“若p,则q”为真命题,那么我们就说 p 是 q 的充分条件,q 是 p 的必要条件。
举个例子,“如果一个数是偶数,那么这个数能被2 整除”,在这里,“一个数是偶数”就是“这个数能被 2 整除”的充分条件,“这个数能被 2整除”就是“一个数是偶数”的必要条件。
充分条件意味着只要满足 p,就一定能推出 q;必要条件则是说若要使 q 成立,p 必须成立。
三、充要条件当 p 既是 q 的充分条件,又是 q 的必要条件时,我们就说 p 是 q 的充要条件。
简单来说,就是“若 p,则q”和“若 q,则p”都为真命题。
例如,“一个三角形是等边三角形”与“这个三角形的三个内角相等”,这两个条件就是互为充要条件。
四、全称量词与存在量词全称量词常见的有“任意”“所有”“一切”等,用符号“∀”表示。
比如“∀x∈R,x²≥0”,意思是对于任意实数 x,x 的平方都大于等于 0。
存在量词常见的有“存在”“至少有一个”等,用符号“∃”表示。
像“∃x∈R,x + 1 =0”,表示存在实数 x,使得 x + 1 等于 0。
理解全称量词和存在量词对于解决一些含有变量的问题非常关键。
五、全称量词命题与存在量词命题的否定对于全称量词命题“∀x∈M,p(x)”,它的否定是“∃x∈M,¬p(x)”;对于存在量词命题“∃x∈M,p(x)”,它的否定是“∀x∈M,¬p(x)”。
高中数学常用逻辑用语

逆否命题: 若 q 则 p
结论1:要写出一个命题的另外三个命
题关键是分清命题的题设和结论(即
把原命题写成“若p则q”的形式)
注意:三种命题中最难写 的是否命题。 高中数学常用逻辑用语
三、四种命题之间的 关系
原命题
பைடு நூலகம்若p则q
互逆 逆命题
若q则p
互
互
否
否
否命题
逆否命题
若﹁p则﹁q
互逆 若﹁q则﹁p
高中数学常用逻辑用语
x∈N”是“x∈M∩N”的
B
A.充要条件
B必要不充分条件
C充分不必要 D既不充分也不必要
注、集合法
2、a∈R,|a|<3成立的一个必要不充分条件是
A.a<3 B.|a|<2 C.a2<9 D.0<a<2
A
高中数学常用逻辑用语
练习5、
1.已知p是q的必要而不充分条件, 那么┐p是┐q的___充__分_不__必__要_条__件__.
(2)从这个假设出发,经过推理 论证,得出矛盾;
(3) 由矛盾判定假设不正确, 从而肯定命题的高中数结学常用论逻辑正用语 确。
归谬 结论
1.写出命题“当c>0时,若a>b, 则ac>bc“的逆命题,否命题 与逆否命题,并分别判断他们的真假
2.写出命题“若x≠a且x≠b, 则x2-(a+b)x+ab≠0”的否命题
充分非必要条件
2) 若A B且B A,则甲是乙的
必要非充分条件
3)若A B且B A,则甲是乙的
既不充分也不必要条件 4)若A=B ,则甲是高中乙数学的常用逻充辑用分语 且必要条件。
注意点
1.在判断条件时,要特别注意的是它们能否互相 推出,切不可不加判断以单向推出代替双向推出.
2020-2021学年高一数学人教A版必修第一册期末复习重难点知识集锦 集合与常用逻辑用语
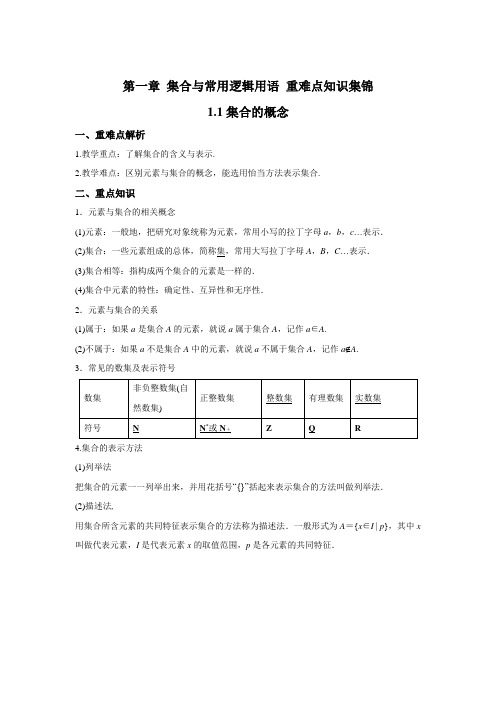
第一章集合与常用逻辑用语重难点知识集锦1.1集合的概念一、重难点解析1.教学重点:了解集合的含义与表示.2.教学难点:区别元素与集合的概念,能选用怡当方法表示集合.二、重点知识1.元素与集合的相关概念(1)元素:一般地,把研究对象统称为元素,常用小写的拉丁字母a,b,c…表示.(2)集合:一些元素组成的总体,简称集,常用大写拉丁字母A,B,C…表示.(3)集合相等:指构成两个集合的元素是一样的.(4)集合中元素的特性:确定性、互异性和无序性.2.元素与集合的关系(1)属于:如果a是集合A的元素,就说a属于集合A,记作a∈A.(2)不属于:如果a不是集合A中的元素,就说a不属于集合A,记作a∉A.3.常见的数集及表示符号4.集合的表示方法(1)列举法把集合的元素一一列举出来,并用花括号“{}”括起来表示集合的方法叫做列举法.(2)描述法,用集合所含元素的共同特征表示集合的方法称为描述法.一般形式为A={x∈I | p},其中x 叫做代表元素,I是代表元素x的取值范围,p是各元素的共同特征.1.2集合间的基本关系一、重难点解析1.教学重点:集合间的包含与相等关系,子集与真子集的概念,空集的概念.2.教学难点:元素与子集,即属于与包含之间的区别.二、重点知识1. 集合与集合的关系(1)子集:对于两个集合A ,B ,如果集合 A 中任意一个元素都是集合 B 中的元素,就称集合A 为集合B 的子集.记作:A B ⊆或B A ⊇.读作:“A 包含于B ”(或“B 包含A ”).(2)集合相等:如果集合A 的任何一个元素都是集合B 的元素,同时集合B 的任何一个元素都是集合A 的元素,那么集合A 与集合B 相等.记作A = B .即:若A B ,且B A ,则A = B .2. 真子集:对于两个集合A 与B ,如果集合A B ⊆,但存在元素x B ∈,且x A ∉,就称集合A 是集合B 的真子集.记作:A B (或B A ).3. 空集:一般地,我们把不含任何元素的集合叫做空集,记为∅.空集是任何集合的子集.4. 子集性质:(1)任何一个集合是它本身的子集,即A A ⊆.(2)对于集合A ,B ,C ,如果A B ⊆,且B C ⊆,那么A C ⊆.5. 结论:含n 个元素的集合的所有子集的个数是2n ,所有真子集的个数是21n -.1.3集合间的基本运算一、重难点解析1.教学重点:理解两个集合的并集与交集的含义,会用集合语言表达数学对象或数学内容.2.教学难点:区别交集与并集的概念及符号表示,二、重点知识1.集合的运算性质a .,,A A A A A A B B A ∅⋃=⋃=⋃=⋃;b .,,A A A A A B B A ∅∅⋂=⋂=⋂=⋂;c .()(),U U A C A A C A U ∅⋂=⋃=;d .,A B A A B A B A B A ⋂=⇔⊆⋃=⇔⊆.2.集合运算中的常用方法(1)数轴法:若已知的集合是不等式的解集,用数轴法求解.(2)图象法:若已知的集合是点集,用图象法求解.(3)V enn 图法:若已知的集合是抽象集合,用Venn 图法求解.1.4充分条件与必要条件一、重难点解析1教学重点:充分理解充要条件的概念2教学难点:命题条件的充要性判断二、重点知识1.定义:若p⇒q且q⇒p,则记作p⇔q,此时p是q的充分必要条件,简称充要条件. 2.条件与结论的等价性:如果p是q的充要条件,那么q也是p的充要条件.3.概括:如果p⇔q,那么p与q互为充要条件.命题按条件和结论的充分性、必要性可分四类:①充分必要条件(充要条件),即p⇒q且q⇒p;②充分不必要条件,即p⇒q且q p.③必要不充分条件,即p q且q⇒p.④既不充分又不必要条件,即p q且q p.1.5全称量词与存在量词一、重难点解析1.教学重点:理解全称量词和存在量词的意义;能判断全称命题和存在命题的真假2.教学难点:全称命題和存在命题真假的判定二、重点知识1.四种命题的关系(1)两个命题互为逆否命题,它们有相同的真假性;(2)两个命题为互逆命题或互否命题,它们的真假性没有关系.2. 含逻辑联结词的命题的真假判断∨”有真则真,其余为假;(1)命题“p q∧”有假则假,其余为真;(2)命题“p q(3)¬p和p为真假对立的命题.3. 全(特)称命题及其否定(1)全称命题p:∀x∈M,p(x).它的否定¬p:∃x0∈M,¬p(x0) ;(2)特称命题p:∃x0∈M,p(x).它的否定¬p:∀x∈M,¬p(x) ;(3)命题p∨q的否定是(¬p)∧(¬q);命题p∧q的否定是(¬p)∨(¬q).。
高中数学常用逻辑用语知识点

高中数学常用逻辑用语知识点一、知识概述《高中数学常用逻辑用语知识点》①基本定义:- 命题:能判断真假的陈述句。
就好比我们在生活中说出的一句有明确对错的话。
比如“今天是晴天”,这就是一个能看出来真假的陈述句,那它就是一个命题。
要是说“你好啊”,这就不是命题,因为它没法判断真假。
- 简单命题:就像简单的一句话表达一个判断。
例如“2大于1”。
- 复合命题:是由简单命题通过一些逻辑连接词(像“且”“或”“非”)组合在一起的命题。
比如说“2大于1且3小于5”,这里就是两个简单命题通过“且”连接起来了。
②重要程度:- 在高中数学里,常用逻辑用语是构建数学推理和证明的基础材料。
就像盖房子的砖头一样重要。
很多数学定理的推导和证明都离不开准确的逻辑判断。
③前置知识:- 需要对基本的数学运算和数的概念比较熟悉。
比如说你得知道数的大小关系才能判断像“3大于2”这样的命题真假。
④应用价值:- 在数学解题的时候,逻辑用语能帮我们准确地分析题目条件,制定解题思路。
在实际生活里,像判断一些事情的合理性,逻辑思维也非常有用。
比如说在判断一个商业计划是否可行的时候,就有点像判断命题真假的过程。
二、知识体系①知识图谱:- 在高中数学整个体系中,常用逻辑用语像经脉一样贯穿于代数、几何等各个领域。
它是我们搞清楚数学概念之间关系,进行数学论证的工具。
②关联知识:- 和集合知识有紧密联系。
比如说集合的关系就可以用逻辑用语来描述。
集合A包含于集合B,就等价于“若元素x属于A,则x属于B”这样一个逻辑关系。
③重难点分析:- 掌握难点在于复合命题真假性的判断。
关键是要理解逻辑连接词“且”“或”“非”在不同情况下对命题真假性的影响。
比如“且”表示两个都要为真才真,“或”是只要有一个为真就真。
④考点分析:- 在考试中频繁出现。
考查方式有直接判断命题真假,根据命题真假求参数范围等。
三、详细讲解【理论概念类】①概念辨析:- 命题这个概念,一定要是陈述句,而且能够判断真假。
高中数学:常用逻辑用语

常用逻辑用语一、知识框架1.命题定义:用语言、符号或式子表达的、可以判断正误的陈述语句,叫做命题。
其中,判断为真的即为真命题,为假的即为假命题。
2.命题的判断以及命题真假的判断(1)命题的判断:①判断该语句是否是陈述句;②能否判断真假。
(2)命题真假的判断:首先,分清条件与结论,其次,再判断命题真假。
3.一般地,用p 和q 分别表示原命题的条件和结论,用¬p 和¬q 表示p 与q 的否定,即如下:(四种命题的关系)4.充分条件和必要条件 (1)充分条件:如果A 成立,那么B 成立,则条件A 是B 成立的充分条件。
(2)必要条件:如果A 成立,那么B 成立,这时B 是A 的必然结果,则条件B 是A 成立的必要条件。
(3)充要条件:如果A 既是B 成立的充分条件,又是B 成立的必要条件,则A 是B 成立的充要条件,与此同时,B 也一定是A 成立的重要条件,所以此时,A 、B 互为充要条件。
【注意】充分条件与必要条件是完全等价的,是同一逻辑关系“A =>B ”的不同表达方法。
5.逻辑联结词(1)不含逻辑联结词的命题是简单命题,由简单命题和逻辑联结词“或”“且”“非”构成的命题是复合命题,它们有以下几种形式:p 或q (p ∨q );p 且q (p ∧q );非p (¬p )。
(2)逻辑联结词“或”“且”“非”的含义的理解 在集合中学习的“并集”“交集”“补集”与逻辑联结词中的“或”“且”“非”关系十分密切。
6.量词与命题量词名称 常见量词表示符号全称量词 所有、一切、任意、全部、每一个、任给等 ∀存在量词 存在一个、至少有一个、某个、有些、某些等∃命 题 表述形式 原命题 若p 则q 逆命题 若q 则p 否命题 若¬p 则¬q 逆否命题若¬q 则¬p(2)全称命题与特称命题 命题全称命题“()x p M x ,∈∀”特称命题“()00,x p M x ∈∃”定义短语“对所有的”“对任意一个”等,在逻辑中通常叫做全称量词,用符号“∀”表示。
版高中数学必修一常用逻辑用语知识点归纳超级精简版

版高中数学必修一常用逻辑用语知识点归纳超级精简版逻辑是数学的重要组成部分,它以推理和证明为基础,帮助我们建立正确的思维方式。
常用逻辑用语主要包括命题、谓词、命题连接词、条件语句和等价语句等。
本文将对这些常用的逻辑用语进行归纳和总结。
一、命题命题是陈述句,可以判断陈述是否为真或为假。
命题常用的表示方式有以下几种:1.用大写字母P、Q、R等表示命题,例如:P表示“数学是一门有趣的学科”。
2.用P(x)表示含有变量x的命题,例如:P(x)表示“x是偶数”。
二、谓词谓词是含有变量的陈述句,变量可以代表任意对象。
常用的谓词有以下几种:1.定义域:谓词的变量所属的集合,例如:P(x)中x的定义域为整数集合。
2.真值:谓词在特定对象上的真假情况,例如:P(2)为真,表示2满足谓词P。
三、命题连接词命题连接词可以用来连接两个或多个命题,形成复合命题。
常用的命题连接词有以下几种:1.否定:连接一个命题,表示命题的相反情况,常用符号为¬,例如:¬P表示“不是所有的数学题都很难”。
2.合取(与):连接两个命题,并且两个命题都为真时,复合命题才为真,常用符号为∧,例如:P∧Q表示“数学和物理都是有趣的学科”。
3.析取(或):连接两个命题,其中至少一个命题为真时,复合命题才为真,常用符号为∨,例如:P∨Q表示“数学或物理是有趣的学科”。
4.异或:连接两个命题,其中有且仅有一个命题为真时,复合命题才为真,常用符号为⊕,例如:P⊕Q表示“数学或物理是有趣的学科,但不是同时有趣”。
5.蕴含(如果...那么...):连接两个命题,如果前提为真,则结论必为真,常用符号为→,例如:如果数学是有趣的学科,那么它的题目也是有趣的。
6.等价(当且仅当):连接两个命题,两个命题真值相等,常用符号为↔,例如:数学是有趣的学科当且仅当它的题目也是有趣的。
四、条件语句条件语句是一种特殊形式的蕴含命题,常用的条件语句有以下几种:1.充分条件:如果A为真,则B也为真,常用符号为A→B。
人教版(新教材)高中数学第一册(必修1)精品课件:第一章集合与常用逻辑用语章末复习课

【例1】 (1)设集合A={1,2,4},集合B={x|x=a+b,a∈A,b∈A},则集合B中元
素的个数是( )
A.4
B.5
C.6
D.7
(2)已知集合A={0,1,2},则集合B={x-y|x∈A,y∈A}中元素的个数是( )
A.1
B.3
ቤተ መጻሕፍቲ ባይዱ
C.5
D.9
解析 (1)∵a∈A,b∈A,x=a+b,所以x=2,3,4,5,6,8,∴B中有6个元素, 故选C. (2)当x=0,y=0时,x-y=0;当x=0,y=1时,x-y=-1;当x=0,y=2时,x-y =-2;当x=1,y=0时,x-y=1;当x=1,y=1时,x-y=0;当x=1,y=2时,x -y=-1;当x=2,y=0时,x-y=2;当x=2,y=1时,x-y=1;当x=2,y=2时, x-y=0.根据集合中元素的互异性知,B中元素有0,-1,-2,1,2,共5个. 答案 (1)C (2)C
【训练4】 (1)若p:x2+x-6=0是q:ax+1=0的必要不充分条件,则实数a的值为 ________. (2) 若 - a<x< - 1 成 立 的 一 个 充 分 不 必 要 条 件 是 - 2<x< - 1 , 则 a 的 取 值 范 围 是 ________.
解析 (1)p:x2+x-6=0,即x=2或x=-3. q:ax+1=0,当 a=0 时,方程无解;当 a≠0 时,x=-1a. 由题意知p q,q p,故a=0舍去;
当 a≠0 时,应有-1a=2 或-1a=-3,解得 a=-12或 a=13. 综上可知,a=-12或 a=13. (2)根据充分条件、必要条件与集合间的包含关系,应有{x|-2<x<-1} {x|-a<x< -1},故有a>2. 答案 (1)-12或13 (2)a>2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)命题 p : x A,命题 q : x B ,且 p 是 q 的必要非充分条件,求实数 m 的取值范围;
(2)若 x A ,都有 x2 m 4 3x ,求实数 m 的取值范围.
p q 且 q⇒p
p 是 q 的既不充分条件也不必要条件
p q 且 q p
A B A B A B 且 A B
2.全称量词与存在量词 量词名称 全称量词 存在量词
常见量词 所有的、一切、任意一个、每一个、任给等 存在一个、至少有一个、有些、对某些等
符号表示 ∀ ∃
3.全称量词命题、存在量词命题及含一个量词的命题的否定
(1)若 m 2 , q 为真命题,求实数 x 的取值范围; (2)若 p 是 q 的充分不必要条件,求实数 m 的取值范围.
21.已知命题 p :存在实数 x R ,使 x2 ax 1 0 成立.
(1)若命题 P 为真命题,求实数 a 的取值范围;
(2)命题 q :任意实数 x 1, 2 ,使 x2 2ax 1 0恒成立.如果 p,q 都是假命题,求实数 a 的取值范围.
12.给出下列命题,其中为真命题的是( )
A. x R , x2 x 1 0 B.当 ac 0 时, x R , ax2 bx c 0 C.命题“ x 1, x2 3x 2 0 ”的否定是:“ x 1 , x2 3x 2 0 ” D. x y x y 成立的充要条件是 xy 0
(2)在判断充分、必要条件时,小可以推大,大不可以推小,如 x 2 (小范围) x 1(大范围), x 1(大 范围) x 2 (小范围).
(3)含有一个量词的命题的否定规律是“改量词、否结论”.
二.题型突破
题型一 充分条件、必要条件及充要条件的判断
【例 1】(1)设 x R ,则“ x 1 1 ”是“ x3 1”的( ) 22
B.命题“任意 x R ,则 x2 x 1 0 ”的否定是“存在 x R ,则 x2 x 1 0 ” C.设 x, y R ,则“ x2 y2 4 ”是“ x 2 且 y 2 ”的充分不必要条件
D.设 a,b R ,则“ a 0”是“ ab 0 ”的必要不充分条件
11.下列说法正确的有( )
三、填空题
13.命题“ x 0 , x2 1 0 ”的否定是:__________. 14.已知条件 p :1 x 0 ,条件 q : x a ,若 p 是 q 的充分不必要条件,则 a 的取值范围是________.
15.命题“ x0 R ,使 m 1 x02 mx0 m 1 0 ”是假命题,则实数 m 的取值范围为__________.
___________.
(2)已知命题 p : x 1,3 , x2 a 2 0 .若 p 为假命题,则 a 的取值范围为( )
A. , 2
B. , 1
C. ,7
D. ,0
巩固训练:
1.已知命题 p : x R , x2 a 1x 1 0 ,若命题 p 是假命题,则 a 的取值范围为( )
16.一名法官在审理一起珍宝盗窃案时,四名嫌疑人甲、乙、丙、丁的供词如下:甲说:“罪犯在乙、丙、 丁三人之中”;乙说:“我没有作案,是丙偷的”;丙说:“甲、乙两人中有一人是小偷”;丁说:“乙说的是 事实”,经过调查核实,四人中有两人说的是真话,另外两人说的是假话,且这四人中只有一人是罪犯, 由此可判断罪犯是________. 四、解答题
A.充分不必要条件 二、多项选择题
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
9.已知 p : x 1,3 , x2 a 0 恒成立,则 p 的一个充分不必要条件可以是( )
A. a 9
B. a 9
10.下面说法正确的是( )
C. a 10
D. a 10
A.“ 1 1”是“ a 1”的必要不充分条件 a
A. x R , x2 x 1 0 4
B.所有正方形既是矩形也是菱形
C. a 0 , x2 2x 2 a 0
D.所有三角形都有外接圆
题型四 含有量词(∀ 、∃ )的参数问题
【例 4】(1)已知命题 p : “ xR , 2kx2 kx 3 0 恒成立”是真命题,则实数 k 的取值范围是 8
巩固训练:
D.既不充分也不必要条件
1.王昌龄《从军行》中有诗句“黄沙百战穿金甲,不破楼兰终不还”,其中“攻破楼兰”是“返回家乡” 的( )
A.必要不充分条件 B.充分不必要条件 C.充要条件 D.既不充分也不必要条件
2.下列不等式中可以作为 x2 1 的一个充分不必要条件的有( )
A. x 1
B. 0 x 1
题型二 充分、必要条件的应用
C. 1 x 0
D. 1 x 1
【例 2】(1)已知“ x k ”是“ 3 1”的充分不必要条件,则 k 的取值范围为( ) x 1
A. ,1
B. 1,
C. 2,
D. 2,
(2)已知关于 x 的不等式 x ax 3 0 成立的一个充分不必要条件是 1 x 1,则 a 的取值范围是
A. x Q ,有 x P
B. x Q ,有 x P
C. x0 Q ,使得 x0 P
D. x0 P ,使得 x0 Q
4.满足“闭合开关 K1 ”是“灯泡 R 亮”的充要条件的电路图是( )
A.
B.
C.
D.
5.已知命题 p : x R , x2 2ax a 0 .若命题 p 是假命题,则实数 a 的取值范围是( )
A.“ a 1”是“方程 x2 x a 0 有一个正根和一个负根”的必要不充分条件 B.对于命题 p :“ x 1, x2 3x 2 0 ”,则非 p 为“ x 1 , x2 3x 2 0 ” C.“ a b ”是“ ac2 bc2 ”的必要不充分条件 D.若 a,b, c R ,则“ ax2 bx c 0 ”的充要条件是“ b2 4ac 0 ”
17.判断下列语句是否为命题,若是,请判断真假并改写成“若 p ,则 q ”的形式.
(1)垂直于同一条直线的两条直线平行吗? (2)三角形中,大角所对的边大于小角所对的边;
(3)当 x y 是有理数时, x, y 都是有理数; (4)1 2 3 2021;
(5)这盆花长得太好了! 18.写出下列命题的否定,并判断其真假:
A.充分不必要条件
B.必要不充分条件 C.充要条件
(2)(多选)下列说法正确的是( )
A.“ ac bc ”是“ a b ”的充分不必要条件
B.“ 1 1 ”是“ a b ”的既不充分也不必要条件 ab
C.若“ x A ”是“ x B ”的充分条件,则 A B
D.“ a b 0 ”是“ an bn n N, n 2”的充要条件
A. 3 2
B. 5 2
题型三 全(特)称命题的否定及真假判断
C. 7 2
【例 3】(1)(多选)下列说法正确的是
D. 7 3
A.若命题 p : x R, x x 0 ,则 p : x R, x x 0
B.命题“梯形的对角线相等”是全称量词命题
C.命题“ x R, x2 x 1 0 ”是真命题
D.“ a 5 是无理数”是“ a 是无理数”的充要条件
(2)命题“ x N , x2 x 2 0 ”的否定是
,此否定命题是 命题(填“真”
或“假”). 巩固训练:
1.命题“ x 0, x2 1 0 ”的否定是:____________________.
2.下列命题的否定中,真命题的是( )
命题名称
语言表示
符号表示
全称量词命题 对 M 中任意一个 x,p(x)成立
∀x∈M,p(x)
存在量词命题 存在 M 中的一个 x,p(x)成立
∃x∈M,p(x)
命题的否定 ∃x0∈M,非 p(x0) ∀x∈M,非 p(x)
4.常用结论和注意点 (1)A 是 B 的充分不必要条件⇔非 B 是非 A 的充分不必要条件.
A. 1,3
B. 1,3
C. 1,3
D. 0,2
2.已知命题“ x0 1,1 , x02 3x0 a 0”为真命题,则实数 a 的取值范围是
A. 9 , 4
B. 4,
C. 2,4
D. 2,
三、反馈练习
一、单项选择题
1.命题“存在实数 x ,使 x 1”的否定是( )
A.对任意实数 x ,都有 x 1
几何体的体积分别为V1 ,V2 ,被平行于这两个平面的任意平面截得的两个截
面面积分别为 S1 , S2 ,则“ S1 , S2 不总相等”是“V1 ,V2 不相等”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
7.已知集合 A x x2 2x 3 0 ,集合 B x 3 x a ,若“ x B ”是“ x A ”的必要不充分
条件,则实数 a 的取值范围是( )
A. 1,
B. 1,
C. 3,1
D. 3,1
8.2020 年 2 月 11 日,世界卫生组织将新型冠状病毒感染的肺炎命名为 COVID-19(新冠肺炎)新冠肺炎,
患者症状是发热、干咳、浑身乏力等外部表征.“新冠肺炎患者”是“患者表现为发热、干咳、浑身乏力” 的已.知.该.患.者.不.是.无.症.状.感.染.者.( )
A. ,0 1, B. ,0 1,
C. 0,1
D. 0,1
6.南北朝时期的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则 积不容异”.其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平行平面的任意平面所截,
如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.如图,夹在两个平行平面之间的两个
