崇文区2008年高三第二次模拟考试数学(文科)试题
中国多媒体教学学报.doc

中国多媒体教学学报中学化学2008年第1期目录2008年第2期目录2008年第3期目录2008年第4期目录2008年第5期目录2008年第6期目录2008年第1期目录【卷首语】1、值得期待的2008/本刊编辑部摘要:作为国内基础教育领域的首家多媒体电子期刊,我们有责任充分发挥载体优势,记录下中国教育史上这浓墨重彩的一笔!我们将紧跟教育改革步伐,贴近教学一线需求,以传播先进教育教学理论和实践经验为己任,竭力奉献更多更优秀的作品。
【专家视角】2、潜下心来教书静下心来育人/陶西平摘要:本期有幸邀到当代著名教育家陶西平先生在2007年中国教育学会生物学教学专业委员会第六次全国代表大会暨第十一届全国学术年会上所作的报告。
报告结合胡锦涛总书记在全国优秀教师代表座谈会上的讲话,从大视野、大角度、高层面就着力提高教育质量,加强教师队伍建设,关注教师职业心态等问题了做了深入浅出的阐述,引起与会代表的高度重视。
本刊对陶先生的发言进行了编辑整理,以期让更多教育工作者受益。
【理论探索】3、中学化学课程资源的开发与利用研究(下)/王耀摘要:本文从模型与实物、文献与论文、书籍与故事、数据与图谱、课件与动画等类型的素材方面继续与大家交流课程资源的开发和利用问题,希望能给广大教育工作者一点可供借鉴的思路和经验。
4、等电子原理与化学新课程/陈凯,赵波,周志华摘要:等电子原理在新课程背景下的化学教学内容中有着独特的地位和作用,本文结合科技知识浅谈怎样运用等电子原理解决一些典型问题,以期对中学化学等电子原理的教与学有所帮助。
5、在初中化学教学中培养学生自主探究/李德胜摘要:本文从自主探究的素材选择、问题创设、拓展探究三个层面,结合丰富的教学实例,对“在初中化学教学中,如何培养学生自主探究学习”做了细致深入的论述。
【整合实践】6、新型无机非金属材料/郑迎红摘要:这是一节基于信息技术环境下的多媒体网络教室中化学学科探索性学习的试验研究课,对多媒体技术和网络技术在中学化学教育中的应用作了新的尝试。
北京市崇文区2009—2010学年度高三第二学期统一练习(二)
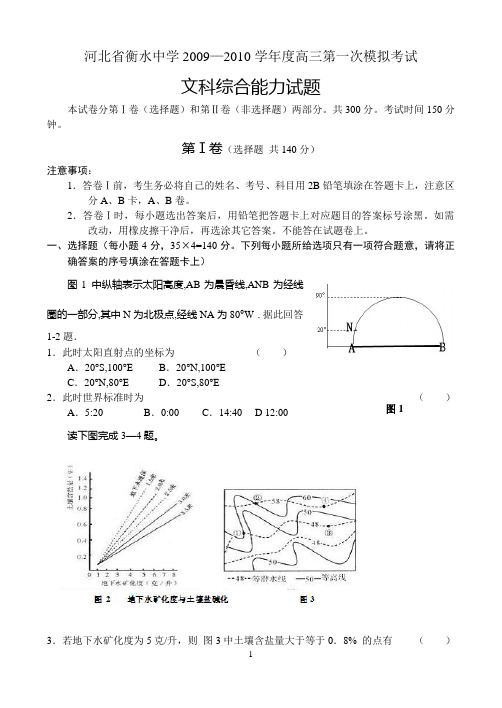
河北省衡水中学2009—2010学年度高三第一次模拟考试文科综合能力试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
共300分。
考试时间150分钟。
第Ⅰ卷(选择题 共140分)注意事项:1.答卷Ⅰ前,考生务必将自己的姓名、考号、科目用2B 铅笔填涂在答题卡上,注意区分A 、B 卡,A 、B 卷。
2.答卷Ⅰ时,每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案。
不能答在试题卷上。
一、选择题(每小题4分,35×4=140分。
下列每小题所给选项只有一项符合题意,请将正确答案的序号填涂在答题卡上)图1 中纵轴表示太阳高度,AB 为晨昏线,ANB 为经线圈的一部分,其中N 为北极点,经线NA 为80°W .据此回答1-2题.1.此时太阳直射点的坐标为 ( )A .20°S,100°EB .20°N,100°EC .20°N,80°ED .20°S,80°E2.此时世界标准时为 ( )A .5:20B .0:00C .14:40D 12:00读下图完成3—4题。
3.若地下水矿化度为5克/升,则 图3中土壤含盐量大于等于0.8% 的点有 ( )A .①B .①②C .②③④D .①③4.读图,下列判断正确的是 ( )A .若地下水矿化度较低则无论地下水埋藏深浅土壤含盐较低图1图4 B .若地下水埋深相同则土壤含盐量与地下水矿化度成负相关C .地下水埋深越大则土壤含盐量越大,土壤盐碱化就越严重D .若地下水矿化度相同则土壤含盐量与地下水埋深成正相关图4 是某月份海平面平均气压沿两条纬线的变化图,回答5—6题。
5.该月份,①、②两地的平均风力相比较 ( )A .①地的较大B .两地相当C .②地的较大D .上半月①地的较大6.③地以南到赤道以北地区,此时的盛行风向为 ( )A .西北风B .西南风C .东北风D .东南风服务外包是指企业将其非核心的业务外包出去,利用外部最优秀的专业化团队来承接业务,从而使其专注核心业务,达到降低成本的一种管理模式。
北京市崇文区2008-2009学年度第二学期高三统一练习(文科)

崇文区2008-2009学年度第二学期高三统一练习高三数学 (文科) 2009.3本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至9页,共150分。
考试时间120分钟。
考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题 共40分)注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
不能答在试卷上。
一、选择题:本大题共8小题.每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 设集合}2,1,0,1{-=A ,}13|{<≤-=x x B ,则A B =A .{}0,1-B .{}1,0,1-C .{}10x x -<< D . {}10x x -≤≤ 2. 抛物线y x 42=的焦点坐标是 A .⎪⎭⎫⎝⎛0,161 B .⎪⎭⎫⎝⎛161,0 C .()1,0 D .()0,1 3. 已知31cos sin =-θθ ,则θ2sin 的值为 A . 32- B .32 C .98-D .984.设{n a }是公差为-2的等差数列,如果,50741=++a a a 则=++1296a a a A . 40 B .30 C .20 D . 105.下列命题中,正确的命题是A .过空间任一点P 均存在着与平面α平行的直线B .过空间任一点P 均存在着与平面α垂直的直线C .过空间任一点P 均存在着与平面α平行的无数多条直线D .过空间任一点P 均存在着与平面α垂直的无数多条直线6.定义在R 上的函数)(x f 是偶函数,且)2()(x f x f -=.若)(x f 在区间[0,1]上是增函数,则)(x fA .在区间[1 ,2--]上是增函数,在区间[6 ,5]上是增函数B .在区间[1 ,2--]上是增函数,在区间[6 ,5]上是减函数C .在区间[1 ,2--]上是减函数,在区间[6 ,5]上是增函数D .在区间[1 ,2--]上是减函数,在区间[6 ,5]上是减函数7.在如下图所示的坐标平面的可行域内(阴影部分且包括边界),若目标函数 z =x +ay 取得最小值的最优 解有无数个,则a 等于A .1B .1-C .3D .3-8.直角坐标系中横坐标、纵坐标均为整数的点称为格点,如果函数f (x )的图象恰好通过k (k ∈N *)个格点,则称函数()f x 为k 阶格点函数.下列函数:① ()f x =sinx ; ② ()f x =π(x -1)2+3; ③ 1()()3xf x = ; ④ x x f 6.0log )(=.其中是一阶格点函数的有 A .①② B .①④ C .①②④ D .①②③ ④崇文区2008-2009学年度第二学期高三统一练习高三数学 (文科) 2009.3第Ⅱ卷(共110分)注意事项:1.用钢笔或圆珠笔将答案直接写在试卷上.二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.9. 已知nxx )21(+展开式的第二项与第三项的系数比是1:2,则n=_____________. 10.若把函数3)2(log 2+-=x y 的图象按向量a 平移,得到函数1)1(log 2-+=x y的图象,则向量a 的坐标为 .11. 某商店要求甲、乙、丙、丁、戊五种不同的商品在货架上排成一排,其中甲、乙两种必须排在一起,而丙、丁两种不能排在一起,不同的排法共有 种.12. 如图,等腰梯形ABCD 中, E,F 分别是BC 边上的三等分点,AD=AE=1,BC=3, ,若把三角形ABE 和DCF 分别沿AE 和DF 折起,使得B 、C 两点重合于一点P ,则二面角P-EF-D 的大小为 .13.点P 为椭圆1162522=+y x 上的动点,21,F F 为椭圆的左、右焦点,则21PF PF ⋅的最小值为__________ ,此时点P 的坐标为________________.14.对于集合N={1, 2, 3,…, n}的每一个非空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减、加后继的数.例如集合{1, 2, 4, 6, 9}的交替和是9–6+4–2+1=6,集合{5}的交替和为5.当集合N 中的n =2时,集合N={1, 2}的所有非空子集为{1},{2},{1, 2},则它的“交替和”的总和2S =1+2+(2–1)=4,则当3n =时,3S = ______________ ;根据2S 、3S 、4S ,猜想集合N ={1, 2, 3,…, n}的每一个非空子集的“交替和”的总和n S =__________.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤15.(本小题满分13分)在△ABC 中,角A 、B 、C 所对的边分别为a,b,c ,向量m)3,(c b a -=,n )cos (cos C A ,=,且m ∥n . (Ⅰ)求cosA 的大小; (Ⅱ) 求)4sin()4sin(22sin2ππ+--+A A C B 的值.16.(本小题满分14分)已知直四棱柱ABCD-A 1B 1C 1D 1中,AB//CD,AB=AD=1, DD 1=CD=2,AB ⊥AD . (I)求证:BC ⊥面D 1DB ;(II)求D 1B 与平面D 1DCC 1所成角的大小.17.(本小题满分13分)已知函数b x x a x a x f +++-=23213)( ,其中,a b ∈R . (Ⅰ)若曲线)(x f y =在点))2(,2(f P 处的切线方程为45-=x y ,求函数)(x f 的解析式; (Ⅱ)当0>a 时,讨论函数)(x f 的单调性.18. (本小题满分13分)某学校进行交通安全教育,设计了如下游戏,如图,一辆车模要直行..通过十字路口,此时前方交通灯为红灯,且该车模前面已.有.4.辆车模...依次在同一车道上排队等候(该车道只可以直行或左转行驶).已知每辆车模直行的概率是35,左转行驶的概率是25,该路口红绿灯转换间隔时间均为1分钟.假设该车道上一辆直行去东向的车模驶出停车线需要10秒钟,一辆左转去北向的车模驶出停车线需要20秒钟,求:(Ⅰ)前4辆车模中恰有2辆车左转行驶的概率;(Ⅱ)该车模在第一次绿灯亮起时的1分钟内通过该路口的概率(汽车驶出停车线就算通过路口).东北19.(本小题满分14分)已知()0,2M ,()2,0N -,动点P 满足2PN PM -=,点P 的轨迹为W ,过点M 的直线与轨迹W 交于B A ,两点.(Ⅰ)求轨迹W 的方程;(Ⅱ)若MB AM =2,求直线AB 斜率k 的值,并判断以线段AB 为直径的圆与直线21=x 的位置关系,并说明理由.20.(本小题满分13分)已知函数()41,()2,f x x g x x x =+=∈R ,数列}{n a ,}{n b 满足条件:11a =, 1()1(n n a g a n +=+∈N *),]3)(][21)(21[1++=n g n f b n .(Ⅰ)求数列}{n a 的通项公式;(Ⅱ)求数列}{n b 的前n 项和n T ,并求使得150mT n >对任意n ∈N *都成立的最大正整数m ;(Ⅲ)求证: 12231(2n n a a a nn a a a +++⋅⋅⋅+<∈N *).崇文区2008-2009学年度第二学期高三统一练习高三数学 (文科)参考答案 2009.3一、选择题(本大题共8小题,每小题5分,共40分) 1.A 2.B 3.D 4.C 5.B 6. B 7. B 8.C 二、填空题(本大题共6小题,每小题5分,共30分) 9. 14 10. (-3,-4) 11.24 12.2π13. 7 ,(0, ±4) 14. 12 , 12n n -,三、解答题(本大题共6小题,共80分) 15.(本小题满分13分)解: (Ⅰ)由m ∥n 得acosC=(3b-c)cosA , --------------------------------1分由正弦定理得 sinAcosC=(3sinB-sinC)cosA , -----------------------3分即sinAcosC+sinCcosA=3sinBcosA , ∴sin(A+C)=3sinBcosA , ABC ∆中,A+C=π-B ,∴sin(π-B)=3sinBcosA , 即sinB=3sinBcosA0sin ),0(≠∈B B π ,∴cosA=31. --------------------------------------------6分(Ⅱ) )4sin()4sin(22sin2ππ+--+A A C B )cos 22sin 22)(cos 22sin 22(22sin 2A A A A A+---=π --------9分)cos (sin 2cos 222A A A --= ------------------------------11分 1cos 22cos 12-++=A A 911)31(223112-=-++=. ---------------------------------13分16.(本小题满分14分)解法一:(I)证明:∵ABCD-A 1B 1C 1D 1为直四棱柱,∴ D 1D ⊥平面ABCD ,∴BC ⊥D 1D .∵AB//CD, AB ⊥AD .∴四边形 ABCD 为直角梯形,又∵AB=AD=1,CD=2,可知BC ⊥DB .∵D 1D ∩ DB=D ,∴BC ⊥平面D 1DB . -----------------------6分 (II)取DC 中点E ,连结BE,D 1E.∵DB=BC ,∴BE ⊥CD.∵ABCD-A 1B 1C 1D 1为直四棱柱,∴ABCD ⊥D 1DCC 1.∴BE ⊥D 1DCC 1.∴D 1E 为D 1B 在平面D 1DCC 1上的射影,∴∠BD 1E 为所求角.在BE D Rt 1∆中,5,11==E D BE .55tan 11==∠E D BE E BD . ∴所求角为55arctan. ---------------------------------14分 解法二:(I)证明:如图建立坐标系D-xyz,1(0,0,0),(1,1,0),(0,2,0),(0,0,2)D B C D .∴1(1,1,0),(0,0,2),(1,1,0)BC DD DB =-== .∵0,01=⋅=⋅DB BC DD BC ,∴BC ⊥DD 1, BC ⊥DB .∵D 1D ∩ DB=D ,∴BC ⊥平面D 1DB . ------------------6分(II) 1(1,1,2),(1,0,0),(1,0,0)D B A DA =-= .∵AD ⊥平面D 1DCC 1,∴平面D 1DCC 1的法向量(1,0,0)m = ,∵111cos ,D B m D B m D B m⋅<>=== . ∴D 1B 与平面D 1DCC 1所成角的大小为66arcsin. --------------------14分 17.(本小题满分13分) 解:(Ⅰ)2()(1)1f x ax a x '=-++, ------------2分由导数的几何意义得(2)5f '=,于是3a =. -----------------3分 由切点(2,(2))P f 在直线54y x =-上可知26b +=,解得4b =. -----5分所以函数()f x 的解析式为32()24f x x x x =-++. ------------6分 (Ⅱ)21()(1)1()(1)f x ax a x a x x a '=-++=--, ------------------7分 当01a <<时,11a>,函数()f x 在区间(, 1)-∞及1(, )a +∞上为增函数; 在区间1(1, )a上为减函数; --------------------------------------------------------9分当1a =时,11a=,函数()f x 在区间(,)-∞+∞上为增函数;------------------11分 当1a >时,11a<,函数()f x 在区间1(, )a -∞及(1, )+∞上为增函数; 在区间1(, 1)a 上为减函数. --------------------------13分 18. (本小题满分13分)(Ⅰ)设前4辆车模中恰有2辆左转行驶为事件A ,则()222432216()()55625P A C =⨯= . --------------------------------------------6分(Ⅱ)设该车在第一次绿灯亮起时的1分钟内通过该路口为事件B ,其中4辆车模均 直行通过路口为事件1B ,3辆直行1辆左转为事件2B ,则事件1B 、2B 互斥.()()()()4433121244332297()()555625P B P B B P B P B C C =+=+=+⨯=. ----13分19.(本小题满分14分)解:(Ⅰ)∵42=<=-MN PM PN ,∴点P 的轨迹是以N M ,为焦点的双曲线的右支,且1,2,3a c b ==∴轨迹W 的方程为 ()11322≥=-x y x . ---------------------------------4分 (Ⅱ)设直线AB 的方程为()2-=x k y .由()⎪⎩⎪⎨⎧=--=,13,222y x x k y 得 ()034432222=--+-k x k x k . ----------------5分 设()()2211,.,y x B y x A ,则0342221>-=+k k x x , ① 03342221>-+=k k x x , ② ()()0343416224>+-+=∆k k k . ③ -------------------8分 由①②③解得 32>k . ------------------------------------------------------------9分 ∵=2,∴()()112222,2,x y x y --=-,∴1226x x -=. 带入 ①②,得 122634x k k -=-, ()112226334x x k k -=-+. 消掉1x 得235,5k k == ---------------------------------11分∵()0,2M 为双曲线右支的焦点,离心率e =2.由双曲线的几何性质,得 ()()31623422222221-+=--⨯=-+=k k k k a x x e AB . 设以AB 为直径的圆的圆心为Q ,Q 到直线l 的距离为d ,则 d =()()32132122221-+=-+k k x x . ∴()()()()()0321331332132222222<-+-=-+--+=-k k k k k k AB d . ∴ 2ABd <,直线l 与圆Q 相交. ---------------------------------------14分20.(本小题满分13分)解:(Ⅰ)由题意121+=+n n a a , --------2分∴)1(211+=++n n a a .∵11=a ,∴数列}1{+n a 是首项为2,公比为2的等比数列. ---------3分∴1221-⨯=+n n a ,∴12-=n n a . ---------4分 (Ⅱ)∵)321121(21)32)(12(1+-+=++=n n n n b n , ---------5分 ∴)32112171515131(21+-++⋅⋅⋅+-+-=n n T n 96)32(3)32131(21+=+⨯=+-=n n n n n . ----------7分 ∵11569156961561221>+++=+⋅++=+nn n n n n n n T T n n ,∴1,n n T T n +<∈N *.∴当1=n 时,n T 取得最小值151. -----------------8分 由题意得150151m >,∴10<m . ∵Z m ∈ , ∴9=m . ------------10分(Ⅲ)证明:∵ n k a a k k k k k k ,,3,2,1,21)22(212121211⋅⋅⋅=<--=--=++ , ∴213221n a a a a a a n n <+⋅⋅⋅+++. ----------------13分。
高考重点总结:近几年排列组合问题全部归纳总结

高考重点总结:近几年排列组合问题全部归纳总结2017年联考题一、选择题1.(山东省济宁市2017年3月高三一模试题理科)从6名男生和2名女生中选出3名志愿者,其中至少有1名女生的选法共有( A )A.36种B.30种C.42种D.60种2.(山东省聊城市2010 年高考模拟数学试题理)从甲、乙、丙、丁四名同学中选出三名同学,分别参加三个不同科目的竞赛,其中甲同学必须参赛,不同的参赛方案共有( B )A.24种B.18种C.21种D.9种3.(山东省日照市2017年3月高三一模理科)某校园有一椭圆型花坛,分成如图四块种花,现有4种不同颜色的花可供选择,要求每块地只能种一种颜色,且有公共边界的两块不能种同一种颜色,则不同的种植方法共有( A )(A)48种(B)36种(C)30种(D)24种4.(湖北省荆州市2017年3月高中毕业班质量检查Ⅱ理科)将5名大学生分配到3个乡镇去任职,每个乡镇至少一名,不同的分配方案有( B )种.A240.B150.C60.D1805.(湖北省八校2010 届高三第二次联考理科)甲、乙、丙、丁、戌5人站成一排,要求甲、乙均不与丙相邻,则不同的排法种数为( C )A.72种B.54种C.36种D.24种6.(湖北省八校2010 届高三第二次联考文科)甲、乙、丙等五人站成一排,要求甲、乙均不与丙相邻,则不同的排法种数为( C )A.72种B.52种C.36种D.24种7.(湖北省襄樊市2017年3月高三调研统一测试文理科)某班要从6名同学中选出4人参加校运动会的4×100m接力比赛,其中甲、乙两名运动员必须入选,而且甲、乙两人中必须有一个人跑最后一棒,则不同的安排方法共有( B )A.24种B.72种C.144种D.360种8.(北京市丰台区2017年4月高三年级第二学期统一考试理科)从0,2,4中取一个数字,从1,3,5中取两个数字,组成无重复数字的三位数,则所有不同的三位数的个数是( B )A.36 B.48 C.52 D.549.(北京市崇文区2017年4月高三年级第二学期统一练习理科)2位男生和3位女生共5位同学站成一排.若男生甲不站两端,3位女生中有且只有两位女生相邻,则不同排法的种数为(A)36 (B)42 (C) 48 (D) 6010. (2017年4月北京市西城区高三抽样测试理科)某会议室第一排共有8个座位,现有3人就座,若要求每人左右均有空位,那么不同的坐法种数为( C )A.12B.16C.24D.32二、填空题:11.(湖北省黄冈市2017年3月份高三年级质量检测理科)将A、B、C、D、E五种不同的文件放入一排编号依次为1、2、3、4、5、6的六个抽屉内,每个抽屉至多放一种文件.若文件A、B必须放入相邻的抽屉内,文件C、D也必须放相邻的抽屉内,则文件放入抽屉内的满足条件的所有不同的方法有种.9612.(湖北省赤壁一中2010届高三年级3月质量检测理科A试题)某车队有7辆车,现在要调出4辆,再按一定顺序出去执行任务.要求甲、乙两车必须参加,而且甲车在乙车前开出,那么不同的调度方案有种.12013.(湖北省八校2010 届高三第二次联考理科)有一种数学推理游戏,游戏规则如下:①在9×9的九宫格子中,分成9个3×3的小九格,用1到9这9个数填满整个格子;②每一行与每一列都有1到9的数字,每个小九宫格里也有1到9的数字,并且一个数字在每行每列及每个小九宫格里只能出现一次,既不能重复也不能少,那么A处应填入的数字为 1 ;B处应填入的数字为 1 。
高三文综高考热点模拟题(四)

武广高铁(广东省深圳高级中学高三一模文科综合) 12月26日,世界上一次性建成里程最长、标准最高、最大的高速铁路——武广高铁正式开通。
武广高铁全线共设15个车站,途经11个地级市,将广州到武汉的铁路运输时间从过去的10小时缩短至3小时。
回答5~6题。
5、武广高铁桥梁和隧道占线路总长度的三分之二,主要原因不包括A.沿线多山地丘陵、河流和交通线B.高速铁路要求线路较平直C.少占用耕地D.经过山区的主要旅游景点6、武广高铁对沿线地区产生的影响,不正确的是A.沿线地区大中小城市之间地租差异进一步扩大B.大城市高速铁路的站点附近将形成卫星城市C.在城际轨道的沿途站点则将形成城市副中心D.加速珠江三角洲地区的产业转移和产业升级西南大旱(北京市海淀区高三第二学期期中文综)自秋季至今,我国西南地区遭遇旱灾,局部地区遭遇百年一遇的严重旱灾。
据图3回答5、6题。
5.下列叙述正确的是A.特旱地区分布在云、贵、川三省 B.该区域旱情严重程度由南向北递减C.此次旱灾是受副热带高压控制形成的伏旱D.降水持续偏少、气温偏高是导致旱灾的原因6.中国气象局对此次旱灾进行了动态监测和预报,应用的地理信息技术是①遥感②全球定位系统③地理信息系统④数字地球A.①② B.③④C.①③ D.②④黄海结冰(广东汕头市普通高等学校招生模拟考试文综地理)新年以来,渤海和黄海北部出现30年来最严重海冰冰情,下图(图5)为我布的1月22日—26日海冰警报示意图,回答9~10题9.从图中可以看出,我国渤海海冰的分布特点是A.从南向北海冰面积递增B.由东向西海冰厚度递增C.海冰的厚度随海水深度而增加 D.海湾处海冰的分布面积大于其他地区10.下列区域,不易形成海冰的是:A.淡水注入的河口B.风浪较大的岬角C.风平浪静的海湾 D.深度不大的浅海莫拉克台风(江苏省南京市高三第二次模拟考试地理) 8月我国台湾省遭受强台湾“莫拉克”袭击,造成巨大的财产损失和人员伤亡,结合图6,回答9-10题9.此次台湾重灾区的人员伤亡主要是由_______导致的A 暴雨洪涝B 强风C 风暴潮D 滑坡泥石流等次生灾害10.图6为台湾岛铁路分布示意图,形成铁路环状分布的原因是A 气候B 地形C 城市分布D 经济发展不平衡美洲地震(江苏省普通高中学业水平测试(必修科目)试卷地理)图3为“北京时间1月13日5时53分海地(西五区)地震示意图”。
2010年北京西城区高考一模试题:数学(文科)

2010年北京崇文区高考一模试题:数学(文科)本试卷分第I 卷和第Ⅱ卷两部分,第I 卷1至2页,第Ⅱ卷3至5页,共150分。
考试时长120分钟。
考生务必将答案答在答题纸上,在试卷上作答无效。
考试结束后,将本试卷和答题纸一并交回。
第I 卷(选择题共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. 1.设集合{|1},{|(1)0}P x x Q x x x =>=->,下列结论正确的是A .P Q =B .P Q R =C .P Q ØD .Q P Ø2.下面四个点中,在平面区域4y x y x<+⎧⎨>-⎩内的点是A .(0,0)B .(0,2)C .(3,2)-D .(2,0)-3.设等差数列{}n a 的前n 项和为,n S 246a a +=,则5S 等于A .10B .12C .15D .304.若0m n <<,则下列结论正确的是A .22mn>B .11()()22m n< C .22log log m n>D .1122log log m n>5.甲乙两名运动员在某项测试中的6次成绩如茎叶图所示,1x ,2x 至z 分别表示甲乙两名运动员这项测试成绩的平均数,1s ,2s 分别表示甲乙两名运动员这项测试成绩的标准差,则有A .1212,x x s s ><B .1212,x x s s =<C .1212,x x s s ==D .1212,x x s s <>6.阅读右面程度框图,运行相应的程序,输出 的结果为A .1321B .2113C .813D .1387.已知双曲线2213yx -=的左顶点为1A ,右焦点为2F ,P 为双曲线右支上一点,则12PA PF的最小值为A .2-B .8116-C .1D .08.如图,平面α⊥平面β,αβ =直线l ,A ,C 是α内不同的两点,,B D是β内不同的两点,且A ,B ,CD ∉直线l ,M ,N 分别是线段AB ,CD 的中点。
2008年北京高考各区各校总体情况
2008年北京高考总体情况(信息汇总)[崇文因成绩垫底,未公布]2008年北京高考总体情况(信息汇总)(2008-06-28 20:34:56)北京市的理科状元——胡梦萦来自人大附中,总分702分。
北京市的文科状元——丁艺莎来自北京四中,总分667分。
数学150,语文132,英语129, 文综256北京市高考理科第二名(700分)、第三名(699分)也均出自北京四中。
各分数段累积分(含加分)理科:720+有2人,710+有8人,700+有27人,690+有66人,680+有148人,670+有316人,660+有580人,650+有934人,640+有1371人,630+有1964人,620+有2619人,610+有3351人,600+有4212人。
文科:670+有5人,660+有7人,650+有23人,640+有65人,630+有126人,620+有227人,610+有366人,600+有559人。
全市理科650分以上有934人,文科650分以上有23人。
600分以上的,文理共4771人。
三门单科出现满分语文:文、理科共有9人在140分以上。
其中,北京二中考生姜伯源语文考了143分,为今年本市高考语文最高分。
数学:文、理科均出现了满分。
数学过140分的考生中,文科有143人、理科有1113人。
英语:过140分的考生文科有6人、理科有12人。
文综:今年考生普遍反映较难,无人上140分,上130分的只有3人。
理综:出现1人满分,290分以上的考生人数为244人。
本市东城西城本科上线率超70%,西城半数理科生过一本本市两大教育强区——西城和东城,均有超过七成的考生高考成绩过本科分数线。
其中,西城区理科生一本上线率突破55%,东城约有四成理科生超过了一本线。
今年西城区高三学生近80%可达本科线。
西城区参加高考的考生约占全市考生总数的十分之一,接近1万人。
其中,文科达到630分以上的考生共有51人,占全市该分段考生总数的40%;理科达到650分以上的考生共有278人,约占全市该分段考生总数的30%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
崇文区2008年高三第二次模拟考试数学(文科)试题 数 学 (文科)
2008.5
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至9页,共150分。考试时间120分钟。考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题 共40分) 注意事项: 答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。不能答在试卷上。
一、选择题:本大题共8小题.每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.函数cosyx的一个单调递增区间为 ( )
A.,22 B.0, C.3,22 D.,2
2.若抛物线pxy22的焦点与椭圆12622yx的右焦点重合,则p的值为 ( ) A.-4 B.4 C.-2 D.2 3.已知数列na中,15a,点1(,)nnaa在直线30xy上,则na= ( ) A23n B32n C23n D32n
4.若函数()fx的反函数是11()2xfx,则(1)f的值为 ( ) A.4 B.4 C.1 D.1 5.若半径为1的球与120°的二面角的两个半平面切于M、N两点,则两切点间的球面距离是 ( )
A.34 B. C.32 D.3 6.按分层抽样的方法,从15个相同的红球和10个相同的黑球中抽出10个球排成一排,则不同的排列方法有 ( ).
A.410C B.410A C.610A D. 1010A
7.给出下列命题,则其中的真命题是 ( ) A.若直线m、n都平行于平面,则m、n一定不是相交直线
B.已知平面、互相垂直,且直线m、n也互相垂直,若,mn则 C.直线m、n在平面内的射影分别是一个点和一条直线,且mn,则//nn或 D.直线m、n是异面直线,若//m,则n必与相交
8.定义域为(,0)(0,+)的偶函数)(xf在区间(0,+)上的图象如图所示,则不等式)x(f)x(f'>0的解集是 ( ) A.(-,-1)(0,1) B.(-1,0)(1,+) C..(-,-1)(1,+) D.(-1,0)(0,1) 崇文区2007-2008学年度第二学期高三期末统一练习 数 学 (文科) 第Ⅱ卷(非选择题 共110分) 注意事项:1.用钢笔或圆珠笔将答案直接写在试卷上. 2.答卷前将密封线内的项目填写清楚. 题号 一 二 三 总分 1--8 9 10 11 12 13 14 15 16 17 18 19 20 分数
二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上. 9.函数2)3lg(xxy的定义域是 . 10.若某椭圆焦点与短轴顶点构成正方形,则该椭圆的离心率为_____________.
11.二项式61(0)xxx的展开式中常数项等于 . 12.已知等比数列{na}的公比q不为1,若向量i=(1a,2a),j=(1a,3a),k=(-1,1)满足
得分 评卷人 (4i-j)k=0,则q= . 13.如图,函数y=f(x)的图象在点P处的切线方程是y= —x+5,则f′(3)= . 14.在如图所示的数阵中,分别按图中虚线,从上到下把划到的数一一列出,构成一个数列{na}:11C,02C ,22C,13C,04C,33C,24C,15C,06C,„„,则22a= .(用数值作答)
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(本小题满分12分)
已知函数)()(Rxxmxxf,且(1)0f. (Ⅰ)求函数()fx的解析式; (Ⅱ)作出函数)(xf的图象,并指出函数)(xf的单调区间.
得分 评卷人 16.(本小题满分14分) 在ABC中,角A,B,C分别所对的边为cba,,,且CBAAB2sincossincossin, ABC的面积为34.:
(Ⅰ)求角C的大小; (Ⅱ)若2a,求边长c.
17.(本小题满分13分)
已知8人组成的抢险小分队中有3名医务人员,将这8人分为A、B两组,每组4人. (Ⅰ)求A组中恰有一名医务人员的概率; (Ⅱ)求A组中至少有两名医务人员的概率;
得分 评卷人 得分 评卷人 18.(本小题满分13分) 如图,已知正方形ABCD与矩形BEFD所在平面互相垂直,AB=2,DF=1,P是线段EF上的动点. (Ⅰ)若点O为正方形ABCD的中心,求直线OP与平面ABCD所成角的最大值; (Ⅱ)当点P为EF的中点时,求直线BP与FA所成角的正弦值;
(Ⅲ)求二面角A—EF—C的大小.
得分 评卷人 19.(本小题满分14分)
已知BA、分别是x轴和y轴上的两个动点,满足2AB,点P在线段AB上且PBAP2,设点P的轨迹方程为C. (Ⅰ)求曲线C的方程; (Ⅱ)若点NM、是曲线C上关于原点对称的两个动点,点Q的坐标为3(,3)2,求QMN的面积S的最大值.
得分 评卷人 20.(本小题满分14分) 已知A(1x,1y),B(2x,2y)是函数21,122()11,2xxxfxx的图像上的任意两点(可以重合),点M在直线12x上,且AM=MB. (Ⅰ)求1x+2x的值及1y+2y的值 (Ⅱ)已知1S=0,当n≥2时,nS=1()fn+2()fn+3()fn+1()nfn,求nS;
(Ⅲ)在(Ⅱ)的条件下,设na=2nS,nT为数列{na}的前n项和,若存在正整数c、m,使得不等式21cTcT1mm成立,求c和m的值.
崇文区2007-2008学年度第二学期高三统一练习(二) 数 学(文科) 参考答案 一、选择题(本大题共8小题,每小题5分,共40分) 1.D 2.B 3.C 4. C 5.D 6. A 7.C 8.B 二、填空题(本大题共6小题,每小题5分,共30分)
得分 评卷人 9.)3,2()2,( 10. 22 11.-20 12.3 13.-1 14.21 三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(本小题满分12分) 解:(Ⅰ)由(1)101fmm, „„„„„3分 22,1()1,1xxxfxxxxxx
;„„„„„„6分
(Ⅱ)图像如图.„„„„„„„„„„„„„„„10分 函数)(xf的单调递增区间是1(,]2和[1,),)(xf的单调递减区间是
]1,21[;„„„„„„„„„„„„12分
16.(本小题满分13分) 解:(Ⅰ)CBAAB2sincossincossin, 化简,CCCBAcossin2sinsin.„„„„„„„„„„„„3分
∵0sinC∴21cosC,3C.„„„„„„„„„„„„„„„„6分 (Ⅱ)∵ ABC的面积为34,∴ ,34sin21Cab∴ 16ab. „„„„„„„„„„„„„„„„„„„„„„„„„„„„„„„„9分
又∵2a,∴ 8b,∴由余弦定理可得:abcbaC2cos222,
∴132c.„„„„„„„„„„„„„„„„„„„„„„„„„„13分 17.(本小题满分13分) 解:(Ⅰ)设“A组中恰有一名医务人员”为事件1A,
1()PA7
3
48
3513
C
CC.„„„„„„„„„„„„„„„„„„„„„„6分
(Ⅱ)设“A组中至少有两名医务人员”为事件2A, 2()PA 2
1
48153348
2523
CCCC
CC.„„„„„„„„„„„„„„„„13分
18.(本小题满分14分) 解:(Ⅰ)连结OP. 设OP与平面ABCD所成角为,则[,]42.当P是线段EF的中点时, OP平面ABCD,直线OP与平面ABCD所成的最大角是2.„„„„„„4分 (Ⅱ)连结AF、FC、OF. 易证FO//PB,∴AFO是直线BP与FA所成的角. „„„„„„„„„„„„„„„„5分
为直角三角形. AD=2,依题意,在等腰AFC中,FOAC,AFODF=1,∴AF=3.又AO=221(2)(2)12, ∴在RtAOF中,3sin3AOAFOAF.„„„„„„„„„„„„„„„„„8分 (Ⅲ)连结AE、EC,则AF=FC=AE=EC=3.取EF的中点P,连结AP、CP,,APEFCPEF,则APC是二面角A—EF—C的平面角.„„„„„„„„„„„„„„„„„„11分 则等腰AEF≌CEF,∴在APC中,AP=CP=2.又AC=2,∴APC是直角三角形. ,且2APC.即二面角A—EF—C的大小是2.„„„„„„„„„„„„„„14分 19.(本小题满分14分) 解:(Ⅰ)设点PBA、、的坐标分别为),(),0()0,(yxba、、,
则,32,3byax 即.23,3ybxa 由2AB得422ba,所以曲线C的方程为11694922yx.„„5分 (Ⅱ)设1111(,),(,)MxyxyN,则22112MNxy. 当10x时,设直线MN的方程为 11yyxx,
则点Q到直线MN的距离112211332yxhxy, ∴QMN的面积112211112211331322322yxSxyyxxy.„„„„11分 ∴22221111113939924Syxxyxy. 又∵2211991416xy,∴22119944xy.∴21149Sxy. 而221111119933912416244xyxyxy,则1194xy.即28,22SS. 当且仅当113324xy时,即1112xy时,“=”成立. 当10x时,48233MN,∴QMN的面积1832232S. ∴S有最大值22.„„„„„„„„„„„„„„„„„„„„„„„„14分 20.(本小题满分14分) 解:(Ⅰ)∵点M在直线x=21上,设MM1(,)2y.又AM=MB,
即111AM(,)2Mxyy,221MB(,)2Mxyy,∴1x+2x=1.„„„„„„2分
