初一下数学能力训练题(B)

合集下载

2020年全国第十三届中学生数学能力测评初一年级模拟试卷及答案解析

第 1 页共 21 页2020年全国第十三届中学生数学能力测评初一年级模拟试卷一．填空题（共10小题）1．若不等式|x ﹣2|+|x +3|+|x ﹣1|+|x +1|≥a 对一切数x 都成立，则a 的取值范围是．2．已知a ，b ，c ，d 分别是一个四位数的千位，百位，十位，个位上的数字，且低位上的数字不小于高位上的数字，当|a ﹣b |+|b ﹣c |+|c ﹣d |+|d ﹣a |取得最大值时，这个四位数的最小值是．3．甲、乙、丙三人到某单人小火锅店就餐，该店共有m 种配菜可以选择，每种配菜都有大盘菜、中盘菜、小盘菜这三种份量，价格分别为a 元、b 元和3元，3＜b ＜a ≤8，a 、b 都为正整数．每个人都选择了所有m 种配菜，而且对于每一种配菜，三个人在份量上的选择都各不相同．结账时，甲乙两人都花费了53元且两人在大盘菜的花费上各不相同，而丙共花费了54元，那么丙在大盘菜上花费元．4．如图，是一个有理数运算程序的流程图，请根据这个程序回答问题：当输入的x 为4时，求最后输出的结果y 是．5．科学考察队的一辆越野车需要穿越650千米的沙漠，但这辆车每次装满汽油最多只能驶600千米，队长想出一个方法，在沙漠中设一个储油点P ，越野车装满油从起点A 出发，到储油点P 时从车中取出部分油放进P 储油点，然后返回出发点A ，加满油后再开往P ，到P 储油点时取出储存的所有油放在车上，再到达终点．用队长想出的方法，这辆越野车穿越这片沙漠的最大距离是千米．6．在环行自行车赛场内，甲、乙、丙三人骑自行车进行训练，他们的速度是：甲每分钟23圈，乙每分钟34圈，丙每分钟12圈，他们同时出发，起点如图所示（甲从A 点出发，沿圆周逆时针运动；乙从B 点出发，沿圆周逆时针运动；丙从C 点出发，沿圆周顺时针运动），则出发后分三人第一次相遇．。

2024-2025学年年七年级数学人教版下册专题整合复习卷8.4 三元一次方程组解法举例(含答案)

2024-2025学年年七年级数学人教版下册专题整合复习卷8.4 三元一次方程组解法举例(含答案)8.4 三元一次方程组解法举例◆回顾归纳1．方程组中含有_____•个相同的未知数，•每个方程中含未知数的项的次数都是____次，并且一共有_____个这样的整式方程，像这样的方程组叫做三元一次方程组． 2．解三元一次方程组的常用方法是_____法和_____法． 3．解三元一次方程组的基本思路是_____． ◆课堂测控知识点三元一次方程组的解法1．三元一次方程组中共有_____个未知数．2．三元一次方程组−−−→消元转化________−−−→消元转化_______． 3．已知三个数x ，y ，z 的和是120，并且x ：y ：z=1：3：4，则x=____，y=_____，z=____．4．（教材变式题）在解三元一次方程组2432215x y x y z x y z -=⎧⎪--=⎨⎪++=⎩时，小颖采用如下方法求解的．解：②+③×2，得5x －y=11 ④ 把①与④组成方程组24511x y x y -=⎧⎨-=⎩解这个方程组，得21x y =⎧⎨=-⎩把x=2，y=－1代入③，得z=4∴214x y z =⎧⎪=-⎨⎪=⎩请问：在②+③×2这一步的目的是_______．在上述解题的过程中主要体现_____________的数学思想．◆课后测控1．解方程组323231112x y zx y zx y z+-=⎧⎪-+=⎨⎪++=⎩时，先消去______较简便．2．解方程组32182731953413x y zx y zx y z+-=⎧⎪+-=⎨⎪-+=⎩时，若先消去z，可以①×4______③，①×③______②．3．解下列方程组．（1）302223x zx y zx y z+-=⎧⎪-+=⎨⎪--=-⎩（2）24317x yx zx y z+=⎧⎪+=⎨⎪++=⎩（3）:1:5:2:327x yy zx y z=⎧⎪=⎨⎪++=⎩（4）32344233322x y zx yzx y z⎧--=⎪⎪⎪+-=⎨⎪⎪-+=⎪⎩4．若（2x －3）+（2x+y ）2+│3z －y │=0，求x －y －z 的值． 5．设342x y z===，求233x y z x y z -+--的值．6．已知x+2y －3z=0，2x+3y+5z=0，求x y zx y z++-+的值．7．已知333x z y z x yy x z+++===k ，求k 的值．8．已知y=ax2+bx+c，且当x=1时，y=5；当x=－2时，y=14；当x=－3时，y=25，求a，b，c•的值．并计算当x=4时y的值．9．一个三位数的各位数字之和等于14，•个位数字与十位数字的和比百位数字大2，如果把百位数字与十位数字对调，所得新数比原数小270，求原三位数．◆拓展创新10．有甲，乙，丙三种商品，若购甲3件，乙7件，丙1件，共需5.8元；若购甲4•件，• 乙10件，丙1件，共需6.3元，问购甲，乙，丙各一件，共需多少元？答案: 回顾归纳1．三；一；三 2．代入；消元；加减3．消元转化为二元一次方程组，再消元转化为一元一次方程．课堂测控1．3 2．二元一次方程组；一元一次方程 3．15，45，60 4．消元未知数z ；转化课后测控1．z 2．十；一3．（1）241x y z =⎧⎪=⎨⎪=⎩ （2）281x y z =-⎧⎪=⎨⎪=⎩ （3）21015x y z =⎧⎪=⎨⎪=⎩ （4）1264x y z =⎧⎪=⎨⎪=⎩4．112 5．－111 6．7297．k=4 8．a=2，b=－1，c=4，当x=4时，y=32． 9．这个三位数为635．10．设购甲，乙，丙各一件分别需x 元，y 元，z 元，则有37 5.8410 6.3x y z x y z ++=⎧⎨++=⎩把方程变式为：2(3)() 5.8,3(3)() 6.3x y x y z x y x y z ++++=⎧⎨++++=⎩解得x+y+z=4.8（元）即购甲，乙，丙各一件共需4.8元．思路点拨：本题采用整体代入法求解．8.4 三元一次方程组解法举例◆知能点分类训练知能点1 三元一次方程组的解法1．在（1）3,1,00,(2)1,(3)10,0,0,x x x y y y z z z ===⎧⎧⎧⎪⎪⎪===-⎨⎨⎨⎪⎪⎪===⎩⎩⎩这三对数值中，______是方程x+2y+z=0的解，_______是方程2x-y-z=1的解，______是方程3x-y-z=2的解，因此________是方程组202132x y z x y z x y z ++=⎧⎪--=⎨⎪--=⎩的解． 2．若满足方程组2234510x y z x y z x y z -+=-⎧⎪+-=⎨⎪++=⎩的x 的值是-1，y 的值是1，则该方程组的解是_______．3．以311x y z =⎧⎪=⎨⎪=-⎩为解建立一个三元一次方程，不正确的是（）．A ．3x-4y+2z=3B ．13x-y+z=-1 C ．x+y-z=-2 D ．2x -23y-z=1564．已知方程组25,589,x y z x y z -+=⎧⎨+-=⎩，则x+y 的值为（）．A ．14B ．2C ．-14D ．-2 5．解下列三元一次方程组．（1）432187x y z x y z x y z -+=-⎧⎪+-=⎨⎪--=⎩4327(2)64621x y z x y z x y z ++=⎧⎪--=⎨⎪-+=⎩◆规律方法应用6．已知等式y=ax2+bx+c，且当x=1时y=2；当x=-1时y=-2；当x=2时y=3，你能求出a，b，c的值吗？7．某企业为了激励员工参与技术革新，设计了技术革新奖，这个奖项分设一、二、三等，按获奖等级颁发一定数额的奖金，每年评选一次，下表是近三年技术革新获奖人数及那么技术革新一、二、三等奖的奖金数额分别是多少万元？◆开放探索创新8．给定方程组111,111112,,,115,x y A B y zx y z z x⎧+=⎪⎪⎪+===⎨⎪⎪+=⎪⎩如果令=C ，则方程组1,2,2,1,5,3,A B x B C y A C z +==⎧⎧⎪⎪+==-⎨⎨⎪⎪+==⎩⎩由此解得，对不对，为什么？答案:1．①② ②③ ② ②2．110x y z =-⎧⎪=⎨⎪=⎩3．C 4．B5．解：（1）①+②，得3x-3y=15，即x-y=5，④②-③，得x+2y=11，⑤ ⑤-④，得3y=6， ∴y=2，把y=2代入④，得x=7．再把x=7，y=2代入③，得z=-2．7,2,2.32(2)11x y z x y z =⎧⎪=⎨⎪=-⎩⎧=⎪⎪=⎨⎪=-⎪⎩所以方程组的解为6．解：由已知可得1,2,32,2,423,1.3a a b c a b c b a b c c ⎧=-⎪++=⎧⎪⎪-+=-=⎨⎨⎪⎪++=⎩⎪=⎩解得 7．解：设一、二、三等奖的奖金额分别为x 万元，y 万元和z 万元．可得10203041,1,12202842,,0.8,14254054,0.5.x y z x x y z y x y z z ++==⎧⎧⎪⎪++==⎨⎨⎪⎪++==⎩⎩解这个方程组得答：技术革新一、二、三等奖的奖金额分别是1万元，0.8万元和0.5万元． 8．不对，没有把解倒过来，应该为x=12，y=-1，z=13．七年级下册第8.3～8.4水平测试一、相信你的选择（每小题3分，共24分） 1. 下列方程组不是三元一次方程组的是（）。

初一下数学能力训练题(D)

1、如图，直线a ∥b ，则∠ACB ＝_____________。

2、下列计算中，正确的是（）A 、2a ＋3b ＝5abB 、a·a 3＝a 3C 、a 6÷a 2＝a 3D 、(－ab)2＝a 2b 2 3、小红、小明、小芳在一起做游戏时，需要确定游戏的先后顺序，他们约定用“剪子、包袱、锤子”的方式确定。

问在一个回合中三个人都出包袱的概率是____________。

4、如右图，在△ABC 中，AD ⊥BC 于D ，再添加一个条件，就可确定△ABD ≌△ACD 。

5、在匀速运动中，路程s （千米）一定时，速度v （千米/时）关于时间t （小时）的函数关系的大致图象是（）6、已知)a 21-6(2=B ),2-a )(2+a (=A 2，求A+B 。

7、化简：1+m ÷)m -m (+)1-m (m 2。

8、如右图，平行四边形ABCD 中，AE ⊥BD ，CF ⊥BD ，垂足分别为E 、F 。

（1）写出图中每一对你认为全等的三角形；（2）选择（1）中的任意一对进行证明。

9、如右图，将矩形纸片ABCD 沿对角线BD 折叠，点C 落在点E 处，BE 交AD 于点F ，连结AE 。

证明：（1）BF=DF ；（2）AE//BD 。

A aB b 28°C 50°ABA 、A B EFCD AB C D EF1、下列运算正确的是（）A、x2·x2=x4B、x6÷x3=x2C、(2x3)3=6x9D、3x3－2x2=x2、下列图案属于轴对称图形的是（）A B C D3、在物理实验课上，小明用弹簧称将铁块A悬于盛有水的水槽中(如图)，然后匀速向上提起，直至铁块完全露出水面一定高度，则能反映弹簧秤的读数y(单位：N)与铁块被提起的高度x(单位：cm)之间的函数关系的图象大致是（）4、有4条长度分别为1，3，5，7的线段，现从中任取三条能构成三角形的概率是__________。

(完整版)初中数学计算能力提升训练测试题

1.化简：b b a a 3)43(4---.2.求比多项式22325b ab a a +--少ab a -25的多项式.3.先化简、再求值)432()12(3)34(222a a a a a a --+-+-- (其中2-=a )4、先化简、再求值)]23()5[(42222y xy x y xy x xy -+--+- (其中21,41-=-=y x )5、计算a a a ⋅+2433)(2)(36、（1）计算1092)21(⋅-=（2）计算532)(x x ÷（3）下列计算正确的是 ( ).(A)3232a a a =+ (B)a a 2121=- (C)623)(a a a -=⋅- (D)aa 221=-计算： (1))3()32()23(32232b a ab c b a -⋅-⋅-； (2))3)(532(22a a a -+-；（3）)8(25.123x x -⋅ ；（4）)532()3(2+-⋅-x x x ;（5）())2(32y x y x +-；（6）利用乘法公式计算:()()n m n m 234234+--+（7）()()x y y x 5225--- （8）已知6,5-==+ab b a ,试求22b ab a +-的值（9）计算:2011200920102⨯-（10）已知多项式3223-++x ax x 能被122+x 整除，商式为3-x ，试求a 的值1、 b a c b a 232232÷-2、 )2(23)2(433y x y x +÷+3、22222335121)433221(y x y x y x y x ÷+-4、当5=x 时,试求整式()()13152322+--+-x x x x 的值5、已知4=+y x ，1=xy ，试求代数式)1)(1(22++y x 的值6、计算:)()532(222223m m n n m n m a a b a a-÷-+-++7、一个矩形的面积为ab a 322+,其宽为a ,试求其周长8、试确定2011201075⋅的个位数字1．（辨析题）不改变分式的值，使分式115101139x y x y -+的各项系数化为整数，分子、分母应乘以（• ）A ．10B ．9C ．45D ．902．（探究题）下列等式：①()a b c --=-a b c -;②x y x -+-=x y x -;③a b c -+=-a b c +; ④m n m --=-m n m-中,成立的是（） A ．①② B ．③④ C ．①③ D ．②④3．（探究题）不改变分式2323523x x x x -+-+-的值，使分子、分母最高次项的系数为正数，正确的是（• ）A ．2332523x x x x +++-B ．2332523x x x x -++-C ．2332523x x x x +--+D ．2332523x x x x ---+ 4．（辨析题）分式434y x a+，2411x x --，22x xy y x y -++，2222a ab ab b +-中是最简分式的有（） A ．1个 B ．2个 C ．3个 D ．4个5．（技能题）约分：（1）22699x x x ++-；（2）2232m m m m-+-．6.（技能题）通分：（1）26x ab ，29y a bc ；（2）2121a a a -++，261a -．7.（妙法求解题）已知x+1x=3，求2421x x x ++的值计算能力训练（分式2）1.根据分式的基本性质，分式a a b--可变形为（） A ．a a b -- B ．a a b + C ．-a a b - D ．a a b + 2．下列各式中，正确的是（）A ．x y x y -+--=x y x y -+;B ．x y x y -+-=x y x y ---;C ．x y x y -+--=x y x y +-;D ．x y x y -+-=x y x y-+ 3．下列各式中，正确的是（）A ．a m a b m b +=+B ．a b a b ++=0C ．1111ab b ac c --=-- D ．221x y x y x y -=-+ 4．（2005·天津市）若a=23，则2223712a a a a ---+的值等于_______． 5．（2005·广州市）计算222a ab a b+-=_________． 6．公式22(1)x x --，323(1)x x --，51x -的最简公分母为（） A ．（x-1）2 B ．（x-1）3 C ．（x-1） D ．（x-1）2（1-x ）37．21?11x x x -=+-，则？处应填上_________，其中条件是__________．拓展创新题8．（学科综合题）已知a 2-4a+9b 2+6b+5=0，求1a -1b 的值．9．（巧解题）已知x 2+3x+1=0，求x 2+21x 的值．计算能力训练(分式方程1)选择1、（2009年安徽）甲志愿者计划用若干个工作日完成社区的某项工作，从第三个工作日起，乙志愿者加盟此项工作，且甲、乙两人工效相同，结果提前3天完成任务，则甲志愿者计划完成此项工作的天数是……………【】A ．8 B.7 C ．6 D ．52、(2009年上海市)3．用换元法解分式方程13101x x x x --+=-时，如果设1x y x -=，将原方程化为关于y 的整式方程，那么这个整式方程是（）A ．230y y +-=B ．2310y y -+=C ．2310y y -+=D ．2310y y --= 3、（2009襄樊市）分式方程131x x x x +=--的解为（） A ．1 B ．-1 C ．-2 D ．-34、（2009柳州）5．分式方程3221+=x x 的解是（） A ．0=x B ．1=x C ．2=x D ．3=x5、（2009年孝感）关于x 的方程211x a x +=-的解是正数，则a 的取值范围是 A ．a ＞－1B ．a ＞－1且a ≠0C ．a ＜－1D ．a ＜－1且a ≠－26、（2009泰安）某服装厂准备加工400套运动装，在加工完160套后，采用了新技术，使得工作效率比原计划提高了20%，结果共用了18天完成任务，问计划每天加工服装多少套？在这个问题中，设计划每天加工x 套，则根据题意可得方程为（A ）18%)201(400160=++x x （B ）18%)201(160400160=+-+xx （C ）18%20160400160=-+x x （D ）18%)201(160400400=+-+x x7、（2009年嘉兴市）解方程x x -=-22482的结果是（） A ．2-=xB ．2=xC ．4=xD ．无解8、（2009年漳州）分式方程211x x =+的解是（） A ．1B ．1-C ．13D ．13- 9、（09湖南怀化）分式方程2131=-x 的解是（） A ．21=x B ．2=x C ．31-=x D ． 31=x10、（2009年安徽）甲志愿者计划用若干个工作日完成社区的某项工作，从第三个工作日起，乙志愿者加盟此项工作，且甲、乙两人工效相同，结果提前3天完成任务，则甲志愿者计划完成此项工作的天数是【】A ．8 B.7 C ．6 D ．511、（2009年广东佛山）方程121x x=-的解是（） A ．0 B ．1 C ．2 D ．312、（2009年山西省）解分式方程11222x x x-+=--，可知方程（） A ．解为2x = B ．解为4x = C ．解为3x = D ．无解13、（2009年广东佛山）方程121x x=-的解是（） A ．0 B ．1 C ．2 D ．314、（2009年山西省）解分式方程11222x x x-+=--，可知方程（） A ．解为2x = B ．解为4x = C ．解为3x = D ．无解计算能力训练(分式方程2)填空1、（2009年邵阳市）请你给x 选择一个合适的值，使方程2112-=-x x 成立，你选择的x ＝________。

2023 年第四届超常(数学)思维与创新能力测评初一年级数学真题

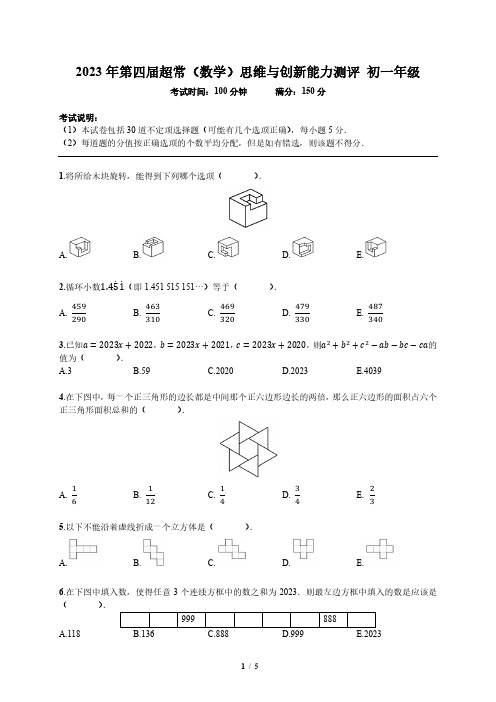
2023年第四届超常（数学）思维与创新能力测评初一年级考试时间：100分钟满分：150分考试说明：（1）本试卷包括30道不定项选择题（可能有几个选项正确），每小题5分．（2）每道题的分值按正确选项的个数平均分配，但是如有错选，则该题不得分．1.将所给木块旋转，能得到下列哪个选项（）．A. B. C. D. E.2.循环小数1.451（即1.451 515 151…）等于（）． A. 459290B.463310C.469320D. 479330E.4873403.已知a =2023x +2022，b =2023x +2021，c =2023x +2020，则a 2+b 2+c 2−ab −bc −ca 的值为（）．A.3 B.59 C.2020 D.2023 E.40394.在下图中，每一个正三角形的边长都是中间那个正六边形边长的两倍，那么正六边形的面积占六个正三角形面积总和的（）．A.16B.112C.14D.34E.235.以下不能沿着虚线折成一个立方体是（）．A. B. C. D. E.6.在下图中填入数，使得任意3个连续方框中的数之和为2023．则最左边方框中填入的数是应该是（）．A.1187.已知202009=102000∙409∙2n，则n的值为（）．A.1991B.2000C.2009D.4018E.50008.如图，某城有一组十分奇怪的限速规定：在离城1km处有一个120km/h的标牌，在离城12km处有一个60km/h的标牌，在离城13km处有一个40km/h的标牌，在离城14km处有一个30km/h的标牌，在离城15km处有一个24km/h的标牌，在离城16km处有一个20km/h的标牌，如果你从120km/h的标牌处出发一直以限定时速行驶，那么需要（）才能到达该城．A.30sB.1min13.5sC.1min42sD.2min27sE.3min9.如图所示，三个正方形以顶点相连接在一起，图中已给出若干角的度数，则x的值是（）．A.41B.42C.43D.44E.4610.一辆自行车的链条在具有48个齿的前链齿轮上运行，通常经过具有18个齿的后轮轴的链齿轮．当后链齿轮每旋转一整圈时，踏板转过的角度是（）．A.135°B.360°C.960°D.120°E.6712°11.如图，一个立方体的八个角都被切去，形成一些三角形面．将该图形的所有24个角都用对角线连起来，这些对角线中穿过图形内部的共有（）条．A.84B.108C.120D.142E.24012.把一个三位数首位前和末位后添写上1，这样得到的五位数比原来的三位数增加14789．则原来三位数的三个数字之和是（）．A.10B.9C.8D.7E.613. Ⅰ号混合液由柠檬汁、油和醋以1:2:3的比例配成，Ⅱ号混合液由同样三种液体以3:4:5的比例配成，将两种混合液倒在一起后，新的混合液的比例不可能是（）．A.2:5:8B.4:5:6C.3:5:7D.5:6:7E.7:9:1114.如图所示的网球场中有（）个长方形．A.19B.29C.23D.30E.3115.已知|x−1|+|x−2|=1，则x的值（）．A.只能为1B.只能为2C．可能为任何实数 D.为满足1≤x≤2的一切实数E.以上都不对16.下图是一张城市的道路平面图，除了一条短对角线外，道路全是东西向或南北向的．由于一条路的修补而不可能从点X通过．从P到Q的所有可能走的路线中，有些路线是最短的．则这样的最短路线有（）条．A.4B.7C.9D.14E.1617.甲、乙一起工作，甲每工作1天休息2天，乙每工作1天休息3天．已知第一天他们都在工作，最后一天乙肯定在工作．甲、乙同时休息时间比同时工作时间多128天．则他们从第一天到最后一天经过了（）天．A.180B.308C.309D.312E.50018.要使关于x的方程ax−1=x+a无解，则a=（）．A.-1B.0C.1D.2E.以上都不对19.小刚和月月搭乘某航空公司的飞机从A地飞往B地，但因为他们的行李超出了航空公司规定的重量，所以要求他们支付附加费．航空公司收费方法是对超出规定的重量每千克收取相同的费用．小刚付了60元，月月付了100元．他们一共有52kg的行李，如果小刚自己带着两人的全部行李走，他将必须付340元．每人最多可带（不需要付附加费的）行李（）kg．A.20B.15C.12D.18E.3020.一个4×4的反幻方是指将数1~16填入4×4方格表内，使得每行、每列、每条对角线上的数之和，经排序后恰好形成十个连续的正整数．如图是一个尚未完成的反幻方，则星号“*”所在方格内应填入（）．A.1B.2C.15D.16E.以上都不对21.某学校新建5个教室，平均每班减少6人．如果再建5个教室，那么平均每班又减少4人．假设学生总数保持不变，这个学校可能有（）名学生．A.560B.600C.650D.720E.80022.在一个2023边形（可以是凹多边形）的内角中，锐角至多有（）个．A.2023B.672C.944D.1345E.134923.在一列数1，2，3，…，10000中，有（）个数恰好包含两个相邻的数字9．例如：993，1992和9929就是这样的数，而9295或1999则不是．A.270B.271C.280D.123E.26124.从1970年起小红开始收集日历且以后每年都这样做，直到以后每一年至少可用一本已经收集到的日历来代用时为止．则必须收集日历的最后年份是（）年．A.1983B.1984C.1997D.2023E.以上都不对25.100个正整数之和为101101，则它们的最大公约数的最大可能值是（）．A.101B.1100C.1001D.2002E.1001026.如图所示，你有一些白色的1×12×1瓦片．当用这些瓦片以紧贴邻边的方式来覆盖一个3×1的矩形时，共可以设计出4种颜色方案（WWW，BWW，WBW，WWB）．那么如果用这些瓦片来覆盖一个10×1的矩形，将可以设计出（）种颜色方案．A.47B.89C.155D.286E.30027.已知A，B，C，D，E，F，G，H，I是9个互不相同的非零数字，满足：A除以B余C，D除以E余F，G除以H余I，那么ABC+DEF+GHI的结果是（）．A.1368B.1458C.1188D.2547E.195328.令s为真分数，即s<t，且为最简分数．若t的值为2到9，s，t为正整数，则符合条件的不同的真t分数有（）．A.26B.27C.28D.30E.3629.有27个同样大小的小正方体，每个小正方体的六个面上写着一个相同的数，且恰为1~27，用这27个小正方体拼成如图所示的大正方体．请根据如图所示的数据以及下面所给出的条件推断，从六个方向都看不见的小正方体的面上所写的数是（）．①数9，13和16在同一条直线上．②数22在9和6之间．③17紧挨着5和13，但与9不相邻．④14紧挨着24和27．⑤数20在14的上面．A.22B.20C.17D.9E.530.一个棱长为6的正方体被切割成若干个棱长为整数的小正方体，若这些小正方体的表面积之和是切割前的大正方体的表面积的10倍，则切割成的小正方体中，棱长为1的小正方体的个数可能为3（）．A.15B.24C.42D.56E.60。

七年级数学下册能力训练 (2)

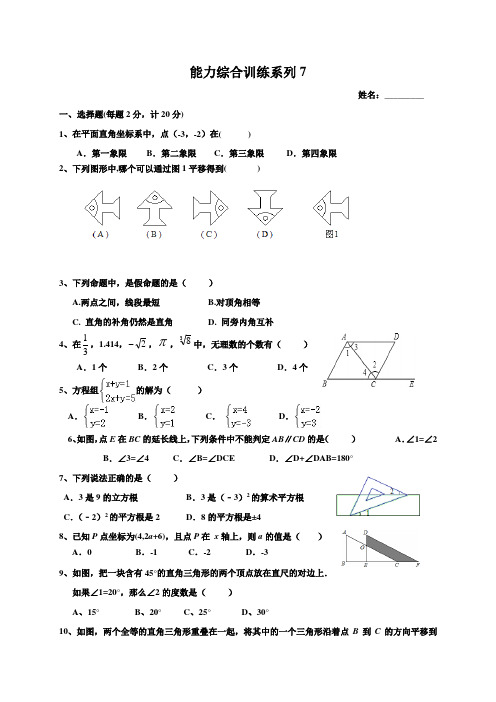
能力综合训练系列7姓名：_________一、选择题(每题2分，计20分)1、在平面直角坐标系中，点（-3，-2）在( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限 2、下列图形中,哪个可以通过图1平移得到( )3、下列命题中，是假命题的是（）A.两点之间，线段最短B.对顶角相等C. 直角的补角仍然是直角D. 同旁内角互补 4、在31，1.414，2-，π，38中，无理数的个数有（） A ．1个 B ．2个 C ．3个 D ．4个 5、方程组的解为（） A．B．C ．D．6、如图，点E 在BC 的延长线上，下列条件中不能判定AB ∥CD 的是（） A ．∠1=∠2B ．∠3=∠4C ．∠B=∠DCED ．∠D+∠DAB=180°7、下列说法正确的是（）A ．3是9的立方根B ．3是（﹣3）2的算术平方根C ．（﹣2）2的平方根是2 D ．8的平方根是±4 8、已知P 点坐标为(4,2a +6)，且点P 在 x 轴上，则a 的值是（） A ．0 B ．-1 C ．-2 D ．-39、如图，把一块含有45°的直角三角形的两个顶点放在直尺的对边上．如果∠1=20°，那么∠2的度数是（） A 、15° B 、20° C 、25° D 、30°10、如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B 到C的方向平移到△DEF 的位置，AB =10，DO =4，平移距离为6，则阴影部分面积为（）A.42B. 48C. 84D. 96 二、填空题（共6小题，每小题3分，满分18分）11、把命题“对顶角相等”写成“如果┉ ，那么┉ 。

”的形式。

12、7的平方根是。

13、如图，计划把河水引到水池A 中，先引AB ⊥CD ，垂足为B ，然后沿AB 开渠，能使所开的渠道最短，这样设计的依据是。

七年级数学下册能力训练 (3)

数学能力训练三一、选择题1．下面四个图形中，∠1与∠2是对顶角的图形是（）A．; B．C．D．2．若点P为直线l外一点，点A、B、C为直线l上的不同的点，其中P A=3，PB=4，PC=5，那么点P到直线l的距离是（）A．小于3 B．3 C．大于或等于3 D．小于或等于33．如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1=15°，那么∠2的度数是（）A．15°B．25°C．30°D．35°4．下列说法中正确的是（）A．过一点有且只有一条直线平行于已知直线B．两条直线被第三直线所截，同位角相等C．两条直线有两种位置关系：平行、相交D．同一平面内，垂直于同一条直线的两条直线平行5．如图，下列说法一定正确的是（）A．∠1和∠4是内错角B．∠1和∠3是同位角C．∠3和∠4是同旁内角D．∠1和∠C是同位角6．如图，∠AOB的一边OA为平面镜，∠AOB=37°36′，在OB上有一点E，从E点射出一束光线经OA上一点D反射，反射光线DC恰好与OB平行，则∠DEB的度数是（）A．74°12′B．74°36′C．75°12′D．75°36′7．观察下列命题：（1）如果a＜0，b＞0，那么a+b＜0；（2）直角都相等；（3）同角的补角相等；（4）如果两条直线被第三条直线所截，那么同位角相等．其中真命题的个数是（）A．0 B．1 C．2 D．38．已知2m﹣4与3m﹣1是同一个正数的两个平方根，则m的值是（）A．0 B．1 C．2 D．39．若=6.356，则=（）A．63.56 B．0.006356 C．635.6 D．0.635610．如图，点E在BC延长线上，下列条件中，不能推断AB∥CD的是（）A．∠4=∠3 B．∠1=∠2 C．∠B=∠5 D．∠B+∠BCD=180°二、填空题11．如下左图，射线DE、DC被直线AB所截得的用数字表示的角中，∠4与是同位角，∠4与是内错角，∠4与是同旁内角．12．如下二图，已知AB∥DE，∠ABC=70°，∠CDE=140°，则∠BCD=．13．如下三图，矩形ABCD中，AB=5，BC=7，则图中五个小矩形的周长之和为．14．如右图图，把一张长方形纸条ABCD沿EF折叠，若∠1=65°，则∠EGF应为．15．的平方根是．三、解答题16．如图，平面上有直线a及直线a外的三点A、B、P．（1）过点P画一条直线m，使得m∥a；（2）过B作BH⊥直线m，并延长BH至B′，使得BB′为直线a、m之间的距离；（3）若直线a、m表示一条河的两岸，现要在这条河上建一座桥（桥与河岸垂直），使得从村庄A 经桥过河到村庄B的路程最短，试问桥应建在何处？画出示意图．17．如图，已知∠2=∠4，∠3=∠B，试判断∠AED与∠C的关系，并说明理由．18．如图，在10×10的正方形网格中，每个小正方形的边长为1个单位长度．△ABC的顶点都在正方形网格的格点上，且通过两次平移（沿网格线方向作上下或左右平移）后得到△A′B′C′，点C的对应点是直线上的格点C′．（1）画出△A′B′C′．（2）△ABC两次共平移了个单位长度．（3）试在直线上画出点P，使得由点A′、B′、C′、P四点围成的四边形的面积为9．19．如图，AD是∠EAC的平分线，AD∥BC，∠B=30°，计算∠EAD、∠DAC、∠C的度数．20．将一副三角板拼成如图所示的图形，∠DCE的平分线CF交DE于点F．（1）求证：CF∥A B．（2）求∠DFC的度数．21．求下列各式中的x的值：（1）x2=25 （2）（x﹣3）2=49．22．（1）如图1，已知，AB∥CD，EF分别交AB、CD于点E、F，EG、EH分别平分∠AEF、∠BEF 交CD于G、H，则EG与EH的位置关系是，∠EGH与∠EHG关系是；（2）如图2，已知：AB∥CD∥EF，BE、DE分别平分∠ABD、∠BDC，求证：BE⊥E D．23．如图，已知EF∥AD，∠1=∠2，∠BAC=70°，求∠AGD（请填空）解：∵E∥F AD∴∠2=（）又∵∠1=∠2∴∠1=∠3（）∴AB∥（）∴∠BAC+=180°（）∵∠BAC=70°（）∴∠AGD=（）24．如图1，AB∥CD，∠P AB=130°，∠PCD=120°，求∠APC的度数．小明的思路是：过P作PE∥AB，通过平行线性质来求∠AP C．（1）按小明的思路，易求得∠APC的度数为度；（2）问题迁移：如图2，AB∥CD，点P在射线OM上运动，记∠P AB=α，∠PCD=β，当点P在B、D两点之间运动时，问∠APC与α、β之间有何数量关系？请说明理由；（3）在（2）的条件下，如果点P在B、D两点外侧运动时（点P与点O、B、D三点不重合），请直接写出∠APC与α、β之间的数量关系．25、如图，已知AM∥BN，∠A=60°．点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D．（1）求∠CB D的度数；（2）当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由；若变化，请写出变化规律．（3）当点P运动到使∠ACB=∠ABD时，∠ABC的度数是．。

七年级思维训练80题(含答案),拔高数学思维能力

1. 计算：七年级思维训练80题（含答案），拔高数学思维能力111113355720212023________． 2. 已知20212021202120222022202220232023202320202020+2020202120212021202220222022a b c，，，则abc ________．3. 123499910001001(1)1(1)1(1)1(1) 的值是________．4. 设11112018201920202050M，则1M的整数部分是________． 5.计算：44444444441032422324343244632458324432416324283244032452324 =________．6.已知5555284110133144□，其中□里的数字是________．7.哪些连续正整数之和为1000？试求出所有的解．8.2023减去它的12，再减去余下的13，再减去余下的14，以此类推，一直到最后减去余下的11000，最后的结果为________．9.n个正数的乘积的n次方根称为这n个数的几何平均数．喜羊羊写了4个数，这4个数的几何平均数是2048；美羊羊也写了4个数，这4个数的几何平均数是8．那么，喜羊羊和美羊羊写的这8个数的几何平均数是________．10.有下列三个命题：（1）若α，β是不相等的无理数，则αβ + α – β是无理数；（2）若α，β是不相等的无理数，则是无理数；（3）若α，β是无理数．其中正确的命题个数是________．11. 如果a ，b ，c 是三个任意整数，那么2a b ，2a c ，2b c（）． A. 都不是整数B. 至少有两个整数C. 至少有一个整数D. 都是整数12. 有理数m ，n 在数轴上的位置如图所示，在m n ，m n ，n m ，m n 中正数的个数是________．13. 如果实数a ，b ，c 在数轴上的位置如图所示，那么代数式||||a b b c 可以化简为（）．A. 2c – aB. 2a – 2bC. –aD. a14. 把4个不同的整数两两相加得到6个和，并且这6个和是5个互不相同的数：23，26，29，32和35．那么这4个整数中最大的是________．15. 从1~26这26个整数中取出两个数，选出的两个数相乘所得的积正好是剩余的24个数之和．选出的两个数分别是________和________．16. 已知a – b = 4，ab + c 2 + 4 = 0，则a + b = ________．17. 已知a 、b 、c 是实数，且13ab a b ，17bc b c ，112ac a c ，则acbc ab abc=________．18. 已知 | x | + x + y =5，x + | y |－y = 10，则 x + y 的值是________．19.________．20. 222 − 4有________个不同的质因数．21. 已知x 是实数，则(x 2－4x +3)(x 2+4x +3)的最小值是________．22. 若实数a ，b ，c 满足等式36b ，96b c ，则c 可能取的最大值为________．23. 已知x ，y 是非负整数，且满足4(2)34x y ，那么满足条件的x + y 的最大值是________．24. 若正整数x ，y ，z 满足11145x y z ，则xyz 的最大值是________．25. 231x x x 的最小值是________．26. 满足24x y y 的整数对（x ，y ）有________个．27. 设a 是整数，关于x 的方程12x a 只有三个不同的整数解，求这三个解．28. 若a 为整数，则关于x 的方程(a – 1) x = a + 1的所有整数解的和是________．29. 已知x 与y 使得x + y ，x – y ，xy ，x y四个数中的三个相等，则这样的数对（x ，y ）有________对．30. 若关于x ，y 的二元一次方程组 132kx y bk x y 有无穷多组解，则22k b 的值为________．31. 若[x ]表示不超过x 的最大整数，且满足方程3x + 5[x ] – 49 = 0，则3x +1=________．32. 如果关于x 的不等式组9080x a x b 的整数解仅有1，2，3，那么整数a ，b 组成的有序数对（a ，b ）共有________对．33. 如果关于x 的不等式组100x x a无解，则a 的取值范围是________．34. 在1~100的自然数中与10互质的自然数共有________个．35. 已知三个质数a ，b ，c 满足133a b c ab bc ac ，则abc ＝________．36.已知三位数abc能被5整除，但不能被6和7整除；三位数cba能被6整除，但不能被5和7整除；三位数cab能被7整除，但不能被5和6整除，则abc ＝________．37.九位数ABCABCBBB能被1~17中的任意整数整除，且A，B，C是不同的数字，则九位数ABCABCBBB是________．38.乘积376×733的个位数字是________．39.四位数aabb是一个整数的平方，aabb=________．p 的不同正因数的个数不超过10，则满足题意的p 40.已知p是质数，且271的个数是________．41.如图所示有4种类型的几何体，每个几何体都是由4个单位正方体组成．选出8个同类型的几何体，把它们组合成一个2×4×4的长方体．可以完成组合的几何体有________种类型．42.已知圆环内直径为a厘米，外直径为b厘米，将50个这样的圆环一个接一个环套地连成一条锁链，那么这条锁链拉直后的长度为________厘米．43.设有一个边长为1的正三角形，记作A1（如图1），将A1的每条边三等分，以中间的线段为一边向形外作正三角形，去掉中间的线段后所得到的图形记作A2（如图2）；将A2的每条边三等分，并重复上述过程，所得到的图形记作A3（如图3）；再将A3的每条边三等分，并重复上述过程，所得到的图形记作A4，那么A4的周长是________．图1 图2 图344. 如图所示，AOB 是一条直线，若1:2:3:41:2:4:5 ，则2 的余角是________度．45. 如图，AB //CD ，那么∠1 –∠2 +∠3 –∠4 +∠5 =________度．46. 如图，∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7=（）．A ．450°B ．540°C ．630°D ．720°47.从一个凸n边形的纸板上剪下一个三角形，剩余的是一个内角和为2160°的多边形，则n最大是________．48.一个凸n边形的内角和小于1998°，那么n的最大值是________．49.如果一个凸多边形的内角和等于外角和的3倍，那么这个多边形的边数是（）．A.4B.6C.8D.10E.1250.如图所示，在△ABC中，AC=7，BC=4，D为AB中点，E为AC边上一点，且1902AED C，则CE =________．51.在△ABC中，已知BD和CE分别是两边上的中线，并且BD⊥CE，BD=4，CE=6，那么△ABC的面积是________．52.△ABC中，∠A为最小角，∠B为最大角，且2∠B = 5∠A，若∠B的最大值为m°，∠B的最小值为n°，则m + n =________．53.如图，在锐角△ABC中，高线CD，BE相交于点F，若∠A=55°，则∠BFC的度数是________度．54.如图，PQ=PR=QS，线段PR与QS相互垂直，则∠PRQ与∠PSQ度数之和是________度．55.在平行四边形ABCD中，AD = 2AB，点M是AD的中点，CE⊥AB于E．如果∠CEM = 40°，那么∠DME的值是（）．A．150° B．140° C．135° D．130°56.若长方形内有一点P，点P到各边的距离从小到大依次为1，2，5，6则长方形面积最小为________．57.如图所示的4×5的方格图中，过格点P的直线与方格图上、下边界相交形成的直角梯形ABCD（其中AB<CD）的面积最大是________．58. 如图，CD 是Rt △ABC 斜边AB 上的高，∠BAC 的平分线AE 交CD 于H ，交∠BCD 的平分线CF 于G ．求证：HF ∥BC ．59. 由8个相同的小正方体搭成的一个几何体，俯视图如下，那么这个几何体的左视图一定不是（）．60. 若n 个人完成一项工程需要m 天，则（m +n ）个人完成这项工程需要（）天． A.nm mnB.m nm nC.m nmnD.2mnm n61. 一个商人用m 元（m 为正整数）买来了n 台（n 为质数）电视机，其中有两台以成本的一半价钱卖给某个慈善机构，其余的电视机在商店出售，每台盈利500元，结果该商人获得利润为5500元，则n 的最小值是________．62. 某商场经销一种商品，由于进货时价格比原进价降低了6.4％，使得利润率增加了8个百分点，那么经销这种商品原来的利润率是________%．（注：100% 销售价进价利润率进价）63. 小倩和小玲每人都有若干面值为整数元的人民币．小倩对小玲说：“你若给我2元，我的钱将是你的n 倍”；小玲对小倩说：“你若给我n 元，我的钱数将是你的2倍”，其中n 为正整数，则n 的最大值是________．64. 图书馆内，在标有号码1，2，3，4的书架上分别有书120，135，142，167本．若干天后，每个书架上都各被借出a 本书，又过了若干天，四个书架又分别被借出0，b ，c ，d 本书，并且四个书架上余下同样本数的书．若b ，c ，d ≥1，b +c +d =a ，则两次借出书后，1号书架剩有________本书．65.五个不同的数，两两之和依次等于3，4，5，6，7，8，11，12，13，15 则这五个数的平均数是________．66.王明在早晨六点至七点之间外出晨练，锻炼时长不超过一小时，出门和回家的时候，时针与分针的夹角都是110°．则王明晨练的时间为________分钟．67.某人骑车沿直线旅行，先前进了a千米，休息了一段时间，又原路返回b千米（b﹤a），再前进c千米，则此人离起点的距离S与时间t的关系示意图是（）．68.某届运动会的十一天的比赛中，醒狮队拿了16块金牌，其中每天至少拿一枚金牌，则醒狮队拿金牌的不同的情况可能有________种．(假设金牌都是一样的)69.将正方形的每条边8等分，再以这些分点为顶点（不包括正方形的顶点），可以得到不同的三角形的个数是________．70.口袋中装有20个只有颜色不同其他都相同的球，其中白球9个，红球5个，黑球6个．现从中任取10个球，使得白球不少于2个但不多于8个，红球不少于2个，黑球不多于3个，那么这样取法有________种．71.将若干红黑两种颜色的球摆成一行，要求两种颜色的球都要出现，且任意中间夹有5个或10个球的两个球必为同一种颜色的球．按这种要求摆放，最多可以摆放________个球．72.在{1000，1001，1002，…，2000}中有________对相邻的数满足下列条件：每对中的两数相加时不需要进位．73.试求所有满足如下性质的四元实数组（a，b，c，d）：组中的任一数都等于其余三个数中某两个数的乘积．（注：四元实数组中的数相同，顺序不同，算作同一组）74.将三位数A各个数位上的数字重新排列，得出的所有数的算术平均值等于A．这样的三位数A共有________个．75.如图，6个人围成一圈做传球游戏，每个人接到球后传给和他不相邻的某一人(如：A接到球后可以传给C、D或E)，开始时，球在A的手中，若球被传递三次后又回到A，此种情况出现的概率是________．76.如图，△ABC中，D、E分别是边BC、AC的中点，从这8个图形△ABD、△ACD、△ABE、△BCE、△GAB、△GAE、△GBD、四边形CEGD中任取2个图形，取出的2个图形面积相等的概率是________．77.按如图的程序进行操作，规定：程序运行从“输入一个值x”到“结果是否>487？”为一次操作．如果操作进行四次才停止，那么x的取值范围是________．78.如图是一个正方体的平面展开图，若该正方体相对的两个面上的代数式的值相等，则x – y – z的值是________．79. 设)(n f 为正整数n （十进制）的各数位上的数字的平方之和，如14321)123(222 f ．记)()(1n f n f ，))(()(1n f f n f k k ，k =1，2，3……，则2016(2016)f 的值是________．80. 有16枚棋子，都是一面黑色，另一面白色，放在4×4的正方形网格里．最初，所有棋子都是黑面朝上．规定：每次操作，将一个2×2正方形中的4枚棋子都正反面翻转一次．那么，要得到如图所示的排列，至少需要经过________次操作．1.计算：7年级思维训练80题答案1111 13355720212023________．答案：1011 20232.已知202120212021202220222022202320232023 20202020+2020202120212021202220222022 a b c，，，则abc ________．答案：13.123499910001001(1)1(1)1(1)1(1)的值是________．答案：–14.设11112018201920202050M，则1M的整数部分是________．答案：615.计算：4444444444 1032422324343244632458324 432416324283244032452324=________．答案：3736.已知5555284110133144□，其中□里的数字是________．答案：77.哪些连续正整数之和为1000？试求出所有的解．答案：198＋199＋200＋201＋202；55＋56＋...＋70；28＋29＋ (52)8. 2023减去它的12，再减去余下的13，再减去余下的14，以此类推，一直到最后减去余下的11000，最后的结果为________．答案：202310009. n 个正数的乘积的n 次方根称为这n 个数的几何平均数．喜羊羊写了4个数，这4个数的几何平均数是2048；美羊羊也写了4个数，这4个数的几何平均数是8．那么，喜羊羊和美羊羊写的这8个数的几何平均数是________．答案：12810. 有下列三个命题：（1）若α，β是不相等的无理数，则αβ + α – β是无理数；（2）若α，β是不相等的无理数，则是无理数；（3）若α，β是无理数．其中正确的命题个数是________．答案：011. 如果a ，b ，c 是三个任意整数，那么2a b ，2a c ，2b c（）． A. 都不是整数B. 至少有两个整数C. 至少有一个整数D. 都是整数答案：C12. 有理数m ，n 在数轴上的位置如图所示，在m n ，m n ，n m ，m n 中正数的个数是________．答案：213. 如果实数a ，b ，c 在数轴上的位置如图所示，那么代数式||||a b b c 可以化简为（）．A. 2c – aB. 2a – 2bC. –aD. a答案：C14. 把4个不同的整数两两相加得到6个和，并且这6个和是5个互不相同的数：23，26，29，32和35．那么这4个整数中最大的是________．答案：1915. 从1~26这26个整数中取出两个数，选出的两个数相乘所得的积正好是剩余的24个数之和．选出的两个数分别是________和________．答案：15，2116. 已知a – b = 4，ab + c 2 + 4 = 0，则a + b = ________．答案：017. 已知a 、b 、c 是实数，且13ab a b ，17bc b c ，112ac a c ，则acbc ab abc=________．答案：11118. 已知 | x | + x + y =5，x + | y |－y = 10，则 x + y 的值是________．答案：119.________．答案：20. 222 − 4有________个不同的质因数．答案：621. 已知x 是实数，则(x 2－4x +3)(x 2+4x +3)的最小值是________．答案：–1622. 若实数a ，b ，c 满足等式36b ，96b c ，则c 可能取的最大值为________．答案：223. 已知x ，y 是非负整数，且满足4(2)34x y ，那么满足条件的x + y 的最大值是________．答案：424. 若正整数x ，y ，z 满足11145x y z，则xyz 的最大值是________．答案：16025. 231x x x 的最小值是________．答案：526. 满足24x y y 的整数对（x ，y ）有________个．答案：627. 设a 是整数，关于x 的方程12x a 只有三个不同的整数解，求这三个解．答案：–3，1，528. 若a 为整数，则关于x 的方程(a – 1) x = a + 1的所有整数解的和是________．答案：429. 已知x 与y 使得x + y ，x – y ，xy ，x y四个数中的三个相等，则这样的数对（x ，y ）有________对．答案：230. 若关于x ，y 的二元一次方程组 132kx y bk x y 有无穷多组解，则22k b 的值为________．答案：531. 若[x ]表示不超过x 的最大整数，且满足方程3x + 5[x ] – 49 = 0，则3x +1=________．答案：2032. 如果关于x 的不等式组9080x a x b的整数解仅有1，2，3，那么整数a ，b 组成的有序数对（a ，b ）共有________对．答案：7233. 如果关于x 的不等式组100x x a无解，则a 的取值范围是________．答案：1a34. 在1~100的自然数中与10互质的自然数共有________个．答案：4035. 已知三个质数a ，b ，c 满足133a b c ab bc ac ，则abc ＝________．答案：15436. 已知三位数abc 能被5整除，但不能被6和7整除；三位数cba 能被6整除，但不能被5和7整除；三位数cab 能被7整除，但不能被5和6整除，则abc ＝________．答案：67537. 九位数ABCABCBBB 能被1~17中的任意整数整除，且A ，B ，C 是不同的数字，则九位数ABCABCBBB 是________．答案：30630600038. 乘积376 ×733 的个位数字是________．答案：739. 四位数aabb 是一个整数的平方，aabb =________．答案：774440. 已知p 是质数，且271p 的不同正因数的个数不超过10，则满足题意的p的个数是________．答案：241. 如图所示有4种类型的几何体，每个几何体都是由4个单位正方体组成．选出8个同类型的几何体，把它们组合成一个2×4×4的长方体．可以完成组合的几何体有________种类型．答案：442. 已知圆环内直径为a 厘米，外直径为b 厘米，将50个这样的圆环一个接一个环套地连成一条锁链，那么这条锁链拉直后的长度为________厘米．答案：49a +b43. 设有一个边长为1的正三角形，记作A 1（如图1），将A 1的每条边三等分，以中间的线段为一边向形外作正三角形，去掉中间的线段后所得到的图形记作A 2（如图2）；将A 2的每条边三等分，并重复上述过程，所得到的图形记作A 3（如图3）；再将A 3的每条边三等分，并重复上述过程，所得到的图形记作A 4，那么A 4的周长是________．图1 图2 图3答案：64944. 如图所示，AOB 是一条直线，若1:2:3:41:2:4:5 ，则2 的余角是________度．答案：6045.如图，AB//CD，那么∠1 –∠2 +∠3 –∠4 +∠5 =________度．答案：046.如图，∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7=（）．A．450° B．540° C．630° D．720°答案：B47.从一个凸n边形的纸板上剪下一个三角形，剩余的是一个内角和为2160°的多边形，则n最大是________．答案：1548.一个凸n边形的内角和小于1998°，那么n的最大值是________．答案：1349.如果一个凸多边形的内角和等于外角和的3倍，那么这个多边形的边数是（）．A.4B.6C.8D.10E.12答案：C50.如图所示，在△ABC中，AC=7，BC=4，D为AB中点，E为AC边上一点，且1902AED C，则CE =________．答案：5.551.在△ABC中，已知BD和CE分别是两边上的中线，并且BD⊥CE，BD=4，CE=6，那么△ABC的面积是________．答案：1652.△ABC中，∠A为最小角，∠B为最大角，且2∠B = 5∠A，若∠B的最大值为m°，∠B的最小值为n°，则m + n =________．答案：17553.如图，在锐角△ABC中，高线CD，BE相交于点F，若∠A=55°，则∠BFC的度数是________度．答案：12554.如图，PQ=PR=QS，线段PR与QS相互垂直，则∠PRQ与∠PSQ度数之和是________度．答案：13555.在平行四边形ABCD中，AD = 2AB，点M是AD的中点，CE⊥AB于E．如果∠CEM = 40°，那么∠DME的值是（）．A．150° B．140° C．135° D．130°答案：A56.若长方形内有一点P，点P到各边的距离从小到大依次为1，2，5，6则长方形面积最小为________．答案：3357.如图所示的4×5的方格图中，过格点P的直线与方格图上、下边界相交形成的直角梯形ABCD（其中AB<CD）的面积最大是________．答案：1258. 如图，CD 是Rt △ABC 斜边AB 上的高，∠BAC 的平分线AE 交CD 于H ，交∠BCD 的平分线CF 于G ．求证：HF ∥BC ．答案：证明：由∠DCB ＝90°－∠B ＝∠BAC ，知∠HCG ＝12∠DCB ＝12∠BAC ＝∠HAD ．而∠CHG ＝∠AHD ，从而∠CGH ＝180°－(∠HCG ＋∠CHG )＝180°－(∠HAD ＋∠AHD )＝90°，知AG ⊥CG ，即AG ⊥CF ．此时，∠FCA ＝90°－∠GAC ＝90°－∠GAF ＝∠CF A ，故AC ＝AF ，即点A 在CF 的垂直平分线AG 上．又H 在AG 上，则HC ＝HF ，即知∠HFC ＝∠FCH ＝∠FCB ，故HF ∥BC ．59. 由8个相同的小正方体搭成的一个几何体，俯视图如下，那么这个几何体的左视图一定不是（）．答案：C60. 若n 个人完成一项工程需要m 天，则（m +n ）个人完成这项工程需要（）天． A.nm mnB.m nm nC.m nmnD.2mnm n答案：A61. 一个商人用m 元（m 为正整数）买来了n 台（n 为质数）电视机，其中有两台以成本的一半价钱卖给某个慈善机构，其余的电视机在商店出售，每台盈利500元，结果该商人获得利润为5500元，则n 的最小值是________．答案：1762. 某商场经销一种商品，由于进货时价格比原进价降低了6.4％，使得利润率增加了8个百分点，那么经销这种商品原来的利润率是________%．（注：100% 销售价进价利润率进价）答案：1763. 小倩和小玲每人都有若干面值为整数元的人民币．小倩对小玲说：“你若给我2元，我的钱将是你的n倍”；小玲对小倩说：“你若给我n元，我的钱数将是你的2倍”，其中n为正整数，则n的最大值是________．答案：864.图书馆内，在标有号码1，2，3，4的书架上分别有书120，135，142，167本．若干天后，每个书架上都各被借出a本书，又过了若干天，四个书架又分别被借出0，b，c，d本书，并且四个书架上余下同样本数的书．若b，c，d≥1，b+c+d=a，则两次借出书后，1号书架剩有________本书．答案：3665.五个不同的数，两两之和依次等于3，4，5，6，7，8，11，12，13，15 则这五个数的平均数是________．答案：4.266.王明在早晨六点至七点之间外出晨练，锻炼时长不超过一小时，出门和回家的时候，时针与分针的夹角都是110°．则王明晨练的时间为________分钟．答案：4067.某人骑车沿直线旅行，先前进了a千米，休息了一段时间，又原路返回b千米（b﹤a），再前进c千米，则此人离起点的距离S与时间t的关系示意图是（）．答案：C68.某届运动会的十一天的比赛中，醒狮队拿了16块金牌，其中每天至少拿一枚金牌，则醒狮队拿金牌的不同的情况可能有________种．(假设金牌都是一样的)答案：300369.将正方形的每条边8等分，再以这些分点为顶点（不包括正方形的顶点），可以得到不同的三角形的个数是________．答案：313670.口袋中装有20个只有颜色不同其他都相同的球，其中白球9个，红球5个，黑球6个．现从中任取10个球，使得白球不少于2个但不多于8个，红球不少于2个，黑球不多于3个，那么这样取法有________种．答案：1671.将若干红黑两种颜色的球摆成一行，要求两种颜色的球都要出现，且任意中间夹有5个或10个球的两个球必为同一种颜色的球．按这种要求摆放，最多可以摆放________个球．答案：1572.在{1000，1001，1002，…，2000}中有________对相邻的数满足下列条件：每对中的两数相加时不需要进位．答案：15673.试求所有满足如下性质的四元实数组（a，b，c，d）：组中的任一数都等于其余三个数中某两个数的乘积．（注：四元实数组中的数相同，顺序不同，算作同一组）答案：（0，0，0，0），（1，1，1，1），（－1，－1，1，1），（－1，－1，－1，1）74.将三位数A各个数位上的数字重新排列，得出的所有数的算术平均值等于A ．这样的三位数A 共有________个．答案：1575. 如图，6个人围成一圈做传球游戏，每个人接到球后传给和他不相邻的某一人(如：A 接到球后可以传给C 、D 或E )，开始时，球在A 的手中，若球被传递三次后又回到A ，此种情况出现的概率是________．答案：22776. 如图，△ABC 中，D 、E 分别是边BC 、AC 的中点，从这 8个图形△ABD 、△ACD 、△ABE 、△BCE 、△GAB 、△GAE 、△GBD 、四边形CEGD 中任取2个图形，取出的2个图形面积相等的概率是________．答案：2777. 按如图的程序进行操作，规定：程序运行从“输入一个值x ”到“结果是否>487？”为一次操作．如果操作进行四次才停止，那么x 的取值范围是________．答案：7＜x ≤1978. 如图是一个正方体的平面展开图，若该正方体相对的两个面上的代数式的值相等，则x – y – z 的值是________．答案：379. 设)(n f 为正整数n （十进制）的各数位上的数字的平方之和，如14321)123(222 f ．记)()(1n f n f ，))(()(1n f f n f k k ，k =1，2，3……，则2016(2016)f 的值是________．答案：14580. 有16枚棋子，都是一面黑色，另一面白色，放在4×4的正方形网格里．最初，所有棋子都是黑面朝上．规定：每次操作，将一个2×2正方形中的4枚棋子都正反面翻转一次．那么，要得到如图所示的排列，至少需要经过________次操作．答案：6。

人教版七年级数学下册能力提升题目专项训练40题(1)

【专题一】非负数1．若+（b+2）2=0，则点M（a，b）所在的象限是（）A．第一象限B．第二象限C．第三象限D．第四象限2．已知点P（x，y），且（x+1）2+=0，则点P的坐标为（）A．（﹣1，0）B．（﹣1，2）C．（0，2）D．（1，﹣2）3．点A的坐标（x，y）满足条件（x+2）2+=0，则点A的位置在（）A．第一象限B．第二象限C．第三象限D．第四象限4．已知（a﹣2）2+=0，则P（﹣a，﹣b）在（）A．第一象限B．第二象限C．第三象限D．第四象限5．若实数x、y满足+（y+3）2=0，则P（x，y）在第几象限（）A．第一象限B．第二象限C．第三象限D．第四象限6．若（a+1）2+=0，则点M（a，b）在（）A．第一象限B．第二象限C．第三象限D．第四象限7．已知x，y为实数，且+3（y﹣2）2=0，则（x，y）在第（）象限．A．第一象限B．第二象限C．第三象限D．第四象限8．已知直角坐标系中，点P（x，y）满足+（y+3）2=0，则点P坐标为（）A．（2，﹣3）B．（﹣2，3）C．（2，3）D．（2，﹣3）或（﹣2，﹣3）9．若点P（x，y）的坐标x，y满足，则点P在（）A．第一象限B．第二象限C．第三象限D．第四象限【专题二】整体思想10．关于x，y的二元一次方程组的解满足不等式x+y＞0，则a的取值范围是．11．若关于x、y的二元一次方程组的解满足x+y＞0，则m的取值范围是．12．若关于x，y的二元一次方程组的解满足x+y＞2，则k的取值范围是．13．已知关于x，y的方程组的解满足不等式x+y＞3，则a的取值范围是．14．关于x，y的二元一次方程组的解满足x+y≥1，则k的取值范围是．15．若关于x，y的二元一次方程组的解满足不等式2x﹣y＞1，则a的取值范围是．16．关于x、y的二元一次方程组的解满足不等式x﹣y＞4，则m的取值范围是．17．已知关于x，y的方程组的解满足x+y＜0，则k的取值范围是．18．已知关于x，y的方程组的解满足x+y＞2，则m的取值范围为．19．若关于x，y的二元一次方程组的解满足x+y＞﹣，则满足条件的m的所有正整数值为．【专题三】平行线的性质20．把一张长方形纸条按如图所示折叠后，若∠AOB′=70°，则∠B′OG=．21．如图，已知a∥b，小亮把三角板的直角顶点放在直线b上．若∠1=35°，则∠2的度数为．22．如图，已知BD∥AC，∠1=65°，∠A=40°，则∠2的大小是．23．如图所示，OP∥QR∥ST，若∠2=110°，∠3=120°，则∠1=度．24．如图，l1∥l2，∠1=120°，∠2=100°，则∠3=度．25．如图，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′位置，若∠EFB=65°，则∠AED′=°．26．如图所示，AB∥EF∥CD，且∠B=∠1，∠D=∠2，则∠BED的度数为°．27．把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G，D、C分别在M、N的位置上，若∠EFG=49°，则∠2﹣∠1=．28．如图，直线a∥b，∠2=∠3，若∠1=45°，则∠4=．29．如图，a∥b，点A在直线a上，点C在直线b上，∠BAC=90°，AB=AC，∠1=30°，则∠2的度数为．30．小丽把一块含30°角的直角三角尺摆成如图所示的造型，其中角的顶点B，C分别在直线a，b上，若a∥b，∠1=55°则∠2=，∠3=．【专题四】31．如果5x3m﹣2n﹣2y n﹣m+11=0是二元一次方程，则2m﹣n=．32．若3x2m﹣3﹣y2n﹣1=5是二元一次方程，则m=，n=．33．若3x a+b﹣2y a﹣b=5是关于x、y的二元一次方程，则ab=．34．若x2m+1+3y n﹣2=3是关于x、y的二元一次方程，则m﹣n=．35．﹣3x a﹣2+4y b﹣1=﹣5是关于x，y的二元一次方程，则ab=．36．若x3m﹣3﹣2y n﹣1=5是二元一次方程，则m+n=．37．若方程（a+2b﹣5）xy+x﹣2y3a﹣b=8是关于x，y的二元一次方程，则a+b=．38．若方程2x2m+1+3y=﹣7是二元一次方程，则m=．39．方程（m2﹣9）x2+x﹣（m﹣3）y=0是关于x，y的二元一次方程，则m的值为．40．若（a+2）x|a|﹣1+3y=1是关于x、y的二元一次方程，则a=．人教版七年级数学下册能力提升题目专项训练40题（1）参考答案一．选择题（共9小题）1．D；2．B；3．B；4．B；5．D；6．B；7．A；8．D；9．B；二．填空题（共31小题）10．a＞﹣1；11．m＞﹣2；12．k＜﹣1；13．a＞1；14．k≥2；15．a；16．m＞3；17．k＜﹣3；18．m＞；19．1、2、3；20．55°；21．55°；22．75°；23．50；24．40；25．57.5；26．90；27．16°；28．45°；29．75°；30．125°；145°；31．2；32．2；1；33．0；34．﹣3；35．6；36．；37．3；38．0；39．﹣3；40．2；。

初一下数学-选择填空题强化训练

54D3E21CBA第一小测选择题（每题3分，共30分）1．通过平移，可将图（1）中的福娃“欢欢”移动到图（）（图1） A B C D 2．一辆汽车在笔直的公路上行驶，两次拐弯后，仍在原来的方向上平行前进，那么两次拐弯的角（）A．第一次右拐50°，第二次左拐130° B．第一次左拐50°，第二次右拐50°C．第一次左拐50°，第二次左拐130° D．第一次右拐50°，第二次右拐50°3．如右图，下列能判定AB∥CD的条件有( )个.(1) ︒=∠+∠180BCDB；(2)21∠=∠； (3) 43∠=∠；(4) 5∠=∠B.A.1B.2C.3D.44．同一平面内的三条直线满足a⊥b，b⊥c，则下列式子成立的是（）A．a∥c B．b⊥a C．a⊥c D．b∥c5．如图，若m∥n，∠1 = 105°，则∠2 =（）A．55° B．60° C．65° D．75°6．命题：①对顶角相等；②过一点有且只有一条直线与已知直线平行；③相等的角是对顶角；④同位角相等。

其中错误的有（）A、1个B、2个C、3个D、4个7、如图13，AB∥CD，AC⊥BC，图中与∠CAB互余的角有（）A、１个B、2个C、3个D、4个8、如图10，点E在AC的延长线上，下列条件中能判断BDAC//的是（）A. 43∠=∠ B. 21∠=∠ C. DCEA∠=∠ D.180=∠+∠ACDA9、如图11，a∥b，∠3=1080，则∠1的度数是（）A、 720B、 800C、 820D、 108010已知点A()2,2-，如果点A关于x轴的对称点是B，点B关于原点的对称点是C，那么C点的坐标是（）A．()2,2B．()2,2-C．()1,1--D．()2,2--21nm第（4）题DCBA二、填空题（每题3分，共30分） 11．如图，直线a ∥b ，则∠ACB=_______。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

初一下数学能力训练题（7）1、下面四个算式，正确的个数有（）。

① 1234a =a •a ② 1055a =a +a ③ a =a ÷a 55④ ()633a =aA 、0个B 、1个C 、2个D 、3个 2、在一个不透明的布袋中装有2个白球，n 个黄球，它们除颜色不同外，其余均相同。

若从中随机摸出一个球，它是黄球的概率是54，则n= 。

3、如右图，AB ∥CD ，∠A=48°，∠C=∠E ，则∠C 的度数为。

4、北京市申办2008年奥运会，得到了全国人民的热情支持。

据统计，某日北京申奥网站的仿问人次为201949，用四舍五入法取近似值保留两个有效数字，得（） A 、2.0×105B 、2.0×106C 、2×105D 、0.2×1065、下列运算正确的是（）Ａ、3x-2x=1 Ｂ、22-x21-=x2- Ｃ、632a =a •-a)( Ｄ、632-a =)-a (6、如图，把一张矩形纸片ABCD 沿EF 折叠后，点C ，D 分别落在C ’,D ’的位置上，EC ’交AD 于点G 。

已知∠EFG=58o ，那么 ∠BEG o。

7、先化简，再求值：)y -x 2)(y +x 2(-)x +y (x 4，其中2-=y ,21=x 。

8、A 口袋中装有2个小球，它们分别标有数字1和2；B 口袋中装有3个小球，它们分别标有数字3，4和5，每个小球除数字外都相同。

甲、乙两人玩游戏，从A ，B 两个口袋中随机地各取出1个小球，若两个小球上的数字之和为偶数，则甲赢；若和为奇数，则乙赢。

这个游戏对甲、乙双方公平吗？请借助图表法说明理由。

9、如图，在△ABC 中，AB ＝AC ，点D 、E 分别是AB 、AC 的中点，点F 是BE 、CD 的交点。

请写出图中两组全等的三角形，并选出其中一组加以证明。

(要求：写出证明过程中的重要依据)CABDE48o ABECDFGC ’D ’ABCDE1、下列运算正确的是（）A 、x 3＋x 5＝x 8B 、(x 3)2＝x 9C 、x 4·x 3＝x 7D 、(x ＋3)2＝x 2＋9 2、我国的陆地面积居世界第三位，约为9597000平方千米，用科学记数法表示为平方千米（保留三个有效数字）。

3、从数字1、2、3中任取两个不同数字组成一个两位数，则这个两位数大于21的概率是。

4、如图：在△ABC 中，∠A=70°，∠B=60°，点D 在BC 的延长线上，则∠ACD= 度.5、如图，ABC Δ中，B ∠，C ∠的平分线相交于点O ，过O 作DE//BC ，若BD+EC=5，则DE 等于（） A 、7B 、6C 、5D 、46、先化简下面的代数式，再求值： )a -4(a +)2-a )(2+a (，其中2=a7、如右图，E 是BC 的中点，∠1=∠2，AE=DE 。

求证：AB=DC 。

8、在一个布口袋中装着只有颜色不同，其它都相同的白、红、黑三种颜色的小球各1只，甲乙两人进行摸球游戏；甲先从袋中摸出一球看清颜色后放回，再由乙从袋中摸出一球。

(1) 试用列表法表示摸球游戏所有可能的结果；(2) 如果规定：乙摸到与甲相同颜色的球为乙胜，否则为负，试求乙在游戏中能获胜的概率。

9、如右图，AB=AD ，AC=AE ，∠1=∠2。

求证：BC=DE 。

70°60° A CDA BCDE12C12ABE C1、计算)m 3-(÷m 623的结果是（）A 、m 3-B 、m 2-C 、m 2D 、m 3 2、如图，水平放置的甲、乙两区域分别由若干大小完全相同的黑色、白色正三角形组成，小明随意向甲、乙两个区域各抛一个小球，P （甲）表示小球停在甲中黑色三角形上的概率，P （乙）表示小球停在乙中黑色三角形上的概率，下列说法中正确的是（） A 、P(甲)>P(乙) B 、P(甲)= P(乙)C 、P(甲)< P(乙)D 、P(甲)与P(乙)的大小关系无法确定 3、有一列数a 1，a 2，a 3，，a n ，从第二个数开始，每一个数都等于1与它前面那个数的倒数的差，若a 1=2，则a 2007为（）Ａ、2007Ｂ、2Ｃ、21Ｄ、-14、如图，已知AB ∥CD ，直线MN 分别交AB 、CD 于E 、F ，∠MFD ＝50°， EG 平分∠MEB ，那么∠MEG 的大小是___________度。

5、2007年4月，全国铁路进行了第六次大提速，提速后的线路时速达200千米。

共改造约6000千米的提速线路，总投资约296亿元人民币，那么，平均每千米提速线路的投资约亿元人民币（用科学记数法，保留两个有效数字）。

6、已知：如右图，直线AD 与BC 交于点O ，OA=OD ，OB=OC 。

求证：AB ∥CD 。

7、如图，分别以ABC ΔRt 的直角边AC ，BC 为边，在ABC ΔRt 外作两个等边三角形ACE Δ和BCF Δ，连结BE ，AF 。

求证：BE=AF 。

8、如图，四边形ABCD 、DEFG 都是正方形，连接AE 、CG 。

（1）求证：AE=CG ；（2）观察图形，猜想AE 与CG 之间的位置关系，并证明你的猜想。

AE甲乙A BCDE FNMGABCDEFGMNH1、下列算式中，正确的是（）A 、-a =3a -a 232 B 、22a =a1•a ÷a C 、2623b a =)b a ( D 、623a =)(-a -2、现有50张大小、质地及背面图案均相同的北京奥运会吉祥物福娃卡片，正面朝下放置在桌面上，从中随机抽取一张并记下卡片正面所绘福娃的名字后原样放回，洗匀后再抽，不断重复上述过程，最后记录抽到欢欢的频率为20℅，则这些卡片中欢欢约为________张。

3、将一副三角板摆放成如图所示，图中∠1= 度。

4、据统计，到2006年底我国大陆总人口数约为13.1448亿，用科学记数法表示这个数(保留4个有效数字)，正确的是（）。

A 、1.315×109B 、1.314×109C 、1.314×108D 、5、如图，将纸片△ABC 沿DE 折叠，点A 落在点A′处，已知 ∠1+∠2＝100°，则∠A 的大小等于____________度。

6、甲、乙两同学设计了这样一个游戏：把三个完全一样的小球分别标上数字1、2、3后，放在一个不透明的口袋里，甲同学先随意摸出一个球，记住球上标注的数字，然后让乙同学抛掷一个质地均匀的、各面分别标有数字1、2、3、4、5、6的正方体骰子，又得到另一个数字，再把两个数字相加。

若两人的数字之和小于7，则甲获胜；否则，乙获胜。

① 请你用列表法把两人所得的数字之和的所有结果都列举出来；② 这个游戏公平吗？如果公平，请说明理由；如果不公平，请你加以改进，使游戏变得公平。

7、已知，如图，点B 、F 、C 、E 在同一直线上，AC 、DF 相交于点G ，A B ⊥BE ，垂足为B ，DE ⊥BE ，垂足为E ，且AB ＝DE ，BF ＝CE 。

求证：（1）△ABC ≌△DEF ；（2）GF ＝GC 。

8、如图，G 是线段AB 上一点，AC 和DG 相交于点E.请先作出∠ABC 的平分线BF ，交AC 于点F ；（尺规作图，保留作图痕迹，不写作法与证明）然后证明：当AD ∥BC ，AD=BC ，∠ABC=2∠ADG 时，DE=BF 。

ADBFGCEEDCE1、下列运算正确的是（）Ａ、633a 2=a +aＢ、853a -=)a -(•)a -(Ｃ、3632b -24a =a 4•)b -2a (Ｄ、22a 91-16b =4b)-a 314b)(-a 31-( 2、某体育训练小组有2名女生和3名男生，现从中任选1人去参加学校组织的“我为奥运添光彩”志愿者活动，则选中女生的概率为。

3、如右图，在ΔABC 中，AB ＝AC ，AD ＝4，BC ＝6，点E ，F 是中线AD 上的两点，则图中阴影部分的面积是（）A 、6B 、12C 、24D 、30 4、如右图，是赛车跑道的一段示意图，其中AB ∥DE ，测得∠B ＝140°， ∠D ＝120°，则∠C 的度数为（）A 、120°B 、100°C 、140°D 、90°5、我国陆地面积居世界第三位，约为9597300平方千米，用科学记数法可表示为平方千米（结果保留三个有效数字）。

6、如右图所示，∠ADB ＝∠ADC ，BD ＝CD 。

求证：△ABD ≌△ACD 。

7、如右图，一个可以自由转动的均匀转盘被分成了4等份，每份内均标有数字，小明和小亮商定了一个游戏，规则如下：（1）连续转动转盘两次；（2）将两次转盘停止后指针所指区域内的数字相加（当指针恰好停在分格线上时视为无效，重转）；（3）若数字之和为奇数，则小明赢；若数字之和为偶数，则小亮赢。

请用“列表”的方法分析一下，这个游戏对双方公平吗？并说明理由。

8、如右图，在△ABC 中，AB=AC ，D 是BC 边上的一点，DE ⊥AB ，DF ⊥AC ，垂足分别为E 、F ，添加一个条件，使DE= DF ，并说明理由。

解：需添加条件是。

理由是：ABC DE ABCDA E BCF D1、根据国务院全面实行农村义务教育经费保障机制改革的精神，据《潇湘晨报》2月28日报道：2007年春季开学，我省投入19.8114亿元，对农村义务教育阶段的学生实行“两免一补”。

19.8114亿元用科学记数法（保留两个有效数字）表示为元。

2、把6张形状完全相同的卡片的正面分别写上数字1、2、3、4、5、6，且洗匀后正面朝下放在桌子上，从这6张卡片中同时随机抽取两张卡片，则两张卡片上的数字之和等于7的概率是___________。

3、如右图，AB ⊥CD ，垂足为C ，o130=1∠，则2∠= 度。

4、计算：0－22008+)21－(＝。

5、化简a(a －2b)－(a －b)2 ＝。

6、如图，用灰白两色正方形瓷砖铺设地面，第6个图案中灰色瓷砖块数为_________。

7、如右图，在ΔABC 中，D 是AB 上一点，DF 交AC 于点E ，DE=FE ，AE=CE ，AB 与CF 有什么位置关系？证明你的结论。

8、如图，已知BE ⊥AD ，CF ⊥AD ，且BE ＝CF 。

请你判断AD 是△ABC 的中线还是角平分线？请说明你判断的理由。

9、如右图，ΔACB 和ΔECD 都是等腰直角三角形，A ，C ，D 三点在同一直线上，连结BD ，AE ，并延长AE 交BD 于F 。