四年级奥数上册:格点与面积
(完整word版)小学奥数模块教程四年级杯赛备战讲义——巧求面积

上课日期: 上课时间: 教师姓名:知识点一:格点面积 一、正方形格点问题在一张纸上,先画出一些水平直线和一些竖直直线,并使任意两条相邻的平行线的距离都相等(通常规定是1个单位),这样在纸上就形成了一个方格网,其中的每个交点就叫做一个格点.在方格网中,以格点为顶点画出的多边形叫做格点多边形,例如,右图中的乡村小屋图形就是一个格点多边形.那么,格点多边形的面积如何计算?它与格点数目有没有关系?如果有,这两者之间的关系能否用计算公式来表达?下面就让我们一起来探讨这些问题吧!用N 表示多边形内部格点,L 表示多边形周界上的格点,S 表示多边形面积,请同学们分析前几个例题的格点数.我们能发现如下规律:12LS N =+-.这个规律就是毕克定理.二、 三角形格点问题1、定义:所谓三角形格点多边形是指:每相邻三点成“∵”或“∴”,所形成的三角形都是等边三角形.规定它的面积为1,以这样的点为顶点画出的多边形为三角形格点多边形.2、公式:关于三角形格点多边形的面积同样有它的计算公式:如果用S 表示面积,N 表示图形内包含的格点数,L 表示图形周界上的格点数,那么有22S N L =⨯+-,就是格点多边形面积等于图形内部所包含格点数的2倍与周界上格点数的和减去2.知识点二:图形剪拼巧求面积知识框架毕克定理若一个格点多边形内部有N 个格点,它的边界上有L 个格点,则它的面积为12LS N =+-.本讲中很多类型的题目还要求同学们去动手尝试.通过本讲知识的学习,让同学们了解不同图形的分割、拼合、剪拼的方法,锻炼同学们的平面想象能力以及增强学生的动手操作能力.(1)把一个几何图形按某种要求分成几个图形,就叫做图形的分割.(2)反过来,按一定的要求也可以把几个图形拼成一个完美的图形,就叫做图形的拼合.(3)将一个或者多个图形先分割开,再拼成一种指定的图形,则叫做图形的剪拼.我们在图形的分割、拼合和剪拼的过程中,都要结合所提供的图形特点来思考.(1)如果把一个图形分割成若干个大小、形状相等的部分,那么就要想办法找图形的对称点,把图形先分少,再分多.(2)图形中,如果有数量方面的要求,可以先从数量入手,找出平分后每块上所含数量的多少,再结合数量来分割图形.(3)如果是要把几个图形拼合成一个大图形,要特别注意每条边的长度,把相等的边长拼合在一起,先拼少的,再拼多的.(4)如果是剪拼图形,要抓住“剪、拼前后图形的面积相等”这个关键,根据已知条件和图形的特点,通过分析推理和必要的计算,确定剪拼的方法.一、解题关键:分割其实就是运用特殊的三角形(等角直角三角形、等边三角形等)、正方形、等边图形的特殊性质进行分割而得,所以分割的关键是利用了特殊图形的关系解题。
四年级上册奥数讲义-第十讲 格点图形的计算-冀教版(无答案)
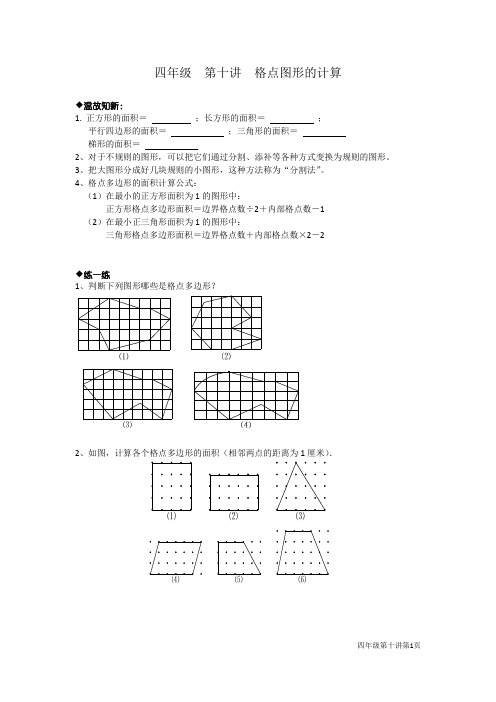
四年级第十讲格点图形的计算◆温故知新:1. 正方形的面积=;长方形的面积=;平行四边形的面积=;三角形的面积=梯形的面积=2、对于不规则的图形,可以把它们通过分割、添补等各种方式变换为规则的图形。
3、把大图形分成好几块规则的小图形,这种方法称为“分割法”。
4、格点多边形的面积计算公式:(1)在最小的正方形面积为1的图形中:正方形格点多边形面积=边界格点数÷2+内部格点数-1(2)在最小正三角形面积为1的图形中:三角形格点多边形面积=边界格点数+内部格点数×2-2◆练一练1、判断下列图形哪些是格点多边形?2、如图,计算各个格点多边形的面积(相邻两点的距离为1厘米).⑴⑵⑶◆例题展示例题1图中相邻两个点间的距离均为1厘米,求多边形的面积分别是多少平方厘米?练习1图中相邻两格点间的距离均为1厘米,求多边形的面积是多少平方厘米?例题2下图中相邻格点围成的最小正方形的面积为1平方厘米。
这个多边形的面积是多少平方厘米?练习2(1)下图中相邻格点围成的最小正方形的面积为1平方厘米.这个多边形的面积是多少?(2)求下列各个格点多边形的面积.例题3下图中相邻格点围成的最小正三角形的面积为1平方厘米。
这个多边形的面积是多少平方厘米?练习3 下图中相邻格点围成的最小正三角形的面积为1平方厘米.这个多边形的面积是多少?(1)(2)(3)(4)例题4 下图中每个最小正方形的面积是2平方厘米。
阴影部分面积是多少平方厘米?练习4图中每个最小正方形的面积是2平方厘米,阴影部分面积是多少平方厘米◆拓展提高拓展1下图中每个最小正三角形的面积是4平方厘米。
阴影部分面积是多少平方厘米?练习1下图中每个最小正三角形的面积是2平方厘米,阴影部分的面积是多少平方厘米?拓展2 如图,正方形网格的总面积等于96平方厘米,求阴影图形的面积。
练习2 如图,每个小方格的面积都是4平方厘米,求阴影图形的面积。
◆思维挑战挑战1如图,每个小等边三角形的面积都是1平方厘米,阴影部分的面积是多少平方厘米?挑战2如图,三角形网格的总面积是36平方厘米。
奥数格点与面积解题法【三篇】

【导语】天⾼鸟飞,海阔鱼跃,学习这舞台,秀出你独特的精彩⽤好分秒时间,积累点滴知识,解决疑难问题,学会举⼀反三。
以下是为⼤家整理的《奥数格点与⾯积解题法【四篇】》供您查阅。
【第⼀篇】 直接将格点图中的不规则图形分成若⼲个可求⾯积的规则图形,然后通过计算规则图形的⾯积来求原图形的⾯积。
例:如图所⽰,计算下⾯格点多边形的⾯积 【详解】这虽然是⼀个规则的三⾓形,但是可以直接⽤⾯积公式计算,或者通过数格⼦么?好像不⾏,因为我们现在不能直接算出相应边的长度和⾼!现在尝试⽤扩展法来解! 解题:如图②将原图扩展成⼀个长⽅形,很明显这个长⽅形的长、宽分别为6、4个单位长度,⽽三个扩展的三⾓形A、B、C的⾯积也是很容易求的!A:6×2÷2=6、B:4×2÷2=4、C:2×4÷2=4,所以原三⾓形的⾯积为:6×4-6-4-4=10(⾯积单位)。
【第⼆篇】 直接将格点图中的不规则图形分成若⼲个可求⾯积的规则图形,然后通过计算规则图形的⾯积来求原图形的⾯积。
例:如图所⽰,计算下⾯格点多边形的⾯积 【详解】这虽然是⼀个规则的三⾓形,但是可以直接⽤⾯积公式计算,或者通过数格⼦么?好像不⾏,因为我们现在不能直接算出相应边的长度和⾼!现在尝试⽤分割法和扩展法来解! 解题:如图①做辅助线,将原图分割成两个⼩三⾓形。
这两个⼩三⾓形都以辅助线为底的话,⾼也是很容易就观察出来的,都是2个单位长度,所以原三⾓形的⾯积为:5×2÷2×2=10(⾯积单位)。
【第三篇】 对于格点图⾥⾯的规则图形,我们有时可以直接通过数图形所占的正⽅形⽅格或者三⾓形⽅格的个数得出规则图形的⾯积,或者由图形得出规则图形相应的⾯积公式需要的量,代⼊公式解出⾯积即可! 例:如下图,计算下列各个格点多边形的⾯积: 【详解】本题所给的图形都是规则图形,它们的⾯积运⽤公式直接可求,只要判断出相应的有关数据就⾏了。
(完整版)第25讲不规则图形的面积四年级奥数格点和面积补充

格点和面积这一讲我们主要介绍利用格点求几何图形的面积,先来介绍什么叫“格点”。
见右图:这是一张由水平线和垂直线组成的方格纸,我们把水平线和垂直线相交的点称为“格点”,水平线和垂直线围成的每个小正方形称为“面积单位”。
借助小格点,我们可以很快地比较和计算图形的面积大小。
利用格点求图形的面积有两种思路,一是直接将图形分成若干个面积单位,然后通过计算有多少个面积单位来求图形的面积;二是将某些图形转化成长方形的面积来求。
当然还可以将这两种方法结合起来,求出某些较复杂图形的面积。
格点面积公式=中间格点数+图形一周的格点数÷2﹢1【典型例题】例1:计算下列各图的面积。
分析:先仔细观察图中的每个图形,选择方法,显然第一、三、五图可以直接数出包含多少个面积单位,而二、四、六显然不适合用数单位面积的方法来求面积,可以采用虚线把这些图形扩展或割补成长方形,通过求长方形的面积来求这些图形的面积。
解:(1)图中长方形的面积包括了3×2=6(个)面积单位,所以它的面积为6个面积单位。
(2)将图中的平行四边形割补成一个长方形,长方形的面积为3×2=6,而平行四边形的面积等于长方形的面积,所以平行四边形的面积是3×2=6(个)面积单位。
(3)将图中三角形用虚线分成3块,它包含1个单位面积和2个单位面积的一半,合起来有2个面积单位,所以它的面积是2个面积单位。
(4)图中三角形扩展成一个长方形,长方形的面积为3×2=6,而三角形面积为长方形面积的一半,则三角形面积为3个面积单位。
(5)将图中梯形用虚线分成3块,它包含了有5个单位面积和2个单位面积的一半。
合起来有6个面积单位。
所以它的面积为6个面积单位。
(6)将图中梯形互相平行的一组对边延长,补出一个与原来梯形方向颠倒,但面积一样的梯形,形成一个大的长方形。
长方形面积为(2+4)×3=18,而梯形的面积为长方形面积的一半,所以梯形的面积是(2+4)×3÷2=9(个)面积单位。
(完整版)小学奥数-格点型面积

板块一 正方形格点问题在一张纸上,先画出一些水平直线和一些竖直直线,并使任意两条相邻的平行线的距离都相等(通常规定是1个单位),这样在纸上就形成了一个方格网,其中的每个交点就叫做一个格点.在方格网中,以格点为顶点画出的多边形叫做格点多边形,例如,右图中的乡村小屋图形就是一个格点多边形.那么,格点多边形的面积如何计算?它与格点数目有没有关系?如果有,这两者之间的关系能否用计算公式来表达?下面就让我们一起来探讨这些问题吧!用N 表示多边形内部格点,L 表示多边形周界上的格点,S 表示多边形面积,请同学们分析前几个例题的格点数.我们能发现如下规律:12LS N =+-.这个规律就是毕克定理.毕克定理若一个格点多边形内部有N 个格点,它的边界上有L 个格点, 则它的面积为12LS N =+-. 例题精讲格点型面积【例 1】用9个钉子钉成相互间隔为1厘米的正方阵(如右图).如果用一根皮筋将适当的三个钉子连结起来就得到一个三角形,这样得到的三角形中,面积等于1平方厘米的三角形的个数有多少?面积等于2平方厘米的三角形有多少个?【解析】面积等于1平方厘米的三角形有32个.面积等于2平方厘米的三角形有8个.(1)面积等于1平方厘米的分类统计如下:①②③底为2,高为1底为2,高为1底为1,高为23×2=6(个)3×2=6(个)3×2=6(个)④⑤⑥底为1,高为2底为2,高为1底为1,高为23×2=6(个)2×2=4(个)2×2=4(个)所以,面积等于1平方厘米的三角形的个数有:6+6+6+6+4+4=32(个).(2)面积等于2平方厘米的分类统计如下:3×2=6(个)1×2=2(个)所以,面积等于2平方厘米的三角形的个数有:6+2=8(个).【例 2】如图,44⨯的方格纸上放了16枚棋子,以棋子为顶点的正方形有个.【解析】根据正方形的大小,分类数正方形.共能组成五种大小不同的正方形(如右图).⨯的正方形:1个;⨯的正方形:4个;3311⨯的正方形:9个;22以11⨯正方形对角线为边长的正方形:4个;以12⨯长方形对角线为边长的正方形:2个.故可以组成9414220++++=(个)正方形.【例 3】判断下列图形哪些是格点多边形?⑴⑵⑶⑷【解析】根据格点多边形的定义可知,图形的边必须是直线段,顶点要在格点上!所以只有⑴是格点多边形.【解析】本题所给的图形都是规则图形,它们的面积运用公式直接可求,只要判断出相应的有关数据就行了.方法一:图⑴是正方形,边长是4,所以面积是4416⨯=(面积单位);图⑵是矩形,长是5,宽是3,所以面积是5315⨯=(面积单位);图⑶是三角形,底是5,高是4,所以面积是54210⨯÷=(面积单位);图⑷是平行四边形,底是5,高是3,所以面积是5315⨯=(面积单位);图⑸是直角梯形,上底是3,下底是5,高是3,所以面积是353212+⨯÷=()(面积单位);图⑹是梯形,上底是3,下底是6,高是4,所以面积是364218+⨯÷=()(面积单位).【巩固】如果两格点之间的距离是2,能利用刚计算的结果说出相应面积么?(教师总结:面积数值均扩大4倍.)方法二:以上部分图形除了利用各自的面积公式直接求出外,我们还可以从推导它们的面积公式过程中得到启发,即用“割补法”或“扩展法”分别转化成长方形来求.这一种方法很重要,在下面的题目中我们还将使用这种方法!如图⑶,我们利用“扩展法”将其转化,如图所示,从图中易知三角形面积是长方形面积的一半.如图⑷,我们利用“割补法”将其阴影部分面积平移到右边,转化成一个长方形,从中易得平行四边形面积.同理,图⑸、⑹也可利用同样的思想.【例 5】如图(a),计算这个格点多边形的面积.【解析】方法一(扩展法).这是个三角形,虽然有三角形面积公式可用,但判断它的底和高却十分困难,只能另想别的办法:这个三角形是处在长是6、宽是4的矩形内,除此之外还有其他三个直角三角形,如下右图(b),这三个直角三角形面积很容易求出,再用矩形面积减去这三个直角三角形面积,就是所要求的三角形面积.矩形面积是6424⨯=;直角三角形Ⅰ的面积是:6226⨯÷=;直角三角形Ⅱ的面积是:4224⨯÷=;直角三角形Ⅲ面积是4224⨯÷=;所求三角形的面积是2464410-++=()(面积单位).方法二(割补法).将原三角形分割成两个我们方便计算面积的三角形,如(c)图.因此三角形的面积是:52252210⨯÷+⨯÷=(面积单位).【例 6】(“新加坡小学数学奥林匹克”竞赛试题)右图是一个方格网,计算阴影部分的面积.【解析】扩展法.把所求三角形扩展成正方形ABCD中.这个正方形中有四个三角形:一个是要求的AEF;另外三个分别是:ABE、FEC、DAF,它们都有一条边是水平放置的,易求它们的面积分别为21.5cm,22cm,21.5cm.所以,图中阴影部分的面积为:33 1.5224⨯-⨯+=()(2cm).⑴ ⑵【解析】 利用“扩展法”和“割补法”我们都可以简单的得到⑴的面积均为9面积单位.⑵的面积均为10面积单位.【点评】“一个格点多边形面积的大小很可能是由哪些因素决定呢?”“格点多边形内部的格点数和周界上的格点数与格点多边形的面积有没有什么内在联系呢?”下面我们就来探讨一下!在巩固中,我们发现两个图形面积相等.进一步还可以发现第一个图形边界上的格点数是8个;第二个图形边界上的格点数是10个,包含在图形内的格点数也相等,都是6个.【巩固】求下列各个格点多边形的面积.⑵⑴⑷⑶【解析】 ⑴ ∵12L =;10N =,∴1211011522L S N =+-=+-=(面积单位); ⑵ ∵10L =;16N =,∴1011612022L S N =+-=+-=(面积单位);⑶ ∵6L =;12N =,∴611211422L S N =+-=+-=(面积单位);⑷ ∵10L =;13N =,∴1011311722L S N =+-=+-=(面积单位).用N 表示多边形内部格点,L 表示多边形周界上的格点,S 表示多边形面积,请同学们分析前几个例题的格点数.我们能发现如下规律:12LS N =+-.这个规律就是毕克定理.【例 8】 我们开始提到的“乡村小屋”的面积是多少?【解析】 图形内部格点数9N =;图形边界上的格点数20L = ;根据毕克定理, 则1182LS N =+-=(单位面积).【例 9】 右图是一个812⨯面积单位的图形.求矩形内的箭形ABCDEFGH 的面积.毕克定理若一个格点多边形内部有N 个格点,它的边界上有L 个格点, 则它的面积为12LS N =+-.HGFEDCBA【解析】箭形ABCDEFGH的面积810214842121232246=+÷-+⨯+÷-⨯=++=()()(面积单位).【例 10】右图中每个小正方形的面积都是1,那么图中这只“狗”所占的面积是多少?【解析】图形内部格点数为54,图形周界上格点数为19.所以图形的面积为:54192162.5+÷-=(面积单位).【巩固】如图,每一个小方格的面积都是1平方厘米,那么用粗线围成的图形的面积是多少平方厘米?【解析】方法一:正方形格点阵中多边形面积公式:(N+L2-1)×单位正方形面积,其中N为图形内格点数,L为图形周界上格点数.有N=4,L=7,则用粗线围成图形的面积为:(4+72-1)×1=6.5(平方厘米)方法二:如右上图,先求出粗实线外格点内的图形的面积,有①=3÷2=1.5,②=2÷2=1,③=2÷2=1,④=2÷2=1,⑤=2÷2=l,⑥=2÷2=1,还有三个小正方形,所以粗实线外格点内的图形面积为1.5+l+1+1+1+1+3=9.5,而整个格点阵所围成的图形的面积为16,所以粗线围成的图形的面积为:16-9.5=6.5平方厘米.【例 11】(“小学数学奥林匹克”竞赛试题)55⨯的方格纸,小方格的面积是1平方厘米,小方格的顶点称为格点.请你在图上选7个格点,要求其中任意3个格点都不在一条直线上,并且使这7个点用直线连接后所围成的面积尽可能大.那么,所围图形的面积是平方厘米.【解析】为了使这7个点围成最大的面积,这7个点应尽量在正方形的边或顶点上,如图选取7个点,围成面积最大.最大面积为550.5323.5⨯-⨯=(平方厘米).【例 12】(“保良局亚洲区城市小学数学”竞赛试题)第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一个小方格的面积是1,那么7、2、1三个数字所占的面积之和是多少?【解析】 要计算三个数字所占的面积之和,可以先分别求出每个数字所占的面积.显然,图中的三个数字都可以看作格点多边形,根据毕克定理,可以很方便地求出每个数字所占的面积.值得注意的是:数字“7”内部有两个格点,而数字“2”和“1”内部都没有格点.7所占的面积为:215218.5+÷-=;2所占的面积为:242111÷-=;1所占的面积为:17217.5÷-=.所以,这三个数字所占的面积之和为:8.5117.527++=.【例 13】 (第六届“从小爱数学”邀请赛试题)两个边长相等的正方形各被分成25个大小相同的小方格.现将这两个正方形的一部分重叠起来,若左上角的阴影部分(块状)面积为25.12cm ,右下角的阴影部分(线状)面积为27.4cm ,求大正方形的面积.【解析】 块状部分与线状部分之间的部分称为D ,则D 与前者共14个方格,与后者共17个方格,因此每个方格的面积是2197.4 5.121714cm 25-÷-=()()()大正方形的面积为219cm .【例 14】 (第六届“华杯赛”试题)图中正六边形ABCDEF 的面积是54,AP =2PF ,CQ =2BQ ,求阴影四边形CEPQ 的面积.B PQFEDCB A【解析】 如图,将正六边形ABCDEF 等分为54个小正三角形.根据平行四边形对角线平分平行四边形面积,PEF 面积3=,CDE 面积9=,四边形ABQP 面积11=.上述三块面积之和为391123++=.因此,阴影四边形CEPQ 面积为542331-=.板块二 三角形格点问题所谓三角形格点多边形是指:每相邻三点成“∵”或“∴”,所形成的三角形都是等边三角形.规定它的面积为1,以这样的点为顶点画出的多边形为三角形格点多边形.关于三角形格点多边形的面积同样有它的计算公式:如果用S 表示面积,N 表示图形内包含的格点数,L 表示图形周界上的格点数,那么有22S N L =⨯+-,就是格点多边形面积等于图形内部所包含格点数的2倍与周界上格点数的和减去2.【例 15】 如图(a ),有21个点,每相邻三个点成“∵”或“∴”,所形成的三角形都是等边三角形.计算三角形ABC 的面积.(b )(a )(c )(d )【解析】 方法一:如图(b )所示,在ABC 内连接相邻的三个点成DEF ,再连接DC 、EA 、FB 后是ABC可看成是由DEF 分别延长FD 、DE 、EF 边一倍、一倍、二倍而成的,由等积变换不难得到2ACD S =, 3AEB S =,4FBC S =,所以123410S =+++=(面积单位).方法二:如图(c )所示,作辅助线把图Ⅰ′、Ⅱ′、Ⅲ′分别移拼到Ⅰ、Ⅱ、Ⅲ的位置,这样可以通过数小正三角形的方法,求出ABC 的面积为10.方法三:如图(d )所示:作辅助线可知:平行四边形ARBE 中有6个小正三角形,而ABE 的面积是平行四边形ARBE 面积的一半,即3AEB S =,平行四边形ADCH 中有4个小正三角形,而ADC 的面积是平行四边形ADCH 面积的一半,即2ACDS =.平行四边形FBGC 中有8个小正三角形,而FBC 的面积是平行四边形FBGC 的一半,即:4FBCS =.所以123410S =+++=(面积单位).【巩固】如图,每相邻三个点所形成的三角形都是面积为1的等边三角形,计算ABC 的面积.【解析】 因为5N =;3L =:所以22253211S N L =⨯+-=⨯+-=(面积单位).【例 16】 求下列格点多边形的面积(每相邻三个点“∵”或“∴”成面积为1的等边三角形).⑴⑵⑶⑷【解析】 ⑴ ∵7L =;7N =,∴22277219S N L =⨯+-=⨯+-=(面积单位);⑵ ∵5L =;8N =,∴22285219S N L =⨯+-=⨯+-=(面积单位); ⑶ ∵6L =;7N =,∴22276218S N L =⨯+-=⨯+-=(面积单位); ⑷ ∵7L =;8N =,∴22287221S N L =⨯+-=⨯+-=(面积单位).【例 17】 把大正三角形每边八等分,组成如右图所示的三角形网.如果大三角形的面积是128,求图中粗线所围成的三角形的面积.【解析】 图中有1357911131564+++++++=(个)小三角形,那么一个小三角形的面积是128642÷=,图形内部格点数为12,图形周界上格点数为4;图形的面积为:2124226⨯+-=(面积单位),进而得图形的面积为:26252⨯=.【例 18】如图,如果每一个小三角形的面积是1平方厘米,那么四边形ABCD 的面积是多少平方厘米?【解析】法一:正三角形方形格点阵中多边形面积公式:(2N+L-2)x单位正三角形面积,其中N为图形内格点数,L为图形周界上格点数.有N=9,L=4,所以用粗线围成的图形的面积为:(9×2+4-2)×1=20(平方厘米).法二:如下图,我们先数出粗实线内完整的小正三角形有10个,而将不完整的小正三角形分成4部分计算,其中①部分对应的平行四边形面积为4,所以①部分的面积为2,②、③、④部分对应的平行四边形面积分别为2,8,6,所以②、③、④部分的面积分别为1,4,3.所以粗实线内图形的面积为10+2+1+4+3=20(平方厘米).【例 19】把同一个三角形的三条边分别5等分、7等分(如图1,图2),然后适当连接这些等分点,便得到了若干个面积相等的小三角形.已知图1中阴影部分面积是294平方分米,那么图2中阴影部分的面积是______平方分米.【解析】图1中阴影部分占整个三角形面积的1225,图2中阴影部分占整个三角形面积的1649,故图2中阴影部分的面积为294÷12162549=200(平方分米).【例 20】将图中的图形分割成面积相等的三块.【解析】如右图所示.【例 21】如图涂阴影部分的小正六角星形面积是16平方厘米,问:大正六角星形面积是多少平方厘米?【解析】如图,涂阴影部分的小正六角星形可分成12个与三角形PMN全等(能完全重叠地放在一起)的小三角形.而图中的大正六角星形除去小正六角星形后.有6×4=24个与三角形PMN全等的小三角形,所以大正六角星形的面是小正六角星形的3倍,即48平方厘米.【例 22】 (第五届“华杯赛”试题)正六边形ABCDEF 的面积是6平方厘米.M 是AB 中点,N 是CD 中点,P 是EF 中点.问:三角形MNP 的面积是多少平方厘米?SRQAB CD EF NM P P M NF EDCBA【解析】 将正六边形分成六个面积为1平方厘米的正三角形,再取它们各边的中点将每个正三角形分为4个小正三角形.于是正六边形ABCDEF 被分成了24个小正三角形,每一个小正三角形的面积是6240.25÷=(平方厘米),三角形MNP 由9个小正三角形所组成,所以三角形MNP 的面积0.259 2.25=⨯=(平方厘米).【例 23】如果下图中任意相邻的三个点构成的三角形面积都是2平方厘米.那么,三角形ABC 的面积是_____平方厘米.【解析】ABC ABD BCD ACD S S S S ∆∆∆∆=++21221229=⨯+⨯+⨯66()=平方厘米。
四年级奥数讲义:格点与面积

四年级奥数讲义:格点与面积在一张方格图中,每个方格都是一个小正方形,并且大小都相等,我们称为一个面积单位。
例如:右图中带阴影的小方格就是一个面积单位。
借助格点图,我们可以很快的比较或计算图形的面积大小。
典型例题例[1] 下图是用皮筋在钉板上分别围成的正方形、长方形、平行四边形和三角形。
它们的面积分别是多少?· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·(1) (2) (3) (4)分析 题中所给的几个图形都是规则图形,它们的面积可以运用公式求得。
