第三章平面机构的运动分析十字滑块联轴器运动简图
平面机构运动简图及自由计算PPT课件

课堂练习
计算下列图示机构自由度,并判断机构是否有确定的相对运动?
F A B E C D
第37页/共46页
计算下列图示机构自由度,并判断机构是否有确定的相对运动?
F
8
6
D
F
7A
6
1
B
52 E
5 3
C
4
E
2
B
4
C 3
1A
D
(1)
(2)
(1) n=8,PL=10,PH=0 F=3n-2PL-PH=3×8-2×10-0=1 W=F>0,机构具有确定的相对
二、机构运动简图
动画
➢1.机构运动简图
撇开实际机构中与运动无关的因素,用简单的线条和符号 表示构件和运动副,并按一定比例定出各运动副的位置,表示机 构各构件间相对运动关系的图。
➢2.机构示意图
只是定性地表示机构的组成及运动原理,而不用严格按比例 绘制的简图,通常称为机构示意图。
第14页/共46页
机构运动简图
F 8
A2
1
3
6
B
E
4
7D
C
5
动画
动画2
第15页/共46页
♥ 3.绘制机构运动简图的方法和步骤
1)找出各构件和选定视图平面
动画
一般选定的视图平面应与各构件平行,由原动件→从动件及 机架
2)找出联接构件的各运动副
由从原动构件出发沿运动的传递路线,分析各构件间的相对 运动性质;确定活动构件数目、运动副的类型和数目根据运动副 类别画上相应的符号,并逐个注上表示运动副的代号A、B、C、 D….,和构件的数目1、2、3、….
面内运动,则称为该机构为平面机构。(实例1、实例2)
第三章平面机构的运动分析

VP23
方向: CCW, 与ω 相反。 2
相对瞬心位于两绝对瞬心之间,两构件转向相反。
青岛科技大学专用
作者: 潘存云教授
3.求传动比 定义:两构件角速度之比传动比。
ω3 /ω2 = P12P23 / P13P23 推广到一般:
2
P ω2 12
1
ωi /ωj =P1jPij / P1iPij
P ω 233
P13
余下的2个用三心定律求出。
P34
③求瞬心P24的速度 。 VP24=μl(P24P12)·ω2
VP24=μl(P24P14)·ω4
VP24
P23 3
2 ω作者:潘存云教授 2 1
P24 P12
4
ω4
P14
ω4 =ω2· (P24P12)/ P24P14
方向: CW, 与ω 相同。 2
相对瞬心位于两绝对瞬心的同一侧,两构件转向相同
青岛科技大学专用
作者: 潘存云教授
b)高副机构 已知构件2的转速ω2,求构件3的角速度ω3 。
解: 用三心定律求出P23 。
n
求瞬心P23的速度 : VP23=μl(P23P12)·ω2
2
P ω2 12 1
P ω 233
3
P13
VP23=μl(P23P13)·ω3
n
∴ω3=ω2·(P13P23/P12P23)
P25
2 作者:潘存云教授
P12
P46 P 作者:潘存云教授
45
4
P34 3
P23
5
青岛科技大学专用
P14 1
P15
∞ P16
6 P 作者: 5潘6存云教授
四、速度瞬心在机构速度分析中的应用
第三章平面机构的运动分析

第三章平⾯机构的运动分析第三章平⾯机构的运动分析§3-1 研究机构运动分析的⽬的和⽅法1、运动分析:已知各构件尺⼨和原动件的运动规律→从动件各点或构件的(⾓)位移、(⾓)速度、(⾓)加速度。
2、⽬的:判断运动参数是否满⾜设计要求?为后继设计提供原始参数3.⽅法:图解法:形象直观、概念清晰。
精度不⾼?(速度瞬⼼法,相对运动图解法)解析法:⾼的精度。
⼯作量⼤?实验法: §3-2速度瞬⼼法及其在机构速度分析上的应⽤1、速度瞬⼼:两构件作平⾯相对运动时,在任意瞬间总能找到这样的点:两构件的相对运动可以认为是绕该点的转动。
深⼊理解速度瞬⼼:1)两构件上相对速度为零的重合点,即同速点; 2)瞬时具有瞬时性(时刻不同,位置不同);3)两构件的速度瞬⼼位于⽆穷远,表明两构件的⾓速度相同或仅作相对移动;4)相对速度瞬⼼:两构件都是运动的;绝对速度瞬⼼:两构件之⼀是静⽌的(绝对速度为零的点;并⾮接触点的变化速度);2、机构中瞬⼼的数⽬年K :2)1(-=n n K n —— 构件数(包括机架) 3、瞬⼼位置的确定1)直接观察法(定义法,由于直接形成运动副的两构件);2=N P 23设:1k V 3、13)曲柄滑块机构4)直动平底从动件凸轮机构62)14(4=-?=N K5)图⽰机构,已知M点的速度,⽤速度瞬⼼法求出所有的瞬⼼,并求出V C,V D,i12。
解:直接观察:P12、P23、P34;P14=(n_-n).×V M ; P13= P12P23. ×P14P34P24= P12P14×C·P24P34 ; ω1= V M/ P14M ; V B= P14B·ω1ω2=V B/ P12P24 ; V C= P24C·ω2ω1/ω2=( V M/ P14M)/( V B/ P12P24); V D= P24D·ω2速度瞬⼼法⼩结:1)速度瞬⼼法仅⽤于求解速度问题,不能⽤于求解加速度问题。
第三章 平面机构的运动分析

• 因为发生相对运动的任意两构件之 间具有一个瞬心,所以根据排列组合的 原理,如果一个机构是由k个构件所组成, 那么它的瞬心的总数为
k (k 1) N 2
(2—1)
3.瞬心的求法 •
当两构件的相对 运动已知时,瞬心 的位置便可确定, 如图2—2中,已知重 合点A2 和Al 及B2 和Bl 的 相 对 速 度 vA2A1 和 vB2B1的方向,则两速 度矢量的垂线的交 点便是瞬心P12 。在 机构中通常是用如 下各法求得瞬心。
(2)根据三心定理求两构件的瞬心(续)
• vS2=vS3
• • • • • • • • 又假设构件1在S处的重合点为S1 vS2=vS1+ vS2S1,vS3=vS1+ vS3S1 则 vS1+ vS2S1= vS1+ vS3S1 即 vS2S1= vS3S1 但是由图可见vS2S1 ⊥P12S, vS3S1⊥P13S,故 vS2S1≠vS3S1 即 vS2≠vS3 因此点S不可能是构件2与3之间的相对速度瞬心;只有 当它位于直线P12P13上时,该两重合点的速度向量才能 相等,所以瞬心P23必位于P12、P13的连线上。至于P23在 直线P12P13上哪一点,只有当构件2和构件3的运动完全 已知时才可以确定。
第三章 平面机构的运动分析
• §3—1 研究机构运动分析的目的和方法 • 研究平面运动分析的方法有图解法、解 析法和实验法三种。图解法较形象直观, 但作图较繁琐,精度不高,常用的方法 有:速度瞬心法和相对运动图解法等。 •
§3—2 速度瞬心法及其在机构速度分析 上的应用 • 当进行某些构件数目较少的机构(如 凸轮机构、齿轮机构和简单的连杆机构 等)的速度分析时,利用速度瞬心的特性 来求解,则颇为简便清楚。
机械原理第三章 平面机构的运动分析课件

机构的运动分析:根据原动件的已知运动规律,分析 机构上某点的位移、速度和加速度以及构件的角位移、角 速度和角加速度。
二、方法 图解法:形象直观,精度不高。 速度瞬心法 矢量方程图解法
P56
P56
P15所在线
P56P34
∞
P36
∞
∞ P36所在线
§3-3 速度、加速度分析中的矢量方
程图解法 1. 矢量方程图解法的基本原理和方法
机构中运动传递的两种情况: ◆ 不同构件重合点; ◆ 同一构件不同点。
E
4
C
1 2 B (B1,B2,B3) A
3
D
(1) 同一构件上两点间的速度及加速度的关系
大小 绝对 牵连 相对 牵连 哥氏 相对移动
方向
平动(⊥导路) 平动(//导路)
注意:akB2B1与arB2B1始终相互垂直。
2、矢量方程图解法的应用举例 例1. 图示为一摆动式运输机的机构运动简图。设已知
机构各构件尺寸。原动件1的角速度w1为等速回转。求 在图示位置VF、aF、w2、w3、w4、e2、e3、e4。
3. 机构中速度瞬心的数目 n个构件组成的机构(包括机架),其总的瞬心数为: N = n(n-1) / 2
4. 机构中速度瞬心位置的确定 如上所述,机构中每两个构件之间就有一个瞬心,如
果两个构件是通过运动副直接联接在一起的,根据瞬心的 定义其瞬心的位置可以很容易地加以确定。
而一般情况下,两构件的瞬心则需藉助于所谓“三心 定理”来确定。现分别介绍如下。
机械原理第三章平面机构的运动分析

2 判定方法
通过违法副法、副移法或 推动法等方法进行判定。
3 应用举例
四连杆机构中的连杆2-连 杆3副是约束运动副。
运动副的数目
1
最大副数
运动副的最大数目取决于机构的自由度。
2
自由度
机构能够独立运动的最少块数。
3
计算方法
自由度 = 3 * (连杆总数 - 框架连杆数 - 3)
极迹法
极迹法是一种利用链接件的相对位置和运动方向进行运动分析的方法,通过 绘制链接件的轨迹,可以分析机构的运动特性。
机械原理第三章平面机构 的运动分析
平面机构是指运动发生在一个平面内的机械装置。本章将详细介绍平面机构 的分类、链接件运动、运动副的命名和判定以及优化设计等内容。
什么是平面机构
平面机构是运动发生在一个平面内的机械装置。它由链接件和运动副组成,可实现各种不同的运动效果。
平面机构的分类
四连杆机构
由四个连杆组成,可实现平面运动和转动。
由滑块和滑道组成的运动副。
键副
通过键配对组成的运动副。
独立运动副的判定
1 定义
独立运动副是能够单独实 现运动的副。
2 判定方法
通过遮挡法、违法副法或 推动法等方法进行判定。
3 应用举例
曲柄滑块机构中的曲柄-连 杆副是独立运动副。
约束运动副的判定
1 定义
约束运动副是通过其他副 的约束实现运动的副。
自由度的计算
自由度是机构能够独立运动的最少块数。通过计算机构的链接件数目和约束数目,可以确定机构的自由度。
平面机构的静力学分析
静力学分析是研究机构在静力平衡条件下的受力分布和力矩平衡的方法。通过分析机构的关节受力和连杆力矩, 可以确定机构的静力学特性。
2012平面机构的运动分析课件PPT教学课件

理论力学方面知识回顾
点的速度合成定理:动点在某一瞬时的绝对速度等于它在该瞬时的牵连速度与相对 速度的矢量和。
va ve vr
点的加速度合成定理:动点在某瞬时的绝对加速度等于该瞬 时它的牵连加速度、相对加速度与哥氏加速度的矢量和。
aa ae ar ak
其中:ak 2e vr ,为哥氏加速度
证明(P23位于P12、P13的连线上)
反证法: (为方便起见,设1固定不动)
VK2
VK3
K
( K2,K3) 2
3
设:K代表P23,假设K不在P12、P13连线上,
2
根据瞬心定义:
P12
VK2=VK3 (同速点)
1
3 P13
由图可知: VK2VK3
假设不成立(连起码的方向都不可能一致),因而K不是瞬心,只有在连线上才能保 证同方向。
解析法:计算精确、迅速,但需推导公式和编制程序,随着计算机技术的 发展,解析法应用越来越广泛。
矢量方程解析法:运用计算器可以求解; 矩阵法:需要借助计算机才能求解。
实验法:需要专门的仪器设备,成本高,投入大。
第4页/共54页
2 速度瞬心及其在平面机构速度分析中应用
2.1 速度瞬心(Instantaneous Center)的定义
P12 1
P14
2 4
P23 3 P34
定P13:
P34、P14 P13(消去脚注中的4);
P13
P12、P23 P13(消去脚注中的2)。
同理可定P24。
第11页/共54页
2 速度瞬心及其在平面机构速度分析中应用
2.5 速度瞬心法在机构速度分析中的应用
(1)铰链四杆机构 例:各构件尺寸、
平面机构的运动分析习题和答案
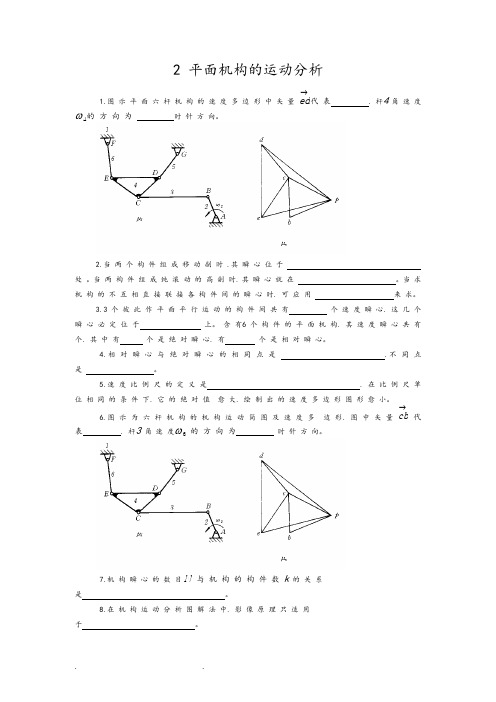
2 平面机构的运动分析1.图 示 平 面 六 杆 机 构 的 速 度 多 边 形 中 矢 量 ed →代 表 . 杆4 角 速 度ω4的 方 向 为时 针 方 向。
2.当 两 个 构 件 组 成 移 动 副 时 .其 瞬 心 位 于 处 。
当 两 构 件 组 成 纯 滚 动 的 高 副 时. 其 瞬 心 就 在 。
当 求 机 构 的 不 互 相 直 接 联 接 各 构 件 间 的 瞬 心 时. 可 应 用 来 求。
3.3 个 彼 此 作 平 面 平 行 运 动 的 构 件 间 共 有 个 速 度 瞬 心. 这 几 个瞬 心 必 定 位 于 上。
含 有6 个 构 件 的 平 面 机 构. 其 速 度 瞬 心 共 有 个. 其 中 有 个 是 绝 对 瞬 心. 有 个 是 相 对 瞬 心。
4.相 对 瞬 心 与 绝 对 瞬 心 的 相 同 点 是 .不 同 点 是 。
5.速 度 比 例 尺 的 定 义 是 . 在 比 例 尺 单 位 相 同 的 条 件 下. 它 的 绝 对 值 愈 大. 绘 制 出 的 速 度 多 边 形 图 形 愈 小。
6.图 示 为 六 杆 机 构 的 机 构 运 动 简 图 及 速 度 多 边 形. 图 中 矢 量 cb →代表 . 杆3 角 速 度ω3 的 方 向 为 时 针 方 向。
7.机 构 瞬 心 的 数 目N 与 机 构 的 构 件 数 k 的 关 系 是 。
8.在 机 构 运 动 分 析 图 解 法 中. 影 像 原 理 只 适 用 于 。
9.当 两 构 件 组 成 转 动 副 时. 其 速 度 瞬 心 在 处; 组 成 移 动 副 时. 其 速 度 瞬 心 在 处; 组 成 兼 有 相 对 滚 动 和 滑 动 的 平 面 高 副 时. 其 速 度 瞬 心 在 上。
10..速 度 瞬 心 是 两 刚 体 上 为 零 的 重 合 点。
11.铰 链 四 杆 机 构 共 有 个 速 度 瞬 心.其 中 个 是 绝 对 瞬 心. 个 是 相 对 瞬 心。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章平面机构的运动分析十字滑块联轴器运动简图第三章平面监管机构的运动分析§3-1 研究机构运动分析最终目标的目的和方法1、运动分析:已知各构件尺寸和原动件的运动规律→从动件各点或构件的(角)位移、(角)速度、(角)加速度。
2、目的:来判断运动参数是否满足设计要求?为后继设计提供原始参数3.方法:图解法:形象直观、概念清晰。
精度不高?(速度瞬心法,相对运动图解法)解析法:高的精度。
工作量大?实验法:§3-2 速度瞬心法及其在机构速度建模上的应用1、速度瞬心:两构件作平面相对运动时,在任意瞬间总能找到这样的点:两构件的相对运动可以认为是绕该点后的转动。
深入概括速度瞬心:1)两构件上相对速度为零的重合点,即同速点; 2)瞬时具有瞬时性(时刻不同,位置不同);3)平行线两构件的速度瞬心位于无穷远,表明两构件的表明角速度相同或仅作相对移动;4)相对速度瞬心:两构件都是运动的;绝对速度瞬心:两构件之一是相对运动的(绝对速度为零的点后;并非接触点的变化速度快);2、咨询机构中瞬心的数目年K:K=n(n-1)n ——构件数(包括机架) 23、瞬心位置的确定1)直接观察法(定义法,由于直接形成运动副的呈现出两构件);2N=P23设:Vk13、1K3)曲柄滑块机构N=4⨯(4-1)=624)直动平底从动件轮轴机构5)图示机构,已知M点的速度,用速度瞬心法求出所有的瞬心,并求出VC,VD,i12。
解:直接观察:P12、P23、P34;P14=(n_-n). × VM ; P13= P12P23. × P14P34P24= P12P14 × C·P24P34 ; ω1= VM/ P14M ; VB= P14B·ω1 ω2=VB/ P12P24 ; VC= P24C·ω2ω1/ω2=( VM/ P14M)/( VB/ P12P24); VD= P24D·ω2速度瞬心法小结:1)速度瞬心法仅用于求解速度问题,不能用于求解加速度环境问题。
2)速度瞬心法用于简单相关机构(构件较少),很方便、几何意义强;3)对于复杂机构,瞬心数目太多,速度瞬心法求解不便(可以只找与帮解题有关的瞬心) 4)瞬心落在图外,解法失效。
5)瞬心多边形求出的实质为三心定理,对超过4个以上构件的机构借助于瞬心多边形求解较方便。
§2—3 用相对运动图解法求机构的速度和一.矢量方程图解法分析方法:用相对运动原理列出构件上点与点之间的矢量方程,然后作图求解矢量方程。
1.矢量方程(高副低代)2。
矢量方程的图解每个矢量方程可以求解两个对顶角二、同一构件上点间的和加速度的关系及求法图示机构,已知:机构各构件的尺寸及φ1、ω1、ε1;求VC、VE、aC、aE、ω2、ε2、ω3、ε3解:1、求速度和角速度VC=VB+VCB大小?lABω ?方向⊥CD ⊥AB ⊥BC → VCVE=VB+VEB=VC+VEC 大小?ω1lAB ?√ ?方向?√ ⊥BE √ ⊥EC → VEω2=VCBV, 方向:顺时针ω3=C,,逆时针 (方向判定采用矢量平移)lCDlBC在速度多边形中,△bce和△BCE相似,图形bce为BC’E的速度影像。
在速度多边形中:P→极点,→VCB 注意:音速影像只能应用于同一并不需要构件上的各点。
小结:1)一个矢量方程最多只能求解两个未知量;2) P称为极点,它代表机构中所有构件上绝对速度为零的点(速度矩形中仅此一点,它可能对应机构中多个点:机架上的点或构件在我看来的绝对瞬心点)3)由P点指向速度多边形中任一点的矢量代表该点的绝对速度大小和方向;4)除P点之外的速度多边形上五点其它四点间的连线,则代表两点间的夹角(注意b→c = VCB) 5)角速度的求法:ω=VCB/LBC 方向判定采用矢量平移;该角速度就是绝对角速度,(随同基点平动+相对转动)6)同一构件上,已知两点的运动速率求第三点时才可以使用速度影象原理。
(机构整体不存在影象) 7)随意在速度矢量图上指定一点,可能在机构图中的每一个构件上按影象原理找到对应的点。
8)多杆机构的运动分析通常按杆组的装设装配顺序进行。
2、求加速度,角加速度aC=aB+aCB或大小+a=a+a+a+a accBBCBCB22ω3lCD ? ω12lAB α1lAB ω2lBC ?方向C→D ⊥CD B→A ⊥AB C→B ⊥BC求aE:=+a+a EBEBEB方向?√ E→B ⊥BE 大小?√ 加速度多边形中:nτ2242aCB=(aCB)2+(aCB)2=(22lCB)+(α2lCB)=lCB2+α2 4242同理:aEB=lEB2+α2 aEC=lEC2+α22ω2lBE α2lBE∴ aCB:aEB:aEC=lCB:lEB:lEC∴ bc:be:ce=BC:EB:EC 即 b"c"e"和BCE相似,称b"c"e"为BCE的加速度影像。
用处:注意:只用于同一构件上。
三、两构件的重合点间的速度和加速度分析已知机构位置,尺寸,ω1等角速求ω3,α3。
解:1、取μc作机构运动简图2、求角速度VB3=VB2+VB3B2大小?ω1lAB ?方向⊥BC ⊥AB ∥BC ∴ω3=VB3,顺时针 lBC3、求角加速度KraB3=aB2+aB3B2+aB3B2 nτkraB+a=a+a+a3B3B2B3B2B3B2方向B→C ⊥BC B→A ⊥BC ∥BC大小2ω3lBC ?ω12lAB 2ω2VB3B2 ?kθ=90°()aB3B2=2ω2VB3B2sinθ ;θ→ω2与VB3B2方向:将VB3B2沿ω2转动90°。
aτ∴ α3=B3,逆时针lBC矢量方程图解法的特点及注意事项 1)合宪性的几何意义强、直观简便,具有普遍的适用含意。
适用两类方程两类可以对绝大多数低副机构作运动分析;2)本方法的工作量大的(尤其分析相关机构整个运动海辛区循环时)、精度低(不绝对,若采用AUTOCAD绘图解的精度很高)。
3)影象法的使用可以大大简化求解过程,但应注意使用条件者(同一构件);例题:图示铰链四杆机构,速度和加速度矢量图已作出,但不完整,请补全,并:. a) 求构件1,2,3,上速度为Vx的X1、X2、X3的位置 b) 构件2上加速度为总和的点Q,标出该点的速度VQ; c) 构件2上速度为零的点E,标出该点的离心力aQ;4)对含有三级杆组的机构需注意,其位置图需描轨迹取交点确定,其运动分析可借助特殊点法求解或结合瞬心法)5)6)速度矢量图随原动件角速度不同按比例变化,可以用此理论变化机架,求解三级机构三级速度统计分析问题。
(但加速度不隐含此原理)同一构件上的两点的速度在其两点的连线上相等;组成移动副两构件重合点处的速度在垂直导路方向的数据传输投影相等;7)某些机构处于特殊位置时飞行速度的速度、角速度多边形可能变成直线、重合点或运动不确定问题,需引起注意;关于科氏加速度ak问题:(2ωV 中,使用拿一个,的方向及有时ak为零)r8)对于某些含有移动副的监管机构,采用加大构件找重合点、杆块对调或导路平移的方法,往往可以使风险问题简化;§2-4 用准则矢量方程解析法解析法作机构的运动分析一.矢量的基本知识 1)矢量的表示方法e -----单位矢量;et -----切矢(切向矢量:反时针转90゜); en -----法矢(法向矢量:反时针转180゜);e =i cosθ+j sinθ (i 、j代表与X、Y轴同向的单位矢量)L=L e =L∠θ=L(i cosθ+ j sinθ)2)单位矢量的运算--------点积运算(1)点积运算:a • b = a b cosθ (标量运算:数量积,与次序无关,θ两矢量间的夹角)(2)e1 • e2 =1 cos(θ2-θ1)-----(理解:投影);(3)e1 • i= cosθ-----(在X轴上的投影) (4)e1 • j= sinθ-----(在Y轴上的投影) (5)e • e =1-----(自身点积为1,用于消去θ)(6)e1 • en =-1-----(反向点积)(7)e1 •e=0(在⊥方向的投影为零,用于消去该矢量)t练习:e1 • e2=cos[(θ2 + 90゜)-θ1]=-sin(θ2 -θ1)te1 • en2= cos[(θ2+ 180゜)-θ1] =-cos(θ2 -θ1)3) 单位矢量的运算--------微分运算(1)对θ的微分:(对θ微分一次转90゜)e′= - i sinθ+ j cosθ= - i cos(90゜+θ)+ jsin(90゜+θ)et″= et′= - i cosθ- j sinθ= - (i cosθ+ jsinθ)= - e = en(2)矢量e对时间t的微分:(e对θ微分,θ再对t微分)de/dt = (de/dθ)(dθ/dt) = ω etde/dt= (de/dθ)(dθ/dt)=ω e d″e/d″t = (de/dt)′=d(ωe)/dt=εe+ ω ett2ttnn(单位矢量的切向加速度+单位矢量的法向加速度)(3)对定长矢量的微分dL/dt = d( Le )/dt= Lωetde/dt= (de/dθ)(dθ/dt)=ω ed″L/d″t = d (L ω e )/dt = L ε e+ L ωtt2ttnen(定长矢量的切向加速度+定长矢量的法向加速度)二、用矢量方程解析法进行机构通过运动剖析(用图示机构方法说明本方法的初学步骤) 1)建立坐标系和封闭矢量图L1 + L2 = L3 + L4大小√ √ √ √ 方向√ ??√2)进行位置分析(1)求解θ3L2 = L3 + L4 -L1方程两端各自点积(消去θ2):L2 •L2 =(整理后,得:A Sinθ3L3 + L4 -L1)•(L3 + L4 -L1)•+ B Cosθ3 + C =01式中:A=2l1l3sinθ ; B=2l3(l1cos-l4) ;1C = l=22 - l=12 - l=32 - l=42+ 2l1l3 cosθ3)进行速度分析由位置方程:l1 e1 + l2e2 = l3 e3 + l4 e 4 (1)对时间进行一次微分;ω1l1 e1 +ω2l2 e2 =ω3l13e3 +ω4l4e4(2)求ω3,用e2 点积上式,消去θ2ttttω3=ω1l1sin(θ1-θ2 )/ l3sin(θ3-θ2 )(3)求ω2,用e3 点积上式,消去θ3ω2=-ω1l1sin(θ1-θ3 )/ l2sin(θ3-θ2 )3)进行加速度分析由速度方程:ω1l1 e1 +ω2l2 e2 =ω3l13e3(1) 将速度方程对时间再进行一次微分解得:tttε1l1 et1 +ω12 l1 en1+ε2l2 et2 +ω22 l2 en2 =ε3l3 et3 +ω32 l3 en3(2)求ε得:ε3=[ω1(3)求ε得:ε2=[-ω122,用23,用e2 点积上式,消去θ2(e2 •e2 = 0;e2 •e2 = -1)t nl1 cos(θ1-θ2)+ ω22 l2 -ω32 l3 cos(θ3-θ2 ) ] / l3 sin(θ3-θ2 )e3 点积上式,消去θ3l1 cos(θ1-θ3) + ω32 l3 -ω22 l2 cos(θ2-θ3)] / l2 sin(θ2-θ1)时间允许情况下再举一个摆动从动件机构的例子,进一步介绍机构右边方程的建立,并验证高副低代。
