对偶原理
对偶原理
分别考察n=3和n=4的情形
平面对偶原则
简单n点(线)形:n=3 简单三点形 ABC 简单三线形 abc
简单n点(线)形:n=4
简单四点形 ABCD 简单四线形 abcd
显然,简单n点(线)形与其顶点(边)的顺序有关
平面对偶原则
(5) 完全n点形:n个点(其中 无三点共线)及其每两点连线 构成的图形. 顶点:n个;
(2) 点 (3) 点
(0 , 0 ,1)
u3 0.
( A, B , 0)
A u1 B u 2 0 .
(3)' 直线
A x1 B x 2 0 .
注:在上述(2), (3)及其对偶中, 为什么不提“原点”, “无穷远 点”等术语? 请在课后尽可能多地练习画出已知图形的对偶图形、写出已知 命题的对偶命题,并从对偶原则出发,重新审视前面所学知识.
注2 对偶原则是一个双射
பைடு நூலகம்
F:
点几何
线几何
因此, 对偶原则可以使得点几何问题与线几何问题相互转化, 可以起到事半功倍的作用.
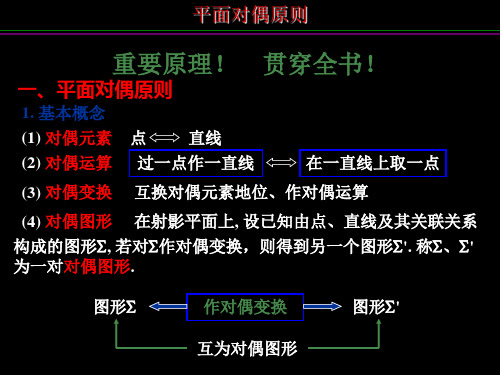
平面对偶原则 二、代数对偶
规定 令坐标相同的点与直线为一对相互对偶的代数对偶元素. 得代数对偶原则 注1 上述规定实际上是RP2与(RP2)*之间的恒同映射. 注2 事实上, 可以有许多种不同的代数对偶映射. 比如将在第四 章学习的配极变换.
平面对偶原则
重要原理! 贯穿全书!
一、平面对偶原则
1. 基本概念 (1) 对偶元素 (2) 对偶运算
(3) 对偶变换 点 直线 过一点作一直线
在一直线上取一点
互换对偶元素地位、作对偶运算
(4) 对偶图形 在射影平面上, 设已知由点、直线及其关联关系 构成的图形, 若对作对偶变换,则得到另一个图形'. 称、' 为一对对偶图形. 图形 作对偶变换 互为对偶图形 图形'
矩阵对偶原理的应用

矩阵对偶原理的应用什么是矩阵对偶原理矩阵对偶原理是线性代数中的一个重要概念。
在数学中,我们可以将一个线性方程组用矩阵来表示,而矩阵对偶原理则是指变换矩阵中的行和列,可以得到与原方程组等价且解唯一的矩阵。
矩阵对偶原理的应用领域矩阵对偶原理在各个领域都有广泛的应用。
下面列举几个常见的应用领域。
1. 图像处理在图像处理中,常常用到矩阵对偶原理来进行图像的变换和处理。
例如,可以将彩色图像转换为灰度图像,通过变换矩阵中的行和列,可以得到一个与原图像等价且灰度唯一的图像。
2. 信号处理矩阵对偶原理在信号处理中也有重要的应用。
例如,可以用矩阵对偶原理来处理音频信号,将一个复杂的音频信号转换为一个简化的信号,从而更方便地进行分析和处理。
3. 机器学习在机器学习领域,矩阵对偶原理也起到了关键的作用。
例如,在支持向量机(SVM)中,可以通过变换矩阵中的行和列来寻找最优的分类超平面,从而实现对数据的分类和预测。
4. 优化问题矩阵对偶原理在优化问题中也有广泛的应用。
例如,在线性规划问题中,可以通过矩阵对偶原理来求解最优解,从而得到一个更有效的优化方案。
矩阵对偶原理的原理解析矩阵对偶原理的原理解析如下:1.对于一个线性方程组,可以用矩阵来表示。
设该方程组为Ax=b,其中A是一个系数矩阵,x是未知数向量,b是常数向量。
2.矩阵对偶原理是指:如果方程组Ax=b有解,则对偶方程组A^T y=0也有解,并且解的形式是唯一的。
3.对偶方程组A^T y=0与原方程组Ax=b是等价的,即它们有相同的解集。
4.对于一个m×n的矩阵A,其秩为r,那么其对偶矩阵A^T的秩也为r。
矩阵对偶原理的示例应用下面通过一个简单的示例来说明矩阵对偶原理的应用。
假设有一个线性方程组2x + 3y = 64x + 5y = 10我们可以将其表示成矩阵的形式:| 2 3 | | x | | 6 || 4 5 | * | y | = | 10 |根据矩阵对偶原理,我们可以变换矩阵中的行和列,得到等价的对偶方程组:2x + 4y = 103x + 5y = 6通过解对偶方程组,我们可以得到唯一的解x=2,y=-1。
对偶原理的应用场景

对偶原理的应用场景1. 逻辑推理与分析•对偶原理是逻辑学中重要的概念,可以应用于逻辑推理和分析中。
通过对偶原理,可以将一个命题的否定转化为其对偶命题的积极描述,从而更容易进行推理和分析。
•在逻辑推理和分析中,对偶原理常用于证明或推导逻辑命题的等价性。
通过对偶原理,可以将一个逻辑公式转化为与之等价的形式,从而更好地理解和解决问题。
•对偶原理的应用场景不仅局限于逻辑推理和分析,在计算机科学、人工智能等领域也得到了广泛的应用。
例如,在编程语言的设计中,对偶原理可以用于设计和优化程序逻辑。
2. 电路设计•对偶原理在电路设计中起着关键作用。
通过对偶原理,可以将一个逻辑门的输入和输出互换,从而实现输入和输出信号的互换,方便电路设计师进行设计和优化。
•例如,在数字电路中,与门和或门是最常用的逻辑门。
通过对偶原理,可以将一个与门的输入和输出互换得到一个或门,从而实现了逻辑门的互换和优化。
•对偶原理还可以应用于多层逻辑门的设计和优化。
通过对偶原理,可以将一个多层逻辑门的输入和输出互换,从而简化电路结构,提高电路的性能和效率。
3. 数据压缩与加密•对偶原理在数据压缩和加密中也有重要的应用。
在数据压缩中,对偶原理可以用于将一个大规模的数据集转化为一个小规模的数据集,从而减少存储空间和传输成本。
•在数据加密中,对偶原理可以用于将一个明文的加密算法转化为一个解密算法,从而实现数据的加密和解密。
•对偶原理的应用使得数据压缩和加密逻辑更加简单和直观,减少了实现的复杂性和成本。
4. 语言翻译与转换•对偶原理在语言翻译和转换中也发挥着重要的作用。
通过对偶原理,可以将一个源语言的表达式转化为目标语言的等价表达式,从而实现不同语言之间的翻译和转换。
•对偶原理的应用使得语言翻译和转换更加简单和高效,减少了翻译过程中可能出现的错误和偏差。
•例如,在编译器的设计中,对偶原理可以用于源代码和目标代码之间的转换,从而实现不同平台上的程序编译和执行。
有关对偶的知识点总结

有关对偶的知识点总结一、对偶的概念1. 对偶的概念起源于古希腊哲学,最早由柏拉图提出。
柏拉图通过对立的概念,强调了现实世界与理念世界之间的关系,认为二者是相互依存、相互对立的。
2. 在逻辑学中,对偶是指针对命题形式P↔Q,当P为真时Q也为真,当P为假时Q也为假。
P与Q的真值相同,称为对偶。
对偶是逻辑推理中的重要概念,有助于推理过程的简化和逻辑等价的判断。
3. 在数学中,对偶的概念也具有重要意义。
在代数学中,对偶空间是指给定向量空间V上的对偶空间V*,表示了V中的线性函数构成的空间。
在几何学中,对偶性可以表示为对偶几何,即在平面几何中,对偶可以对应于点与线的对偶关系。
在范畴论中,对偶由自然变换定义,在范畴理论中具有重要的作用。
4. 在物理学中,对偶的概念也具有重要的意义。
例如,在粒子物理学中,粒子-波对偶原理指出了粒子和波具有双重性质,在不同条件下会呈现出不同的行为。
在相对论和量子力学中,对偶的原理也有着深远的意义。
二、对偶的类型对偶的类型可以从不同的角度进行分类,包括逻辑对偶、数学对偶、物理对偶、文学对偶等等。
下面将针对不同类型的对偶进行详细介绍。
1. 逻辑对偶在逻辑学中,对偶是指一个蕴涵式的两部分,一般都是以“如果……那么……”的形式出现。
逻辑对偶是一个很重要的逻辑等价关系,在命题逻辑和谓词逻辑中都有广泛的应用。
在命题逻辑中,对偶是指P↔Q的真值表达式为真。
换言之,当P为真时Q也为真,当P为假时Q也为假。
例如,“如果今天下雨,那么地面会潮湿”与“如果地面不潮湿,那么今天没有下雨”就是一个对偶关系。
在谓词逻辑中,对偶是指量词的对偶,即∀xP(x)与∃x~P(x)的对偶关系。
其中∀表示全称量词,∃表示存在量词,P(x)表示一个关于x的命题函数。
2. 数学对偶数学中的对偶概念涉及到多个领域,例如代数学、几何学、范畴论等。
在代数学中,对偶空间是一个重要概念。
对于一个向量空间V,它的对偶空间V*是由所有从V到其定义域中的标量域的线性函数组成的。
电路对偶原理

电路对偶原理
电路对偶原理是电路理论中一个重要的概念,它指的是通过互换电路中的电源和电阻的位置,可以得到一个等效的电路。
换句话说,如果一个电路能够满足一定的电路特性,那么交换其中的电源和电阻的位置后,新得到的电路也将满足相同的电路特性。
电路对偶原理的应用非常广泛,例如在逻辑电路设计中,我们可以通过对偶原理来简化电路设计和分析。
以与门和或门为例,它们的逻辑功能是互补的,通过应用对偶原理,我们可以很容易地从一个门的逻辑功能推导出另一个门的逻辑功能。
同时,电路对偶原理也可以用于简化电路分析的过程。
通过交换电源和电阻的位置,我们可以将电源视为电阻,电阻视为电源,进而将电路转化为等效电路,从而简化分析的过程。
需要注意的是,电路对偶原理只适用于一些特定的电路特性和性质。
因此,在应用电路对偶原理时,需要明确电路所具有的特性,并合理选择是否使用对偶原理进行简化或分析。
总而言之,电路对偶原理是一个重要的电路理论概念,通过互换电路中的电源和电阻的位置,可以得到等效的电路。
它在电路设计和分析中有着广泛的应用,可以简化电路设计和分析的过程。
对偶问题的原理和应用

对偶问题的原理和应用1. 对偶问题的概述对偶问题是线性规划领域的一个重要概念,它通过将原始问题转化为对偶形式,从另一个角度来解决问题。
对偶问题在优化领域有着广泛的应用,尤其在线性规划中起到了重要的作用。
2. 对偶问题的原理对偶问题的转化是基于线性规划的标准形式进行的。
假设我们有一个原始线性规划问题:最小化:c T x约束条件:$Ax \\geq b$ 变量约束:$x \\geq 0$其中,c是目标函数的系数向量,A是约束矩阵,b是约束条件的右侧常数向量。
对于原始问题,我们可以定义一个对偶问题。
对偶问题的定义如下:最大化:b T y约束条件:$A^Ty \\leq c$ 变量约束:$y \\geq 0$其中,y是对偶问题的变量向量。
对偶问题的目标函数和约束条件是原始问题的线性组合,并且满足一定的对偶性质。
3. 对偶问题的求解方法对偶问题的求解方法有两种:一种是通过求解原始问题得到对偶问题的最优解,另一种是通过求解对偶问题得到原始问题的最优解。
这两种方法都可以有效地解决线性规划问题。
3.1 原始问题到对偶问题的转换原始问题到对偶问题的转换可以通过拉格朗日对偶性定理来实现。
该定理表明,原始问题的最优解与对偶问题的最优解之间存在一种对偶性关系。
通过求解原始问题的对偶问题,我们可以获得原始问题的最优解。
3.2 对偶问题到原始问题的转换对偶问题到原始问题的转换可以通过对偶定理来实现。
该定理表明,对偶问题的最优解与原始问题的最优解之间存在一种对偶性关系。
通过求解对偶问题,我们可以获得原始问题的最优解。
4. 对偶问题的应用对偶问题在实际应用中具有广泛的应用,下面介绍几个常见的应用场景。
4.1 线性规划问题对偶问题在线性规划中得到了广泛的应用。
通过将原始问题转化为对偶形式,我们可以使用对偶问题的求解方法来求解线性规划问题。
对偶问题可以提供原始问题的最优解,并且可以帮助我们理解原始问题的性质和结构。
4.2 经济学和管理学对偶问题在经济学和管理学中也有重要的应用。
电路对偶原理
电路对偶原理电路对偶原理是电路分析中的一种重要方法,它可以帮助我们在分析电路时,通过对电路中元件的对偶变换,得到等效的电路,从而简化电路分析的过程。
在电路对偶原理中,我们可以通过对电路中的电阻、电容和电感等元件进行对偶变换,得到等效的电路,从而更加方便地进行分析和计算。
首先,我们来看一下电路中电阻的对偶变换。
在电路中,我们可以将电阻对偶变换为导纳,即电阻的对偶是导纳。
对于一个电阻为R的元件,其对偶导纳为1/R。
通过这种对偶变换,我们可以将电路中的电阻网络转换为等效的导纳网络,从而简化电路分析的过程。
接下来,我们再来看一下电路中电容的对偶变换。
在电路中,我们可以将电容对偶变换为电感,即电容的对偶是电感。
对于一个电容为C的元件,其对偶电感为C。
通过这种对偶变换,我们可以将电路中的电容网络转换为等效的电感网络,从而更加方便地进行电路分析。
除了电阻和电容,电路中的电感也可以进行对偶变换。
在电路中,我们可以将电感对偶变换为电容,即电感的对偶是电容。
对于一个电感为L的元件,其对偶电容为L。
通过这种对偶变换,我们可以将电路中的电感网络转换为等效的电容网络,从而简化电路分析的过程。
通过对电路中的电阻、电容和电感等元件进行对偶变换,我们可以得到等效的电路,从而更加方便地进行电路分析。
在实际的电路分析中,电路对偶原理可以帮助我们简化电路分析的过程,提高分析的效率。
因此,掌握电路对偶原理对于电路分析来说是非常重要的。
总的来说,电路对偶原理是电路分析中的一种重要方法,通过对电路中元件的对偶变换,可以得到等效的电路,从而简化电路分析的过程。
通过对电路中的电阻、电容和电感等元件进行对偶变换,可以得到等效的电路,提高分析的效率。
因此,掌握电路对偶原理对于电路分析来说是非常重要的。
希望本文对大家理解电路对偶原理有所帮助。
2.3对偶原理
解:先把第二个约 束改写为
2 x2 x3 2
则其对偶问题为
则定义其对偶问题为
MinW b1 y1 b2 y2 bm ym a11 y1 a21 y 2 am1 ym c1 a y a y a y c 22 2 m2 n 2 12 1 s.t. a y a y a y c 2n 2 mn n n 1n 1 y1 , y2 , , ym 0
这两个式子之间的变换关系称为 “对称形式的对偶关系”。
(2)对称形式的对偶关系的矩阵描述
MaxZ CX
MinW bY
(D) s.t.YA C AX b (L)s.t. Y 0 X 0 (3)怎样从原始问题写出其对偶问题?
按照定义;
记忆法则:
“上、下”交换,“左、右”换位, 不等式变号,“极大”变“极小”
(3)无界性:用反证法,假设对偶问题有最优解Y 则由弱对偶性得 CX Yb ,这与原问题无界矛盾。 (4)可行解是最优解定理。设X 是原问题的任意 可行解,由弱对偶性知道
CX Yb CX
可见 X 是最优解。同理可证 Y 是对偶问题的最优解 (5)强对偶性:设 X 是原问题的最优解,B为最优 基,此时最优值 z CB B 1b ,相应所有的检验数应满 足:
例2-3 写出下面线性规划的对偶问题:
MaxZ 2 x1 x 2 3 x1 4 x 2 15 s.t.5 x1 2 x 2 10 x , x 0 1 2
代数中对偶原理的应用
代数中对偶原理的应用1. 简介对偶原理是代数中一种重要的概念,它在很多领域中得到广泛的应用。
本文将介绍代数中对偶原理的基本概念及其应用。
2. 对偶原理的定义对偶原理是指对于一个代数表达式,可以通过对变量和运算符的取反来得到一个新的表达式,其结果与原表达式相同。
3. 对偶原理的应用举例对偶原理在许多代数学的领域中都有重要的应用,下面将介绍一些常见的应用。
3.1 逻辑代数在逻辑代数中,对偶原理被广泛应用于逻辑运算的简化和化简。
例如,对于逻辑表达式A AND B,根据对偶原理,可以得到其对偶表达式为NOT (NOT A OR NOT B)。
通过应用对偶原理,可以简化复杂的逻辑表达式,使其更易于理解和计算。
3.2 线性代数在线性代数中,对偶原理可以用来解决向量空间的对偶空间问题。
对偶空间是指一个向量空间中的线性函数组成的空间。
利用对偶原理,可以将一个向量空间的问题转化为对应的对偶空间问题,从而简化问题的求解。
3.3 组合代数在组合代数中,对偶原理被应用于多项式的因式分解和化简。
对于一个多项式,可以通过对其系数取反来得到一个新的多项式。
通过应用对偶原理,可以找到多项式的因子以及进行多项式的化简。
3.4 集合代数在集合代数中,对偶原理用于集合的运算和化简。
例如,通过对一个集合的补集进行运算,可以得到与原集合有相同元素的集合。
对偶原理也可以用于集合的交、并等运算的化简。
4. 对偶原理在实际应用中的意义对偶原理在代数中的应用具有以下意义:4.1 简化复杂问题通过对偶原理的应用,可以将一个复杂的代数表达式或问题转化为一个等价但更简单的表达式或问题,从而降低问题的复杂度和求解难度。
4.2 解决对偶问题通过对偶原理的应用,可以将一个代数问题转化为对应的对偶问题,从而利用已知的结论和方法来解决问题。
4.3 推广应用对偶原理的思想可以推广到其他领域中,例如计算科学、控制理论等,从而解决相关问题。
5. 总结对偶原理是代数中一种重要的概念,其应用广泛存在于逻辑代数、线性代数、组合代数和集合代数等领域。
对偶定理实验报告
一、实验目的1. 理解对偶定理的基本概念和原理。
2. 掌握对偶定理的证明方法。
3. 通过实验验证对偶定理的正确性。
4. 培养学生的逻辑思维能力和实际操作能力。
二、实验原理对偶定理是图论中的一个重要定理,它揭示了两个图之间的对偶关系。
对偶定理的表述如下:设G=(V,E)是一个简单无向图,V为顶点集,E为边集。
若G的对偶图G'=(V',E')满足以下条件:(1)G'的顶点集V'与G的边集E一一对应;(2)G'的边集E'与G的顶点集V一一对应;(3)若G中存在一条从顶点u到顶点v的路径,则G'中存在一条从边u到边v的路径,反之亦然。
则称G和G'为对偶图。
三、实验内容1. 选择一个简单无向图G,并画出其图形。
2. 根据对偶定理的原理,构造G的对偶图G'。
3. 证明G和G'为对偶图。
4. 分析对偶图G'的性质。
四、实验步骤1. 选择一个简单无向图G,例如K3,3(三个顶点的完全图)。
2. 画出G的图形,并标注顶点和边。
3. 根据对偶定理的原理,构造G的对偶图G'。
对于G中的每条边,在G'中找到对应的顶点,并将G'中的顶点两两相连,形成G'的边。
4. 证明G和G'为对偶图。
具体步骤如下:(1)证明G'的顶点集V'与G的边集E一一对应。
由于G中有6条边,G'中有6个顶点,且G'的顶点与G的边一一对应,因此满足条件。
(2)证明G'的边集E'与G的顶点集V一一对应。
由于G中有3个顶点,G'中有3条边,且G'的边与G的顶点一一对应,因此满足条件。
(3)证明若G中存在一条从顶点u到顶点v的路径,则G'中存在一条从边u到边v的路径,反之亦然。
对于G中的一条从顶点u到顶点v的路径,将其对应的边u 和边v在G'中相连,即可得到一条从边u到边v的路径。
