2011年高考试题分类汇编数学理科立体几何精华版
2011届高考数学第一轮复习立体几何专题题库11
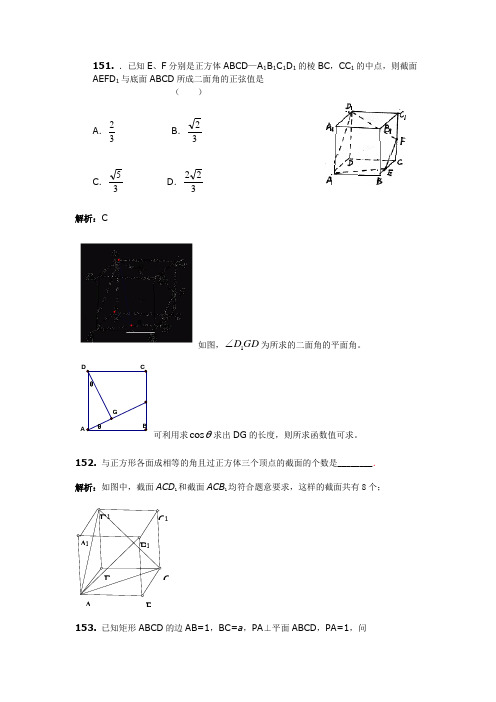
151. .已知E 、F 分别是正方体ABCD —A 1B 1C 1D 1的棱BC ,CC 1的中点,则截面AEFD 1与底面ABCD 所成二面角的正弦值是 ( )A .32B .32C .35 D .322 解析:C如图,1D GD ∠为所求的二面角的平面角。
A可利用求cos θ求出DG 的长度,则所求函数值可求。
152. 与正方形各面成相等的角且过正方体三个顶点的截面的个数是________. 解析:如图中,截面ACD 1和截面ACB 1均符合题意要求,这样的截面共有8个;153. 已知矩形ABCD 的边AB=1,BC=a ,PA ⊥平面ABCD ,PA=1,问AB1BC 边上是否存在点Q ,使得PQ ⊥QD ,并说明理由.解析:连接AQ ,因PA ⊥平面ABCD ,所以PQ ⊥QD AQ ⊥QD ,即以AD 为直经的圆与BC有交点.当AD=BC=a ≥AB=1,即a ≥1时,在BC 边上存在点Q ,使得PQ ⊥QD ;.........5分当0<a<1时,在BC 边上不存在点Q ,使得PQ ⊥QD ...154. 如图,正三棱柱ABC —A 1B 1C 1的底面边长的3,侧棱AA 1=,233D 是CB 延长线上一点,且BD=BC.(Ⅰ)求证:直线BC 1//平面AB 1D ; (Ⅱ)求二面角B 1—AD —B 的大小; (Ⅲ)求三棱锥C 1—ABB 1的体积.(Ⅰ)证明:CD//C 1B 1,又BD=BC=B 1C 1, ∴ 四边形BDB 1C 1是平行四边形, ∴AABC 1//DB 1.又DB 1⊂平面AB 1D ,BC 1⊄平面AB 1D ,∴直线BC 1//平面AB 1D....................5分(Ⅱ)解:过B 作BE ⊥AD 于E ,连结EB 1, ∵B 1B ⊥平面ABD ,∴B 1E ⊥AD ,∴∠B 1EB 是二面角B 1—AD —B 的平面角, ∵BD=BC=AB , ∴E 是AD 的中点,.2321==AC BE 在Rt △B 1BE 中,.32332311===∠BEB B BE B tg ∴∠B 1EB=60°。
2011年全国各地高考数学试题及解答分类汇编大全(11解析几何初步)

2011年全国各地高考数学试题及解答分类汇编大全(11解析几何初步)一、选择题:1. (2011全国大纲卷文)设两圆G、C2都和两坐标轴相切,且都过点(4,1),则两圆心的距离C1C2 ( )(A)4 (B) 4、、2 (C)8 (D) 8 21. 【答案】C【命题意图】本题主要考查圆的方程与两点间的距离公式【解析】由题意知圆心在直线y=x上并且在第一象限,设圆心坐标为(a,a)(a .0),则a —,(a -4)2• (a -1)2,即a2 -10a 17 =0,所以由两点间的距离公式可求出CQ2| =(2[(印+a2)2—4印82] = J2x(100—4如7) =8.. . . . 2 2 . .2. (2011四川文)圆x …4x::;£y =0的圆心坐标是( )(A ) (2 , 3) ( B) ( —2, 3) ( C) (—2,- 3) ( D) (2, - 3)答案:D解析:圆方程化为(x -2)2(y - 3)2=13,圆心(2, —3),选D.3. (2011重庆理)在圆x2y2-2x-6y =0内,过点E (0, 1)的最长弦和最短弦分别是AC和BD,则四边形ABCD的面积为( )A. 5、2 B . 10、2 C. 15'、2 D . 20 24. (2011安徽文)若直线?x y [.过圆X———y二i-的圆心,则a的值为( )(A) -1 (B) 1 (C) 3 (D) -34. B【解析】本题主要考查了圆和直线的方程以及直线和圆的位置关系。
圆的方程可变为X-]亠,因为直线经过圆的圆心,所以' (-1)*亡*£二[.,即a「.【技巧点拨】解题关键是把圆的方程化为标准方程,求出圆心坐标。
5. (2011北京文)已知点A 0,2 , B 2,0。
若点C在函数y = x?的图象上,则使得L ABC的面积为2 的点C的个数为(A) 4 (B)3 (C)2 (D)1KS1 A【解析1:设C(x T^},因为凶62}』(2「0)所以“迪的直线方程为- + ^- = 1即艾卡y—2=0■—■+据二由= 2昙;= 忑fjw忑技=2却丹二忑*由点到育「.r三画:w/S SPx2 +x—2 »十序耳却令恋故选A6. (2011 北京理)设 A 0,0 , B 4,0 , C t 4,4 , D t,4 t R •记 Nt 为平行四边形 ABCD 内 部(不含边界)的整点的个数,其中整点是指横、 纵坐标都是整数的点, 则函数N t 的值域为() (A ) {9,10,11} (B ) {9,10,12}(C ) {9,11,12}(D ) {10,11,12} 在平丙直角坐标系中画出平行四边形其中一■!位于原点,3位于斗正丰轴F 设 ―如“⑶与蛊D 边的交点为站・边的奁点为跌’四辺据内部{不 礙迦跖 碍厢都在疑段上砸,匸4 /.线段人冬上的聲鬲訪个竝j 个.所以3x3"如3x*=12,神嘶妬』.空.功妬4①不是整数时,謂,」却比都不是整点,"0) = 12②为4起型整較时,4,且▼廷均沟整点■,丫(0 = 9甜倉4 + 2型整数时,* 右 ▲申只有A 是整点,.¥(/) = !!「-J j ■ U 谨4n + 3型整数瞅 胡不.竺虽,—12 (以上表谨中n 为宜上面4种情形涵概了 t 的所有可能取值,所以 N(t)的值域为{ 9 , 11, 12 },如图所示,故选 C二、填空题:1. (2011湖北文)过点(一1 — 2)的直线I 被圆x 2 y 2 -2x-2y 10 截得的弦长为、• 2,则直线 I 的斜率为 。
高三数学立体几何历年高考题(2011年-2017的年的).doc
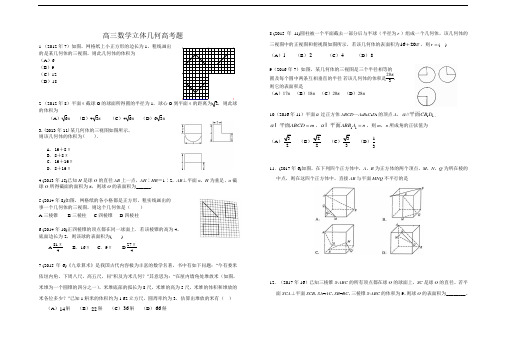
高三数学立体几何高考题1.(2012年7)如图,网格纸上小正方形的边长为1,粗线画出 的是某几何体的三视图,则此几何体的体积为 (A )6 (B )9 (C )12 (D )182.(2012年8)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为(A )6π (B )43π (C )46π (D )63π3.(2013年11)某几何体的三视图如图所示, 则该几何体的体积为( ).A .16+8πB .8+8πC .16+16πD .8+16π4.(2013年15)已知H 是球O 的直径AB 上一点,AH ∶HB =1∶2,AB ⊥平面α,H 为垂足,α截球O 所得截面的面积为π,则球O 的表面积为______.5.(2014年8)如图,网格纸的各小格都是正方形,粗实线画出的 事一个几何体的三视图,则这个几何体是( ) A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱6.(2014年10)正四棱锥的顶点都在同一球面上.若该棱锥的高为4, 底面边长为2,则该球的表面积为( )A.81π4 B .16π C .9π D.27π47.(2015年6)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问”积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,米堆的体积和堆放的米各位多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米有( ) (A )14斛 (B )22斛 (C )36斛 (D )66斛8.(2015年11)圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为1620π+,则r =( ) (A )1 (B )2 (C )4 (D )89(2016年7)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3,则它的表面积是(A )17π (B )18π (C )20π (D )28π10(2016年11)平面α过正方体ABCD —A 1B 1C 1D 1的顶点A ,11//CB D α平面,ABCD m α=I 平面,11ABB A n α=I 平面,则m ,n 所成角的正弦值为(A )32 (B )22 (C )33 (D )1311.(2017年6)如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直接AB 与平面MNQ 不平行的是12.(2017年16)已知三棱锥S-ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径。
【数学文】2011届高考模拟题(课标)分类汇编:立体几何
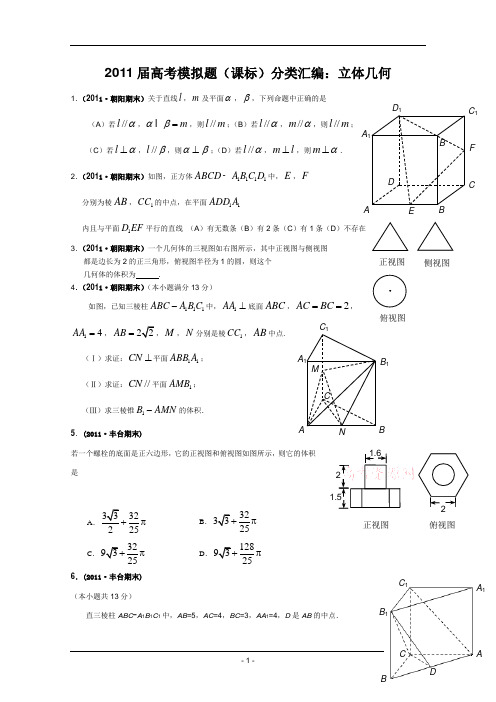
正视图俯视图2011届高考模拟题(课标)分类汇编:立体几何1.(2011·朝阳期末)关于直线l ,m 及平面α,β,下列命题中正确的是(A )若//l α,m αβ=I ,则//l m ;(B )若//l α,//m α,则//l m ; (C )若lα⊥,//l β,则αβ⊥;(D )若//l α,m l ⊥,则m α⊥.2.(2011·朝阳期末)如图,正方体1111ABCD A B C D -中,E ,F分别为棱AB ,1CC 的中点,在平面11ADD A内且与平面1D EF 平行的直线 (A )有无数条(B )有2条(C )有1条(D )不存在 3.(2011·朝阳期末)一个几何体的三视图如右图所示,其中正视图与侧视图都是边长为2的正三角形,俯视图半径为1的圆,则这个 几何体的体积为 .4.(2011·朝阳期末)(本小题满分13分)如图,已知三棱柱111ABC A B C -中,1AA ⊥底面ABC ,2AC BC ==,14AA =,AB =M ,N 分别是棱1CC ,AB 中点.(Ⅰ)求证:CN⊥平面11ABB A ;(Ⅱ)求证://CN 平面1AMB ;(Ⅲ)求三棱锥1B AMN -的体积.5.(2011·丰台期末)若一个螺栓的底面是正六边形,它的正视图和俯视图如图所示,则它的体积是A.32225+π B.3225π C.3225π D.12825π 6.(2011·丰台期末) (本小题共13分)直三棱柱ABC -A 1B 1C 1中,AB =5,AC =4,BC =3,AA 1=4,D 是AB 的中点.ABCDA 1BC 1D 1EF正视图 侧视图俯视图AB CA 1B 1C 1M NA 1B 1C 1(Ⅰ)求证:AC ⊥B 1C ; (Ⅱ)求证:AC 1∥平面B 1CD ; 7.(2011·东莞期末) 把边长为1的正方形ABCD 沿对角线BD 折起,使得平面⊥ABD 平面CBD ,形成三棱锥ABD C -的正视图与俯视图如右图所示,则侧视图的面积为A.21B.22 C.42D.418.(2011·东莞期末)(本小题满分14分)在三棱锥ABC S -中,ABC ∆是边长为32的正三角形,平面SAC ⊥平面ABC ,2==SC SA ,M 、N 分别为AB 、SB 的中点。
2012年-2021年(10年)全国高考数学真题分类汇编 立体几何客观题(精解精析版)

2012-2021十年全国高考数学真题分类汇编立体几何客观题(精解精析版)一、选择题1.(2021年高考全国乙卷理科)在正方体1111ABCD A B C D -中,P 为11B D 的中点,则直线PB 与1AD 所成的角为()A .π2B .π3C .π4D .π6【答案】D解析:如图,连接11,,BC PC PB ,因为1AD ∥1BC ,所以1PBC ∠或其补角为直线PB 与1AD 所成的角,因为1BB ⊥平面1111D C B A ,所以11BB PC ⊥,又111PC B D ⊥,1111BB B D B ⋂=,所以1PC ⊥平面1P B B ,所以1PC PB ⊥,设正方体棱长为2,则111112BC PC D B ===1111sin 2PC PBC BC ∠==,所以16PBC π∠=.故选:D2.(2021年高考全国甲卷理科)在一个正方体中,过顶点A 的三条棱的中点分别为E ,F ,G .该正方体截去三棱锥A EFG -后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是()()A.B.C.D.【答案】D解析:由题意及正视图可得几何体的直观图,如图所示,所以其侧视图为故选:D3.(2021年高考全国甲卷理科)已如A.B.C是半径为1的球O的球面上的三个点,且,1AC BC AC BC⊥==,则三棱锥O ABC-的体积为()A.212B.312C.24D.34【答案】A解析:,1AC BC AC BC ⊥== ,ABC ∴ 为等腰直角三角形,AB ∴=,则ABC 外接圆的半径为22,又球的半径为1,设O 到平面ABC 的距离为d ,则22d =,所以1112211332212O ABC ABC V S d -=⋅=⨯⨯⨯⨯=.故选:A .【点睛】关键点睛:本题考查球内几何体问题,解题的关键是正确利用截面圆半径、球半径、球心到截面距离的勾股关系求解.4.(2020年高考数学课标Ⅰ卷理科)已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC 的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为()A .64πB .48πC .36πD .32π【答案】A【解析】设圆1O 半径为r ,球的半径为R ,依题意,得24,2r r ππ=∴=, ABC 为等边三角形,由正弦定理可得2sin 60AB r =︒=,1OO AB ∴==,根据球的截面性质1OO ⊥平面ABC ,11,4OO O A R OA ∴⊥====,∴球O 的表面积2464S R ππ==.故选:A【点睛】本题考查球的表面积,应用球的截面性质是解题的关键,考查计算求解能力,属于基础题.5.(2020年高考数学课标Ⅰ卷理科)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为()()A .514-B .512-C .514+D .512+【答案】C【解析】如图,设,CD a PE b ==,则22224a PO PE OEb =-=-,由题意212PO ab =,即22142a b ab-=,化简得24()210b b a a -⋅-=,解得154b a =(负值舍去).故选:C .【点晴】本题主要考查正四棱锥的概念及其有关计算,考查学生的数学计算能力,是一道容易题.6.(2020年高考数学课标Ⅱ卷理科)已知△ABC 是面积为934的等边三角形,且其顶点都在球O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为()A .3B .32C .1D .32【答案】C解析:设球O 的半径为R ,则2416R ππ=,解得:2R =.设ABC 外接圆半径为r ,边长为a ,ABC 是面积为934的等边三角形,21393224a ∴⨯=,解得:3a =,22229933434a r a ∴=-=-=,∴球心O 到平面ABC 的距离22431d R r =-=-=.故选:C .【点睛】本题考查球的相关问题的求解,涉及到球的表面积公式和三角形面积公式的应用;解题关键是明确球的性质,即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.7.(2020年高考数学课标Ⅱ卷理科)如图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应的点为M ,在俯视图中对应的点为N ,则该端点在侧视图中对应的点为()()A .EB .FC .GD .H【答案】A解析:根据三视图,画出多面体立体图形,14D D 上的点在正视图中都对应点M ,直线34B C 上的点在俯视图中对应的点为N,∴在正视图中对应M ,在俯视图中对应N 的点是4D ,线段34D D ,上的所有点在侧试图中都对应E ,∴点4D 在侧视图中对应的点为E .故选:A【点睛】本题主要考查了根据三视图判断点的位置,解题关键是掌握三视图的基础知识和根据三视图能还原立体图形的方法,考查了分析能力和空间想象,属于基础题.8.(2020年高考数学课标Ⅲ卷理科)下图为某几何体的三视图,则该几何体的表面积是()()A .6+4B .C .D .【答案】C解析:根据三视图特征,在正方体中截取出符合题意的立体图形根据立体图形可得:12222ABC ADC CDB S S S ===⨯⨯=△△△根据勾股定理可得:AB AD DB ===∴ADB △是边长为的等边三角形根据三角形面积公式可得:211sin 60222ADB S AB AD =⋅⋅︒=⋅=△∴该几何体的表面积是:632=⨯++.故选:C .【点睛】本题主要考查了根据三视图求立体图形的表面积问题,解题关键是掌握根据三视图画出立体图形,考查了分析能力和空间想象能力,属于基础题.9.(2019年高考数学课标Ⅲ卷理科)如图,点N 为正方形ABCD 的中心,ECD △为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则()A .BM EN =,且直线,BM EN 是相交直线B .BM EN ≠,且直线,BM EN 是相交直线C .BM EN =,且直线,BM EN 是异面直线D .BM EN ≠,且直线,BM EN 是异面直线【答案】B 【解析】取DC 中点E ,如图连接辅助线,在BDE △中,N 为BD 中点,M 为DE 中点,所以//MN BE ,所以BM ,EN 共面相交,选项C ,D 错误. 平面CDE ⊥平面ABCD ,EF CD ⊥,EF ∴⊥平面ABCD ,又DC CD ⊥,∴DC ⊥平面DCE ,从而EF FN ⊥,BC MC ⊥.所以MCB △与EFN△均为直角三角形.不妨设正方形边长为2,易知3,1MC EF NF ===,所以22(3)27BM =+=,22(3)12EN =+=,BM EN ∴≠,故选B .【点评】本题比较具有综合性,既考查了面面垂直、线面垂直等线面关系,还考查了三角形中的一些计算问题,是一个比较经典的题目.10.(2019年高考数学课标全国Ⅱ卷理科)设α、β为两个平面,则αβ//的充要条件是()()A .α内有无数条直线与β平行B .α内有两条相交直线与β平行C .α,β平行于同一条直线D .α,β垂直于同一平面【答案】B【解析】由面面平行的判定定理知:α内两条相交直线都与β平行是αβ//的充分条件,由面面平行性质定理知,若αβ//,则α内任意一条直线都与β平行,所以α内两条相交直线都与β平行是αβ//的必要条件,故选B .【点评】本题考查了空间两个平面的判定与性质及充要条件,渗透直观想象、逻辑推理素养,利用面面平行的判定定理与性质定理即可作出判断.面面平行的判定问题要紧扣面面平行判定定理,最容易犯的错误为定理记不住,凭主观臆断,如:“若,,//a b a b αβ⊂⊂,则//αβ”此类的错误.11.(2019年高考数学课标全国Ⅰ卷理科)已知三棱锥P ABC -的四个顶点在球O 的球面上,PA PB PC ==,ABC △是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,90CEF ∠=︒,则球O 的体积为()A .B .C .D 【答案】D解析:三棱锥P ABC -为正三棱锥,取AC 中点M ,连接,PM BM ,则,AC PM AB BM ⊥⊥,PM BM M = ,可得AC ⊥平面PBM ,从而AC PB ⊥,又//,PB EF EF CE ⊥,可得PB CE ⊥,又AC CE C = ,所以PB ⊥平面PAC ,从而,PB PA PB PC ⊥⊥,从而正三棱锥P ABC -的三条侧棱,,PA PB PC 两两垂直,且PA PB PC ===,,PA PB PC 为棱的正方体,正方体的体对角线即为球O 的直径,即22R R ==,所以球O 的体积为343V R π==.12.(2018年高考数学课标Ⅲ卷(理))设,,,A B C D 是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为,则三棱锥D ABC -体积的最大值为()A.B.C.D.【答案】B解析:设ABC △的边长为a,则21sin 6062ABC S a a =︒=⇒=△,此时ABC △外接圆的半径为112sin 60232a r =⋅=⨯︒,故球心O 到面ABC2==,故点D 到面ABC 的最大距离为26R +=,此时11633D ABC ABC D ABC V S d --=⋅=⨯=△,故选B.点评:本题主要考查三棱锥的外接球,考查了勾股定理,三角形的面积公式和三棱锥的体积公式,判断出当DM ⊥平面ABC 时,三棱锥D ABC -体积最大很关键,由M 为三角形ABC 的重心,计算得到23BM BE ==,再由勾股定理得到OM ,进而得到结果,属于较难题型.13.(2018年高考数学课标Ⅲ卷(理))中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫,凹进部分叫卯眼,图中木构件右边的小长方体是榫头,若如图摆放的木构件与某一带卯眼的木构件咬合成长方体.则咬合时带卯眼的木构件的俯视图可以是()()【答案】A解析:依题意,结合三视图的知识易知,带卯眼的木构件的俯视图可以是A 图.14.(2018年高考数学课标Ⅱ卷(理))在长方体1111ABCD A B C D -中,1AB BC ==,1AA =线1AD 与1DB 所成角的余弦值为()A .15B .56C .55D .22【答案】C解析:以D 为坐标原点,1,,DA DC DD DA 为,,x y z 轴建立空间直角坐标系,则11(0,0,0),(1,0,0),(1,1,3),(0,0,3)D A B D ,所以11(1,0,3),(1,1,3)AD DB =-=因为111111135cos ,5||||25AD DB AD DB AD DB ⋅-+<>===⋅⨯所以异面直线1AD 与1DB 所成角的余弦值为55,故选C .15.(2018年高考数学课标卷Ⅰ(理))已知正方体的校长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面而积的最大值为()A .334B .233C .324D .32【答案】A【解析一】根据题意,平面α与正方体对角线垂直,记正方体为111ABCD A B C D -不妨设平面α与1AC 垂直,且交于点M .平面ABD 与平面11B D C 与1AC 分别交于,P Q .正方体中心为O ,则容易证明当M 从A 运动到P 时,截面为三角形且周长逐渐增大:当M 从P 运动到Q 时,截面为六边形且周长不变;当M 从Q 运动到1C 时,截面为三角形且周长还渐减小。
2011年数学高考分类汇编解答题(文)03——立体几何

03 立体几何1. (天津文)17.(本小题满分13分)如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,045ADC ∠=,1AD AC ==,O 为AC 中点,PO ⊥平面ABCD ,2PO =,M 为PD 中点.(Ⅰ)证明:PB //平面ACM ; (Ⅱ)证明:AD ⊥平面PAC ;(Ⅲ)求直线AM 与平面ABCD 所成角的正切值.【解析】(17)本小题主要考查直线与平面平行、直线与平面垂直、直线与平面所成的角等基础知识,考查空间想象能力、运算能力和推理论证能力.满分13分。
(Ⅰ)证明:连接BD ,MO ,在平行四边形ABCD中,因为O 为AC 的中点,所以O 为BD 的中点,又M 为PD 的中点,所以PB//MO 。
因为PB ⊄平面ACM ,MO ⊂平面ACM ,所以PB//平面ACM 。
(Ⅱ)证明:因为45ADC ∠=︒,且AD=AC=1,所以90DAC ∠=︒,即AD AC ⊥,又PO ⊥平面ABCD,AD ⊂平面ABCD ,所以,PO AD AC PO O ⊥⋂=而,所以AD ⊥平面PAC 。
(Ⅲ)解:取DO 中点N ,连接MN ,AN ,因为M 为PD 的中点,所以MN//PO ,且11,2MN PO PO ==⊥由平面ABCD ,得MN ⊥平面ABCD ,所以MAN ∠是直线AM 与平面ABCD 所成的角,在Rt DAO ∆中,11,2AD AO ==,所以5DO =,从而152AN DO ==, 在45,tan 54MN Rt ANM MAN AN ∆∠===中即直线AM 与平面ABCD 所成角的452。
(北京文)17.(本小题共14分) 如图,在四面体PABC 中,PC ⊥AB ,PA ⊥BC ,点D,E,F,G 分别是棱AP,AC,BC,PB 的中点. (Ⅰ)求证:DE ∥平面BCP ; (Ⅱ)求证:四边形DEFG 为矩形; (Ⅲ)是否存在点Q ,到四面体PABC 六条棱的中点的距离相等?说明理由。
2011届高考数学第一轮复习立体几何专题题库39
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
2011年高考数学试题分类解析(八)——立体几何
2 1 年 的高考 已经 落下帷 幕 ,综 观全 国各地 的数 学试 卷 , 平面所成 的角 、二面角 的计算问题. 0 1 不难 发现对立 体几何 内容 的考 查 ,都严 格遵 循 《 普通 高 中数 学 课程标准 ( 实验) ( 《 学大纲》 》或 教 )和 O 1 1 年高考考试说 明》
的概念 ;会用几何 法和 向量法解决 异面直 线所成 的角 、直线 与
思维.分析 和研 究 2 1 高考 立体几何试题 的命题特 点、热点 0 1年 容的复 习教 学具有很 好的导向性和前瞻性. 关键 词 :立体几何 ;试题特点 ;命题 意 图;复 习建议
题 型和创 新试题 的命题意 图和解 法 ,对做好 新一轮 立体 几何 内 平行 、垂直 的有 关性质 与判定 ;会 用几何 法和 向量 方法证 明有
好的指导性和前瞻性.
一
大纲 课程全 国文理卷 、四川文理 卷 、浙 江文理卷 、辽宁文 理卷
、
分 析 特 点
等 . 有个别试 卷以 “ t 题两 大题 ”的形 式出现 ,分值 为 2 也 -l , 9 分 ,占总分 比为 1 . 45 %,例如 江苏理科卷. 考查难度一般 为中等 ,解答题所处位置基本上 在前 3道题 。
N - 8 01 O7 2 1 —
J u n lo ie e Mah mais E u ain o r a fChn s te t d c t c o
21 0 1年
第 7 8期 —
摘要 :2 1 年 高考数 学已经落下帷幕 ,与 2 1 01 0 0年相 比,各 识别 三视 图所表示 的空 间几何体 ;理解三视 图和直观 图的联系 ,
三视 图 ;球 、柱 、锥 、台 的表 面积和体 积计算 ;空间位 置 离等.解答题 的考法 与往 年类似 ,仍然注重在一个具体 的立体几 关 系的判断与证明 ;空间角 、距离的计 算.
【2022高考必备】2012-2021十年全国高考数学真题分类汇编 立体几何大题(原卷版)
2012-2021十年全国高考数学真题分类汇编 立体几何大题(原卷版)1.(2021年高考全国甲卷理科)已知直三棱柱111ABC A B C -中,侧面11AA B B 为正方形,2AB BC ==,E ,F 分别为AC 和1CC 中点,D 为棱11A B 上地点.11BF A B ⊥(1)证明:BF DE ⊥。
(2)当1B D 为何值时,面11BB C C 与面DFE 所成地二面角地正弦值最小?2.(2021年高考全国乙卷理科)如图,四棱锥P ABCD -地底面是矩形,PD ⊥底面ABCD ,1PD DC ==,M 为BC 地中点,且PB AM ⊥.(1)求BC 。
(2)求二面角A PM B --地正弦值.3.(2020年高考数学课标Ⅰ卷理科)如图,D 为圆锥地顶点,O 是圆锥底面地圆心,AE 为底面直径,AE AD =.ABC 是底面地内接正三角形,P 为DO 上一点,PO =.的(1)证明:PA ⊥平面PBC 。
(2)求二面角B PC E --地余弦值.4.(2020年高考数学课标Ⅱ卷理科)如图,已知三棱柱ABC -A 1B 1C 1地底面是正三角形,侧面BB 1C 1C 是矩形,M ,N 分别为BC ,B 1C 1地中点,P 为AM 上一点,过B 1C 1和P 地平面交AB 于E ,交AC 于F .(1)证明:AA 1∥MN ,且平面A 1AMN ⊥EB 1C 1F 。
(2)设O 为△A 1B 1C 1地中心,若AO ∥平面EB 1C 1F ,且AO =AB ,求直线B 1E 与平面A 1AMN 所成角地正弦值.5.(2020年高考数学课标Ⅲ卷理科)如图,在长方体1111ABCD A B C D -中,点,E F 分别在棱11,DD BB 上,且12DE ED =,12BF FB =.(1)证明:点1C 平面AEF 内。
(2)若2AB =,1AD =,13AA =,求二面角1A EF A --地正弦值.6.(2019年高考数学课标Ⅲ卷理科)图1是由矩形ADEB ,Rt △ABC 和菱形BFGC 组成地一个平面图形,其中AB =1,BE =BF =2,∠FBC =60°,将其沿AB ,BC 折起使得BE 与BF 重合,连结DG ,如图2.(1)证明:图2中地A ,C ,G ,D 四点共面,且平面ABC ⊥平面BCGE 。
2011年高考数学—立体几何(解答题)
1、江苏16、如图,在四棱锥ABCD P -中,平面PAD ⊥平面ABCD , AB=AD ,∠BAD=60°,E 、F 分别是AP 、AD 的中点 求证:(1)直线EF ‖平面PCD ; (2)平面BEF ⊥平面PAD2、上海文20、(14分)已知1111ABCD A BC D -是底面边长为1的正四棱柱,高12AA =。
求: ⑴ 异面直线BD 与1AB 所成的角的大小(结果用反三角函数表示);⑵ 四面体11AB D C 的体积。
3、全国文20.(本小题满分l2分)(注意:在试题卷上作答无效.........) 如图,四棱锥S ABCD -中, AB CD ,BC CD ⊥,侧面SAB 为等边三角形,2,1AB BC CD SD ====.(I )证明:SD ⊥平面SAB ;(II )求AB 与平面SBC 所成的角的大小。
4、北京文17.(本小题共14分)如图,在四面体PABC 中,PC⊥AB,PA⊥BC,点D,E,F,G 分别是棱AP,AC,BC,PB 的中点. (Ⅰ)求证:DE∥平面BCP ; (Ⅱ)求证:四边形DEFG 为矩形;(Ⅲ)是否存在点Q ,到四面体PABC 六条棱的中点的距离相等?说明理由.ADBD 11B5、四川文19.(本小题共l2分)如图,在直三棱柱ABC -A 1B 1C 1中,∠BAC =90°,AB =AC =AA 1=1,延长A 1C 1至点P ,使C 1P =A 1C 1,连接AP 交棱CC 1于D .(Ⅰ)求证:PB 1∥平面BDA 1;(Ⅱ)求二面角A -A 1D -B 的平面角的余弦值;6、天津文17.(本小题满分13分)如图,在四棱锥P ABCD -中,底面ABCD 为 平行四边形,045ADC ∠=,1AD AC ==,O 为AC 中点,PO ⊥平面ABCD , 2PO =,M 为PD 中点.(Ⅰ)证明:PB //平面ACM ; (Ⅱ)证明:AD ⊥平面PAC ;(Ⅲ)求直线AM 与平面ABCD 所成角的正切值.7、安徽文(19)(本小题满分13分)如图,ABEDFC 为多面体,平面ABED 与平面ACFD 垂直,点O 在线段AD 上,1OA =,2OD =,△OAB,△OAC,△ODE,△ODF 都是正三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年高考试题数学(理科)立体几何一、选择题:1. (2011年高考山东卷理科11)下图是长和宽分别相等的两个矩形.给定下列三个命题: ①存在三棱柱,其正(主)视图、俯视图如下图;②存在四棱柱,其正(主)视图、俯视图如 下图;③存在圆柱,其正(主)视图、俯视图如下图.其中真命题的个数是 (A)3 (B)2 (C)1 (D)0 【答案】A【解析】对于①,可以是放倒的三棱柱;容易判断②③可以.2.(2011年高考浙江卷理科3)若某几何体的三视图如图所示,则这个几何体的直观图可以是【答案】D【解析】由正视图可排除A 、B 选项;由俯视图可排除C 选项. 3.(2011年高考浙江卷理科4)下列命题中错误的是(A )如果平面αβ⊥平面,那么平面α内一定存在直线平行于平面β (B )如果平面不垂直于平面β,那么平面α内一定不存在直线垂直于平面β (C )如果平面αγ⊥平面,平面βγ⊥平面,=l αβ⋂,那么l γ⊥平面 (D )如果平面αβ⊥平面,那么平面α内所有直线都垂直于平面β 【答案】D【解析】若面⊥α面β,在面α内与面的交线不相交的直线平行平面β,故A 正确;B 中若α内存在直线垂直平面β,则βα⊥,与题没矛盾,所以B 正确;由面⊥面的性质知选项C 正确.4.(2011年高考安徽卷理科6)一个空间几何体得三视图如图所示,则该几何体的表面积为(A ) 48 (B)32+817 (C) 48+817 (D) 80 【答案】C【命题意图】本题考查三视图的识别以及空间多面体表面积的求法.【解析】由三视图可知几何体是底面是等腰梯形的直棱柱.底面等腰梯形的上底为2,下底为4,高为4,。
故S 2+4=⨯4⨯2+4⨯2+4⨯4+4⨯17⨯22=48+817表 【解题指导】:三视图还原很关键,每一个数据都要标注准确。
5.(2011年高考辽宁卷理科8)如图,四棱锥S-ABCD 的底面为正方形,SD ⊥底面ABCD ,则下列结论中不正确...的是( )(A) AC ⊥SB (B) AB ∥平面SCD(C) SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 (D)AB 与SC 所成的角等于DC 与SA 所成的角 答案: D解析:对于A:因为SD ⊥平面ABCD ,所以DS ⊥AC.因为四边形ABCD 为正方形,所以AC ⊥BD ,故AC ⊥平面ABD,因为SB ⊂平面ABD,所以AC ⊥SB ,正确.对于B :因为AB//CD,所以AB//平面SCD.对于C:设AC BD O =I .因为AC ⊥平面ABD ,所以SA 和SC 在平面SBD 内的射影为SO ,则∠ASO 和∠CSO 就是SA 与平面SBD 所成的角和SC 与平面SBD 所成的角,二者相等,正确.故选D.6.(2011年高考辽宁卷理科12)已知球的直径SC=4,A,B 是该球球面上的两点,AB=3,︒=∠=∠30B SC ASC ,则棱锥S-ABC 的体积为()(A )33 (B )32 (C )3 (D )17.(2011年高考全国新课标卷理科6)在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的侧视图可以为8.(2011年高考江西卷理科8)已知1α,2α,3α是三个相互平行的平面.平面1α,2α之间3 32正视图侧视图俯视图图1的距离为1d ,平面2α,3α之间的距离为2d .直线l 与1α,2α,3α分别相交于1P ,2P ,3P ,那么“12P P =23P P ”是“12d d =”的A.充分不必要条件B.必要不充分条件 C .充分必要条件 D .既不充分也不必要条件 【答案】C【解析】过点1P 作平面2α的垂线g,交平面2α,3α分别于点A 、B 两点,由两个平面平行的性质可知2P A ∥3P B ,所以121122PP d PP d =,故选C. 9. (2011年高考湖南卷理科3)设图1是某几何体的三视图,则该几何体的体积为 A.1229+π B. 1829+πC. 429+πD. 1836+π 答案:B解析:由三视图可以还原为一个底面为边长是3的正方形, 高为2的长方体以及一个直径为3的球组成的简单几何体, 其体积等于=⨯⨯+⋅⋅233)23(343π1829+π。
故选B 评析:本小题主要考查球与长方体组成的简单几何体的三视图 以及几何体的体积计算.10.(2011年高考广东卷理科7)如图l —3.某几何体的正视图(主视图)是平行四边形,侧视图(左视图)和俯视图都是矩形,则该几何体的体积为( )A.3B.93C.123D.183【解析】B.由题得三视图对应的直观图是如图所示的直四棱柱,.ABCD EA 平面⊥HGFE DCBA 31233931232=⨯-⨯=•=h S V ABCD 平行四边形。
所以选B11.(2011年高考陕西卷理科5)某几何体的三视图如图所示,则它的体积是 (A )283π-(B )83π- (C )82π-(D )23π【答案】A【解析】:由三视图可知该几何体为立方体与圆锥, 立方体棱长为2,圆锥底面半径为1、高为2, 所以体积为3212123π-⋅⨯⨯=283π-故选A 12.(2011年高考重庆卷理科9)高为24的四棱锥S-ABCD 的底面是边长为1的正方形,点S 、A 、B 、C 、D 均在半径为1的同一球面上,则底面ABCD 的中心与顶点S 之间的距离为 (A 2 (B 2 (C )1 (D 2解析:选C. 设底面中心为G ,球心为O ,则易得2AG =,于是22OG =,用一个与ABCD 所在平面距离等于24的平面去截球,S 便为其中一个交点,此平面的中心设为H ,则222244OH =-=,故22227148SH ⎛=-= ⎝⎭,故22272184SG SH HG ⎛⎫=+=+= ⎪ ⎪⎝⎭ 13.(2011年高考四川卷理科3)1l ,2l ,3l 是空间三条不同的直线,则下列命题正确的是( )(A)12l l ⊥,23l l ⊥13l l ⇒P (B )12l l ⊥,23l l P ⇒13l l ⊥(C)233l l l P P ⇒ 1l ,2l ,3l 共面 (D )1l ,2l ,3l 共点⇒1l ,2l ,3l 共面 答案:B解析:A 答案还有异面或者相交,C 、D 不一定14.(2011年高考全国卷理科6)已知直二面角l αβ--,点,A AC l α∈⊥,C 为垂足,,,B BD l D β∈⊥为垂足.若AB=2,AC=BD=1,则D 到平面ABC 的距离等于(A)3(D) 1【思路点拨】本题关键是找出或做出点D 到平面ABC 的距离DE ,根据面面垂直的性质不难证明AC ⊥平面β,进而β⊥平面平面ABC,所以过D 作DE BC ⊥于E ,则DE 就是要求的距离。
【答案】C【解析】如图,作DE BC ⊥于E ,由l αβ--为直二面角,AC l ⊥,得AC ⊥平面β,进而AC DE ⊥,又BC DE ⊥,BC AC C =I ,于是DE ⊥平面ABC 。
故DE 为D 到平面ABC 的距离。
在Rt BCD ∆中,利用等面积法得BD DC DE BC ⨯===15. (2011年高考全国卷理科11)已知平面α截一球面得圆M ,过圆心M 且与α成060,二面角的平面β截该球面得圆N ,若该球的半径为4,圆M 的面积为4π,则圆N 的面积为(A)7π (B)9π (c)11π (D)13π 【答案】D【解析】:由圆M 的面积为4π得2MA =,2224212OM =-=OM ⇒=030Rt ONM OMN ∠=V 中,12ON OM ∴===13N S π∴=圆故选D16.(2011年高考北京卷理科7)某四面体的三视图如图所示,该四面体四个面的面积中,最大的是A .8B .62C .10D .82【答案】C 二、填空题:1.(2011年高考辽宁卷理科15)一个正三棱柱的侧棱长和底面边长相等,体积为32,它的三视图中的俯视图如右图所示,左视图是一个矩形,则这个矩形的面积是____________.答案: 3解析:设正三棱柱的侧棱长和底面边长为a 2323a ⋅=,解得a=2,正三棱柱的左视图与底面一边垂直的截面大小相同,故该矩形的面积是322232⋅=2. (2011年高考全国新课标卷理科15)已知矩形ABCD 的顶点都在半径为4的球O 的球面上,且6,23AB BC ==则棱锥O ABCD -的体积为 。
答案: 38解析:如图,连接矩形对角线的交点1O 和球心O ,则,3221,341===AC A O AC ,四棱锥的高为o 1Do2)32(4221=-=OO ,所以,体积为38232631=⨯⨯⨯=V 点评:本题考查多面体和旋转体的有关概念和性质以及体积的计算。
关键是确定棱锥高的大小,正确运用公式求解。
3.(2011年高考天津卷理科10)一个几何体的三视图如图所示(单位:m ),则这个几何体 的体积为__________ 3m 【答案】6π+【解析】由题意知,该几何体为一个组合体,其下面是一个长方体(长为3m,宽为2m, 高为1m),上面有一个圆锥(底面半径为1,高为3),所以其体积为1321363V V ππ+=⨯⨯+⨯=+长方体圆锥.4. (2011年高考四川卷理科15)如图,半径为R 的球O 中有一内接圆柱.当圆柱的侧面积最大时,求球的表面积与该圆柱的侧面积之差是 .答案:22R π解析:22222max 224()S r R r r R r S ππ=⋅-=-⇒侧侧时,22222222R r R r r r R =-⇒=⇒=,则222422R R R πππ-=5.(2011年高考全国卷理科16)己知点E 、F 分别在正方体ABCD -A 1B 2C 3D 4的棱BB 1 、CC 1上,且B 1E =2EB, CF=2FC 1,则面AEF 与面ABC 所成的二面角的正切值等于 .【思路点拨】本题应先找出两平面的交线,进而找出或做出二面角的平面角是解决此问题的关键,延长EF 必与BC 相交,交点为P ,则AP 为面AEF 与面ABC 的交线.【答案】23【精讲精析】延长EF 交BC 的延长线于P ,则AP 为面AEF 与面ABC 的交线,因为90CAP ∠=o,所以FCA ∠为面AEF 与面ABC 所成的二面角的平面角。
223tan 32FC FCA CA ∠===6.(2011年高考福建卷理科12)三棱锥P-ABC 中,PA ⊥底面ABC ,PA=3,底面ABC 是边长为2的正三角形,则三棱锥P-ABC 的体积等于______。
【答案】37.(2011年高考上海卷理科7)若圆锥的侧面积为2π,底面积为π,则该圆锥的体积为 。
