人教A高中数学必修二2.3.4 平面与平面垂直的性质[王丽]【市一等奖】优质课
六盘水市2017年度初,高级中学数学录像优质课评选评审结果
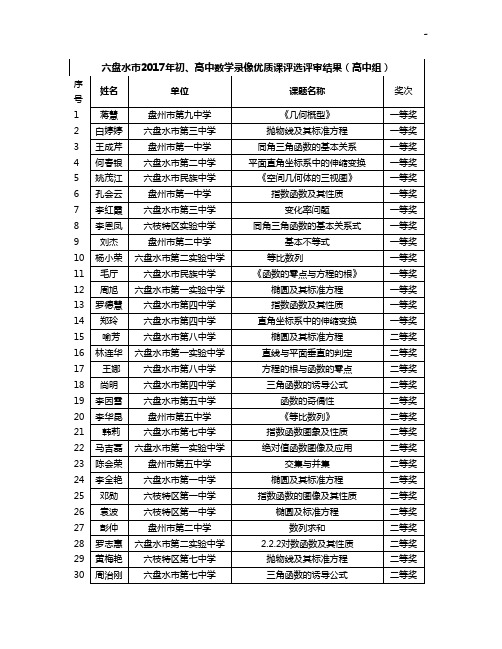
序号
姓名
单位
课题名称
奖次
1
蒋慧
盘州市第九中学
《几何概型》
一等奖
2
白婷婷
六盘水市第三中学
抛物线及其标准方程
一等奖
3
王成芹
盘州市第一中学
同角三角函数的基本关系
一等奖
4
何春银
六盘水市第二中学
平面直角坐标系中的伸缩变换
一等奖
5
姚茂江
六盘水市民族中学
椭圆及其标准方程
二等奖
25
邓勋
六枝特区第一中学
指数函数的图像及其性质
二等奖
26
袁波
六枝特区第一中学
椭圆及标准方程
二等奖
27
彭仲
盘州市第二中学
数列求和
二等奖
28
罗志惠
六盘水市第二实验中学
2.2.2对数函数及其性质
二等奖
29
黄梅艳
六枝特区第七中学
抛物线及其标准方程
二等奖
30
周治刚
六盘水市第七中学
三角函数的诱导公式
二等奖
31
李洪敦
六盘水市第二中学
平面几何与立体几何之新解行列式在高中的应用
三等奖
32
祖杏
六盘水市第二中学
随机事件的概率
三等奖
33
蒋娇娇
盘州市第十二中学
直线与平面的垂直判定
三等奖
34
许丹
六盘水市第一中学
算法的概念
三等奖
35
李弢
盘州市第六中学
直线与圆的位置关系
三等奖
36
苏教版七下数学第七章——平面图形的认识(2)PPT省名师优质课赛课获奖课件市赛课一等奖课件

A. 1cm, 2cm, 3cm B. 2cm, 3cm , 4cm
C. 2cm, 3cm , 5cm D. 2cm, 3cm , 6cm
分析:鉴别3条线段能否构成三角形, 只要计算两条较短线段旳和,看其是 否不小于最长旳线段即可.
1.有两根长度分别为5cm和8cm旳木棒.
A. 锐角三角形 B. 钝角三角形
C.直角三角形 D. 以上都可能
◆已知,如图,AD、AE分别是 △ABC旳中线和高,BC=6cm,AE=4cm. ①求△ABC、△ABD旳面积.
◆已知,如图,AD、AE分别是 △ABC旳中线和高,BC=6cm,AE=4cm.
②由此你能得出什么结论?
动脑筋
已知,如图,△ABC中,
认识三角形(二)
A
B
.C
D
在三角形中,从一种顶点向它旳对边所在直线
作垂线,顶点和垂足之间旳线段叫做三角形旳
高线,简称三角形旳高.
线段AD⊥BC,垂足为D,我们把线段AD叫做
△ABC旳高.
2.下图中, 在△ABC中画出边AC上
旳高,画法正确旳是( C )
(A)
(B)
(C)
(D)
·
锐角三角形旳三条高交于形内一点
①与长度为2cm旳木棒一起能摆成三角 形吗?为何?
②与长度为13cm旳木棒呢?
③若能摆成一种三角形,则第三根木棒 旳长度xcm应在什么范围内?
8-3<5<x<x<138+5
2.有长度分别为2cm、3cm、4cm和5cm 旳4根小木棒,任取其中3根,能搭出
不同旳三角形旳种数是( C )
A.1种
B. 2种
三角形内角和(一)
高一物理必修2总复习课件省名师优质课赛课获奖课件市赛课一等奖课件

a b
c d
如图一辆质量为500kg旳汽车静止在一座半径为50m旳 圆弧形拱桥顶部.(取g=10m/s2) (1)此时汽车对圆弧形拱桥旳压力是多大?
(2)汽车以多大速度经过拱 桥旳顶部时,汽车对圆弧形拱 桥旳压力恰好为零?
离
心
运 动
离心运动:0 ≤F合<Fn
与
向 心 匀速圆周运动:F合= Fn
运
弹 簧
x1+x=l
链
接
问
题
功
率
功率旳定义式:
P=
W
t
功率旳另一体现式: P Fv cos
※ F:所指旳力
瞬时速度:瞬时功率
※ v:物体旳运动速度
平均速度:平均功率
※ :F、 v旳夹角,若F、v同向,则有:
P=Fv
汽车开启问题
(1)汽车以额定功率起动
P一定,P=F v
Ff一定
F -Ff=ma
a
做 功
做
功 一、静摩擦力做功(74)
专
题 静摩擦力能够对物体做负功(例6) 2 : 静摩擦力能够对物体做正功(例7) 摩 擦 静摩擦力能够对物体不做功(例8)
力
做 功
做
功 二、滑动摩擦力做功(74)
专
题 滑动摩擦力能够对物体做负功(例9) 2 : 滑动摩擦力能够对物体做正功(例10) 摩 擦 滑动摩擦力能够对物体不做功(例11)
1 :
功以及经过量度值求功旳问题。
变
力 一、微元法 做 功 求变力做功一般是采用微元法,即:将运动过程无限分小,
每一小段就可看成是恒力做功,然后把各小段恒力做旳功
求出来,再求出代数和,即为变力所做旳功。实质就是将
高一数学必修4221向量加法运算及其几何意义市公开课一等奖课件名师大赛获奖课件

人教A版 ·必修4
路漫漫其修远兮 吾将上下而求索
第二章
平面向量
第二章
2.2 平面向量的线性运算
第二章
2.2.1 向量加法运算及其几何意义
课前自主预习
温故知新 1.向量的有关概念: (1)所谓向量是___既__有__大__小__又__有__方__向_____的量,其三要素 是___始_点__,__大__小__,__方__向____. (2)相等向量应满足__大__小__相__等__,__方__向__相__同____,所谓共线 向量是指__方__向__相__同__或__相__反_____的向量.
[答案] ①⑤
4.设O为正六边形ABCDEF的中心,在如图所标出的向量 中,
(1)找出与F→E共线的向量; (2)找出与F→E相等的向量; (3)向量O→A与B→C相等吗?
[解析]
(1)O→A,B→C
→ (2)BC
(3)不相等,方向不同.
新课引入 飞机从北京到上海,再从上海到香港,两次位移的结果与 飞机直接从北京到香港的位移显然是相同的,物理中把后一次 位移称为前两次位移的和,类似地,我们可以获得向量的加法 运算,类比实数的减法运算,还可以得到向量的减法运算.
化简P→B+O→P+B→O=________. [答案] 0 [解析] P→B+O→P+B→O=(O→P+P→B)+B→O=O→B+B→O=0.
课堂典例讲练
命题方向 1 向量的三角形法则 如下图中(1)、(2)所示,试作出向量 a 与 b 的和.
[分析] 依据向量加法的三角形法则,在平面上任取一点 O,以O为起点作出一个向量等于a,再以终点为起点作下一 个向量等于b,可得出a+b.
若a、b反向,则||O→A|-|A→B||=|O→B|,即 ||a|-|b||=|a+b|,如图(3) 综上知,||a|-|b||≤|a+b|≤|a|+|b|.
高中数学单元教学设计思路与策略探析

2021年12期46扫描二维码,获取更多本文相关信息教学研究引 言所谓单元教学设计,主要是基于教材本身,对其中存在较大联系的内容展开全面分析,并完成重组和合并。
教师应基于整体教学理念的引导,对现有的要素予以全面规划,促使教学设计变得更为合理。
然而从实际情况来看,很多教师并未认识到单元教学设计的重要性,造成了教学质量下降。
因此,相关问题理应得到广泛重视。
一、单元教学设计的思路从当前情况来看,对于高中数学教学来说,单元教学设计的类型主要包括三个方面。
其一,基于数学概念本身进行教学设计。
诸如《普通高中课程标准》提出的四个主题分别是函数、几何代数、统计概率及数学建模。
从结构层面来看,这些都属于大型单元,教师可以基于单元中的某些小知识点作为主题,对教学活动予以设计。
其二,基于数学方法进行教学设计。
此类设计模式往往需要跨越多个章节,如数形结合部分,就会包括函数、方程及导数的知识内容,因此可以将多个内容全部联系在一起,并完成整合[1]。
其三,基于数学核心思想展开教学设计。
在高中数学知识内容中,核心素养主要包括六个方面,分别是直观想象、数学抽象、数学建模、数据分析、逻辑推理和数学运算。
在进行教学设计工作时,教师应合理筛选其中的内容,并制订针对性策略。
由于整体实施难度较高,教师需要花费较多的时间进行准备。
二、单元教学设计存在的问题(一)对教学设计缺乏认知现如今,很多高中教师对单元教学设计的理解存在高中数学单元教学设计思路与策略探析郭 茂(甘肃省庆阳市镇原中学,甘肃庆阳 744500)摘 要:在高中数学教学中,一些教师出现了设计缺失及目标偏离的情况,造成教学活动的开展受到了诸多影响。
因此,教师便需要对此有所重视,结合早期教学工作的不足,及时优化设计思路,促使学生更好地完成学习任务。
本文主要描述了单元设计的思路,探讨了单元设计教学存在的问题,并对具体方法发表一些个人的观点和看法。
关键词:高中教育;数学单元教学;设计思路;教学策略中图分类号:G 427 文献标识码:A 文章编号:2095-9192(2021)12-0046-02一定偏差,认为学生只要掌握知识即可,因此一直在采用传统的教学模式,导致整个课堂缺乏足够的吸引力,无法将学生潜在的积极性激发出来。
优质课 精品教案 (省一等奖)《二次函数与一元二次方程(第1课时)》公开课教案

22.2 二次函数与一元二次方程教学时间课题22.2 二次函数与一元二次方程课型新授课教 学 目 标知 识 和能 力 通过探索,使学生理解二次函数与一元二次方程、一元二次不等式之间的联系。
过 程 和方 法 使学生能够运用二次函数及其图象、性质解决实际问题,提高学生用数学的意识。
情 感 态 度 价值观进一步培养学生综合解题能力,渗透数形结合思想。
教学重点 使学生理解二次函数与一元二次方程、一元二次不等式之间的联系,能够运用二次函数及其图象、性质去解决实际问题教学难点 进一步培养学生综合解题能力,渗透数形结合的思想 教学准备教师多媒体课件学生“五个一〞课 堂 教 学 程 序 设 计设计意图一、引言 在现实生活中,我们常常会遇到与二次函数及其图象有关的问题,如拱桥跨度、拱高计算等,利用二次函数的有关知识研究和解决这些问题,具有很现实的意义。
本节课,请同学们共同研究,尝试解决以下几个问题。
二、探索问题问题1:某公园要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子,上面的A 处安装一个喷头向外喷水。
连喷头在内,柱高为。
水流在各个方向上沿形状相同的抛物线路径落下,如图(1)所示。
根据设计图纸:如图(2)中所示直角坐标系中,水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是y =-x 2+2x +45。
(1)喷出的水流距水平面的最大高度是多少?(2)如果不计其他的因素,那么水池至少为多少时,才能使喷出的水流都落在水池内?教学要点1.让学生讨论、交流,如何将文学语言转化为数学语言,得出问题(1)就是求函数y =-x 2+2x +45最大值,问题(2)就是求如图(2)B 点的横坐标;2.学生解答,教师巡视指导; 3.让一两位同学板演,教师讲评。
问题2:一个涵洞成抛物线形,它的截面如图(3)所示,现测得,当水面宽AB =时,涵洞顶点与水面的距离为。
这时,离开水面处,涵洞宽ED 是多少?是否会超过1m?教学要点1.教师分析:根据条件,要求ED 的宽,只要求出FD 的长度。
青岛市信息技术与学科融合优质课获奖名单.doc
董秀红
走进机器人世界
城阳区惜福镇小学
范玉明
用数对确定位置
青岛市即墨区通济山东小学
郭雪丽
盛开的紫荆花
城阳区田村小学
赫卫丽
RevisionofModule5
城阳区赵红路小学
胡妮军
《海底两万里》整本书阅读汇报课
胶州市向阳小学
纪子成
《百分数》
山东省平度实验小学
姜国英
小数的意义
胶州市第四实验小学
圆
青岛西海岸新区江山路第一小学
秦加彬
《长方体和正方体的认识》
胶州市中云振华教育总校(集团)
秦江楠
《分数的初步认识》
青岛市即墨区第一实验小学
秦淑青
时分的认识
青岛四流中路第三小学
宋亚男
精彩ppt——ppt复习课
崂山区华楼海尔希望小学
苏贞秀
《练习二》
莱西市实验小学
孙丽雪
五彩缤纷新世界
青岛西海岸新区黄岛小学
孙宇
认识新朋友
城阳区第二实验小学
万初伟
红绿灯,安全伴我行
城阳区流亭小学
王佳
洋娃娃和小熊跳舞
平度经济开发区小学
王莉
《6.变色龙》
城阳区流亭街道天河小学
王盼盼
古意新曲:国学儿歌开心学堂----《啄木鸟》
平度市白沙河街道麻兰小学
王培
体感游戏我来做---视频侦测巧应用
红岛中心小学
王钦明
Are you sad?
姜青蔚
《圆的面积》
崂山区华楼海尔希望小学
姜艳
《乡下孩子》
城阳区春阳路小学
矫苏玲
我的魔法师爸爸--对称
人教版高中数学选修2-1《圆锥曲线起始课》教学设计(特级教师一等奖)
人教版高中数学选修2-1《圆锥曲线起始课》教学设计(特级教师一等奖)“圆锥曲线起始课”教学设计一.【教学内容解析】1.圆锥曲线是平面解析几何的重要组成部分,也可以说是核心内容.它是继研究了以直线和圆为代表的简单图形之后,用平面几何的方法无法研究的较为复杂的图形.圆锥曲线能充分体现解析几何研究方法.2.圆锥曲线是体现数形结合思想的重要载体.圆锥曲线的研究不是采用逻辑推理的形式,而是运用代数的方法.即以代数为工具解决几何问题,用代数的语言来描述几何图形,把几何问题转化为代数问题,实施代数运算,求解代数问题,再将代数解转化为几何结论,这一过程体现了从形到数的数形结合的思想.3.圆锥曲线是二次曲线非常重要的数学模型,同时它的几何性质在日常生活,社会生产以及其他科学中都有着重要而广泛的应用,宇宙天地的运动,光学仪器,建筑学等等.因此圆锥曲线的研究对学生进一步理解数学模型的意义,树立观念都非常有价值.本节课的内容是选自XXX《高中数学选修2-1》第三章知识的引言部分,属于策略性和介绍性为主的起始课.二.【教学目标设置】1.知识与技能目标本节课的主线为圆锥曲线的发展史,从中参插各种情景.通过用平面对圆锥面的不同的截法,产生三种不同的圆锥曲线,经历概念的形成过程,从整体上认识三种圆锥曲线的内在关系,通过具体情境,从中抽象出椭圆、双曲线、抛物线模型的过程,理解它们的定义(主要是椭圆).2.过程与方法目标初步了圆锥曲线研究的内容;通过动手试验、互相讨论等环节,使学生形成自主研究以及相互协作的团队精神;通过对具体情形的分析,归纳得出一般规律,让学生具备初步归纳能力;借助实物模型,通过整体观察、直观感知,使学生形成积极主动、勇于探索的研究方式,完善思维结构,体会解析几何的研究方法.3.情感、态度与价值观目标通过以圆锥曲线的发展史为主线,设立多种情景引入方式,让学生激发研究圆锥曲线的兴趣,能够自主研究、自我探索,形成注重实践、热爱科学、勇于创新的情感、态度与价值观.4.重难点重点:圆锥曲线的发展史及定义,椭圆的定义.难点:用Dandelin双球发现椭圆的定义,通过椭圆的定义类比双曲线定义.三.【学生学情阐发】1.这节课的授课工具是高中二年级的学生,他们有较好的研究惯,有一定的口头和书面表达的能力.在知识层面上,高一阶段已研究了立体几何空间旋转体中的圆锥,学生具有一定的空间想象能力,学生还研究相识析几何中的直线和圆,具有一定的用解析方法处理题目的能力.在方法的层面,学生在高1、高二年级的研究中基本把握了数形结合的脑筋与类比与转化脑筋.2.学生在研究过程中,也可能会遇到诸多艰巨:从空间的圆锥截出平面图形的转化题目,特别是通过Dandelin双球发觉椭圆的定义;还有理解椭圆,双曲线定义时点的轨迹及静态题目.四.【讲授策略阐发】1.整个课堂的主线是圆锥曲线的发展史,使学生产生兴趣,并以润物细无声的方法安排各种情景,让学生很自然进入研究圆锥曲线的研究,为后面采用解析的方法研究埋下了伏笔.2.由于是起始课,因此多采取直观的演示幻灯片、动画、实验和使用实物模型,直观感知、操1作确认,避免过分抽象.思争吵证、度量计算等手腕在后续课程中再接纳.3.在处理椭圆定义的环节,创造条件让学生亲自动手画出椭圆,并安排了一系列情节引导学生在操作过程中注意细节,鼓励学生通过动手实验、独立思考、相互讨论等手段得出结论,鼓励学生表达自己的见解.4.从多种具体情形出发,引导学生归纳出一般规律,培养学生的归纳总结能力.采用模型和软件,使学生的想法能够即时得到实现,所想即所见,快速形成正确认知,提高教学实效性.五.【教学过程】环节1.课题引入教学过程和师生活动通过生活中的一系列图片让学生在认知的曲线.意图,理念与备注1.从实践生活出发,直观感知各种圆锥曲线的存在,使学生在脑筋中产生各类曲线的开端印象,为下一步的数学抽象做准备.2.特别是“愤怒的小鸟”这个抛物线段片让学生马上产生兴趣,积极参与发现与探索,加深直观印象.师生活动:让学生踊跃讲话.2.复和准备1.温圆锥的形成2.由圆锥的形成过程引入圆锥面注:这里还要提出圆锥的轴截面是等腰三角形,并引入顶角的一半,为后面轴截面和旋转轴所成的角的大小截出分歧的曲线留下知识.师生活动:教师引导学生回忆知识,尽量让学生口述其过程。
2018年青岛信息技术与学科融合优质课
常见的天气系统—锋面系统
青岛市崂山区第一中学
江汶
助盲神器的设计与实现
胶州市第二中学
希望
《通过神经系统的调节》
山东省青岛市第六中学
金姗姗
M2B5Writing英文求职信写作
山东省青岛第二中学
高磊
《常用轨迹方程的求法》
山东省青岛第三十九中学
柳艳
细胞呼吸——果酒制作
山东省青岛第一中学
管延琴
空间几何体的三视图
刘瑞静
拼布
青岛市实验初级中学
张聪Hale Waihona Puke 制作植物细胞模型与观察质壁分离
青岛第四十二中学
高玉香
《Unit5Doyouhaveasoccerball?SectionA(1a-2d)》
平度市实验中学
孙丰收
第三章变量之间的关系第一节用表格表示的变量间关系
山东省青岛第二中学分校
张玉波
冷光条彩灯装饰
山东省青岛第一中学
周苑
姜青蔚
《圆的面积》
崂山区华楼海尔希望小学
姜艳
《乡下孩子》
城阳区春阳路小学
矫苏玲
我的魔法师爸爸--对称
莱西市院上镇武备小学
李宝杰
想象
城阳区惜福镇牟家小学
李翠
喜庆吉祥的民间美术—剪纸
平度市南京路小学
李华芳
《认识水》
青岛实验学校
李吉祥
建筑艺术的美
平度市旧店镇旧店小学
李雯雯
二十世纪的艺术大师—马蒂斯
莱西市月湖小学
崂山区第六中学
刘国栋
《用表格表示的变量间关系》
莱西市第三中学
李燕
景物描写习作训练
莱西市第三中学
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
练习3.如图,已知PA⊥平面ABC,平面PAB⊥平面PBC, 求证:BC⊥平面PAB.
面面垂直
性质定理 判定定理
线面垂直
1、平面与平面垂直的性质定理:两个平面 垂直,则一个平面内垂直于交线的直线与另 一个平面垂直。 2、证明线面垂直的两种方法: 线线垂直→线面垂直;面面垂直→线面垂直 3、线线、线面、面面之间的关系的转化是解 决空间图形问题的重要思想方法。
[思考题目] 4.如图所示,在平行四边形 ABCD 中,已知 AD=2AB=2a, BD= 3a,AC∩BD= E, 将其沿对角线 BD 折成直二面角.
b
a
即可。而题中条件有 又 a , b a , ,因此,
a //ቤተ መጻሕፍቲ ባይዱ 必有b .
即直线a与平面平行
规律方法:
面面垂直的性质是作平面的垂线的重要的
方法,因此,在有面面垂直的条件下,若
需要平面的垂线,要首先考虑面面垂直的 性质。
Ⅲ.知识应用
练习1:判断正误。
求证:(1)AB⊥平面 BCD; (2)平面 ACD⊥平面 ABD.
证明:(1)在△ABD 中,AB=a, AD=2a,BD= 3a, ∴AB2+BD2=AD2, ∴∠ABD=90° ,∴AB⊥BD. 又∵平面 ABD⊥平面 BCD, 平面 ABD∩平面 BCD=BD,AB⊂平面 ABD, ∴AB⊥平面 BCD.
证明:过点A作AE⊥PB,垂足为E, ∵平面PAB⊥平面PBC, 平面PAB∩平面PBC=PB, ∴AE⊥平面PBC.
P
∵BC 平面PBC,∴AE⊥BC
∵PA⊥平面ABC,BC 平面ABC,
A
C
∴PA⊥BC.
故BC⊥平面PAB
B
解题反思
1、面面垂直的性质定理给我们提供了一 种证明线面垂直的方法 2、本题充分地体现了面面垂直与 线面 垂直之间的相互转化关系。
面面垂直
线面垂直
线面、面面之间的关系的转化是解决空间图 形问题的重要思想方法。
应用举例
例2:已知平面 , , , 直线a满足a , a ,判断直线a与平面的位置关系。 解:在内作垂直于与 分析:
交线的直线b 要证a // , 只需在平
b 面内作一直线b // a a a // b
人教A版2003课标版
2.3.4平面与平面垂直的性质定理
主讲教师: 王丽 工作单位:巨鹿中学
巨鹿中学 王丽
1、平面与平面垂直的定义
两个平面相交,如果它们所成的二面角是 直二面角,就说这两个平面互相垂直。
2、平面与平面垂直的判定定理
一个平面过另一个平面的垂 线,则这两个平面垂直。
符号表示:
该命题正确吗?
已知: , CD,AB , AB CD 求证:AB 证明: 在内过点B作BE CD 分析:要证明直线垂 直于平面,须证明直 则ABE是二面角
线垂直于平面内两条 - CD 的平面角 相交直线,而题中条 件已有一条,故可过 该直线作辅助线 . AB BE
已知平面α⊥平面β,α∩β=l下列命题
(1)平面α内的任意一条直线必垂直于平面β ( ×)
(2)垂直于交线l的直线必垂直于平面β ( ×)
(3)过平面α内任意一点作交线的垂线,则此 垂线必垂直于平面β(× )
练习2:如图,AB是⊙O的直径,C是圆周上不 同于A,B的任意一点,平面PAC⊥平面ABC, (1)判断BC与平面PAC的位置关系,并证明。 (2)判断平面PBC与平面PAC的位置关系。
b
b b
新知探究一:黑板所在的平面与地面所在的平面垂直,
你能否在黑板上画出一条直线与地面垂直?
新知探究二:平面与平面垂直的性质
如图,在长方体ABCD—A1B1C1D1中,
平面AC 平面D1C 平面AC 平面D1C DC
D1D 平面D1C
A1
(2)∵折叠前四边形 ABCD 是平行四边形,且 AB⊥BD, ∴CD⊥BD.∵ AB⊥平面 BCD,∴AB⊥CD. 又∵AB∩BD=B,∴CD⊥平面 ABD. 又∵CD⊂平面 ACD,∴平面 ACD⊥平面 ABD.
D A B D1 B1 C1
D1D CD
D1D 平面AC
C
平面与平面垂直的性质定理
两个平面垂直,则一个平面内垂 文字语言 直于交线的直线与另一个平面垂直.
图形语言
D
C
B
A
符号语言
, AB , AB CD CD,
AB
平面与平面垂直的性质定理
E
B
D
A
C
AB CD
CD , BE , BE CD B AB
平面与平面垂直的性质定理
CD, AB , AB CD ,
AB
简记: 线面垂直 面面垂直
性质定理 判定定理
D A
C
B
定理的作用:证明线面垂直。
