全等三角形sas练习题
12.2 三角形全等的判定(SAS)

①先在池塘旁取一个能直接到达A和B处的点C,
②连结AC并延长至D点,使AC=DC
③连结BC并延长至E点,使BC=EC
④连结DE,测出DE的长,这 个长度就等于A,B两点的距离
A
1
B
C
隐含条件:对顶角相等
E
2
D
典型例题
例2 如图, AB=CB ,∠ABD= ∠CBD , 求证:△ABD≌△CBD 变式1: 求证AD=CD 变式2:求证∠ADB=∠CDB
A
O
D
C
在△ ABO 和△ ADO中, AB = AD (已知),∠BAO = ∠DAO (已证), AO= AO (公共边) ∴ △ ABO ≌ △ ADO(SAS), ∴ ∠AOB = ∠AOD (全等三角形的对应角相等) 又∵∠AOB + ∠AOD =180°(邻补角定义) ∴ ∠AOB = ∠AOD= 90°. ∴AC⊥BD(垂直定义).
A
∠B=∠E BC=EF
B
C D
∴△ABC≌△DEF(SAS) 3、证明线段或角相等 转化为证明线段或角所在的两个三角形全等。
E
F
练 习 二
如右图, 已知:AB=AD,CB=CD. 求证:AC⊥BD. B 分析:欲证AC⊥BD,只需证∠AOB= ∠AOD, 证明: 在△ABC 和△ADC中,
练习2。 (1)如图,AB=CD,AC=BD,△ABC和△DCB是否 全等?试说明理由。 A D 解: △ABC≌△DCB 理由如下: B C AB = CD AC = BD BC = BC △ABD ≌△DCB ( SSS ) E A (2)如图,D、F是线段BC上的两点, AB=CE,AF=DE,要使△ABF≌△ECD , 还需要条件 BF=DC或 BD=FC B D F C
12全等三角形判定一SSS,SAS提高巩固练习
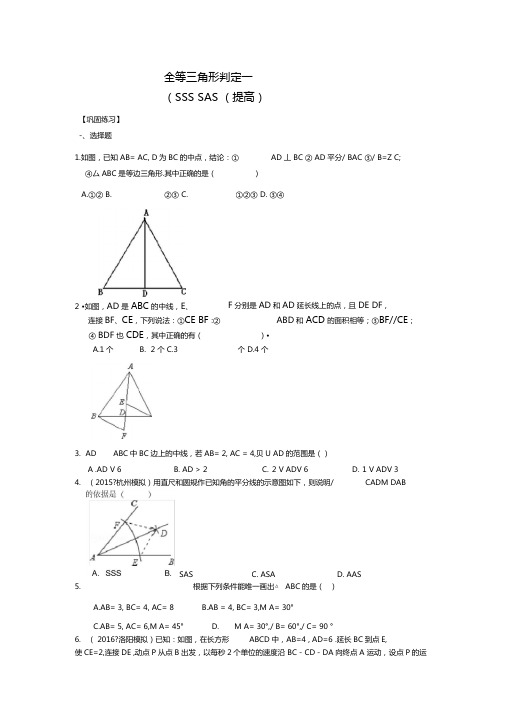
全等三角形判定一(SSS SAS (提高)【巩固练习】-、选择题1.如图,已知 AB= AC, D为BC的中点,结论:①④厶ABC是等边三角形.其中正确的是()F分别是AD和AD延长线上的点,且DE DF ,连接BF、CE,下列说法:①CE BF :②ABD和ACD的面积相等;③BF//CE;④ BDF也CDE,其中正确的有()•3.AD ABC中BC边上的中线,若AB= 2, AC = 4,贝U AD的范围是()4.(2015?杭州模拟)用直尺和圆规作已知角的平分线的示意图如下,则说明/ CADM DAB5.根据下列条件能唯一画出△ABC的是()A.AB= 3, BC= 4, AC= 8B.AB = 4, BC= 3,M A= 30°C.AB= 5, AC= 6,M A= 45°D. M A= 30°,/ B= 60°,/ C= 90 °6.( 2016?洛阳模拟)已知:如图,在长方形ABCD中,AB=4 , AD=6 .延长BC到点E,使CE=2,连接DE ,动点P从点B出发,以每秒2个单位的速度沿 BC - CD - DA向终点A 运动,设点P的运A.①② B. ②③ C. ①②③ D. ③④AD丄 BC ② AD平分/ BAC ③/ B=Z C;2 •如图,AD是ABC的中线,E、B.2 个C.3 个D.4 个A .AD V 6 B. AD > 2 C.2 V ADV 6 D.1 V ADV 3C. ASAD. AASA.1个SAS动时间为t秒,当t的值为()秒时,△ ABP和厶DCE全等.如图,△ ABC 是三边均不等的三角形, 使所作的三角形与△ ABC 全等,这样的三角形最多可以画△ABC 和△FED 中,AD=FC ,AB=FE ,当添加条件(只需填写一个即可)12. 把两根钢条AA', BB'的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳)A . 1B . 1 或 3C . 1 或 7 D.二、填空题如图,AB= CD AC= DB,Z ABD= 25° 7. ,/ AOB= 82° ,则/ DCB=DE= BC,以D E 为两个顶点画位置不同的三角形,个•C Dr(2016?微山县二模)如图,四边形 9. 使厶 ABC ◎△ CDA .ABCD 中,/ 1 = / 2,请你补充一个条件8.B» ED,若/ ABC= 54°,则/ E=10. (2014春?鹤岗校级期末)如图:在如图,若测得 AB= 5厘米,则槽宽为 厘米.三、解答题13. (2014秋?天津期末)如图在 △ ABE 中,已知 AB=AE , AD=AC , /仁/ 2 .求证:△ ABC 也△ AED .14. 如图, B= C, BD = CE, CD = BF.1求证:EDF = 90 - - A 215. 已知:如图,BE CF 是厶ABC 的高,且 BP= AC, CQ= AB, 求证:API AQ.【答案与解析】 一.选择题1.【答案】C【解析】由SSS 证全等可得①②③是正确的2.【答案】D;3.【答案】D;【解析】用倍长中线法;4.【答案】A;【解析】解:从角平分线的作法得出,△ AFD与厶AED的三边全部相等,则厶 AFD^A AED故选A.5.【答案】C;【解析】A不能构成三角形,B没有SSA定理,D没有AAA定理.6.【答案】C;【解析】解:因为 AB=CD,若/ ABP= / DCE=90 ° BP=CE=2,根据SAS证得△ ABP◎△ DCE,由题意得:BP=2t=2,所以 t=1 ,因为 AB=CD,若/ BAP= / DCE=90 ° AP=CE=2,根据 SAS 证得△ BAP◎△ DCE,由题意得:AP=16 - 2t=2,解得t=7 .所以,当t的值为1或7秒时.△ ABP和厶DCE全等. 故选C.二.填空题7.【答案】66°;82【解析】可由 SSS证明厶AB3A DCB / OBC=Z OCB^ —41,所以/ DCB=/ ABG= 25°+ 41 °= 66 °8.【答案】4;【解析】在DE的两侧可以各画2个.9.【答案】AD=BC ;【解析】由题意知,已知条件是△ABC与厶CDA对应角/ 1 = / 2、公共边AC=CA,所以根据全等三角形的判定定理SAS来证△ ABC ◎△ CDA时,需要添加的条件是 AD=BC.10. 【答BC=ED 或/ A= / F.11. 【答27;【解可证△ ADB^A CDB^A CDE.12. 【答5;_ -解答题13. 【解证明:•••/仁/ 2,••• / 1 + / DAC= / 2+ / DAC ,••• / BAC= / EAD ,在厶ABC和厶AED中,\ ZBAC=ZEAD ,I AC=AB•••△ ABC ◎△ AED ( SAS).14.【解析】证明:在厶 ABC中,/ B=Z C,1•••/ B = 90/ A2在厶 DBF和△ ECD中BD CEB CBF CD•••△ DBF^A ECD( SAS•••/ BFD=Z CDE1 •••/ EDM 180°—/ BD1/ CDE= 180° -(Z BDF^Z BFD) =Z B = 90 —/ A .215.【解析】证明:T BEX AC CF丄AB(已知)•Z ACF+Z BAC= 90°,/ ABE^Z BAC= 90°,(三角形内角和定理)/ ACF=Z ABE(等式性质)在厶ACQ^n^ PBA中CQ ABACF ABPAC BP• △ ACQ^ PBA( SAS•Z Q=Z BAP (全等三角形对应角相等)•/ CFX AB (已知)•Z Q+Z QAF= 90°,(垂直定义)•Z BAP+Z QAF= 90°,(等量代换)•AP丄AQ.(垂直定义)。
全等三角形的判定证明题sss、sas

全等三角形的判定训练题(SSS、SAS)判定定理1:简单的表示为:SSS数学语言:在△ABC和△A'B'C'中AC=A'C'(已知)BC=B'C'(已知)AB=A'B'(已知)∴△ABC≌△A'B'C'(SSS)1、若AB=CD,AC=DB,可以判定哪两个三角形全等?请证明。
2、△ABC中,AB=AC,AD是BC边上的中线,∠B与∠C有什么关系?请证明。
3、点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF,则AB和DE有怎样的位置关系?请证明。
C4、已知AB=CD,BE=DF,AF=CE,则AB与CD有怎样的位置关系?5、如图,AC=DF,BC=EF,AD=BE,∠BAC=80o,∠F=60o,求∠ABC6、如图,AC=AD,BC=BD,∠1=35o,∠2=65o,求∠C1.1数学八年级上册同步练习:12.2.1三角形全等的判定SSS 37、如图,△ABC 中,AD=AE , BE=CD ,AB=AC ,说明△ABD ≌△ACE判定定理2: 简单的表示为:SAS 数学语言:在△ABC 和△A 'B 'C ' 中 AB=A 'B ' (已知) ∠B=∠B ' (已知)BC=B 'C '(已知) ∴△ABC ≌△A 'B 'C '(SSS ) 8、如图,已知AC ,BD 相交于O ,AO=DO ,BO=CO ,证明:∠A=∠D9.如图,AE 是,BAC 的平分线 AB=AC.证明 △ABD ≌△ACDCDE1 210、已知:如图,AB=AC,AD=AE,求证:BE=CD.11、如图,已知:点D、E在BC上,且BD=CE,AD=AE,∠1=∠2,求证:△ADB≌△AEC12、如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,求证: BE=DC13、如图,点C是AB中点,CD∥BE,且CD=BE,试探究AD与CE的关系。
全等三角形练习题及答案

全等三角形练习题及答案.求证如图已知C B =BC :AC.=C A AB,=B A AC,A C AB,A B ,:.1''''⊥'⊥'2.已知:如图,△ABC 中,点E 、F 分别在AB 、AC 边上,点D 是BC 边中点,且EF ∥BC,DE=DF . 求证:∠B=∠C3. 已知:如图,AC=AB,AE=AD,∠1=∠2.求证:∠3=∠44. 已知:如图 , AB=DC ,AD=BC , O 是BD 中点 ,过O 的直线分别与DA 、BC 的延长线交于E 、F . 求证:OE=OF5. 已知:如图,AB=AC,AE 平分∠BAC.求证:∠DBE=∠DCE .6. 已知:如图:AB=CD , BE=CF , AF=DE.求证:△ABE≌△DCF7. 已知:如图,∠1=∠2,BD=CD,求证:AD是∠BAC的平分线.8. 已知:如图,AD是BC上的中线,且DF=DE.求证:BE∥CF.9. 如图,已知:AC=DF,AC∥FD,AE=DB,求证:△ABC≌△DEF10. 已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.求证:AC∥DF.答案1. C B =BC C A B BAC C A B =BAC AC B +C CA =AC B +B BA 90=C CA =B BA AC A C AB,A B :''''''''''''⊥'⊥'∴≌△∴△∠∠即∠∠∠∠∴°∠∠∴∵证明 2. 证:∵BD=CD,EF ∥BC∴∠1=∠2,∠3=∠4∵DE=DF,∴∠2=∠4∴∠1=∠3∵D 是BC 的中点,∴BD=DC,又∠1=∠3,DE=DF ∴△BED ≌△CFD(SAS)∴∠B=∠C3. 证明:∵∠1=∠2∴∠1+∠5=∠2+∠5,即∠EAC=∠DAB 在△EAC 和△DAB 中∵∠∠AC ABEAC DABAE AD ===⎡⎣⎢⎢⎢⎢∴△EAC ≌△DAB(SAS)∴∠3=∠44. 提示:先证△ABD ≌△CDB , 再证△DOE ≌△BOF .5. 证明:在△ABE 和△ACE 中 ∵∠∠平分∠AB ACABE BAC AE AE ===⎡⎣⎢⎢⎢⎢12()∴△ABE ≌△ACE(SAS)∴BE=CE ∠3=∠ 4在△EBD 和△ECD 中∵∠∠BE CEDE ED ===⎡⎣⎢⎢⎢⎢34∴△EBD ≌△ECD(SAS) ∴∠DBE=∠DCE6. 证 明:∵AF=DE , ∴AF+FE=DE+EF .即AE=DF 在△ABE 和△DCF 中AB=CD , BE=CF , AE=DF , ∴△ABE ≌△DCF(SSS).7. 证明:∵BD=CD,∠1=∠2, ∴∠ADB=∠ADCAD=AD∴△ADB ≌△ADC(SAS) ∴∠BAD=∠CAD .即AD 平分∠BAC .8. 证:∵D 是BC 的中点,∴BD=CD ∵∠1=∠2,DF=DE,∴△BED ≌△CFD(SAS) ∴∠E=∠CFD∴BE ∥CF9. 证明:∵AE=BD∴AB=DE∵AC=DF AC ∥DF∴∠1=∠2∴△ABC ≌△DEF(SAS)10. 证明:∵BE=CF∴BE+EC=CF+EC 即BC=EF 又 AB ∥DE∴∠B=∠DEF∵AB=DE∴△ABC ≌△DEF∴∠ACB=∠F∴AC ∥DF。
全等三角形的判定(SAS)

练习: 在下列图中找出全等三角形进行连线.
30º
Ⅰ
Ⅱ
ⅣⅣ ⅢⅢ
5 cm
30º
Ⅴ
Ⅵ
30º
Ⅶ
Ⅷ
例.如果AB=CB ,∠ ABD= ∠ CBD,那么 △ ABD 和△ CBD 全等吗?
已知:如图,BA=BC,∠1= ∠2.
求证: (1) AD=CD;
(2) DB 平分∠ ADC.
1
证明: (1)在△ABD与△CBD中,B
2
AB=CB ∠1=∠2
BD=BD
(已知), (已知), (公共边),
∴△ABD≌△CBD(SAS), ∴AD=CD. (2)∵△ABD≌△CBD(已证),
∴∠3=∠4,
全等三角形的判定(SAS)
复习回顾
全等三角形的性质
全等三角形的对应边相等; 全等三角形的对应角相等.
A
D
B
C
E
F
问题1:如果两个三角形的有1个角对应相等, 那么这两个三角形会全等吗?
问题2:如果两个三角形有2个角分别对应相等, 那么这两个三角形会全等吗?
问题3:如果两个三角形有3个角分别对应相等, 那么这两个三角形会全等吗?
A
D
O
B
C
(2)如图, 在ΔABD和ΔACD中,
BD = CD
(已知)
∠ADB =∠ADC(已证)
A—D—=——AD———(—公——共——边—)——
∴ΔABD ΔACD(SAS).
A
D
B
全等三角形的判定精选练习题分SSSSASAASASAHL分专题

全等三角形的判定(SSS)1、如图1,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是()A。
120°B.125°C。
127° D。
104°2、如图2,线段AD与BC交于点O,且AC=BD,AD=BC,•则下面的结论中不正确的是( )A.△ABC≌△BAD B。
∠CAB=∠DBA C.OB=OC D。
∠C=∠D3、在△ABC和△A1B1C1中,已知AB=A1B1,BC=B1C1,则补充条件____________,可得到△ABC≌△A1B1C1.4、如图3,AB=CD,BF=DE,E、F是AC上两点,且AE=CF.欲证∠B=∠D,可先运用等式的性质证明AF=________,再用“SSS”证明______≌_______得到结论。
5、如图,已知AB=CD,AC=BD,求证:∠A=∠D.6、如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:⑴∠D=∠B;⑵AE∥CF.7、已知如图,A、E、F、C四点共线,BF=DE,AB=CD.⑴请你添加一个条件,使△DEC≌△BFA;⑵在⑴的基础上,求证:DE∥BF.全等三角形的判定(SAS)1、如图1,AB∥CD,AB=CD,BE=DF,则图中有多少对全等三角形( )A.3 B。
4 C.5 D。
6CBA 2、如图2,AB=AC ,AD=A E,欲证△A BD ≌△A CE ,可补充条件( ) A 。
∠1=∠2B .∠B=∠C C.∠D=∠ED 。
∠BAE=∠C AD 3、如图3,AD=B C,要得到△AB D和△CD B全等,可以添加的条件是( )A .AB∥CD B。
AD ∥B CC .∠A=∠C D.∠ABC =∠CDA4、如图4,AB 与CD 交于点O ,O A=OC ,OD =OB ,∠A OD =________,•根据_________可得到△AOD ≌△COB ,从而可以得到AD=_________.5、如图5,已知△ABC 中,AB=AC ,A D平分∠BAC ,请补充完整过程说明△A BD≌△ACD 的理由。
08-16全等三角形的判定精选练习题SSS、SAS、AAS、ASA、HL分专题
全等三角形的判定 (SSS )3、在△ ABC 和△A 1B 1C 1 中,已知 AB=A 1B 1,BC=B 1C 1,则补充条件 ___________ ,可得到△ ABC ≌△A 1B 1C 1 .4、如图 3,AB=CD ,BF=DE ,E 、F 是 AC 上两点,且 AE=CF .欲证∠ B= ∠ D ,可先运用等式的性质证明AF= ________ ,再用“ SSS ”证明 _______ ≌ _________ 得到结论. 5、如图, AB=AC , BD=CD ,求证:∠ 1= ∠ 2.6、如图,已知 AB=CD ,AC=BD ,求证:∠ A=∠ D .7、如图, AC 与BD 交于点 O ,AD=CB ,E 、F 是 BD 上两点,且 AE=CF ,DE=BF.请推导下列结论:⑴∠8、已知如图, A 、E 、F 、C 四点共线, BF=DE ,AB=CD. ⑴请你添加一个条件,使△ DEC ≌△BFA ; ⑵在⑴的基础上,求证: DE ∥ BF.1、如图 1, AB=AD ,CB=CD ,∠A.120 °B.125°2、如图 2,线段 AD 与 BC 交于点 B. ∠ CAB= ∠DBA A.△ABC ≌△BAD AD=BC C.OB=OC , ?则下面的结论中不正确的是 ( D.∠C=∠ D D= ∠B ;⑵ AE ∥CF .B=30°C.127°O ,且AC=BD ,全等三角形的判定 (SAS )1、如图 1, AB ∥ CD , AB=CD , BE=DF ,则图中有多少对全等三角形 ( )A. 3B.4C.5D.62、如图 2,AB=AC ,AD=AE ,欲证△ ABD ≌△ACE ,可补充条件 ( ) A.∠1=∠2 B.∠B=∠CC.∠D=∠ED. ∠BAE= ∠CAD3、如图 3, AD=BC ,要得到△ ABD 和△ CDB 全等,可以添加的条件是 ( )A.AB ∥CDB.AD ∥BCC.∠A=∠CD. ∠ABC= ∠CDA4、如图 4,AB 与 CD 交于点 O ,OA=OC ,OD=OB ,∠ AOD= ________ ,?根据 _________ 可得到△ AOD ≌△ COB ,从而可以得到 AD= ________ .5、如图 5,已知△ ABC 中,AB=AC ,AD 平分∠ BAC ,请补充完整过程说明△ ABD ≌△ACD 的理由. ∵AD 平分∠ BAC , ∴∠ _______ = ∠ __________ (角平分线的定义 ). 在△ABD 和△ ACD 中,∵ __________________________________ , ∴△ ABD ≌△ ACD ( ) 6、如图 6,已知 AB=AD , AC=AE ,∠1=∠2,求证∠ ADE= ∠B.7、如图,已知 AB=AD ,若 AC 平分∠ BAD ,问 AC 是否平分∠ BCD ?为什么?8、如图,在△ ABC 和△ DEF 中, B 、E 、F 、C ,在同一直线上,下面有 为题设,余下的一个作为结论,写一个真命题,并加以证明 . ① AB=DE ; ②AC=DF ; ③∠ ABC= ∠ DEF ; ④ BE=CF.9、如图⑴, AB ⊥BD ,DE ⊥BD ,点C 是BD 上一点,且 BC=DE ,CD=AB . ⑴试判断 AC 与 CE 的位置关系,并说明理由.⑵如图⑵,若把△ CDE 沿直线 BD 向左平移,使△ CDE 的顶点 C 与 B 重合,此时第⑴问中 AC 与 BE 的位置关系还成立吗? (注意字母的变化 )4 个条件,请你在其中选 3 个作C全等三角形(三) AAS 和 ASA知识要点 】1.角边角定理( ASA ):有两角及其夹边对应相等的两个三角形全等 2 .角角边定理( AAS ):有两角和其中一角的对边对应相等的两个三角形全等【典型例题 】例 1.如图, AB ∥ CD , AE=CF ,求证: AB=CD例 2 .如图,已知: AD=AE , ACD ABE ,求证: BD=CE.例 4.如图已知: AB=CD ,AD=BC ,O 是 BD 中点,过 O 点的直线分别交 DA 和 BC 的延长线于 E ,F. 求证:AE=CF.例 5.如图,已知 1 23 , AB=AD.求证: BC=DE.例 6.如图,已知四边形 ABCD 中, AB=DC ,AD=BC ,点 F 在 AD 上,点 E 在 BC 上, AF=CE ,EF 的对角线 BD 交于 O ,请问 O 点有何特征?例 3.如图,已知: C D. BAC ABD ,求证:OC=OD.CABE【经典练习】1. △ABC 和△ ABC 中, AA ',BC BC , C C 则△ ABC 与△ A BC.2.如图,点C ,F 在 BE 上, 12,BC EF ,请补充一个条件, 使△ ABC ≌DFE,补充的条件是.3.在△ ABC 和△ AB C 中,下列条件能判断△ ABC 和△ ABC 全等的个数有( )①A A B B , BC BC ②A A , B B , AC AC③A A B B , AC BC ④A A , BB , AB AC A . 1 个B. 2 个C. 3 个D. 4 个4.如图,已MB=ND , MBA NDC , 下列条件不能判定ABM ≌△ CDN 的是( )6.如图 3 所示,在△ ABC 和△ DCB 中, AB =DC ,要使△ ABO ≌DCO ,请你补充条件 一个你认为合适的条件 ).7. 如图,已知∠ A=∠ C ,AF=CE ,DE ∥BF ,求证:△ ABF ≌△ CDE.A MNB. AB=CDC . AM=CND. AM ∥ CN5.如图 2 所示, ∠E =∠F =90°,∠ B =∠C ,AE =AF ,给出下列结论:①∠1=∠2 ② BE=CF ③△ ACN ≌△ ABM ④CD=DN( 注:将你认为正确的结论填上 ) 其中正确的结B图28.如图, CD ⊥AB ,BE ⊥AC ,垂足分别为 D 、E ,BE 交 CD 于 F ,且 AD=DF ,求证: AC= BF 。
全等三角形的判定精选练习题简单(分SSS、SAS、AAS、.
⑵如图2,若把△CDE沿直线BD向左平移,使△CDE的顶点C与B重合,此时第⑴问中AC与BE的位置关系还
成立吗?(注意字母的变化
全等三角形(三AAS和ASA
【典型题】
1.如图1,AB∥CD,AE=CF,求证:AB=CD
图5
图4
图1图2图3
2.如图2,已知:AD=AE,ABE
11.如图11,在Rt△ABC中,AB=AC,∠BAC=90º,多点A的任一直线AN,BD⊥AN于D,
CE⊥AN于E,你能说说DE=BD-CE的理由吗?
B
A
E
2
1
F
C
D
B
A
E F
C
D
图9图11图7图8
A E B
D C
F
O
A
D E
B C
A B
O
D C
D
F
C
O
B
A
E
A
B D C
E
O
1
2
3
A F D
O
B E C
ACD∠
=
∠,求证:BD=CE.
3.如图3,已知:ABD
BAC
D
C∠
=
∠
∠
=
∠.,求证:OC=OD.图6
4.如图4已知:AB=CD,AD=BC,O是BD中点,过O点的直线分别交DA和BC的延长线于E,F.求证:AE=CF.
5.如图5,已知3
2
1∠=Leabharlann ∠=∠,AB=AD.求证:BC=DE.
6.如图6,已知四边形ABCD中,AB=DC,AD=BC,点F在AD上,点E在BC上,AF=CE,EF的对角线BD交于O,求证:OF=OE
全等三角形的判定练习题
全等三角形的判定练习题一、选择题1、如图,已知点A、D、C、F在同一直线上,AB=DE,AD=CF,且∠B=∠E=90°,判定∠ABC∠∠DEF 的依据是()A.SAS B.ASA C.AAS D.HL答案:D2、如图,AC和BD相交于O点,若OA=OD,用“SAS”证明∠AOB∠∠DOC还需()A.AB=DC B.OB=OC C.∠C=∠D D.∠AOB=∠DOC答案:B3、下列说法中,正确的个数是()①斜边和一直角边对应相等的两个直角三角形全等;②有两边和它们的对应夹角相等的两个直角三角形全等;③一锐角和斜边对应相等的两个直角三角形全等;④两个锐角对应相等的两个直角三角形全等.A.1个B.2个C.3个D.4个答案:C解析:①②③正确,④错误。
4、如图,下列条件中不能证明∠ABD∠∠ACD的是()A.BD=DC,AB=AC B.∠ADB=∠ADC,BD=DCC.∠B=∠C,BD=DC D.∠BAD=∠CAD,AB=AC答案:C解析:选项A,利用SSS可证;选项B,利用SAS可证;选项C,不可以;选项D,利用SAS 可证。
5、如图,EA//DF,AE=DF,要使∠AEC∠∠DFB,只要()A.AB=CD B.EC=BF C.∠A=∠D D.AB=BC答案:A解析:EA//DF,有∠A=∠F;AE=DF;若AB=CD,则有AC=BD,于是∠AEC∠∠DFB(SAS)。
6、如图为作一个角的角平分线的示意图,该作法的依据是全等三角形判定的基本事实,可简写为()A.SSS B.SAS C.ASA D.AAS答案:A7、如图,已知AB=AC,BD=CD,E是AD上的一点,则下列结论中不成立的是()A.BE=CE B.AE=DE C.∠BAD=∠CAD D.∠BED=∠CED答案:B解析:AB=AC,BD=CD,AE=AE,DE=DE,AD=AD,可得△ACE ≌△ABE,△DCE≌△DBE,△ACD≌△ABD。
11.3探索三角形全等的条件(1)(SAS)
B
C
∠1 ∠2 ______=________( 对顶角相等 ) BO=CO(已知 已知) 已知 ∴ △AOB≌△DOC( SAS ) ≌ (
如图,已知 = , = 。 如图,已知AB=AC,AD=AE。 求证:∠B=∠C 求证: = 证明: 证明:在△ABD和△ACE中 E 和 中 已知) AB=AC(已知) 公共角) B ∠A=∠A(公共角) AD=AE(已知) A 已知) ∴△ABD≌△ACE(SAS) ≌ ( ) ∴∠B= ∴∠ =∠C(全等三角形 ( 对应角相等) 对应角相等)
C
它既是△ACB
看看线 段AB AB
的一条边, 的一条边
A
△ACB 和△ADB的 ADB的 公共边
B
D 又是△ADB
的一条边
已知: 例1已知
如图,AC=AD ,∠CAB=∠DAB. 如图 ∠ ∠ 求证: 求证 △ACB ≌ △ADB.
C
证明: 证明
在△ACB 和 △ADB中 中 AC = A D ∠CAB=∠DAB ∠
1、全等三角形的定义? 全等三角形的定义 能够完全重合的两个三角形叫 全等三角形
2、全等三角形的性质? 全等三角形的性质
A A’ ∠A=∠A’ ∠A=∠A’ ∠B=∠B’ ∠B=∠B’ ∠C=∠C’ ∠C=∠C’ AB=A’ AB=A’B’ BC=B’ BC=B’C’ AC=A’C’ AC=A’ B’ C’
S ——边 ——边
A——角 ——角
三角形全等判定方法1 三角形全等判定方法1 两边和它们的夹角对应相等的两个三 角形全等。简写成“边角边” SAS” 角形全等。简写成“边角边”或“SAS” 用符号语言表达为: 用符号语言表达为: 在△ABC与△DEF中 与 中 AB=DE
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精品文档
2016
1 / 8
全等三角形sas练习题
1.如图,AB=AC,AD=AE,欲证△ABD≌△ACE,可补充条
件A.∠1=∠ B.∠B=∠C C.∠D=∠E D.∠BAE=∠CAD.能判定
△ABC≌△A′B′C′的条件是 A.AB=A′B′,AC=A′C′,
∠C=∠C′ B. AB=A′B′, ∠A=∠A′,BC=B′C′ C.
AC=A′C′, ∠A=∠A′,BC=B′C D. AC=A′C′,
∠C=∠C′,BC=B′C
3.如图,AB与CD交于点O,OA=OC,OD=OB,∠AOD=, 根
据_________可得到△AOD≌△COB,从而可以得到
AD=_________..如图,已知BD=CD,要根据“SAS”判定
△ABD≌△ACD, 则还需添加的条件是。.如图,AD=BC,要
根据“SAS”判定△ABD≌△BAC, 则还需添加的条件是.如
图,已知△ABC中,AB=AC,AD平分∠BAC, 请补充完整过
程说明△ABD≌△ACD的理由. 解:∵AD平分∠BAC,
∴∠________=∠_________.在△ABD和△ACD中,
∵
∴△ABD≌△ACD
7.如图,AC与BD相交于点O,已知OA=OC,OB=OD, 求
证:△AOB≌△COD 证明:在△AOB和△COD中∵
∴△AOB≌△COD
8.已知:如图,AB=CB,∠1=∠△ABD 和△CBD 全等吗?
9.已知:如图,AB=AC,AD=AE ,∠1 =∠。试说明:
精品文档
2016
2 / 8
△ABD ≌△ACE 。
10.已知:如图,△ABC中, AD⊥BC 于D,AD=BD,
DC=DE, ∠C=50°。 求∠ EBD的度数。
1.在△ABC和△A?B?C?中,若AB=A?B?,AC=A?C?,还
要加一个角的条件,使△ABC≌△
A?B?C?,那么你加的条件是
A.∠A=∠A? B.∠B=∠B? C.∠C=∠C?
D.∠A=∠B?.下列各组条件中,能判断△ABC≌△DEF的是
A.AB=DE,BC=EF;CA=CD B.CA=CD;∠C=∠F;AC=EF
C.CA=CD;∠B=∠E D.AB=DE;BC=EF,两个三角形周
长相等
3.已知△ABC的6个元素,则下面甲乙丙三个三角形
中,和△ABC全等的图形是
甲
A.甲和乙
B. 乙和丙
C. 没有乙
D. 没有甲
4.如图工作师傅做门时,常用木条EF固定矩形门框
ABCD,使其不变形这种做法根据是.
A、两点之间线段最短 B、矩形的对称性 C、矩形的
精品文档
2016
3 / 8
四个角都是直角 D、三角形的稳定性
5.如果△ABC≌△DEF,且△ABC的周长95cm,A、B
分别与D、E对应并且AB=30cm,DF=2cm,
那么BC的长等于
A.40cm B.35cm C.30cm D.25cm
6.如图,AB∥DE,CD=BF,若△ABC≌△DEF,还需要
补充的条件可以是 A.AC=EFB.AB=DEC.∠B=∠E D.不
用补充.如图,∠CAB=∠DBA,AC=BD,则下列结论中,不正
确的是
A、BC=AD B、CO=DO C、∠C=∠D D、∠AOB=∠C+∠D
A
F
B
C
B
B
8.如图,AB=AC,若AD平分?BAC,则AD与BC的位
置关系是 .
9.阅读理解题:
如图:已知AC,BD相交于O,OA=OB,OC=OD.
那么△ABC与△BAD全等吗?请说明理由.△ABC与
△BAD全等吗?请说明理由.小明的解答:
精品文档
2016
4 / 8
OA=OB?
1??OD=OC
而BAD=△AOD+△ADB所以△ABC≌△BAD
你认为小明的解答有无错误;
如有错误给出正确解答;
AOD≌△BOC
△ABC=△BOC+△AOB
10.如图,点C是AB中点,CD∥BE,且CD=BE,试探
究AD与CE
11.如图,AE是?
BAC的平分线,AB=AC
D
若D是AE
上任意一点,则△ABD≌△ACD,说明理由.
若D
是AE
12.如图,已知AB=AC,EB=EC,请说明BD=CD的理由
13. 如图,△ABC,△BDF为等腰直角三角形。求证:
CF=AD;BE=DC,BE⊥DC.
B
A
D
精品文档
2016
5 / 8
P
C
全等三角形的判定
1、如图1,AB∥CD,AB=CD,BE=DF,则图中有多少
对全等三角形
A.3B. C. D.6
2、如图2,AB=AC,AD=AE,欲证△ABD≌△ACE,可补
充条件
A.∠1=∠ B.∠B=∠C C.∠D=∠E D.∠BAE=∠CAD
3、如图3,AD=BC,要得到△ABD和△CDB全等,可以
添加的条件是
A.AB∥CD B.AD∥BC C.∠A=∠C D.∠ABC=∠CDA
4、如图4,AB与CD交于点O,OA=OC,OD=OB,
∠AOD=________,?根据_________可得到△AOD
≌△COB,从而可以得到AD=_________.
5、如图5,已知△ABC中,AB=AC,AD平分∠BAC,
请补充完整过程说明△ABD≌△ACD的理由. ∵AD平分
∠BAC, ∴∠________=∠_________.
在△ABD和△ACD中,
∵____________________________, ∴△ABD≌△ACD
6、如图6,已知AB=AD,AC=AE,∠1=∠2,求证∠ADE=∠B.
B
精品文档
2016
6 / 8
7、如图,已知AB=AD,若AC平分∠BAD,问AC是否
平分∠BCD?为什么?
AC
8、如图,在△ABC和△DEF中,B、E、F、C,在同一
直线上,下面有4个条件,请你在其中选3个作
为题设,余下的一个作为结论,写一个真命题,并加
以证明.
①AB=DE; ②AC=DF; ③∠ABC=∠DEF; ④BE=CF.
9、如图⑴,AB⊥BD,DE⊥BD,点C是BD上一点,且
BC=DE,CD=AB.
⑴试判断AC与CE的位置关系,并说明理由.
⑵如图⑵,若把△CDE沿直线BD向左平移,使△CDE
的顶点C与B重合,此时第⑴问中AC与BE的位置关系还成
立吗?
1、已知:如图,B?A?AB,C?A?AC,AB?=AB,AC?=AC.
求证:△ABC≌△AB’C‘第1题
2、已知:如图,△ABC中,点E、F分别在AB、AC边上,
点D是BC边中点,且 DF∥AB,BE=DF.求证: △BED≌△DFC
第2题
3、已知:如图,AC=AB,AE=AD,∠1=∠2.求证:∠3=∠4
第3题
4、已知:如图 , AB=DC ,AD=BC , ∠DAB=∠BCD,求
精品文档
2016
7 / 8
证:△ABD≌△CDB
第4题
5、已知:如图,AB=AC,AE平分∠BAC.求
证:∠DBE=∠DCE. 第5题
6、已知:如图,AB=CD , AE=DF , AB∥CD.D、E、F、
A在同一条直线上。求证:△ABE≌△DCF
第6题
7、已知:如图,∠1=∠2,BD=CD,求证:AD是∠BAC的平
分线. 第7题
8、已知:如图,AD是BC上的中线,且DF=DE.求
证:BE∥CF. 第8题
9、已知:如图, AC=DF,AC∥FD,AB=DE,求
证:△ABC≌△DEF 第9题
10、已知:如图,点B,E,C,F在同一直线上,AB∥DE,且
AB=DE,BE=CF. 求证:AC∥DF 第10题
11、已知:如图 , 四边形ABCD中 , AB∥CD , AD∥BC.求
证:△ABD≌△CDB
第11题
12、如图,点C是AB中点,CD∥BE,且CD=BE,试探
究AD与CE的关系。
D
第12题
精品文档
2016
8 / 8
