第二节 函数的求导法则
x
arcsin x
x x ( a ) arcsin x
x x a (arcsin x )
1 x 1 x 2 a arcsin x 2
x a
x
ln a arcsin x
x a
x
1 1 x 2
上一页下一页 返回
3、函数商的求导法则 法则4 两个可导的函数的商当除数函数（或分母） 不为０时可导，它们商的导数等于被除函数（分 子）的导数乘于除数（分母）减去被除函数（分 子）乘于除数（分母）的导数后，再除于除数函 数（分母）的平方，即
上一页下一页 返回
三、基本求导法则和求导公式
1.常数和基本初等函数的导数公式
(C ) 0 (sin x ) cos x
2 (tan x ) sec x
1 ( x ) x
(cos x ) sin x
2 (cot x ) csc x
(sec x ) sec x tan x
2 10
Q dy dx dy du
dy dx
dy du
10u ,
9
du dx
2x
9 2 9
du dx
1 0 x 1 2 x 2 0 x x 1
2
2 9 2
解2
10( x 1) ( x 1)
10( x 1) 2 x 20 x ( x 1) .
x x ( a ) a ln a
(csc x ) csc x cot x
'
10
7 2
5
7
1
x
2
1 2e x 2
3 2
1 2
1
3 5 x 2 ex
y ' x 1 3 5 e
上一页下一页 返回
例4
求函数 y xa x arcsin x 的导数．
y ( x a arcsin x )
x
解
( x )a
dy du dy dx 1 u dy du ; du dx du dx 2x u 2x 1 x
2
2x
上一页下一页 返回
推广 设 y f ( u), u (v ), v ( x ),
则复合函数 y f { [ ( x )]}的导数为 dy du dv . dx du dv dx dy
(u )v u (v ) u 2 v v
'
上一页下一页 返回
例5 求 y tan x 的导数 . 解
y (tan x ) (
sin x cos x
)
(sin x ) cos x sin x (cos x ) cos x
2
cos x sin x
u
2x 1
2x 1
上一页下一页 返回
y e
sin
2 x 1
解：y' e e e e
sin 2 x 1
sin
2 x 1
sin
2x 1 ' 2x 1 '
co s co s co s
2x 1 2x 1 2x 1
sin
2 x 1
2 x 1 '
2 2x 1
2
2
9
2
2
9
x 2x 0 x 2x
上一页下一页 返回
2、函数乘积的求导法则 两个可导的函数的积可导，乘积的导数等于这两个函数 中每一个函数的导数分别乘于另一函数后的和，即
(uv) uv uv
推广 uvw ' u ' vw uwv ' uvw '
上一页下一页 返回
例8 求函数 y ln sin x 的导数.
解
y ln u, u sin x .
dy du dx du dx 1 u cos x sin x
dy
cos x
cot x
上一页下一页 返回
例9 求函数 y ( x 2 1)10 的导数 . 解1 y x 1 是 由 y u 1 0 , u x 2 1复 合 而 成 的
• 函数的四则运算法则和复合运算法则
上一页下一页 返回
一、导数的四则运算法则
1、函数的和、差的求导法则 两个可导的函数和（差）可导，它们的和（差）导 数等于这两个函数的导数的和（差），即
u v ' u ' v '
可以推广到有限个可导函数的代数和的情形，如
u v w
3y x 2 0
0
y
1 3
x
2
2 3
kl
1 3
依 题 意 得 y ' x x 3
即 3 x0 6 x0 6 3
x0 2 x0 3 0
2
x 0 3或 x 0 1
这 个 点 的 坐 标 为 3 , - 2 0 , 1, 0
通过以上例子，我们可以发现运用复合函数的求导 法则的关键在于把复合函数分解成为若干个基本初 等函数和常数的复合或者是它们的四则运算，然后 运用法则和适当的导数公式进行计算． • 在计算函数的导数时，有时必须注意化简后求 导，以及需要综合地运用导数的四则运算求导法则 和复合函数的求导法则．
上一页下一页 返回
)
sin x cos x
2
sec x tan x .
同理可得
(csc x ) csc x cot x .
上一页下一页 返回
例7
求下列函数的导数．
2 x x3 x 1
5 2 7
（1） y
（2） s
2t sin t 3t 2 4t 4 2t
解（1）y
si n
2 x 1
2x 1
上一页下一页 返回
例 11 求下列函数 y ln (3 tan x 7) 的导数．
2
解法１（用链式法则）
y 是 由 y u , u ln v , v 3 tan x 7 复 合 而 成 的
2
Q
dy du
2u ,
du dv
1 v
,
dv dx
上一页下一页 返回
例如 y sin 2 x 是由 y sin u 与u 2 x 复合而成的。且
dy du dy dx dy du du dx co s u du dx
co s u 2 2 co s u 2 co s 2 x
2
再如 y ln x 2 1 是由 y ln u ，u x 2 1 复合而成的。且
u v w
上一页下一页 返回
例１
求函数 y sin x tan x x 9 的导数．
2 2
解： y sin x tan x x
sin x tan x x
co s x sec co s x sec 2 2
3 sec x
2
dy dx
dy du
2
du dv
dv dx
2 ln 3 tan x 7
1 3 tan x 7
3 ec x
2
6 sec x ln 3 tan x 7 3 tan x 7
上一页下一页 返回
解法２（逐层求导）
y ' ln (3 tan x 7 ) 2 ln 3 tan x 7 ln 3 tan x 7
(x
2
x 3) ( x 1) ( x ( x 1)
2
2
x 3)( x 1)
2
( 2 x 1)( x 1) ( x x 3) 1 ( x 1) x 2x 4
2 2
( x 1)
2
上一页下一页 返回
（2）通常为了便于计算，把商的形式转化成和差 或积的形式，再进行求导．
上一页下一页 返回
推论 常数与可导函数的积的导数等于常数乘于 该可导函数的导数，即
(cu ) cu
也就是说常数因子可以直接提到求导记号外面去.
上一页下一页 返回
例2 求 y sin 2 x ln x 的导数 . 解 y 2 sin x cos x ln x
y 2 cos x cos x ln x 2 sin x ( sin x ) ln x 1 2 sin x cos x x 1 2 cos 2 x ln x sin 2 x . x
2 9 2 9
上一页下一页 返回
例 10 求下列函数 y a
3 x 1
的导数．
解
y a
3 x 1
是 由 y a , u 3 x 1复 合 而 成 的 ，
u
Q
dy du
a ln a ,
u
du dx
3
dy dx
dy du
du dx
3a
3 x 1
ln a
上一页下一页 返回
y e 解：y e
sin
2 x 1
sin
2 x 1
是 由 y e ; u sin v ; v
u
w ; w 2 x 1复 合 而 成
导数的运算法则
cos x
(sin
x
)
cos x cos2
sin x
x(cos
x)
cos2 x cos2
sin2 x
x
1 cos2
x
sec2
x
即 (tan x) sec2 x.
同理可得 (cot x) csc2 x.
例4 y sec x 求y
解
y
1 cos
若u ( x)在I上可导，y f (u)在I1上可导 x I ,u ( x) I1,则复合函数y f [ ( x)]
在I上可导，且有dy dy du dx du dx
注
链式法则——“由外向里，逐层求导”
推广 设 y f (u), u (v), v ( x), 则复合函数 y f {[ ( x)]}的导数为
dx du dx
四、二阶导数
问题:变速直线运动的加速度.
设 s f (t), 则瞬时速度为v(t) f (t) 加速度a是速度v对时间t的变化率
a(t) v(t) [ f (t)].
定义
如果函数f (x)的导数f (x)在点x处可导,则称 ( f (x))为函数f (x)在点x处的二阶导数.
( y)
即 反函数的导数等于直接函数导数的倒数.
例5 求函数 y arcsinin
y在
I
y
(
2
,
)内单调、可导 2
,
且 (sin y) cos y 0, 在 I x (1,1)内有
(arcsin x) 1 1 (sin y) cos y
1 1 sin2 y
2(3x 2 1) (1 x 2 )3
2.
导数运算法则
设函数 x = ϕ ( t )具有单调连续的反函数 t = ϕ ( x ),
−1
∴ y = ψ [ϕ −1 ( x )]
再设函数 x = ϕ ( t ), y = ψ ( t )都可导, 且ϕ ′( t ) ≠ 0,
例1 求由方程 xy − e x + e y = 0所确定的隐函数
dy dy y的导数 , dx dx
解
x=0
.
方程两边对x 方程两边对 求导, dy dy y + x − ex + ey =0 dx dx
dy e x − y 解得 , = y dx x + e
dy ∴ dx
x=0
由原方程知 x = 0, y = 0,
y= x
sin x
.
多个函数相乘和幂指函 数 u( x )
v( x)
的情形 .
( x + 1)3 x − 1 例1 设 y = , 求y′ . 2 x ( x + 4) e
解 等式两边取对数得
1 ln y = ln( x + 1) + ln( x − 1) − 2 ln( x + 4) − x 3 上式两边对 x求导得
∴ (a )′ =
x
1 (log a y ) ′
= ylna = a x ln a
即：
特别地：
(a )′ = a x ln a
x
(e )′ = e
x
x
三、复合函数的求导法则
定理
如 函 u = ϕ(x)在 x0可 , 而 = f (u) 果 数 点 导 y 在 u0 = ϕ(x0 )可 , 则 点 导 复合 数 y = f [ϕ(x)]在 函 点 x0可 , 且 导 其导 为 数 dy dx
课件：复合函数的求导法则,反函数的求导法则
dy
即：反函数的导数等于原函数的导数的倒数.
证 任取x I x , 给x以增量x (x 0, x x I x ) 由y f ( x)的单调性可知 y 0,
于是有
y x
1 x
,
f ( x)连续,
y
当x 0时，必有 y 0.又知 ( y) 0
f ( x) lim y x0 x
lim 1 y0 x
例1
y lntan x，求
dy dx
.
解 令 u tan x ，则 y ln u
故 dy ln utan x 1 sec2 x
dx
u
1 sec2 x tan x
1 sin x cos x
例2
y 3 1 2x2 ，求 dy
dx
.
解
dy
1 2x2
1 3
dx
1
1 2x2
证 由 y f (u)在u处可导,可得
f (u) lim y u0 u
则有 y f (u) o(1),其中lim o(1) 0
u
u0
即 y f (u)u o(1)u
所以 y f (u) u o(1) u
x
x
x
注意到:当x 0时, 由u (x) 的连续性
可得 u 0,从而 lim o(1) lim o(1) 0
2 3
1 2x2
3
1
1 2x2
2 3
4x
3
4x
33 (1 2x2 )2
例3 y sin nx sinn x ,求y. nsinn1 x sin(n 1)x
例4 y ln( x x2 1), 求 yy. 1
例5
y
1
微积分3-2-1导数的四则运算法则
微
积
分
例1(3). y x ( x 3 4 cos x sin 1) ,
3 ( x 4 cos x sin 1) 解: y ( x )
2 x 1 ( x 3 4 cos x sin 1) x (3x2 +4sinx) 2 x 1 y x 1 (1 4 cos1 sin 1) ( 3 4 sin 1) 2 7 7 sin 1 2 cos1 2 2
微
积
分
第三章
第二节 求导法则
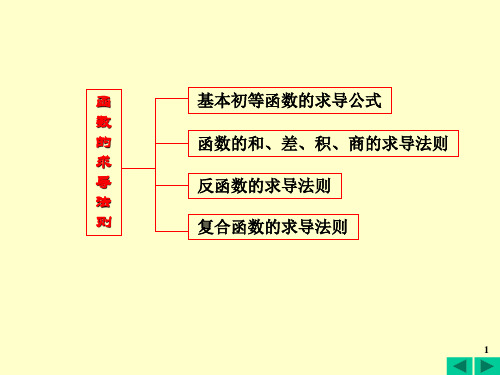
一、四则运算求导法则 二、反函数的求导法则 三、复合函数求导法则
四、初等函数的求导问题
微
积
分
第一节根据导数的定义已经求出了一些简
单函数的导数。但对于比较复杂的函数，直接
用定义求其导数往往比较困难。
本节将介绍求导数的几个 基本法则和基本
初等函数的导数公式，利用这些法则和公式，
h v( xC h v( xC ) v ) 推论: ( C为常数 ) 2
v ( x h) v ( x ) u ( x h) u ( x ) v ( x ) u ( x) h h
v
v
微
积
分
例3. 求证
sin x (sin x) cos x sin x (cos x) 证: (tan x) cos2 x cos x
1
x ( x 3 4 cos x sin 1)
( x 3 4 cos x sin 1) x （ -（4cosx） -(sin1) ] [ x3）
微
积
分
例2. 解:
y a cos x ln x,
医学高数6(求导数的一般方法)
3 x 2 − y − xy′ + y′ cos y = 0
3x 2 − y y′ = x − cos y
例2-16 已知 x4 + xy – 2y2 = 0，求 y′ | x=1 ， ′ 解 方程两边同时关于自变量 x 求导得 所以
4 x 3 + y + xy′ − 4 yy′ = 0
4x + y y′ = 4y − x
dy = f ′(u ) ⋅ g ′( x) dx
的导数。 例2-13 求函数 y = sin3x 的导数。 解 设 y =u3，u = sin x 则根据法则 2-4 得
y′ = (u 3 )′ ⋅ (sin x)′x = 3u 2 ⋅ cos x = 3sin 2 x ⋅ cos x u
的导数。 例2-14 求函数 y =cot[ ln(x2-5x+6)]的导数。 的导数 则根据法则2-4得 解 设 y = cot u, u = ln v, v = x 2 − 5 x + 6 ，则根据法则 得 1 2 2 y′ = (cot u )′ ⋅ (ln v)′ ⋅ ( x − 5 x + 6)′x = − csc u ⋅ ⋅ (2 x − 5) u v v 1 2 2 = − csc [ln( x − 5 x + 6)] ⋅ 2 ⋅ (2 x − 5) x − 5x + 6
3
当 x =1 时，1+y - 2y2 = 0 , y =1 或 y =-1/2 ，所以 1 4− 4 +1 5 2 = −7 y′ x =1 = = 或 y′ x =1 = 4 −1 3 −2 − 1 6
（二）参数方程的求导公式 表示时， 当函数关系用参数方程 x = ϕ (t ) 表示时，
第二节 导数的求导法则、求导
主
页 后退 目录
退
相应地, f ( x)称为零阶导数; f ( x)称为一阶导数.
出
2020年5月2日6时21分
23
第二节 导数的运算
高阶导数的计算
本节
知识
引入 1.直接法:由高阶导数的定义逐步求高阶导数.
本节
目的 与要
例1 设 y arctan x, 求f (0), f (0).
求
本节 重点 与难
1 2x2
19
第二节 导数的运算
本节 知识
例13 求函数 y ( x2 1)10 的导数 .
引入
本节
目的 与要
解
求
本节 重点 与难 点
本节 复习 指导
dy 10( x 2 1)9 ( x 2 1) dx
10( x2 1)9 2x 20x( x2 1)9 .
主 页 后退 目录 退 出
点
本节 复习
解
y ln u, u sin x.
指导
dy dy du 1 cos x cos x cot x
dx du dx u
sin x
主
页
后退 目录
退
出
2020年5月2日6时21分
15
复合函数的导数
设复合函数y=f[g(x)]关于x可导，则 y f [g(x)]• g(x)
2
第二章 导数与微分
前言
• 本节预备 知识
求函数的导数的方法叫微分法。
• 本节目的
与要求
微分法是指运用求导数的基本法则和基本
本节重点 初等函数的导数公式，求出初等函数导数 与难点 的方法。
本节复习
指导 • 因此我们将要建立最基本的一组求导数的
函数的和、差、积、商的求导法则
f '(x) 1
'( y)
或者记为dy 1 dx dx
dy
注意：1、这里反函数的记法，并不把自变量按习惯记作x.
2、反函数关系是相互的。
即：x ( y)是 y f ( x)的反函数， y f ( x)也是 x ( y)的反函数。
6
例1 y a x的反函数x loga y在（0， ）内单调连续 且x R相应的y (0, )
1 x2
8
二、复合函数的导数
函数u ( x)在x处可导，y f (u)在与x相应的点u处可导，
则：复合函数y f ( x)在x处可导,且
y' f '(u) '( x)
或者 dy dy du dx du dx
由 于y f (u)在 点u处 可 导 ， 故lim y f '(u) u0 u
dx
x lna 2
4
例6：g( x)
( x 2 1)2 x2
求：g '( x)
解： 由于：g( x) x 2 2 x 2
先化简函数表达式， 大大方便了计算。
所以：g '( x)
2x 2x3
2 x3
(x4
1)
5
第三节 反函数的导数 复合函数的求导法则
一、反函数求导法则
设：x ( y)单调连续并在点y可导，且'( y) 0 x ( y)的反函数y f ( x)在对应点x处可导，则
x）'
1 x lna
.
（a
0, a
1）
解： log a
x' ln x '
lna
1 (ln x)' ln a
1 x lna
2-2,2-3求导法及反函数与复合函数的求导法则
8
现在看： 现在看：
dy ∆y , ⇒ y′ y 可导， = 函数 y= f (x) 对x可导， ′ = = lim x ∆x → 0 ∆ x dx dy ∆y , ⇒ y′ y = 可导， 函数 y= f (u) 对u可导， ′ = = lim u ∆u→ 0 ∆ u du dy ∆y , ⇒ y ′ 于是 = lim = 可导， 函数 y= f (t) 对t可导，y′ = t ∆t → 0 ∆ t dt du ∆u = 可导， t 函数 u= f (t) 对t可导， ′ = u , = lim dt ∆t → 0 ∆ t dx ∆x = 可导， t 函数 x= f (t)对t可导，x′ = , = lim dt ∆ t → 0 ∆ t dx ∆x x , = lim = 可导， y 函数 x= f (y)对y可导， ′ = dy ∆ y → 0 ∆ y
= (2x2 )′ex + 2x2 (ex )′ + (23 x)′
2 = 4xe + 2x e + x 3
x 2 x − 2 3
[
]
6
例4. 求证
′ sin x (sin x)′ cos x − sin x (cos x)′ 证: (tan x)′ = = cos x cos 2 x
= 3x2 + cos x
y′ x=1 = 3+ cos1.
5
例2.
y = x sin x ,
3
解: y′ =
(x3 sin x )′
= (x3 )′sin x + x3 (sin x)′
= 3x2 sin x + x3 cos x
y = 2x2ex + 23 x , 例3.
22函数的求导法则85651
16
五、基本求导法则与导数公式
1. 常数和基本初等函数的导数
(C) 0
(x ) x1
(sin x) cos x (tan x) sec2 x
(cos x) sin x
(cot x) csc2 x
(sec x) sec x tan x (csc x) csc x cot x
6
（2）(uv) uv u v
证: 设 f (x) u(x)v(x) , 则有
f (x) lim f (x h) f (x) lim u(x h)v(x h) u(x)v(x)
h0
h
h0
h
lim
h 0
u(
x
h) h
v(x)
(a x ) a x ln a
(ex ) ex
(loga
x)
1 x ln a
(arcsin x) 1
1 x2
(arctan
2019/7/11
x)
1 1 x2
(ln x) 1
x
(arccos x) 1
1 x2
(arccot x) 1
1 x2
17
x)
1 x ln
a
(a 0, a 1)
（8）(ln x ) 1 x
2019/7/11
3
但是，对于比较复杂的函数，直接根据定义求它 们的导数往往很困难.
例如，求下列函数的导函数：
（1） y x3 ax 2cos x ； （2） y arctan x ；
（3） y e 12x ；
第二节 导数运算(知识梳理)
第二节 导数运算复习目标学法指导能利用基本初等函数的导数公式和导数的四则运算法则求简单函数的导数,并了解复合函数求导法则,能求简单复合函数(仅限于形如y=f(ax+b)的复合函数)的导数.1.熟记基本初等函数的导数公式及导数的运算法则,是解决复杂导数问题的基础.2.注意导数的运算法则的符号.3.复合函数求导,要分清复合函数的结构,恰当引入中间变量,将复合函数分解成较为简单的函数,然后求导.一、导数的运算法则1.[f(x)±g(x)]′=f ′(x)±g ′(x).2.[f(x)g(x)]′=f ′(x)g(x)+f(x)g ′(x).3.[()()f xg x ]′=()()()()()2f xg x f x g x g x ''-⎡⎤⎣⎦(g(x)≠0).二、复合函数的导数复合函数y=f(ax+b)的导数和函数y=f(u),u=ax+b的导数间的关系为y x′=[f(ax+b)]′=af′(u).与导数运算有关的结论(1)若c为常数,则[cf(x)]′=cf′(x);(2)[f1(x)+f2(x)+…+f n(x)]′=f′1(x)+f′2(x)+…+f′n(x);(3)[f1(x)·f2(x)·f3(x)·…·f n(x)]′=[f′1(x)·f2(x)·f3(x)·…·f n(x)]+[f1(x)·f′2(x)·f3(x)·…·f n(x)]+[f1(x)·f2(x)·f′3(x)·…·f n(x)]+…+[f1(x)·f2(x)·f3(x)·…·f′n(x)];(4)设y=f(u),u=g(x),则复合函数y=f(g(x))的导数为y′x=y′u·u′x.1.曲线y=13x3-2在点(-1,-73)处的切线的倾斜角为( B )(A)30°(B)45°(C)135° (D)-45°2.曲线y=xe x-1在点(1,1)处切线的斜率等于( C )(A)2e (B)e (C)2 (D)1解析:对y=xe x-1求导,得y′=e x-1+xe x-1,由导数的几何意义,得所求切线的斜率k=y′|x=1=2,故选C.3.若函数f(x)的导函数的图象关于原点对称,则函数f(x)的解析式可能是( A )(A)f(x)=3cos x (B)f(x)=x3+x2(C)f(x)=1+2sin x (D)f(x)=e x +x解析:A 中f ′(x)=-3sin x 为奇函数,B 中 f ′(x)=3x 2+2x 非奇非偶函数,C 中f ′(x)=2cos x 为偶函数,D 中f ′(x)=e x +1非奇非偶函数. 故选A.4.已知函数f(x)=x 3-3x,函数f(x)的图象在x=0处的切线方程是 ;函数f(x)在区间[0,2]内的值域是 . 解析:函数f(x)=x 3-3x,切点坐标(0,0),导数为y ′=3x 2-3,切线的斜率为-3,所以切线方程为y=-3x; 3x 2-3=0,可得x=±1,x ∈(-1,1),y ′<0,函数f(x)是减函数,x ∈(1,+∞),y ′>0,函数f(x)是增函数,f(0)=0,f(1)=-2,f(2)=8-6=2, 函数f(x)在区间[0,2]内的值域是[-2,2]. 答案:y=-3x [-2,2]5.已知函数f(x)=(ax+1)ln x,f ′(x)为f(x)的导函数,若f ′(1)=3,则实数a 的值为 .解析:根据题意,f ′(x)=1 ax x +aln x,所以f ′(1)=a+1=3,故a=2. 答案:2考点一 导数的四则运算 [例1] 求下列各函数的导数. (1)y=4x+1x ; (2)y=e x sin x;(3)y=ln xx;(4)y=cos(2x+5).解:(1)y=4x+1x ,则y′=4-21x.(2)y=e x sin x,则y′=e x sin x+e x cos x.(3)y=ln xx ,则y′=21ln xx-.(4)y=cos(2x+5),则y′=-sin(2x+5)·(2x+5)′=-2sin(2x+5).导数的计算方法(1)连乘积形式:先展开化为多项式的形式,再求导.(2)分式形式:观察函数的结构特征,先化为整式函数或较为简单的分式函数,再求导.(3)对数形式:先化为和、差的形式,再求导.(4)根式形式:先化为分数指数幂的形式,再求导.(5)三角形式:先利用三角函数公式转化为和或差的形式,再求导. 求满足下列条件的函数f(x).(1)f(x)是三次函数,且f(0)=3,f′(0)=0,f′(1)=-3,f′(2)=0;(2)f(x)是二次函数,且x2f′(x)-(2x-1)f(x)=1.解:(1)由题意设f(x)=ax3+bx2+cx+d(a≠0),则f′(x)=3ax2+2bx+c,由已知得()()()()03,00,1323,21240.⎧==⎪'==⎪⎨'=++=-⎪⎪'=++=⎩f df cf a b cf a b c解得a=1,b=-3,c=0,d=3,故f(x)=x 3-3x 2+3.(2)由题意设f(x)=ax 2+bx+c(a ≠0), 则f ′(x)=2ax+b.所以x 2(2ax+b)-(2x-1)(ax 2+bx+c)=1, 化简得(a-b)x 2+(b-2c)x+c=1, 因为此式对任意x都成立,所以,2,1,=⎧⎪=⎨⎪=⎩a b b c c解得a=2,b=2,c=1, 故f(x)=2x 2+2x+1.考点二 导数运算的综合问题[例2] (1)设曲线y=11x x +-在点(3,2)处的切线与直线ax+y+1=0垂直,则a 等于( )(A)2 (B)1 (C)-1 (D)-2(2)设函数f(x)在R 上可导,f(x)=x 2f ′(1)-2x+1,则f(a 2-a+2)与f(1)的大小关系是( )(A)f(a 2-a+2)>f(1) (B)f(a 2-a+2)=f(1) (C)f(a 2-a+2)<f(1) (D)不确定解析:(1)因为y=11x x +-, 所以y ′=-()221x -.因为x=3,所以y ′=-12即切线斜率为-12, 因为切线与直线ax+y+1=0垂直, 直线ax+y+1=0的斜率为-a.所以-12·(-a)=-1得a=-2.故选D.(2)由题意,f ′(x)=2f ′(1)x-2,则f ′(1)=2f ′(1)-2,可得f ′(1)=2,则f(x)=2x 2-2x+1,由二次函数性质可知,函数f(x)在(12,+∞)上单调递增,因为a 2-a+2=(a-12)2+74>1>12,所以f(a 2-a+2)>f(1),故选A.[例3] (1)设函数f(x)=g(x)+x 2,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则曲线y=f(x)在点(1,f(1))处切线的斜率是( )(A)4 (B)-14 (C)2 (D)-12(2)已知曲线y=x+ln x 在点(1,1)处的切线与曲线y=ax 2+(a+2)x+1相切,则a= .解析:(1)由导数的几何意义,得g ′(1)=2,求导函数得 f ′(x)=g ′(x)+2x,k=f ′(1)=g ′(1)+2=4,故选A. (2)法一 因为y ′=1+1x , 所以y ′|x=1=2,所以y=x+ln x 在点(1,1)处的切线方程为 y-1=2(x-1), 所以y=2x-1.又切线与曲线y=ax 2+(a+2)x+1相切, 当a=0时,y=2x+1与y=2x-1平行,故a ≠0,由()221,21,y ax a x y x ⎧=+++⎪⎨=-⎪⎩得ax2+ax+2=0,因为Δ=a2-8a=0,所以a=8.法二因为y′=1+1x,所以y′|x=1=2,所以y=x+ln x在点(1,1)处的切线方程为y-1=2(x-1), 所以y=2x-1,又切线与曲线y=ax2+(a+2)x+1相切,当a=0时,y=2x+1与y=2x-1平行,故a≠0.因为y′=2ax+(a+2),所以令2ax+a+2=2,得x=-12,代入y=2x-1,得y=-2,所以点(-12,-2)在y=ax2+(a+2)x+1的图象上,故-2=a×(-12)2+(a+2)×(-12)+1,所以a=8.答案:(1)A (2)8[例4] 设函数y=x2-2x+2的图象为C1,函数y=-x2+ax+b的图象为C2,已知过C1与C2的一个交点的两切线互相垂直.(1)求a,b之间的关系;(2)求ab的最大值.解:(1)对于C1:y=x2-2x+2,有y′=2x-2,对于C2:y=-x2+ax+b,有y′=-2x+a,设C1与C2的一个交点为(x0,y0),由题意知过交点(x0,y0)的两条切线互相垂直.所以(2x 0-2)·(-2x 0+a)=-1, 即420x -2(a+2)x 0+2a-1=0,①又点(x 0,y 0)为C 1与C 2的交点,故有200020022,,y x x y x ax b ⎧=-+⎪⎨=-++⎪⎩ ⇒220x -(a+2)x 0+2-b=0.②由①②消去x 0,可得a+b=52.(2)由(1)知,b=52-a, 所以ab=a(52-a)=-(a-54)2+2516. 所以当a=54时,(ab)max =2516. 曲线f(x)在点(x 0,f(x 0))处的切线方程为Ax+By+C=0有三层含义:一是点在曲线上,二是点在切线上,三是函数f(x)在点x=x 0处的导数等于切线的斜率,即f ′(x 0)=- A B .1.若函数f(x)满足f(x)=13x 3-f ′(1)·x 2-x,则f ′(2)的值为( A ) (A)3 (B)1 (C)0 (D)-1 解析:f ′(x)=x 2-2f ′(1)x-1,令x=1,得f ′(1)=-2f ′(1) ,解得f ′(1)=0, 所以f ′(x)=x 2-1. 所以f ′(2)=3. 故选A.2.设函数f(x)=ax 3+3x,其图象在点(1,f(1))处的切线l 与直线x-6y-7=0垂直,则直线l 与坐标轴围成的三角形的面积为( B )(A)1 (B)3 (C)9 (D)12解析:f′(x)=3ax2+3,由题设得f′(1)=-6,所以3a+3=-6,a=-3,所以f(x)=-3x3+3x,f(1)=0,切线l的方程为y-0=-6(x-1),即y=-6x+6.所以直线l与坐标轴围成的三角形的面积为S=12×1×6=3.故选B.3.直线y=kx+1与曲线y=x3+ax+b相切于点A(1,3),则2a+b的值为( C )(A)2 (B)-1 (C)1 (D)-2解析:因为y=x3+ax+b,所以y′=3x2+a;由题意得13,3,13,ka ka b+=⎧⎪+=⎨⎪++=⎩解得2,1,3,kab=⎧⎪=-⎨⎪=⎩则2a+b=-2+3=1.故选C.4.设点P是曲线y=x3-3x+23上的任意一点,则P点处切线倾斜角α的取值范围为( C )(A)[0,π2)∪[5π6,π) (B)[2π3,π)(C)[0,π2)∪[2π3,π) (D)(π2,5π6]解析:因为y′=3x2-3≥-3,故切线斜率k≥-3,所以切线倾斜角α的取值范围是[0,π2)∪[2π3,π).故答案为C.类型一导数的计算1.设f0(x)=sin x,f1(x)=f′0(x),f2(x)=f′1(x),……,f n+1(x)=f′n(x),x∈N,则f2 020(x)等于( C )(A)cos B·cos C=14(B)-cos x(C)sin x (D)-sin x解析:根据题意,f0(x)=sin x,f1(x)=f′0(x)=cos x,f2(x)=f′1(x)=-sin x,f3(x)=f′2(x)=-cos x,f4(x)=f′3(x)=sin x,则有f0(x)=f4(x),f1(x)=f5(x),……则f2 020(x)=f4(x)=sin x.故选C.2.已知函数f(x)的导函数为f′(x),满足f(x)=2xf′(2)+x3,则f′(2)等于( B )(A)-8 (B)-12 (C)8 (D)12解析:因为f(x)=2xf′(2)+x3,所以f′(x)=2f′(2)+3x2;令x=2,则f′(2)=2f′(2)+12,得f′(2)=-12.故选B.类型二导数运算的综合问题3.直线y=12x+b与曲线y=-12x+ln x相切,则b的值为( A )(A)-1 (B)-2 (C)-12(D)1解析:设切点为(x0,-12x0+ln x0),则斜率为k=-12+1x,由题意知-12+1x=12,所以x0=1.所以切点为(1,-12),又因为切点在切线y=12x+b上,所以-12=12+b.所以b=-1.故选A.4.已知f′(x)是函数f(x)的导函数,如果f′(x)是二次函数,f′(x)的图象开口向上,顶点坐标为那么曲线y=f(x)上任意一点处的切线的倾斜角α的取值范围是( B )(A)(0,π3] (B)[π3,π2)(C)[π2,2π3] (D)[π3,π)解析:由题意知f′(x)=a(x-1)2所以f′(x)=a(x-1)2即tan所以α∈[π3,π2).故选B.5.(2019·全国Ⅰ卷)曲线y=3(x2+x)e x在点(0,0)处的切线方程为.解析:y′=3(x2+3x+1)e x,故切线斜率k=y′|x=0=3,故切线方程为y=3x. 答案:y=3x6.已知函数y=f(x)及其导函数y=f′(x)的图象如图所示,则曲线y=f(x)在点P处的切线方程是.解析:根据导数的几何意义及图象可知,曲线y=f(x)在点P 处的切线的斜率k=f ′(2)=1,又过点P(2,0),所以切线方程为x-y-2=0. 答案:x-y-2=07.已知f(x)=ln x,g(x)=12x 2+mx+72(m<0),直线l 与函数f(x),g(x)的图象都相切,且与f(x)图象的切点为(1,f(1)),则m 等于 . 解析:因为f ′(x)=1x, 所以直线l 的斜率为k=f ′(1)=1,又f(1)=0,所以切线l 的方程为y=x-1.g ′(x)=x+m,设直线l 与g(x)的图象的切点为(x 0,y 0), 则有00020001,1,17,22x m y x y x mx ⎧⎪+=⎪=-⎨⎪⎪=++⎩又m<0,于是解得m=-2.答案:-28.已知函数f(x)=12x 2-aln x,(a ∈R). (1)若y=f(x)在x=2处的切线方程为y=x+b,求a,b 的值;(2)若f(x)在(1,+∞)上为增函数,求a 的取值范围.解:(1)因为f ′(x)=x-a x(x>0), 又f(x)在x=2处的切线方程为y=x+b,所以2ln 22,21,2a b a -=+⎧⎪⎨-=⎪⎩所以2,2ln 2.a b =⎧⎨=-⎩(2)因为f(x)在(1,+∞)上为增函数,所以f ′(x)=x-a x≥0在(1,+∞)上恒成立. 即a ≤x 2在(1,+∞)上恒成立,所以有a ≤1.。