LTI系统的单位冲激响应.ppt
合集下载
§2-1 LTI系统的时间方程

⑶ 求齐次通解中的待定系数,确定自由响应。
由于自由项中没有出现冲激,初始条件 y(0 ) y(0 ) y(0 ) y(0 ) 1 于是有
1 y (0 ) 1 A1 A2 2 3 y(0 ) 1 A1 2 A2 2
y(t ) yh (t ) y p (t ) 1 3t t 2t A1e A2 e e 2
大连海事大学信息科学技术学院
《信号与系统》
§2-1 线性时不变系统的时间方程
系统方程只涉及到输入信号:e(t)与输出信号:i(t),因此成为 系统的输入输出方程。方程中各项的系数均是常数,且左边的各项, 就是输出信号与其各阶导函数的组合,因此称方程为常系数线性微 分方程。
N阶常系数线性微分方程的一般形式为:
a 1
于是系统输出在t=0时刻的跳变值:
y(0 ) 1 , y(0 ) 0
y(0 ) y(0 ) y(0 ) 1
大连海事大学信息科学技术学院
因此,系统的初始条件为:
y(0 ) y(0 ) y(0 ) 2
《Signals & Systems》
《Signals & Systems》 大连海事大学信息科学技术学院
《信号与系统》
§2-1 线性时不变系统的时间方程
因为回路的输入电压
2 1
C
L
e(t ) 10u(t ) 20u(t ) 10 10u(t )
R
20V 10V
e(t )
i (t )
de (t ) 10 (t ) dt
将其代入方程左边,并使方程平衡
d 2 y p (t ) dt 2
《Signals & Systems》
信号与系统 系统函数完美版PPT

m
j
j1
H(s) H(z) 当t -> ∞ 时,对应的响应函数趋近于零。 n
n
A(s) A(z) 4) H(z)在单位圆上的二阶及二阶以上的极点,
(s p ) (z p ) 全通函数:如果系统的幅频响应|H(jω)|对所有的ω均为常数,i 则称该系统为全通系统,相应的系统函数称为全通函数。 i
极点pi 和零点ζj 的值可能是实数或复数。若A(·)和 B(·)的系数
都是实数,则零、极点若为复数,必共轭成对。
二、系统函数与时域响应
系统的冲激响应或单位序列响应的函数形式由A(·)的根确定, 即由H(·)的极点确定;而自由响应的形式也由H(·)极点确定。
t
jω
t
t σ
t
t
t
H(s)的极点与所对应的响应函数
ห้องสมุดไป่ตู้
2π
1
H| jω | Φ(ω)
一律平等地传输,因而被称为全通系统,其系统函
数称为全通函数。
()121222arc2 t2a 2n 2)ω(
最小相移函数:
如有一系统函数Ha(s),
有两个极点-s1和-s1*, 两个零点-s2和-s2*, 都在左半开平面:
H 系统a函(s数)Ha(s)(可(ss以写为ss:12))((ssjωss1*2*))
Hi(1j)bmB1B2Bm
A1A2An
幅频响应
() (1 2 m ) (1 2 n )相频响应
全通函数:如果系统的幅频响应|H(jω)|对所有的ω均为常
数,则称该系统为全通系统,相应的系统函数称为全通函数。
如有二阶系统,
其系统函数在左半平面有一对共轭极点:p1,2 =-α±jβ,
信号与系统第三章

例3.1-2 描述一阶LTI系统的常系数微分方程如 式(3.1-3)所示
设 f (t) 2 a 2, b 1 则有
dy(t) 2 y(t) 2 dt
已知初始值 y(0) 4 求 t 0时系统的响应 y(t)
解:第一步,由方程可知系统的特征方程为 2 0
2 由此可得系统的齐次解为
2
处理教研室
第三章 连续信号与系统的时域分析
教学重点:
1、常微分方程的建立及其解的基本特点; 2、阶跃响应和冲激响应的概念; 3、卷积及其在系统分析中的应用。
2020/6/7
信号
3
处理教研室
应用实例:汽车点火系统
汽车点火系统主要由电源(蓄电池和发电机)、电阻、 点火开关、点火线圈、分压器等组成。
系数 a,b都是常量。系统的阶数就是其数学模型——
微分方程的阶数。
而 n 阶常系数线性微分方程的一般形式为
an
dn y(t) dt n
an1
dn1 y(t) dt n1
L
a1
dy(t) dt
a0
y (t )
bm
dm f (t) dt m
bm1
dm1 f (t) dt m1
L
b1
df (t) dt
b0
即yf’(0+) = yf’(0-) = 0,yf(0+) = yf(0-) = 0
对t>0时,有 yf”(t) + 3yf’(t) + 2yf(t) = 6
不难求得其齐次解为Cf1e-t + Cf2e-2t,其特解为常数3,
于是有
yf(t)=Cf1e-t + Cf2e-2t + 3
代入初始值求得
设 f (t) 2 a 2, b 1 则有
dy(t) 2 y(t) 2 dt
已知初始值 y(0) 4 求 t 0时系统的响应 y(t)
解:第一步,由方程可知系统的特征方程为 2 0
2 由此可得系统的齐次解为
2
处理教研室
第三章 连续信号与系统的时域分析
教学重点:
1、常微分方程的建立及其解的基本特点; 2、阶跃响应和冲激响应的概念; 3、卷积及其在系统分析中的应用。
2020/6/7
信号
3
处理教研室
应用实例:汽车点火系统
汽车点火系统主要由电源(蓄电池和发电机)、电阻、 点火开关、点火线圈、分压器等组成。
系数 a,b都是常量。系统的阶数就是其数学模型——
微分方程的阶数。
而 n 阶常系数线性微分方程的一般形式为
an
dn y(t) dt n
an1
dn1 y(t) dt n1
L
a1
dy(t) dt
a0
y (t )
bm
dm f (t) dt m
bm1
dm1 f (t) dt m1
L
b1
df (t) dt
b0
即yf’(0+) = yf’(0-) = 0,yf(0+) = yf(0-) = 0
对t>0时,有 yf”(t) + 3yf’(t) + 2yf(t) = 6
不难求得其齐次解为Cf1e-t + Cf2e-2t,其特解为常数3,
于是有
yf(t)=Cf1e-t + Cf2e-2t + 3
代入初始值求得
§2-1 LTI系统的零状态响应

1
1 2
x(τ)
1 −1 0 1
τ
τ2 t2 1 当1<t<2 y (t ) = ∫ (t − τ + 1)dτ = (tτ − + τ) t −1 = 2 − 2 2 t −1
∞
h(t − τ)
1
t − 10 t
1
t +1
τ
当t>2
y (t ) =
−∞
∫ x(τ)h(t − τ)dτ = 0
h(t − τ)
−∞
u (t − τ ) d τ
1
0
1
u (−τ)
以上积分式的积分的上下限为(1~t),积 分结果的定义区间为(1~∞),所以后面要乘 分结果的定义区间为(1~ (1~∞ 以u(t-1)。
t t
1
0
t =0
τ
u (t − τ)
1 t <1 0 t
y 2 (t ) = − ∫ e − ( t − τ ) d τ = − e − t ∫ e τ d τ
大连海事大学信息科学技术学院
《信号与系统》 信号与系统》
∞ ∞
第二章
LTI系统的时域分析 LTI系统的时域分析
y (t ) =
=
−∞ ∞
∫ x ( τ ) h (t − τ ) d τ =
−(t − τ)
−∞
u ( τ ) e − ( t − τ ) u (t − τ ) d τ ∫
u (τ)
1
0
x (t ) = u (t )
,
h (t ) = e − t u (t )
求系统的零状态响应 解:
y (t ) = x (t ) ∗ h (t )
1 2
x(τ)
1 −1 0 1
τ
τ2 t2 1 当1<t<2 y (t ) = ∫ (t − τ + 1)dτ = (tτ − + τ) t −1 = 2 − 2 2 t −1
∞
h(t − τ)
1
t − 10 t
1
t +1
τ
当t>2
y (t ) =
−∞
∫ x(τ)h(t − τ)dτ = 0
h(t − τ)
−∞
u (t − τ ) d τ
1
0
1
u (−τ)
以上积分式的积分的上下限为(1~t),积 分结果的定义区间为(1~∞),所以后面要乘 分结果的定义区间为(1~ (1~∞ 以u(t-1)。
t t
1
0
t =0
τ
u (t − τ)
1 t <1 0 t
y 2 (t ) = − ∫ e − ( t − τ ) d τ = − e − t ∫ e τ d τ
大连海事大学信息科学技术学院
《信号与系统》 信号与系统》
∞ ∞
第二章
LTI系统的时域分析 LTI系统的时域分析
y (t ) =
=
−∞ ∞
∫ x ( τ ) h (t − τ ) d τ =
−(t − τ)
−∞
u ( τ ) e − ( t − τ ) u (t − τ ) d τ ∫
u (τ)
1
0
x (t ) = u (t )
,
h (t ) = e − t u (t )
求系统的零状态响应 解:
y (t ) = x (t ) ∗ h (t )
第五章1-连续LTI系统频域分析

第5章 系统的频域分析
连续时间LTI系统的频域分析 离散时间LTI系统的频域分析 信号的幅度调制和解调
时域分析的要点是,以冲激函数为基本信号,
任意输入信号可分解为一系列冲激函数;而系统零 状态响应yzs(t) = x(t)*h(t)。 由单位冲激函数δ (t)所引起的零状态响应称为单位 冲激响应,简称冲激响应,记为h(t)。
解: 利用H(j)与h(t)的关系
H ( j) F[h(t)] 1 1 j 1 j 2
1
( j)2 3( j) 2
只有当连续系统是稳定的LTI系统时,才存在H(j), 且可以由h(t)计算出H(j)。
电路系统的频率响应:
分析电路系统的频率响应,主要有两种方法。
H ( j) Yzs ( j)
( j) 3
X ( j) ( j)2 3( j) 2
在实际应用中, 只有当连续系统是稳定的LTI系统时,
才存在H(j),且频响函数才有意义。
例 已知某LTI系统的冲激响应为
h(t) = (e-t-e-2t) u(t),求系统的频率响应H(j)。
vR (t) RiR (t)
VR ( jw) R IR ( jw)
ZR
VR ( IR(
jw) jw)
R
vL
(t)
L
diL (t) dt
VL ( jw) jwLIL ( jw)
ZL
VL ( jw) IL ( jw)
jwL
iC
(t)
C
d
vC (t) dt
IC ( jw) jwCVC ( jw)
例 已知某LTI系统的动态方程为 y"(t) + 3y'(t) + 2y(t) = x(t),
连续时间LTI系统的频域分析 离散时间LTI系统的频域分析 信号的幅度调制和解调
时域分析的要点是,以冲激函数为基本信号,
任意输入信号可分解为一系列冲激函数;而系统零 状态响应yzs(t) = x(t)*h(t)。 由单位冲激函数δ (t)所引起的零状态响应称为单位 冲激响应,简称冲激响应,记为h(t)。
解: 利用H(j)与h(t)的关系
H ( j) F[h(t)] 1 1 j 1 j 2
1
( j)2 3( j) 2
只有当连续系统是稳定的LTI系统时,才存在H(j), 且可以由h(t)计算出H(j)。
电路系统的频率响应:
分析电路系统的频率响应,主要有两种方法。
H ( j) Yzs ( j)
( j) 3
X ( j) ( j)2 3( j) 2
在实际应用中, 只有当连续系统是稳定的LTI系统时,
才存在H(j),且频响函数才有意义。
例 已知某LTI系统的冲激响应为
h(t) = (e-t-e-2t) u(t),求系统的频率响应H(j)。
vR (t) RiR (t)
VR ( jw) R IR ( jw)
ZR
VR ( IR(
jw) jw)
R
vL
(t)
L
diL (t) dt
VL ( jw) jwLIL ( jw)
ZL
VL ( jw) IL ( jw)
jwL
iC
(t)
C
d
vC (t) dt
IC ( jw) jwCVC ( jw)
例 已知某LTI系统的动态方程为 y"(t) + 3y'(t) + 2y(t) = x(t),
【VIP专享】第三章(2)冲激序列响应及卷积和
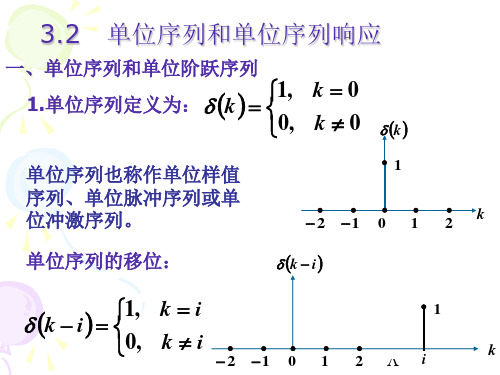
1 1, 2 2
hk C1 1k C22k
代入初值得
h0 h1
C1 C2 1 C1 2C2
1
hk
1 3
1k
2 3
2k
k
C1
C 2
1 3 2 3
例3.2-2 求图示离散系统的单位序列响应。
1
D D f k
xk
xk 1
xk 2
1
yk
1
2
解(1)写差分方程
xk xk 1 2xk 2 f k
g1
g 2
0
由方程利用迭代得:
g0 g1 2g 2 1 1
g1
g0
2g
1
1
2
阶跃响应满足方程:
gk gk 1 2gk 2 k
g0 1, g1 2
1 1, 2 2
gk
C1 1k
C2 2k
1 2
,
k0
g0 g1
C1
C2
1 2
1
1 C1 2C2 2
2
C1 C2
a1 a1
k0
k1, k2 可为正或 负整数,但 k2 k1
3
aj
1
j0
1a
a 1
4
aj
a k1
j k1
1a
a 1
k1 可为正或负 整数
序号 5 6
7
公式
说明
k j kk 1
j0
2
k0
k2
j
j k1
k1 k2
k2 k1 1 2
k1, k2 可为正或负 整数,但 k2 k1
yk
xk
xk
§3.7 用单位抽样响应表示系统的性质
目 录 29
2)、可否由已知的三个初始条件确定系数? 不行!
由于输入 2 (n) 在n=0时加入系统,
必然 y(0) 1已经含有输入引起的初始 条件,必须剔除它。而 y0(3)是在n=0 之前就有的初始条件,我们设法求解它
目 录 30
对原方程设n=0,则
2 y(0) 12 y(1) 24 y(2) 16 y(3) 2
2 y(n) 12 y(n 1) 24 y(n 2) 16 y(n 3) x(n) 2 (n)
y(0) 1, y(1) 1, y(2) 11 8
解:1)根据特征方程 2 p3 12 p2 24 p 16 2( p 2)3 0 y0(n) (C1 C2n C3n2 )(2)n
的零输入响应?
y0[1] 1 y0[2] 11/ 8 y0[3] 21/16
解: 其特征方程为 ( 2)3 0 2 为方程的三重特征根
y[n] (c1n2 c2n c3 )(2)n
代入初始条件,得 c1 0,c2 5/ 4,c3 3/ 4, y0[n] 5 / 4n[2]n 3 / 4[2]n
目 录 27
3、在用经典法求全响应时,可以用以上
y(k )求得全响应的待定系数。因为它
同时反映了系统初态及输入信号作用 共同引起的初态的变化;但是不能用 Y(k)确定零输入响应的待定系数 4、为了确定零输入响应的系数,必须求 得信号没有加入之前的系统的初始状 态引起的初始条件
目 录 28
例:已知系统的差分方程,求零输入响应
目 录 26
有关初始条件的讨论 1、以上两个例题所给的初始条件 y0(1)
y0(2) y0(k) 等都是系统在未加入输入 信号时的起始状态,可以用来求解零 输入响应的未知系数 2、但是当微分方程有x(n)作用时,它同样 对系统的初态有影响,记为 yx (k)。它 们共同引起的初始条件记为y(k) y0(k) yx (k)
2)、可否由已知的三个初始条件确定系数? 不行!
由于输入 2 (n) 在n=0时加入系统,
必然 y(0) 1已经含有输入引起的初始 条件,必须剔除它。而 y0(3)是在n=0 之前就有的初始条件,我们设法求解它
目 录 30
对原方程设n=0,则
2 y(0) 12 y(1) 24 y(2) 16 y(3) 2
2 y(n) 12 y(n 1) 24 y(n 2) 16 y(n 3) x(n) 2 (n)
y(0) 1, y(1) 1, y(2) 11 8
解:1)根据特征方程 2 p3 12 p2 24 p 16 2( p 2)3 0 y0(n) (C1 C2n C3n2 )(2)n
的零输入响应?
y0[1] 1 y0[2] 11/ 8 y0[3] 21/16
解: 其特征方程为 ( 2)3 0 2 为方程的三重特征根
y[n] (c1n2 c2n c3 )(2)n
代入初始条件,得 c1 0,c2 5/ 4,c3 3/ 4, y0[n] 5 / 4n[2]n 3 / 4[2]n
目 录 27
3、在用经典法求全响应时,可以用以上
y(k )求得全响应的待定系数。因为它
同时反映了系统初态及输入信号作用 共同引起的初态的变化;但是不能用 Y(k)确定零输入响应的待定系数 4、为了确定零输入响应的系数,必须求 得信号没有加入之前的系统的初始状 态引起的初始条件
目 录 28
例:已知系统的差分方程,求零输入响应
目 录 26
有关初始条件的讨论 1、以上两个例题所给的初始条件 y0(1)
y0(2) y0(k) 等都是系统在未加入输入 信号时的起始状态,可以用来求解零 输入响应的未知系数 2、但是当微分方程有x(n)作用时,它同样 对系统的初态有影响,记为 yx (k)。它 们共同引起的初始条件记为y(k) y0(k) yx (k)
第2章 线性时不变系统
y(t ) x( )h(t )d h( ) x(t )d
0 t
2.4 LTI系统的性质
举例:累加系统(accumulator)
y[n]
k
x[k ]
n
它是LTI系统,其单位脉冲响应为
h[n] u[n]
h[n] k [n] Memory h[n] 0, n 0 Causal
2.4 LTI系统的性质
从以上推导得出以下结论: DT LTI 系统的单位阶跃响应是其单位脉冲响应的求和函数; DT LTI 系统的单位脉冲响应是其单位阶跃响应的一次差分 同理,对于CT LTI 系统: 单位阶跃响应是其单位冲激响应的积分函数
s(t ) h( )d
t
单位冲激响应是其单位阶跃响应的一阶导数
2.7小结
2.1概述
(1)线性与时不变性(Linearity and Time-Invariance): 很多物理过程都具有这两个性质 这些物理过程能用LTI系统表征 可以对LTI系统进行详细的分析:
能够将LTI系统的输入用一组基本信号的线性组合表示 根据该系统对基本信号的响应,利用叠加性质求得整个系统的输出
2.4 LTI系统的性质
离散时间LTI系统用 卷积和表示
连续时间LTI系统用 卷积积分表示
LTI系统的特性可以 完全由其单位冲激响 应决定
2.4 LTI系统的性质
卷积的交换律性质 The Commutative Property of Convolution
2.4 LTI系统的性质
卷积的三个代数性质:交换律、结合律、分配律 Three algebraic properties of convolution
0 t
2.4 LTI系统的性质
举例:累加系统(accumulator)
y[n]
k
x[k ]
n
它是LTI系统,其单位脉冲响应为
h[n] u[n]
h[n] k [n] Memory h[n] 0, n 0 Causal
2.4 LTI系统的性质
从以上推导得出以下结论: DT LTI 系统的单位阶跃响应是其单位脉冲响应的求和函数; DT LTI 系统的单位脉冲响应是其单位阶跃响应的一次差分 同理,对于CT LTI 系统: 单位阶跃响应是其单位冲激响应的积分函数
s(t ) h( )d
t
单位冲激响应是其单位阶跃响应的一阶导数
2.7小结
2.1概述
(1)线性与时不变性(Linearity and Time-Invariance): 很多物理过程都具有这两个性质 这些物理过程能用LTI系统表征 可以对LTI系统进行详细的分析:
能够将LTI系统的输入用一组基本信号的线性组合表示 根据该系统对基本信号的响应,利用叠加性质求得整个系统的输出
2.4 LTI系统的性质
离散时间LTI系统用 卷积和表示
连续时间LTI系统用 卷积积分表示
LTI系统的特性可以 完全由其单位冲激响 应决定
2.4 LTI系统的性质
卷积的交换律性质 The Commutative Property of Convolution
2.4 LTI系统的性质
卷积的三个代数性质:交换律、结合律、分配律 Three algebraic properties of convolution
冲激响应的拉普拉斯变换
冲激响应的拉普拉斯变换
冲激响应是指输入信号为单位冲激函数(Dirac函数)时,系
统的输出信号。
拉普拉斯变换是一种用于分析线性时不变(LTI)系统的数学工具。
假设系统的输入信号为 x(t),输出信号为 y(t),冲激响应为
h(t)。
根据拉普拉斯变换的定义,可以得到以下关系:
Y(s) = H(s) * X(s)
其中,Y(s)和X(s)分别为输出信号和输入信号的拉普拉斯变换,H(s)为系统的传递函数的拉普拉斯变换。
对于冲激响应,输入信号 X(s) 可以表示为:
X(s) = 1
将 X(s) 和 Y(s) 的值代入上述关系式,可以得到:
Y(s) = H(s)
因此,冲激响应的拉普拉斯变换即为系统的传递函数的拉普拉斯变换。
总结:冲激响应的拉普拉斯变换等于系统的传递函数的拉普拉斯变换。
第2章线性时不变系统
求解系统响应的卷积方法是系统分析的重要工具。
单位冲激响应h[n]完全描述了线性时不变系统的变换 规律。不同的系统输入,都在h[n]的作用下产生相应的 响应,因此,给定了一个LTI系统的单位冲激响应h[n]就 等于给定了该系统。
本书由天疯上传于世界工厂网-下载中心
从计算某一个特定点的角度来看
yy [n [n 0]
单冲激响应
本书由天疯上传于世界工厂网-下载中心
由时不变性可得:
[n k ] h[n k ]
利用LTI系统的齐次性可得:
x[n] [n k ] x[n]h[n k ]
利用LTI系统的叠加性和式:
y[n]
k
x[k ]h[n k ]
上式称为卷积和或者简称卷积。
单位冲激响应同样完全刻画了LTI系统的变 换规律。 不同的系统输入,都在单位冲激响应的作 用下产生相应的响应; 因此,给定了一个LTI系统的单位冲激响应, 就等于给定了该系统。
本书由天疯上传于世界工厂网-下载中心
例题2.3 已知给定的LTI系统的输入信号为
x(t ) e
t
u(t )
h(t ) u (t )
本书由天疯上传于世界工厂网-下载中心
M
N
M+N-1
本书由天疯上传于世界工厂网-下载中心
举一个限长度序列卷积的例子。
例题2.2 试求:
其中,
y[n] x[n] h[n]
x[n] [n] [n 1] [n 2] [n 3]
h[n] [n] [n 1] [n 2] [n 3]
特别地,我们有
u[n]
[n k ]
单位冲激响应h[n]完全描述了线性时不变系统的变换 规律。不同的系统输入,都在h[n]的作用下产生相应的 响应,因此,给定了一个LTI系统的单位冲激响应h[n]就 等于给定了该系统。
本书由天疯上传于世界工厂网-下载中心
从计算某一个特定点的角度来看
yy [n [n 0]
单冲激响应
本书由天疯上传于世界工厂网-下载中心
由时不变性可得:
[n k ] h[n k ]
利用LTI系统的齐次性可得:
x[n] [n k ] x[n]h[n k ]
利用LTI系统的叠加性和式:
y[n]
k
x[k ]h[n k ]
上式称为卷积和或者简称卷积。
单位冲激响应同样完全刻画了LTI系统的变 换规律。 不同的系统输入,都在单位冲激响应的作 用下产生相应的响应; 因此,给定了一个LTI系统的单位冲激响应, 就等于给定了该系统。
本书由天疯上传于世界工厂网-下载中心
例题2.3 已知给定的LTI系统的输入信号为
x(t ) e
t
u(t )
h(t ) u (t )
本书由天疯上传于世界工厂网-下载中心
M
N
M+N-1
本书由天疯上传于世界工厂网-下载中心
举一个限长度序列卷积的例子。
例题2.2 试求:
其中,
y[n] x[n] h[n]
x[n] [n] [n 1] [n 2] [n 3]
h[n] [n] [n 1] [n 2] [n 3]
特别地,我们有
u[n]
[n k ]
