材料力学 第02章作业(刘)06
材料力学答案第二章
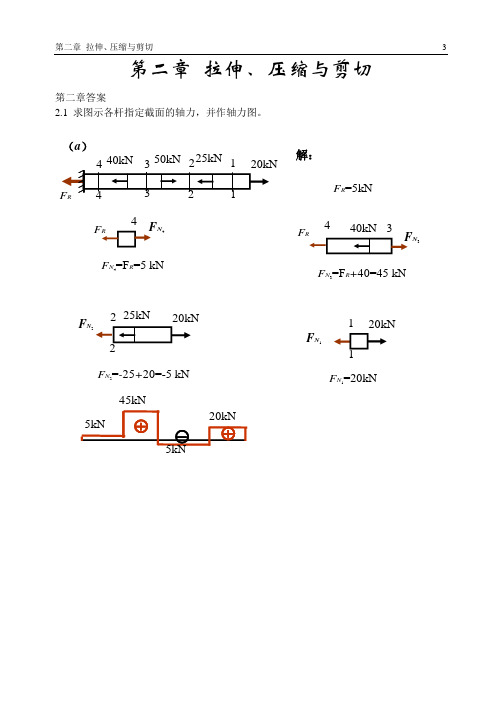
第二章 拉伸、压缩与剪切第二章答案2.1 求图示各杆指定截面的轴力,并作轴力图。
40kN 50kN 25kN(a )44F RF N440kN 3F N325kN 2F N220kN11F N1解:F R =5kN F N 4=F R =5 kNF N 3=F R +40=45 kNF N 2=-25+20=-5 kNF N 1=20kN45kN 5kN20kN5kN(b)110kN6kNF N1=10 kNF N2=10-10=0F N3=6 kN1—1截面:2—2截面:3—3截面:10kNF N11110kN10kN22F N26kN33F N32.2 图示一面积为100mm 200mm的矩形截面杆,受拉力F = 20kN的作用,试求:(1)6π=θ的斜截面m-m 上的应力;(2)最大正应力max σ和最大剪应力max τ的大小及其作用面的方位角。
解:320101MPa0.10.2P A σ⨯===⨯2303cos 14σσα==⨯=3013sin600.433MPa 222στ==⨯=max 1MPaσσ==max 0.5MPa2στ==F2.3 图示一正方形截面的阶梯形混凝土柱。
设重力加速度g = 9.8m/s 2, 混凝土的密度为33m /kg 1004.2⨯=ρ,F = 100kN ,许用应力[]MPa 2=σ。
试根据强度条件选择截面宽度a和b 。
ba解:24,aρ⋅3422.0410ρ=⨯⨯11[]aσσ=0.228ma ≥==22342424431001021040.2282104a b b ρρ=⋅+⋅=⨯⨯+⨯⨯⨯+⨯⨯⨯2[],bσσ≥0.398m 398mmb ≥==2.4 在图示杆系中,AC 和BC 两杆的材料相同,且抗拉和抗压许用应力相等,同为[]σ。
BC 杆保持水平,长度为l ,AC 杆的长度可随θ角的大小而变。
为使杆系使用的材料最省,试求夹角θ的值。
F F N Fθθsin ,0sin ,022F F F F F N N Y ==-=∑F F F F F N N N Xθθcos ,0cos ,0112==-=∑1A =2A A 2A 1解:[])sin cos cos sin 1(cos 1221θθθθσθ+=+=+=Fl l A l A V V V [])cot 2(tan θθσ+=Fl)cot tan cos sin cos sin cos sin 1(22θθθθθθθθ+=+=θθθθθ22sin 1)(,cos 1)(tan ,0-='='=ctg d d 由V 0sin 2cos 1)2(tan 22=-=+θθθθθctg d d 0cos 2sin ,0cos sin cos 2sin 222222=θ-θ=θθθ-θ44.54,2tan ,2tan 2===θθθ2.5 图示桁架ABC ,在节点C 承受集中载荷F 作用。
材料力学 第2章拉压

F1 + F2 + W cos 60o − FN cos15o = 0 得: FN sin15o − W cos 30o = 0
F2 = W cos 30o 解得:FN = W = 3.35W o sin15 F1 = FN cos15o − W (1 + cos 60o ) = 1.74W
§2.4
、概念
材料在拉伸时的力学性能
1、材料的力学性能: 材料的力学性能:
•材料在外力作用下表现出的变形、破坏等方面的特性称为材 料的力学性能也称为材料的机械性能或机械性质。 •材料的力学性能由材料试验分析系确定。 •常温静载试验:室温(20°C)下缓慢加载。
2、材料在拉伸时的力学性能: 材料在拉伸时的力学性能:
§2.7
一、 失效的概念
失效、 失效、安全系数和强度计算
1、定义:构件丧失正常承载功能称为失效。 构件失效的类型: 2、构件失效的类型:
•强度失效 由于材料屈服或断裂所致。 强度失效: 强度失效 •刚度失效 由于构件弹性变形过大不能正常工作所致。 刚度失效: 刚度失效 •失稳失效 失稳失效:不能维持原有平衡状态所致。 失稳失效
二、其他塑性材料拉伸时的力学性能
1、性能比较: 性能比较:
•均有线弹性阶段。 •均有强化阶段。 •不一定有屈服阶段。 •不一定有颈缩阶段。
2、无屈服阶段材料的屈 服指标: 服指标:
σ0.2—名义屈服极限。
三、铸铁拉伸时的力学性能
1、拉断前应变很小,伸长率也 拉断前应变很小, 很小。 很小。 应力应变非线性关系。 2、应力应变非线性关系。 3、强度极限:σb(唯一的强度 强度极限:
指标)
材料力学(金忠谋)第六版答案第02章

材料力学(金忠谋)第六版答案第02章习题2-1 一木柱受力如图示,柱的横截面为边长20cm的正方形,材料服从虎克定律,其弹性模量E??105MPa.如不计柱自重,试求:作轴力图;各段柱横截面上的应力;各段柱的纵向线应变;柱的总变形.解:轴力图AC段应力???100??260????106?a????a CB 段应力?????106?a????a AC段线应变???4N- 图??????10??105CB段线应变????????10?4 5??10 总变形??????10?4???10?4???10?3m 2-2 图(a)所示铆接件,板件的受力情况如图所示.已知:P=7 kN,t=,b1=,b2=,b3=。
试绘板件的轴力图,并计算板内的最大拉应力。
解: 轴力图?1?1???22?73?2??107?1 0?6???a ??2?107?10?6???a ?3? 7?107?10?6???a ??2最大拉应力?max??3???a 2-3 直径为1cm 的圆杆,在拉力P=10 kN的作用下,试求杆内最大剪应力,以及与横截面夹角为?=30o的斜截面上的正应力与剪应力。
解: 最大剪应力?max??2?12?2?107?6??10?10???a 221?d??14 ??30?界面上的应力???????2?1?cos2????3???a 2?sin2???sin30????a ?22-4 图示结构中ABC与CD均为刚性梁,C与D均为铰接,铅垂力P=20kN作用在C铰,若杆的直径d1=1cm,杆的直径d2=2cm,两杆的材料相同,E=200Gpa,其他尺寸如图示,试求两杆的应力;C点的位移。
解1杆的应力?(1)??1?d1244?20??12?107?10?6???a 2杆的应力?(2)?2?1?d2422?20??22?107?10? 6???a ?l1? C点的位移?(1)?l1?200?103?2??10?3m? ?20 0?10?c?2?2??1? ?l2??(2)l2??2??10? 3m? 2-5 某铣床工作台进给油缸如图示,缸内工作油压p?2MPa,油缸内径D=,活塞杆直径d=,已知活塞杆材料的许用应力????50Mpa。
材料力学课件刘鸿文第二章拉压X2资料

强度极限σb— 整个 σ — ε 曲线最高点
B、塑性指标(韧性指标)
e
延伸率 L1 L 100%
L
b
e P
a c s
b
f
5% 脆性材料
5% 塑性材料(韧性材料)
o
面积收缩率
A A1 100%
L
A
L1
3、卸载定律及冷作硬化:
e
d b f
b
e P
a c s
卸载定律:塑性材料被加
1、对 图的分析
分四个阶段:
第一阶段: (ob)弹性阶段
特点: 载荷去掉,变形会完
全消失
b
e P
a c s
弹性极限σe—
弹性阶段最高点b对应的应力值。
o
该段的oa段: (线弹性区)
σ 、ε成正比阶段的最高点对
、 成正比 比例极限σP— 应的应力值。
E ——胡克定律
E(=tgα)——弹性模量
特点(:二)、铸铁压缩
σ—ε曲线线型与拉伸时类似 (无σp、σs只有σb同样近似服
从胡克定律) 抗压强度极限远大于抗拉强度极限(高4 — 5倍) 破坏断口与轴线约成45°(39°)
※ 一般塑性材料、脆性材料的划分是就常温静载条件而言 ※塑性、脆性材料力学行为比较:
塑性材料抗拉能力远大于脆性材料;
就脆性材料本身讲,其抗压能力远大于抗拉能力;
塑性材料抗冲击、抗震动能力远大于脆性材料;由于塑性材 料破坏前变形较大,因而易于发现,脆性材料则易发突发性 的事故。故通过化学成分或工艺过程的改变,设法提高塑性 是有关的材料学科一直在研究着的。
三、 铸铁拉伸时的力学性能
特点: 应力小,变形很小便破坏,
材料力学(刘鸿文)第02章05、剪切和挤压

(2)若铆钉按图(b)排列,所需板宽b为多少?
F F F
b
F
材料力学
F
F
图(a) F
F
图(b)
材料力学
解: 可能造成的破坏: (1)因铆钉被剪断而使铆接被破坏;
(2)铆钉和板在钉孔之间相互挤压过大,而使铆接被 破坏;
(3)因板有钉孔,在截面被削弱处被拉断。 可采用假设的计算方法: 假定每个铆钉所受的力都是一样的。
L
材料力学
解:剪切面如图所示。剪
F/2 F
切面面积为:
A Lb
由剪切强度条件:
剪切面
F/2
Fs F / 2 [ ] A Lb
由挤压强度条件:
F L 100 mm 2b[ j ]
jy
Fb F /2 [ jy ] A jy b
材料力学
F 10mm 2b[ jy ]
例题5 厚度为
的主钢板用两块厚度为 t1 12mm
的同样 t2 6cm
材料的盖板对接如图示。已知铆钉直径为d=2cm,钢板的许用拉应 力 [ ] 160MPa ,钢板和铆钉许用剪应力和许用挤压应力相同,分 别为 [ j ] 100MPa, [ jy ] 280MPa 。若F=250KN,试求 (1)每边所需的铆钉个数n;
练习:P68,2.55-2.68
Fs A
材料力学
剪切强度条件:
Fs [ ] A
可解决三类问题: 1、选择截面尺寸; 2、确定最大许可载荷, 3、强度校核。
材料力学
名义许用剪应力
在假定的前提下进行 实物或模型实验,确 定许用应力。
例题1 图示冲床的最大冲压力为400KN,被冲剪钢板的剪切极限 应力为 300103 KN / m2 t。已知 d=34mm。 ,试求此冲床所能冲剪钢板的最大厚度 F 冲头 钢板 d 冲模 t
刘鸿文材力第二章拉压应力 机械 ...

轴力图,并求σmax . 解:⑴计算轴力 AB段:1—1截面
FN1 P A1 x1
BC段:2—2截面
(0 x1 l1 )
FN 2 P A1x1 A2 x2 l1
(l1 x2 l1 l2 )
工程认为,在弹性范围内材料服从胡克定律。
b
E
C F
2. 屈服阶段
s D e B C ' p A
O
C点对应应力s——屈服极限(下屈服点的应力值)。 试件出现大的塑性变形。
3. 强化(硬化)阶段
b s D C' e B p A
C
E F
O
E点对应应力b —— 强度极限,材料的最大抗力。
2
解:⑴计算木柱压力
P st A1
cos2 sin 2
2
P st A1 35106 2 2 104 14kN
压
⑵计算木柱的剪应力 P 14 103 2.19MPa 横截面上 4 A2 8 8 10 顺纹方向 30
m
1.截面法:
P Y
P
m
P
}
F N
FN
x P
保留左段时: Fx 0, FN P = 0,
FN = P
保留右段时:
P FN= 0,
F N =P
FN与FN等值反向,为一对作用力与反作用力,称轴力。
2.符号规定:
正号轴力 — FN 的方向与截面外法线方向一致。 负号轴力 — FN 的方向与截面外法线方向相反。 即: 拉伸为正、压缩为负。先设正方向。
材料力学网上作业题参考答案
东北农业大学网络教育学院材料力学网上作业题(2015更新版)绪论一、名词解释1.强度2. 刚度3. 稳定性4. 变形5. 杆件6.板或壳7.块体二、简答题1.构件有哪些分类2. 材料力学的研究对象是什么3. 材料力学的任务是什么4. 可变形固体有哪些基本假设5. 杆件变形有哪些基本形式6. 杆件的几何基本特征7.载荷的分类8. 设计构件时首先应考虑什么问题设计过程中存在哪些矛盾第一章轴向拉伸和压缩一、名词解释1.内力2. 轴力3.应力4.应变5.正应力6.切应力7.伸长率8.断面收缩率9. 许用应力 10.轴向拉伸 11. 冷作硬化二、简答题1.杆件轴向拉伸或压缩时,外力特点是什么2. 杆件轴向拉伸或压缩时,变形特点是什么3. 截面法求解杆件内力时,有哪些步骤4.内力与应力有什么区别5.极限应力与许用应力有什么区别6.变形与应变有什么区别7.什么是名义屈服应力8.低碳钢和铸铁在轴向拉伸时,有什么样的力学特性9.强度计算时,一般有哪学步骤10.什么是胡克定律11.表示材料的强度指标有哪些12.表示材料的刚度指标有哪些13.什么是泊松比14. 表示材料的塑性指标有哪些15.拉压杆横截面正应力公式适用范围是什么16.直杆轴向拉伸或压缩变形时,在推导横截面正应力公式时,进行什么假设三、计算题1. 试用截面法求下列各杆指定截面的轴力。
2. 试用截面法求下列各杆指定截面的轴力。
3. 试用截面法求下列各杆指定截面的轴力。
4. 试用截面法求下列各杆指定截面的轴力。
5. 试用截面法求下列各杆指定截面的轴力。
6. 试用截面法求下列各杆指定截面的轴力。
7 高炉装料器中的大钟拉杆如图a所示,拉杆下端以连接楔与大钟连接,连接处拉杆的横截面如图b所示;拉杆上端螺纹的小径d = 175 mm。
已知作用于拉杆上的静拉力F=850 kN,试计算大钟拉杆横截面上的最大静应力。
8 一桅杆起重机如图所示,起重杆AB为一钢管,其外径D = 20 mm,内径d≈18 mm;钢绳CB的横截面面积为10 mm2。
材料力学第二章习题选及其解答
2-1. 试求图示各杆1-1、2-2、3-3截面的轴力, 并作轴力图。
解: (a)(1)求约束反力kNR R X 500203040 0==-++-=∑(2)求截面1-1的轴力kNN NR X 500011==+-=∑(3)求截面2-2的轴力kNN NR X 10040 022==++-=∑(4)求截面3-3的轴力(a) (b)kNN NR X 2003040 033-==+++-=∑(5)画轴力图(b)(1)求截面1-1的轴力01=N(2)求截面2-2的轴力 PN4022==(3)求截面3-3的轴力PN P P NX 304 033==-+=∑(4)画轴力图2-2. 作用图示零件上的拉力P=38kN ,试问零件内最大拉应力发生于哪个横截面上?并求其值。
解:(1)1-1截面MPa A P 86.6720)2250(3103811=⨯-⨯==σ(2)2-2截面MPa A P 33.63152021038322=⨯⨯⨯==σ(3)3-3截面MPa A P 24.45215)2250(1038333=⨯⨯-⨯==σ(4)最大拉应力MPa 86.671max ==σσ2-3. 在图示结构中,若钢拉杆BC 的横截面直径为10mm ,试求拉杆内的应力。
设由BC 联接的两部分均为刚体。
3 3解:(1)以刚体CAE 为研究对象∑=⨯-⨯+⨯=035.15.4 0'P N N mC E A (2)以刚体BDE 为研究对象075.05.1 0=⨯-⨯=∑B E DN N m(3)联立求解kNN N N N N C EE C B 6 '=∴==(4)拉杆内的应力MPa A N B 4.7610410623=⨯⨯⨯==πσ 2-4. 图示结构中,1、2两杆的横截面直径分别为10mm 和20mm ,试求两杆内的应力。
设两根横梁皆为刚体。
解:(1)以整体为研究对象,易见A 处的水平约束反力为零; (2)以AB 为研究对象由平衡方程知0===A B B R Y X(3)以杆BD由平衡方程求得KNN N NY KNN N mC20010 01001101 021211==--===⨯-⨯=∑∑(4)杆内的应力为1MPa A N MPa A N 7.63204102012710410102322223111=⨯⨯⨯===⨯⨯⨯==πσπσ2-7. 某拉伸试验机的示意图如图所示。
材料力学作业及练习题参考答案(2、3章2016级)
※评分标准:Abs与Fbs正确,得3分(即Abs=d1、Fbs=F/2,或Abs=d2、Fbs =F/4);正确代入数据,结果正确,单位正确,得1分; 结论正确,得1分。
※要点:挤压强度条件;要明确挤压面及其上面的挤压力。
※易犯的错误:挤压面积、挤压力计算错误;计算结果无单位。 ※忌:① 不看题的要求,连同剪切强度一起校核;② 无结论。
第二章填空练习题参考答案
(1). ① d2/4 ② M/(2D) ③ [M/(2D)]/(d2/4) ④ db ⑤ M/(2D) ⑥ [M/(2D)]/(db)
(2). ① dh ② F ③ F/(dh) ④ (D2-d2)/4 ⑤ F ⑥ F/[(D2-d2)/4] (3). ① 2.4 (4). ① lb ② F ③ F/(lb) ④ ab ⑤ F ⑥ F/(ab) (5). ① 平板 (6). ① d (7). ① d=8t/ (8). ① 1 ② 1和2 (9). ① 300×106×(0.1×2+2×0.05)×0.005 N (注:R=0.05 m) (10). ① 刚度校核 (11). ① 强度小的构件 (12). ① (F/2)/(d2/4) ② F/(d1)
1
1
150 MPa,构件1和2的厚度1=16 mm,
2=8 mm,请校核螺栓的挤压强度。
2
2
2 F
解:1=22,挤压面d1上的bs 与挤压面d2上的bs 大小相同,按其中之一计 算。
挤压面d1上挤压力为F/2, bs=Fbs/Abs=(F/2)/(d1)
=(30×103/2)/(0.01×0.016)=93.75×106 Pa<[bs] 螺栓满足挤压强度条件。
1000 Nm 400 Nm
※评分标准:求得外力偶矩MA、MB、MC(最少须求出其中2个),且单位正 确,得2分;求得AD段及DB段的扭矩,并正确地画出扭矩图,得3分, 如扭矩图中无特征值,扣1分。
材料力学作业习题
第二章 轴向拉伸与压缩1、试求图示各杆1-1与2-2横截面上的轴力,并做轴力图。
(1) (2)2、图示拉杆承受轴向拉力F =10kN,杆的横截面面积A =100mm 2。
如以α表示斜截面与横截面的夹角,试求当α=10°,30°,45°,60°,90°时各斜截面上的正应力与切应力,并用图表示其方向。
3、一木桩受力如图所示。
柱的横截面为边长200mm 的正方形,材料可认为符合胡克定律,其弹性模量E =10GPa 。
如不计柱的自重,试求:(1)作轴力图;(2)各段柱横截面上的应力; (3)各段柱的纵向线应变;(4)柱的总变形。
4、(1)试证明受轴向拉伸(压缩)等于直径方向的线应变d ε。
(2)一根直径为d =10mm 的圆截面杆,在轴向拉力F 作用下,直径减小0、0025mm 。
如材料的弹性摸量E =210GPa,泊松比ν=0、3,试求轴向拉力F 。
(3)空心圆截面钢杆,外直径D =120mm,内直径d =60mm,材料的泊松比ν=0、3。
当其受轴向拉伸时, 已知纵向线应变ε=0、001,试求其变形后的壁厚δ。
5、图示A 与B 两点之间原有水平方向的一根直径d =1mm 的钢丝,在钢丝的中点C 加一竖直荷载F 。
已知钢丝产生的线应变为ε=0、0035,其材料的弹性模量E =210GPa,钢丝的自重不计。
试求:(1) 钢丝横截面上的应力(假设钢丝经过冷拉,在断裂前可认为符合胡克定律);(2) 钢丝在C点下降的距离∆;(3) 荷载F的值。
6、简易起重设备的计算简图如图所示、一直斜杆AB应用两根63mm×40mm×4mm不等边角钢组[σ=170MPa。
试问在提起重量为P=15kN的重物时,斜杆AB就是否满足强成,钢的许用应力]度条件?7、一结构受力如图所示,杆件AB,AD均由两根等边角钢组成。
已知材料的许用应力[σ=170MPa,试选择杆AB,AD的角钢型号。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4m C
4m
4m
正确解题步骤:(1)求出各杆内力; (2)由各杆强度求出载荷大小; (3)取最小值为许可载荷. 错误解题步骤: (1)设1杆达到最大值,判断2杆是否破坏; (2)2杆破坏,设2杆达到最大值,判断3杆是否破坏; (3) 如此循环
[孙题 孙题2-22] 图示结构,各杆均为两根等边角钢组成, 孙题 (P48) ) [σ] =170MPa, 试选择杆AC和CD的角钢型号.
3 =200(MPa)
σ bc 600
n
=
FN2 5 F ≤[σ c ] σ2 = = A2 2 A2
5F 5 × 28.2×10 3 ∴A2 ≥ =157(mm 2 ) = 2[σ c ] 2× 200
[单题 单题2-16] 图示结构,杆1和杆2为圆截面钢杆, [σ] =160MPa, 单题 d1=30mm, d2=20mm,确定许可载荷.
1 A a C a
2 E a B F
1 A a N1 A a C a C a
2 E a N2 E a B F B F
N1 A a C a
N2 E a B F
平衡方程:
∑m A =0 , N1 a + N 2 2 a F 3a = 0
1 A C l1
2 E l2 B F
变形协调方程: 物理方程:
B 30 1° 45 ° 2 C
A F 正确的解题步骤:(1)求出各杆内力; (2)由各杆强度求出载荷大小; (3)取最小值为许可载荷.
FN1 = 0.732 F
B 30 1° 45 ° 2 C
FN2 = 0.518F
FN1 0.732 F ≤[σ ] σ1 = = A1 A1
∴F ∴ ≤154.5kN
[孙题 孙题6-9] 图示阶梯状杆,下端 孙题 与支座距离δ=1mm,上,下段杆
A
的横截面面积分别为600mm2和 300mm2,材料的弹性模量E=
60kN
D
210GPa,试作杆的轴力图.
C 40kN B
δ
解:
A A
RAD 60kND源自60kNC 40kN B[例1] 图示结构,杆1为35号钢, σs =315MPa, 例
σb =530MPa, A1=3cm2,杆2为铸铁,抗拉强度极限σbt =180MPa ,抗拉强度极限σbc =600MPa , 安全因数均 为n=3.求:(1)按1杆的强度确定许可载荷; (2)在上 述的许可载荷下确定2杆的面积. C
RA A
220kN
220kN
RB B RA
4m C
4m
D
4m
A FAC FAC FCD C
解:[整体] 求支反力 [A节点] [C节点]
R A = RB = 220 kN
N AC = 366.7 kN
N CD = 293kN
AC杆:
N AC σ AC = ≤[σ ] 2 AAC
N AC 366.7×103 ∴AAC ≥ = =1078(mm 2 ) 2×170 2[σ ]
N2 N3 σ2= = 25( MPa ) σ 3 = = 25( MPa ) A A
试画出杆的轴力图. [刘题 刘题2.1a] 试画出杆的轴力图. 刘题 1 1 50 FN图 +
40kN 2
2
30kN 3
3
20kN
10 +
单位:kN
–
20
要求:上下对齐,标出大小, 要求:上下对齐,标出大小,标出正负
A1 60kN 20kN 200 40kN
40kN
A2
200
FN图 解: l =
+ –
20kN
FN1 = 20kN
FN 2 = 40kN
n F N i li ∑ i =1 E i Ai
F N1 l1 F N2 l 2 = + = 0.025+ 0.1 E1 A1 E 2 A2 = 0.075 mm
2
A
1 木
30°
B F
FN1 3F 3F ≤[σ ] σ1 = = 1 A1 A1 [σ ]1 A1 = 40.4( kN ) ∴F ≤ 3 FN2 = 2 F ≤[σ ]2 σ2=
A2
A2
[ F ]≤ 40.4( kN )
[σ ]2 A2 = 48( kN ) ∴F ≤ 2
[刘题 刘题2.18] 变截面杆,已知A1=8cm2, A2=4cm2, 刘题 E=200GPa,求杆的总伸长l.
315 [1杆]: ] = [σ = =105(MPa) n 3 F 5F σ 1 = N1 = ≤ [σ ] A1 2 A1
σs
∴F ≤
2[σ ] A1 = 2×105×300 5
5
= 28.2×10 3 ( N) = 28.2(kN )
∴许可载荷 [2杆]:[σ c ]=
[ F ]≤ 28.2(kN )
A F
FN2 0.518 F ≤[σ ] σ2= = A2 A2 ∴F ≤ 97.2kN
∴[ F ]= 97.2kN
[例3]图示结构,各杆均为圆截面钢杆,1,2,3杆的直径为 例 d1=30mm, 4,5,6,7,8杆的直径为 d2=20mm, 9杆 的直径为d3=40mm, [σ] =160MPa, 确定许可载荷. F
B 30 1° 45 ° 2
C
A F 错误解题步骤:1)设1杆达到最大值,判断2杆是否破坏; 2)2杆破坏,由2杆确定结构许可载荷; 3)设2杆达到最大值,求出1杆的内力 4)求许可载荷.
此方法不可取!
[单题 单题2-16] 图示结构,杆1和杆2为圆截面钢杆, [σ] =160MPa,
d1=30mm, d2=20mm,确定许可载荷.
A = 2×11.503= 23.006( cm 2 )
[孙题 孙题2-7] 等直杆,已知杆的横截面面积A和材料的弹性 孙题 模量E,试作轴力图,并求杆端点D的位移.
A
2F
l 3
B
2F
l 3
C
D F
l 3
+
FN图
+
F
–
F
F
[孙题 孙题6-4] 图示结构,AB为刚性杆,1杆和2杆的长度相等, 孙题 横截面面积相等,材料相同, A=1000mm2,F=50kN .试 求两杆的轴力和应力.
变形协调方程:
2l2 = l1 + l3
FN1l l1 = EA FN 2l l 2 = EA
物理方程:
FN 3l l3 = EA
[刘题 刘题2.43] 刘题 另解
1 A 2 B 3 C
l
a F FN1
A
a
FN2
B
FN3
C
a F
a
FN1
A
FN2
B
FN3
C
a F 平衡方程:
a
∑M A =0 ,
N 2 a N 3 2a = 0
N1 + N 2 N 3 F = 0
∑ Fy = 0 ,
1 A
2 B
3
5 FN1 = F 6
l3 l2
1 FN 2 = F 3
1 FN 3 = F 6
l1
变形协调方程: 物理方程:
2(l2 + l3 ) = l1 + l3
FN1l l1 = EA
FN 2l l 2 = EA
FN 3l l3 = EA
[例2] 图示结构,1杆为35号钢, σs =315MPa, 例
σb =530MPa, A1=3cm2,2杆为铸铁,抗拉强度极限σbt =180MPa ,抗压强度极限σbc =600MPa , 安全因数均 为n=3.求:(1)按1杆的强度确定许可载荷; (2)在上 述的许可载荷下确定2杆的面积.
D F H
试作轴力图, [单题 单题2-1(c)] 试作轴力图, 单题
2kN 3kN 2kN 3kN
FN
1kN
3kN
+
–
2kN
[刘题 刘题2.12] 刘题 图示结构,BC为钢杆,AB为木杆, 木杆的横截面面积 A1=100cm2,许用应力 [σ] 1 =7MPa,钢杆横截面面积 A2=6cm2,许用应力 [σ] 2 =160MPa,试求许可载荷F. 解: FN1 = 3 F C FN 2 = 2 F 钢
l2 = 2l1
N1l l1 = EA
N 2l l 2 = EA
[孙题 孙题6-5] 图示结构,AB为刚性杆,1杆和2杆为钢杆, [σ] 孙题 =170MPa, A1=400mm2, l1=1m, A2=200mm2, l2=1.8m,试 校核杆的强度. D q=30kN/m A 1 1m 2 B C E 2m
[孙题 孙题2-2] 试画出杆的轴力图.若横截面面积 孙题 A=400mm2,试求各横截面上的应力. 3 3 FN图 单位:kN 10 + – 10 – 20 20kN 2 2 10kN 1 1 20kN
要求:上下对齐,标出大小, 要求:上下对齐,标出大小,标出正负
N1 σ 1 = = 50( MPa ) A
l
FN1
A
FN2
B
FN3
C
a F
a
a F
a
FN1
A
FN2
B
FN3
C
a F 平衡方程:
a
∑M A =0 ,
N 2 a + N 3 2a = 0
N1 + N 2 + N 3 F = 0
∑ Fy = 0 ,
1 A
2 B
3 C
l
5 FN1 = F 6
1 FN 2 = F 3
