9-5简谐运动动的合成
大学物理 机械振动 框架图和解题方法

第5章 机械振动一、基本要求1.掌握描述简谐运动各物理量的物理意义及相互关系,能根据给定的初始条件建立简谐运动方程;2.掌握旋转矢量法,并能用以求解初相、相位、相位差、时间差;理解简谐运动合成规律; 3.理解振幅、周期、频率、相位等描述机械波的重要物理量。
二、基本内容(一)本章重点和难点:重点:理解简谐运动特征并能根据给定的初始条件写出简谐运动方程。
难点:掌握旋转矢量法在解题中的应用。
(二)知识网络结构图:⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧=+===⎪⎩⎪⎨⎧=+''+=-=李萨如图形垂直方向频率整数比椭圆运动垂直方向同频率拍同方向不同频率仍为简谐运动同方向同频率简谐运动的合成总能量弹性势能动能简谐运动的能量复摆单摆弹簧振子典型例子初相相位角频率频率周期振幅基本物理量谐运动微分方程谐运动方程回复力公式简谐运动的定义振动::::212121,,:,,,,,:0:)cos(::2222kA E E E kx E m v E x x t A x kx F p k p k ωϕω(三)容易混淆的概念: 1.初相和相位简谐振动运动方程 简谐振动能量 简谐振动合成速度方程 加速度方程 动能 势能 合振幅合相位初相ϕ反映简谐运动物体在初始时刻的运动状态;相位ϕω+t 反映简谐运动物体在任意时刻的运动状态。
2.角频率和频率角频率(圆频率)ω反映角位置随时间的变化,对于谐振子而言,由劲度系数和质量决定,又称固有频率;频率ν是单位时间内完成全振动的次数,是周期的倒数。
(四)主要内容:1.简谐运动的基本概念:(1) 运动方程:)cos(ϕω+=t A x ,A x m =(2) 速度方程:)sin(ϕωω+-=t A v ,A v m ω= (3) 加速度方程:)cos(2ϕωω+-=t A a ,A a m 2ω= (4) 周期:ωπ2=T(5) 频率:πων21==T (6) 时间差与相位差的关系:ωϕ∆=∆t2.旋转矢量法:在平面上画一矢量A ,初始位置与x 轴正方向的夹角等于初相位ϕ,其尾端固定在坐标原点上,其长度等于振动的振幅A ,并以圆频率ω为角速度绕原点作逆时针匀速转动,则矢量A在x 轴上的投影为:)cos(ϕω+=t A x 。
简谐运动实验的原理及应用

简谐运动实验的原理及应用1. 简谐运动的定义和特点•简谐运动是指一个物体在恢复力作用下沿着直线振动,并且振动的加速度与位移成正比,方向相反。
•简谐运动的特点包括周期性、振幅、频率和相位等。
2. 简谐运动的数学描述•简谐运动可以通过数学函数来描述,最常用的是正弦函数。
•位移函数可以表示为x(t) = A * sin(ωt + φ),其中 A 为振幅,ω 为角频率,t 为时间,φ 为初相位。
3. 简谐运动实验的原理•简谐运动实验可以通过弹簧振子或摆锤等装置来实现。
•实验中,通过测量物体的振动周期和振幅,可以得到振动的频率和相位,进而计算出物体的动能和势能。
4. 简谐运动实验的步骤1.准备实验装置,包括弹簧振子或摆锤等。
2.将物体振动至平衡位置,并记录下平衡位置的位置信息。
3.以合适的角度将物体拉开或释放,使其开始振动。
4.用计时器测量物体完成一个完整振动的时间,即振动周期。
5.反复实验多次,取平均值来增加测量的精确度。
6.根据振动周期和振幅,计算出振动的频率和相位差。
5. 简谐运动实验的应用•简谐运动实验具有广泛的应用价值,包括以下几个方面:1.物理教学:简谐运动实验是物理教学中的经典实验之一,通过实施实验可以帮助学生深入理解简谐运动的概念和特点。
2.工程设计:简谐运动是许多工程设计中的基础概念,例如建筑物的结构抗震设计、机械振动系统的优化等。
3.医学应用:许多生物系统,如心脏的跳动和呼吸运动等,都可以近似地看作简谐运动,通过研究简谐运动可以帮助医学领域的疾病诊断和治疗。
4.乐器制作:乐器音调的产生和调节离不开简谐运动的原理,通过研究简谐运动可以优化乐器的设计和制作。
5.科学研究:简谐运动的原理和应用广泛存在于各个科学领域,如天文学、电磁学、光学等,研究简谐运动可以帮助我们更好地理解自然界的规律。
6. 总结•简谐运动是一个重要的物理概念,通过实验可以对其原理和应用进行研究。
•简谐运动实验的步骤包括准备装置、记录平衡位置、测量振动周期以及计算频率和相位差等。
《大学物理学》机械振动练习题
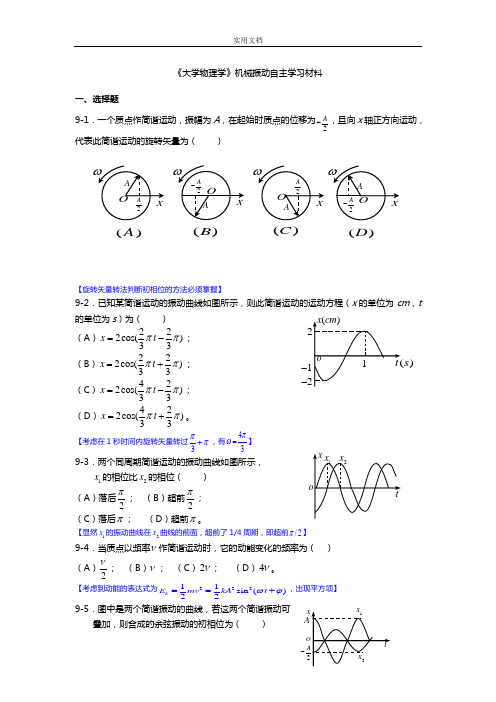
《大学物理学》机械振动自主学习材料一、选择题9-1.一个质点作简谐运动,振幅为A ,在起始时质点的位移为2A -,且向x 轴正方向运动,代表此简谐运动的旋转矢量为( )【旋转矢量转法判断初相位的方法必须掌握】9-2.已知某简谐运动的振动曲线如图所示,则此简谐运动的运动方程(x 的单位为cm ,t 的单位为s )为( )(A )222cos()33x t ππ=-;(B )222cos()33x t ππ=+;(C )422cos()33x t ππ=-;(D )422cos()33x t ππ=+。
【考虑在1秒时间内旋转矢量转过3ππ+,有43πω=】9-3.两个同周期简谐运动的振动曲线如图所示,1x 的相位比2x 的相位( )(A )落后2π; (B )超前2π;(C )落后π; (D )超前π。
【显然1x 的振动曲线在2x 曲线的前面,超前了1/4周期,即超前/2π】9-4.当质点以频率ν作简谐运动时,它的动能变化的频率为( ) (A )2ν; (B )ν; (C )2ν; (D )4ν。
【考虑到动能的表达式为22211sin ()22kE mv kA t ωϕ==+,出现平方项】9-5.图中是两个简谐振动的曲线,若这两个简谐振动可叠加,则合成的余弦振动的初相位为( )()A ()B()C()D )s--(A )32π; (B )2π; (C )π; (D )0。
【由图可见,两个简谐振动同频率,相位相差π,所以,则合成的余弦振动的振幅应该是大减小,初相位是大的那一个】9--1.一物体悬挂在一质量可忽略的弹簧下端,使物体略有位移, 测得其振动周期为T ,然后将弹簧分割为两半,并联地悬挂同 一物体,再使物体略有位移,测得其振动周期为'T ,则'/T T 为( )(A )2; (B )1; (C; (D )12。
【弹簧串联的弹性系数公式为12111k k k =+串,弹簧对半分割后,其中一根的弹性系数为2k ,两弹簧并联后形成新的弹簧整体,弹性系数为4k ,公式为12k k k =+并,利用ω=2T πω=,所以,'22T T π==】9--2.一弹簧振子作简谐运动,当位移为振幅的一半时,其动能为总能量的( ) (A )12;(B;(C(D )34。
大学物理A第九章 简谐振动

第九章 简谐振动一、填空题(每空3分)9-1 质点作简谐振动,当位移等于振幅一半时,动能与势能的比值为 ,位移等于 时,动能与势能相等。
(3:1,22A ±)9-2两个谐振动方程为()120.03cos (),0.04cos 2()x t m x t m ωωπ==+则它们的合振幅为 。
(0.05m )9-3两个同方向同频率的简谐振动的表达式分别为X 1=6.0×10-2cos(T π2t+4π) (SI) , X 2=4.0×10-2cos(T π2t -43π) (SI) ,则其合振动的表达式为______(SI).( X=2.0×10-2cos(T π2t+4π) (SI)) 9-4一质点作周期为T 、振幅为A 的简谐振动,质点由平衡位置运动到2A处所需要的最短时间为_________。
(12T) 9-5 有两个同方向同频率的简谐振动,其表达式分别为 )4cos(1πω+=t A x m 、)43cos(32πω+=t A x m ,则合振动的振幅为 。
(2 A)9-6 已知一质点作周期为T 、振幅为A 的简谐振动,质点由正向最大位移处运动到2A处所需要的最短时间为_________。
(6T) 9-7有两个同方向同频率的简谐振动,其表达式分别为 )75.010cos(03.01π+=t x m 、)25.010cos(04.02π-=t x m ,则合振动的振幅为 。
(0.01m )9-8 质量0.10m kg =的物体,以振幅21.010m -⨯作简谐振动,其最大加速度为24.0m s -⋅,通过平衡位置时的动能为 ;振动周期是 。
(-32.010,10s J π⨯) 9-9一物体作简谐振动,当它处于正向位移一半处,且向平衡位置运动,则在该位置时的相位为 ;在该位置,势能和动能的比值为 。
(3,1:3π)9-10质量为0.1kg 的物体,以振幅21.010m -⨯作谐振动,其最大加速度为14.0m s -⋅,则通过最大位移处的势能为 。
8-5简谐运动的合成

(1)相位差 2k π (k 0,1,)
A A1 A2
相互加强
(2)相位差 (2k 1) π (k 0,1,)
A A1 A2
(3)一般情况
相互削弱
A1 A2 A A1 A2
第八章 机械振5 动
8-5 简谐运动的合成
思考
例 图中所画的是两个简谐振动的振动曲线. 若这 两个简谐振动可叠加,则合成的余弦振动的初相为
arctan11rad
第八章 机械振8 动
O A1
O
A2
A
T t
A A1 A2
2 1 2kπ
x ( A1 A2 ) cos(t )
第八章 机械振3 动
8-5 简谐运动的合成
A A12 A22 2A1A2 cos(2 1)
(2)相位差 2 1 (2k 1)π (k 0,1, )
tan A1 sin 1 A2 sin 2 A1 cos1 A2 cos2
第八章 机械振2 动
8-5 简谐运动的合成
讨论 A A12 A22 2A1A2 cos(2 1) (1)相位差 2 1 2kπ (k 0,1, 2,)
xx
8-5 简谐运动的合成
两个同方向同频率简 当 t 0时
谐运动的合成
x1 A1 cos(t 1) x2 A2 cos(t 2 )
x x1 x2
A2
2 1
O x20
A1
x10
A x Acos(t )
两个同方向、同频率 简谐运动的合振动仍是简 谐运动,其频率与分振动
(A)3π / 2
9-1简谐运动 振幅 周期和频率 相位(大学物理)

x t 图
T
T 2
A
o
A
t
振 动
18
t
第九章
振 动
11
物理学
第五版
9-1
简谐运动 振幅 周期和频率 相位
三 周期、频率 x A cos(t ) A cos[ (t T ) ]
周期 T
2π
A
x
注意
弹簧振子周期
x t 图
T
T 2
o
A
t
m T 2π k
第九章
振 动
12
物理学
第五版
9-1
简谐运动 振幅 周期和频率 相位
振 动
17
物理学
第五版
9-1
简谐运动 振幅 周期和频率 相位
讨论
已知t 0, x 0, v0 0 求
v
x
π 0 A cos 2 v0 A sin 0 π sin 0 取 2 π x A cos(t ) 2
第九章
o
x A cos(t ) A cos[ (t T ) ] 1 频率 T 2π x
圆频率
x t 图
T 2
A
2π 2 π T
o
A
T
t
周期和频率仅与振动系统本身的 物理性质有关
第九章 振 动
13
物理学
第五版
9-1
简谐运动 振幅 周期和频率 相位
作简谐运动的物体
第九章
振 动
4
物理学
第五版
9-1
简谐运动 振幅 周期和频率 相位
弹簧振子的振动
9-3单摆和复摆
dt
θ l
v FT m
o
J = ml
振 动
θ = θ m cos( ω t + ϕ )
T = 2π l g
v P
2
2
第九章
物理学
第五版
二
复摆 (θ < 5 )
o
9-3
单摆和复摆 转动正向
振动时的周期? 振动时的周期
v v v M =l ×F M = −mgl sin θ
d 2θ = Jβ = J 2 dt
第九章 振 动
A
θ
l
m
o
θ <5
o
1
物理学
第五版
动力学分析: 动力学分析:
9-3
单摆和复摆
转动 正向
θ < 5 时 , sinθ ≈ θ M = − mgl sin θ ≈ − mglθ d 2θ − mglθ = J 2
o
A
dθ g g 2 = − θ 令ω = 2 dt l l d 2θ 2 = −ω θ 2 dt
F = − kx 平衡位置 x = 0
d x 2 = −ω x 2 dt
2
x = A cos(ωt + ϕ )
单摆 弹簧振子 ω = k m 由振动系统本身性质决定) (由振动系统本身性质决定)
第九章 振 动
a = −ω x
2
v = − A ω sin( ω t + ϕ )
ω= g l
ω = mgl
π 2
Q0 I 0
O
﹡ π
2π
﹡
(ωt +ϕ)
π q = Q0 cos(ωt +ϕ) i = I0 cos(ωt +ϕ + ) 2
9-3 简谐运动的图示法
第九章 振 动
5 t =0 24 3
3)到达点P相应位置所需时间
t P= .6s 1
9
物理学
第五版
物理学
第五版
9-3 简谐运动的图示法
二 简谐运动的矢量图示法
旋转矢量:自
原点O作一矢量 A ( A A ),且 A
在Oxy平面内绕点O 作逆时针匀角速转
v
0.08 0.04
x/m
o
0.04
0.08
28
第九章 振 动
物理学
第五版
物理学
第五版
9-3 简谐运动的图示法
法二
t
时刻
t
π3 π3
起始时刻
x/m
0.08
2 3
0.08 0.04
o
0.04
π t 3
π3 1 t T T 2π 6
第九章 振 动
0.667 s
29
x/m
x A cos( t )
解一(解析法):
0.10 0.05
0
P 4.0 t/s
A 0.10m t 0 0 x0 0.05m
0.05 0.10 cos
=
v0 A sin 0
t1 4.0s x1 0m
,
3 π 0 0.10 cos(4 )
x/m
0.10 0.05
0
P t/s
4.0
第九章 振 动
21
物理学
第五版
物理学
第五版
9-3 简谐运动的图示法
x/m 0.10 0.05 0 P
x A cos( t )
9-1简谐运动 振幅 周期和频率 相位
当 x0 0 、v0 0时的 取在第三象限的值;
当 x0 0 、v0 0时的 取在第四象限的值;
第九章 振 动
22
物理学
第五版
9-1 讨论
简谐运动 振幅 周期和频率 相位
已知: t 0, x 0, v0 0 求:
0 A cos π 2 v0 A sin 0
12
物理学
第五版
9-1
简谐运动 振幅 周期和频率 相位
A
v A sin(t ) π A cos(t ) 2 2 a A cos( t )
A cos( t π)
2
x A cos(t ) 2π T 取 0
20
物理学
第五版
9-1
简谐运动 振幅 周期和频率 相位
五、常数 A和 的确定 x A cos( t )
v A sin(t )
初始条件 t
2
0 x x0 v v0
v0
2 2
A x0
v0 tan x0
第九章
对给定的振动系统, 周期T或角频率由系统 本身性质决定,振幅A和 初相由初始条件决定.
第九章 振 动
6
物理学
第五版
9-1
简谐运动 振幅 周期和频率 相位
振动的成因:
F kx
——回复力
回复力
+
惯性
振 动
7
第九章
物理学
第五版
9-1
简谐运动 振幅 周期和频率 相位
根据胡克定律和牛顿第二定律得
F kx ma k a x m k 2 2 a x 得 令 m
简谐运动,相位差!【极好!】只是分享
上的投影点的
运动为简谐运
动.
第九章 振 动
2
xA co ts ()
9-2 旋转矢量
点旋以转o 矢为量原A
的端点在 x轴
上的投影点的 运动为简谐运 动.
第九章 振 动
3
9-2 旋转矢量
用旋转矢量图画简谐运动的xt图
第九章 振 动
4
9-2 旋转矢量
➢ 相位差:表示两个相位之差
(1)对同一简谐运动,相位差可以给出 两运动状态间变化所需的时间.
x1A 1co ts (1) x2A 2cot s2 ()
(t 2 ) (t 1 )
2
1
第九章 振 动
7
9-2 旋转矢量
2
1
0同步
x
超前
π反相 为其它 落后
x
x
o
o
o
t
t
t
第九章 振 动
8
9-2 旋转矢量
旋转矢量
t 0
o
自Ox轴的 原点
O作一矢量 A ,使 它的模等于振动的
振幅A,并使矢量A
A 在 Oxy平面内绕点
O作逆时针方向的
x 0
x 匀角速转动,其角
x0Acos
速度 与振动频率
相等,这个矢量就
叫做旋转矢量.
第九章 振 动
1
9-2 旋转矢量
A
t t
t
o
x
xAcots()
点旋以转o 矢为量原A
x1A co t1 s () x2A co ts 2 ()
( t ) ( t )
2
1
t t2 t1
第九章 振 动
5
