生成树的发展历程
生成树简介.

简介STP(生成树协议SpanningTreepProtocol)能够提供路径冗余,使用STP可以使两个终端中只有一条有效路径。
在实际的网络环境中,物理环路可以提高网络的可靠性,当一条线路断掉的时候,另一条链路仍然可以传输数据。
但是,在交换网络中,当交换机接收到一个未知目的地址的数据帧时,交换机的操作是将这个数据帧广播出去,这样,在存在物理的交换网络中,就会产生一个双向的广播环,甚至产生广播风暴,导致交换机死机。
如何既有物理冗余链路保证网络的可靠性,又能避免冗余环路所产生的广播风暴呢?STP协议是在逻辑上断开网络的环路,防止广播风暴的产生,而一旦正在用的线路出现故障,逻辑上被断开的线路又被连通,继续传输数据。
交换网络环路交换网络环路会带来3个问题:广播风暴、同一帧的多个拷贝和交换机CAM表不稳定。
交换网络环路的产生:PC1和PC2通过交换机相连。
网络初始状态时,PC1与PC2通信过程如下:1.在网络通信最初,PC1的ARP条目中没有PC2的MAC地址,PC1首先会向SW1发送一个ARP广播请求PC2的MAC地址;2.当SW1收到ARP的广播请求后,SW1会将广播帧从除接收端口之外的所有端口转发出去即会从F0/1和F0/2发出;3.SW2收到广播后,会将广播帧从F0/2和连接PC2的端口转发,同样SW3收到广播后,将其从F0/2端口转发;4.SW2收到SW3的广播后,将其从F0/1和连接PC2的端口转发,SW3收到SW2的广播后将其从F0/1端口转发;5.SW1分别从SW2、SW3收到广播帧,然后将从SW2收到的广播帧转发给SW3,而将从SW3收到的广播帧发给SW2。
SW1、SW2和SW3会将广播帧相互转发。
这时网络就形成了一个环路,而交换机并不知道,这将导致广播帧在这个环路中永远循环下去。
STP工作原理STP运行STA(生成树算法Spanning Tree Algorithm)。
STA算法很复杂,但是其过程可以归纳为以下三个步骤:1.选择根网桥(Root Bridge);1>网桥ID最小。
写出最小生成树的构造过程

写出最小生成树的构造过程最小生成树(Minimum Spanning Tree,简称MST)是一个连通图上的生成树,它的边权重之和是所有可能生成树中最小的。
最小生成树在许多实际问题中有着广泛的应用,比如网络设计、电力输送、通信等领域。
下面我将为大家介绍最小生成树的构造过程。
一、Prim算法:Prim算法是一种贪心算法,它的基本思想是从一个顶点开始,逐渐扩展生成树,每一步选择一个与树相邻的权重最小的边,并将该边所指向的顶点加入树中。
具体的步骤如下:1.随机选择一个顶点作为起始点,将该顶点加入生成树。
2.在生成树中选择一个顶点v,寻找与v相邻的顶点中权重最小的边(u, v (u∈生成树,v∉生成树)),将该边加入生成树。
3.将顶点v加入生成树。
4.重复执行第2、3步,直到生成树中包含了所有的顶点。
在Prim算法中,我们需要用一个数组distance来记录各个顶点到生成树的最小距离(weight)。
在每一步中,通过更新distance数组的值,选择其中的最小值并将对应的顶点加入生成树。
二、Kruskal算法:Kruskal算法是一种基于边贪心策略的算法,其基本思想是将图中的所有边按照权重的非递减顺序排序,然后逐步加入生成树,直到生成树包含了所有的顶点。
具体的步骤如下:1.将图中的所有边按照权重的非递减顺序排序。
2.初始化一个空的生成树。
3.依次选择排好序的边,如果该边所连接的两个顶点不属于同一个连通分量,就将该边加入生成树。
如果加入该边之后,生成树中的边数等于顶点数减一,则结束算法。
4.重复执行第3步,直到生成树中的边数等于顶点数减一。
在Kruskal算法中,我们需要用一个数组parent来记录每个顶点所属的连通分量。
在每一步中,通过查找顶点的连通分量是否相同,判断是否可以加入生成树。
三、比较:Prim算法的时间复杂度为O(V^2),其中V为顶点数。
由于Prim算法需要维护一个数组distance,因此适用于稠密图,即顶点数较多的情况。
生成树的名词解释

生成树的名词解释生成树(Spanning Tree)是图论中的一个重要概念,用来描述在一个无向连通图中连接所有顶点的极小连通子图。
在一个无向连通图中,如果能够找到一颗包含所有顶点且边数最少的子图,那么这个子图就是该图的生成树。
生成树的概念最早由Otto Schönflies于1885年提出,并且在图论研究和实际应用中得到了广泛的运用。
生成树在电网规划、通信网络设计、计算机网络以及城市交通规划等领域都有着重要的应用价值。
生成树的定义可以用简洁的方式表述:在一个无向连通图中,生成树是保留了原图的所有顶点,但只保留了足够的边来使得这个子图连通,并且不包含任何环的一种连通子图。
换句话说,生成树是一个无向连通图中的极小连通子图,它连接了所有的顶点,并且不存在回路。
生成树具有很多重要的性质和应用。
首先,生成树的边数比原图的顶点数少一个。
这是因为生成树是一个连通子图,而且不包含任何环。
因此,生成树中的边数等于原图的顶点数减去1。
这个性质经常用于生成树的构造和推导。
其次,生成树可以用于表示图中的最小连接网络。
在一个无向连通图中,如果存在多个连通子图,那么通过连接这些子图的最少的边,就可以得到一个生成树。
这个生成树可以看作是一个最小的连通网络,其中所有顶点都能够通过最短路径相互到达。
此外,生成树还可以用于网络设计和优化问题。
在电网规划、通信网络设计和计算机网络中,生成树常常被用于实现信息的传输和路由的优化。
通过构造合适的生成树,可以使得信息的传输路径更加简洁和高效。
生成树有多种构造算法,其中最常用的是Prim算法和Kruskal算法。
Prim算法是一种贪心算法,它从一个任意选定的顶点开始,逐步构建生成树。
具体地,Prim算法每次选择与已有的生成树连接边权值最小的顶点,并将其加入生成树。
重复这个过程,直到生成树包含了所有的顶点。
Kruskal算法是一种基于边的方法,它首先将图中的边按照权值从小到大排序,然后依次将边加入生成树,直到生成树包含了所有的顶点为止。
离散数学生成树

离散数学生成树一、引言离散数学是数学的一个分支,它研究的是不连续的、离散的数学结构。
生成树是离散数学中的一个重要概念,它在图论中有着广泛的应用。
本文将介绍生成树的定义、性质以及应用领域。
二、生成树的定义在图论中,生成树是指包含图中所有顶点的一个连通子图,并且该子图是一个树。
换句话说,生成树是从图中选择一些边,构成一个没有回路的子图,同时保持图的连通性。
三、生成树的性质1. 生成树的边数等于顶点数减一。
这个性质可以通过数学归纳法证明。
假设一个图有n个顶点,那么它的生成树一定有n-1条边。
2. 生成树是连通图的最小连通子图。
也就是说,对于一个连通图来说,它的生成树是包含所有顶点的子图中边数最少的一个。
3. 生成树中任意两个顶点之间都是互联的。
也就是说,生成树中任意两个顶点之间存在且仅存在一条路径,这个路径就是生成树中的边。
四、生成树的应用生成树在计算机科学中有着广泛的应用,以下是一些常见的应用领域:1. 网络设计:生成树可以用于设计计算机网络中的最优传输路径,以提高网络的稳定性和可靠性。
2. 电力传输:生成树可以用于规划电力传输网络,以确保电力的高效传输和供应。
3. 数据压缩:生成树可以用于数据压缩算法中,通过构建最优编码树来减少数据的存储空间。
4. 优化问题:生成树可以用于解决一些优化问题,比如旅行商问题中的最短路径搜索。
5. 连接关系:生成树可以用于分析社交网络、物流网络等复杂系统中的连接关系。
五、总结生成树作为离散数学中的重要概念,在图论和计算机科学中有着广泛的应用。
它不仅可以用于网络设计和电力传输等实际问题,还可以用于解决优化问题和分析复杂系统中的连接关系。
通过对生成树的研究和应用,我们可以更好地理解和优化各种实际问题。
生成树的定义和性质使得它成为离散数学中的重要研究对象。
希望本文对读者理解生成树的概念和应用有所帮助。
生成树协议的发展历程浅析

由于生 成树协议本 身比较小 ,所 以并 不像路 由协 议那样 广
为人 知 。 但 是 它 却 掌 管 着 端 口的 转 发 和 开 关 的 大 权 。 在 和 别 的
垡戚树协议 的 展历程浅桥
_吴
[ 摘
专题 的定期资料简报) 专题情报报告 ( 一般由情报人 员与研究分 析人 员共 同其工作成
果最直接 的方式。其优点是其资料直观 系统 有条理 .易于把 握 不足之处在于其工作周期一般较长 .情报需求方难于控制其 工作的进度与方向 .容易产生偏 差。第二种是情报服务类 .情报 服务是情报部 门使其工作成果发生效益的一种高级形式 .它往往 需要情报部 门与人力 行政部 门紧密配合 .针对某些专题组织专 项的培训 、在 公司内部局域网上进行互动式的讨论等 。这种方式 的优点是针对性强 信息量大且可针对实际效果及 时做出调整 : 协同能力要 求较高 .要 搞好有一定难度。
络流量 的碰撞 . 但是透 明网桥 也有它的不足之处 . 就是透 明网桥
并 不 能 像 路 由 器 那 样 知 道 数 据 帧 可 以经 过 多 少 次 转 发 . 一旦 网络
敏感 的重要 的资讯。所 以,在对方有明显不道 德行 为的前提下 ,
存在环路就会造成数据帧在环路内不断循环和增生甚至造成广播
的薄 弱 环 节 。最 后 .根 据上 述 的分 析 结 果 实施 具 体 的 保 密 措施 并 成树协议 。
一
、
第一代生成树协议 S P和 R T T SP
树的诞生故事(数学)

树的诞生故事(数学)【最新版4篇】目录(篇1)1.引言:介绍树的概念及其在数学中的应用2.树的基本结构:节点、边、叶子节点、度、生成树等3.树的种类:满二叉树、完全二叉树、平衡二叉树(AVL 树)和二叉搜索树4.树的遍历:前序遍历、中序遍历和后序遍历5.树的应用:图论、数据结构和算法6.结论:总结树的重要性和在数学领域的发展正文(篇1)树的诞生故事 (数学)树的概念在生活中非常常见,它既是生物学中的基本结构,也是数学中的一个重要研究对象。
在数学领域,树被广泛应用于图论、数据结构和算法等方面,为我们理解和解决许多实际问题提供了有力的工具。
接下来,我们将探讨树的诞生故事,了解其在数学中的基本结构、种类和应用。
首先,让我们来了解一下树的基本结构。
在数学中,树是由节点(vertex)和边(edge)组成的一种非线性数据结构。
树的节点表示元素,边表示元素之间的关系。
树中还存在叶子节点(leaf node),即没有子节点的节点。
度(degree)是树中节点的子节点数量,根节点的度为 0,而叶子节点的度为 1。
生成树(spanning tree)是指一个树覆盖一个图的所有节点,且保持图的连通性。
接下来,我们来探讨树的种类。
满二叉树是一种特殊的完全二叉树,它的每一层都充满了节点,且最后一层可能不完全填充。
完全二叉树是一种特殊的平衡二叉树(AVL 树),它的每一层都充满了节点,且最后一层可能不完全填充。
平衡二叉树是一种保持左右子树高度差不超过 1 的二叉树,它的调整操作使其保持平衡。
二叉搜索树是一种特殊的平衡二叉树,它的左子树中的所有节点的值都小于根节点的值,右子树中的所有节点的值都大于根节点的值。
在树的遍历方面,有前序遍历、中序遍历和后序遍历三种方式。
前序遍历是指先访问根节点,然后遍历左子树,最后遍历右子树。
中序遍历是指先遍历左子树,然后访问根节点,最后遍历右子树。
后序遍历是指先遍历左子树,然后遍历右子树,最后访问根节点。
第九章 树(生成树)
9
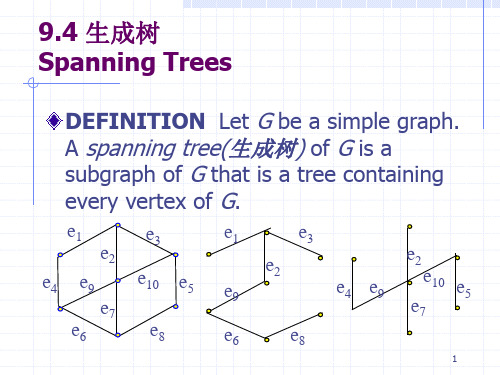
9.4 生成树 Spanning Trees
回溯(Backtracking) 回溯 基本做法是深度优先搜索, 基本做法是深度优先搜索,可以避免不 必要重复搜索的穷举式搜索算法(Bruteforce search)。 。
10
9.4 生成树 Spanning Trees
例:图着色
11
9.4 生成树 Spanning Trees
25
9.5 最小生成树 Minimum Spanning Trees
例:
26
9.5 最小生成树 Minimum Spanning Trees
Example:Find a spanning tree of : minimum weight for this graph
27
PageRank from Google
2
9.4 生成树 Spanning Trees
破圈法:连通图G 个点m条边, 破圈法:连通图G有n个点m条边,则G要删除 (n- 条边, 破坏m (n- 个回路, m-(n-1) 条边 , 破坏 m-(n-1) 个回路 , 得 的一棵生成树。 到G的一棵生成树。 避圈法: 条边中选取n 避圈法 : 从 m 条边中选取 n-1 条边并使它不 含有回路,得到G的一棵生成树。 含有回路,得到G的一棵生成树。
( i , j )∈T
∑ W (i , j )
在带权图G所有生成树中 在带权图 所有生成树中, 权最小的那棵树称 所有生成树中 的最小生成树。 为G的最小生成树。 的最小生成树
17
9.5 最小生成树 Minimum Spanning Trees
克鲁斯卡尔算法(Kruskal 1956) 克鲁斯卡尔算法 1.在G(n,m)中选取权最小的边 记作 1,置i=1 中选取权最小的边,记作 在 中选取权最小的边 记作e 置 2.当i=n-1时结束 否则转 。 时结束,否则转 当 时结束 否则转3。 3.设已选择边为 1,e2,……ei,此时无回路。 设已选择边为e 此时无回路。 设已选择边为 此时无回路 在 G 中 除 这 i 条 边 外 , 选 择 边 ei+1, 该 边 使 得 {e1,…,ei+1}生成的子图中无回路 且 ei+1 是满 生成的子图中无回路,且 生成的子图中无回路 足该条件中权最小的一条边。 足该条件中权最小的一条边。 4.置i:=i+1,转2。 置 转 。
生成树

生成树协议中树的形成与维护学生姓名:薛明杨学号:2011019020015 老师:唐伟摘要:本文主要讨论生成树协议形成一棵树的过程,当拓扑变化时生成树是如何感知,如何重新形成新的树。
1.生成树形成的过程:1.生成树概述生成树算法的网桥协议STP(Spanning Tree Protocol) 它通过生成生成树保证一个已知的网桥在网络拓扑中沿一个环动态工作。
网桥与其他网桥交换BPDU消息来监测环路,然后关闭选择的网桥接口取消环路,统指IEEE802·1生成树协议标准和早期的数字设备合作生成树协议,该协议是基于后者产生的。
IEEE版本的生成树协议支持网桥区域,它允许网桥在一个扩展本地网中建设自由环形拓扑结构。
2.生成树的功能生成树协议的主要功能有两个:一是在利用生成树算法、在以太网络中,创建一个以某台交换机的某个端口为根的生成树,避免环路。
二是在以太网络拓扑发生变化时,通过生成树协议达到收敛保护的目的。
3.生成树的结构思路不论网桥(交换机)之间采用怎样物理联接,网桥(交换机)能够自动发现一个没有环路的拓扑结构的网路,这个逻辑拓扑结构的网路必须是树型的。
生成树协议还能够确定有足够的连接通向整个网络的每一个部分。
所有网络节点要么进入转发状态,要么进入阻塞状态,这样就建立了整个局域网的生成树。
当首次连接网桥或者网络结构发生变化时,网桥都将进行生成树拓扑的重新计算。
为稳定的生成树拓扑结构选择一个根桥, 从一点传输数据到另一点, 出现两条以上条路径时只能选择一条距离根桥最短的活动路径。
生成树协议这样的控制机制可以协调多个网桥(交换机)共同工作, 使计算机网络可以避免因为一个接点的失败导致整个网络联接功能的丢失, 而且冗余设计的网络环路不会出现广播风暴。
4.关键概念(1)网桥标识(bridge ID):①非扩展的:网桥优先级(2bytes)+ MAC地址②扩展的:网桥优先级(4bits) + 系统标识(VLAN ID;12bits) + MAC地址(2)网桥协议数据单元(BPDU):①配置(CFG)BPDU: 初始时每个网桥都会发送,假设自己就是根网桥收敛后,只从根网桥发出,其他网桥在根端口接收后向下中继。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
生成树(STP)技术的部署与调试案例
8.1 生成树(STP)技术与实现原理
在一个包含有交换机与网桥的网络中,消除环路对于获得可靠通信与防止流量在网络中不停循环必不可少。
生成树协议(Spanning-tree Protocol,STP),工作在ISO七层模型中第二层,其应用能够使交换机或者网桥通过构成“生成树”,在网络拓扑中动态执行“环路遍历”,通过逻辑判断网络的链路,达到网络无环路和链路冗余的目的。
8.1.1 生成树的发展历程
网络发展过程中,以太网设备由Hub发展到透明网桥到智能交换机。
透明网桥比Hub
智能,Hub收到数据包后,向除自己外的其他所有端口进行广播,而透明网桥则记录物理端口上连接设备的MAC,收到数据帧后按照记录的MAC地址向该端口发送数据帧,这样大大减少数据帧冲突。
但是透明网桥由于他的透明性,一旦网络中存在环路,一台透明网桥收到的数据帧,又会在环路中返回,这样数据帧不停在网络中增生,最终形成广播风暴,导致整个网络瘫痪;一种阻止网络环路的协议——生成树协议(STP),IEEE 802.1D标准,生成树模拟自然界树的生长规律,从树根到树梢不会形成环路,生成树协议通过对比环路网络中的设备属性的优先级、链路的开销、端口优先级等来判断环路中链路的优先级,从而逻辑上阻断优先级低的网络链路。
生成树从阻断到转发状态需要经过阻断、监听、学习、转发延迟等阶段,这个阶段大约需要30~50s的时间,对于要求高可靠性的网络来,这是不允许的。
快速生成树协议(RSTP)IEEE 802.1W按结构需求产生,RSTP将阻断的端口设置备用端口,一旦检测到主链路中断,备用端口直接进入转发状态,大大加大收敛速度。
上一章介绍了VLAN在园区网中的应用与划分,很多企业在网络中都会规划多个VLAN。
STP和RSTP只支持一个VLAN,对于只有一个VLAN的网络非常适用,但现在网络中全部是多VLAN的结构,每VLAN生成树和多VLAN生成树协议被提上议程。
其中,每VLAN生成树 PVST 为Cisco专有的协议,该协议不兼容其他厂家的生成树协议。
同时,如果VLAN多的话,过多的生成树可能导致交换机CPU、内存过载,而IEEE 802.1S 制定的多生成树协议(MSTP)通过划分域的概念,解决了CPU过度运算的问题,同时向下兼容STP、RSTP协议。
本章的后续案例将分别介绍各种生成树技术的应用。
