自由网平差
合集下载
自由网平差结果的相互转换

3
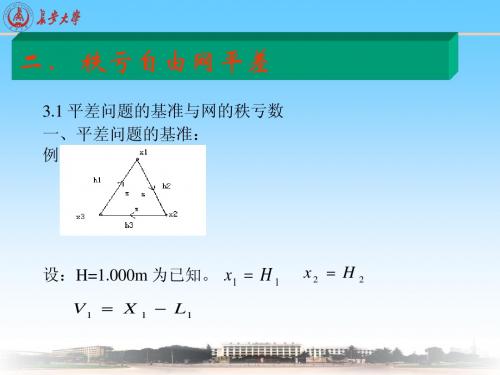
x2
h1
h2
解:
1 1 0 ˆ1 x v 0 1 0 ˆ2 x 0 1 6
2 1 N 1 2
6 v 0
x1
h3
x3
ˆ1 1 2 x ˆc x ˆ2 3 1 x
QP ( N Px GGT Px ) I QP N I QP Px GGT Px
同时右乘G
又
令
0 G QP PxG QP PxG G
QP N I GG Px
T
NG=0、GTPxG=I
ˆ p ( I GG Px ) x ˆc x
T
TP c I GGT Px
同一、数据可以采用:
经典最小二乘平差、普通秩亏网平差、加权秩亏网平差、拟稳平差 不同平差基准下的数据处理 避免因基准不同,对同一网进行多次平差
坐标转换 不同基准下平差解的相互转换
一
经典平差结果转换至秩亏网平差结果
加权秩亏网平差结果
1. 经典平差
经典平差:
ˆc L V Ax T ˆc 0 GC x T V PV min
tr (Qx ˆ2 ) min
结论: 1、最小范数条件与最小方差条件一致 2、所得参数为最优无偏解
注意: 1、对于线性问题,近似值可以任意给定! 2、近似值提供了基准信息 思考: 1、对于非线性问题,近似值如何给定?为什么? 2、以上三种结果的关系是什么?
主要内容
秩亏自由网平差的性质 秩亏自由网结果的相互转换 秩亏自由网平差的应用举例
T
tr ((Px Qx ˆ PL )
x2
h1
h2
解:
1 1 0 ˆ1 x v 0 1 0 ˆ2 x 0 1 6
2 1 N 1 2
6 v 0
x1
h3
x3
ˆ1 1 2 x ˆc x ˆ2 3 1 x
QP ( N Px GGT Px ) I QP N I QP Px GGT Px
同时右乘G
又
令
0 G QP PxG QP PxG G
QP N I GG Px
T
NG=0、GTPxG=I
ˆ p ( I GG Px ) x ˆc x
T
TP c I GGT Px
同一、数据可以采用:
经典最小二乘平差、普通秩亏网平差、加权秩亏网平差、拟稳平差 不同平差基准下的数据处理 避免因基准不同,对同一网进行多次平差
坐标转换 不同基准下平差解的相互转换
一
经典平差结果转换至秩亏网平差结果
加权秩亏网平差结果
1. 经典平差
经典平差:
ˆc L V Ax T ˆc 0 GC x T V PV min
tr (Qx ˆ2 ) min
结论: 1、最小范数条件与最小方差条件一致 2、所得参数为最优无偏解
注意: 1、对于线性问题,近似值可以任意给定! 2、近似值提供了基准信息 思考: 1、对于非线性问题,近似值如何给定?为什么? 2、以上三种结果的关系是什么?
主要内容
秩亏自由网平差的性质 秩亏自由网结果的相互转换 秩亏自由网平差的应用举例
T
tr ((Px Qx ˆ PL )
论秩亏自由网平差的性质及稳健基准的意义

论秩亏自由网平差的性质及稳健基准的意义
自由网平差是一种网络平差方法,它可以用来解决复杂的网络平差问题。
自由网平差具有三个特点:1、自由网平差是一种秩亏的网络平差方法,它可以解决复杂的网络平差问题;2、自由网平差是一种稳健的网络平差方法,它可以抵消网络中的噪声和误差;3、自由网平差是一种有效的网络平差方法,它可以有效地提高网络的精度和稳定性。
秩亏的自由网平差是指在网络平差过程中,网络的观测数据和计算结果之间存在着秩亏的状态,即观测数据和计算结果之间存在着不可解释的差异。
这种秩亏的状态可以通过调整网络中的参数来消除,从而达到网络平差的目的。
稳健基准是指在网络平差过程中,通过调整网络中的参数,使网络对噪声和误差具有较强的抗干扰能力,有效地抵消噪声和误差,从而提高网络的精度和稳定性。
稳健基准的意义在于,可以有效地抵消网络中的噪声和误差,保证网络的精度和稳定性。
6秩亏自由网平差S的求法与基准

(2)
X 3 X 30
ˆ 设 X 3 X 30 X 3
ˆ 0 X 3
称为基准条件方程
T 0 0 1 T ˆ ,G X GC C
13
ˆ X ˆ X ˆ ˆ 0 , 其中 X X 1 2 3
2. 二维测角网
假设所有点的纵横坐标为未知数,给定网中两个点的坐标为固定 (已知)坐标或一个点的纵横坐标、一条边方位角、一条边的边长为 固定值(已知)。 ——这些固定数据构成二维网的平差基准。
ˆ Q AT Pl X r 11
S T Q11 0
T T -1 T QX Q A PQ PAQ Q NQ Q Q S ( S S ) S Q11 ˆ X ˆ 11 ll 11 11 11 11 11 r r
NQ11 I S( S T S )1 S T
可以证明
d u
Q11 N N m
S
T
ˆ 0 X r
u1
ˆTX ˆ min X
主要内容
秩亏自由网平差的三种解法回顾 各类自由网S的确定 S与基准的关系
各类自由网S和G的确定
1、水准网
d=1。由于误差方程系数阵A中的每一行元素总是出现两个基 本元素+1和-1,其元素结构总是形如:
ˆ 0 0 X 1 V1 1 1 V 0 X ˆ 0 1 1 2 2 6 ˆ 1 0 1 V3 X 3
x2 h1 h2 x3
(1)
x1
h3
0 ym 0 xm
0 1 0
0 zm
y10
0 zm
0
0 xm 0 ym
测绘数据处理自由网平差

(1-7-1) 系数矩阵B最大线性无关的行(列)向量的个数,及B矩阵
的秩R(B)等于未知参数 的个数t.即 (1-7-2)
2020/7/9
2
在最小二乘准则下,得其法方程为
(1-7-3)
其中N= PB,W=
。此时,系数阵N为满秩方阵,即
det(N) ,N为非奇异阵,有唯一解,其解为
(1-7-4)
当平差网没有起算数据时,网中所有的点均为待定点。设未知
方程,从而可以按附有限制条件的间接平差法求解。
等价于约束条件
的限制条件方程为
式中
BG=0
故加权秩亏网平差函数模型为
(1-7-9) (1-7-10)
(1-7-11)
2020/7/9 11
此处的系数矩阵B不是列满矩阵,而是列亏矩阵。 将式(1-7-11)组成法方程,得
(1-7-12)
式中
, 因N为降秩方阵,无正常逆,所以
2020/7/9
5
(2)、秩亏网平差。它是在最小二乘
和最小范数
的条件
下求定未知参数的最佳估值。
(3)、加权秩亏网平差。它是在最小二乘
和加权最
小范数的条件
下求定未知参数的最佳估值。式
中, 为表示未知参数稳定程度的先验权矩阵。
(4)、拟稳平差。若将平差网中的未知参数分为两类,即
(s>d)
(1-7-7)
平均距离)。 对于一维的高程网,这种约束是使平差前后网店的平均高程保持 不变。 这些约束条件我们称之为重心基准条件。
2020/7/9
9
(三)加权秩亏自由网平差基准 和秩亏自由网平差基准类似,但应考虑各网点的权重,采用了带 权重心基准条件。 (四)拟稳平差基准 也和秩亏自由网平差基准类似,但仅仅是采用所有拟稳点的重心 基准条件。
的秩R(B)等于未知参数 的个数t.即 (1-7-2)
2020/7/9
2
在最小二乘准则下,得其法方程为
(1-7-3)
其中N= PB,W=
。此时,系数阵N为满秩方阵,即
det(N) ,N为非奇异阵,有唯一解,其解为
(1-7-4)
当平差网没有起算数据时,网中所有的点均为待定点。设未知
方程,从而可以按附有限制条件的间接平差法求解。
等价于约束条件
的限制条件方程为
式中
BG=0
故加权秩亏网平差函数模型为
(1-7-9) (1-7-10)
(1-7-11)
2020/7/9 11
此处的系数矩阵B不是列满矩阵,而是列亏矩阵。 将式(1-7-11)组成法方程,得
(1-7-12)
式中
, 因N为降秩方阵,无正常逆,所以
2020/7/9
5
(2)、秩亏网平差。它是在最小二乘
和最小范数
的条件
下求定未知参数的最佳估值。
(3)、加权秩亏网平差。它是在最小二乘
和加权最
小范数的条件
下求定未知参数的最佳估值。式
中, 为表示未知参数稳定程度的先验权矩阵。
(4)、拟稳平差。若将平差网中的未知参数分为两类,即
(s>d)
(1-7-7)
平均距离)。 对于一维的高程网,这种约束是使平差前后网店的平均高程保持 不变。 这些约束条件我们称之为重心基准条件。
2020/7/9
9
(三)加权秩亏自由网平差基准 和秩亏自由网平差基准类似,但应考虑各网点的权重,采用了带 权重心基准条件。 (四)拟稳平差基准 也和秩亏自由网平差基准类似,但仅仅是采用所有拟稳点的重心 基准条件。
6秩亏自由网平差S的求法与基准解析

a jh
(
y
0 h
y
0 j
)
(
s
0 jh
)
2
, b jh
(x
0 h
x
0 j
)
(s
0 jh
)
2
自由测角网中没有固定点,因此每个水平角为两水平方向之
差。三个坐标点的坐标未知数必同时出现在误差方程中,故
系数阵中的每一行元素结构总是形如
(a jh a jk ) (bjh bjk ) a jh bjh a jk bjk
• 参考: Xu P L. A General Solution in Geodetic Nonlinear Rank-defect Models [ J ] . Bollettino di Geodesia e Scienze Affini , 1997 ,56 (1) :1225.
• /special/opencourse/daishu.h tml 讲师:Gilbert Strang 职业:麻省理工学院 教授
1
0
1
0 1
0
m
m
m
GT
0
y10
1
0
m
x10
y
0 2
1 0
m
x
0 2
y
0 m
1
m xm0
H H
HH
H H
此时
1 0 0
G TG 0 1 0 I
0 0 1
➢ 由于测边网中的观测方程为非线性方程,在线性 化处理中,总假定坐标改正数为微小量,因此仅 取其一次项(即线性)。所以在假定坐标近似值 时,应尽量逼近坐标平差值,以减少因线性化所 带来的误差。一般可先假定任一点的坐标,再根 据相应的观测值推算网中其余点的近似坐标。
第二章1秩亏自由网平差与拟稳平差
秩亏网平差方法
1)是一种广义逆法:通过求法方程N的某些广义逆 N m , N T ,
或求A的位逆,求出其特解(最优唯一解)。(从原理出发) 2)从传统平差方法出发,寻求秩亏网平差的解法——直接法、 附加条件法、转换法。 规定: ˆ X Qˆ 加权秩亏网平差: P 、 X P ˆ 普通秩亏网平差: 、 ˆ X r QX r 普通拟稳平差:ˆ S 、 X S X Qˆ ˆ 经典自由网平差: C 、 X X Q ˆC
当网中没有足够的起算数据: R(A)=T0
T
d 0 = R ( A) R( A) T T0 d (秩亏数基准数)
一般: 几维几何空间大地网,当以点位和尺度比为未知数,而观 测量为边长(高差)和方向(角度)。 基准的类型和个数 尺度基准:
0 d1 Cn 1
位置基准:
1 d 2 Cn n
1
X L L 0 2 2 2 3 L1 1 1 0 T A L L2 0 1 1 L 3
ˆ 所以 X N 1 AT L ( AT A) 1 AT L 其中( AT A) 1 AT 左逆,
( N m1 NN T N m2 NN T ) ( N m1 N m2 ) NN T 0
两边右乘
( N m1 N m2 )T
( N m1 N m2 ) NN T ( N m1 N m2 ) T 0 [(N m1 N m2 ) N ][(N m1 N m2 ) N ]T 0 ( N m1 N m2 ) N 0
测边网,边角网,导线网:测边长,方向(角度) 需:一个点的位置,和一个方位基准,所以d=3。 如果考虑尺度比作未知参数,仍需一个尺度基准,这 时d=4。 三维大地网,三维坐标为未知数,需要一个位置基 准(一个固定点x、y、z),一个定向基准(固定方 向,三个方向余铉角 , , ),一个定大小基准 (固定边长),一共有7个基准信息,d=7。
测绘数据处理-自由网平差

2019/2/15
4
d就是网中必要的起算数据个数。且有:
二、秩亏自由网平差思路 为了求得未知参数的唯一确定解,除了遵循最小二乘准则外 ,还必须增加新的约束条件,从而达到求得唯一解的目的 。由于约束条件不同,秩亏自由网平差可分为如下几种情 况: (1)、经典自由网平差。它是在假设网中有d个必要起算数据 的条件下,求定未知参数的最佳估计。这种方法早就已为 人们所熟知。不难理解,该法的平差结果(未知参数X的 解及其协因数阵 )将随着假设的d个必要起算数据的不同 而不同,即随着已知点位置的改变而改变。
第七行划去,剩下的6三行u列的阵即为三维测边网平差时的附
加阵。 很明显,上述的附加阵G均未标准化,即只是满足了BG=0, 但尚未满足的条件。
2019/2/15
17
阵标准化
1、用原始阵 2、设 和 阵,求出相应的阵 ; 相应 中第i行主对角元素为gii,把原始阵
的第i行数据均乘以
即可得到标准化阵的相应数据;
2019/2/15
2
在最小二乘准则下,得其法方程为 (1-7-3) 其中N= PB,W= 。此时,系数阵N为满秩方阵,即 (1-7-4) 当平差网没有起算数据时,网中所有的点均为待定点。设未知 参数的个数为u,误差方程为 (1-7-5) 组成的法方程为
2019/2/15
det(N)
,N为非奇异阵,有唯一解,其解为
2019/2/15
26
点号
P1 P2 P3 P4
/m
2019/2/15
27
(1)计算网的重心点坐标
(2)计算以加权重心点坐标为坐标原点的各待定点的坐标值
点号
P1 P2 P3
/km
P4
2019/2/15
4
d就是网中必要的起算数据个数。且有:
二、秩亏自由网平差思路 为了求得未知参数的唯一确定解,除了遵循最小二乘准则外 ,还必须增加新的约束条件,从而达到求得唯一解的目的 。由于约束条件不同,秩亏自由网平差可分为如下几种情 况: (1)、经典自由网平差。它是在假设网中有d个必要起算数据 的条件下,求定未知参数的最佳估计。这种方法早就已为 人们所熟知。不难理解,该法的平差结果(未知参数X的 解及其协因数阵 )将随着假设的d个必要起算数据的不同 而不同,即随着已知点位置的改变而改变。
第七行划去,剩下的6三行u列的阵即为三维测边网平差时的附
加阵。 很明显,上述的附加阵G均未标准化,即只是满足了BG=0, 但尚未满足的条件。
2019/2/15
17
阵标准化
1、用原始阵 2、设 和 阵,求出相应的阵 ; 相应 中第i行主对角元素为gii,把原始阵
的第i行数据均乘以
即可得到标准化阵的相应数据;
2019/2/15
2
在最小二乘准则下,得其法方程为 (1-7-3) 其中N= PB,W= 。此时,系数阵N为满秩方阵,即 (1-7-4) 当平差网没有起算数据时,网中所有的点均为待定点。设未知 参数的个数为u,误差方程为 (1-7-5) 组成的法方程为
2019/2/15
det(N)
,N为非奇异阵,有唯一解,其解为
2019/2/15
26
点号
P1 P2 P3 P4
/m
2019/2/15
27
(1)计算网的重心点坐标
(2)计算以加权重心点坐标为坐标原点的各待定点的坐标值
点号
P1 P2 P3
/km
P4
2019/2/15
秩亏自由网平差

ˆ N BT Pl ( E N N )M 中挑选一个解,使得 从X
X min
所以,平差问题成为:
即求误差方程的最小 二乘、最小范数解。 最小二乘指改正数, 最小范数指参数。亦 即求长度最短的最小 二乘解。 武汉大学测绘学院 孙海燕
V T PV min ˆ l V BX ˆTX ˆ min X
武汉大学测绘学院 孙海燕
第四章 秩亏自由网平差
例:如图水准网,1)设 H 3 已知,则误差方程为
0 v1 1 l1 ˆ1 v 1 1 x l2 2 x ˆ2 v3 0 1 l3
法方程系数阵
rank( B) R( B) u t 2
2 1 B B 1 2
T T T 1
rank( BT B) t u 2
1 2 1 | B B | 3, ( B B) 3 1 2
ˆ ( BT B) 1 BT l x
(5) 若矩阵 P 正定,则
A( AT PA) AT PA A
(6) G 为 AT A 的广义逆,则 G T 也是 AT A的广义逆。 3、广义逆 A 的计算 若
rank ( A) r (n, m)
,设
1 A O 11 A m.n O O
A11 r .r A n.m A21 n r .r
4、不同基准下平差的各种量有什么变化
5、基准如何变换
武汉大学测绘学院 孙海燕
第四章 秩亏自由网平差
第二节 广义逆与线性方程组的解
m,n n ,1
线性方程组
Axb
m,1
a1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求导
ˆ T P 2 K T N 0 得到 K N 1P X ˆ 2X 1 X1 11 11 X 1 1 ˆ1 x
ˆ T P 2K T N 0 得到 X ˆ Q N K 2X 2 X2 12 2 X 2 21 X 2
于是
1 ˆ ˆ X 2 QX 2 N 21 N11 PX1 X 1
V BT ( BBT ) 1W
BR BT ( BBT ) 1
右逆
第三讲 秩亏平差(Free Net Adjustment)
关于广义逆 2、广义逆(generalized Inverse)
设A是m×n矩阵,秩R(A)=r<=min(m,n), 如果G满足如下方程,
AGA A
定义为A的广义逆,G为n×m矩阵,并记为 A 一般不唯一。
第三讲 秩亏平差(Free Net Adjustment)
一、自由网平差概述
4、秩亏网平差方法分类(根据约束条件)
加权最小二乘最小范数解
V T PV min ˆTP X ˆ min X
X
最小二乘最小范数解
逆稳平差
V T PV min ˆTX ˆ min X
ˆ X ˆ 1 X ˆ X 2 V T PV min ˆ TX ˆ min X 2 2
关于向量范数(Norm of Vector) ——范数是比长度更广泛的概念
设
X ( x1, x2 xn )
1-范数
X xi
i 1
n
X
p
( xi )1/ p
i 1
n
p
p-范数
X
( x x x )
2 1 2 2
2 1/ 2 n
X
T 1/ 2 ( X AX ) A
结论1:最小二乘原则与附加条件无关, V T PV 是不变量
结论2:附加约束解与最小范数解一致
结论3:令P=I,Px=I
Q11 ( N GGT )1
可以证明Q11是N的伪逆。
P176——例4-2
第三讲 秩亏平差(Free Net Adjustment)
二、加权秩亏网平差解法
3、转换法(Transformed From Classical Estimation)
二、加权秩亏网平差解法
2、附加约束解(Estimation given by Constraints)
ˆ U 0 NX
d t T ˆ 0 G PX X t t
联立法方程和约束条件
(2)式左乘 易得
ˆ 0 PX G 得到 PX GGT PX X
ˆ U 0 ( N PX GGT PX ) X
ˆ N X ˆ N 21 X 1 22 2 U 2 0
无唯一解
第三讲 秩亏平差(Free Net Adjustment)
二、加权秩亏网平差解法
3、转换法(Transformed From Classical Estimation)
给定约束条件
ˆ PX ˆ X 1 ˆ P X ˆ X ˆ ˆ 1 X X ˆ X P ˆ X 2 X 2 ˆ T Pˆ X ˆ X ˆ T Pˆ X ˆ min X 1 1 2 2 X X
第三讲 秩亏平差(Free Net Adjustment)
关于广义逆 3、伪逆(Pseudo Inverse , Moore-Penrose)
如果有 A 满足
AA A A
A AA A
( AA )T AA
( A A)T A A
伪逆是唯一的
第三讲 秩亏平差(Free Net Adjustment)
数学模型 估值
L AX
PI
ˆ ( AT A) 1 AT L X
AL ( AT A) 1 AT
左逆
第三讲 秩亏平差(Free Net Adjustment)
关于广义逆 1、左逆和右逆(Left and Right Inverse)
数学模型 改正数
BV W 0
PI
T 1 T 1 QX GG P ) ˆ ( N PX GG PX ) N ( N P X X
ˆ ( N P GGT P ) 1U X X X
第三讲 秩亏平差(Free Net Adjustment)
二、加权秩亏网平差解法
2、附加约束解(Estimation given by Constraints)
二、加权秩亏网平差解法
4、直接解法(设Px=I)
V A1
A列满秩,令
ˆ X A2 1 L ˆ X 2
Байду номын сангаас
ˆ L1 L A2 X 2
得到 解得
ˆ L V A1 X 1 1
ˆ N 1 AT PL N 1 AT P(L A X ˆ ) X 1 11 1 1 11 1 2 2
将A矩阵分块
A A1 nt0 A2 nd
R( A) R( A1 ) t 0 t d
A1矩阵列满秩
第三讲 秩亏平差(Free Net Adjustment)
二、加权秩亏网平差解法
3、转换法(Transformed From Classical Estimation)
则 令 于是
K ( NQX N ) U
P
ˆ Q N ( NQ N ) AT PL X P X X
T
A QX N ( NQX N ) A P
ˆ X P AP L
T QX A Q ( A ˆ P P)
P
注意: Px 是基准权,不是先验权。X不是随机参数
第三讲 秩亏平差(Free Net Adjustment)
T T 1 T 2
1 2
构造极值函数
X X 2K ( N11 X1 N12 X 2 U1 ) X P ˆT ˆ ˆ ˆ T
第三讲 秩亏平差(Free Net Adjustment)
二、加权秩亏网平差解法
3、转换法(Transformed From Classical Estimation)
则
ˆ ( N N M ) 1U [ N ( I N 1 N M )]1U X 1 11 12 1 11 11 12 1
1 1 ( I N11 N12 M ) 1 N11 U1
第三讲 秩亏平差(Free Net Adjustment)
二、加权秩亏网平差解法
3、转换法(Transformed From Classical Estimation)
第三讲 秩亏平差(Free Net Adjustment)
一、自由网平差概述
3、各种网的基准数(necessary Datum)
水准网:1个点的高程 二维水平网
测角网:4个(2个坐标,1个方位角,1个边长) 测边网,边角同测网:3个(2个坐标,1个方位角)
三维空间网:区分各种情况(7,6,3等)
GPS网在WGS84坐标系中平差,需3个位置基准; 在其它坐标系中,所需基准数有变化。
第三讲 秩亏平差(Free Net Adjustment)
1、Introduction
2、Free Net Adjustment
3、Quasi-Stable Adjustment
4、Datum of Adjustment
第三讲 秩亏平差(Free Net Adjustment)
关于广义逆 1、左逆和右逆(Left and Right Inverse)
1 11
1 ˆ (N 1N )T N 1 AT PL 0 N12 )T (N11 N12 ) I T I X 2 11 12 11 1
上式有唯一解。令
R N11 N11
可解得
1 T ˆ X 2 N21 ( R N12 N21 ) A1 PL 1 T ˆ X1 N11 (R N12 N21 ) A1 PL
1、最小范数法(Minimum Norm)
特例 令 于是
PX I , P I
ˆ N ( N N ) AT L A L X r
QX N ( NN ) N ( NN ) N N ˆ
r
为等精度观测的普通秩亏网平差解(P117——水准网例题)
第三讲 秩亏平差(Free Net Adjustment)
2-范数
加权范数、椭圆范数
第三讲 秩亏平差(Free Net Adjustment)
一、自由网平差概述
1、自由网平差综合模型
L AX
nt
E ( L) AX
2 2 1 0 Q 0 P
If If
R( A) t ,Full rank G-M model R( A) q t ,Deficiency G-M model
第三讲 秩亏平差(Free Net Adjustment)
二、加权秩亏网平差解法
1、最小范数法(Minimum Norm) 2、附加约束法 3、转换法 4、直接解法
第三讲 秩亏平差(Free Net Adjustment)
二、加权秩亏网平差解法
1、最小范数法(Minimum Norm)
ˆ L V AX
函数模型
约束条件
V T PV min ˆTP X ˆ min X
X
由
ˆ U 0 V T PV min NX
ˆTP X ˆ 2K T ( NX ˆ U ) min X X
目标函数
第三讲 秩亏平差(Free Net Adjustment)
1、最小范数法(Minimum Norm) X ˆ X 2 K N 0 X P PX NK Q X NK 2X P ˆ ˆ T T 1 求导
