最短航线
高三地理 最困难系列 利用经纬网定“最短航线”知识点
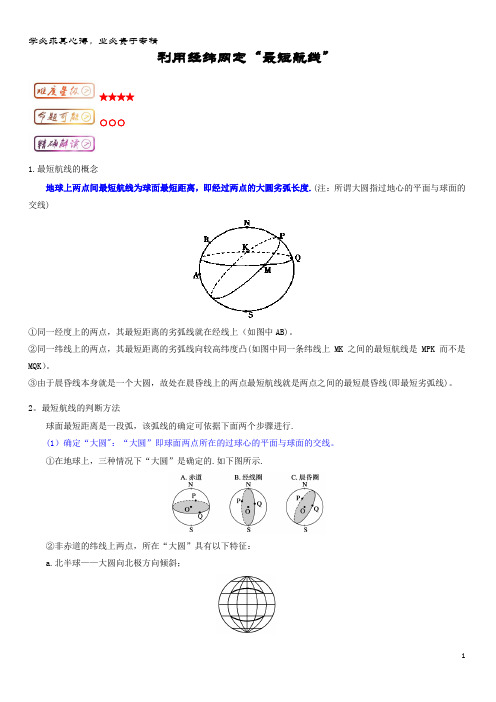
利用经纬网定“最短航线”★★★★○○○1.最短航线的概念地球上两点间最短航线为球面最短距离,即经过两点的大圆劣弧长度.(注:所谓大圆指过地心的平面与球面的交线)①同一经度上的两点,其最短距离的劣弧线就在经线上(如图中AB)。
②同一纬线上的两点,其最短距离的劣弧线向较高纬度凸(如图中同一条纬线上MK之间的最短航线是MPK而不是MQK)。
③由于晨昏线本身就是一个大圆,故处在晨昏线上的两点最短航线就是两点之间的最短晨昏线(即最短劣弧线)。
2。
最短航线的判断方法球面最短距离是一段弧,该弧线的确定可依据下面两个步骤进行.(1)确定“大圆":“大圆”即球面两点所在的过球心的平面与球面的交线。
①在地球上,三种情况下“大圆”是确定的.如下图所示.②非赤道的纬线上两点,所在“大圆”具有以下特征:a.北半球——大圆向北极方向倾斜;b.南半球——大圆向南极方向倾斜。
(2)确定“劣弧”:大圆上两点间的最短距离具体应该是哪一段弧线,则由“劣弧”来决定,所谓“劣弧”,即两点间的弧度小于180°。
如图6中的两段劣弧。
如果记忆不牢固的话,可通过下图进行推导。
如图A、B为位于北半球的两点且不在常见的大圆上,则其最短航线为一个向北弯曲的弧线,C、D为位于南半球的两点且不在常见的大圆上,则其最短航线为一个向南弯曲的弧线。
具体是:同北偏北,同南偏南,同一条经线圈上走极点。
寻“最短航线"的技巧(1)若两地经度差等于180°,过这两点的大圆便是经线圈。
最短航线经过两极点,具体分三种情况:①同在北半球,先向北,过极点后再向南,如A到E.②同在南半球,先向南,过极点后再向北,如B到D.③两地位于不同半球,则看劣弧过哪个极点再做讨论,如A至C.(2)同一纬线上但不在同一经线圈上①同在北纬,从A到B的最短距离;先向东北,再向东南方向.②同在南纬,从A到B的最短距离:先向东南,再向东北方向。
读下图,从E点到F点的最短航线是()A.先西北后西南 B.先东南后东北C.先西南后西北 D.先东北后东南【答案】A某飞行员驾机从A机场(30°N,120°E)起飞,为了经济省时,飞机必须沿最短航线飞往B机场(35°S,60°W)执行任务.据此回答1-2题.1。
最短航线和两点间距离

三、利用经纬网定“最短航线”
地球上两点间最短航线为球 面最短距离,即经过两点的大圆 劣弧长度。(注:所谓大圆指过 地心的平面与地球表面的交线) 1.同一经线圈上的两点,其最短距离的劣弧就在该经 线圈上(如右图中AB)。 2.同一纬线上的两点(经度和不等于180°),其最 短距离的劣弧线向较高纬度凸(如右图中同一条纬线上 ,MK之间的最短航线是MPK而不是MQK)。 3.由于晨昏线本身就是一个过地心的大圆,故处在晨 昏线上的两点之间的最短晨昏线(即最短劣弧线)就是两 点的最短航线。
60°
30°
东南方
3、M点和P点的实际距离是 A 4444千米
C 2222千米
D 1823 千米
S
F
M
P
P点坐标 45°S,150°W ;M点坐标 60°S,150°E 。
P点位于M点的
东北 方;M点位于北京的 东南 方。
P点关于地心对称的点坐标为 45°N,30°E 。
弧FM长度约为 3330 千米;弧PF长度约为 1665 千米。
依据: 任意一条纬线都跨360 °的经度(纬线是圆)。 同一纬线上,经度相差1°的两地距离= 此纬线的周长/360 ° 任意一条纬线(纬度为α)的周长=赤道周长× cos α
3、赤道上经度相差1°的两地距离为111千米; 南北纬60°上经度相差1°的两地距离为111/2千米 4、纬度越大,同一纬线上经度相差1°的两地距离越短。 (纬线的长度由赤道向两极递减)
二、利用经纬网计算两地距离
1、同一条经线上,纬度相差1°的两地距离相差约111千米。
依据: 经线长度都相等(约2万千米);任意一条经线都跨180°的 纬度(经线是半圆)。 同一条经线上,纬度相差1°的两地距离= 2万千米/经度相差1°的两地距离 相差约 111×cos α 千米。
高考地理专题1.2 最短航线图的判读-解图释含义含解析

定“最短航线”图[知识点拨]1.确定最短距离球面最短距离是一段劣弧,沿劣弧的行进方向即为最短航线,该弧线的确定可分两个步骤进行:(1)确定“大圆”:“大圆”即球面两点所在的过球心的平面与球面的交线,如图所示:①在地球仪上,三种情况下“大圆”是确定的:一是赤道(图A) 二是经线圈(图B) 三是晨昏圈(图C)。
②非赤道的纬线上两点,所在“大圆”具有以下特征:北半球——大圆向北极方向倾斜;南半球——大圆向南极方向倾斜。
(2)确定“劣弧”:大圆上两点间的最短距离具体应该是哪一段弧线,是由“劣弧”来决定,所谓“劣弧”即两点间的弧度<180°,如图D中PQ间的劣弧为上侧一段弧,P′Q′间的劣弧为下侧一段弧。
2.沿劣弧的行进方向即为最短航线(3)航向的判读(以图中从M点到K点最短航线为例)①首先判读两点的东西相对位置。
K点(目的地)在M点东侧,若想到达K点必须向东航行。
②航行过程需要经过较高纬的P点,故需要先向较高纬(向北)航行,后向较低纬(向南)航行。
③结合上面两点分析,其航行方向为东北—(正东)—东南。
[典题示例](2018·湖北武汉华师附中期中测试)读经纬网图,回答1~2题。
1.设A、B两点和B、C两点之间的最短距离分别为L1和L2,则( )A.L1和L2相等B.L1约为L2的一半C.L2约为L1的1.5倍D.L1约为L2的两倍2.若飞机从图中B点飞往D点,沿最短航线飞行,合理的方向是( )A.一直向东 B.一直向西C.先向东南,再向东北 D.先向西南,再向西北[对点练习]1.新加坡(采用的是东八区的计时方法)是亚洲与大洋洲的航空枢纽,也是伦敦到悉尼的重要航空中转站。
由新加坡沿最短线路飞往伦敦的航班( )A.航程小于10 000 km B.航程大于15 000 kmC.航向一直朝西北 D.航向先向西北再向西南解析:选D 最短航线跨经度需小于180°,故整体向西飞,但在同一半球中跨经度大于90°则有方向上的拐点,故航向先向西北再向西南。
两地间最短航线方向的确定

两地间最短航线方向的确定
(1)若两地经度和等于180度,过这两点的大园便是经线圈,最短航线经过极点,具体又分三种情况:同位于北半球,最近航程一定是先向北,过北极点后,再向南;同位于南半球,最近航程一定是先向南,过南极点后,再向北;两地位于不同半球,这时需要讨论要看过北极点的为劣弧还是过南极点的为劣弧,确定后再讨论。
(2)两地经度和不等于180,则过两点的大园不是经线圈,而是与经线圈斜交。
最短航线不过极点,而是过两极地区(或上空),具体又分两种情况:甲位于乙地的东方,从甲到乙的最近航程为:同在北半球,先向西北,再向西,最后向西南;同地南半球,先向西南。
再向西,最后向西北;位于不同半球时需要讨论哪一段为劣弧段。
甲位于乙地的西方,从甲到乙的最近航程为:同在北半球,先向东北,再向东,最后向东南;同地南半球,先向东南。
再向东,最后向东北;位于不同半球时需要讨论哪一段为劣弧段。
最短航线的判定方法

最短航线的判定方法
判定最短航线的方法是使用最短路径算法。
最短路径算法是一种寻找图中连接两个节点间最短距离的算法。
以下是两种常用的最短路径算法:
1. Dijkstra算法:该算法适用于没有负权边的有向图或无向图。
它通过从起始节点开始,逐步更新其他节点的距离,直到找到最短路径为止。
2. Floyd-Warshall算法:该算法适用于有向图或无向图,可以处理边权值为负数的情况。
Floyd-Warshall算法通过一个动态规划的过程,计算所有节点间的最短路径。
在使用最短路径算法判定最短航线时,需要将航线抽象为一个图,节点表示地点,边表示航班,边的权值表示航班的飞行时间或距离。
根据实际情况,选择合适的最短路径算法,并给出起始节点和目标节点,即可计算出最短航线的距离或路径。
最短航线的三种判定方法

最短航线的三种判定方法以最短航线的三种判定方法为标题,写一篇文章一、最短航线的定义与重要性最短航线是指在给定的起点和终点之间选择的距离最短的航行路径。
在航空、航运和航天领域,寻找最短航线对于节省时间、燃料和资源具有重要意义。
为了确定最短航线,有三种常用的判定方法:直线距离法、曲线距离法和大圆航线法。
二、直线距离法直线距离法是最简单的判定方法,它基于两点间的直线距离。
这种方法忽略了地球的曲率和地球表面的不规则性,只考虑了两点之间的直线距离。
在实际应用中,直线距离法常用于短距离航线的计算,例如城市之间的航线。
然而,当航线跨越较大的距离时,直线距离法会引入较大的误差,因为地球的曲率不能被忽略。
三、曲线距离法曲线距离法是一种考虑地球表面曲率的判定方法。
它通过在地球表面上选择一条曲线路径来计算航线距离。
常用的曲线路径包括大圆弧和小圆弧。
大圆弧是连接两个点的最短路径,它是地球表面上的一段大圆。
小圆弧是连接两个点的路径,它不一定是最短路径,但比直线距离更接近最短航线。
曲线距离法考虑了地球的曲率,因此可以在计算较长航线时提供更准确的结果。
四、大圆航线法大圆航线法是寻找最短航线的一种常用方法,它基于大圆弧路径。
大圆弧是连接两个点的最短路径,它是地球表面上的一段大圆。
在计算大圆航线时,需要使用球面三角学公式,如球面余弦定理和球面正弦定理。
这些公式可以根据给定的起点和终点的经纬度来计算大圆航线的距离和方向。
大圆航线法是最精确的判定方法之一,广泛应用于航空和航运领域。
五、总结最短航线的判定方法有直线距离法、曲线距离法和大圆航线法。
直线距离法简单易用,适用于短距离航线的计算。
曲线距离法考虑了地球的曲率,提供了更准确的结果。
大圆航线法是最精确的判定方法之一,广泛应用于航空和航运领域。
在实际应用中,选择适当的判定方法可以帮助我们找到最短航线,节省时间和资源。
经纬网应用--最短航线

图中由E到F的最短航线为 先向西北,再向西南 北半球,向西行
例外:当给出像左图形式的非常明显的图示 或材料说明时,则根据图中信息及材料判断。
图中由A到F最短航线 一直向东北
五、利用经纬网确定球面两点间“最短航线”
地球上两点间的最短航线为球面最短距离,即经过两点 的大圆劣弧长度。(大圆指的是过地心的平面与地面的交线)
航向为先向正北,再向正南 (如图中A、B两地) (2)两地都在南半球,最短航线过南极点。
航向为先向正南,再向正北 (如图中C、D两地)
N
A
Q
B
地心O
C
F
D S
(3)若一地在南半球,一地在北半球时,比较两地纬度值的大小, 最短航线经过两地中纬度值较大者所在半球的极点。
由A到D时 先向南,过南极点,然后向北
5、最短航线的特殊情况
(1)一地位于赤道,另一地不在赤道和极点上
① 两地经度差≤ 90°时,最短航线方向不变。
② 两地经度差 > 90°时,最短航线方向变化。
由C到A时 方向为向东北
由C到F时 方向为向东北
N
由C到B时 方向为先向东北,然后向东南
F
A
B
C
D
S
(2)两地同位于一个半球,并且不在同一条纬线上时
4.假若一架飞机从A飞到B,实际最短的飞行线路是
A 弧ANB C 弧AMB
B 弧AGB D 弧ACB
A
5、上图中从D点到E点的最短航线是( D)
A.先西北后西南
B.先东南后东北
C.先西南后西北
D.先东北后东南
D:60°N,165°W E:60°N,45°W
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
●Hale Waihona Puke S(2)若两地的经度差等于 180°,则经过这两点大圆是 经线圈。这两点间的最短距离 是经过极点。
①同在北半球,最短航线必须经 过北极点,其航行方向一定是先 向正北,过北极点后再向正南。
N A
● ●
B
S
②同在南半球,最短航线必须经 过南极点,其航行方向一定是先 向正南,过南极点后再向正北。
先向东北再向东南 ________________。
B
图中ACB为晨昏线,C点在格陵兰岛上 若图中A地点正当日落,两 个小时后,太阳直射点的 45° 地理位置是( B ) C 70°
A.20°S,75°W B. 20°N,105°E C.23°26′N,165°E D.23°26′S,105°W
D
A 30°
B
(二)非赤道的纬线上两点,所在“ 大圆”具有以下特征: 北半球——大圆向北极方向倾斜
B A
C
D
飞机从②处沿图中箭头路线飞往①的航向是 ( ) D
A.从东南向西北 B.从南向北 C.先向西北再向 西南 D.先向东北再向 东南
南半球——大圆向南极方向倾斜
A
D
B
C
a
如图,AB、AC为两条经线(局 部),弧线a为晨昏线,B、C两点纬 度相同,D为BC中点。回答1-2题。 1.AD间的球面距离不可能是 A.10千米 B.1000千米 C.2000千米 D.3000千米
A D
B
C
a
如图,AB、AC为两条经线(局 部),弧线a为晨昏线,B、C两点 纬度相同,D为BC中点。
2.若A为北极点,C点位于晨线上, 则D点时刻为 A.0:00 B.6:00 C.12:00 D.18:00
N
A
●
●
B
S
③两地位于不同半球,这时需要 考虑经过北极点为劣弧,还是经 过南极点为劣弧,然后确定最短 航线的走向和航程。
A N
●
●
B
S
3.晨昏圈 晨昏线上 两点之间的 最短距离即 该晨昏线上 两点之间的 劣弧部分。 (如图中的 GH之间)
图中ACB为晨昏线,C点在格陵兰岛上
1.由A到B的最短航线是 70° ( B ) A.由A点出发沿纬线向东 到B B.沿ACB C.沿ADB D.从A出发过极点再到B 30° 2.飞行方向的变化是 A 45° C D
N P N N P● O
● ● ●
P
Q
●
●
O
●
● ●
Q
O
Q
S
S
S
(二)在其他情况下“大圆”的 确定:
二、判断最短距离:找“劣弧” 1.赤道 则两点间最短航线应是沿 着赤道朝两点间的劣弧方向运动, 即向东或向西。 N
所谓“劣弧” 即两点间的弧 度<180°
P
●
O
●
Q
●
S
2.经线圈
(1)若两点在同一条经线上,则 两点间最短航线应是沿着经线朝 两点间的劣弧方向运动,即向北 N 或向南。
球面最短距离
雅丹地貌是一种典型的风蚀性地貌
有陡崖的陆相红层地貌称为丹霞地貌
要点 探究
球面上两点间的最短距离 确定最短距离球面最短距离是一 段弧,该弧线的确定可依据下面两 个步骤进行: 一、确定“大 圆”: 即球面两点所 在的过球心的圆
(一)在地球仪上,三种情况下 “大圆”是确定的: 1.赤道 2.经线圈 3.晨昏圈
