第10章二重积分的习题课
高等数学(下)课件D10_习题课

f ( x, y )dy
(2) I= ∫1 dy ∫1 f ( x, y )dx + ∫ dy ∫ f ( x, y )dx
2 y 1 y
2
2
2
2
解:根据积分限可得积分区域
1 1 D = {( x, y ) | ≤ y ≤ 1, ≤ x ≤ 2} 2 y U{( x, y ) |1 ≤ y ≤ 2, y ≤ x ≤ 2}
2 2 1 1 D − x 1
1 1 1[+−)1x 1(|−x 2 2 2 d − | 31 = ∫( x y ] = ∫ x ) − 1 d x − − 1 1 3 3 1 2 x1 = =∫3 ) 1 − ( −x . d 0 3 2 3
D 直x 及 2 3 ∫ y ,其是 =2 物 线 线 例算 σ 中由y − 抛yx 计x = d ∫
6、会用二重积分计算质量、质心、一阶矩和转动惯 量等。 7、掌握第一型曲面积分的概念,会确定曲面在坐标 平面上的投影区域,会计算简单曲面上的第一型 曲面积分。 8、对三重积分可以理解为密度函数为的所占的区域 为的物体的质量。理解这一点对三重积分的许多 性质的理解有极大的帮助。 9、还应将三重积分和以前各类积分比较,一方面可 以加强理解,另一方面也使同学不易忘记和混淆。
xσ [ xx d ∫ y = yy] ∫ d ∫∫ dy 1
22 D
3 4 2 x2y 2 yyd [2 y2 9 = y ] = 2 ) = −] . [ ( y 1 ∫ ⋅2d ∫ − y y 8= 1 1 8 2 2
D 直1 = 2 ∫ +−d 其是 = x 1 线 − 例算12 yσ 中由y 、 计y x 2 , ∫
习题课10--二重积分部分

9计算二重积分 ,其中
10计算二重积分 ,其中D是由直线 , , 以及曲线
所围成的平面区域。
11设函数 在区间 上连续,并设 ,
求 。
解法1:化为二重积分,然后利用二重积分的性质。
如图, : , : 。
∵ ,
∴
。
解法2:更换二次积分顺序
∵
∴
。
解法3:利用定积分换元法。
。
解法3:利用分部积分
,
得所求二重积分的方程,解之得 。
宁波工程学院高等数学AI教案
习题课10--重积分
1选择填空
(1) ,其中 的大小
关系为:( )
(A) (B) (C) (D)无法判断
(2) ,且 在 上连续.
(A) (B) (C) (D)
(3) 区域 ,按Y型区域应为( )
(A) (B) (C) (D)
(4) 已知
,则( )
(A) (B) (C) (D)
12设 连续,且 ,其中D是由 , ,
所围成区域,则 等于(C)
(A) ;(B) ;(C) ;(D) 。
解:设 (常数)。在D上对 两边积分得:
,解得 ,
故 。
(5)设 连续,且 ,其中D由 所围成,则
(A) (B) (C) (D)
2 填空
(1) 在Y型区域下的二次积分为
(2) 将 转换为极坐标形式下的二次积分
(3) 所围成,且 连续。
(4)
(5) 。
解: 。
(6) 。
解:
。
(7) 。
解:该积分不是二重积分的二次积分。
。
(8) 在极坐标系下的二次积分
为 。
(二)、客观题
1设 在 上连续,证明: .
二重积分习题课

所以 2xyd 0 。
O
x
D
( x y)2d ( x2 y2 )d
D
D
上页 下页 返回16
又因为x2 y2关于 x 为偶函数,
y 2a
若设D1为D中x 0的部分,则
D a
( x y)2d ( x2 y2 )d
D
D
O
2
( x2 y2 )d 2
2 d
2a sin r 2 rdr
上页 下页 返回 7
(三)有关二重积分的对称性的应用
1、若D关于y轴对称 即当(x,y)∈D时,必有(x,y) ∈D,则
f ( x, y)d
D
0,
2
D1
f (x,
y)d ,
当f ( x, y) f ( x, y)时 当f ( x, y) f ( x, y)时
其中D1是D的右半区域
上页 下页 返回 8
(1) F(t) 2 tf (t2 )
(2) 由洛必达法则:
lim F (t) lim F(t) lim 2 tf (t 2 ) 0.
t t 0
t0
t0
上页 下页 返回31
例10 设f ( x)为闭区间[a,b]上的连续函数且恒大于0,
试利用二重积分证明不等式 y
b
b
f ( x)dx
1
y),则
c y d
y x 1( y) d
D
D
f ( x, y)d
d
dy
c
2( y) 1( y)
f
( x,
y)dxc
o
x 2( y) x
上页 下页 返回 4
(3) 交换积分顺序 由所给的二次积分的顺序及积分限,确定积
二重积分

0
0
D
∫ ∫ =
π 0
(x2 y − 1 3
y3)
sin x 0
dx
=
π (x2 sin x − 1 sin3 x)dx
0
3
∫ ∫ =
π x2 sin xdx − 1 (2
π
2 sin3 xdx)
0
30
∫ =
(−x2
cos x)
π 0
+
2
π 0
x cos xdx − 1 (2 • 3
2) 3
∫ = π 2
D
次积分,其中积分区域 D 为:
∫∫ ∫∫ ( y2 − x)dσ = 2 ( y2 − x)dσ = − 24
D
D1
5
(3) ∫∫ (x 2 − y 2 )dσ , D : 0 ≤ y ≤ sin x,0 ≤ x ≤ π .
D
∫∫ ∫ ∫ 解:
(x2 − y2 )dσ =
π
dx
sin x (x2 − y2 )dy
≤y r2
≤r − y2
≤
x≤
,故
r2 − y2
∫ ∫ ∫∫
f (x, y)dσ
=
r dy
0
r2 − y2 − r2−y2
f (x, y)dx
D
(3)环形闭区域:1 ≤ x 2 + y 2 ≤ 4 .
D : X − 型区域
⎧⎪−2 ≤ x ≤ −1
⎨ ⎪⎩−
4 − x2 ≤ y ≤
4−
x2
∪
⎧⎪−1 ≤ ⎨ ⎪⎩2 )
3−2 y2 y2
dy
=
1 (y2x −
−1
二重积分的计算习题课
y= x
x x = ∫1 (− ) 1 dx y x
2
2
x
1
o
D
1
x=2
9 = ∫1 ( x − x)dx = . 4
2 3
2
x
型区域计算可以吗? 按Y-型区域计算可以吗 型区域计算可以吗
6
P155:15(2) P155:15(2)
∫∫
D
π 2 1 1− ρ 1 − x2 − y2 dxdy = ∫ 2 dθ ∫ ρ dρ 2 2 2 0 0 1+ x + y 1+ ρ
• 确定积分序
• 写出积分限
• 计算要简便 (充分利用对称性,几何意义和性质等 充分利用对称性, 充分利用对称性 几何意义和性质等)
2
P154:2(3) P154:2(3)
e x + y d σ , 其 中 D = {( x , y ) x + y ≤ 1 ∫∫
D
}.
1
0 ≤ x ≤1 解: X-型 D1: 型 x − 1 ≤ y ≤ 1 − x
12
6. (10分)计算二重积分 ∫∫ r 2 sin θ 1 − r 2 sin 2θ drdθ ,
D
π 其中D = ( r ,θ ) 0 ≤ r ≤ sec θ , 0 ≤ θ ≤ . 4
(10数学二 数学二) 数学二
7. (10分)计算二重积分 ∫∫ ( x + y )3 dxdy , 其中D由曲线x = 1 + y 2
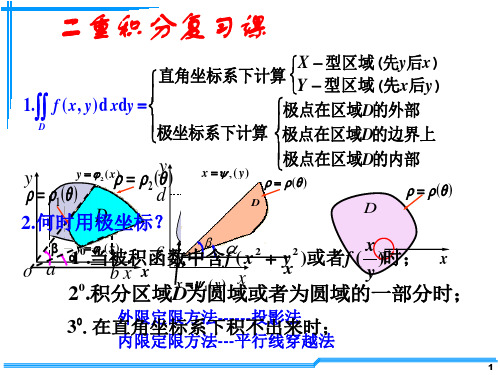
二重积分复习课
1.∫∫ f ( x, y)d xdy = 极点在区域D的外部 D 极坐标系下计算 极点在区域D的边界上 极点在区域D的内部 y x =ψ ( y) y = ϕ ( x) y ρ = ρ2(θ) ρ = ρ(θ ) ρ = ρ(θ) d ρ=ρ (θ)
二重积分习题课(简)

1
错误点:大多同学都做错了, 错误点:大多同学都做错了,可能是正切函数的导数 不清楚了。 不清楚了。
11
目录 上页 下页 返回
第三次作业共有2 第三次作业共有2题 P13) 多元函数微分法 习题课二 (习题册第一本 P13) 填空 1. f ( x, y )在 ( x0 , y0 ) 处有极值,则 D 处有极值, (A) f x ( x0 , y0 ) = 0, f y ( x0 , y0 ) = 0 ) 内唯一驻点, (B) ( x0 , y0 ) 是D内唯一驻点,则必为最大值点;且 ) 内唯一驻点 则必为最大值点;
1 2 1 2 −0 ≤ x + y < × 2ε = ε 2 2 x2 + y2 xy
即
( x , y ) →(0,0)
lim
f ( x, y ) = 0 = f (0, 0).
处连续。 因此函数 f ( x, y ) 在点 (0, 0) 处连续。 错误作法: 取极限, 错误作法: 有的同学令 y = kx 取极限,得到
∆y →0
= lim
∆y ∆y
∆y →0
g (0, 0),
存在, 因为 f x (0, 0) 和 f y (0, 0) 存在,并且
∆x → 0
lim
∆x ∆x
不存在, 不存在,所以 g (0, 0) = 0.
错误:多数同学做得不好,从偏导数的形式得不到 错误:多数同学做得不好,
g (0, 0) = 0
x →0, y = kx →0
lim
f ( x, y ) = 0 = f (0, 0) 从而得到结论。 从而得到结论。
3
目录 上页 下页 返回
第二节:( :(习题册第一本 P4) (2)第二节:(习题册第一本 P4)四 四、设 f ( x, y ) = x − y g ( x, y ), 其中 g ( x, y ) 在点 (0, 0) 的邻域内连续。 应满足什么条件, 的邻域内连续。问:g ( x, y ) 应满足什么条件,使
习题课 二重积分的计算

( x, y) 1 2. J . ( u, v ) ( u, v ) ( x, y)
二、例题分析
2 2 2 2 ( x y ) d 例1 计算 D : 2x x y 4 x D
解
积分区域由不等式给出 在不等式中取等号所得的曲线是两个半圆 但它们围不成区域 要使 2 x x 2 , 4 x 2 都有意义 必须限制 x [0,2]
v
D
1 f ( x y )dxdy f ( u)dudv 2 D
0 A u A A u
u
1 1 f ( u)du dv f ( u)du dv 2 A 20 A u u A
1 f ( u)( A u)du f ( u)( A u)du 2 A 0
2 2 xyf ( x y )d 0 D
0
D D
D2
xd xd xdx dy D D
1
x
3
D1
1
x
3
2 5
2 I 5
例6 设 f (x) 在 [0,1] 上连续
求
dx f ( x ) f ( y )dy 0 x
1
1
f ( x )dx A 0
③若D关于原点对称
D3 ( x, y ) D, x 0, y 0
D3
④若 D 关于直线
y=x
对称
f ( x , y )dxdy f ( y , x )dxdy D D
——称为关于积分变量的轮换对称性 是多元积分所独有的性质
①、②、③简单地说就是
奇函数关于对称域的积分等于0,偶函数关 于对称域的积分等于对称的部分区域上积分的两 倍,完全类似于 对称区间上奇偶函数的定积分的 性质
高等数学 课后习题答案 第十章

习题十1. 根据二重积分性质,比较ln()d Dx y σ+⎰⎰与2[ln()]d Dx y σ+⎰⎰的大小,其中:(1)D 表示以(0,1),(1,0),(1,1)为顶点的三角形;(2)D 表示矩形区域{(,)|35,02}x y x y ≤≤≤≤.解:(1)区域D 如图10-1所示,由于区域D 夹在直线x+y=1与x+y=2之间,显然有图10-112x y ≤+≤从而0l n ()1x y ≤+<故有2l n ()[l n ()]x y x y +≥+ 所以2l n ()d [l n ()]dDDx y x yσσ+≥+⎰⎰⎰⎰(2)区域D 如图10-2所示.显然,当(,)x y D ∈时,有3x y +≥.图10-2 从而 ln(x+y)>1 故有2l n ()[l n ()]x y x y +<+ 所以2l n ()d [l n ()]dDDx y x yσσ+<+⎰⎰⎰⎰2. 根据二重积分性质,估计下列积分的值:(1),{(,)|02,02}I D x y x y σ==≤≤≤≤⎰⎰;(2)22sin sin d ,{(,)|0π,0π}DI x y D x y x y σ==≤≤≤≤⎰⎰;(3)2222(49)d ,{(,)|4}DI x y D x y x y σ=++=+≤⎰⎰.解:(1)因为当(,)x y D ∈时,有02x ≤≤, 02y ≤≤因而04xy ≤≤.从而2≤≤故2d DD σσσ≤≤⎰⎰⎰⎰⎰⎰即2d d DDσσσ≤≤⎰⎰⎰⎰而d Dσσ=⎰⎰(σ为区域D 的面积),由σ=4得8σ≤≤⎰⎰(2) 因为220sin 1,0sin 1x y ≤≤≤≤,从而220sin sin 1x y ≤≤故 220d sin sin d 1d DDDx y σσσ≤≤⎰⎰⎰⎰⎰⎰即220sin sin d d DDx y σσσ≤≤=⎰⎰⎰⎰而2πσ=所以2220sin sin d πDx y σ≤≤⎰⎰(3)因为当(,)x y D ∈时,2204x y ≤+≤所以 22229494()925x y x y ≤++≤++≤故229d (49)d 25d DDDx y σσσ≤++≤⎰⎰⎰⎰⎰⎰即 229(49)d 25Dx y σσσ≤++≤⎰⎰而2π24πσ=⋅=所以 2236π(49)d 100πDx y σ≤++≤⎰⎰3. 根据二重积分的几何意义,确定下列积分的值:(1)222(,{(,)|};Da D x y x y a σ=+≤⎰⎰(2)222,{(,)|}.D x y x y a σ=+≤⎰⎰解:(1)(,Da σ-⎰⎰在几何上表示以D 为底,以z 轴为轴,以(0,0,a )为顶点的圆锥的体积,所以31(π3D a a σ=⎰⎰(2)σ⎰⎰在几何上表示以原点(0,0,0)为圆心,以a为半径的上半球的体积,故32π.3a σ=⎰⎰4. 设f(x ,y)为连续函数,求2220021lim(,)d ,{(,)|()()}πDr f x y D x y x x y y r r σ→=-+-≤⎰⎰.解:因为f(x ,y)为连续函数,由二重积分的中值定理得,(,),D ξη∃∈使得2(,)d (,)π(,)Df x y f r f σξησξη=⋅=⋅⎰⎰又由于D 是以(x0,y0)为圆心,r 为半径的圆盘,所以当0r→时,00(,)(,),x y ξη→于是:0022200000(,)(,)11lim(,)d limπ(,)lim (,)ππlim (,)(,)Dr r r x y f x y r f f r r f f x y ξησξηξηξη→→→→=⋅===⎰⎰5. 画出积分区域,把(,)d Df x y σ⎰⎰化为累次积分:(1){(,)|1,1,0}D x y x y y x y =+≤-≤≥;(2)2{(,)|2,}D x y y x x y =≥-≥(3)2{(,)|,2,2}D x y y y x x x =≥≤≤解:(1)区域D 如图10-3所示,D 亦可表示为11,01y x y y -≤≤-≤≤.所以1101(,)d d (,)d yDy f x y y f x y xσ--=⎰⎰⎰⎰(2) 区域D 如图10-4所示,直线y=x-2与抛物线x=y2的交点为(1,-1),(4,2),区域D 可表示为22,12y x y y ≤≤+-≤≤.图10-3 图10-4所以2221(,)d d (,)d y Dyf x y y f x y xσ+-=⎰⎰⎰⎰(3)区域D 如图10-5所示,直线y=2x 与曲线2y x =的交点(1,2),与x=2的交点为(2,4),曲线2y x =与x=2的交点为(2,1),区域D 可表示为22,1 2.y x x x ≤≤≤≤图10-5所以2221(,)d d (,)d xDxf x y x f x y yσ=⎰⎰⎰⎰.6. 画出积分区域,改变累次积分的积分次序:(1)2220d (,)d yy y f x y x⎰⎰; (2)eln 1d (,)d xx f x y y⎰⎰;(3)1320d (,)d y y f x y x-⎰; (4)πsin 0sin2d (,)d xxx f x y y-⎰⎰;(5)123301d (,)d d (,)d yyy f x y y y f x y x-+⎰⎰⎰⎰.解:(1)相应二重保健的积分区域为D :202,2.y y x y ≤≤≤≤如图10-6所示.图10-6D 亦可表示为:04,.2xx y ≤≤≤所以22242d (,)d d (,)d .yx yy f x y x x f x y y =⎰⎰⎰⎰(2) 相应二重积分的积分区域D:1e,0ln.x y x≤≤≤≤如图10-7所示.图10-7D亦可表示为:01,e e,yy x≤≤≤≤所以e ln1e100ed(,)d d(,)dyxx f x y y y f x y x=⎰⎰⎰⎰(3) 相应二重积分的积分区域D为:01,32,y x y≤≤≤≤-如图10-8所示.图10-8D亦可看成D1与D2的和,其中D1:201,0,x y x≤≤≤≤D2:113,0(3).2x y x≤≤≤≤-所以2113213(3)200010d(,)d d(,)d d(,)dy x xy f x y x x f x y y x f x y y--=+⎰⎰⎰⎰⎰.(4) 相应二重积分的积分区域D为:0π,sin sin.2xx y x≤≤-≤≤如图10-9所示.图10-9D亦可看成由D1与D2两部分之和,其中D1:10,2arcsinπ;y y x-≤≤-≤≤D2:01,arcsinπarcsin.y y x y≤≤≤≤-所以πsin 0π1πarcsin 0sin12arcsin 0arcsin 2d (,)d d (,)d d (,)d xyx yyx f x y y y f x y x y f x y x----=+⎰⎰⎰⎰⎰⎰(5) 相应二重积分的积分区域D 由D1与D2两部分组成,其中 D1:01,02,y x y ≤≤≤≤ D2:13,03.y x y ≤≤≤≤-如图10-10所示.图10-10D 亦可表示为:02,3;2xx y x ≤≤≤≤-所以()123323012d ,d d (,)d d (,)d yyxxy f x y x y f x y x x f x y y--+=⎰⎰⎰⎰⎰⎰7. 求下列立体体积:(1)旋转抛物面z=x2+y2,平面z=0与柱面x2+y2=ax 所围; (2)旋转抛物面z=x2+y2,柱面y=x2及平面y=1和z=0所围. 解:(1)由二重积分的几何意义知,所围立体的体积V=22()d d Dx y x y+⎰⎰其中D :22{(,)|}x y x y ax +≤由被积函数及积分区域的对称性知,V=2122()d d D x y x y+⎰⎰,其中D1为D 在第一象限的部分.利用极坐标计算上述二重积分得cos πππcos 344442220001132d d 2d cos d π4232a a V r r r a a θθθθθθ====⎰⎰⎰⎰.(2) 由二重积分的几何意义知,所围立体的体积22()d d ,DV x y x y =+⎰⎰其中积分区域D 为xOy 面上由曲线y=x2及直线y=1所围成的区域,如图10-11所示.图10-11D 可表示为:211, 1.x x y -≤≤≤≤所以21122221()d d d ()d DxV x y x y x x y y-=+=+⎰⎰⎰⎰2111232461111188d ()d .333105x x y y x x x x x --⎡⎤=+=+--=⎢⎥⎣⎦⎰⎰ 8. 计算下列二重积分:(1)221d d ,:12,;Dx x y D x y x y x ≤≤≤≤⎰⎰(2)e d d ,x yDx y ⎰⎰D 由抛物线y2=x,直线x=0与y=1所围;(3)d ,x y ⎰⎰D 是以O(0,0),A(1,-1),B(1,1)为顶点的三角形;(4)cos()d d ,{(,)|0π,π}Dx y x y D x y x x y +=≤≤≤≤⎰⎰.解:(1)()22222231221111d d d d d d xx Dx xx x x x y x y x x x x y yy ==-=-⎰⎰⎰⎰⎰⎰2421119.424x x ⎡⎤=-=⎢⎥⎣⎦(2) 积分区域D 如图10-12所示.图10-12D 可表示为:201,0.y x y ≤≤≤≤所示22110000e d d d e d d e d()xx x y y y y yD xx y y x y y y ==⎰⎰⎰⎰⎰⎰ 21111ed (e 1)d e d d y x y y yy y y y y y y y==-=-⎰⎰⎰⎰1111120000011de d e e d .22yy yy y y y y y =-=--=⎰⎰⎰(3) 积分区域D 如图10-13所示.图10-13 D 可表示为:01,.x x y x ≤≤-≤≤所以2110d d arcsin d 2xxx x y x y x y xx --⎡==+⎢⎣⎰⎰⎰⎰⎰112300ππ1πd .2236x x x ==⋅=⎰ππππ0πππ0(4)cos()d d d cos()d [sin()]d [sin(π)sin 2]d (sin sin 2)d 11.cos cos 222x Dxx y x y x x y y x y xx x x x x xx x +=+=+=+-=--⎡⎤==+⎢⎥⎣⎦⎰⎰⎰⎰⎰⎰⎰9. 计算下列二次积分:10112111224sin (1)d d ;(2)d e d d e d .yy y xxyxy x xy x y x +⎰⎰⎰⎰解:(1)因为sin d xx x ⎰求不出来,故应改变积分次序。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(三)有关二重积分的对称性的应用
1、若D关于y轴对称 即当(x,y)∈D时,必有(x,y) ∈D,则
f (x, y)d
D
0,
当 f(x,y)f(x,y)时
2D 1 f(x,y)d, 当 f(x,y)f(x,y)时
其中D1是D的右半区域
上页 下页 返回 8
2、若D关于x轴对称
即当(x,y)∈D时,必有(x, y) ∈D,则
f (x, y)d
D
0,
若 f(x,y)f(x,y)
2D 1 f(x,y)d, 若 f(x,y)f(x,y)
D1是D的上半部分区域
上页 下页 返回 9
3、若D关于原点对称, 即当(x,y)D时,必有( x,y) D,则
f (x, y)d
D
0,
0
y2
O
1
(1
y2
y2)e 2 dy
y2 1
e 2dy
y2
1
yde2
0
0
0
y2
y2
1
e 2d yye2
0
1 0
y2
1
e 0
2dy
ye
y2 2
1 0
e
1 2
。
上页 下页
x
返回14
例2 计算下列二重积分
(1) (xy)2d,
D
x2y22ay D : x2y2a(ya0)
(2)
D
x2 (a2
D既是X —型区域又是Y —型区域时,选择不需 分块或分块较少的积分顺序。
上页 下页 返回 3
若D:1(x)y2(x),则 y
axb
f(x,y)dbdx 2(x)f(x,y)dy
D
a 1(x)
oa
y2(x) D y1(x)
bx
若D:1(y)x2(y),则
cyd
y x1(y)
d
D
f(x,y)d
D
D
上页 下页 返回16
又 因 为 x 2 y 2 关 于 x 为 偶 函 数 ,
y 2a
若 设 D 1 为 D 中 x 0 的 部 分 ,则 a D
(xy)2d(x2y2)d
D
2
D
(x2 y2)d2
2d
O
2asinr2rdr
D1
0
as i n
x
22(1a 64si4n a4si4n )d15a4
(四)有关二重积分的一些证明题
中值定理、变上限积分、换元等
上页 下页 返回11
例1 当被积函数的原 是函 初数 等不 函数时, e x 2 ,e x y ,sy i,c nx o ,ss x i,s n x ik ,n cx o k (k s2 )等 ,
xx x 对这些函数要 y再先对 x积 积分 .
上页 下页 返回 5
(1)极点在D外
r 2()
D : 1 ( ) r 2 ( ), D
(2 )极 点 在 D 的 边 界 上 时
r 1()
D :0 r ( ) , O
r x2()
(3)极 点 在 D 的 内 部 时
D
D :0 r ()0 , 2
如D的边界是由直角坐标方 程:y =f (x) 给出,通常可从几何 意义去确定D的极坐标表示(图
D
cdd y 12 ((yy))f(x,y)dcx
o
x2(y)
x
上页 下页 返回 4
(3) 交换积分顺序 由所给的二次积分的顺序及积分限,确定积
分区域 D(画出图形),再按新的积分顺序将 D用新的不等式表出,即定出新的积分限。
2、利用极坐标计算二重积分
(1) 积分顺序通常是先 r后
(2) D的极坐标表示
2sin4d
40
20
15a4 3 1 45 a 4 。
2 4 2 2 32
上页 下页 返回17
(2)
x2 D(a2
by22)d,
D:x2y2R2
y
D
因为积 D 关 分于 区 y 直 x域 对线 称o R x
应先积y
I
1
x2
dx
sinx3dy
00
y
x y
1x2sinx3dx 0
O
x
1 cos x3 1 1(1 cos1)。
3
03
上页 下页 返回13
( 2 ) ey 2 2dxdy,D :yx,x1,y0所 围 。
D
y
D :y2x1,0y1
y x
应先积x
1
1 y2
I dy e 2 dx
y2 b2
)d,
D: x2 y2 R2(a0,b0)。
上页 下页 返回15
解(1)(xy)2d
D D :x 2 y 2 2 a ,x 2 y y 2 a ( a y 0 )
y
2a
因 为 区 域 D 关 于 y轴 对 称 ,
D a
2xy关于 x为奇函数
所 以 2xyd 0。
O
x
D
(xy)2d(x2y2)d
d
oa
D y1(x)
c
bx
o
D
x2(y)
x
上页 下页 返回 2
积分区域的不等式表示的是二重积分化为二 次积分确定积分限的基本依据。
(2) 积分顺序的确定 先积y还是先积x,要结合被积函数f (x,y)及积
分区域两个方面的特点加以考虑。
首先是“能积出”,其次是“易积出”。 如仅从积分区域的特点看,D是X —型区域时先 积y;D是Y —型区域先积x。
二重积分习题课
一、内容提要 (一)二重积分的概念、性质
n
1、定义 Df(x,y)dli m 0i1f(i,i) i
2、几何意义:曲顶柱体的体积 3、性质
上页 下页 返回 1
(二)二重积分的计算 1 、直角坐标系中
(1) 积分区域D的类型:
X—型区域,Y—型区域,一般区域分划。
y2(x)
y
y x1(y)
(1 )s in x 3 d x d y ,D :x y ,x 1 ,y 0 所 围 。
Dy2
( 2 ) e2dxdy,D :yx,x1,y0所 围 。 D
上页 下页 返回12
(1 )s in x 3 d x d y ,D :x y ,x 1 ,y 0 所 围 。
D
解 (1) D的图形如右。
2D 1 f(x,y)d,
若 f(x,y)f(x,y) 若 f(x,y)f(x,y)
其中D1是D的上半部分(或右半部分)区域。
上页 下页 返回10
4、若D关于直线 y =x对称, 即当(x,y)∈D时,必有(y,x)∈D,则
f (x, y)d f(y,x)d
D
D
1 2D[f(x,y)f(y,x)d]
形是重要的)或利用x=rcos, y=rsin 进行变换。
O
r 1()
x
r ()
oD
上页 下页
x
返回 6
(3)坐 标 系 的 选 取 当 D 的 边 界 用 极 坐 标 表 示 比 较 简 单 或 D 是
圆 域 、 圆 的 一 部 分 时 , 当 被 积 函 数 形 如 f(x 2 y 2 )、 f x y 、 f x y 时 可 考 虑 选 用 极 坐 标 系 。
