数字逻辑2-1
数字逻辑第二章课后答案

2-1
2-2
均可以作为反相器使用。
与非门:
或非门:
异或门:
2-3 1
Y V
CMOS 与非门的一个输入端通过电阻接地,相当于该输入端输入低电平,输出Y1是高电平。
2Y V
CMOS 或非门的一个输入端通过电阻接高电平与直接接高电平是一样的,输出Y2是低电平。
V 3
Y V 低电平有效的三态门的使能端EN 接高电平,则Y3为高阻态。
4
Y V
与或非门的一个与门输入全为高电平,则输出Y4是低电平。
2-4
E D C B A Y ⋅⋅⋅⋅=1 E D C B A Y ++++=2
))((3F E D C B A Y ++++=
F E D C B A Y ⋅⋅+⋅⋅=4 2-5
当1=EN ,T1`和T2截止,Y=Z (高阻)。
当0=EN ,T1`导通,A A Y ==。
2-7
(1)忽略所有门电路的传输延迟时间,除去开始的一小段时间,与非门的两个输入端总有一个是低电平,输出一直为高电平。
(2)考虑每个门都有传输延迟时间。
假设1级门的传输延迟时间为tpd ,则与非门的两个输入端的输入信号变化实际上并不是同时的。
信号A 经过两级门的传输延迟,比信号B 要晚2tpd 时间到达与非门的输入端。
因此,将出现,在短暂时间里,两个输入端的输入信号都是高电平的情况,输出电压波形出现毛刺。
数字逻辑(第二版)习题答案

第一章1. 什么是模拟信号?什么是数字信号?试举出实例。
模拟信号-----指在时间上和数值上均作连续变化的信号。
例如,温度、压力、交流电压等信号。
数字信号-----指信号的变化在时间上和数值上都是断续的,阶跃式的,或者说是离散的,这类信号有时又称为离散信号。
例如,在数字系统中的脉冲信号、开关状态等。
2. 数字逻辑电路具有哪些主要特点?数字逻辑电路具有如下主要特点:●电路的基本工作信号是二值信号。
●电路中的半导体器件一般都工作在开、关状态●电路结构简单、功耗低、便于集成制造和系列化生产。
产品价格低●由数字逻辑电路构成的数字系统工作速度快、精度高、功能强、可3. 数字逻辑电路按功能可分为哪两种类型?主要区别是什么?根据数字逻辑电路有无记忆功能,可分为组合逻辑电路和时序逻辑电路两类。
组合逻辑电路:电路在任意时刻产生的稳定输出值仅取决于该时刻电路输入值的组合,而与电路过去的输入值无关。
组合逻辑电路又可根据输出端个数的多少进一步分为单输出和多输出组合逻辑电路。
时序逻辑电路:电路在任意时刻产生的稳定输出值不仅与该时刻电路的输入值有关,而且与电路过去的输入值有关。
时序逻辑电路又可根据电路中有无统一的定时信号进一步分为同步时序逻辑电路和异4. 最简电路是否一定最佳?为什么?一个最简的方案并不等于一个最佳的方案。
最佳方案应满足全面的性能指标和实际应用要求。
所以,在求出一个实现预定功能的最简电路之后,往往要根据实际情况进行相应调整。
5. 把下列不同进制数写成按权展开形式。
(1) (4517.239)10 (3) (325.744)8(2) (10110.0101)2 (4) (785.4AF)16解答(1)(4517.239)10 = 4×103+5×102+1×101+7×100+2×10-1+3×10-2+9×10-3(2)(10110.0101)2= 1×24+1×22+1×21+1×2-2+1×2-4(3)(325.744)8 = 3×82+2×81+5×80+7×8-1+4×8-2+4×8-3 (4) (785.4AF)16 = 7×162+8×161+5×160+4×16-1+10×16-2+15×16-36.将下列二进制数转换成十进制数、八进制数和十六进制数。
第二章 逻辑代数基础

A B A B
______
A (B C) A (B C) A B C
__________ _____
A ( B C ) A B C A B C
________
3.反演定理
对于任意一个逻辑式 Y ,若将其中所有的“•”换成 “+”, “+”换成“•”,0换成1,1换成0,原变量 __ 换成反变量,反变量换成原变量,则得到的结果就是 Y
2、非逻辑真值表 A 0 1 Y
3 、非逻辑函数式
Y=A 或: Y A
1
0
4、 非逻辑符号
A
1
Y
或: 5 、 非逻辑运算 0=1 1=0
四、 几种最常见的复合逻辑运算
1 、 与非 Y=A B A B & Y
A 0 0 1 1
B 0 1 0 1
Y 1 1 1 0
3 、 同或 Y= AB+A B =A⊙B A B Y
(还原律)
证明: A B A B A ( B B ) A 1 A
4.
A ( A B) A
(吸收律)
证明: A ( A B) A A A B A A B A (1 B) A 1 A
5. A B A C B C A B A C
c. 非非律: ( A) A
A+A=A
d. 吸收律:A + A B = A
A (A+B) = A
A AB A B
e. 摩根定律: ( AB) A B
A .B A B 反演律(摩根定律): A B A B
二选一多路选择器原理

二选一多路选择器原理二选一多路选择器(Multiplexer,简称MUX)是一种能够将多个输入信号选中其中一个并输出的数字逻辑电路。
在数字电路中,MUX是一种广泛应用的电路之一,在数字信号处理、通信、计算机等领域都有着非常重要的作用。
二选一多路选择器通过一组控制信号,将多个输入信号中的一个输出到信号线上。
其结构通常由选择输入端、数据输入端和输出端组成。
多路选择器的输入端可选输入多个数据信号,由控制信号确定输出哪一个数据信号到输出端,因此多路选择器也称为“数据选择器”。
为了更好地理解多路选择器的原理,以下将多路选择器原理分为三个部分:1. 控制器多路选择器的控制器表示多路选择器的选择输入端,用于选择哪个输入端输出到输出端。
多路选择器的控制信号可以是一个或多个不同的信号,但这些信号所代表的值必须是二进制值。
多路选择器的控制器可以使用 AND 或 OR 门实现,当控制信号和输入信号同时为 1 时,对应输入信号会输出到输出线上。
2. 数据输入多路选择器的数据输入就是该选择器的多个输入端。
可以选择其中的一个输入端作为输出,这个输出端的值等于该输入端的值。
这些输入信号可以是数字信号、模拟信号或混合信号。
3. 输出多路选择器的输出端是计算机或其他设备使用的信号线。
多路选择器的输出值取决于选择输入端和输入端的状态。
当控制器的状态为0 时,多路选择器输出与第一个输入信号连接的值。
当控制器为 1 时,多路选择器输出与第二个输入信号相连的值。
这个选择过程由控制器完成。
综上所述,二选一多路选择器是一种能够将多个输入信号中的一个输出的数字逻辑电路。
其结构由选择输入端、数据输入端和输出端组成。
多路选择器通过一组控制信号,确定输出哪一个数据信号到输出端。
在数字信号处理、通信、计算机等领域中,多路选择器都有着广泛的应用,是非常重要的电路之一。
列表:1. 二选一多路选择器是什么?2. 多路选择器的控制器是如何实现的?3. 多路选择器的数据输入是什么?4. 多路选择器的输出是什么?5. 多路选择器在哪些领域有广泛的应用?。
数字逻辑第2章-逻辑代数

例如:
Y AB CDE
Y A B C D E
Y AB C
Y ( A B )(C D E)
(B A) B
证明:由于(A B ) (A B) (A B A) B
A (B B)
A 1
1
而且(A B ) (A B) A B A A B B
00
0 所以,根据公理 5的唯一性可得到:
A B A B
A A
定理6:反演律
A B A B
A B A B
定理7:还原律
A B A B A ( A B ) ( A B ) A
定理8:冗余律
AB A C BC AB A C
( A B)(A C)(B C) ( A B)(A C)
A B B A 交换律: A B B A
公理2
( A B) C A ( B C ) 结合律: ( A B) C A ( B C )
公理3
公理4
A (B C) A B A C 分配律: A B C ( A B) ( A C )*
判断两个逻辑函数是否相等,通常有两种方法。
①列出输入变量所有可能的取值组合,并按逻 辑运算法则计算出各种输入取值下两个逻辑 函数的相应值,然后进行比较。
②用逻辑代数的公理、定律和规则进行证明。
2.2 逻辑代数的基本定理和重要规则
数字逻辑电路基础知识整理(属于个人笔记)
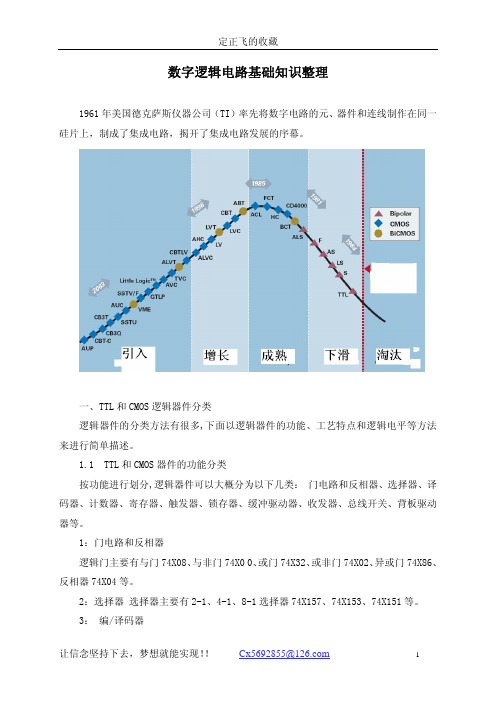
1.2 TTL 和 CMOS 逻辑器件的工艺分类特点
按工艺特点进行划分,逻辑器件可以分为 Bipolar、CMOS、BiCMOS 等工艺,其中包括
器件系列有:
Bi polar(双极)工艺的器件有: TTL、S、LS、AS、F、ALS。
CMOS 工艺的器件有: HC、HCT、CD40000、ACL、FCT、LVC、LV、CBT、ALVC、AHC、
5VTTL 的输出 0 低于 0.4V,可以被 CMOS 识别。至于 TTL 的高电平输出能力非常微 弱(<1mA),CMOS 电路的输入有嵌位二极管,防止可控硅闩锁,一般都有 5~10mA 的吸收 能力,此时 TTL 的输出大约是 3.3+0.7=4.0V,是 1。
TTL 电平: 输出高电平>2.4V,输出低电平<0.4V。在室温下,一般输出高电平是 3.5V,输出低电 平是 0.2V。最小输入高电平和低电平:输入高电平>=2.0V,输入低电平<=0.8V,噪声容限 是 0.4V。 CMOS 电平: 逻辑电平电压接近于电源电压,0 逻辑电平接近于 0V。而且具有很宽的噪声容限。 电平转换电路: 因为 TTL 和 COMS 的高低电平的值不一样(ttl 5v<==>cmos 3.3v),所以互相连 接时需要电平的转换:就是用两个电阻对电平分压,没有什么高深的东西。 OC 门,即集电极开路门电路,OD 门,即漏极开路门电路,必须外界上拉电阻和电源才 能将开关电平作为高低电平用。否则它一般只作为开关大电压和大电流负载,所以又叫 做驱动门电路。 TTL 和 COMS 电路比较: 1)TTL 电路是电流控制器件,而 coms 电路是电压控制器件。 2)TTL 电路的速度快,传输延迟时间短(5-10ns),但是功耗大。COMS 电路的速度慢, 传输延迟时间长(25-50ns),但功耗低。COMS 电路本身的功耗与输入信号的脉冲频率有关, 频率越高,芯片集越热,这是正常现象。 TTL 和 CMOS 的逻辑电平关系
数字逻辑设计习题参考答案 (第2章)
数字逻辑设计习题册班级:学号:姓名:哈尔滨工业大学(威海)计算机科学与技术学院体系结构教研室第2章 逻辑代数基础2—1 填空1.摩根定理表示为:=⋅B A _B A +__;=+B A _B A ⋅__。
2. 函数表达式D C AB Y ++=,则其对偶式为='Y _D C B A ⋅⋅+)(_______。
3.根据反演规则,若C D C B A Y +++=,则=Y C D C B A ⋅++)(。
4.函数式CD BC AB F ++=写成最小项之和的形式结果为()15,14,113,12,11,7,6,3∑m ,写成最大项之积的形式结果为)10,9,8,5,4,2,1,0(∏M。
5. (33.33)10 =(100001.0101 )2 =( 41.2 )8 =( 21.5 )162—2 证明1.证明公式()()A BC A B A C +=++成立。
2.证明此公式B A B A A +=+成立。
3.证明此公式)()()()()(C A B A C B C A B A +⋅+=+⋅+⋅+成立。
左边 (由分配律得)右边BCA BCB C A BC BA AC AA C A B A +=+++=+++=++)1())((BA A AB B B A B A B A AB AB B A B A AB BA B B A +=+++=+++=++=++=)()()(ACBC A B C A AC B C A C B B A ++=+⋅+=+⋅+⋅+=)()()()()(ACBC A B BC A B AC A A ++=+++=4. 证明此公式1))(((=+++⋅++C B D B A C B D C C B A 成立。
左边5.证明此公式D C D C B A D AC D C B D C A ⊕=+++⊕)(成立。
左边2—3 用代数法化简下列各式 1.B A BC A F +=1 2.D C A ABD CD B A F ++=2F 1 F 23.CD D AC ABC C A F +++=3 F 34.)()(4C B A C B A C B A F ++⋅++⋅++=F 41))((0))((=+++=+++⋅=C B D B A C B C B D B A C B D C C B A DC DC BD C D C D C A D C B D C A D AC D C A D C B D C A D AC A B D C D C A D AC B A B D C D C A ⊕=++=⊕++⊕=+++⊕=+++⊕=+++⊕=)()()()()()()(1=++++=B A C B A ADC B C B AD C B C B AD =+=++=)()(CDA CDC B C A CD AC AB C A D A C B C A D D A C BC C A +=+++=+++=+++=+++=)()()()()(CB AC B C B A A C A C B A C A C B A +=++=++=+++=)()(x y x y x =+⋅+)()(5.C DE C BE CD B B A AC F ++++=5F 56.C B A AD C B A CD AB F ++++=6F 67.D BC A BD A BD CD B B A C A F +++++=7F 78. D D C C A B A F +++=8F 8 1=++++=D D C C A B A9. D AC D C A D C B D C D C A F ++++=)(9F 9CE B AC CE D B B AC C E D B AC B AC C E D B C A B AC C E D B D B C B B A AC C E D B D C B B A AC ++=+++=+++=++++=++++=+++++=)()()(DC B A AD B C AB AD D C B C AB AD A A C B D C AB +++=++++=++++=+++++=)()(1)()()()()(=++++=+++++=+++++=+++++=+++++=+++++=A CD B BD A C A A CD B BD B B A C A A CD B B A D A B C A A CD B B A BD D B A C A A BD CD B B A D B C A BD A BD CD B B A D BC C A DC D C D C B D C D C D C D C A D C B D C D C A +=++=++++=)()(10.D B AB C D B AB F +++++=10(y x y x x +=+)2—4用卡诺图化简下列各式1.C B A AB C B F ++=1 2.C B BC B A F ++=2F 1ABC += F 2B A +=3.C B C B C A C A F +++=3F 3C B B A C A ++=4.D C A C B AD C D C A ABD ABC F +++++=4D A F +=4111111111111AB CD0001111000011110D B AB C DB ABCD B AB ++=++⋅⋅=5.D B A AC C B A F ++=5 6.C B A AD C B A D C AB F ++++=6AC D B B A F ++=5 A C B DC F ++=6 7.D BC A BD A CD B B A C A F +F 7=18.D B D B C A C A F +++=8D)⊙(B C)⊙(8⋅=+++=A D C B A ABCD D C B A D C B A F11111111AB CD 00011110000111109.D C B A D AC D C B D C A F +++⊕=)(9D C D C F +=9 10. ))((10C AB B A F ++=C B C A F +=1011. C B AC D C A B A F +++=11AC C B B A F ++=1112.∑=mC B A P )7,6,5,2,1,0(),,(1AC C B B A P ++=2 13.=D C B A P )14,11,10,9,8,7,6,4,3,2,1,0(),,,(2D C C A D A B P +++=2 14.∑=mD C B A P )15,14,13,12,10,9,8,6,4,1,0(),,,(3D A D B C B AB D C P ++++=315. ∑=m D C B A P )15,14,13,11,9,7,6,5,3,1(),,,(4F 15=D+BC2—5 用卡诺图化简下列带有约束条件的逻辑函数 1.∑∑+=d mD C B A P )15,14,13,2,1,0()12,11,9,8,6,3(),,,(1CD A D B C A P ++=1 2.∑∑+=d mD C B A P )15,14,13,10,9,8()12,11,6,5,4,3,2,0(),,,(2C B C BD P ++=23.D C B A D C B A D C A P ++++=3, 约束:0=+AC ABD C B D C A D C A P ++=34.CD B A CD B A P +=4, 约束:A B C D 为互相排斥的一组变量,即在任何情况下它们之中不可能两个同时为1。
数字逻辑实验二
数字逻辑实验⼆实验⼆数据选择器、译码器、全加器实验⼀、实验⽬的1.熟悉数据选择器的逻辑功能。
2.熟悉译码器的⼯作原理和使⽤⽅法。
3.设计应⽤译码器的电路,进⼀步加深对它的理解。
4.掌握全加器的实现⽅法。
5.学习⽤中规模集成电路的设计⽅法。
⼆、实验所⽤器件和仪表1.双4选1数据选择器74LS153 1⽚2.双2-4线译码器74LS139 2⽚3.⼆输⼊四与⾮门74LS00 1⽚4.⼆输⼊四异或门74LS86 1⽚5.万⽤表6.⽰波器7.实验箱三、实验内容1.测试74LS153中⼀个4选1数据选择器的逻辑功能。
2.测试74LS139中⼀个2-4译码器的逻辑功能。
3.⽤2-4线译码器74LS139和与⾮门74LS00实现逻辑函数。
4.⽤两⽚2-4线译码器74LS139设计⼀个8通道的数据分配器。
5.⽤数据选择器74LS153设计⼀个全加器。
四、实验接线图1.74LS153实验接线图和74LS153真值表(每个芯⽚的电源和地端要连接)4个数据输⼊引脚C0─C3分别接实验台上的10MHz、1MHz、500KHz、100KHz脉冲源。
变化地址选择引脚A、B和使能引脚G的电平,产⽣不同的组合。
观测并记录每种组合下数据选择器的输出波形。
Output输出送到⽰波器上的红⾊线端,⽰波器上的⿊⾊线端接地。
观察⽰波器上输出波形和右下⽅频率的数值。
K1、K2和K3是实验箱上3个不同的开关。
图4.1 74LS153实验接线图表4.1 74LS153真值表2.74LS139实验接线图和74LS139真值表图4.2 74LS139实验接线图表4.2 74LS139真值表4个译码输出引脚Y0─Y3接电平指⽰灯。
改变引脚G、B、A的电平,产⽣8种组合。
观测并记录指⽰灯的显⽰状态。
=+。
输⼊来源于开关,输出送到LED 3.⽤74LS139和74LS00实现逻辑函数F AB AB灯上,观察在不同的输⼊时,灯的亮灭情况)4.⽤两⽚74LS139设计⼀个8通道的数据分配器(输⼊来源于开关,输出送到LED灯A图4.4 74LS139实现数据分配器的接线图5.⽤数据选择器74LS153设计⼀个全加器(输⼊来源于开关,输出送到LED灯上,观察在不同的输⼊时LED 灯的亮灭情况)。
数字逻辑电路__刘常澍主编____第二章习题答案
第2章 习题答案2-1 二极管、三极管用于数字电路中与用于模拟电路有什么不同?答:二极管和三极管在数字电路中主要用作开关,工作于大信号状态,即二极管工作在正向导通和反向截止两个状态,三极管工作在饱和于截止两个状态; 模拟电路中二极管一般工作在小信号状态或反向击穿状态,三极管一般工作在放大状态。
2-2 有两个二极管A 和B ,在相同条件下测得A 管的I F =10mA ,I R =2mA ;B 管的I F=30mA ,I R =0.5μA ;比较而言,哪个性能更好?答:B 管更好,因为其反向漏电流较小而正向允许电流大。
2-3 三极管工作在截止、饱和、放大状态的外部条件各是什么?答:截止时,使发射结反偏即v BE ≤0;饱和时,使基极电流等于或大于基极饱和电流,即i B ≥I BS =V CC /βR C ;放大时,使发射结正偏,而i B <I BS =V CC /βR C 。
2-4 MOS 管工作在截止、恒流、可变电阻区的外部条件各是什么? 答:对于常用的增强型NMOS 管,截止时,使栅源电压小于开启电压V T 即v GS >V GS(th)N ;工作于恒流区时,使v DS >v GS - V GS(th)N ;工作于可变电阻区时,使v DS <v GS - V GS(th)N2-5 二极管电路如图P2-5所示。
v I =5sin ωt (V ),假设二极管是理想二极管,试画出输出 v O 的波形。
若考虑二极管的导通压降V D =0.7V ,画出输出v O 的波形。
解:输出波形如图解P2-5所示。
(a)为输入波形, D 为理想二极管时输出波形为(b), 考虑D 导通压降为0.7伏时输出波形为(c)。
2-6 二极管开关电路如图P2-6所示。
二极管导通电压为0.7V ,试分析输入端A 、B 分别为0V 和5V 时管子的工作状态,输出电压v O =?解:v A =5V ,v B =0V 时,D 2、D 1均导通 v O =–0.7V ; v A =5V ,v B =5V 时, D 2、D 1均导通 v O =4.3V ; v A =0V ,v B =5V 时,D 1 导通、D 2截止 v O =4.3V ; v A =5V, v B =0V 时, D 1截止、D 2导通 v O =4.3V 。
数电实验二 组合逻辑电路
实验二 组合逻辑电路一、实验目的1、熟悉组合逻辑电路的一些特点及一般分析、设计方法。
2、熟悉中规模集成电路典型的基本逻辑功能和简单应用设计。
二、实验器材1、直流稳压电源、数字逻辑电路实验箱、万用表、示波器2、74LS00、74LS04、74LS10、74LS20、74LS51、74LS86、74LS138、74LS148、74LS151、 74LS153三、实验内容和步骤 1、组合逻辑电路分析(1)图2-1是用SSI 实现的组合逻辑电路。
74LS51芯片是“与或非”门(CD AB Y +=), 74LS86芯片是“异或”门(B A Y ⊕=)。
建立实验电路,三个输入变量分别用三个 逻辑开关加载数值,两个输出变量的状态分别用两只LED 观察。
观察并记录输出变 量相应的状态变化。
整理结果形成真值表并进行分析,写出输出函数的逻辑表达式, 描述该逻辑电路所实现的逻辑功能。
(2)图2-2和2-3是用MSI 实现的组合逻辑电路。
图2-2中的74LS138芯片是“3-8译码 器”,74LS20芯片是“与非”门(ABCD Y =)图2-3中的74LS153芯片是四选一 数据选择器。
建立实验电路,对两个逻辑电路进行分析,列出真值表,写出函数的逻 辑表达式,描述逻辑电路所实现的功能。
图2-1:SSI 组合逻辑电路图2-2 :MSI 组合逻辑电路(74LS138)2、组合逻辑电路设计(1)SSI 逻辑门电路设计——裁判表决电路举重比赛有三名裁判:一个主裁判A 、两个副裁判B 和C 。
在杠铃是否完全举起裁 决中,最终结果取决于至少两名裁判的裁决,其中必须要有主裁判。
如果最终的裁决 为杠铃举起成功,则输出“有效”指示灯亮,否则杠铃举起失败。
(2)MSI 逻辑器件设计——路灯控制电路用74LS151芯片和逻辑门,设计一个路灯控制电路,要求能够在四个不同的地方都 能任意的开灯和关灯。
四、实验结果、电路分析及电路设计方案1、组合逻辑电路分析 (1)图2-1: 逻辑表达式:)()(11i i i i i i i i i i B A C S B A C B A C ⊕⊕=⊕+=--逻辑功能:实现A i 、B i 、C i-1三个一位二进制数 的加法运算功能,即全加器。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Examples :
101110001011 5613 B8B
2
8
16
1011100010. 11 1342 . 6 2E2 . C
2
8
16
Conversion: from one system to another
Summary: p.31 Table 2-2
Operations for unsigned numbers
00110110 2 25 24 22 21 5410 0.00110110 2 23 24 26 27 0.2109375 10
0.2109375 28 54
Conversion: from one system to another
binary to decimal Examples : 0010 .1101 2 ?10 00101101 2 32 8 4 1 4510 0010 .1101 2 45 / 24 2.8125 10
Example for an 8-bit binary number:
0.00110110 00110110
MSB/LSB
Conversion: from one system to another
binary to decimal: based on definitions; Examples :
Positional number systems
D d2 r 2 d1 r1 d0 r 0 d1 r 1 d2 r 2
D Number d digit r base/radix Number: a string of digits; Each digit position has a different weight; Radix is written as 10 in any system.
0.17—0.34 —0.68—1.36—0.72—1.44—0.88—1.76—1.52
Different number systems
P.28 Table 2-1
A short way to represent numbers
Binary to octal: 3-bit to one digit; Binary to hexadecimal: 4-bit to one digit; Key point: divide from the radix point !
101 .012 1 22 0 21 1 20 0 21 1 22
bit: one digit in binary system;
Positional number system in digital design
Binary numbers withlways be set as 0.xxxxxxxx; We can take these numbers as integers !
Shift-add : use adders and shift-registers; The product width will be 2n !
Conversion: from Decimal to binary
For integer numbers : divided by 2, get its remainders; Examples for 8-bit binary numbers: 179 10 10110011 2
179—89 —44—22—11—5—2—1 1 1 0 0 1 1 01
Chapter 2: Number systems and codes
Positional number system : representation and conversion
Representations of negative binary numbers BCD codes and Gray code
Addition and subtraction Basic rules:
0+0=0 1+0=1 1+1=10 10-1=1
C:carry S:sum
B:borrow D:difference
Operations for unsigned numbers
Multiplication Basic rules: 0×A = 0 1×A = A
2.1 Positional number systems
Use few digit to express infinite values Each digit position has a different weight
Definition:
p 1
D d2d1d0.d1d2 di r i in
Examples of positional number system
Decimal system: base is 10, the digit may be 0 to 9
101 .110 110 2 0 101 1100 110 1
Binary system: base is 2, the digit may be 0 or 1
Conversion: from Decimal to binary
For decimal fraction numbers : multiplied by radix, and get its integers; Examples for 8-bit binary numbers:
0.1710 0.00101011 2
