第九章二重积分习题课
理学第九章重积分

1
1
2
2
(
1 2
,
2)
y
(
1 2
,1)
yx (1,1)
2
dy
1
y f (x, y)dx
1
1 2
(
1 2
,
1 2
)
y
1 x
o 11 2
x
机动 目录 上页 下页 返回 结束
4. 计算 I
2 dy
2
sin
x
dx.
0
yx
解: 积分区域如图. 交换积分顺序得:
I
2
sin
x
dx
0x
x
dy
0
x
cos(x y)dy
2
x
2
1
D2
o
D1
2
x
机动 目录 上页 下页 返回 结束
x y , x2 y 2x2
8. 设 f (x, y)
0 , 其他
,求 I f (x, y)dxdy,
D
其中 D {(x, y) 0 x 1 , 0 y 1}.
解: 积分区域如图.
I f (x, y)dxdy f (x, y)dxdy f (x, y)dxdy
z
1
解: 积分区域如图.
x2 y2 z2 6
z x2 y2
Dxy : x2 y2 2
y
2
o Dxy
x
1 : z 6 x2 y2
2 : z x2 y2
机动 目录 上页 下页 返回 结束
S1 Dxy
6 6 x2 y2 dxdy
2
2
6 d
0
0
rdr 6 r2
二重积分的计算习题课
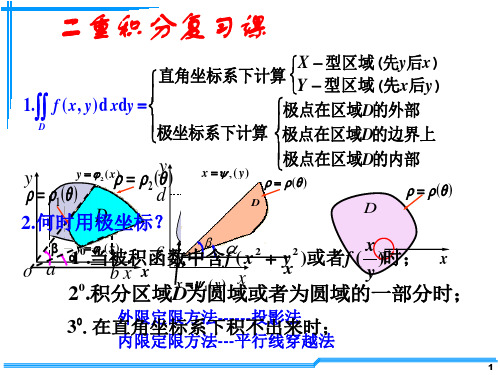
y= x
x x = ∫1 (− ) 1 dx y x
2
2
x
1
o
D
1
x=2
9 = ∫1 ( x − x)dx = . 4
2 3
2
x
型区域计算可以吗? 按Y-型区域计算可以吗 型区域计算可以吗
6
P155:15(2) P155:15(2)
∫∫
D
π 2 1 1− ρ 1 − x2 − y2 dxdy = ∫ 2 dθ ∫ ρ dρ 2 2 2 0 0 1+ x + y 1+ ρ
• 确定积分序
• 写出积分限
• 计算要简便 (充分利用对称性,几何意义和性质等 充分利用对称性, 充分利用对称性 几何意义和性质等)
2
P154:2(3) P154:2(3)
e x + y d σ , 其 中 D = {( x , y ) x + y ≤ 1 ∫∫
D
}.
1
0 ≤ x ≤1 解: X-型 D1: 型 x − 1 ≤ y ≤ 1 − x
12
6. (10分)计算二重积分 ∫∫ r 2 sin θ 1 − r 2 sin 2θ drdθ ,
D
π 其中D = ( r ,θ ) 0 ≤ r ≤ sec θ , 0 ≤ θ ≤ . 4
(10数学二 数学二) 数学二
7. (10分)计算二重积分 ∫∫ ( x + y )3 dxdy , 其中D由曲线x = 1 + y 2
二重积分复习课
1.∫∫ f ( x, y)d xdy = 极点在区域D的外部 D 极坐标系下计算 极点在区域D的边界上 极点在区域D的内部 y x =ψ ( y) y = ϕ ( x) y ρ = ρ2(θ) ρ = ρ(θ ) ρ = ρ(θ) d ρ=ρ (θ)
高等数学 二重积分习题课

y
1
D
1
dx
1 x 2e y2 dy
1
dy
y x 2e y2 dx
0
x
0
0
.
0
y x 1x
1 y 3 e y2 dy 1
03
6
1 y 2e y2 d( y 2 () 令 y 2 u )
D
D1
D2
0
dx
1 x e x y dy
1
dx
1
x
e
x
y
dy
1
1 x
0
x 1
0 (e 2 x1 e 1 )dx
1
(e
e 2 x1 )dx
e e1
1
0
【例3】计算二重积分
D
y dxdy. x
其中D 是由圆周 x 2
y2
重积分的几何意义将所求立体的体积用二重积分来表示,再 利用极坐标计算即可。
解:令
Байду номын сангаас
2
x2
y2
x2
y2,
求得曲线
z
2 x2 y2
z x 2 y2
在xoy坐标面上的投影曲线方程为 x2 y2 1;
故立体在 xoy坐标面上投影区域为Dxy : x2 y2 1.
f (i ,
i ) i
2.几何意义:表示曲顶柱体的体积
V f ( x, y)d ( f ( x, y) 0)
D
顶 : z f ( x, y) 底 : D
第九章第2节二重积分的计算(1)
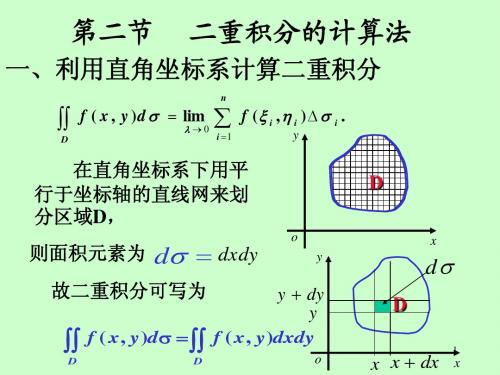
y + dy y ∫∫ f ( x, y)dσ =∫∫ f ( x, y)dxdy
D D
dσ
D
x
o
x x + dx
1
x
直角坐标系下的计算公式
a 如果积分区域为: 如果积分区域为: ≤ x ≤ b, ϕ 1 ( x ) ≤ y ≤ ϕ 2 ( x ).
y = ϕ2 ( x )
y = ϕ2 ( x )
ϕ1 ( x )
f ( x , y )dy
4
如果积分区域为: 如果积分区域为:
c ≤ y ≤ d , ϕ 1 ( y ) ≤ x ≤ ϕ 2 ( y ).
d
d
x = ϕ1 ( y )
D
x = ϕ2 ( y)
x = ϕ1 ( y )
D
c
c
x = ϕ2 ( y)
∫∫ f ( x , y )dσ = ∫
π
例4. 求 ∫∫ x e
D
2 − y2
dxdy ,其中 D 是以(0,0), (1,1),
(0,1)为顶点的三角形.
解 Q∫ e
− y2
dy 无法用初等函数表示
∴ 积分时必须考虑次序
∫∫ x e
D
2 − y2
dxdy = ∫ dy ∫ x e
0 0
1
y
2 − y2
dx
=∫ e
0
1
− y2
y ⋅ dy = − 3
2 2 2
2
2
2
利用对称性, 考虑第一卦限部分, 其曲顶柱体的顶为
R
o x
R2 −x2
x2 + y2 = R2
z = R2 − x2 0 ≤ y ≤ R2 − x2 (x, y) ∈D: 0 ≤ x ≤ R
二重积分习题课(简)

1
错误点:大多同学都做错了, 错误点:大多同学都做错了,可能是正切函数的导数 不清楚了。 不清楚了。
11
目录 上页 下页 返回
第三次作业共有2 第三次作业共有2题 P13) 多元函数微分法 习题课二 (习题册第一本 P13) 填空 1. f ( x, y )在 ( x0 , y0 ) 处有极值,则 D 处有极值, (A) f x ( x0 , y0 ) = 0, f y ( x0 , y0 ) = 0 ) 内唯一驻点, (B) ( x0 , y0 ) 是D内唯一驻点,则必为最大值点;且 ) 内唯一驻点 则必为最大值点;
1 2 1 2 −0 ≤ x + y < × 2ε = ε 2 2 x2 + y2 xy
即
( x , y ) →(0,0)
lim
f ( x, y ) = 0 = f (0, 0).
处连续。 因此函数 f ( x, y ) 在点 (0, 0) 处连续。 错误作法: 取极限, 错误作法: 有的同学令 y = kx 取极限,得到
∆y →0
= lim
∆y ∆y
∆y →0
g (0, 0),
存在, 因为 f x (0, 0) 和 f y (0, 0) 存在,并且
∆x → 0
lim
∆x ∆x
不存在, 不存在,所以 g (0, 0) = 0.
错误:多数同学做得不好,从偏导数的形式得不到 错误:多数同学做得不好,
g (0, 0) = 0
x →0, y = kx →0
lim
f ( x, y ) = 0 = f (0, 0) 从而得到结论。 从而得到结论。
3
目录 上页 下页 返回
第二节:( :(习题册第一本 P4) (2)第二节:(习题册第一本 P4)四 四、设 f ( x, y ) = x − y g ( x, y ), 其中 g ( x, y ) 在点 (0, 0) 的邻域内连续。 应满足什么条件, 的邻域内连续。问:g ( x, y ) 应满足什么条件,使
习题课

使
∫∫ f ( x , y )dσ =
D
f (ξ ,η ) s
3. 二重积分的计算 计算方法: 化二重积分为二次积分. 计算方法: 化二重积分为二次积分 问题: (1)根据什么选择坐标系 问题: (1)根据什么选择坐标系? 根据什么选择坐标系? 根据被积函数和积分区域的特点。 根据被积函数和积分区域的特点。 (2)根据什么选择积分次序? (2)根据什么选择积分次序? 根据什么选择积分次序 的边界的特点: 根据积分区域 D 的边界的特点: 原则:分块尽可能少,并且积分上、下限简单; 原则:分块尽可能少,并且积分上、下限简单; 容易根据第一次积分结果计算第二次积分。 容易根据第一次积分结果计算第二次积分。 注意: (1)无论在什么坐标系下 转化成二次积分计算时 无论在什么坐标系下, 二次积分计算时, 注意: (1)无论在什么坐标系下, 转化成二次积分计算时, 积分的下限要小于积分的上限。 积分的下限要小于积分的上限。 (2)灵活运用二重积分的性质简化计算过程。 (2)灵活运用二重积分的性质简化计算过程。 灵活运用二重积分的性质简化计算过程 (3)善于利用被积函数在对称积分区域上的奇偶性 (3)善于利用被积函数在对称积分区域上的奇偶性 简化计算。具体如下: 简化计算。具体如下:
0
π
sin x 0
f ( x, y ) d y − ∫
2
2π
π
d x∫
0 sin x
f ( x, y ) d y
= ∫∫
0
D1
f ( x, y ) d σ − ∫∫D f ( x, y ) d σ
π − arcsin y
arcsin y
= ∫ dy ∫
1
f ( x, y ) d x
二重积分习题练习及解析ppt课件
(2)设f (x, y)在有界闭区域D上连续. 若D关于
y轴对称, f (x, y)对x为奇函数, 即
f ( x , y ) f ( x , y ), ( x , y ) D,
则
f ( x , y )dxdy 0, D
f (x, y)对x为偶函数, 即 D
f ( x , y ) f ( x , y ), ( x , y ) D,
D
n
0
i 1
4
f ( x , y ) d xOy平面上方的曲顶柱体体积 D
减xOy平面下方的曲顶柱体体积. 3. 物理意义 若平面薄片占有平面内有界闭区域D, 它的面 密度为连续函数 ( x , y ), 则它的质量M为:
M ( x , y ) d .
D
5
(二)二重积分的性质 (重积分与定积分有类似的性质) 性质1(线性运算性质) 设、 为常数, 则
序后的积分限;
2. 如被积函数为 f ( x 2 y 2 ), f ( x 2 y 2 ),
y y f ( ), f (arctan ) 或积分域为 圆域、扇形域、 x x
圆环域时, 则用极坐标计算;
18
3. 注意利用对称性质, 以便简化计算; 4. 被积函数中含有绝对值符号时, 应 将积分域分割成几个子域, 使被积函数在 每个子域中保持同一符号, 以消除被积函 数中的绝对值符号.
y
1
1
y x2
O
1
x
20
2.利用对称性
例 计算
x 2 y 2 a 2
( x 2 x 3 y 2)d .
2
解 积分域是圆 x 2 y 2 a 2 , 故关于x、y轴、 直线 y x 对称, 故将被积函数分项积分:
第九章-2二重积分的计算法市公开课获奖课件省名师示范课获奖课件
2 x
应为_________________________.
6、将二次积分
dx
sin x x
f ( x, y)dy 改换积分次序,
0
sin
2
应为_________________________.
7、将二次积分 1 dy 2 f ( x, y)dx
e2
ln y
1 2
2
dy
f ( x, y)dx 改换积分次序,
若是X—型, 就先 y 后 x 若是Y—型,就先 x 后 y ,
注意内层积分限是外层积分变量旳函数,外层 积分限是常数。
例1 解
改变积分
1
dx
1x f ( x, y)dy的次序.
00
积分区域如图
y 1 x
原式
1 1 y
dy f ( x, y)dx .
00
例 2 改变积分
1
dx
2 x x2
若区域如图, 则必须分割.
在分割后旳三个区域上分别 使用积分公式
.
D
D1
D2
D3
注ⅰ)二重积分化累次积分旳环节
①画域,②选序,③定限
D3 D1
D2
ⅱ)累次积分中积分旳上限不不大于 下限
ⅲ)二重积分化累次积分定限是关键,积分限 要根据积分区域旳形状来拟定,这首先要画好 区域旳草图,——画好围成D旳几条边界线,
2 1
1
(3
sin
3)
2
以上各例阐明
化二重积分为累次积分时选择积分顺序旳 主要性,有些题目两种积分顺序在计算上难易程 度差别不大,有些题目在计算上差别很大,甚至 有些题目对一种顺序能积出来,而对另一种顺序 却积不出来
高数课后习题九详细答案
第9章课后习题详解 重积分课后习题全解习题9-1★1.设有一平面薄板(不计其厚度),占有xOy 面上的闭区域D ,薄板上分布着面密度为),(y x μμ=的电荷,且),(y x μ在D 上连续,试用二重积分表达该板上的全部电荷Q .解:将D 任意分割成n 个小区域{}i σ∆,在第i 个小区域上任取一点),(i i ηξ,由于),(y x μ在D 上连续和i σ∆很小,所以用),(i i ηξμ作为i σ∆上各点函数值的近似值,则i σ∆上的电荷i i i i Q σηξμ∆≈∆),(从而该板上的全部电荷⎰⎰∑=∆==→Dni i i i d y x Q σμσηξμλ),(),(lim 1其中λ是各i σ∆中的最大直径。
★★2.利用二重积分定义证明:(1)σσ=⎰⎰Dd (σ为区域D 的面积);(2)⎰⎰⎰⎰=DDd y x f k d y x kf σσ),(),((其中k 为常数);(3)⎰⎰⎰⎰⎰⎰+=21),(),(),(D D Dd y x f d y x f d y x f σσσ,其中21D D D=, 21,D D 为两个无公共内点的闭区域。
证明:(1)这里,被积函数1),(≡y x f ,由二重积分的定义,对任意分割和取点法,=∙⎰⎰Dd σ1∑∑=→=→∆∙=∆n i i ni iiif 111lim ),(lim σσηξλλ∑=→∆=ni i 1lim σλσσλ==→0lim ,∴σσ=⎰⎰Dd ,其中λ是各iσ∆中的最大直径。
(2)=⎰⎰Dd y x kf σ),(∑∑=→=→∆=∆ni i i i ni iiif k kf 101),(lim ),(lim σηξσηξλλ∑=→∆=ni i i i f k 1),(lim σηξλ⎰⎰=Dd y x f k σ),((3)将1D 任意分割成1n 个小区域{}1i σ∆,1λ是其各小区域的最大直径,将2D 任意分割成2n 个小区域{}2i σ∆,2λ有类似的意义。
微积分第九章二重积分作业
第1次作业一、填空题1.设区域D 为01,01x y ≤≤≤≤,则()Dx y d σ+⎰⎰的取值范围是_________________;2.依二重积分的概念可知=--⎰⎰≤≤-≤≤dxdy y x x x y 10102221 ;3.设函数(),f x y 在有界闭区域D 上连续,闭区域D 关于x 轴对称,1D 为闭区域D 在上半平面0y ≥中的部分闭区域,若()(),,f x y f x y -=,则(),_____________Df x yd x d y =⎰⎰,若()(),,f x y f x y -=-,则(),_____________Df x y dxdy =⎰⎰。
二、选择题1.若11(1)D I x d σ=+⎰⎰,其中1D 是1,1x y ≤≤,22D I xyd σ=⎰⎰,其中2D 是221x y +≤,则12I I 与的值为( );A .120,0I I <>;B .120,0I I >=;C .120,0I I ==;D .120,0I I ><。
2.若 1222322312(),()D D I x y d I x y d σσ=+=+⎰⎰⎰⎰, 其中12:1,2,:01,20D x y D x y ≤≤≤≤-≤≤,则12I I 与的关系是( );A .12I I =;B .122I I ≤;C .124I I =;D .128I I =。
三、根据二重积分的性质比较下列积分的大小:1.()Dx y d σ+⎰⎰与2()Dx y d σ+⎰⎰,其中D 是由x 轴、y 轴与直线1x y +=所围成的区域;2.ln()Dx y d σ+⎰⎰与2[ln()]Dx y d σ+⎰⎰,其中D 是矩形区域:35,01x y ≤≤≤≤;四、利用二重积分的性质估计下列积分值: ()⎰⎰++=Dy x I σd 1,其中(){}20,10,≤≤≤≤=y x y x D第2次作业一、填空题1. (,)DI f x y dxdy =⎰⎰,D 是3,y x y x ==所围成区域,则其先y 后x 的二次积分是_________________;先x 后y 的二次积分是_________________;3.若(,)()()f x y h x g y = ,在:,D a x b c y d ≤≤≤≤上连续,则(,)Df x y dxdy =⎰⎰_________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章二重积分习题课
高等数学课讲教案主讲人
课题第九章重积分习题课
目的任务使学生进一步理解本章的知识要点,熟练重积分的计算。
重点难点本章知识要点的进一步理解,重积分计算的熟练掌握。
教学方法讲授法
使用教具
提问作业
备课时间年月日上课时间年月日
查阅抽查
一、本章内容小结
1. 二重积分的定义及其几何意义
1) 重积分的定义:
2) 说明:
n
* 二重积分是和式的极限值,故是一个数,这个数只与被积函数
f(,,,),,,iii,1i
及积分区域有关,与积分变量的字母无关,即有 f(x,y)
f(x,y)d,,f(s,t)d,,,,,DD
* 和式的极限若存在,则与区域D如何划分及点如何选无关,为此常选方便(,,,)ii计算的分割方法,如选用平行于坐标轴的直线网来分割区域,则,此时二重d,,dxdy
积分 f(x,y)d,,f(x,y)dxdy,,,,DD
D * 若函数在有界闭区域上连续,则函数在上的二重积分总存在,称
f(x,y)f(x,y)
D函数在上可积。
f(x,y)
3) 重积分的几何意义.
2. 二重积分的性质:
注意性质所适用的条件,中值定理的几何意义
3. 二重积分的计算法:
二重积分的计算法采用累次积分,即把二重积分化为二次积分,通过两次定积分的计算即求得二重积分值,分以下两种情况。
y,x,1) 在直角坐标系下:将区域划分为型或型计算.
2) 在极坐标系下:将区域按照与极点的位置来划分并计算.
* 两种坐标系的适用范围、面积元素、表达式及变量替换对照表如下:
直角坐标极坐标
积分区域矩形、三角形或任意形圆形、环形、扇形
dxdyrdrd,面积元素
x,rcos,y,rsin,变量替换
f(x,y)dxdyf(rcos,,rsin,)rdrd,积分表达式 ,,,,DD
* 计算二重积分关键步骤是确定累次积分的上、下限,而上、下限的确定关键在于正确画出积分区域草图和正确运用不等式表示积分区域,把不等式小的一端列为积分下限,大的一端为积分上限。
注意:先一次积分的上、下限一般是后面积分变量的函数,且最后一次积分的上、下限应是常数。
d,,rdrd,* 若在极坐标系中要注意,不能丢:正确写出积分区域的边界曲线在r 极坐标系下的方程;选正确公式。
4. 二重积分的应用:
1) 曲顶柱体的体积;
2) 平面区域的面积 ; S,d,,,D
二、习题讲解(课后习题)
三、课堂练习(复习题九)。
