高中数列经典例集
高中数列经典习题含答案

高中数列经典习题 ( 含答案 )1、在等差数列 {a n}中,a1=-250,公差 d=2,求同足以下条件的全部 a n的和 , (1)70≤n≤ 200;(2)n 能被7 整除 .2、等差数列 {a n}的前 n 和 S n.已知 a3=12, S12>0,S13<0.(Ⅰ)求公差 d 的取范;(Ⅱ)指出S1,S2,⋯,S12,中哪一个最大 ,并明理由.3、数列 { a n }是首23,公差整数的等差数列,且前 6 正,从第 7 开始的,回答以下各: (1)求此等差数列的公差d;(2) 前n和 S n,求 S n的最大;(3)当 S n是正数,求n的最大 .4、数列 { a n}的前 n 和S n.已知首1a =3,且S n 1+ S n=2a n 1,求此数列的通公式a n及前n 和Sn .5、已知数列 { a n }的前 n 和S n13n(n+1)(n+2),求数列 { 1a n}的前 n 和 .6、已知数列 { a n}是等差数列 ,此中每一 及公差d均不 零 ,a i x 2 2a i 1xa i 2=0(i=1,2,3,⋯)是对于x 的一 方程 .回答: (1)求全部 些方程的公共根;(2) 些 方 程 的 另 一 个 根m i, 求m1, m1, m1,⋯ ,1 ,⋯也成等差数列 .112131m n17、假如数列 { a n} 中 ,相 两 a n和 a n 1是二次方程 x n23nx n c n=0(n=1,2,3⋯)的两个根 ,当 a 1=2 , 求c 100 的 .8、有两个无 的等比数列 { a n }和{ a n }, 它 的公比的 都小于 1,它 的各 和分 是 1 和 2, 而且 于全部自然数 n,都有 a n 1, 求 两个数列的首 和公比 .9、有两个各 都是正数的数列{ a n},{ b n}. 假如a =1,b =2,a =3.且, ,an 1 成等差数列 ,,an 1 , bn 1 成112a nb nb n等比数列 ,试求这两个数列的通项公式.10、若等差数列 {log2x n}的第 m 项等于 n,第 n 项等于 m(此中 m n),求数列 {x n}的前 m+n 项的和。
高中数学-数列应用题-老师-(七)

4、户,一月初向银行贷款10万元作开店资金,每月底获得的利润是该月初投入资金的20%,每月需交所得税为该月所得金额(含利润)的10%,每月生活费和其它开支三千元,余款作为资金全部投入再营业.如此继续,问到这一年底,这位个体户还清银行贷款后,纯收入还有多少?
2.由1.得{an}是等比数列a1=0.2 ,q=
3、有一个细胞集团,每小时死亡2个,余下的各个分裂成2个,设最初有细胞7个,问n小时后有多少个细胞?
解:设n小时后的细胞总数为an,则a0=7,且an+1=2(an-2),即an+1-4=2(an-4),数列{(an-4}是首项为a0-4=3,公比为2的等比数列,∴an=3·2n+4 (n∈N)。因此,第n个小时后的细胞总数为3·2n+4个。
欲使Tn最大,则: ,得 ,故n=5,此时s=7875。
即该厂家应生产7875件产品,做5千元的广告,能使获利最大。
三、an= C·an-1+B,其中B、C为非零常数且C≠1
例3、某企业投资1千万元于一个高科技项目,每年可获利25%,由于企业间竞争激烈,每年底需要从利润中取出资金200万元进行科研、技术改造与广告投入,方能保持原有的利润增长率,问经过多少年后,该项目的资金可以达到或超过翻两番(4倍)的目标?(lg2=0.3)。
解:由上面的分析可知: ,即
得t1=40.所以这次运送共持续了40小时.
2、为了保护某处珍贵文物古迹,政府决定建一堵大理石护墙,设计时,为了与周边景点协调,对于同种规格的大理石用量须按下述法则计算:第一层用全部大理石的一半多一块,第二层用剩下的一半多一块,第三层…依次类推,到第十层恰好将石块用完,问共需大理石多少块?每层各用大理石多少块?
高中数学数列经典题型及解析

高中数学数列经典题型及解析1. 求数列的通项公式:题目描述:已知数列的前几项为1,4,9,16,...,求该数列的通项公式。
解析:观察该数列可以发现,每一项都是前一项的平方加1,所以可以得到通项公式为an =n^2 + 1。
2. 求数列的和:题目描述:已知数列的前几项为2,5,8,11,...,求前100项的和。
解析:观察该数列可以发现,每一项都是前一项加3,所以可以得到通项公式为an = 3n - 1。
根据等差数列的求和公式,前n项的和可以表示为Sn = (n/2)(a1 + an),所以前100项的和为S100 = (100/2)(2 + a100),代入通项公式,得到S100 = (100/2)(2 + (3*100 - 1)) = 10100。
3. 求等差数列的前n项和:题目描述:已知数列的前几项为3,7,11,15,...,求前20项的和。
解析:观察该数列可以发现,每一项都是前一项加4,所以可以得到通项公式为an = 4n - 1。
根据等差数列的求和公式,前n项的和可以表示为Sn = (n/2)(a1 + an),所以前20项的和为S20 = (20/2)(3 + (4*20 - 1)) = 820。
4. 求数列的极限:题目描述:已知数列的前几项为1,1/2,1/3,1/4,...,求该数列的极限值。
解析:观察该数列可以发现,每一项都是前一项的倒数,即an = 1/n。
当n趋向于无穷大时,an趋向于0,所以该数列的极限值为0。
5. 求数列的递推关系:题目描述:已知数列的前几项为1,2,4,7,11,...,求该数列的递推关系。
解析:观察该数列可以发现,每一项都是前一项加一个递增的数,递增的数可以依次为1,2,3,4,...,所以可以得到递推关系为an = an-1 + (n-1)。
以上是高中数学中数列的经典题型及解析,希望对你有帮助!。
高中数列经典例集(习题)

一、 经典例题剖析考点一:等差、等比数列的概念与性质 例题1.(1)数列{a n }和{b n }满足)(121n n b b b na +++=(n=1,2,3…), (1)求证{b n }为等差数列的充要条件是{a n }为等差数列。
(2)数列{a n }和{c n }满足*)(21N n a a c n n n ∈+=+,探究}{n a 为等差数列的充分必要条例题 2.已知数列{}n a 的首项121a a =+(a 是常数,且1a ≠-),24221+-+=-n n a a n n (2n ≥),数列{}n b 的首项1b a =,2n a b n n +=(2n ≥)。
(1)证明:{}n b 从第2项起是以2为公比的等比数列;(2)设n S 为数列{}n b 的前n 项和,且{}n S 是等比数列,求实数a 的值; (3)当a>0时,求数列{}n a 的最小项。
考点二:求数列的通项与求和 例题3..已知数列{}n a 中各项为:12、1122、111222、……、111n ⋅⋅⋅⋅⋅⋅ 个222n ⋅⋅⋅⋅⋅⋅个…… (1)证明这个数列中的每一项都是两个相邻整数的积. (2)求这个数列前n 项之和S n .例题4. 已知数列{}n a 满足411=a ,()),2(2111N n n a a a n nn n ∈≥--=--. (Ⅰ)求数列{}n a 的通项公式n a ; (Ⅱ)设21nn a b =,求数列{}n b 的前n 项和n S ;(Ⅲ)设2)12(sinπ-=n a c n n ,数列{}n c 的前n 项和为n T .求证:对任意的*∈N n ,74<n T .考点三:数列与不等式的联系例题5.已知α为锐角,且12tan -=α,函数)42sin(2tan )(2παα+⋅+=x x x f ,数列{a n }的首项)(,2111n n a f a a ==+. ⑴ 求函数)(x f 的表达式; ⑵ 求证:n n a a >+1;⑶ 求证:),2(21111111*21N n n a a a n∈≥<++++++<例题6已知数列{}n a 满足()111,21n n a a a n N *+==+∈(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若数列{}n b 满足n n b nb b b b a )1(44441111321+=---- ,证明:{}n a 是等差数列; (Ⅲ)证明:()23111123n n N a a a *++++<∈例题7. 已知函数()()ln 1f x x x =-+,数列{}n a 满足101a <<,()1n n a f a +=; 数列{}n b 满足1111,(1)22n n b b n b +=≥+, *n N ∈.求证:(Ⅰ)101;n n a a +<<<(Ⅱ)21;2n n a a +<(Ⅲ)若12a =则当n ≥2时,!n n b a n >⋅. 考点四:数列与函数、向量等的联系 例题8.已知函数f(x)=52168xx+-,设正项数列{}n a 满足1a =l ,()1n n a f a +=.(1)写出2a 、3a 的值; (2)试比较n a 与54的大小,并说明理由; (3)设数列{}n b 满足n b =54-n a ,记S n =1ni i b =∑.证明:当n ≥2时,S n <14(2n-1).例题9.在平面直角坐标系中,已知三个点列{A n },{B n },{C n },其中),(),,(n n n n b n B a n A )0,1(-n C n ,满足向量1+n n A A 与向量n n C B 共线,且点(B ,n )在方向向量为(1,6)的线上.,11a b a a -==(1)试用a 与n 表示)2(≥n a n ;(2)若a 6与a 7两项中至少有一项是a n 的最小值,试求a 的取值范围。
高中数学数列基础知识与典型例题
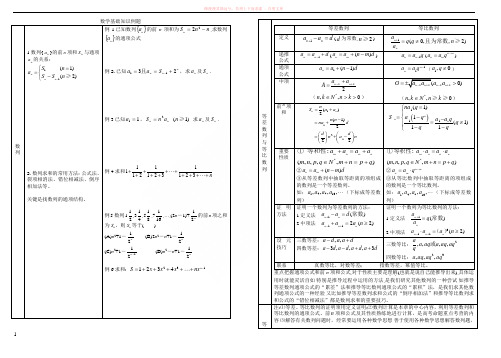
数列1.数列{na}的前n项和n S与通项na的关系:11(1)(2)nn nS naS S n-=⎧=⎨-⎩≥2.数列求和的常用方法:公式法、裂项相消法、错位相减法、倒序相加法等。
关键是找数列的通项结构。
例1.已知数列{}n a的前n项和为nnSn-=22,求数列{}na的通项公式.例2.已知nnnSaa2311+==-且,求na及nS.例3.已知11=a,nnanS2=(1)n≥求na及nS.例4.求和n+++++++++++321132112111.例5.数列121,341,581,7161,…,(2n-1)+n21的前n项之和为S n,则S n等于( )(A)n2+1-n21(B)2n2-n+1-n21(C)n2+1-121-n(D)n2-n+1-n21例6.求和: 2311234nS x x x nx-=+++++.等差数列与等比数列等差数列等比数列定义1n na a d+-=(d为常数,2n≥) 1(0,2)nnaq q na+=≠且为常数,≥递推公式1n na a d-=+(()n ma a n m d=+-)1n na a q-=(n mn ma a q-=)通项公式1(1)na a n d=+-11nna a q-=(1,0a q≠)中项2n k n ka aA-++=(*,,0n k N n k∈>>)(0)n k n k n k n kG a a a a-+-+=±>(*,,0n k N n k∈≥≥)前n项和1121()2(1)222n nnS a an nna dd dn a n=+-=+⎛⎫⎛⎫=+-⎪ ⎪⎝⎭⎝⎭()111(1)1(1)11nn nna qS a q a a qqq q=⎧⎪=-⎨-=≠⎪--⎩重要性质*(,,,,)m n p qa a a am n p q N m n p q+=+∈+=+①等和性:②()n ma a n m d=+-③从等差数列中抽取等距离的项组成的数列是一个等差数列。
数列求通项公式典型例题及答案

数列求通项公式1、累加法 :适用于:1()n n a a f n +=+ ----------这是广义的等差数列,累加法是最基本的二个方法之一。
例1.1 已知数列{}n a 满足11211n n a a n a +=++=,,求数列{}n a 的通项公式。
【答案:2n a n =】例1.2 已知数列{}n a 满足112313n n n a a a +=+⨯+=,,求数列{}n a 的通项公式。
【答案:3 1.nn a n =+-】练1.1 已知数列{}n a 的首项为1,且*12()n n a a n n N +=+∈写出数列{}n a 的通项公式.【答案:12+-=n n a n 】练1.2 已知数列}{n a 满足)2()1(1,311≥-+==-n n n a a a n n ,求此数列的通项公式. 【答案:n a n 12-=】2、累乘法适用于: 1()n n a f n a += ----------这是广义的等比数列,累乘法是最基本的二个方法之二。
例2.1 已知数列{n a }中,n n a a a n n 2,111+==+,求数列的通项公式。
【答案:)(2)1(*∈+=N n n n a n 】 例2.2 已知数列{n a }中,n n a n na a )1(2,111+==+,求数列的通项公式。
【答案:12-=n n na 】 练2.1【理科】 已知数列{}n a 满足112(1)53nn n a n a a +=+⨯=,,求数列{}n a 的通项公式。
【答案:(1)12325!.n n n n a n --=⨯⨯⨯】练2.2.设{}n a 是首项为1的正项数列,且()011221=+-+++n n n n a a na a n (n =1,2, 3,…),则它的通项公式是n a =________.【答案:na n 1=】3、待定系数法适用于1()n n a qa f n +=+ 基本思路是转化为等差数列或等比数列,而数列的本质是一个函数,其定义域是自然数集的一个函数。
极限经典例题集
之阿布丰王创作时间:二O二一年七月二十九日例题1.在数列{a n}中,a1=1,当n≥2时,a n,S n,成等比数列.(1)求a2,a3,a4;(2)猜想a n的表达式并用数学归纳法证明;(3)求;(4)(思考题)不使用猜想a n的表达式并用数学归纳法证明的方法直接求a n.1..解析:∵a n,S n,成等比数列,∴(n≥2)(*)(1)把a1=1,S2=a1+a2=1+a2代入(*)式得:把a1=1,,代入(*)得:.同理可得:由此可以推出(2)(i)当n=1,2,3,4时,由(*)知猜想成立.(ii)假设n=k(k≥2)时,成立.故∴或(舍去)由得即n=k+1时,命题也成立.由(i)(ii)可知,对一切n∈N成立.(3)由(2)得数列前n项的和,所有项和(4)对{a n}的通项还可以这样来求:∵, ∴,故是以为首项,为公差的等差数列故,注:对含有a n,S n的关系式中,常将a n用S n-S n-1(n≥2)代(或S n+1-S n用a n+1代),化成S n,S n+1(或a n,a n+1)的递归关系式.例 1.数列{a n}满足下列条件,求其通项公式a n.(1)a1=1,(2)a1=2,(3)a1=2,{a n}的前n项和S n满足解:(1)……将以上各式叠加,得∴又n=1时,(2)……将以上各式叠乘,得∴a n=n(n+1)(n≥2)当n=1时,1×(1+1)=2 = a1∴a n=n(n+1)(n∈N*)(3)∴2S n-1S n=S n-1-S n(n≥2)在上式两边同除以S n S n-1,得∴数列为首项,公差为2的等差数列.例2、在等差数列{a n}中(1)若a p=q,a q=p(p、q∈N*且q≠p),求a p+q;(2){a n}共有n项,其前四项之和为124,其最后四项之和为156,其所有项之和为210,求项数n;(3)若{a n}前n项和记为S n,且有,求S m+n的范围解:(1)∵a q=a p+(q-p)d∴a p+q=a p+(q+p-p)d=q+q×(-1)=0(2)∵a1+a2+a3+a4=124a n+a n-1+a n-2+a n-3=156∴(a1+a n)+(a2+a n-1)+(a3+a n-2)+(a4+a n-3)=280∴4(a1+a n)=280∴a1+a n=70∴n=6(3)设前n项和将以上两式相减得:两边同除以m-n,得例3、在数列{a n}中,S n是其前n项和,a1=1,S n+1=4a n+2(n∈N*)(1)设b n=a n+1-2a n,求证数列{b n}为等比数列并求其通项公式;(2)设 ,求证数列{C n}是等差数列并求其通项解:(1)∵S n+1=4a n+2∴S n+2=4a n+1+2 将以上两式相减,得a n+2=4a n+1-4a n∴a n+2-2a n+1=2(a n+1-2a n)又s2=4a1+2=a1+a2∴a2=5 ∴数列{b n}是以b1=a2-2a1=5-2=3为首项,q=2为公比的等比数列.∴b n=3×2n-1(2)数列{C n}是以为首项,为公差的等差数列.例4、在等差数列{a n}中,公差d≠0,a2是a1与a4的等比中项,已知数列成等比数列,求数列{k n}的通项k n解:∵a2是a1与a4的等比中项∵d≠0∴a1=d ∵是等差数列中的第k n项,是等比数列中的第n+2项且 =a1+(k n-1)d=d+(k n-1)d=k n d ∴∴ 2.数列的极限应用恒等变换和极限的四项运算法则,将数列的极限转化为三个基本极限来求解.3.数学归纳法数学归纳法有两个基本步伐:第一步,验证n=n0时,命题成立;第二步,假设n=k时,命题成立,然后利用归纳假设证明n=k+1时成立.用数学归纳法证明命题时特别要求证明的逻辑严密性.数学归纳法通经常使用来证明有关等式,不等式,整除,几何命题等.例 5.数列{a n}满足 ,a1=2(1)求数列{a n}的通项;(2)令 ,求出n∈(1,10000)内使b1b2b3…b n为整数的n的所有值的和. 解:(1)由a1=2得:由a2=3得:由a3=4得:猜想:a n=n+1(n∈N*) 下用数学归纳法证明该猜想1°当n=1时,a1=1+1=2,命题成立2°假设n=k(k∈N*)时,命题成立,即有a k=k+1,则=(k+1)+1 即n=k+1时,命题也成立.综合1°,2°知,a n=n+1(n∈N*)(2)∵将a n=n+1代入得=log2(n+2)欲使b1b2b3…b n为整数,须使n+2为2的整数幂∵n∈(1,10000) ∴n+2可是以22,23,24,213∴所求和为(22-2)+(23-2)+(24-2)++(213-2)=22+23+24+…+213-24=214-28=16356例6.无穷数列{a n}的前n项和为b n,无穷数列{b n}的前n项和C n,对n∈N*,恒有b n+c n=n,(1)证明:数列{1-b n}是等比数列;(2)求(3)比力的年夜小关系解:(1)首先b1+C1=1而C1=b1,得由已知:b n+C n=n,有b n+1+C n+1=n+1将两式相减,有b n+1-b n+b n+1=1∴数列{1-b n}是以的等比数列.(2)由(1)知:(3)n=1时,n≥2时,综上,当n=1或2时,显然有当n≥3时,这时例7.设 ,不论α、β为何实数,恒有f(cosα)≤0,f(2-sinβ)≥0,正数数列{a n}的前n项和S n=f(a n),n∈N*(1)求b值;(2)求{a n}的通项公式;(3)令 ,{c n}的前n项和为T n,比力T n与的年夜小.解:(1)当cosα=1时,有f(1)≤0当sinβ=1时,有f(2-sinβ)=f(1)≥0∴f(1)=0(2)令n=1,有解得a1=3或a1=-1(舍)将以上两式相减,∵{a n}为正数数列,∴a n,a n-1>0,∴a n+a n-1>0∴a n-a n-1=2(n≥2)∴{a n}是以a1=3为首项,公差为2的等差数列∴a n=3+(n-1)×2=2n+1(3)∴T n=C1+C2+…+C n[课后练习]1.数列{a n}的通项公式是a n=n2-kn,若数列{a n}是递增的,则实数k的取值范围是()(A)k<3(B)k≤3(C)k<2(D)k≤22.数列{a n}的通项公式是 ,当a n取最年夜值时,n即是()(A)4(B)5(C)6(D)73.数列{a n}满足a1=0, ,则a20即是( )(A)0(B)(C)(D)4.等比数列{a n}中,a n>0,a5a6=16,则log4a1+log4a2+…+log4a10=_____5.在等比数列{a n}中,a5,a9是方程7x2-18x+7=0的两个根,则6.数列{a n}的前n项和S n满足a n+2S n S n-1=0(n≥2),(1)求证:是等差数列;(2)求a n;(3)若b n=2(1-n)a n(n≥2),求证:7.已知数列{a n}的首项a1=5,前n项和为S n,且S n+1=2S n+n+5(n∈N*)(1)证明数列{a n+1}是等比数列;(2)令f(x)=a1x+a2x2++a n x n,求函数f(x)在点x=1处的导数f′(1)[参考谜底]1.选 A∵a n+1-a n=(n+1)2-k(n+1)-(n2-kn)=2n+1-k>0(n∈N*)∴k<2n+1对任意n∈N*成立而2n+1最小值为3,∴k<32.选 A∴a n图象可看作是函数个单元,再上移个单元而获得(a n图象是一些孤立点)画草图可知,a4最年夜3.选 B∴可知{a n}的各项数值以3为周期重复呈现4.5.又a5,a7,a9符号相同,∴a7=16.(1)由a n+2S n S n-1=0 (n≥2)∴S n-S n-1+2S n S n-1=0 (n≥2)为首项,公差为2的等差数列.(2)(3)7.(1)∵S n+1=2S n+n+5∴S n=2S n-1+(n-1)+5(n≥2)∴S n+1-S n=2(S n-S n-1)+1(n≥2)即a n+1=2a n+1(n≥2)∴a n+1+1=2(a n+1)(n≥2)∴{a n+1}从第2项起,是公比为2的等比数列又a1=5,由S n+1=2S n+n+5令n=1有S2=2S1+6∴a1+a2=2a1+6∴a2=11∴{a n+1}是以a1+1=6为首项,公比为2的等比数列(2)∵f′(x)=a1+2a2x+3a3x2+…+na n x n-1∴f′(1)=a1+2a2+3a3+…+na n 由(1)知a n+1=6×2n-1∴a n=6×2n-1-1令T n=6×20+2×6×21+3×6×22+…+n×6×2n-1∴2T n=6×21+2×6×22+3×6×23+…+n×6×2n∴-T n=6×20+6×21+6×22+…+6×2n-1-n×6×2n∴T n=(n-1)×6×2n+6时间:二O二一年七月二十九日。
高中常见数列的公式及经典例题
数列 知识点及解题技巧1.等差数列:一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,即n a -1-n a =d ,(n ≥2,n ∈N +),这个数列就叫做等差数列,这个常数就叫做等差数列的公差(常用字母“d ”表示)2.等差数列的通项公式:d n a a n )1(1-+= =n a d m n a m )(-+或 n a =pn+q (p 、q 是常数))3.有几种方法可以计算公差d ① d=n a -1-n a ② d =11--n a a n ③ d =mn a a mn -- 4.等差中项:,,2b a ba A ⇔+=成等差数列 5.等差数列的性质: m+n=p+q ⇒q p n m a a a a +=+ (m, n, p, q ∈N ) 等差数列前n 项和公式6.等差数列的前n 项和公式 (1)2)(1n n a a n S +=(2)2)1(1d n n na S n -+= (3)n )2da (n 2d S 12n -+=,当d ≠0,是一个常数项为零的二次式8.对等差数列前项和的最值问题有两种方法:(1) 利用n a :当n a >0,d<0,前n 项和有最大值可由n a ≥0,且1+n a ≤0,求得n 的值当n a <0,d>0,前n 项和有最小值n a ≤0,且1+n a ≥0,求得n 的值(2) 利用n S :由n )2da (n 2d S 12n -+=二次函数配方法求得最值时n 的值 等比数列1.等比数列:如果一个数列从第二项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列.这个常数叫做等比数列的公比;公比通常用字母q 表示(q ≠0),即:1-n na a =q (q ≠0) 2.等比数列的通项公式: )0(111≠⋅⋅=-q a q a a n n , )0(1≠⋅⋅=-q a qa a mn m n 3.{n a }成等比数列⇔nn a a 1+=q (+∈N n ,q ≠0) “n a ≠0”是数列{n a }成等比数列的必要非充分条件 4.既是等差又是等比数列的数列:非零常数列.5.等比中项:G 为a 与b 的等比中项. 即G =±ab (a ,b 同号). 6.性质:若m+n=p+q ,q p n m a a a a ⋅=⋅7.判断等比数列的方法:定义法,中项法,通项公式法8.等比数列的增减性:当q>1, 1a >0或0<q<1, 1a <0时, {n a }是递增数列; 当q>1, 1a <0,或0<q<1, 1a >0时, {n a }是递减数列; 当q=1时, {n a }是常数列; 当q<0时, {n a }是摆动数列; 等比数列前n 项和等比数列的前n 项和公式:∴当1≠q 时,qq a S n n --=1)1(1 ① 或q q a a S n n --=11 ②当q=1时,1na S n =当已知1a , q, n 时用公式①;当已知1a , q, n a 时,用公式②.数列通项公式的求法一、定义法直接利用等差数列或等比数列的定义求通项的方法叫定义法,这种方法适应于已知数列类型的题目.例1.等差数列{}n a 是递增数列,前n 项和为n S ,且931,,a a a 成等比数列,255a S =.求数列{}n a 的通项公式. 解:设数列{}n a 公差为)0(>d d∵931,,a a a 成等比数列,∴9123a a a =,即)8()2(1121d a a d a +=+d a d 12=⇒∵0≠d , ∴d a =1………………………………①∵255a S = ∴211)4(2455d a d a +=⋅⨯+…………② 由①②得:531=a ,53=d∴n n a n 5353)1(53=⨯-+=点评:利用定义法求数列通项时要注意不用错定义,设法求出首项与公差(公比)后再写出通项。
高中数列知识点总结(附例题)
高中数列知识点总结(附例题)知识点1:等差数列及其前n 项 1.等差数列的定义 2.等差数列的通项公式如果等差数列{a n }的首项为a 1,公差为d ,那么它的通项公式a n =a 1+(n -1)d .3.等差中项如果 A =a +b2 ,那么A 叫做a 与b 的等差中项. 4.等差数列的常用性质(1)通项公式的推广:a n =a m +(n-m )d ,(n ,m ∈N *).(2)若{a n }为等差数列,且k +l =m +n ,(k ,l ,m ,n ∈N *),则a k +a l =a m +a n . (3)若{a n }是等差数列,公差为d ,则{a 2n }也是等差数列,公差为2d .(4)若{a n },{b n }是等差数列,则{pa n +qb n }也是等差数列.(5)若{a n }是等差数列,公差为d ,则a k ,a k +m ,a k +2m ,…(k ,m ∈N *)是公差为md 的等差数列.5.等差数列的前n 项和公式设等差数列{a n }的公差d ,其前n 项和S n =n (a 1+a n )2或S n =na 1+n (n -1)2d .6.等差数列的前n 项和公式与函数的关系S n =d 2n 2+⎝ ⎛⎭⎪⎫a 1-d 2n .数列{a n }是等差数列⇔S n =An 2+Bn ,(A 、B 为常数).7.等差数列的最值在等差数列{a n }中,a 1>0,d <0,则S n 存在最 大 值;若a 1<0,d >0,则S n 存在最 小 值.[难点正本 疑点清源] 1.等差数列的判定(1)定义法:a n -a n -1=d (n ≥2); (2)等差中项法:2a n +1=a n +a n +2.2.等差数列与等差数列各项和的有关性质(1)a m ,a m +k ,a m +2k ,a m +3k ,…仍是等差数列,公差为kd . (2)数列S m ,S 2m -S m ,S 3m -S 2m ,…也是等差数列. (3)S 2n -1=(2n -1)a n .(4)若n 为偶数,则S 偶-S 奇=n2d . 若n 为奇数,则S 奇-S 偶=a 中(中间项).例1(等差数列的判定或证明):已知数列{a n }中,a 1=35,a n =2-1a n -1(n ≥2,n ∈N *),数列{b n }满足b n =1a n -1(n ∈N *).(1)求证:数列{b n }是等差数列;(2)求数列{a n }中的最大项和最小项,并说明理由.(1)证明 ∵a n =2-1a n -1 (n ≥2,n ∈N *),b n =1a n -1.∴n ≥2时,b n -b n -1=1a n -1-1a n -1-1=1⎝⎛⎭⎪⎫2-1a n -1-1-1a n -1-1=a n -1a n -1-1-1a n -1-1=1.∴数列{b n }是以-52为首项,1为公差的等差数列.(2)解 由(1)知,b n =n -72,则a n =1+1b n=1+22n -7,设函数f (x )=1+22x -7,易知f (x )在区间⎝ ⎛⎭⎪⎫-∞,72和⎝ ⎛⎭⎪⎫72,+∞内为减函数. ∴当n =3时,a n 取得最小值-1;当n =4时,a n 取得最大值3.例2(等差数列的基本量的计算)设a 1,d 为实数,首项为a 1,公差为d 的等差数列{a n }的前n 项和为S n ,满足S 5S 6+15=0.(1)若S 5=5,求S 6及a 1 (2)求d 的取值范围.解 (1)由题意知S 6=-15S 5=-3,a 6=S 6-S 5=-8.所以⎩⎨⎧5a 1+10d =5,a 1+5d =-8.解得a 1=7,所以S 6=-3,a 1=7. (2)方法一 ∵S 5S 6+15=0,∴(5a 1+10d )(6a 1+15d )+15=0,即2a 21+9da 1+10d 2+1=0.因为关于a 1的一元二次方程有解,所以 Δ=81d 2-8(10d 2+1)=d 2-8≥0,解得d ≤-22或d ≥2 2. 方法二 ∵S 5S 6+15=0,∴(5a 1+10d )(6a 1+15d )+15=0, 9da 1+10d 2+1=0.故(4a 1+9d )2=d 2-8.所以d 2≥8.故d 的取值范围为d ≤-22或d ≥2 2.例3(前n 项和及综合应用)(1)在等差数列{a n }中,已知a 1=20,前n 项和为S n ,且S 10=S 15,求当n 取何值时,S n 取得最大值,并求出它的最大值; (2)已知数列{a n }的通项公式是a n =4n -25,求数列{|a n |}的前n 项和.解 方法一 ∵a 1=20,S 10=S 15,∴10×20+10×92d =15×20+15×142d ,∴d =-53.∴a n =20+(n -1)×⎝ ⎛⎭⎪⎫-53=-53n +653.∴a 13=0,即当n ≤12时,a n >0,n ≥14时,a n <0,∴当n =12或13时,S n 取得最大值,且最大值为S 13=S 12=12×20+12×112×⎝ ⎛⎭⎪⎫-53=130.方法二 同方法一求得d =-53.∴S n =20n +n (n -1)2·⎝ ⎛⎭⎪⎫-53=-56n 2+1256n =-56⎝ ⎛⎭⎪⎫n -2522+3 12524. ∵n ∈N *,∴当n =12或13时,S n 有最大值,且最大值为S 12=S 13=130. (2)∵a n =4n -25,a n +1=4(n +1)-25, ∴a n +1-a n =4=d ,又a 1=4×1-25=-21.所以数列{a n }是以-21为首项,以4为公差的递增的等差数列. 令⎩⎨⎧a n =4n -25<0, ①a n +1=4(n +1)-25≥0, ②由①得n <614;由②得n ≥514,所以n =6. 即数列{|a n |}的前6项是以21为首项,公差为-4的等差数列,从第7项起以后各项构成公差为4的等差数列, 而|a 7|=a 7=4×7-24=3. 设{|a n |}的前n 项和为T n ,则T n =⎩⎪⎨⎪⎧21n +n (n -1)2×(-4) (n ≤6)66+3(n -6)+(n -6)(n -7)2×4 (n ≥7)=⎩⎨⎧-2n 2+23n (n ≤6),2n 2-23n +132 (n ≥7).例4,已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则其公差为 3例5等差数列{},{}n n a b 的前n 项和分别为{},{}n n S T ,且7453n nS n T n,则使得n na b 为正整数的正整数n 的个数是 3 . (先求an/bn n=5,13,35)已知递推关系求通项:这类问题的要求不高,但试题难度较难把握.一般有三常见思路:(1)算出前几项,再归纳、猜想;(2)“a n+1=pa n+q ”这种形式通常转化为an +1+λ=p (an +λ),由待定系数法求出,再化为等比数列; (3)逐差累加或累乘法.例6 已知数列{}n a 中,113a =,当2≥n 时,其前n 项和n S 满足2221nn n S a S =-,则数列{}n a 的通项公式为例7在数列{}n a 中,12a =,11ln(1)n n a a n+=++,则n a = .知识点2:等比数列及其n 项和 1.等比数列的定义 2.等比数列的通项公式 3.等比中项若G 2=a ·b (ab ≠0),那么G 叫做a 与b 的等比中项.4.等比数列的常用性质(1)通项公式的推广:a n =a n q n-m,(n ,m ∈N *).(2)若{a n }为等比数列,且k +l =m +n ,(k ,l ,m ,n ∈N *),则a k ·a l =a m ·a n . (3)若{a n },{b n }(项数相同)是等比数列,则{λa n }(λ≠0),21221nn n n S S S S --=-1.21n S n ⇒=+1111122(2)n n n n n n S S S S n S S ---⇒-=⇒-=≥()()21132214n n a n n ⎧=⎪=⎨⎪-⎩≥13211221, 2.≥n n n n n a a a a a a n a a a a ---=⋅⋅⋅⋅⋅2ln n+⎩⎨⎧⎭⎬⎫1a n ,{a 2n },{a n ·b n },⎩⎨⎧⎭⎬⎫a nb n 仍是等比数列.5.等比数列的前n 项和公式等比数列{a n }的公比为q(q ≠0),其前n 项和为S n , 当q =1时,S n =na 1;当q ≠1时,S n =a 1(1-q n )1-q =a 1-a n q1-q.6.等比数列前n 项和的性质公比不为-1的等比数列{a n }的前n 项和为S n ,则S n ,S 2n -S n ,S 3n -S 2n 仍成等比数列,其公比为q n .7. 等比数列的单调性【难点】1.等比数列的特征从等比数列的定义看,等比数列的任意项都是非零的,公比q 也是非常数. 2.等比数列中的函数观点利用函数、方程的观点和方法,揭示等比数列的特征及基本量之间的关系.在借用指数函数讨论单调性时,要特别注意首项和公比的大小. 3.等比数列的前n 项和S n(1)等比数列的前n 项和S n 是用错位相减法求得的,注意这种思想方法在数列求和中的运用.(2)等比数列的通项公式a n =a 1q n -1及前n 项和公式S n =a 1(1-q n )1-q =a 1-a n q 1-q(q ≠1)共涉及五个量a 1,a n ,q ,n ,S n ,知三求二,体现了方程的思想的应用.(3)在使用等比数列的前n 项和公式时,如果不确定q 与1的关系,一般要用分类讨论的思想,分公比q =1和q ≠1两种情况.例1:(1)在等比数列{a n }中,已知a 6-a 4=24,a 3a 5=64,求{a n }的前8项和S 8; (2)设等比数列{a n }的公比为q (q >0),它的前n 项和为40,前2n 项和为3 280,且前n 项中数值最大的项为27,求数列的第2n 项. (1)设数列{a n }的公比为q ,由通项公式a n =a 1q n -1及已知条件得: ⎩⎨⎧a 6-a 4=a 1q 3(q 2-1)=24, ①a 3·a 5=(a 1q 3)2=64. ②由②得a 1q 3=±8.将a 1q 3=-8代入①式,得q 2=-2,无解将a 1q 3=8代入①式,得q 2=4,∴q =±2.,故舍去.当q =2时,a 1=1,∴S 8=a 1(1-q 8)1-q =255;当q =-2时,a 1=-1,∴S 8=a 1(1-q 8)1-q =85.(2)若q =1,则na 1=40,2na 1=3 280,矛盾.∴q ≠1,∴⎩⎪⎨⎪⎧a 1(1-q n )1-q =40, ①a 1(1-q 2n )1-q =3 280, ②②①得:1+q n =82,∴q n=81, ③ 将③代入①得q =1+2a 1. ④又∵q >0,∴q >1,∴a 1>0,{a n }为递增数列. ∴a n =a 1q n -1=27, ⑤ 由③、④、⑤得q =3,a 1=1,n =4. ∴a 2n =a 8=1×37=2 187.例2 已知数列{a n }的前n 项和为S n ,数列{b n }中,b 1=a 1,b n =a n -a n -1 (n ≥2),且a n +S n =n.(1)设c n =a n -1,求证:{c n }是等比数列; (2)求数列{b n }的通项公式. 1)证明 ∵a n +S n =n , ① ∴a n +1+S n +1=n +1. ②②-①得a n +1-a n +a n +1=1,∴2a n +1=a n +1,∴2(a n +1-1)=a n -1, ∴a n +1-1a n -1=12,∴{a n -1}是等比数列. ∵首项c 1=a 1-1,又a 1+a 1=1,∴a 1=12,∴c 1=-12,公比q =12. 又c n =a n -1,∴{c n }是以-12为首项,12为公比的等比数列.(2)解 由(1)可知c n =⎝ ⎛⎭⎪⎫-12·⎝ ⎛⎭⎪⎫12n -1=-⎝ ⎛⎭⎪⎫12n , ∴a n =c n +1=1-⎝ ⎛⎭⎪⎫12n . ∴当n ≥2时,b n =a n -a n -1=1-⎝ ⎛⎭⎪⎫12n -⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫12n -1=⎝ ⎛⎭⎪⎫12n -1-⎝ ⎛⎭⎪⎫12n =⎝ ⎛⎭⎪⎫12n.又b 1=a 1=12代入上式也符合,∴b n =⎝ ⎛⎭⎪⎫12n .例3 在等比数列{a n }中,(1)若已知a 2=4,a 5=-12,求a n ;(2)若已知a 3a 4a 5=8,求a 2a 3a 4a 5a 6的值.解 (1)设公比为q ,则a 5a 2=q 3,即q 3=-18,∴q =-12,∴a n =a 5·q n -5=⎝ ⎛⎭⎪⎫-12n -4.(2)∵a 3a 4a 5=8,又a 3a 5=a 24,∴a 34=8,a 4=2.∴a 2a 3a 4a 5a 6=a 54=25=32.例4已知数列{a n }满足a 1=1,a 2=2,a n +2=a n +a n +12,n ∈N *. (1)令b n =a n +1-a n ,证明:{b n }是等比数列; (2)求{a n }的通项公式. 规范解答(1)证明 b 1=a 2-a 1=1, [1分]当n ≥2时,b n =a n +1-a n =a n -1+a n2-a n=-12(a n -a n -1)=-12b n -1, [5分]∴{b n }是首项为1,公比为-12的等比数列. [6分](2)解 由(1)知b n =a n +1-a n =⎝ ⎛⎭⎪⎫-12n -1, [8分]当n ≥2时,a n =a 1+(a 2-a 1)+(a 3-a 2)+…+(a n -a n -1) [10分]=1+1+⎝ ⎛⎭⎪⎫-12+…+⎝ ⎛⎭⎪⎫-12n -2=1+1-⎝ ⎛⎭⎪⎫-12n -11-⎝ ⎛⎭⎪⎫-12=1+23⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫-12n -1=53-23⎝ ⎛⎭⎪⎫-12n -1当n =1时,53-23⎝ ⎛⎭⎪⎫-121-1=1=a 1, ∴a n =53-23⎝ ⎛⎭⎪⎫-12n -1 (n ∈N *). [14分]例4 (07 重庆11)设11a a -+是和的等比中项,则a +3b 的最大值为 2 .(三角函数)例5 若数列1, 2cos θ, 22cos 2θ,23cos 3θ, … ,前100项之和为0, 则θ的值为( )例 6 △ABC 的三内角成等差数列, 三边成等比数列,则三角形的形状为__等边三角形__________.【综合应用】例7.已知等差数列{a n }的首项a 1=1,公差d >0,且第2项、第5项、第14项分别是等比数列{b n }的第2项、第3项、第4项. (1)求数列{a n }与{b n }的通项公式;22,Z 3k k ππ±∈(2)设数列{c n }对n ∈N *均有c 1b 1+c 2b 2+…+c nb n=a n +1成立,求c 1+c 2+c 3+…+c 2 013.解 (1)由已知有a 2=1+d ,a 5=1+4d ,a 14=1+13d , ∴(1+4d )2=(1+d )(1+13d ).解得d =2 (∵d >0). ∴a n =1+(n -1)·2=2n -1.又b 2=a 2=3,b 3=a 5=9,∴数列{b n }的公比为3, ∴b n =3·3n -2=3n -1.2)由c 1b 1+c 2b 2+…+c nb n=a n +1得当n ≥2时,c 1b 1+c 2b 2+…+c n -1b n -1=a n .两式相减得:n ≥2时,c nb n=a n +1-a n =2.∴c n =2b n =2·3n -1 (n ≥2).又当n =1时,c 1b 1=a 2,∴c 1=3.∴c n =⎩⎨⎧3 (n =1)2·3n -1 (n ≥2).∴c 1+c 2+c 3+…+c 2 013=3+6-2×32 0131-3=3+(-3+32 013)=32 013.知识点3:数列的基本知识1,1-1)1(n n n n n S S n S a S a -==或的关系:与例1:设{}n a 数列的前n 项和2n S n =,则8a 的值为 15 .2,数列的递推公式及应用:利用数列的递推公式求数列的通项公式,一般有三种方法:累加法,累积法,构造法①对形如q pa a a a n n +==+11;的递推公式()1.≠p q p 为常数且,可令()λλ+=++n n a p a 1,整理得()λλλ+=+=+n n a p a p q1,1-,所以是{}λ+n a 等比数列②对形如q pa a a n n n +=+1的递推公式,两边取倒数后换元转化为nn a qp a +=+11,再求出⎭⎬⎫⎩⎨⎧n a 1即可例2:已知数列{}n a 满足n a a a n n 2-,3311==+,则na n的最小值为 10.5。
高中数学数列经典九例
数学数列经典例题1. 已知等比数列432,,,}{a a a a n 中分别是某等差数列的第5项、第3项、第2项,且1,641≠=q a 公比 (Ⅰ)求n a ;(Ⅱ)设n n a b 2log =,求数列.|}{|n n T n b 项和的前2.已知数列}{n a 满足递推式)2(121≥+=-n a a n n ,其中.154=a (Ⅰ)求321,,a a a ; (Ⅱ)求数列}{n a 的通项公式; (Ⅲ)求数列}{n a 的前n 项和n S3.已知数列{}n a 的前n 项和为n S ,且有12a =,11353n n n n S a a S --=-+(2)n ≥(1)求数列n a 的通项公式;(2)若(21)n n b n a =-,求数列n a 的前n 项的和n T 。
4.已知数列{n a }满足11=a ,且),2(22*1N n n a a nn n ∈≥+=-且.(Ⅰ)求2a ,3a ;(Ⅱ)证明数列{n na 2}是等差数列;(Ⅲ)求数列{n a }的前n 项之和n S5.数列{}n a 的前n 项和为n S ,11a =,*12()n n a S n +=∈N(Ⅰ)求数列{}n a 的通项n a ;(Ⅱ)求数列{}n na 的前n 项和n T6.22,,4,21121+=-===++n n n n n b b a a b a a . 求证:⑴数列{b n +2}是公比为2的等比数列; ⑵n a n n 221-=+;⑶4)1(2221-+-=++++n n a a a n n .7.已知各项都不相等的等差数列}{n a 的前六项和为60,且2116a a a 和为 的等比中项.(1)求数列}{n a 的通项公式n n S n a 项和及前;(2)若数列}1{,3),(}{11nn n n n b b N n a b b b 求数列且满足=∈=-*+的前n 项和T n .8.已知n S 是数列{}n a 的前n 项和,123,22a a ==,且113210n n n S S S +--++=,其中*2,n n N ≥∈. ①求证数列{}1n a -是等比数列;②求数列{}n a 的前n 项和n S .9.已知n S 是数列{n a }的前n 项和,并且1a =1,对任意正整数n ,241+=+n n a S ;设,3,2,1(21=-=+n a a b n n n ).(I )证明数列}{n b 是等比数列,并求}{n b 的通项公式;(II )设}log log 1{,32212++⋅=n n n n n C C T b C 为数列的前n 项和,求n T .高考数列解答题参考答案1.解析:(1)设该等差数列为{}n c ,则25a c =,33a c =,42a c=533222()c c d c c -==- ∴2334()2()a a a a -=-即:223111122a q a q a q a q -=-∴12(1)q q q -=-,1q ≠, ∴121,2q q ==,∴1164()2n a -= (2)121log [64()]6(1)72n n b n n -==--=-,{}n b 的前n 项和(13)2n n n S -=∴当17n ≤≤时,0n b ≥,∴(13)2n n n n T S -==(8分) 当8n ≥时,0n b <,12789n n T b b b b b b =+++----789777()()2n n n S b b b S S S S S =-+++=--=-(13)422n n -=-∴(13)(17,)2(13)42(8,)2n n n n n T n n n n -⎧≤≤∈⎪⎪=⎨-⎪-≥∈⎪⎩**N N 2.解:(1)由151241=+=-a a a n n 及知,1234+=a a解得:,73=a 同理得.1,312==a a(2)由121+=-n n a a 知2211+=+-n n a a)1(211+=+-n n a a {}1+∴n a 构成以211=+a 为首项以2为公比的等比数列; 112)1(1-⋅++∴n n a a ;,21n n a =+∴.12-=∴n n a 为所求通项公式(3)12-=nn a 123......n n S a a a a ∴=++++123(21)(21)(21)......(21)n =-+-+-++-123(222......2)nn =++++-n n ---=21)21(2.221n n --=+3.解:由11335(2)n n n n S S a a n ---=-≥,12n n a a -∴=,又12a =,112n n a a -=, {}n a ∴是以2为首项,12为公比的等比数列,122112()()222n n n n a ---∴=⨯== 2(21)2n n b n -=-,1012123252(21)2n n T n --∴=⨯+⨯+⨯++-⋅ (1) 012111232(23)2(21)22n n n T n n ---=⨯+⨯++-⋅+-⋅ (2) (1)—(2)得0121122(222)(21)22n n n T n ---=++++--⋅ 即:1111112[1(2)]2(21)26(23)2212n n n n T n n ------=+--⋅=-+⋅- ,212(23)2n n T n -∴=-+⋅ 4.解:(Ⅰ)622212=+=a a ,2022323=+=a a .(Ⅱ)),2(22*1N n n a a n n n ∈≥+=-且 , ∴),2(122*11N n n a a n n n n ∈≥+=--且, 即),2(122*11N n n a a n n n n ∈≥=---且. ∴数列}2{n n a 是首项为21211=a ,公差为1=d 的等差数列. (Ⅲ)由(Ⅱ)得,211)1(21)1(212-=⋅-+=-+=n n d n a n n ∴n n n a 2)21(⋅-=. )2(2)21(2)211(2252232212)1(2)21(2252232211432321+⋅-+⋅--++⋅+⋅+⋅=⋅-++⋅+⋅+⋅=n n n n n n n S n S 1322)21(2221)2()1(+⋅--++++=--n n n n S 得 12)21(2222132-⋅--++++=+n n n12)21(21)21(21-⋅----=+n n n 32)23(-⋅-=n n . ∴32)32(+⋅-=n n n S . 5.解:(Ⅰ)12n n a S +=,12n n n S S S +∴-=,13n n S S +∴= 又111S a ==,∴数列{}n S 是首项为1,公比为3的等比数列,1*3()n n S n -=∈N 当2n ≥时,21223(2)n n n a S n --==≥,21132n n n a n -=⎧∴=⎨2⎩, ,,≥.(Ⅱ)12323n n T a a a na =++++, 当1n =时,11T =;当2n ≥时,0121436323n n T n -=++++,…………①12133436323n n T n -=++++,………………………②-①②得:12212242(333)23n n n T n ---=-+++++-213(13)222313n n n ---=+-- 11(12)3n n -=-+-1113(2)22n n T n n -⎛⎫∴=+- ⎪⎝⎭≥ 又111T a ==也满足上式, 1113(2)22n n T n n -⎛⎫∴=+- ⎪⎝⎭≥ 6.解: ⑴ )2(221+=++n n b b 2221=++∴+n n b b 2121=-=a a b 62222=+=b b 数列{b n +2}是首项为4公比为2的等比数列;⑵由⑴知 112242+-=⨯=+n n n b221-=∴+n n b 2211-=-++n n n a a22212-=-∴a a22323-=-a a……221-=--n n n a a上列(n-1)式子累加:n a n n 2)222(232-+++=-n a n n 221-=∴+⑶2)1(2)222(13221+-+++=++++n n a a a n n . 4)1(2221-+-=+++∴+n n a a a n n7.解:(1)设等差数列}{n a 的公差为d ,则⎩⎨⎧+=+=+21111)5()20(,60156d a d a a d a 解得⎩⎨⎧==.5,21a d32+=∴n a n . )4(2)325(+=++=n n n n S n (2)由).,2(,111*--+∈≥=-∴=-N n n a b b a b b n n n n n n112211121112,()()()(1)(14)3(2).3,n n n n n n n n b b b b b b b b a a a b n n n n b -----≥=-+-++-+=++++=--++=+=当时对也适合 ))(2(*∈+=∴N n n n b n ).211(21)2(11+-=+=∴n n n n b n )211123(21)2114121311(21+-+-=+-++-+-=n n n n T n )2)(1(4532+++=n n n n8.解:①113210n n n S S S +--++=⇒112()1n n n n S S S S +--=--⇒121(2)n n a a n +=-≥ 又123,22a a ==也满足上式,∴*121()n n a a n N +=-∈⇒112(1)n n a a +-=-(*n N ∈) ∴数列{}1n a -是公比为2,首项为1112a -=的等比数列 (2)由①,1211222n n n a ---=⨯=221n n a -⇒=+ 于是12...n n S a a a =+++()()()()1012212121...21n --=++++++++ ()1012222...2n n --=++++212n n -=+9.解析:(I )),2(24,2411≥+=∴+=-+n a S a S n n n n两式相减:),2(4411≥-=-+n a a a n n n *),(2)2(2,2)(42,2),2)((41111121111N n b a a b a a a a a b a a b n a a a n n n n n n n n n n n n n n n n ∈=-=--=-=∴-=∴≥-=∴++++++++-+ ,21=∴+nn b b }{n b ∴是以2为公比的等比数列, ,325,523,24,2112121121=-==+=∴+=+-=b a a a a a a a b 而 *)(231N n b n n ∈⋅=∴-(II ),231-==n n n b C ,)1(12log 2log 1log log 11222212+=⋅=⋅∴+++n n C C n n n n 而,111)1(1+-=+n n n n .111)111()4131()3121()211(+-=+-++-+-+-=∴n n n T n。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、 经典例题剖析
考点一:等差、等比数列的概念与性质
例题1.(1)数列{a n }和{b n }满足)(121n n b b b n
a +++= (n=1,2,3…), (1)求证{
b n }为等差数列的充要条件是{a n }为等差数列。
(2)数列{a n }和{c n }满足*)(21N n a a c n n n ∈+=+,探究}{n a 为等差数列的充分必要条例题2.已知数列{}n a 的首项
121a a =+(a 是常数,且1a ≠-),24221+-+=-n n a a n n (2n ≥),数列{}n b 的首项1b a =,2n a b n n +=(2n ≥)。
(1)证明:{}n b 从第2项起是以2为公比的等比数列;
(2)设n S 为数列{}n b 的前n 项和,且{}n S 是等比数列,求实数a 的值;
(3)当a>0时,求数列{}n a 的最小项。
例题4. 已知数列{}n a 满足411=a ,()),2(2
111N n n a a a n n n n ∈≥--=--. (Ⅰ)求数列{}n a 的通项公式n a ; (Ⅱ)设21
n n a b =,求数列{}n b 的前n 项和n S ; (Ⅲ)设2
)12(sin
π-=n a c n n ,数列{}n c 的前n 项和为n T .求证:对任意的*∈N n ,74<n T . 考点三:数列与不等式的联系
例题5.已知α为锐角,且12tan -=α,函数)4
2sin(2tan )(2παα+⋅+=x x x f ,数列{a n }的首项)(,2
111n n a f a a ==+. ⑴ 求函数)(x f 的表达式;
⑵ 求证:n n a a >+1;
⑶ 求证:),2(21111111*21N n n a a a n
∈≥<++++++< 例题6已知数列{}n a 满足()111,21n n a a a n N
*+==+∈
(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)若数列{}n b 满足n n b n
b b b b a )1(44441111321+=---- ,证明:{}n a 是等差数列; (Ⅲ)证明:()23111123n n N a a a *++++<∈。
