第4讲_2-3几何组成分析_习题课
2.6 几何组成分析及示例
一个形状复杂的刚片如果仅有两个单铰（可为虚铰例18）与
其它部分连接也可简化为一直线链杆
B
DB
B
A
AC
A
聊城大学建筑工程学院
d. 连接两刚片的两根链杆(并联)等效于它们交点处的虚铰。
a
O 即：可将二个链杆看作一个
铰（虚铰）
b
e. 用等效的多个单约束代替一个复约束。
AB
B
C
A
C
BD
B
D
A
C
A
C
注意：右图中A、B、C三铰是不共线的（因复链杆本身几何不
注：运用三刚片原则时，尽量“拉开距离”选择刚片。
聊城大学建筑工程学院
【例2-9】试对图示体系进行几何组成分析。
J
I B
F
K
D
C
III
B
D
C
G
E
A
H
I
II
A
解：首先，进行简化，将“不变部分，并为一杆（刚
片）”，其中刚片I、III分别按三刚片规则和二元体规则 组成；
其次，对刚片I、II、III进行几何组成分析，该三刚片用 三铰（铰A、B、C）两两相连，组成几何不变体系，但 有一个多余约束（杆AD）。
G
A
B
E
III(地基)
G
解：首先找出第一个构造单元，它是由刚片I、II、III（地基）
用三铰A、B、C两两相连所组成的几何不变的新的大刚片
ABC；
其次，该大刚片与刚片IV用一铰D一链杆（E处链杆）相连， 组成更大刚片ABCDE；
第三，该更大刚片与刚片V用两个铰（铰F、G）相连，组成 几何不变，但有一个多余约束的体系。
聊城大学建筑工程学院
第四讲 几何综合(二)
A a c b B H E G F D
C
可知：S正方形 ABCD =4S△ABE +S正方形 EFGH =4×
2 1 ab+（a − b） 2
=a2 + b2 =c 2
2013 年春季六年级（第 12 级上）A++教材
课后作业
1、如图所示，由边长为 2，3，5，7 的四个三角形拼成一个大三角形，具体面 积见三角形内部数字，那么三角形 BEF 的面积是 ．
C
E
84
O A
40 30
D
35
F
B
【随堂练】 如图， 在三角形 ABC 中， BD=2DC， AE=2ED， FC=7． 那么， AF=
．
A
E B
F
D
C
2013 年春季六年级（第 12 级上）A++教材
【拓展】难度★★★★ 如图，△ABC 中,
DC EA FB 1 ,求△GHI 和△ABC 的面积比的比值． DB EC FA 2
B C P 9 5
A R F
D
Q E
2013 年春季六年级（第 12 级上）A++教材
课堂小结
1、燕尾定理：如图，在三角形中，AD，BE，CF 相交于同一点 O，那么 （1）S△AOB : S△AOC = （2）S△BOA : S△BOC = （3）S△COA : S△COB = : : : = = = : : : ； ； ．
2013 年春季六年级（第 12 级上）A++教材
【例 8】难度★★★★ 如图，∠A=∠B=60°，且 AB=24，BD=16，AC=8，而且三角形 CDE 的面积 等于四边形 ABEC 的面积．请问：DE 的长度是多少？
研究生入学考试辅导丛书----结构力学第三版习题
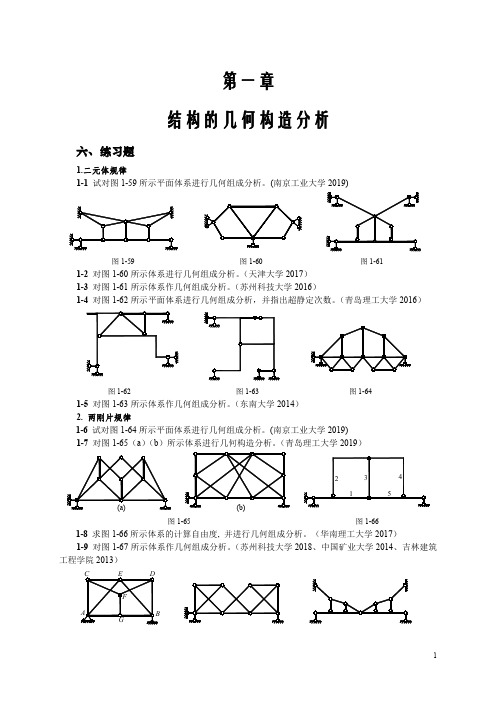
第一章结构的几何构造分析六、练习题1.二元体规律1-1试对图1-59所示平面体系进行几何组成分析。
(南京工业大学2019)(b)a)(c)图1-59图1-60图1-611-2对图1-60所示体系进行几何组成分析。
（天津大学2017）1-3对图1-61所示体系作几何组成分析。
（苏州科技大学2016）1-4对图1-62所示平面体系进行几何组成分析，并指出超静定次数。
（青岛理工大学2016）图1-62图1-63图1-641-5对图1-63所示体系作几何组成分析。
（东南大学2014）2.两刚片规律1-6试对图1-64所示平面体系进行几何组成分析。
(南京工业大学2019)1-7对图1-65（a ）（b ）所示体系进行几何构造分析。
（青岛理工大学2019）图1-65图1-661-8求图1-66所示体系的计算自由度,并进行几何组成分析。
（华南理工大学2017）1-9对图1-67所示体系作几何组成分析。
（苏州科技大学2018、中国矿业大学2014、吉林建筑工程学院2013）图1-67图1-68图1-69 1-10图1-68所示体系的机动分析结论是。
（重庆交通大学2015）3.三刚片规律3.1三个铰都对应于有限点1-11对图1-69所示平面体系进行几何组成分析。
(南京工业大学2019)1-12对图1-70所示体系进行几何组成分析(各点均为铰结点)。
(长沙理工大学2017)图1-70图1-71 1-13图1-71所示体系的计算自由度W=，有个多余约束，为体系。
（哈尔滨工业大学2017）1-14试对图1-72所示平面体系进行几何组成分析。
（哈尔滨工业大学2015）图1-72图1-73图1-74 1-15计算图1-73所示杆件体系的计算自由度，并判断体系符合哪种几何组成规律？（北京工业大学2014）3.2一个无穷远瞬铰1-16对图1-74所示体系进行几何构成分析。
（西安交通大学2015）1-17图1-75所示为（）。
（山东科技大学2018）A.无多余约束的几何不变体系；B.有多余约束的几何不变体系；C.瞬变体系；D.常变体系。
(0729)《结构力学》题目及答案
分。
图1 图2 图3解：对图1所示体系进行几何组成分析时，可把地基作为一个刚片，当中的T 字形部分BCE 作为一个刚片。
左边的AB 部分虽为折线，但本身是一个刚片而且只用两个铰与其他部分相联，因此它实际上与A 、B 两铰连线上的一根链杆（如图中虚线所示）的作用相同。
同理，右边的CD 部分也相当于一根链杆。
这样，此体系便是两个刚片用AB 、CD 和EF 三根链杆相联而组成，三杆不全平行也不同交于一点，故为几何不变体系，而且没有多余约束。
对图2所示体系有：去二元体DEBF ；去二元体FBC ；去二元体CB ；AB 杆件与地基刚接构成刚片；整个体系为无多余约束的几何不变体系。
AB 为基本部分，其它为附属部分。
对图3所示体系有：DE 杆件与地基构成几何不变体系；CB 刚片与地基之间用AB 链杆和C 处两个平行链杆相连接，三个链杆不平行也不交与一点满足二刚片规则，故CB 与地基构成几何不变体系；BD 链杆为多余联系；故整个体系为有一个多余约束的几何不变体系。
2、结构位移求解：本题共2题，任选1题作答，计20分。
（1）试求如图4所示外伸梁C 点的竖向位移Cy ∆。
梁的EI 为常数。
（2）已知图5所示结构，422.110 kN m ,10 kN/m EI q =⨯⋅=求B 点的水平位移。
图4 图51、解作P M 和M 图，分别如图(b)、(c)。
BC 段P M 图是标准二次抛物线图形；AB 段P M 图不是标准二次抛物线图形，现将其分解为一个三角形和一个标准二次抛物线图形。
由图乘法可得2224113213828384283()128Cyql l l ql l ql l l l EI ql EI⎡⎤⎛⎫⎛⎫⎛⎫∆=⨯-⨯⨯+⨯⨯⎢⎥⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎣⎦=↓ 2、解：单位和荷载弯矩图，用图乘可求得：29700.14 m B EI∆==3、超静定结构求解：本题共2题，任选1题作答，计20分。
（1）用力法作图6所示结构的M 图.EI =常数。
几何组成分析解题要点
几何组成分析解题要点
⏹一、机动分析时应灵活运用规则
⏹通常的顺序是：
⏹ 1.二元体规则；
⏹ 2.两钢片规则；
⏹ 3.三钢片规则；
⏹ 4.联合使用多个规则。
⏹二、机动分析的解题要点：
⏹ 1.去掉二元体（若存在）
⏹ 2.当体系用三根链杆按“两钢片规则”与地基相
⏹联时，可去掉支座链杆和地基，只对体系
⏹本身进行分析。
⏹若体系本身几何不变，那么，整个体
⏹系即为几何不变；反之，则为几何可变。
⏹当体系支座链杆多于三根时，则必须把基础视为一钢片，与体系本身一起分析。
⏹ 3.等效代换
⏹⑴等效钢片：
⏹一个几何不变的部分可视为一个钢片。
⏹⑵等效链杆：
⏹复杂形状的链杆（如曲链杆、折线型链
⏹杆）可看作通过铰心的直链杆。
⏹⑶等效虚铰：
⏹联结两钢片的两链杆可用交点的虚铰代
⏹替。
⏹ 4.逐步扩大分析法
⏹⑴从基础出发逐步扩大；
⏹⑵从内部出发逐步扩大。
⏹ 5.两两相联（三钢片规则中）
⏹运用三钢片规则分析时，往往体系比较复杂，应注意以下几点：
⏹⑴选用三个合适的钢片；
⏹⑵找出三个单铰；
⏹⑶注意“两两相联”。
⏹ 6.若体系较复杂，而通过W的计算已知W＞0，
⏹则为可变体系，无需再进行分析。
2几何组成分析习题课.
D
(II, III) C
零载法 例7：试计算图示体系的自由度。 解法 I: 将AC、CB、CG和CI视为 刚片，则 m 4
A F G D I E C H B
C点为复铰，相当于3个单 铰，故 h 3
单链杆数为：7，即 b 7
故体系自由度为： W 3m (3g 2h b)
3 4 (2 3 7) 1
平面结构几何构造分析习题课
一、分类： 二、目的： 三、方法： 几何不变体系的组成规律： 规律1 （双杆系组成规律） ——二元体
连接一个铰结点的两根不共线的链杆构成一无多余约束的
几何不变体系
在体系上增加或拆除一个二元体， 应用： 不会影响原体系的几何构造性质。 规律2 （二刚片结合规律） 两刚片通过一铰和一延长线不通 过该铰的链杆相连，构成一无多 余约束的几何不变体系。
m 2, j 2 单铰数： h 1 单链杆数： b 9 体系自由度为：
W (3m 2 j ) (3g 2h b) (3 2 2 2) (2 1 9) 1
注意： 一般情况下，存在复链杆时，取刚片计算；而当存在复铰 时，选择可动质点计算较为简单。
解法II： 将A、B、C、F、G、H、 G、I视为可动质点，则
A F G D
C H I
B
j7
AC、CB为复链杆，每个
E
复链杆相当于（2n —3） 个单链杆，故 2n 3 3 b 2 3 9 15 体系自由度为： W 2 j b 2 7 15 1
解法 III：将AC、CB视为刚片，将G、I视为可动质点，则
例6：
(I, III)
F G A
II B II) (I,
高中数学1.1空间几何体1.1.1构成空间几何体的基本元素课后训练新人教B版必修2(2021学年)
高中数学1．１空间几何体1.1.１构成空间几何体的基本元素课后训练新人教B版必修２编辑整理：尊敬的读者朋友们:这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望（高中数学 1.１空间几何体1.1．1 构成空间几何体的基本元素课后训练新人教Ｂ版必修２)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中数学 1.1 空间几何体 1．1.１构成空间几何体的基本元素课后训练新人教Ｂ版必修2的全部内容。
1。
1．1 构成空间几何体的基本元素课后训练１.下列叙述中,一定是平面的是( ）．A．一条直线平行移动形成的面Ｂ．三角形经过延展得到的面C.组成圆锥的面D.正方形围绕一条边旋转形成的面2.下面空间图形的画法中错误的是( )．３．下列说法正确的是( ).Ａ.四边形是平面图形B.有三个公共点的两个平面必重合C.两两相交的三条直线必在同一个平面内Ｄ.三角形是平面图形４．如图，在正方体ABCD－Ａ１B1C1Ｄ1中，M,N,P，Q分别是线段Ｃ1D1，A1D１,BD1,BC的中点,给出下面四个命题:①ＭＮ∥平面APＣ；②B1Q∥平面AＤD1A１;③A,Ｐ，M三点共线；④平面MNQ∥平面ＡBCD.其中正确的序号为( ).A.①②B.①④C.②③D.③④５．纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北．现在沿该正方体的一些棱将正方体剪开、外面朝上展平,得到下侧的平面图形,则标“△”的面的方位是( ）．Ａ.南Ｂ.北Ｃ．西Ｄ.下６.在长方体ＡBCD-Ａ1B1C１D1中（如图所示)，和棱Ａ1B1不相交的棱有__＿_＿＿＿___条．7．若空间三个平面两两相交，则它们的交线条数是__＿_____＿_．８.如图,是一个无盖正方体盒子的表面展开图，A,B,Ｃ为其上三点,则在正方体盒子中,∠AＢC等于____＿__＿__．９.如下图所示,画出(1),（2)中直线ｌ′围绕直线ｌ旋转一周形成的空间几何体．10.如图是边长为1 m的正方体,有一蜘蛛潜伏在A处,B处有一小虫被蜘蛛网粘住,请制作出实物模型，将正方体剪开，描述蜘蛛爬行的最短路线.ﻬ参考答案１.答案:B 直线平行移动可以形成平面或曲面，只有在方向不变的情况下才能得到平面．2。
《几何组成分析》课件
几何组成分析的工具和软件
CAD软件
几何分析工具
例如AutoCAD、SolidWorks等， 用于创建、编辑和分析几何模型。
包括模型检查、尺寸测量和形状 优化等功能，帮助实现几何组成 分析的目标。
可视化软件
用于生成精美的几何分析报告和 图形展示，提供直观的分析结果。
点、线、面的几何分析方法
1 点的坐标与位置
个元素内部，用于空间分析和约束。
3
连接与组合方式
研究几何元素的连接方式，分析组合对 元素功能和性能的影响。
几何组成分析中的常见误差和处理方法
1 测量误差
由于测量设备和方法的限 制，导致几何数据存在一 定的误差和偏差。
2 模型误差
几何模型的构建和简化过 程中，可能引入形状、尺 寸和拓扑结构的误差。
3 数据修复与校正
《几何组成分析》PPT课 件
通过本课件，您将深入了解几何组成分析的应用领域、基本原理、常见工具 与软件，以及其在产品开发、工业设计、制造过程等领域中的重要性和影响。
什么是几何组成分析
几何组成分析涉及对几何构造和形状的定量和定性分析，以揭示其内部结构、 关系和性能特征。
几何组成分析的应用领域
产品开发
质量控制中的几何组成分析
通过对产品外形、尺寸和位置的几何分析，实现对生产过程中产品质量的控 制与管理。
几何组成分析在制造过程中的应用
几何组成分析可以应用于质量检验、装配过程控制和模具设计等制造环节，提高产品质量和制造效率。
通过几何计算方法，对模型进行变换、剖析、比较和关系计算。
3 数据可视化
将分析结果以图形方式呈现，便于理解和决策。
几何组成分析中的常见概念
1
拓扑关系
几何组成分析习题课
F
G
H
C
A
B
D
E
F
G
H
(2,3)
A
BC D
E
J
K
(1,2)
F
G
H
(2,3)
C
A
B
D
E
J
K
(1,3)
刚片二等效替 代为链杆
F
G
(2,3) (1,2)
A
BC D E
几何不变体系
F
G
H
I
A
B
C
DE分析：该体系源自支座约束多于3个，因此将基础作为1个刚片 对整个体系进行分析。除基础外，从中可找出AF、BFG、 CGH、DHI和EI共5部分作为刚片，但这些刚片之间的约束不 完全符合基本组成规则的要求，无法按照基本刚片的扩大装配 法进行分析。
刚片法则或三刚片法则进行分析，继续 尝试进行替代。
刚片BFG与体系其他部 分之间仅通过单铰G和支 座链杆AF、 BJ联结， AF、 BJ组成瞬铰O1， 可认为刚片BFG与基础 （刚片）间通过瞬铰O1 E 联接，而与CGH之间通 过实铰G联结。刚片 CGH与基础之间通过铰 G及瞬铰O1与基础发生 联接，刚片BFG及相应 约束可用通过两铰铰心 的链杆O1G替代，瞬铰 O1是位于基础上的， O1G视为1支座链杆。
而体系中又无二元体，也无法按照撤除部件的方法进行分析。 尝试采用等效替代法进行分析。
O1
F
G
O2
H
I
A
B
C
D
J
替代体系1
折杆AF与体系其余部分之间通过单铰A 和F联接，可用链杆AF替代；同样，折 杆EI可用链杆EI替代。 该体系仍有5根支座链杆，仍将基础视 为一个刚片，体系中共有BFG、CGH、 DHI及基础4个刚片。此时还不能采用两
几何组成分析课件
地理信息系统中的离散组成 分析
离散组成分析在地理信息系 统中有着广泛的应用。通过 对地理实体进行离散化处理 ，可以更好地理解和分析地 理数据的空间分布和相互关 系，为地理信息系统提供更 加准确和可靠的数据支持。
THANKS
感谢观看
地形分析
通过几何组成分析对地形地貌进 行详细分析，为土地利用、城市
规划等提供依据。
地图制作
在地图制作中，利用几何组成分析 对地图要素进行精确绘制，提高地 图的精度和可视化效果。
遥感影像处理
在遥感影像处理中，利用几何组成 分析对影像进行校正、配准等操作 ，提高遥感数据的处理效率和精度 。
05
案例研究
应用广泛性
几何组成分析在许多领域都有广泛的应用，如建筑设计、机 械设计、电子工程等。通过对实际问题的几何组成进行分析 ，可以更好地理解其性质和变化，为解决实际问题提供思路 和方法。
几何组成分析的基本原则
01
系统性
几何组成分析需要遵循系统性原则，对几何图形进行全面、系统的分析
。分析过程中需要综合考虑形状、大小、位置和方向等属性，探究其内
总结词
建筑设计中的几何元素
总结词
建筑设计中的几何元素
详细描述
建筑设计中的几何元素，如点、线、面、体等，是构成建 筑形态的基本要素。通过对这些几何元素的运用，可以创 造出各种不同的建筑风格和空间效果。
案例二：几何操作在机器人视觉中的应用
总结词
机器人视觉中的几何操作
详细描述
在机器人视觉中，几何操作是至关重要的。通过对图像进 行几何变换，如缩放、旋转、平移等，可以纠正图像的畸 变，提高机器人的定位精度和识别能分析概述 • 几何元素与几何操作 • 几何组成分析方法 • 几何组成分析的应用 • 案例研究
第四讲 不定积分 .doc
第四讲 不 定 积 分Ⅰ.考试要求1. 理解原函数的概念，理解不定积分的概念.2. 掌握不定积分的基本公式,掌握不定积分的性质,掌握换元积分法与分部积分法.3. 会求有理函数、三角函数有理式和简单无理函数的积分.Ⅱ. 考试内容一. 原函数的概念1. 定义：原函数定义 如果)()(x f x F =', 或者dx x f x dF )()(=, 则称)(x F 是)(x f 的原函数. 2. 存在性：连续函数有原函数.推论 初等函数在有定义的区间上有原函数. 注：（1）原函数有无穷多.（2）任意两个原函数差一个常数.二. 不定积分的的概念与性质1. 定义：函数)(x f 的全部原函数{+∞<<-∞+C C x F |)(}称为)(x f 的不定积分, 记作⎰dx x f )(.注：（1）不定积分不是一个函数, 而是一个函数的集合.（2）11s i n s i n d x d x C x x-=⎰⎰ 2. 性质基本性质：[])()(x f dx x f dxd=⎰, 或者[]dx x f dx x f d )()(=⎰ ⎰+='C x F dx x F )()(, 或者⎰+=Cx F x dF )()( 运算性质：[()()]f x g xd x αβ+⎰=()()f x d x g x d xαβ+⎰⎰注：当积分号消失时加任意常数三.基本公式1.k d x k x C =+⎰,2.(1)1x x dx C μμμμ=+≠-+⎰, 3. 1ln||d x x C x=+⎰,4.ln x xa a dx C a=+⎰, x xed x e C =+⎰, 5.s i n c o s x d x x C=-+⎰, 6.c o s d s i n xx x C =+⎰, 7.2s e c d t a n x x x C=+⎰, 8.2c s cd c o t x x x C=-+⎰, 9.s e ct a n d s e c x x x xC =+⎰， 10.c s c c o td c s c x x x xC =-+⎰，11. 221a r c s i n xd x Ca a x=+-⎰, 12.2211a r c t a n xd x C a x a a=++⎰, 13.s e c d l n |s e c t a n |x x x xC =++⎰， 14. c s c d l n |c s c c o t|x x x xC =-++⎰，15.2211l n ||2a xd x C a x a a x+=+--⎰. 16. 22221l n ()d x x x a Cx a=+±+±⎰. 注：不能用初等函数表示的积分2x e d x ⎰,2x ed x -⎰,s in x d x x ⎰,1ln d x x⎰. 四. 基本积分方法1. 换元积分法：()()[()]()x t f x d x f t td t ϕϕϕ='⎰⎰ 2.常见换元公式 （1）1()()()fa xb d x fa xb d a xb a +=++⎰⎰,（2）11()()f x x d x f x d x μμμμμ-=⎰⎰, （3）1()()l n x x x xf aa d x f ad a a=⎰⎰,（4）(s i n )c o s (s i n )s i n f x x d x f x dx =⎰⎰, （5）(c o s )s i n (c o s )c o s f x x d x f x dx =-⎰⎰, （6）21(s i n )(s i n )s i n 1f a r c x d x f a r c x d a r c x x=-⎰⎰, （7）21(a r c t a n )(a r c t a n )a r c t a n 1f x d x f x d x x=+⎰⎰, （8）22(,)Rxa x d x -⎰， 令22a x -，令t a x sin =,22ππ≤≤-t ；（9）22(,)Rxa x d x +⎰， 令t a x tan =, 22ππ<<-t .（10）22(,)Rx x a d x -⎰，令t a x sec =, 20π<<t 或02<<-t π, （11）(,)nax bR x dx cx d++⎰，令na x bu cx d+=+，其中，0a d b c -≠，2,3,4,n =（12）(s i n ,c o s )R x xd x ⎰，令ta n 2x u = 分母次数较高时，倒代换1x t=；a xe t =，a r c s i n x t = 3.分部积分法:⎰⎰'-='vdxu uv dx v u . 注：反对幂三指（1）()s i n n P x a x d x ⎰，()c o s n P x a x d x ⎰，()a xn P x e dx ⎰ （2）()a r c s i n nPx a x d x ⎰，()a r c c o s nPx a x d x ⎰，()l n nP x x d x ⎰ （3）s i n ()k xe a x bd x+⎰Ⅲ．题型与例题【例1】d xx x ++-⎰11.【例2】计算下列不定积分 【例3】计算不定积分dx x x x⎰-)1(arccos 2.【例4】求计算不定积分.)1(232arctan dx x xe x ⎰+【例5】⎰+dx exe xx 1【例6】计算不定积分⎰+dx xx xcos sin sin 【例7】求dx xxx x ⎰-2sin cos sin .【例8】（11317）（本题满分10分）求arcsin ln x xdx x+⎰. 【例9】设x xx f sin )(sin 2=，求⎰-dx x f xx )(1 【例10】设函数f x ()有连续导函数, 且f x d x x x C ()(s i n )l n =++⎰1, 求 xf x d x '⎰().第五讲 定积分及其应用Ⅰ.考试要求1. 理解定积分的概念．2. 掌握定积分的性质及定积分中值定理，掌握换元积分法与分部积分法．3. 会求有理函数、三角函数有理式和简单无理函数的积分．4. 理解积分上限的函数，会求它的导数，掌握牛顿－莱布尼茨公式．5. 了解反常积分的概念，会计算反常积分． 注：（1）数一、数二要求：掌握用定积分表达和计算一些几何量与物理量（平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等）及函数的平均值．（2）数三要求：会利用定积分计算平面图形的面积、旋转体的体积和函数的平均值，会利用定积分求解简单的经济应用问题．Ⅱ.考试内容一、定积分的概念与性质1. 定义∑⎰=→∆∆ni i i ba x f dx x f 1)(lim )(ξλ； 注：（1）积分与所用变量的符号无关. （2）规定：()()baab f xd x f xdx =-⎰⎰, ()0a af x dx =⎰.（3）几何意义（4）设)(x f 在[,]a b 上可积，则1011l i m ()()nn k ba ba fa k fx d x n n n →∞=--+=∑⎰ 特别地， ⎰∑==∞→101)()(1lim dx x f n kf n n k n ． 【例1】求和式极限（1）222121l i m []n n n n n→∞-+++ （2）222222l i m []12n n n nn n n n→∞++++++（3）12l i m [1c o s 1c o s 1c o s ]n n nnn nπππ→∞++++++（4）!l i mnn n n→∞2. 可积的条件（1）可积的必要条件：若)(x f 在],[b a 上可积，则)(x f 在],[b a 上有界． （2）可积的充分条件：若)(x f 在],[b a 上连续或仅有有限个间断点，则)(x f 在],[b a 上可积； 3. 定积分的性质假设各性质中所列出的定积分都是存在的． （1）⎰⎰⎰±=±bababa dx x g dx x f dx x g x f )()()]()([βαβα． （2）⎰⎰⎰+=bcc a ba dx x f dx x f dx x f )()()(． 注：分段函数的积分（3）若在],[b a 上()()f x g x ≤，则()()bbaaf xd xg xd x ≤⎰⎰．|()||()|()bbaaf x d x f x d x b a ≤>⎰⎰． （4）设M 与m 分别是)(x f 在],[b a 上最大值与最小值，则 )()()(a b M dx x f a b m ba -≤≤-⎰． （5）积分中值定理：若)(x f 在],[b a 上连续，则存在],[b a ∈ξ，使得)()()(ξf a b dx x f ba-=⎰. 注：① ξ可以在区间内部取到.② 若)(x f 在],[b a 上连续，()g x 在],[b a 上可积且定号,则],[b a ∈ξ，使得()()()()b baaf xg x d x f g x d x ξ=⎰⎰. 【例2】 （11304）设⎰=4sin ln πxdx I ,⎰=4cot ln πxdx J ,⎰=40cos ln πxdxK ,则I ,J ,K 的大小关系是[ ]．)(A K J I <<. )(B J K I <<. )(C K I J <<. )(D I J K <<. 【例3】 设函数)(x f y =在区间]1,0[上可导, 且⎰=2/10)(2)1(dx x xf f , 则存在(0,1)ξ∈, 使得0)()(=+'ξξξf f二、奇偶函数与周期函数的积分性质1. 若)(x f 在],[a a -上可积，则⎪⎩⎪⎨⎧=⎰⎰-为偶函数若为奇函数若)(,)(2)(,0)(0x f dx x f x f dx x f a aa ． 2. 若)(x f 在],[a a -上可积，则⎩⎨⎧⎰为偶函数若奇函数为奇函数若偶函数为)(,)(,)(0x f x f dt t f x． 注：若)(x f 为奇函数，则)(x f 的原函数均为偶函数．若)(x f 为偶函数，则原函数中只有一个原函数是奇函数． 3. 设)(x f 是以T 为周期的可积函数，则任意周期上的积分相等.⎰⎰⎰-+==2/2/0)()()(T T T Ta a dxx f dx x f dx x f ， ⎰⎰=T nTdx xf n dx x f 00)()(． 4. 设)(x f 是以T 为周期的连续函数，则)(x f 的原函数以T 为周期的充分必要条件是0)(0=⎰Tdx x f ．【例4】积分=+⎰-22223cos )sin (ππxdt x x ________． 【例5】设)(x F 是连续函数)(x f 的一个原函数，“N M ⇔”表示M 的充要条件是N ，则必有 [ ]．（A ）)(x F 是偶函数 ⇔)(x f 是奇函数．（B ）)(x F 是奇函数 ⇔)(x f 是偶函数． （C ）)(x F 是周期函数 ⇔)(x f 是周期函数． （D ）)(x F 是单调函数 ⇔)(x f 是单调函数． 【例6】设函数⎰=xdt t x S 0cos)(， （1）当n 为正整数，且ππ)1(+≤≤n x n 时，证明：)1(2)(2+<≤n x S n ； （2）求xx S x )(lim+∞→.三、计算定积分1. 微积分基本公式（牛顿－莱布尼茨公式）：若)(x f 在],[b a 上连续，)(x F 是)(x f 在],[b a 上的一个原函数，则)()()(a F b F dx x f ba-=⎰． 2. 换元积分法与分部积分法 注：换元要换限 【例7】计算⎰--2ln 021dx e x 。
解析几何第四章习题及解答
第4章 二次曲线和二次曲面习题4.11.在直角坐标系x O y 中，以直线:43120l x y -+=为新坐标系的x '轴，取通过(1,3)A -且垂直于l 的直线为y '轴，写出点的坐标变换公式， 并且求直线1:3250l x y -+=在新坐标系中的方程。
解：直线:43120l x y -+=的方向是(3,4)，与它垂直的方向是(4,3)±-，新坐标系的x '轴的坐标向量取为34(,)55，y '轴坐标向量取为43(,)55-，与直线:43120l x y -+=垂直且的直线方程可设为340x y c ++=，由于过点(1,3)A -，得到直线方程是3490x y ++=，两直线的交点(3,0)-是新坐标原点，所以点的坐标变换公式：34355.43055x x y y ⎡⎤-⎢⎥'-⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦直线1:3250l x y -+=在新坐标系中的方程：13443:3(3)2()505555l x y x y ''''---++=，化简有1:18200.l x y ''--=2.作直角坐标变换，已知点(6,5),(1,4)A B --的新坐标分别为(1,3),(0,2)-，求点的坐标变换公式。
解：设同定向的点的坐标变换公式是：cos sin .sin cos x x a y y b θθθθ'-⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎣⎦它的向量的坐标变换公式是：cos sin .sin cos u u v v θθθθ'-⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦由题意知向量(5,1) A B =-变为(1,5)A B ''=-，于是有5cos sin 1.1sin cos 5θθθθ---⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦得到125s i n ,c o s .1313θθ==于是点的坐标变换公式是：5121313.1251313x x a y y b ⎡⎤-⎢⎥'⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦将点(1,4)B -及它的像点(0,2)代入得到3713,6213a b ⎡⎤⎢⎥⎡⎤=⎢⎥⎢⎥⎣⎦⎢⎥-⎢⎥⎣⎦所以点的坐标变换公式是： 51237131313.12562131313x x y y ⎡⎤⎡⎤-⎢⎥⎢⎥'⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦设反定向的点的坐标变换公式是：cos sin .sin cos x x a y y b θθθθ'-⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎣⎦它的向量的坐标变换公式是：cos sin .sin cos u u v v θθθθ'-⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦由题意知向量(5,1)A B =-变为(1,5) A B ''=-，于是有5cos sin 1.1sin cos 5θθθθ---⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦得到s i n 1,c o s 0.θθ=-=于是点的坐标变换公式是：01.10x x a y y b '-⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'-⎣⎦⎣⎦⎣⎦⎣⎦将点(1,4B -及它的像点(0,2)代入得到3,4a b ⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦所以点的坐标变换公式是： 013.104x x y y '-⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥'--⎣⎦⎣⎦⎣⎦⎣⎦3.设新旧坐标系都是右手直角坐标系，点的坐标变换公式为5,3,22(1)(2) 2.3;22x x y x y y x y x y ⎛''=++ '=-+⎧⎨' =-⎩''=-+- ⎝ 其中，(,)x y 与(,)x y ''分别表示同一点的旧坐标与新坐标，求新坐标系的原点的旧坐标，并且求坐标轴旋转的角θ。
(完整版)几何组成分析习题及答案
题15．7试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 2j -6-r=2×8-9-7=0(2)几何组成分析。
首先把三角形ACD和BCE分别看做刚片I和刚片Ⅱ，把基础看做刚片I，则三个刚片用不共线的三个铰A、B、C分别两两相联，组成一个大的刚片。
在这个大的刚片上依次增加二元体12、DGF、CHG、EIH、IJ3。
最后得知整个体系为几何不变，且无多余约束。
题15.8试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 3m - 2h -r=3×6-2×7—4=0(2)几何组成分析。
刚片AF和AB由不共线的单铰A以及链杆DH相联，构成刚片I，同理可把BICEG部分看做刚片Ⅱ，把基础以及二元体12、34看作刚片I，则刚片I、Ⅱ、Ⅲ由不共线的三个铰F、B、G两两相联，构成几何不变体系，且无多余约束。
题15.9试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 3m - 2h -r=3×14 -2×19 -4一O(2)几何组成分析。
在刚片HD上依次增加二元体DCJ、CBI、BAH构成刚片I，同理可把DMG部分看做刚片Ⅱ，把基础看做刚片I，则刚片I、Ⅱ、Ⅲ由不共线的单铰D，虚铰N、O 相联，构成几何不变体系，且无多余约束。
题15.10试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W-2j—b-r=2×7—11-3一O(2)几何组成分析。
由于AFG部分由基础简支，所以可只分析AFG部分。
可去掉二元体BAC只分析BFGC部分。
把三角形BDF、CEG分别看做附片I和I，刚片I和I由三根平行的链杆相联，因而整个体系为瞬变。
题15.11试对图示体系进行几何组成分析。
解 (1)计算自由度。
体系的自由度为W- 2j -6-r=2×9-13—5一O(2)几何组成分析。
首先在基础上依次增加二元体12、AE3、AFE、ABF、FI4，成一个大的刚片I。
结构力学龙驭球第四版第二章课后习题答案
图 2-10-a b. 解：如图 2-10-b 所示刚片 I，ll，IⅢl，三刚片分别由饺(1,3)，(2,3）及杆 1，2 交于无穷
图 2-8-a b. 解：如图 2-8-b 所示刚片Ⅰ﹐及大地Ⅲ，I，Ⅱ交于无穷远处饺(1,2),l，Ⅲ由支座链杆相
联交于(1,3)，ll，Ⅲ交于(2，3); (1,3）及(2,3)的连线与杆 5,6 平行﹐故体系为瞬变。
图 2-8-b 2-9 试分析所示体系的几何构造。 a. 解：按一般思路分析，如图 2-9-a 所示刚片 I，ll,大地刚片Ⅲ,分别交于饺 A，(1,3),(2,3),
4，5;6,7;8,9;10,1l;12,13 后仍为几何不变,大地视为刚片Ⅱ﹐由不平行且不交于一点的链 14,15,16 相联，所以为几何不变体系且无多余约束。
图 2-2-b c. 解：去掉二元体 8,9,不予考虑。如图 2-2-c 所示刚片 I，ll,Ⅲ由三饺相联，但三个铰在一
条直线上,不满足规则要求，为瞬变体系。
图 2-1-c 2-2 试分析所示体系的几何构造。 a. 解：如图 2-2-a 所示,依次去掉二元体 l,2;3,4;5,6;7,8;9,10;11,12;只剩下大地刚片，为几何
不变体系，且无多余约束。
图 2-2-a b. 解：如图 2-2-b 所示,杆 1,2,3 由不在一条直线上的三个饺相联﹐构成刚片Ⅰ,加上二元体
w= 2j-b= 2×10-(16＋4)= o b. 解：w = 3m-（3g ＋2h＋b
=3×14-(3 ×2＋2×18) =o
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
铰无穷远的探讨，几何组成分析举例，复习组成规 则、几何组成与静定性的关系
Structural Mechanics
教学要求：
1、 了解铰无穷远与几何性质的关系； 2、深刻理解组成规则； 3、熟练掌握几何组成分析的方法、技巧。
重点：几何组成分析 难点：刚片的选取
E( 1 , 3 )
H G F
I
G
本题还可以将三 铰三角形ADJ、 CEJ分别视为刚 片II、III
习 题 2-3b
2-3b：只须分析体系内部是否几何不变。去掉三对二元体只 须分析下半部分的几何性质。在三铰三角形FDH上加二对二 元体视为刚片I，三刚片和三铰如图所示，三铰共线，不满足 刚片规则，该体系是瞬变体系。
几何组成分析习题评讲：
D D
Structural Mechanics
II F
B A
I F
B A
E
C
E
C
习 题 2-5b
2-5b：支承约束多于三个。把悬臂刚架和大地看成刚片I， DFE为刚片II。两刚片通过D铰和链杆BF联结，满足两刚片 规则。该体系有三个多余约束的几何不变体系。
几何组成分析习题评讲：
C B
(2,3)
III
习 题 2-6a
几何组成分析习题评讲： Structural Mechanics
2-6b：支承链杆多于三根，
D
A
把大地看成一个刚片。取 刚片如图所示，刚片间链
(2,3)
I
(1,3)
II
(1,2)
杆形成的虚铰如图所示，
其中I、II由无穷远虚铰相 链，另外两个虚铰重合， 故该体系不满足三刚片规 则，是瞬变体系。
2-6a：支承链杆多于三根， 把大地看成一个刚片。取
A (1,3)
D
Structural Mechanics
刚片，以及用刚片间链杆 形成的虚铰如图所示，其
I
II
(1,2)
中I、II由无穷远虚铰相链，
但形成该虚铰的链杆不与 另外两虚铰的连线平行， 故该体系满足三刚片规则， 是无多余约束的几何不变 体系。
§ 2.4 几何组成分析举例
练习7：
O
Structural Mechanics
瞬变
O II
I
§ 2.4 几何组成分析举例
练习8：
II I
Structural Mechanics
不变
(1,2)
II
(2,3)
I
(1,3)
III
§ 2.4 几何组成分析举例
练习9：
II
Structural Mechanics
习 题 2-3a
规则，该体系是无多余约束的
分析体系内部是否几何不变。去掉五对二元体，得到几何不 变的三铰三角形ABC。满足二元体规则，该体系是无多余约 束的几何不变体系。
几何组成分析习题评讲：
B B C
Structural Mechanics
A
A
C
D J H F
E
D (1,2)
II
III
(2,3)
D E F B C E
(1,2) B
D
(2,3)
F
(1,3) C
Structural Mechanics
III II
A
A G
G
I
习 题 2-8a
2-8a：支承链杆多于三根，把大地看成一个刚片。取刚片，以 及刚片间链杆形成的虚铰如图所示，其中I、III由无穷远虚铰 相链，但形成该虚铰的链杆不与另外两虚铰的连线平行，故该 体系满足三刚片规则，是无多余约束的几何不变体系。
几何组成分析习题评讲：
B C
(2,3) (1,3)
E
A D
C
E
III
Structural Mechanics
A D
F G
(1,2)
F G
II
H
I
H
习 题 2-8b
2-8b：支承链杆多于三根，把大地看成一个刚片。由于ABCD 是无多余约束的铰结体系，且只有三处与外界相联，故可以视 为铰结三角形ACD。取刚片，以及刚片间链杆形成的虚铰如图 所示，故该体系满足三刚片规则，是几何不变体系。
III
O13
O23
几何瞬变体系
§ 2.4 几何组成分析举例
1
一铰无穷远 O12
Structural Mechanics
I
2
II
O13
III
O23
平 行 等 长
几何常变体系
一个无穷远处铰： 形成无穷 远处虚铰的链杆与另外两个铰的 连线平行且等长→常变体系。
§ 2.4 几何组成分析举例
一铰无穷远
O2 (2,3)
几何组成分析习题评讲：
(1,3)
D
(1,2)
D B III C
(2,3)
E
B
C
II
Structural Mechanics
E
G
I
A
G
I
A
习 题 2-7b
2-7b：支承链杆多于三根，把大地看成一个刚片。取刚片，
以及刚片间链杆形成的虚铰如图所示，故该体系满足三刚片 规则，是几何不变体系。
几何组成分析习题评讲：
几何组成分析习题评讲：
B C J (1 ,3 ) K M F
Structural Mechanics
(1 ,2 ) E
II
(2
,3
)
III
N H D
A D G L
习 题 2-9b
I
2-9b：支承链杆多于三根，把大地看成一个刚片。AB、LM是
悬臂梁，可以将其与大地看成一个新刚片。三固定支座、二元
体BCD、MKL本质上是加在这个新刚片上的二元体。取刚片， 以及刚片间链杆形成的虚铰如图所示，故该体系满足三刚片规 则，是几何不变体系。
几何组成分析习题评讲： Structural Mechanics
A
B
2-3a：方法一：支承链杆只有
A
B
三根。可以去除三根支承链杆
只须分析体系内部是否几何不
C C
变。取ABC刚片如图所示，刚
片上加五对二元体不会改变其
几何不变的性质。满足二元体 几何不变体系。 方法二： 支承链杆只有三根。可以去除三根支承链杆，只须
几何组成分析习题评讲：
B
Structural Mechanics
D
G
A B D G
C
F
E B D G
I
A C
方法一
II F
E A
I
C
方法二
II F
E
题 2-5(a)图
2-5a：支承链杆只有三根。可以去除三根支承链杆，只须分
析分析桁架本身是否几何不变。取刚片如图所示，两刚片通 过B铰和链杆CF联结，满足两刚片规则。该体系有二个多余 约束的几何不变体系。
III O13
O23
四 杆 平 行 等 长
几何常变体系
§ 2.4 几何组成分析举例
(c) 三铰无穷远情况
(1,2) (1,2)
Structural Mechanics
I
(1,2) (1,2)
I
II II
III III (1,3) (1,3)
III III I I II II
(2,3) (2,3)
(1,3) (1,3)
一个无穷远处铰： 形 O12
成无穷远处虚铰的链杆与
另外两个铰的连线不平行
→几何不变体系。
几何不变体系
O23
§ 2.4 几何组成分析举例
1 一铰无穷远 O12 平 行 但 不 等 长
Structural Mechanics
II
2
一个无穷远处 铰： 形成无穷远处 虚铰的链杆与另外 两个铰的连线平行 →瞬变体系。
II
1 2 3
F
I
H
C
E
G
方法二
2-4c：支承链杆只有三根。可 以去除三根支承链杆，只须分 析体系内部是否几何不变。三 铰三角形ABC上增加两对二元 体后视为刚片I，三铰三角形 HFG上增加一对二元体后视为 刚片II。两刚片采用一个铰D 和不通过此铰的链杆3联结， 满足两刚片规则。该体系有无 多余约束的几何不变体系。
Structural Mechanics
E
D A B C
A B II
(1,2)
E
O1 (1,3) C I
III D
瞬变(ACDE为各边中点) 一个无穷远处铰： 形成无穷远处虚铰的链杆与另 外两个铰的连线平行且等长→常变体系。
§ 2.4 几何组成分析举例
(b) 两铰无穷远情况
O12
Structural Mechanics
B
C
III
习 题 2-6b
几何组成分析习题评讲：
A B C E F
A (1 ,2 )
C (2 ,3 )
B II III E
F (1 ,3 )
Structural Mechanics
D H
G
D H I
G
习 题 2-7a
2-7a：支承链杆多于三根，把大地看成一个刚片。取刚片，
以及取刚片间链杆形成的虚铰和实铰如图所示，三铰共线， 故该体系不满足三刚片规则，是瞬变体系。
1
C
瞬变
2
O1 C I
E
A
3
E
O2
4
B
D
F
G
两铰无穷远→瞬变体系。 形成无穷远处虚铰的链
不变
I C