关于两个简谐振动合成的思考
简谐振动的合成及应用

简谐振动的合成及应用简谐振动是一种周期性的、能够用正弦函数的形式来描述的振动。
它可以通过合成多个简谐振动来实现不同形态的振动,且在实际应用中具有广泛的用途。
简谐振动的合成是指将多个简谐振动叠加在一起,形成一个复合振动的过程。
这种合成可以通过简单叠加每个简谐振动的位移、速度或加速度来实现。
例如,当多个简谐振动具有相同的频率和相位时,它们的位移叠加在一起,形成一个更大的振幅的振动。
当简谐振动具有不同的频率或相位时,它们的合成将产生出现谐波现象的复合振动。
简谐振动的合成在实际应用中具有很大的意义。
首先,它可以用来模拟各种复杂的振动现象。
例如,在音乐中,各种乐器发出的声音可以看作是不同频率和相位的简谐振动的叠加。
通过合成这些简谐振动,我们可以模拟出乐曲中的各种音调和音色。
此外,合成简谐振动还可以用来模拟地震、力学振动等实际现象,从而为工程设计和科学研究提供参考。
其次,简谐振动的合成可以用来解决实际问题。
例如,在无线通信中,调制信号的合成就是通过合成不同频率和相位的简谐振动来实现的。
调制信号的合成可以实现信号的调频、调幅、调相等功能,从而满足不同的通信需求。
另一个例子是振动传感器中的信号处理。
振动传感器通常可以检测到复杂的振动信号,但我们通常只对其中某些特定频率范围的振动感兴趣。
通过合成多个简谐振动,我们可以提取出目标频率范围的振动信号,从而实现信号的滤波和分析。
最后,简谐振动的合成也可以用来研究物体的振动性质。
通过合成不同频率和相位的简谐振动,我们可以得到物体在不同条件下的振动响应。
这对于研究物体的固有振动频率、共振现象等具有重要意义。
例如,在工程设计中,我们需要确定一个物体的固有振动频率,以避免共振现象。
通过合成简谐振动,我们可以模拟不同频率的激励对物体产生的响应,从而确定合适的工作频率范围。
总之,简谐振动的合成及其应用具有广泛的意义。
它可以用来模拟各种复杂的振动现象,解决实际问题,研究物体的振动性质等。
谐振动分析(三)两个同方向同频率简谐运动的合成
o
o
A1
A2
A
T
t
A A1 A2
x (A A )cos(t )
1
2
2 1 2k π
3
物理学
第五版
谐运动分析(三)
(2)相位差 (2k 1) π(k 0,1, )
2
1
x
x
A1
2 o
o
Tt
A
A2
A A1 A2
x (A2 A1)cos(t )
2
1
(2k
1)π
4
物理学
第五版
小结
(1)相位差
2
1
2k
π
A A1 A2
谐运动分析(三)
(k 0,1, ) 加强
(2)相位差
2
1
(2k 1) π
(k 0,1, )
A A A
1
2
减弱
(3)一般情况
A1 A2 A A1 A2
5
物理学
第五版
谐运动分析(三)
二 两个相互垂直的同频率的简谐
运动的合成 x A1 cos(t 1)
x 阻尼振动位移时间曲线
A
Ae t
Aet cost
O
T A
t
( 0)
21
物理学
第五版
三种阻尼的比较
谐运动分析(三)
(a)欠阻尼
2 0
2
(b)过阻尼
2 0
2
(c)临界阻尼
2 0
2
x
b
oc
t
a
22
物理学
第五版
谐运动分析(三)
例 有一单摆在空气(室温为 20C)中来 回摆动. 摆线长l 1.0 m,摆锤是半径r 5.0103 m 的铅球.求(1)摆动周期;(2)振幅减小 10%所需的时间;(3)能量减小10%所需 的时间;(4)从以上所得结果说明空气的 粘性对单摆周期、振幅和能量的影响.
任意方向简谐振动的合成

任意方向简谐振动的合成简谐振动是物理学中的一个基本概念,它指的是以一定周期,向同一方向重复运动的振动。
这种振动形式在自然界中有着广泛的应用,比如海浪、风力、地震、电磁波、声波等等。
因此,对简谐振动的理解和利用对于探索自然界的规律和机制具有重要意义。
简谐振动可以分为任意方向简谐振动和水平简谐振动。
任意方向简谐振动指的是在一个固定的方向上,按照一定的频率、振幅和相位进行的振动。
这种振动的特点是其旋转方向及频率是可以改变的,而旋转变换的特性在研究自然界的规律中具有重要的意义。
水平简谐振动是指振动的方向和幅度在一个水平的方向上按照一定的频率和振幅进行的振动。
这种振动的特点是其幅度和频率是不变的,而这种不变的特性使其在实际应用中具有广泛的应用,比如电力系统、工业机械设备等等。
由于任意方向简谐振动和水平简谐振动具有不同的特点,因此在实际应用中,需要将这两种振动方式结合起来,以达到更好的应用效果。
在汽车工业、船舶工业等众多行业中,都大量应用了任意方向简谐振动的合成技术。
任意方向简谐振动的合成实现的关键在于对任意方向简谐振动和水平简谐振动进行有效的整合,以达到最优的应用效果。
针对这一问题,目前,科学家们已经提出了许多有效的解决方案,比如控制系统、智能控制系统、万联系统等等。
其中,控制系统是一种早期的任意方向简谐振动的合成技术,它通过检测水平简谐振动的特性以及任意方向简谐振动的特性,实现两者之间的匹配,从而达到最优的应用效果。
另外,智能控制系统则是通过大量的计算机算法和算法,实现对任意方向简谐振动和水平简谐振动的有效整合,从而实现更加高效和智能化的任意方向简谐振动的合成技术。
此外,更为重要的是,利用万联系统可以实现任意方向简谐振动和水平简谐振动的结合,从而实现更加精确的任意方向简谐振动的合成技术。
万联系统以一种多处理器的方式,将水平简谐振动和任意方向简谐振动分别划分到不同的处理器上,通过有效的数据通信和控制,实现对任意方向简谐振动和水平简谐振动的高效融合。
两个互相垂直的简谐振动合成的几个问题

两个互相垂直的简谐振动合成的几个问题
关于两互相垂直的简谐振动合成的几个问题,笔者在此对此话题进行深入探讨。
简谐振动与传统弹性振动有着很大的不同,它依赖于应力和拉力的作用,而非仅凭于回复力,也因而改变了原振动的对称和规律性。
互相垂直的简谐振动合成,指的是两个相互垂直的振动的合成,它的定义是令一定的力测出一定的位移,以产生向后的非线性振动。
这种特性可以让原有简谐振动有着不同的形态,也带来了更多实用价值。
重点探讨可以归纳为:首先,它究竟可以应用于哪些领域?其次,如何通过互相垂直的简谐振动合成来获得理想的振动状态?“
从实用角度来看,有许多领域可以运用互相垂直的简谐振动合成,如汽车底盘的粘滞振动吸收、电梯的非线性振动消噪、离心泵轴的驱动突现等。
而如何获得理想的振动状态,则需依赖于智能测控设备,使用模拟系统加以测量和控制,建立交互式、可视化的仿真模型,以实现准确的测控管理。
最后,本文重点探讨了两个互相垂直的简谐振动合成的几个问题,其应用的范围广泛,即使是对于复杂的振动也可以采取有效的管理策略。
同时,需要搭配先进的测控设备和模拟系统,来实现对合成振动的有效控制。
同方向同频率简谐振动合成问题求解方法的研究

电子技术与软件工程Electronic Technology & Software Engineering电子技术Electronic Technology 同方向同频率简谐振动合成问题求解方法的研究贾冬梅(中北大学信息商务学院山西省晋中市030600 )摘要:本文分别运用解析法和旋转矢量法来求解两个同方向同频率简谐振动的合成问题并分析总结了它们冬自的特点.通过对比发 现:运用旋转矢量法比解析法更为直观有效,它可以生免去对物理公式的记忆和复杂的数学计算.但是在一般情形下,运用解析法求解更为有效.对于合振动初相位的确定,运用旋转矢量法比解析法更加直观、有效和便捷.关键词:振动合成;解析法;旋转矢量法;振幅;初相简谐振动是机械振动中最简单、最基本的振动形式,任何复杂 的振动都可以看作是简谐振动的合成旳。
而同方向同频率的简谐振 动的合成又是简谐振动的合成中最简单最重要的形式,它为波干涉 和衍射现象的分析奠定了理论基础,因此研究同方向同频率简谐振 动的合成有着十分重要的意义。
寻求一种高效便捷的求解简谐振动 合振动的振动的方法成为了解决同方向同频率简谐振动的合成的关 键3」。
对于同方向同频率简谐振动的合成问题,大学物理教材中 常使用旋转矢量法和解析法来进行讨论分析‘网。
下面分别运用解 析法和旋转矢量法来求解同方向同频率简谐振动合成问题,分析总 结它们各自的特点,为这类问题的分析和求解提供一些参考和借鉴。
1两个同方向同频率简谐振动的合成设两个简谐振动都沿着x 轴方向振动,平衡位置都为坐标原点, 它们振动的角频率3,振幅分别为A]和A2,初相分别为®和%, 它们的振动方程分别为:x,=A| cos ((ot+(p]) x 2=A 2 cos ((ot+(p 2)求这两个解析振动的合振动。
1. 1解析法由于两个简谐振动都沿着X 轴方向振动,所以这两个简谐振动在任一时刻合振动的位移也应在X 轴方向上,且合振动的位移X 等 于这两个分振动位移的代数和,即:X=X]+x 2将分振动的方程X1和X2代入上式展开整理:x = x }+x 2= A } COS (<zX + % ) + 厦2 COS (m + 02 )=4 cos (p 、cos - /1] sin (p } cos cotA 2 cos (p 2 cos cot- A 2s\n (p 2 sin cut=(A, cos (p 、+ A 2 cos %) cos cot sin (p 、4- A 2 sin (p 2) sin cot 令 A cos (p=A] cos (p]+A 2 cos (p 2 A sin (p=A 1 sin (P]+A 2 sin (p 2 得至lj x=A cos (p coscot-A sin (p sin (ot=A cos ((ot+(p )这一结果表明:两个同方向同频率简谐振动的合振动依旧是一 个简谐振动,且合振动的频率与分振动的频率相同都等于3,合振 动的振幅和初相可以表示为:A = J (/sin 0)2 +(/cos (p )2=J A : + / j + 2A t A 2 cos (02 - %)川 sin 0 _ A x sin ® + A 2 sin (p 2t a n (p =------—-------------------A cos (p A x cos (p 、+ A 2 cos (p 21.2旋转矢量法如图1所示,4和力2分别为两个分振动的旋转矢量,它们以相 同的角速度绕o 点做逆时针转动,t=Os 时它们与x 轴正向的夹角分 别为卩和①。
谐振动分析(三)两个同方向同频率简谐运动的合成

A
f (02 p2 )2 4 2p2
t
dA 0 d p
x A0 e
cos(t ) A cos( p t )
28
物理学
第五版
谐运动分析(三)
共振频率
r | 2 |
2 0 2
A
共振频率 小阻尼 阻尼 0
3
物理学
第五版
谐运动分析(三)
(2)相位差 2 1 (2k 1) π (k 0 , 1, )
x
A1
x
2
o
o
T
t
x ( A2 A1 ) cos( t ) A A1 A2 2 1 (2k 1)π
4
A
A2
物理学
第五版
物理学
第五版
谐运动分析(三)
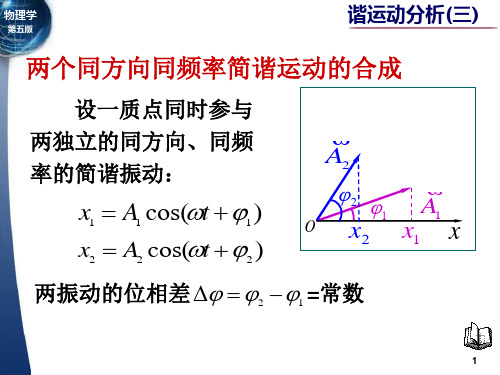
两个同方向同频率简谐运动的合成
设一质点同时参与 两独立的同方向、同频 率的简谐振动:
A2
2
O
x1 A1 cos( t 1 )
x2 A2 cos( t 2 )
x2
1
x1
A1
x
两振动的位相差 2 1 =常数
1
物理学
第五版
5
解 (2) 有阻尼时 A' Ae t ln( 1 ) 0 . 9 t t 174 s 3 min 0.9 A Ae 1
1
E 0.9E, t ? ( 3)
E ' A ' ( 3) ( ) 2 e 2t E A 1 ) ln( 2t 0.9 87 s 1.5 min 0.9 e t2 2
同方向同频率的两简谐振动合成后初相位
同向相位相同的两个简谐振动合成后初相位
的重要性
简谐振动是一个基本的物理现象,它是一个周期性运动,能够被描述为一个正弦或余弦函数。
同向相位相同的两个简谐振动合成后,初相位的设置非常重要,它决定了合成振动的特性。
在这篇文章中,我们将讨论初相位的重要性以及如何在实际应用中正确设置初相位。
对于同向相位相同的两个简谐振动,合成后的振动可以表示为:y = A sin (ωt + φ)
其中,A为振幅,ω为角频率,t为时间,φ为初相位。
如果两个振动的初相位不同,那么合成后的振动将不再是简谐振动,而是一个复杂的非周期性振动。
因此,初相位的设置对于合成振动的稳定性和周期性是非常关键的。
如果初相位设置不当,合成振动可能会失去稳定性,出现不期望的高频或低频分量。
在实际应用中,初相位的设置通常需要通过实验进行。
一种常见的方法是使用相干解调器。
相干解调器是一种电子设备,可以将两个简谐振动合成为一个新的简谐振动,并自动调整初相位,使合成振动以最大振幅、最小畸变的方式出现。
总之,同向相位相同的两个简谐振动合成后初相位的设置是非常重要的。
在实际应用中,正确设置初相位可以保证合成振动的周期性和稳定性,从而获得更准确、可靠的测量结果。
两个相互垂直同频率简谐运动的合成推导
两个相互垂直同频率简谐运动的合成推导好啦,今天咱们来聊聊两个相互垂直同频率简谐运动的合成。
你别看这名字听起来有点高大上,其实就是把两个上下或者左右的运动加在一起,看看它们会变成什么样的奇妙组合。
就像是你和你的朋友一起跳舞,虽然你们的舞步不同,但合在一起能跳出一种新花样。
这两种看似不相干的运动,如何在合成的过程中创造出新奇的结果呢?嘿,咱们慢慢往下聊。
首先啊,你想象一下,你有两个简单的摆动运动,一个在水平方向,一个在垂直方向。
这两个运动的频率是一样的,也就是说,它们每秒钟摇摆的次数是一样的。
每当一个摆动到最高点,另一个也在它的最高点摇晃。
是不是很有趣?就好像你左手跟右手同时开始做动作,虽然它们各自独立,但当合起来就能形成一种协调的美感。
现在问题来了,这俩摆动怎么加在一起呢?合成的原理并不复杂。
你可以把它想成一个在平面内活动的小球,这个小球每次摆动的方向都不一样,但它的速度、幅度却保持一致。
就像你用两根弹簧做实验,一个垂直拉伸,另一个水平方向拉伸,合起来以后,你会发现弹簧的运动方向变化了,但它们合成的结果给了你一个新的动力。
你看,不管是横着摆还是竖着摆,最终的结果就是一个新的路径。
假设你现在站在原点,左边那个摆动沿着x轴做运动,右边那个沿着y轴做运动。
它们的合成就是这样,合成的结果在某个时刻的位置,既有水平方向的位移,也有竖直方向的位移。
嗯,就像你既能向前跑也能向上跳,但最后你的位置是前面加上上面两者的结果。
合成后的运动轨迹就像是斜着的线,你根本猜不到它的样子,毕竟你只知道它是从两个方向合成来的。
你是不是有点懵了?别急,咱们先给这条轨迹取个名字,叫做“合成轨迹”。
你可以把它看作是从原点出发的小球,既向左又向上跳跃的轨迹。
这小球的运动,像是有点儿跳跃,但又不失稳重,给人一种干脆利落的感觉。
啥时候它能走得更远?当它的速度快、幅度大时,它就能从原点跳得越来越远,走得越来越快。
接下来嘛,咱们不妨再深入一点,看看合成的轨迹到底是啥样的。
简谐运动合成的讨论
为 了计算方便 ,建立两个直角三 角形 ,如图 2 ,有 e。s 。= (17)
根据 三角形 的和差关 系 ,整 理 (1)和(2) c。s∞ 。c。s 1+sinmt‘sin l (4)
上A c。s £。c。s 2+sin∞z’s in 2 (5)
= AlCOS(o)t+ 1) (1) Y=A2COS(tot+ 2) (2) 消去时 间 t,可得合运动 的轨迹方程 为 :
+ + 告一 cos( z一 。-)_= sin( : 一 。l)J (【3 j)
合运动轨迹 方程 是 一个 椭 圆方 程 ,它 的形 状 由两个
收 稿 日期 :2018—02—20 作者简介 :金 锋(1982.5一),男 ,辽 宁省沈 阳人 ,硕士研 究生 ,讲 师,从 事普通物理和 普通物理 实验教 学. 基金项 目:本论文是校级 大学物理精 品课程 建设 项 目(编号 :JP20140009)阶段 性建设成果.
c。s 一上 A 。。s : sin 。
2
cos
Az os
cos cos = sin2 ̄t‘
sin ( l一 2) (9) (4)乘 以 sin :,(5)乘 以 sin 。后得 :
siI 2=cos ‘cos l‘sin 2+sin ‘8in 1。sin 2 ( 0)
c。s = 上A2 (18)
根据 (17)和 (18)的关 系 ,(15)与 (16)两边 做差 ,整
理 后 得 :
02—0l: 2一 1 (19)
对 (19)两 沩 取 正 弦 ,得 :
sin(02—01)=sin( 2一 1) (2O)
二、同方向不同频率两个简谐振动的合成剖析
一个拍
合振幅变化的频率即拍频
拍
|
2 1 2
|| 2
1
|
拍现象是一种很重要的物理现象。
手风琴的中音簧: 键 盘 式 手 风 琴 ( Accordion) 的 两 排 中 音 簧 的 频 率大概相差6到8个赫兹,其作用就是产生“拍” 频。而俄罗斯的“巴扬”---纽扣式手风琴则是单 簧片的,因此没有拍频造成的颤音效果。
如果 A1 A2 则 A=0
合成振动
T 2
T
3T 2
2T
t
x2
x1
T 合成振动 3T
2
2
T
2T t
一般情况 为其他任意值,则:
A1 A2 A ( A1 A2 )
x
合成振动
T
3T
2
2
o
T
2
t
T
上述结果说明两个振动的相位差对合振动起着 重要作用。
例: 两个沿同一直线且具有相同振幅和周期的谐振动
两个同方向频率相近的简谐振动的合成 为合振幅随时间作缓慢变化的准简谐振动(拍)
合振幅变化的频率即拍频 拍 | 2 1 |
两个振动方向垂直频率相同的简谐振动的合成可能仍 为直线振动(而且是谐振动)也可能是圆运动,和椭 圆运动。
课后实验:
1. 请你测量一根吉他琴弦的振动频率。
2. 敲击盛水的玻璃酒杯能产生清晰的音调.试用 音叉把这些音调校准到你所需要的频率看看是否 能把他们排列起来构成一个八度音阶。
4
2
9
4
与合成相反:一个圆运动或椭圆运动可分解为
相互垂直的两个简谐振动。
四、两个互相垂直不同频率简谐振动的合成
如果两个相互垂直的振动的频率不相同,它们 的合运动比较复杂,而且轨迹是不稳定的。下面只 讨论简单的情形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于两个简谐运动合成的思考
曾骥敏
(能源与环境学院一卡通:213093696)
【摘要】现在,笔者想着重谈谈李萨茹图形。
笔者想首先从大一下学期用示波器做的关于振动的实验中谈起……
【关键词】简谐运动、李萨茹图形、振动
Thought Of Superposition of Two Simple Harmonic
Motions
Jimmy Zeng
(School of Energy& Environment, number:213093696) Abstract: And now, I want to tell something about Lissajous figures. Let me introduce the experiment used by an oscilloscope I have done in the last semester.
Key words: Simple Harmonic Motions, Lissajous figures, oscillation
经过一年大学物理的学习,笔者学习了包括力学、声学、光学、电磁学等许多基础的物理学知识,而笔者想在这里提出的自己关于两个简谐运动合成的一些粗略的思考。
首先,笔者想先提出关于前辈们在这方面所做的贡献。
大学物理中,简单的两个简谐运动的合成可以分成两种类型:
(1)两个简谐运动的振动方向一致;
(2)两个简谐运动的振动方向相互垂直。
而在每一种分类中,又可将其再细分成两种类型:
(a)两个简谐运动拥有相同的角速度ω;
(b)两个简谐运动的角速度各不相同,分别为ω
1、ω
2 。
让笔者再对这几种分类简单地做一下具体的说明:
(1)当两个简谐运动的振动方向一致时,假设:
(a)当两者拥有相同的角速度ω时,
(b ) 当两者角速度不相同时,假设:
(2) 当两个简谐运动振动方向相互垂直时,
(a ) 当两者拥有相同的角速度ω时,假设:
笔者在此假设了21ϕϕφ-=,这样,我们就能够得到如下的图片:
(b)当两者角速度不相同时,假设:
对于这个方程的轨迹不是一个闭合的曲线。
但是,我们都知道,如果我们假设两个周期
T x 和 T
y
,当
(m,n为整数)
这个轨迹就将成为一个闭合的曲线,这个曲线就是我们所说的李萨茹图形,而(2)-
(a)中提到的图形是当:1:1
x y
T T 时的李萨茹图形。
现在,笔者想着重谈谈李萨茹图形。
笔者想首先从大一下学期用示波器做的关于振动的实验中谈起。
如果示波器的X轴和Y轴偏转板上输入的都是正弦电压,荧光屏上亮点的运动将是两个
相互垂直振动的合成。
当两个正弦电压信号的频率相等或成简单整数比时,荧光屏上亮点的合成轨迹为一稳定的闭合曲线,叫李萨茹图形。
例如,当
Y
V 的频率为
Y
f 为
X
V 的频率
X
f 的两倍时,亮点的轨迹如图20-8所示,图20-9是频率比成简单整数时形成的若干李萨茹图形。
利用李萨茹图形可以比较两个电信号的频率。
如果其中一个电信号的频率是已知的,即可用此法测定另一个电信号的频率。
而笔者记录的实验结果如下所示:
李萨茹图
从图中和表中,我们可以看到,当
:2:1
Y X
f f=
时,为什么李萨茹图形不是一个闭合
的曲线呢?
其实,这个李萨茹图形仍然是一条闭合的曲线,只是我们观察的位置导致我们视觉上觉得它不是一条闭合的曲线,而在实验过程中,这条曲线是如同下图中缓慢地旋转的:
此外,笔者还想提一下
:?
X Y
T T=
的问题。
我们看到,
11::
:X Y Y X
X
Y
T T f f f f =
=
当:1:1
Y X f f =时,x 轴上的节点有两个,y 轴上的节点也有两个。
当
:2:1
Y X f f =时,x 轴上的节点有两个,而y 轴上的节点仅有一个。
当
:1:2
Y X f f =时,x 轴上的节点仅有一个,而y 轴上的节点有两个。
当
:1:3
Y X f f =时,x 轴上的节点有两个,y 轴上的节点有六个。
这样,我们可以得到
结论:
nodes of Y -axis : nodes of X -axis
Y X the f f the =
最后,笔者想对整篇文章做一个小结。
(I ) 当两个简谐运动有相同的振动方向和相同的角速度时,合成的运动的振幅取决于两简谐运动的振幅和相位角。
(II ) 当两个简谐运动有相同的振动方向,但是角速度不同时,我们将
观察到“拍”现象。
(III ) 当两个简谐运动的振动方向相互垂直但却有相同的角速度时,合成运动的图形取决于两运动的振幅和相位角。
(IV ) 当两个简谐运动的振动方向相互垂直且含有不同的角速度时,我
们便能得到李萨茹图形。
参考文献:
[1]/view/600826.htm
[2]Sears and Zemansky’s University Physics, China Machine Press, Hugh D. Young and Roger A. Freedman.
[3]《物理学(第五版)》,高等教育出版社,马文蔚改编
[4]《大学物理学(第四册)-波动与光学》,清华大学出版社,张三慧主编
[5]《大学物理实验(修订版)》,高等教育出版社,钱锋潘人培主编。
