福建省宁德市2017-2018学年高二上学期期末质量检测数学(理)试题
高二数学上学期期末考试试题 理(扫描版)1

福建省宁德市2015-2016学年高二数学上学期期末考试试题理(扫描版)宁德市2015—2016学年度第一学期高二期末质量检测数学(理科)试题参考答案及评分标准说明:1.本解答指出了每题要考察的主要知识和能力,给出一种或几种解法供参考。
如果考生的解法与给出的解法不同,可根据试题的主要考察内容比照评分标准确定相应的评分细则。
2.对解答题,当考生的解答在某一步出现错误,但整体解决方案可行且后续步骤没有出现推理或计算错误,则错误部分依细则扣分,并根据对后续步骤影响的程度决定后继部分的给分,但不得超过后续部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分。
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数。
4.解答题只给整数分数,选择题和填空题不给中间分。
一、选择题:本题考查基础知识和基本运算。
本大题共12小题,每小题5分,共60分。
1.D2. C3. B4. B5.A6.A7.A8.C9.D 10.B 11.A 12.B二、填空题 :本题考查基础知识和基本运算。
本大题共4小题,每小题5分,共20分。
13.1(,0)4F 14.21212n n a n n =⎧=⎨-≥⎩ 15.111442a b c +- 16.103 三、解答题:本大题 共6小题,共70分。
17. 本题主要以不等式恒成立为载体来考查简易逻辑等基本知识,考查运算求解能力和逻辑推理能力。
满分10分。
解:(Ⅰ)p ⌝:[1, 2]x ∃∈,2m x > ……………………….3分 (II )因为p q ∧为真命题,所以命题p 、q 都是真命题. ……………………….5分由p 是真命题,得2m x ≤恒成立. 因为[1, 2]x ∀∈,所以1m ≤. ………………………………………………………7分由q 是真命题,得240m ∆=-<,即22m -<<. ………………………………9分所以21m -<≤. 即所求m 的取值范围是(2, 1]-. ………………………………..10分18. 本题主要考查数列部分的基本知识,考查运算求解能力及化归思想转化。
2017-2018学年福建省宁德市高二(上)期末数学试卷(理科)(解析版)

10.(5 分)在等差数列{an},{bn}中,a1=1,a3=7,{an}的前 n 项和为 Sn,若 bn= (c
≠0),则 c=( )
A.
B.﹣
C.3
D.﹣3
11.(5 分)已知△ABC 的三个内角 A,B,C 的对边分别为 a,b,c,角 A,B,C 的大小依
次成等差数列,且 b= ,若函数 (f x)=cx2+2x+a 的值域是[0,+∞),则 a+c=( )
C.﹣4<a≤0
D.a<﹣4 或 a>0
7.(5 分)△ABC 中,已知
,则△ABC 为( )
A.等边三角形 B.等腰直角三角形 C.有一个内角为 30°的直角三角形 D.有一个内角为 30°的等腰三角形 8.(5 分)以椭圆 +y2=1 的焦点为顶点,同时以椭圆的顶点为焦点的双曲线方程是( )
A. ﹣y2=1
第 3 页(共 13 页)
直达航线,使 ON=8km,OM=4km.勘测时发现以 O 为圆心,3km 为半径的扇形区域为 浅水区,不适宜船只航行,问此航线是否影响船只航行? (2)为了发展经济需要,政府计划填海造陆,建造一个商业区(如图四边形 OACB 所示), 其中∠OAC=45°,∠AOC=θ,θ∈[30°,60°],求该商业区的面积 S 的取值范围.
(2)若
,求二面角 E﹣AC﹣D 的大小.
21.(14 分)已知 O,A,B 分别是海岸线 l1,l2 上的三个集镇,A 位于 O 的正南方向 10km 处,B 位于 O 的北偏东 60°方向 10kml1,l2 上分别修建码头 M,N,开辟水上
A.7
B.6
C.5
D.4
12.(5 分)过双曲线 ﹣ =1(a>0,b>0)的右焦点 F 作平行于一条渐近线的直线与
精品解析:【全国市级联考】福建省宁德市2016-2017学年高二第二学期期末质量检测数学理试题(原卷版)

宁德市2016-2017学年度第二学期高二期末质量检测数学(理科)试题第I卷(选择题共60分)选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一个项是符合题目要求的.1. 复数的共扼复数对应的点所在象限是A. 第一象限B. 第二象限C. 第三象限D. 第四象限2. 为考察数学成绩与物理成绩的关系,在高二随机抽取了300名学生,统计数据如下表数学85~100分85分以下合计物理85~100分37 85 12285分以下35 143 178合计72 228 3000.050 0.010 0.0013.841 6.635 10.828附:经计算,现判断数学成绩与物理成绩有关系,则判断出错的概率不会超过A. 0.5%B. 1%C. 2%D. 5%3. 某校高考数学成绩近似地服从正态分布,且,的值为A. 0.02B. 0.04C. 0.48D. 0.494. 某校9人入选3人篮球赛,若训练时分为三组,每组3人,则不同的分法种数有A. 280B. 1680C. 10080D.5. 篮子里装有3个红球,4个白球和5个黑球,球除颜色外,形状大小一致.某人从篮子中随机取出两个球,记事件A=“取出的两个球颜色不同”,事件B= “取出一个红球,一个白球”,则 =A. B. C. D.6. 如图,设不等式组表示的平面区域为长方形ABCD,长方形ABCD内的曲线为抛物线的一部分,若在长方形ABCD内随机取一个点,则此点取自阴影部分的概率等于学&科&网...学&科&网...学&科&网...A. B.C. D.7. 某单位为了了解用电量度与气温之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表气温()20 16 12 8用电量(度)14 28 44 62由表中数据得回归直线方程中,预测当气温为时,用电量的度数是A. 62B. 64C. 76D. 778. 函数的图象如图,则的单调递减区间是A. B.C. D.9. 直线与曲线相切,则的值为A. B. C. 2 D. 410. 某高校从7名大学生志愿者中选派4名去4个村庄进行环保宣传(每村1人),其中甲和乙两人中有且只有一个人去,甲和丙只能同去或同不去,则不同的选派方案种数有A. 10B. 96C. 144D. 24011. 已知三角形的三边长分别为,有以下四个命题:(1)以为边长的三角形一定存在;(2)以为边长的三角形一定存在;(3)以为边长的三角形一定存在;(4)以为边长的三角形一定存在;其中错误命题的个数为A. 0B. 1C. 2D. 312. 设函数,其中,若存在唯一整数,使得,则的取值范围是A. B. C. D.第II卷(非选择题共90分)二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.13. 随机变量服从二项分布,且,则 =__________.14. __________.。
精品解析:【全国市级联考】福建省宁德市2016-2017学年高二第二学期期末质量检测数学理试题(解析版)
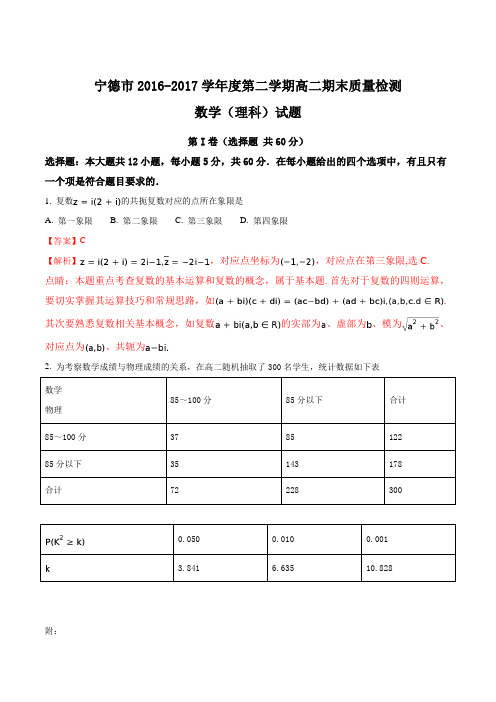
宁德市2016-2017学年度第二学期高二期末质量检测数学(理科)试题第I卷(选择题共60分)选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一个项是符合题目要求的.1. 复数的共扼复数对应的点所在象限是A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】C【解析】,对应点坐标为,对应点在第三象限,选C.点睛:本题重点考查复数的基本运算和复数的概念,属于基本题.首先对于复数的四则运算,要切实掌握其运算技巧和常规思路,如. 其次要熟悉复数相关基本概念,如复数的实部为、虚部为、模为、对应点为、共轭为2. 为考察数学成绩与物理成绩的关系,在高二随机抽取了300名学生,统计数据如下表附:经计算,现判断数学成绩与物理成绩有关系,则判断出错的概率不会超过A. 0.5%B. 1%C. 2%D. 5%【答案】D【解析】,则,出错概率不超过5%选D.3. 某校高考数学成绩近似地服从正态分布,且,的值为A. 0.02B. 0.04C. 0.48D. 0.49【答案】C【解析】选C.4. 某校9人入选3人篮球赛,若训练时分为三组,每组3人,则不同的分法种数有A.280 B. 1680 C. 10080 D.【答案】A【解析】选A.点睛:求解排列、组合问题常用的解题方法:(1)元素相邻的排列问题——“捆邦法”;(2)元素相间的排列问题——“插空法”;(3)元素有顺序限制的排列问题——“除序法”;(4)带有“含”与“不含”“至多”“至少”的排列组合问题——间接法.5. 篮子里装有3个红球,4个白球和5个黑球,球除颜色外,形状大小一致.某人从篮子中随机取出两个球,记事件A=“取出的两个球颜色不同”,事件B= “取出一个红球,一个白球”,则 =A. B. C. D.【答案】B【解析】选B.6. 如图,设不等式组表示的平面区域为长方形ABCD,长方形ABCD内的曲线为抛物线的一部分,若在长方形ABCD内随机取一个点,则此点取自阴影部分的概率等于A. B.C. D.【答案】A【解析】选A.点睛:1.求曲边图形面积的方法与步骤(1)画图,并将图形分割为若干个曲边梯形;(2)对每个曲边梯形确定其存在的范围,从而确定积分的上、下限;(3)确定被积函数;(4)求出各曲边梯形的面积和,即各积分的绝对值的和.2.利用定积分求曲边图形面积时,一定要找准积分上限、下限及被积函数.当图形的边界不同时,要分不同情况讨论.7. 某单位为了了解用电量度与气温之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表)由表中数据得回归直线方程中,预测当气温为时,用电量的度数是A. 62B. 64C. 76D. 77【答案】D【解析】选D.点睛:函数关系是一种确定的关系,相关关系是一种非确定的关系.事实上,函数关系是两个非随机变量的关系,而相关关系是非随机变量与随机变量的关系.如果线性相关,则直接根据用公式求,写出回归方程,回归直线方程恒过点.8. 函数的图象如图,则的单调递减区间是A. B.C. D.【答案】A【解析】;令,则的零点为,对称轴为图象先增再减再增,则函数开口向上,先减后增,单调减区间为选A.9. 直线与曲线相切,则的值为A. B. C.2 D. 4【答案】A【解析】设直线与曲线切点为,切点斜率为-2,则,从而,切点为选A.10. 某高校从7名大学生志愿者中选派4名去4个村庄进行环保宣传(每村1人),其中甲和乙两人中有且只有一个人去,甲和丙只能同去或同不去,则不同的选派方案种数有A. 10B. 96C. 144D. 240【答案】D【解析】分配人员:(1)甲去,则乙不去丙去,剩余两人选法有种(2)乙去,则甲丙都不去,剩余三人选法有种则分配人员共10种分配村庄:有种则共有240种,选D.11. 已知三角形的三边长分别为,有以下四个命题:(1)以为边长的三角形一定存在;(2)以为边长的三角形一定存在;(3)以为边长的三角形一定存在;(4)以为边长的三角形一定存在;其中错误命题的个数为A. 0B. 1C. 2D. 3【答案】B【解析】假设选项1:选项2:当时,,错误选项3:选项4:综上,只有一个错误,选B.12. 设函数,其中,若存在唯一整数,使得,则的取值范围是A. B. C. D.【答案】B【解析】;,在单调减,则时,;时,,则原题转换为存在唯一整数,使得;,令因为为整数,则,而,则所以,解得,即选B.点睛:涉及函数的零点问题、方程解的个数问题、函数图像交点个数问题,一般先通过导数研究函数的单调性、最大值、最小值、变化趋势等,再借助函数的大致图象判断零点、方程根、交点的情况,归根到底还是研究函数的性质,如单调性、极值,然后通过数形结合的思想找到解题的思路.第II卷(非选择题共90分)二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.13. 随机变量服从二项分布,且,则 =__________.【答案】【解析】14. __________.【答案】0【解析】15. 若函数在定义域上是增函数,则实数的取值范围为__________.【答案】【解析】定义域,在上恒成立,即在上恒成立,,当且仅当时成立,则点睛:函数单调性问题,往往转化为导函数符号是否变号或怎样变号问题,即转化为方程或不等式解的问题(有解,恒成立,无解等),而不等式有解或恒成立问题,又可通过适当的变量分离转化为对应函数最值问题.16. 定义:分子为1且分母为正整数的分数称为单位分数.我们可以把1分拆为若干个不同的单位分数之和.如:,,,依此类推可得:,其中,,则 =__________.【答案】33【解析】三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17. 已知是复数,且,均为实数(为虚数单位).(Ⅰ)求复数;(Ⅱ)若,求实数的值.【答案】(1)(2)或【解析】试题分析:(1)设,根据复数为实数条件列方程组,解得(2)根据复数模的定义得方程,解方程可得实数的值.试题解析:解:(1)设则;均为实数,(2)由得或18. 已知.(Ⅰ)求;(Ⅱ)求.【答案】(1)(2)【解析】试题分析:(1)令,则展开式右边为,左边为(2)即求展开式中含x2的项的系数:根据对应关系可得,即为.试题解析:解:(1)令,得,(2)展开式中含x2的项为: ,.点睛:赋值法研究二项式的系数和问题“赋值法”普遍适用于恒等式,是一种重要的方法,对形如的式子求其展开式的各项系数之和,常用赋值法,只需令即可;对形如的式子求其展开式各项系数之和,只需令即可.19. 已知.(Ⅰ)当时,求的极值;(Ⅱ)若在上不单调,求实数的取值范围.【答案】(1),,(2)【解析】试题分析:(1)先求函数导数,再求导函数零点,列表分析导函数符号变化规律,进而确定极值取法(2)即在上存在导函数零点,根据零点存在定理可得, 解不等式可得实数的取值范围.试题解析:(Ⅰ)当时,由得或由得在和上单调递增,在上单调递减,(Ⅱ),在上单调递增,所以,要使函数在区间上不单调,只需,即.20. 电视剧《人民的名义》中有一个低矮的接待上访服务窗口,假设群众办理业务所需的时间互相独立,且都是10分钟的整数倍,对以往群众办理业务所需的时间统计结果如下:假设排队等待办理业务的群众不少于3人,从第一个群众开始办理业务时开始计时.(Ⅰ)估计第三个群众恰好等待40分钟开始办理业务的概率;(Ⅱ)表示至第20分钟末已办理完业务的群众人数,求的分布列及数学期望.【答案】(1)(2)见解析【解析】试题分析:(1)先确定前两个群主所需时间:①第一个10分钟,且第二个30分钟;②第一个30分钟,且第二个10分钟;③第一个和第二个均为20分钟.根据互斥事件概率加法可得所求概率(2)先确定随机变量取法:.再分别确定对应事件及对应概率,列表可得分布列,最后根据数学期望公式求期望学,科,网...学,科,网...学,科,网...学,科,网...学,科,网...学,科,网...学,科,网...学,科,网...试题解析:解:设表示顾客办理业务所需的时间,用频率估计概率,得的分布列如下:(Ⅰ)表示事件“第三个顾客恰好等待40分钟开始办理业务”,则事件对应三种情形: ①第一个顾客办理业务所需的时间为10分钟,且第二个顾客办理业务所需的时间为30分钟;②第一个顾客办理业务所需的时间为30分钟,且第二个顾客办理业务所需的时间为10分钟;③第一个和第二个顾客办理业务所需的时间均为20分钟.所以.(Ⅱ)X 所有可能的取值为.对应第一个顾客办理业务所需的时间超过20分钟, 所以;对应第一个顾客办理业务所需的时间为10分钟且第二个顾客办理业务所需的时间超过10分钟,或第一个顾客办理业务所需的时间为20分钟,所以;对应两个顾客办理业务所需的时间均为10分钟, 所以;所以X 的分布列为21. 已知().(Ⅰ)求证:;(Ⅱ)若不等式在时恒成立,求最小正整数,并给出证明.【答案】(1)见解析(2)最小正整数等于5.【解析】试题分析:(1)利用分析法证不等式:两边平方,整理转化,再平方即得已知事实(2)先逐个代入验证并归纳猜想最小正整数.再利用数学归纳法进行证明: 当时,利用放缩及归纳假设得,即可证明试题解析:证明:(Ⅰ)要证:即证:只需证:即证:只需证:只需证:上式显然成立不等式成立.(Ⅱ)即当时,左边=,右边=,不等式不成立;当时,左边=,右边=,不等式不成立;当时,左边=,右边=,不等式不成立;当时,左边=,右边=,不等式不成立;当时,左边=,右边=,不等式成立;当时,左边=,右边=,不等式成立;故猜想最小正整数.下面证明时成立:证法一:(数学归纳法)①当时,左边=,右边=,不等式成立②假设当时,不等式成立,即,则当时,当时,显然故即时不等式成立综上,不等式在时恒成立,且最小正整数等于5.证法二:当时,由得即所以,不等式在时恒成立,且最小正整数等于5.22. 已知,(Ⅰ)求的值域;(Ⅱ)若时,,求的取值范围.【答案】(1)(2)【解析】试题分析:(1)先求函数导数,再导函数零点,列表分析导函数符号变化规律,确定函数单调性,结合函数图像确定函数值域(2)利用变量分离转化为求对应函数最值: ,利用导数及罗比特法则可得,因此,也可分类讨论求最值试题解析:解:(Ⅰ)定义域为,令,即得,当时,;当时,,当时,取得极小值即最小值函数的值域为.(Ⅱ)令,,令,,①若,,在上单调递增,,即,在上单调递增,,不符合题意;②若,由得,当时,,在上单调递增,从而,即,在上单调递增,从而,不符合题意;③若,则,在上单调递减,,即,在上单调递减,,从而. 综上所述,的取值范围是.。
2017年宁德质检数学卷

2017年宁德市普通高中毕业班第二次质量检查试卷理 科 数 学本试卷分第I 卷和第II 卷两部分.第I 卷1至3页,第II 卷4至6页,满分150. 考生注意:1.答题前,考生务必将自己的准考号、姓名填写在答题卡上.考生要认真核对答题卡上粘贴的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致.2.第I 卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.第II 卷用0.5毫米的黑色墨水签字笔在答题卡上书写作答.若在试题卷上作答,答案无效.3.考试结束,监考员将试题卷和答题卡一并交回 .第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设全集{|13}U x x =∈-≤≤Z ,0.5{1,2},{|log ,}A B y y x x A ===∈,则集合()U C AB =(A ){3}(B ){1,0,3}-(C ){1,0,1,2}-(D ){1,0,1,2,3}-(2)若复数z 满足i1i z z =-,其中i 是虚数单位,则复数z 的共轭复数为 (A )11i 22-+ (B )11i 22-- (C )11i 22- (D )11i 22+(3)等差数列{}n a 的公差为2,若2a ,4a ,8a 成等比数列,则{}n a 的前8项和8S = (A )72(B )56(C )36(D ) 16(4)已知函数()2cos (0)f x x ωω=>图象的两相邻对称轴间的距离为2π.若将函数()y f x =的图象向右平移6π个单位后,再将得到图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到()y g x =的图象,则()y g x =在下列区间上为减函数的是 (A )2233ππ⎡⎤-⎢⎥⎣⎦, (B )[]π0, (C )[]2ππ,3 (D )23π⎡⎤π⎢⎥⎣⎦,(5)阅读右图所示的程序框图,运行相应的程序,则 输出的结果是(A )12 (B )23(C )89(D )1(6)已知定义在R 上的函数()f x 满足(2)2()f x f x +=-,当(]0,2x ∈时,()=2x f x ,则在区间(]4,6上满足 ()=(3)12f x f +的实数x 的值为(A ) 6 (B )5(C )92(D )2log 21(7)若关于x 的不等式224k k kx -+≥的解集是M ,则对任意的正实数k ,总有(A ){}01x x M ≤<⊆ (B ){}13x x M ≤≤⊆ (C ){}13x x M ≤<⊆ (D ){}24x x M <≤⊆(8)等腰梯形ABCD 中,//AD BC ,2AB AD DC ===,60B ∠=.若抛物线Γ恰过,,,A B C D 四点,则该抛物线的焦点到其准线的距离为(A 3 (B 3 (C 3 (D 3(9)设1e ,2e 为单位向量,满足1212⋅=e e ,非零向量112212,,λλλλ=+∈R a e e ,则1||||λa 的最大值为 (A )12(B 3(C )1 (D 23(10)榫卯(sŭn măo )是我国古代工匠极为精巧的发明,它是在两个构件上采用凹凸部位相结合的一种连接方式. 我国的北京紫禁城、山西悬空寺、福建宁德的廊桥等 建筑都用到了榫卯结构.如图所示是一种榫卯构件中 卯的三视图,其体积为(A )21 (B ) 22.5 (C )23.5 (D ) 25开始1k =1?ba≤输出b 结束是否 2,03a b ==2()3ka k =⋅b a =1k k =+(11)已知F是双曲线C:22221(0,0)x ya ba b-=>>的右焦点,P是y轴正半轴上一点,以OP 为直径的圆在第一象限与双曲线的渐近线交于点M.若点P,M,F三点共线,且MFO∆的面积是PMO∆面积的5倍,则双曲线C的离心率为(A(B(C(D(12)已知直线1:l y x a=+分别与直线2:2(1)l y x=+及曲线:lnC y x x=+交于A,B两点,则A,B两点间距离的最小值为(A(B)3 (C(D)2017年宁德市普通高中毕业班第二次质量检查试卷理 科 数 学第II 卷注意事项:用0.5毫米黑色签字笔在答题卡上书写作答. 在试题卷上作答,答案无效.本卷包括必考题和选考题两部分.第(13)~(21)题为必考题,每个试题考生都必须做答.第(22)、(23)题为选考题,考生根据要求做答. 二、填空题:本大题共4小题,每小题5分.(13)若3(1)(1)x ax -+的展开式中2x 的系数为2,则实数a 的值为__________.(14)“微信抢红包”自2015年以来异常火爆.在某个微信群某次进行的抢红包活动中,若所发红包的总金额为9元,被随机分配为1.49元,1.31元,2.19元,3.40元,0.61元,共5份,供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于4元的概率是__________.(15)已知菱形ABCD 的边长为6,60A ∠=.沿对角线BD 将该菱形折成锐二面角A BD C --,连结AC .若三棱锥A BCD -表面积为__________.(16)若数列{}n a 满足211()()lg(1)n n n n a a a n n n+-=+++,且11a =,则100a =__________.三、解答题:本大题共6小题,满分70分.解答须写出文字说明、证明过程和演算步骤. (17)(本小题满分12分)如图,在ABC ∆中,3B π∠=.D 为边BC 上的点,E 为AD 上的点,且8AE =,AC =4CED π∠=.(Ⅰ)求CE 的长;(Ⅱ)若5CD =,求cos DAB ∠的值.EDCBA(18)(本小题满分12分)某公司计划明年用不超过6千万元的资金投资于本地养鱼场和远洋捕捞队.经对本地养鱼场年利润率的调研,得到如图所示年利润率的频率分布直方图.对远洋捕捞队的调研结果是:年利润率为60%的可能性为0.6,不赔不赚的可能性为0.2,亏损30%的可能性为0.2.假设该公司投资本地养鱼场的资金为(0)x x ≥千万元,投资远洋捕捞队的资金为(0)y y ≥千万元.(Ⅰ)利用调研数据估计明年远洋捕捞队的利润ξ的分布列和数学期望E ξ. (Ⅱ)为确保本地的鲜鱼供应,市政府要求该公司对本地养鱼场的投资不得低于远洋捕捞队的一半.试用调研数据,给出公司分配投资金额的建议,使得明年两个项目的利润之和最大.(19)(本小题满分12分)在多面体ABCDEF 中,四边形ABCD 是正方形,//EF AB ,1DE EF ==,2DC BF ==,30EAD ︒∠=.(Ⅰ)求证:AE ⊥平面CDEF ;(Ⅱ)在线段BD 上确定一点G ,使得平面EAD 与平面FAG 所成的角为30.0.6年利润率频率/组距-0.2-0.40.40.22.01.00.5OGFEDCBA(20)(本小题满分12分)已知过点(1,3)-,(1,1)且圆心在直线1y x =-上的圆C 与x 轴相交于,A B 两点,曲线Γ上的任意一点P 与,A B 两点连线的斜率之积为34-.(Ⅰ)求曲线Γ的方程;(Ⅱ)过原点O 作射线OM ,ON ,分别平行于PA ,PB ,交曲线Γ于M ,N 两点,求OM ON ⋅的取值范围.(21)(本小题满分12分)已知定义在(0,)+∞上的函数()f x 满足1()()f x f x=,且当[1,)x ∈+∞时,11()e ln ()x f x x a x t x-=++--,t ∈R .(Ⅰ)若0a ≥,试讨论函数()f x 的零点个数; (Ⅱ)若1t =,求证:当1a ≥-时,()0f x ≥.请考生在第22、23题中任选一题做答,如果多做,则按所做的第一题记分.做答时请写清题号.(22)(本小题满分10分)选修4—4:坐标系与参数方程在直角坐标系xOy ,直线l 的参数方程是+cos ,sin .x m t y t αα=⎧⎨=⎩(t 是参数).在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线C :4cos ρθ=.(Ⅰ)当1m =-,=30α时,判断直线l 与曲线C 的位置关系;(Ⅱ)当1m =时,若直线l 与曲线C 相交于,A B 两点,设(1,0)P ,且1PA PB -=,求直线l 的倾斜角.(23)(本小题满分10分)选修4—5:不等式选讲 已知函数()()212f x x x t t =+--∈R . (Ⅰ)当3t =时,解关于x 的不等式()1f x <; (Ⅱ)x ∃∈R ,使()5f x ≤-,求t 的取值范围.。
2017-2018学年福建省宁德市高二(上)期末数学试卷(文科)(解析版)

2017-2018学年福建省宁德市高二(上)期末数学试卷(文科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)若焦点在x轴的椭圆+=1(a>0)的焦距为2,则a=()A.B.C.D.12.(5分)已知x为实数,则“<1”是“x>2”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.(5分)某学生通过某种数学游戏的概率为,他连续操作2次,则恰有1次通过的概率为()A.B.C.D.4.(5分)若等比数列的前3项为x,x+1,2x+2,则该数列的第4项是()A.2B.4C.8D.165.(5分)执行下面的程序框图,若输入的n是8,则输出的值是()A.12B.37C.86D.1676.(5分)某产品的广告支出x(单位:万元)与销售收入y(单位:万元)之间有如表所对应的数据:已知y对x的回归直线方程是=﹣2,则m的值是()A.15B.16C.17D.187.(5分)已知等差数列{a n}的前n项和为S n,且a4=4,S5=15,则数列{}的前100项和为()A.B.C.D.8.(5分)已知△ABC中,a=2,b=2,B=60°,则△ABC的面积是()A.3B.3C.6D.69.(5分)已知{a n}为等比数列,下面结论中正确的是()A.a22+a42≥2a32B.a3+a5≥2a4C.若a2<a4,则a1<a3D.若a2=a4,则a2=a310.(5分)已知正实数a,b满足a+b=2,则+的最小值是()A.8B.10C.12D.1811.(5分)已知△ABC的三个内角A,B,C的对边分别为a,b,c,角A,B,C的大小依次成等差数列,且b=,若函数f(x)=cx2+2x+a的值域是[0,+∞),则a+c=()A.7B.6C.5D.412.(5分)已知F1,F2分别是双曲线﹣=1(a>0,b>0)的左、右焦点,过点F1与双曲线的一条渐近线平行的直线交双曲线的另一条渐近线于点P,若点P在以线段F1F2为直径的圆内,则双曲线离心率的取值范围是()A.(1,2)B.(1,)C.(,2)D.(2,+∞)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.(5分)若实数x,y满足,则z=2x+y的最大值是.14.(5分)若“∀x∈R,x2+3x+m>0”是假命题,则实数m的取值范围是.15.(5分)△ABC中,D是BC边上的一点,已知BD=﹣,∠B=30°,∠ADC=45°,DC=2,则AC=.16.(5分)将大于1的正整数n拆分成两个正整数的和(如5=2+3),求出这两个正整数的乘积,再将拆分出来的大于1的正整数拆分成两个正整数的和,求出这两个正整数的乘积,如此下去,直到不能再拆分为止,则所有这些乘积的和为.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(8分)命题p:关于x的方程x2﹣ax+a+3=0有实根,命题q:实数a满足不等式|a﹣2|≤5.若¬p∨q为真命题,¬p∧q为假命题,求实数a的取值范围.18.(10分)已知等比数列{a n}的前n项和S n=2n﹣1;(1)求数列{a n}的通项公式;(2)设b=log2a n+1,求数列{a n b n}的前n项和T n.19.(12分)已知抛物线x2=2py(p>0)的焦点为F,准线为l,过抛物线上一点A(x0,3)(x0>0)作准线l的垂线,垂足为H,若|FH|=|F A|;(1)求抛物线的方程;(2)延长AF交抛物线于B,求△AOB的面积(O为坐标原点).20.(12分)已知△ABC的三个内角A,B,C的对边分别为a,b,c ,且+=1;(1)求B;(2)若b =,求a2+c2的取值范围.21.(14分)某中学为了解高二学生对“地方历史”校本课程的喜欢是否与在本地成长有关,在全校高二学生中随机抽取了20名,得到一组不完全的统计数据如表:(Ⅰ)补齐上表数据,并分别从被抽取的喜欢“地方历史”校本课程与不喜欢“地方历史”校本课程的学生中各选1名做进一步访谈,求两名学生均属于在本地成长的概率;(Ⅱ)试回答:能否在犯错误的概率不超过0.10的前提下认为“是否喜欢地方历史校本课程与在本地成长有关”.附:参考公式:x2=,其中n=a+b+c+d22.(14分)已知椭圆Γ:+=1(a>b>0)过点P(﹣1,),离心率e=;(1)求椭圆Γ的方程;(2)过椭圆Γ的左焦点F1作两条互相垂直的直线,分别交椭圆Γ于A,B和C,D,证明+为定值.2017-2018学年福建省宁德市高二(上)期末数学试卷(文科)参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.【解答】解:焦点在x轴的椭圆+=1(a>0)的焦距为2,可得a,所以a2﹣2=1,可得a=.故选:B.2.【解答】解:根据题意,当x<0时,有“<1”,则“x>2”不成立,则“<1”不是“x>2”的充分条件,反之,若“x>2”,则必有“<1”成立,则“<1”是“x>2”的必要条件,则“<1”是“x>2”的必要不充分条件;故选:B.3.【解答】解:某学生通过某种数学游戏的概率为,他连续操作2次,则恰有1次通过的概率为:p==.故选:C.4.【解答】解:x,x+1,2x+2是一个等比数列的前3项,可得(x+1)2=x(2x+2),解得x=﹣1或x=1,当x=﹣1时,x,x+1,2x+2化为:﹣1,0,0,不是等比数列,当x=1时,x,x+1,2x+2化为:1,2,4,是等比数列第四项为:8故选:C.5.【解答】解:根据题意得,运行程序得S=2+12+32+52+72+92=167,故选:D.6.【解答】解:=,=,将(,)代入回归方程得:=×﹣2,解得:m=18,故选:D.7.【解答】解:设等差数列{a n}的公差为d,∵a4=4,S5=15,∴a1+3d=4,5a1+d=15,联立解得a1=d=1,∴S n=n+=.∴=2.数列{}的前n项和=2=.∴数列{}的前100项和=.故选:D.8.【解答】解:设AB=c,在△ABC中,由余弦定理知AC2=AB2+BC2﹣2AB•BC cos B,即28=c2+4﹣2×2×c×cos60°,c2﹣2c﹣24=0,又c>0,∴c=6.S△ABC=AB•BC sin B=×=.故选:B.9.【解答】解:根据题意,依次分析选项:对于A,a22+a42≥2a2a4=2a32,正确;对于B,当a1<0,q<0时,a3、a5为负值,a4为正值,a3+a5≥2a4不成立,错误;对于C,当a1<0,q<﹣1时,有0<a2<a4,但a1<a3<0,错误;对于D,当q=﹣1时,a2=a4,则a2=﹣a3,错误;故选:A.10.【解答】解:由基本不等式可得═,所以,,当且仅当,即当时,等号成立,所以,的最小值为8,故选:A.11.【解答】解:根据题意,△ABC的三个内角A,B,C的大小依次成等差数列,则2B=A+C,又由A+B+C=180°,则有B=60°,函数f(x)=cx2+2x+a的值域是[0,+∞),则有△=4﹣4ac=0,即ac=1,∵b=,∴cos B===,∴a2+c2=14,∴(a+c)2=a2+c2+2ac=16,解得a+c=4.故选:D.12.【解答】解:设F1(﹣c,0),双曲线﹣=1的渐近线方程为y=±x,过点F1与双曲线的一条渐近线平行的直线方程为y=(x+c),联立渐近线方程y=﹣x,可得交点P(﹣c,),点P在以线段F1F2为直径的圆内,可得(﹣c)2+()2<c2,即有<3,可得双曲线的离心率e==<2,但e>1,即1<e<2.故选:A.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.【解答】解:实数x,y满足,作出不等式组对应的平面区域如图:由z=2x+y得y=﹣2x+z,平移直线y=﹣2x+z,则当直线y=﹣2x+z经过点A时,直线的截距最大,此时z最大,由可得A(1,0).此时z=2,故答案为:214.【解答】解:由x2+3x+m>0恒成立,可得32﹣4m<0,即m>.而命题“∀x∈R,x2+3x+m>0”是假命题,∴实数m的取值范围是:(﹣∞,].故答案为:(﹣∞,].15.【解答】解:由∠ADC=45°,那么∠ADB=135°,∵∠B=30°,∴∠DAB=15°在△ABD中,正弦定理,可得,可得AD=2,在△CAD中,余弦定理,可得AC2=AD2+CD2﹣2ADCD cos∠ADC=4+8﹣8×cos45°=4,∴AC=2,故答案为:2.16.【解答】解:记满足条件所有这些乘积的和为S,当n=2时,2=1+1,则y=1,当n=3时,3=2+1,2=1+1,则y=3,当n=4时,4=3+1,3=2+1,2=1+1,则y=6,当n=5时,5=4+1,4=3+1,3=2+1,2=1+1,则y=10,…故S=1+2+3+…+(n﹣1)=,故答案为:.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.【解答】解:命题P:△=(﹣a)2﹣4(a+3)≥0,即a≤﹣2或a≥6;命题q:﹣5≤a﹣2≤5,即﹣3≤a≤7;∵¬p∨q为真,¬p∧q为假,∴¬p和q必然是一真一假,p与q都真或都假,当p与q都真时,∴﹣3≤a≤﹣2或6≤a≤7当p与q都假时,∴a∈∅综上所述:实数a的取值范围是:[﹣3,﹣2]∪[6,7]18.【解答】解:(1)因为等比数列{a n}的前n项和S n=2n﹣1,当n≥2时,a n=S n﹣S n﹣1=(2n﹣1)﹣(2n﹣1﹣1)=2n﹣1,a1=S1=1也满足该式,所以数列{a n}通项公式为a n=2n﹣1,n∈N*;(2)b n=log2a n+1=log22n=n,则a n b n=n•2n﹣1,T n=1•20+2•21+3•22+…+n•2n﹣1,2T n=1•2+2•22+3•23+…+n•2n,两式相减可得﹣T n=1+21+22+…+2n﹣1﹣n•2n=﹣n•2n,化简可得T n=(n﹣1)•2n+1.19.【解答】解:(1)∵|FH|=|F A|,则y A﹣y F=y F﹣y H,又A(x0,3),F(0,),H(x0,﹣),∴3﹣=p,解得:p=2,所以抛物线的方程为x2=4y.(2)由x02=4×3得x0=2,∴A(2,3).从而直线AF的方程为y﹣1=x,代入x2=4y,整理得3y2﹣10y+3=0,∴y A+y B=,由抛物线定义知:|AB|=y A+y B+p==.原点O到直线AB的距离为d==,∴S△OAB=|AB|•d==.20.【解答】解:(1)∵+=1,∴=1,化简得:bc+c2+a2+ab=ab+ac+b2+bc,即a2+c2﹣b2=ac,∴cos B==,又∵B∈(0,π),∴B=.(2)在△ABC中,由余弦定理:b2=a2+c2﹣2ac cos B,∴()2=a2+c2﹣2ac cos B,即2=a2+c2﹣ac,可得:ac=(a2+c2)﹣2,∵ac≤,第11页(共12页)∴(a 2+c 2)﹣2≤,可得:a 2+c 2≤4,(当且仅当a =c 时取等号) 又∵B 为锐角,∴a 2+c 2>b 2=2, ∴a 2+c 2的取值范围是(2,4].21.【解答】解:(Ⅰ)补齐表格如下:…(2分)由上表知,在喜欢“地方历史”校本课程的12名学生中抽取1人,在本地成长的概率为, 在不喜欢“地方历史”校本课程的8名学生中抽取1人,在本地成长的概率为, 设从中抽取的2名学生中至少有1名学生是在本地成长的事件为A , 则…(6分) (Ⅱ)x 2===≈3.3333>2.706,…(10分)∴能在犯错误的概率不超过0.10的前提下认为“是否喜欢‘地方历史’校本课程与本地成长有关”.…(12分)22.【解答】解:(1)依题意:解得a 2=1,b 2=1. 所以椭圆Γ的方程为+y 2=1; 证明:(2)易知F 1(﹣1,0),①当直线AB (或CD )与x 轴重合时,|AB |=2a =2,|CD |== 则+=+=,②当直线AB(或CD)与x轴不重合时,不妨设AB:y=k(x+1),k≠0,则CD:y =﹣(x+1),将y=k(x+1)代入+y2=1整理得:(1+2k2)x2+4k2x+2k2﹣2=0设点A(x1,y1),B(x2,y2),由韦达定理x1+x2=,x1x2=∴|AB|==•=2•,将﹣代换k可得|CD|=2•;∴+=(+)=•=综上①②可知,+为定值.第12页(共12页)。
2017-2018学年福建省宁德市高三(上)期末数学试卷(理科)
2017-2018学年福建省宁德市高三(上)期末数学试卷(理科)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合A={x|x2﹣2x≤3},B={x|2x>1},则A∩B=()A.[0,3]B.(0,3]C.[﹣1,+∞)D.[﹣1,1)2.(5分)已知复数z1对应复平面上的点(﹣1,1),复数z2满足z1z2=﹣2,则|z2+2i|=()A.B.2 C. D.103.(5分)若tan(﹣α)=﹣,则c os2α=()A.B.﹣ C.﹣ D.4.(5分)执行如图所示的程序框图,运行相应的程序,则输出的a的值为()A.10 B.lg99 C.2 D.lg1015.(5分)设x,y满足约束条件,若目标函数z=x﹣2y的最小值大于﹣5,则m的取值范围为()A.B.C.[﹣3,2)D.(﹣∞,2)6.(5分)福建省第十六届运动会将于2018年在宁德召开.组委会预备在会议期间将A,B,C,D,E,F这六名工作人员分配到两个不同的地点参与接待工作.若要求A,B必须在同一组,且每组至少2人,则不同的分配方法有()A.15种B.18种C.20种D.22种7.(5分)一个几何体的三视图如图所示,则它的表面积为()A.B.C.D.8.(5分)已知a=log0.62,b=log20.6,c=0.62,则()A.a>b>c B.b>c>a C.c>b>a D.c>a>b9.(5分)设抛物线y2=2px(p>0)的焦点为F,过F点且倾斜角为的直线l 与抛物线相交于A,B两点,若以AB为直径的圆过点,则该抛物线的方程为()A.y2=2x B.y2=4x C.y2=8x D.y2=16x10.(5分)我国古代数学名著《孙子算经》中有如下问题:“今有三女,长女五日一归,中女四日一归,少女三日一归.问:三女何日相会?”意思是:“一家出嫁的三个女儿中,大女儿每五天回一次娘家,二女儿每四天回一次娘家,小女儿每三天回一次娘家.三个女儿从娘家同一天走后,至少再隔多少天三人再次相会?”假如回娘家当天均回夫家,若当地风俗正月初二都要回娘家,则从正月初三算起的一百天内,有女儿回娘家的天数有()A.58 B.59 C.60 D.6111.(5分)函数f(x)=asinωx+bcosωx(a,b∈R,ω>0),满足,且对任意x∈R,都有,则以下结论正确的是()A.f(x)max=|a|B.f(﹣x)=f(x) C.D.ω=312.(5分)设函数f(x)=ae x﹣1﹣1﹣e x ln(x+1)存在零点x0,且x0>1,则实数a的取值范围是()A.(﹣∞,1+eln2)B.(﹣eln2,+∞)C.(﹣∞,﹣eln2)D.(1+eln2,+∞)二、填空题:本大题共4小题,每小题5分.13.(5分)已知向量,的夹角为60°,||=2,|+2|=2,则||=.14.(5分)若双曲线C的右焦点F关于其中一条渐近线的对称点P落在另一条渐近线上,则双曲线C的离心率e=.15.(5分)若正三棱台ABC﹣A'B'C'的上、下底面边长分别为和,高为1,则该正三棱台的外接球的表面积为.16.(5分)设函数f(x)=|x2﹣2x﹣1|,若a>b≥1,f(a)=f(b),则对任意的实数c,(a﹣c)2+(b+c)2的最小值为.三、解答题:本大题共5小题,满分60分.解答须写出文字说明、证明过程和演算步骤.17.(12分)已知数列{a n}的前n和为S n,若a n>0,.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)若,求数列{b n}的前n项和T n.18.(12分)如图,矩形ABCD中,AB=6,,点F是AC上的动点.现将矩形ABCD沿着对角线AC折成二面角D'﹣AC﹣B,使得.(Ⅰ)求证:当时,D'F⊥BC;(Ⅱ)试求CF的长,使得二面角A﹣D'F﹣B的大小为.19.(12分)如图,岛A、C相距海里.上午9点整有一客轮在岛C的北偏西40°且距岛C10海里的D处,沿直线方向匀速开往岛A,在岛A停留10分钟后前往B市.上午9:30测得客轮位于岛C的北偏西70°且距岛C海里的E 处,此时小张从岛C乘坐速度为V海里/小时的小艇沿直线方向前往A岛换乘客轮去B市.(Ⅰ)若V∈(0,30],问小张能否乘上这班客轮?(Ⅱ)现测得,.已知速度为V海里/小时(V∈(0,30])的小艇每小时的总费用为()元,若小张由岛C直接乘小艇去B 市,则至少需要多少费用?20.(12分)已知椭圆的左、右焦点分别为F1,F2.过且斜率为k的直线l与椭圆C相交于点M,N.当k=0时,四边形MNF1F2恰在以MF1为直径,面积为的圆上.(Ⅰ)求椭圆C的方程;(Ⅱ)若,求直线l的方程.21.(12分)已知函数f(x)=ax2+lnx(a∈R)有最大值,g(x)=x2﹣2x+f(x),且g'(x)是g(x)的导数.(Ⅰ)求a的值;(Ⅱ)证明:当x1<x2,g(x1)+g(x2)+3=0时,.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分.作答时请写清题号.[选修4-4:坐标系与参数方程]22.(10分)在平面直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系.曲线C1的极坐标方程为ρ=4sinθ,M为曲线C1上异于极点的动点,点P在射线OM上,且成等比数列.(Ⅰ)求点P的轨迹C2的直角坐标方程;(Ⅱ)已知A(0,3),B是曲线C2上的一点且横坐标为2,直线AB与C1交于D,E两点,试求||AD|﹣|AE||的值.[选修4-5:不等式选讲]23.已知f(x)=x2+a(a∈R),g(x)=|x+1|+|x﹣2|(Ⅰ)若a=﹣4,求不等式f(x)≥g(x)的解集;(Ⅱ)若x∈[0,3]时,f(x)>g(x)的解集为空集,求a的取值范围.2017-2018学年福建省宁德市高三(上)期末数学试卷(理科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.【解答】解:A={x|x2﹣2x≤3}={x|x2﹣2x﹣3≤0}={x|﹣1≤x≤3},B={x|2x>1}={x|x>0},则A∩B={x|0<x≤3},故选:B.2.【解答】解:由题意可得,z1=﹣1+i,则由z1z2=﹣2,得=1+i,∴|z2+2i|=|1+3i|=.故选:C.3.【解答】解:∵tan(﹣α)==﹣,解得:tanα=2,∴cos2α====﹣.故选:B.4.【解答】解:由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量a=lg(1+1)+lg(1+)+lg(1+)+…+lg(1+)的值,a=lg(1+1)+lg(1+)+lg(1+)+…+lg(1+)=lg2+lg+lg+…+lg=lg2+lg3﹣lg2+lg4﹣lg3+…+lg101﹣lg100=lg101.故选:D.5.【解答】解:x,y满足约束条件的可行域如图:目标函数z=x﹣2y 的最小值大于﹣5,可知目标函数经过可行域A时,截距最大,目标函数取得最小值,解得B(﹣1,﹣3),由可得A(﹣1,m),所以m≥﹣3.并且:﹣1﹣2m>﹣5,解得m<2,所以m的取值范围为:[﹣3,2).故选:C.6.【解答】解:根据题意,分3种情况讨论:①、A,B在一组,C,D,E,F都分在另一组,将两组全排列,对应两个校区即可,有A22=2种分配方法;②、C,D,E,F中取出1人,与A、B一组,剩下3人一组,再将两组全排列,对应两个校区,有C41×A22=8种分配方法;③、C,D,E,F中取出2人,与A、B一组,剩下2人一组,再将两组全排列,对应两个校区,有C42×A22=12种分配方法;故一共有2+8+12=22种分配方法;故选:D.7.【解答】解:由三视图得该几何体是一个半圆锥P﹣ABOD和一个三棱锥P﹣BCD 的组合体,其中半圆的底面半径r=1,高PO=,母线长l=2,三棱锥P﹣BCD中,高PO=,BD⊥BC,PB⊥BC,BC=BD=2=PB=PD=2,DC=PC=2,如图,∴PC=CD==2,∴该几何体的表面积:S=S半圆锥表面积+S△BDC+S△PBC+S△PCD=++=++=.故选:A.8.【解答】解:a=log0.62=﹣1,又ab=×=1.∴b=log20.6∈(﹣1,0),c=0.62>0,则c>b>a.故选:C.9.【解答】解:抛物线y2=2px(p>0)的焦点为F,过F点且倾斜角为的直线l 与抛物线相交于A,B两点,以AB为直径的圆与抛物线的准线相切,以AB为直径的圆过点,可知AB的中的纵坐标为:2,直线l的方程为:y=x﹣,则,可得y2﹣2py﹣p2=0,则AB中的纵坐标为:=2,解得p=2,该抛物线的方程为:y2=4x.故选:B.10.【解答】解:大女儿每五天回一次娘家,二女儿每四天回一次娘家,小女儿每三天回一次娘家,当地风俗正月初二都要回娘家,则从正月初三算起的一百天内,小女儿、二女儿和大女儿回娘家的天数分别是33,25,20,小女儿和二女儿、小女儿和大女儿、二女儿和大女儿同时回娘家的天数分别为8,6,5,三个女儿同时回娘家的天数是1,从正月初三算起的一百天内,有女儿回娘家的天数有:33+25+20﹣(8+6+5)+1=60.故选:C.11.【解答】解:函数f(x)满足,∴f(x)关于点(﹣,0)对称,且对任意x∈R,都有,∴x=﹣是f(x)的对称轴,利用﹣f(0)=asin0+bcos0=b=f(﹣)=0,∴b=0,f(x)=asinωx,A正确;∴f(x)是定义域R上的奇函数,B错误;可得a≠0,b=0,a≠b,C错误;由题意,ω=6k+3,k∈Z,∴D错误;综上,正确的结论是A.故选:A.12.【解答】解:函数f(x)=ae x﹣1﹣1﹣e x ln(x+1),令f(x)=0,可得a=e1﹣x+eln(x+1),设g(x)=e1﹣x+eln(x+1),x>1,则g′(x)=﹣e1﹣x+=e•,由y=e x﹣x﹣1的导数为y′=e x﹣1,当x>1时,e x﹣1>e﹣1>0,则函数y=e x﹣x﹣1递增,可得y=e x﹣x﹣1>0,则g(x)在(1,+∞)递增,可得g(x)>g(1)=1+eln2,则a>1+eln2,故选:D.二、填空题:本大题共4小题,每小题5分.13.【解答】解:根据题意,设||=t,若向量,的夹角为60°,则•=2tcos60°=t,又由|+2|=2,则有(+2)2=2+4•+42=4+4t+4t2=28,即t2+t﹣6=0,解可得t=2或t=﹣3(舍);故t=2,即||=2;故答案为:214.【解答】解:双曲线C:﹣=1的左焦点为F(﹣c,0),渐近线方程为y=±x,设F关于y=x的对称点为(m,﹣m),由题意可得=﹣,(*)且(0﹣m)=•(m﹣c),可得m=c,代入(*)可得b2=3a2,c2=a2+b2=4a2,则离心率e==2.故答案为:2.15.【解答】解:∵正三棱台ABC﹣A'B'C'的上、下底面边长分别为和,高为1,取△A1B1C1的重心E1,取△ABC的重心E,则EE1=1是正三棱台ABC﹣A'B'C'的高,AE==2,A1E1==1,则球心O在E1E的延长线上,半径R=OA=OA1,即=,解得OE=1,∴R==,∴该正三棱台的外接球的表面积S=4πR2=4π×5=20π.故答案为:20π.16.【解答】解:根据题意,函数f(x)=|x2﹣2x﹣1|=,其图象如图:(a﹣c)2+(b+c)2=(a2﹣2ac+c2)+(c2+2bc+c2)=2c2+2(b﹣a)c+(a2+b2),c为任意的实数,令t=2c2+2(b﹣a)c+(a2+b2),看成是以c为自变量的二次函数,其最小值为t()=2()2﹣2(a﹣b)()+(a2+b2)=,分析可得:a+b≥2(+1),则有t的最小值为=6+4;故答案为:6+4.三、解答题:本大题共5小题,满分60分.解答须写出文字说明、证明过程和演算步骤.17.【解答】解法一:(Ⅰ)∵,∴.…(1分)当n=1时,,得a1=1.…(2分)当n≥2时,,∴,…(3分)∴,即(a n+a n﹣1)(a n﹣a n﹣1)=2(a n+a n﹣1),∵a n>0,∴a n﹣a n﹣1=2.…(4分)∴数列{a n}是等差数列,且首项为a1=1,公差为2,…(5分)∴a n=1+2(n﹣1)=2n﹣1.…(6分)(Ⅱ)由(Ⅰ)可知,,∴,﹣﹣①…(7分),﹣﹣②…(8分)①﹣②得…(9分)=,…(10分)化简得.…(12分)解法二:(Ⅰ)同解法一.(Ⅱ)由(Ⅰ)可知,,设,∴解得,∴,…(9分)∴T n=b1+b2+…+b n==.…(12分)18.【解答】满分(12分).(Ⅰ)证明:连结DF,BF.在矩形ABCD中,,∴,∠DAC=60°.…(1分)在△ADF中,∵,∴DF2=DA2+AF2﹣2DA•AF•cos∠DAC=9,.…(2分)∵DF2+AF2=9+3=DA2,∴DF⊥AC,即D'F⊥AC.…(3分)又在△ABF中,BF2=AB2+AF2﹣2AB•AF•cos∠CAB=21,…(4分)∴在△D'FB中,,∴BF⊥D'F,…(5分)又∵AC∩FB=F,∴D'F⊥平面ABC.∴D'F⊥BC.…(6分)(Ⅱ)解:在矩形ABCD中,过D作DE⊥AC于O,并延长交AB于E.沿着对角线AC翻折后,由(Ⅰ)可知,OE,OC,OD'两两垂直,以O为原点,的方向为x轴的正方向建立空间直角坐标系O﹣xyz,则O(0,0,0),E(1,0,0),, (7))k AB=﹣1平面AD'F,∴为平面AD'F的一个法向量.…(8分)设平面BD'F的法向量为=(x,y,z),∵F(0,t,0),∴,由得取y=3,则,∴.…(10分)∴,即,∴.∴当时,二面角A﹣D'F﹣B的大小是.…(12分)19.【解答】满分(12分).解:(Ⅰ)如图,根据题意得:CD=10,,,∠DCE=70°﹣400=300.在△CDE中,由余弦定理得,==10,…(2分)所以客轮的航行速度V1=10×2=20(海里/小时).…(3分)因为CD=DE,所以∠DEC=∠DCE=30°,所以∠AEC=180°﹣300=1500.在△ACE中,由余弦定理得,AC2=AE2+CE2﹣2AE•CE•cos∠AEC,整理得:AE2+30AE﹣400=0,解得AE=10或AE=﹣40(不合舍去).…(5分)所以客轮从E处到岛A所用的时间小时,小张到岛A所用的时间至少为小时.由于,所以若小张9点半出发,则无法乘上这班客轮…(6分)(Ⅱ)在△ABC中,,,所以∠ACB为锐角,,.…(7分)所以sinB=sin[1800﹣(∠BAC+∠ACB)]=sin(∠BAC+∠ACB)=sin∠BACcos∠ACB+cos∠BACsin∠ACB==.…(8分)由正弦定理得,,所以,…(9分)所以小张由岛C直接乘小艇去城市B的总费用为(V∈(0,30]),…(10分)当且仅当,即V=10时,(元)…(11分)所以若小张由岛C直接乘小艇去B市,其费用至少需元.…(12分).20.【解答】满分(12分).解:(Ⅰ)当k=0时,直线l∥x轴,又四边形MNF1F2恰在以MF1为直径,面积为的圆上,∴四边形MNF1F2为矩形,且.…(1分)∴点M的坐标为.…(2分)又,∴.…(3分)设,则c=k.在Rt△MF1F2中,,|F1F2|=2k,∴,∴k=1.∴,…(5分)∴椭圆C的方程为.…(6分)(Ⅱ)将与椭圆方程联立得(3+4k2)x2+12kx﹣3=0,设M(x1,y1),N(x2,y2),得,.…(7分)故=.…(9分)又,…(10分)∴,即,解得,∴直线l的方程为.…(12分)21.【解答】解:(Ⅰ)f(x)的定义域为(0,+∞),.…(1分)当a≥0时,f'(x)>0,f(x)在(0,∞)上为单调递增函数,无最大值,不合题意,舍去;…(2分)当a<0时,令f'(x)=0,得,当时,f'(x)>0,函数f(x)单调递增;当时,f'(x)<0,函数f(x)单调递减,…(3分)∴,∴,…(4分)∴.…(5分)(Ⅱ)由(Ⅰ)可知,,∴.∵,∴g'(x)≥0,∴g(x)在(0,+∞)上单调递增.…(6分)又∵x1<x2,g(x1)+g(x2)=﹣3且,∴0<x1<1<x2.…(7分)∵,∴当x>1时,g''(x)>0,g'(x)单调递增,要证,即g'(x1+x2)>g'(2),只要证x1+x2>2,即x2>2﹣x1.…(8分)∵x1<1,∴2﹣x1>1,所以只要证g(2﹣x1)<g(x2)=﹣3﹣g(x1)⇔g(x1)+g(2﹣x1)<﹣3﹣﹣﹣﹣(*),…(9分)设G(x)=g(x)+g(2﹣x)=x2﹣2x﹣2+lnx+ln(2﹣x)(其中0<x<1),∴==,∴G(x)在(0,1)上为增函数,…(11分)∴G(x)<G(1)=﹣3,故(*)式成立,从而.…(12分)请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分.作答时请写清题号.[选修4-4:坐标系与参数方程]22.【解答】解:(1)设P(ρ,θ),M(ρ1,θ),则由成等比数列,可得|OP|•|OM|=20,…(1分)即ρ•ρ1=20,.…(2分)又M(ρ1,θ)满足ρ1=4sinθ,即,…(3分)∴ρsinθ=5,…(4分)化为直角坐标方程为y=5.∴点P的轨迹C2的直角坐标方程为y=5.…(5分)(Ⅱ)依题意可得B(2,5),故k AB=1,即直线AB倾斜角为,…(6分)∴直线AB的参数方程为…(7分)代入圆的直角坐标方程x2+(y﹣2)2=4,得,…(8分)故,t1t2=﹣3<0,…(9分)∴.…(10分)[选修4-5:不等式选讲]23.【解答】解:(Ⅰ)当a=﹣4时,f(x)≥g(x)化为x2﹣4≥|x+1|+|x﹣2|,…(1分)当x≤﹣1,不等式化为x2+2x﹣5≥0,解得或,故;…(2分)当﹣1<x<2时,不等式化为x2≥7,解得或,故x∈∅;…(3分)当x≥2,不等式化为x2﹣2x﹣3≥0,解得x≤﹣1或x≥3故x≥3;…(4分)所以f(x)≤x解集为或x≥3}.…(5分)(Ⅱ)由题意可知,即为x∈[0,3]时,f(x)≤g(x)恒成立.…(6分)当0≤x≤2时,x2+a≤3,得a≤(3﹣x2)min=﹣1;…(8分)当2≤x≤3时,x2+a≤2x﹣1,得a≤(﹣x2+2x﹣1)min=﹣4,综上,a≤﹣4.…(10分)。
福建省宁德市2017-2018学年度第二学期期末高二质量检测有答案
宁德市2017-2018学年度第二学期期末高二质量检测生物试题(考试时间:90分钟满分:100分)第Ⅰ卷选择题本卷共35题,1-20每题1分,21-35每题2分,共50分,每小题只有一个选项符合题意。
1. 下列关于DNA分子复制的叙述,正确的是A. 复制发生在细胞分裂前期B. 复制特点是边解旋边复制C. 复制只以其中的一条链为模板D. 一次复制后产生四个DNA分子2. 下列属于单倍体的是A. 二倍体种子长成的幼苗B. 四倍体水稻的杂交后代C. 六倍体小麦花粉离体培养的幼苗D. 蛙受精卵发育成的蝌蚪3. 基因工程中拼接基因的工具是A. DNA连接酶B. DNA酶C. 限制酶D. DNA聚合酶4. 下图表示细胞核中进行的一项生理过程,下列说法正确的是A. 该过程共涉及5种核苷酸B. 该过程需要DNA聚合酶C. 该过程遵循碱基互补配对原则D. 不同组织细胞中该过程的产物相同5. 下列关于变异的叙述正确的是A. 基因重组是生物变异的根本来源B. 可遗传变异可以为生物进化提供原材料C. 染色体易位不改变基因数量,对个体性状不会产生影响D. 基因突变一定会引起基因结构的改变,也一定会引起生物性状的改变6. 下图表示细胞中蛋白质合成的部分过程,相关叙述正确的是A.过程a主要在细胞核中进行B.图示过程没有遗传信息的传递C.甲、乙中均含有起始密码子D.组成甲、乙的基本单位是脱氧核苷酸7. 生产上培育无子西瓜、青霉素高产菌株、杂交培育矮杆抗锈病水稻的原理依次是①基因突变②基因重组③染色体变异A. ③①②B. ③②①C.②①③D. ①②③8. 下列关于实验或调查活动中调查方法的叙述不正确...的是 A. 用样方法调查草地上蒲公英的种群密度B. 用标志重捕法调查土壤中蚯蚓的种群密度C. 用取样器取样法探究土壤中小动物类群丰富度D. 用抽样检测法计数培养液中酵母菌的种群数量9. 下列与免疫有关的叙述不正确...的是 A .唾液中的溶菌酶可杀死病原体B .吞噬细胞的保卫作用属于特异性免疫C .免疫系统具有防卫、监控和清除的功能D .B 细胞对病原菌的免疫应答属于体液免疫10.下图是甲状腺激素分泌活动的调节示意图。
福建省宁德市2017-2018学年高二上学期期末考试数学(理)Word版含答案
宁德市 2017-2018 学年度第一学期期末高二质量检测数学(理科)试题第Ⅰ卷(共 60 分)一、选择题:本大题共12 个小题 , 每题 5 分, 共 60 分.在每题给出的四个选项中,只有一项为哪一项切合题目要求的.1.已知命题p : x R, x0 ,那么命题p 为()A.x R, x0D.x R , x0B.x R , x0C.x R , x02.已知ABC 中, a 6 , b 4 , A60,则 cos B()A.32C.6D.3 3B.3233a, b,c R,且 a b ,则().已知A.ac bc B. b b1C.a a1x5y211D.a3b3 a b4x, y 知足x y4,则z x 2 y的最大值是().若实数y1A. -9B. 3C. 5D. 6uur r uuur r uuur r uuur uur 5.空间四边形OABC中,OA a , OB b , OC c ,点M在OA上,且OM1OA,uuur2N 为 BC 的中点,则MN()A.1r1r1rB.1r1r1ra b c a b c 222222C.1r1r1rD.1r1r1r a b c a b c 2222226.命题x R , ax2ax 1 0为假命题,则实数 a 的取值范围为()A.4 a 0B. 4 a 0C. 4 a 0D. a4 或 a 07.ABC 中,已知a b c,则ABC 为()sin A cos B cosCA.等边三角形B.等腰直角三角形C.有一个内角为30°的直角三角形D.有一个内角为30°的等腰三角形8.以椭圆x2y21的焦点为极点,同时以椭圆的极点为焦点的双曲线方程是()4A. x2y 21B. x2y 21C. x2y21D. x2y 21 434339.如图,正方体ABCD ABC D 中,下边结论错误的选项是()1111A.BD∥平面CB1D1B.异面直线 AD 与CB1所成的角为45°C.AC1平面 CB1D1D. AC1与平面ABCD所成的角为30°10.在等差数列a n,b n a11a37a n n S n S n,中,,,的前项和为,若b c 0ncn则 c ()A.1B.1C.3D.-3 3311.已知ABC 的三个内角A, B, C 的对边分别为 a,b,c ,角 A, B,C 的大小挨次成等差数列,且 b13 ,若函数 f x cx2 2 x a 的值域是0,,则a c()A. 4B. 5C.6D.712.过双曲线x2y2 1 a0, b0的右焦点 F作平行于一条渐近线的直线与另一条渐近a2b2线交于点 P ,若点 P 在圆心为2c,0,半径为5a的圆内,则该双曲线离心率的取值范围是()A.1, 2B.1,5C.2,D.5,第Ⅱ卷(共 90 分)二、填空题(每题 5 分,满分 20 分,将答案填在答题纸上)13.已知椭圆C :x2y21,F1, F2分别为椭圆的两焦点,点 P 椭圆在椭圆上,且PF2 3 ,1612则 PF1 F2的面积为.14.若数列a n的通项公式为 a n1,则其前 n 项和S n.2n n115.若m1,n0 , m n 3 ,则21的最小值为.m 1n16.将大于 1 的正整数n拆分红两个正整数的和(如 5 2 3 ),求出这两个正整数的乘积,再将拆分出来的大于 1 的正整数拆分红两个正整数的和,求出这两个正整数的乘积,这样下去,直到不可以再拆分为止,则全部这些乘积的和为.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知等比数列a n的各项均为正数, 2a1 5a23 ,a3a79a42;( 1)求数列a n的通项公式;( 2)设b n a n log3 a n,求数列b n的前 n 项和 S n.18.设命题p:实数x知足12x8 ,命题q:实数x知足x23ax2a20 a 0 ;41,p q 为真命题时,务实数x的取值范围;()当 a 2( 2)若p的必需不充足条件是q ,务实数a的取值范围 .19.在平面直角坐标系xOy中,动点P x, y(此中 y 0)到定点 M0,1 的距离比到 x 轴的距离大 1.( 1)求动点P的轨迹C的方程;( 2)若直线l : y kx 1 与曲线 C 订交于 A, B 两点,点 N 在直线 y1上,BN 垂直于x轴,证明直线 AN 过坐标原点 O .20.已知直角梯形ABCD,如图( 1)所示,AB∥CD,AB BC ,AB BC2,CD 4,连结 AC ,将ABC 沿 AC 折起,使得平面ABC平面 ACD ,获得几何体 B ACD ,如图( 2)所示 .( 1)求证:AD平面 ABC ;uur1 uuurAC D的大小.( 2)若BE BD ,求二面角 E321.已知O, A, B分别是海岸线l1 ,l 2上的三个集镇, A 位于O的正南方向10km处, B 位于O 的北偏东60°方向10km处;( 1)为了缓解集镇O的交通压力,拟在海岸线l1 , l2上分别修筑码头M , N,开拓水上直抵航线,使 ON8km ,OM4km .勘察时发现以 O 为圆心, 3km 为半径的扇形地区为浅水区,不适合船只航行,问此航线能否影响船只航行?( 2)为了发展经济需要,政府计划填海造陆,建筑一个商业区(如图四边形OACB 所示),此中 OAC45 ,AOC,30,60 ,求该商业区的面积S 的取值范围.22.已知椭圆 E 的中心在原点,焦点在y 轴上离心率e 2,且经过点P 1, 2;2( 1)求椭圆E的方程;( 2)过椭圆E的焦点F作两条相互垂直的直线,分别交椭圆 E 于A, B和C , D,求AB CD 的最小值.数学(理科)试题(参照答案与评分标准)一、选择题1-5:ACDCB6-10:CBCDB11、 12:AA二、填空题13. 614.n15.3216n n 1.2n222三、解答题17.解:( 1)设数列a n的公比 q q0 ,由 2a1 5a2 3 ,a3a79a422a1q 5a13得,a12q89a12 q6a13∴,q 3∴a n 3n , n N( 2)b n a n log 3 a n n 3n∴S n13232 3 33L n 1 3n 1n 3n∴3S n 1 32 2 33L n 13n n 3n 1相减得233233L3n n3n13 13nn 3n113∴ S n2n 1 3n 134418.解:( 1)命题 p :实数 x 知足12x8 ,得实数 x 知足 2 x 34当 a 2 时,命题 q :实数 x 知足 x 2 6x8 0 ,∴ x2 或 x4 ,因为 pq 为真命题,∴ x 3 或 x 4( 2)因为 p 的必需不充足条件是 q ,∴ pq 且 q p又∵ x 2 3ax2a 20 ∴ x a x 2a当 a0 时,命题 q :实数 x 知足 x 2a 或 xaa 0a 0 3∴或a ∴ a2a23当 a0 时,命题 q :实数 x 知足 x a 或 x 2aa 0a 0 ∴ a2∴或a2a 32综上所述: a2 或 a 319.解:( 1)动点 P x, y (此中 y 0 )到 x 轴的距离为 y ,到 x 轴的距离为 y 1∴ PM y 1,又M 0,1 ,∴ x2y 1 2y1得轨迹 C 的方程: x 24 y(2)设A x 1 , y 1, Bx 2 , y 2,由x 2 4 y得 x 24kx 4 0y kx 1∴ x 1 x 2 4k , x 1 x 24 ,①点 N 在直线 y 1上, BNx轴,∴ N x 2 , 1又 A 在抛物线 x24y 上,∴ Ax ,x 1214x 12 x 11 ∴ AO 斜率 k 14, NO 的斜率 k 2x 14 ,x 2x 11 ,∴直线 AN 过原点 O .由①k 1k 2 4x 220.( 1)证明:如图( 1),过 A 作 AM CD 交 CD 于 M ,得正方形 ABCM ,∴ AB BC CMMA 2∴ MD 2∴ACAB 2 BC 22 2,ADAM 2 MD 22 2∴ AC 2 AD 2 CD 2 ∴ ADAC如图( 2),∵平面 ABC 平面 ACD ,且两面交线为 AC ,AD平面 ACD∴ AD 平面 ABC( 2)解:取 AC 中点 O ,连结 BO 、 MO ,则 BO 平面 ACD∵ M 、 O 分别为 CD 、AC 中点 ∴MO ∥AD∴ MOAC以 O 为原点, OC 、 OM 、 OB 所在的直线为 x 轴、 y 轴、 z 轴,成立如图坐标系 O xyz ,A2,0,0 , B 0,0, 2 , C2,0,0 , D2,2 2,0uur1 uuur∵ BEBD31∴ a, b, c22, 22,23∴ a2,b2, c 2 233 3∴ E2 , 2,2 2333uuur22,22,22uuur∴AE, AC 2 2,0,0333urx, y, z为平面 EAC 的一个法向量,则设 mur uuur2 2 x 2 2 y 2 2 z 0m AEur uuur33322x0m AC取 y1,则 x0, z1ur0,1,1∴ mr0,0,1为平面 ACD 的一个法向量又 nur r ur rm n2∴ cos m, n ur r2m n∵二面角 E AC D 为锐角∴二面角 E AC D 为45°.21.解:( 1)由已知,得MON 120 , OM 4 , ON8由余弦定理,得MN 2OM 2ON 22OM ON cos MON112∴MN 47设 OMN 的边 MN 上的高为 h ,则1MN h1OM ON sin MON22421∴h37∴此航线会影响船只航线.( 2)由已知,得 BOC 120在 OAC 中,∵OCOA,sin OAC sinOCA即OC sin 10sin 45 45∴ OC5 2sin 45∴ S1OA OC sinAOC1OBOCsin BOC221 105 2sin110 5 222 sin 120sin 45sin 4575sin25 3 cossincos75tan 25 375 75 25 3tan 1tan 1 ∵ S 在30 ,60 单一递加,且S3075375, S 60150 50 3∴ S753 75,150 50 322.解:( 1)依题意,设椭圆方程为y 2 x 2 1 a b 0,则a2b2由 e2 ,得 a2c , b c2将点P1,2 代入得 b 2c 2 2 , a 24∴椭圆 E 的方程为y 2x 2 1.42( 2)得椭圆 E 的上焦点 F 0, 2 ,当弦 AB 垂直或平行x 轴时, ABCD 4 2 6当弦 AB 不垂直或平行x 轴时,设 AB 方程y kx2,则 CD 方程 y 1 x 2 ,ky 2x21得 k 2 2 x2设A x1 , y1, B x2 , y2,由42 2 2kx 2 0y kx2∴x1x222k, x1x22,①k2k 222AB 1 k 2x124x1 x2 x28k 284 k21k 21k 2 2 2 2k 2k 222同理, CD 4 k 21 12k2得11k 222k 213AB CD 4 k 2 1 4 k 2 14∴AB CD11224 AB CD16∴AB CD,3当且仅当 k 1 时取等号,∴AB CD 最小值16. 3。
2016-2017学年福建省高二上学期期末考试数学(理)试题Word版含答案
2016-2017学年福建省高二上学期期末考试数学(理)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.为了解1000名学生的学习情况,采用系统抽样的方法,从中抽取容量为40的样本,则分段的间隔为( ) A .50 B .40 C .25 D .202.已知随机变量ξ服从正态分布()20,N σ,若()30.023P ξ>=,则()33P ξ-≤≤=( ) A .0.954 B .0.023 C .0.977 D .0.0463.执行如图所示的程序框图,如果输入的[]2,2t ∈-,则输出的S 属于( )A .[]62--,B .[]51--,C .[]4,5-D .[]3,6- 4.如图所示的程序表示的算法是( )A .交换m 与n 的位置B .辗转相除法C .更相减损术D .秦九韶算法 5.已知随机变量,X Y 满足8X Y +=,若()10,0.6X B ~,则()(),E Y D Y 分别是( ) A .6和2.4 B .2和2.4 C .2和5.6 D .6和5.66.通过随机询问110名性别不同的大学生是否爱好某处运动,得到如下的列联表:由卡方公式算得:27.8K ≈ 附表:参照附表:得到的正确的结论是( )A .在犯错的概率不超过0.1%的前提下,认为“爱好该运动与性别无关”B .在犯错的概率不超过0.1%的前提下,认为“爱好该运动与性别有关”C .有99%以上的把握认为“爱好该运动与性别有关”D .有99%以上的把握认为“爱好该运动与性别无关”7.已知点(),P x y 是直线()400kx y k ++=>上的一动点,,PA PB 是圆22:20C x y y +-=的两条切线(C 为圆心),,A B 是切点,若四边形PACB 的面积的最小值是2,则k 的值为( )A .3B ..2 8.设某大学的女生体重y (单位:kg )与身高x (单位:cm )具有线性相关关系,根据一组样本数据()(),1,2,,i i x y i n = ,用最小二乘法建立的回归方程为0.8585.71y x =-,则下列结论中不正确的是( )A .y 与x 具有正的线性相关关系B .回归直线过样本点的中心(),x yC .若该大学某女生身高增加1cm ,则其体重约增加0.85kgD .若该大学某女生身高增加170cm ,则可断定其体重必为58.79kg9.已知圆2221:24C x y mx m +-+=,圆()2222:2283C x y x my m m ++-=->,则两圆的位置关系是( ) A .相交 B .内切 C .外切 D .外离10.有4位同学在同一天的上午、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学测试两个项目,分别在上午和下午,且每人上午和下午测试的项目不能相同.若上午不测“握力”,下午不测“台阶”,其余项目上午、下午都各测试一人,则不同的安排方式的种数为( )A .264B .72C .266D .274 11.若()()2013201301201312x a a x a x x R -=+++∈ ,则201312232014222a a a +++值为( ) A .1 B .0 C .12- D .1-12.在平面直角坐标系xOy 中,点()0,3A ,直线:24l y x =-,设圆C 的半径为1,圆心在l 上,若圆C 上存在点M ,使2MA MO =,则圆心C 的横坐标的取值范围为( ) A .120,5⎡⎤⎢⎥⎣⎦ B .[]0,1 C .121,5⎡⎤⎢⎥⎣⎦ D .120,5⎛⎫ ⎪⎝⎭第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.如图是某学校一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的方差为 .14.一个盒子中装有4只产品,其中3只是一等品,1只是二等品,从中取产品两次,每次任取1只,做不放回抽样.设事件A 为“第一次取到的是一等品”,事件B 是“第二次取到的是一等品”,则()/P B A .(()/P B A 为A 在发生的条件下B 发生的概率)15.若,x y 满足约束条件11y xx y y ≤⎧⎪+≤⎨⎪>-⎩,则1y z x =+的范围是 .16.已知函数()()y f x x I =∈,对函数()()y g x x I =∈,定义()g x 关于()f x 的“对称函数”为函数(),y h x x I =∈.即(),y h x x I =∈满足对任意x I ∈,两点()()()(),,,x h x x g x 关于点()(),x f x 对称.若()h x 是()g x =()3f x x m =+的对称函数,且()()h x g x >恒成立,则实数m 的取值范围是 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. (本小题满分12分)(1)设集合{}1,2,3M =和{}1,1,2,3,4,5N =-,从集合M 中随机取一个数作为a ,从N 中随机取一个数作为b .求所取的两数中能使2b a ≤时的概率;(2)设点(),a b 是区域6000x y x y +-≤⎧⎪>⎨⎪>⎩内的随机点,求能使2b a ≤时的概率.18. (本小题满分12分)已知圆22:4230C x y x y +-+-=和圆外一点()4,8M -.(1)过M 作圆C 的切线,切点为,D E ,圆心为C ,求切线长及DE 所在的直线方程; (2)过M 作圆的割线交圆于,A B 两点,若4AB =,求直线AB 的方程.19. (本小题满分12分)某校100位学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[)[)[)[)[]50,6060,7070,8080,9090,100、、、、.(1)求图中a 的值;(2)根据频率分布直方图,估计这100名学生语文成绩的中位数;(3)若这100名学生的语文成绩某些分数段的人数x 与数学成绩相应分数段的人数y 之比如下表所示,求数学成绩在[)50,90之外的人数.(分数可以不为整数)20. (本小题满分12分)设平面直角坐标系xOy 中,设二次函数()()2f x x x b x R =++∈的图象与两坐标轴有三个交点,经过这三个交点的圆记为C .求: (1)求实数b 的取值范围;(2)求圆C 的方程(用含b 的方程表示)(3)问圆C 是否经过某定点(其坐标与b 无关)?请证明你的结论.21. (本小题满分12分)某中学高二年级共有8个班,现从高二年级选10名同学组成社区服务小组,其中高二(1)班选取3名同学,其它各班各选取1名同学.现从这10名同学中随机选取3名同学到社区老年中心参加“尊老爱老”活动(每位同学被选到的可能性相同). (1)求选出的3名同学来自不同班级的概率;(2)设X 为选出的同学来自高二(1)班的人数,求随机变量X 的分布列和数学期望.22. (本小题满分10分)一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同.随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为,,a b c . (1)求“抽取的卡片上的数字满足a b c +=”的概率; (2)求“抽取的卡片上的数字,,a b c 不完全相同”的概率.2016-2017学年福建省高二上学期期末考试数学(理)试题答案一、选择题1-5: CADBB 6-10:CDDDA 11、12:CA 二、填空题 13.534 14. 32 15. 1(,]3-∞ 16. 102>m 三、解答题17. 解(1)∵2b≤a,若a=1则b=-1, 若a=2则b=-1,1,若a=3则b=-1,1,记事件A 为“所取的两数中能使2b ≤a ”,则事件A 包含基本事件的个数是1+2+2=5 ∴所求事件A 的概率为P(A)= 518(2)依题设条件可知试验的全部结果所构成的区域为⎩⎪⎨⎪⎧a+b-6≤0a >0b >0 ,而构成所求事件的区域为三角形AOB 部分,如图所示.由⎩⎪⎨⎪⎧a+b-6=0b= a 2解得交点为B(4,2).∴所求事件的概率为P=S △AOB S △AOC = 12 ×6×212 ×6×6 = 1318.解(1)圆方程22(2)(1)8x y -++=,||CM ==由于,,,C D M E 四点共圆,则过,,,C D M E 的圆方程为22953(3)()24x y -++=由于DE 为两圆的公共弦,则两圆相减得DE 直线方程为:27190x y --=. (如用圆的切线方程求出的相应给分)(2)①若割线斜率存在,设:8(4)AB y k x +=-,即480kx y k ---=. 设AB 的中点中点为N ,则||CN =||CN ⇒=由222||||()2AB CN r +=,得4528k =-;直线:4528440AB x y ++=. ②若割线斜率不存在,:4AB x =.代入圆方程得2122301,3y y y y +-=⇒==-,符合题意. 综上直线:4528440AB x y ++=或4x =.19、解:(1)由概率和为1可得:005.01204.03.02.0=⇒=+++a a(2)区间]70,50的概率和为45.04.005.0=+,则区间]80,70[中还需拿出概率05.0的区域才到达概率为5.0,即区间]80,70[要拿出61的区域,故中位数为3271106170=⨯+.(3)根据上表知:)90,50[外的人数为:10)2540205(100=+++- 20、解:(Ⅰ)令x =0,得二次函数图象与y 轴交点是(0,b );因为二次函数二次项系数为1,由二次函数性质得二次函数()()2f x x x b x R =++∈的图象必与x 轴有两个交点.令()20f x x x b =++=,由题意b ≠0 且Δ>0,解得14b <且b ≠0. (Ⅱ)设所求圆的一般方程为2x 20y Dx Ey F ++++=令y =0 得20x Dx F ++=这与20x x b ++= 是同一个方程,故D =1,F =b . 令x =0 得20y Ey b ++=,此方程有一个根为b 且b ≠0,代入得出E =―b ―1. 所以圆C 的方程为22(1)0x y x b y b ++-++=.(Ⅲ)圆C :22(1)0x y x b y b ++-++=方程化为22(1)0x y x y b y ++---= 则圆C 必过定点(0,1)和(-1,1).证明如下:将(0,1)代入圆C 的方程,得左边=02+12+0-(b +1)+b =0,右边=0, 所以圆C 必过定点(0,1).同理可证圆C 必过定点(-1,1).21.解:(1)三名学生均不来自高二(1)班的概率为24712035310371===C C p 三名学生有1名来自高二(1)班的概率为40211206331027132==⨯=C C C p 三名学生来自不同班级的概率为60494021247=+=p (2)0=X 时,2471203531037===C C p ,1=X 时,4021120633101327==⨯=C C C p 2=X 时,407120213102317==⨯=C C C p ,3=X 时,120131033==C C p . X 的分布列如下表:9.0101203402401240)(==⨯+⨯+⨯+⨯=x E22.解:(1)由题意,随机有放回的抽取3次,基本事情(1,1,1),(1,1,2),(1,1,3),(1,2,1),(1,2,2),(1,2,3),(1,3,1),(1,3,2),(1,3,3)……(3,3,3)共有27个 又c b a =+包含三个基本事件:(1,1,2),(1,2,3),2,1,3)源:Z+xx+] 对应的概率31279p ==. (2)“c b a ,,不完全相同”的对立事件是“c b a ,,完全相同”, “c b a ,,完全相同”包含三个基本事件:“3,2,1=========c b a c b a c b a ” 所以381279p =-=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宁德市2017-2018学年度第一学期期末高二质量检测数学(理科)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知命题:,0p x x ∀∈≥R ,那么命题p ⌝为( )A .,0x x ∃∈<RB .,0x x ∀∈<RC .,0x x ∃∈≤RD .,0x x ∀∈≤R2.已知ABC ∆中,6a =,4b =,60A =︒,则cos B =( ) A.23 C3.已知,,a b c ∈R ,且a b >,则( ) A .ac bc > B .11b b a a +>+ C .11a b< D .33a b > 4.若实数,x y 满足5241x y x y y -≥-⎧⎪+≤⎨⎪≥-⎩,则2z x y =+的最大值是( )A .-9B .3C .5D .65.空间四边形OABC 中,OA a =uu r r ,OB b =uu u r r ,OC c =u u u r r,点M 在OA 上,且12OM OA =uuu r uu r ,N 为BC 的中点,则MN =uuu r( )A .111222a b c ++r r rB .111222a b c -++r r rC .111222a b c --+r r rD .111222a b c +-r r r6.命题2,10x ax ax ∃∈+-≥R 为假命题,则实数a 的取值范围为( )A .40a -<<B .40a -≤≤C .40a -<≤D .4a <-或0a > 7.ABC ∆中,已知sin cos cos a b cA B C==,则ABC ∆为( ) A .等边三角形 B .等腰直角三角形C .有一个内角为30°的直角三角形D .有一个内角为30°的等腰三角形8.以椭圆2214x y +=的焦点为顶点,同时以椭圆的顶点为焦点的双曲线方程是( ) A .2214x y -= B .22134x y -= C .2213x y -= D .2213y x -= 9.如图,正方体1111ABCD A BC D -中,下面结论错误的是( ) A .BD ∥平面11CB D B .异面直线AD 与1CB 所成的角为45° C .1AC ⊥平面11CB D D .1AC 与平面ABCD 所成的角为30° 10.在等差数列{}{},n n a b 中,11a =,37a =,{}n a 的前n 项和为n S ,若()0nn S b c n c=≠+,则c =( )A .13 B .13- C .3 D .-3 11.已知ABC ∆的三个内角,,A B C 的对边分别为,,a b c ,角,,A B C 的大小依次成等差数列,且b =()22f x cx x a =++的值域是[)0,+∞,则a c +=( )A .4B .5C .6D .712.过双曲线()222210,0x y a b a b-=>>的右焦点F 作平行于一条渐近线的直线与另一条渐近线交于点P ,若点P 在圆心为()2,0c ,的圆内,则该双曲线离心率的取值范围是( )A .(B .(C .)+∞ D .)+∞第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知椭圆22:11612x y C +=,12,F F 分别为椭圆的两焦点,点P 椭圆在椭圆上,且23PF =,则12PF F ∆的面积为 .14.若数列{}n a 的通项公式为()121n a n n =+,则其前n 项和n S = .15.若1,0m n >>,3m n +=,则211m n+-的最小值为 . 16.将大于1的正整数n 拆分成两个正整数的和(如523=+),求出这两个正整数的乘积,再将拆分出来的大于1的正整数拆分成两个正整数的和,求出这两个正整数的乘积,如此下去,直到不能再拆分为止,则所有这些乘积的和为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知等比数列{}n a 的各项均为正数,12253a a -=,23749a a a =;(1)求数列{}n a 的通项公式;(2)设3log n n n b a a =⋅,求数列{}n b 的前n 项和n S . 18.设命题p :实数x 满足1284x <<,命题q :实数x 满足()223200x ax a a -+>≠; (1)当2a =,p q ∨为真命题时,求实数x 的取值范围; (2)若p 的必要不充分条件是q ,求实数a 的取值范围.19.在平面直角坐标系xOy 中,动点(),P x y (其中0y ≥)到定点()0,1M 的距离比到x 轴的距离大1.(1)求动点P 的轨迹C 的方程;(2)若直线:1l y kx =+与曲线C 相交于,A B 两点,点N 在直线1y =-上,BN 垂直于x 轴,证明直线AN 过坐标原点O .20.已知直角梯形ABCD ,如图(1)所示,AB CD ∥,AB BC ⊥,2AB BC ==,4CD =,连接AC ,将ABC ∆沿AC 折起,使得平面ABC ⊥平面ACD ,得到几何体B ACD -,如图(2)所示.(1)求证:AD ⊥平面ABC ;(2)若13BE BD =uur uu u r,求二面角E AC D --的大小.21.已知,,O A B 分别是海岸线12,l l 上的三个集镇,A 位于O 的正南方向10km 处,B 位于O 的北偏东60°方向10km 处;(1)为了缓解集镇O 的交通压力,拟在海岸线12,l l 上分别修建码头,M N ,开辟水上直达航线,使8km ON =,4km OM =.勘测时发现以O 为圆心,3km 为半径的扇形区域为浅水区,不适宜船只航行,问此航线是否影响船只航行?(2)为了发展经济需要,政府计划填海造陆,建造一个商业区(如图四边形OACB 所示),其中45OAC ∠=︒,AOC θ∠=,[]30,60θ∈︒︒,求该商业区的面积S 的取值范围.22.已知椭圆E 的中心在原点,焦点在y 轴上离心率2e =,且经过点(P ; (1)求椭圆E 的方程;(2)过椭圆E 的焦点F 作两条互相垂直的直线,分别交椭圆E 于,A B 和,C D ,求AB CD +的最小值.宁德市2017-2018学年度第一学期高二期末质量检测数学(理科)试题(参考答案与评分标准)一、选择题1-5:ACDCB 6-10:CBCDB 11、12:AA二、填空题13.6 14.22n n + 15.322+ 16.()12n n -三、解答题17.解:(1)设数列{}n a 的公比()0q q >,由12253a a -=,23749a a a =得112826112539a q a a q a q-=⎧⎨=⎩, ∴133a q =⎧⎨=⎩,∴()3,n n a n N +=∈(2)3log 3n n n n b a a n =⋅=⋅∴()231132333133n n n S n n -=⨯+⨯+⨯++-⨯+⨯L∴()23131323133nn n S n n +=⨯+⨯++-⨯+⨯L相减得231233333nn n +-=++++-⨯L()1313313n n n +-=-⋅-∴1213344n n n S +-=⋅+ 18.解:(1)命题p :实数x 满足1284x <<,得实数x 满足23x -<< 当2a =时,命题q :实数x 满足2680x x -+>,∴2x <或4x >,由于p q ∨为真命题,∴3x <或4x > (2)因为p 的必要不充分条件是q , ∴p q ⇒且q p ⇒又∵22320x ax a -+>∴()()20x a x a -->当0a >时,命题q :实数x 满足2x a >或x a <∴022a a >⎧⎨≤-⎩或03a a >⎧⎨≥⎩∴3a ≥当0a <时,命题q :实数x 满足x a >或2x a <∴023a a <⎧⎨≥⎩或02a a <⎧⎨≤-⎩∴2a ≤-综上所述:2a ≤-或3a ≥19.解:(1)动点(),P x y (其中0y ≥)到x 轴的距离为y ,到x 轴的距离为1y + ∴1PM y =+,又()0,1M 1y =+得轨迹C 的方程:24x y =(2)设()11,A x y ,()22,B x y ,由241x y y kx ⎧=⎨=+⎩得2440x kx --=∴124x x k +=,124x x =-,①点N 在直线1y =-上,BN x ⊥轴,∴()2,1N x -又A 在抛物线24x y =上,∴211,4x A x ⎛⎫⎪⎝⎭∴AO 斜率2111144x x k x ==,NO 的斜率221k x -=,由①112214x k k x -===,∴直线AN 过原点O . 20.(1)证明:如图(1),过A 作AM CD ⊥交CD 于M ,得正方形ABCM , ∴2AB BC CM MA ==== ∴2MD =∴AC =AD ==∴222AC AD CD +=∴AD AC ⊥ 如图(2),∵平面ABC ⊥平面ACD ,且两面交线为AC ,AD ⊂平面ACD ∴AD ⊥平面ABC(2)解:取AC 中点O ,连接BO MO 、,则BO ⊥平面ACD ∵M O 、分别为CD AC 、中点 ∴MO AD ∥ ∴MO AC ⊥以O 为原点,OC OM OB 、、所在的直线为x 轴、y 轴、z 轴,建立如图坐标系O xyz -,()A,(B,)C,()D∵13BE BD =uur uu u r∴((1,,3a b c =∴,333a b c =-==∴333E ⎛⎫- ⎪ ⎪⎝⎭∴AE =⎝⎭uu u r,()AC =uuu r设(),,m x y z =u r为平面EAC 的一个法向量,则03330m AE x y z m AC ⎧⋅=++=⎪⎨⎪⋅==⎩u r uu u r u r uuu r 取1y =,则0,1x z ==-∴()0,1,1m =-u r又()0,0,1n =r为平面ACD 的一个法向量∴cos ,2m n m n m n⋅==-⋅u r ru r r u r r∵二面角E AC D --为锐角∴二面角E AC D --为45°.21.解:(1)由已知,得120MON ∠=︒,4OM =,8ON = 由余弦定理,得2222cos 112MN OM ON OM ON MON =+-⋅⋅∠=∴MN =设OMN ∆的边MN 上的高为h ,则11sin 22MN h OM ON MON ⋅⋅=⋅⋅⋅∠∴37h =< ∴此航线会影响船只航线.(2)由已知,得120BOC θ∠=︒- 在OAC ∆中,∵sin sin OC OAOAC OCA=∠∠,即()10sin 45sin 45OC θ=︒︒+∴()sin 45OC θ=︒+∴11sin sin 22S OA OC AOC OB OC BOC =⋅⋅⋅∠+⋅⋅⋅∠()()()1110sin 10sin 1202sin 452sin 45θθθθ=⋅⋅⋅+⋅⋅⋅︒-︒+︒+=75==∵()S θ在[]30,60θ∈︒︒单调递增,且()3075S ︒=,()60150S ︒=-∴75,150S ⎡∈-⎣22.解:(1)依题意,设椭圆方程为()222210y x a b a b+=>>,则由2e =,得a =,b c =将点(P 代入得222b c ==,24a =∴椭圆E 的方程为22142y x +=.(2)得椭圆E 的上焦点(F ,当弦AB 垂直或平行x 轴时,426AB CD +=+= 当弦AB 不垂直或平行x 轴时,设AB方程y kx =CD方程1y x k=-+, 设()11,A x y ,()22,B x y,由22142y x y kx ⎧+=⎪⎨⎪=⎩得()22220k x ++-=∴1222x x k -+=+,12222x x k -=+,①AB =()22412k k +==+ 同理,()224112k CD k+=+得()()222211221344141k k AB CD k k +++=+=++ ∴()11224AB CD AB CD ⎛⎫++≥+= ⎪ ⎪⎝⎭ ∴163AB CD +≥, 当且仅当1k =±时取等号,∴AB CD +最小值163.。
