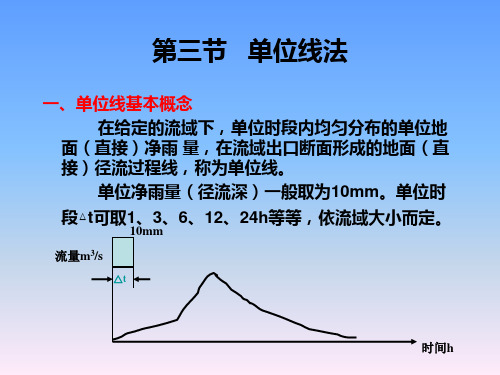
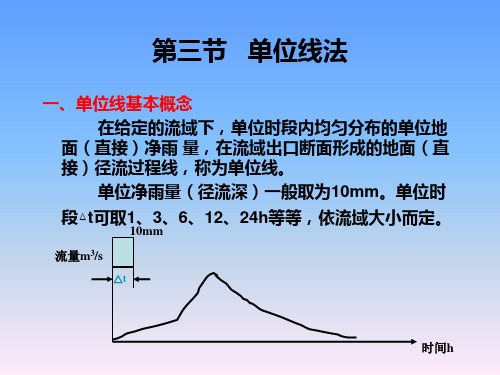
第三章 单位线分析计算

第三章 单位线分析计算本章着重介绍如何由净雨量过程预报流域出口的流量过程。

净雨量经过流域汇流形成出口的流量过程线，流域汇流历时是降雨径流预报预见期的来源，流域汇流物理过程是编制预报方案的理论依据。

3.1 舍尔曼时段单位线 3.1.1 基本原理舍尔曼(L. K. Sherman)于1932年提出了单位线的概念。

其定义为：流域上分布均匀的1个单位净雨直接径流产流量，所形成的直接径流过程线，即为单位线，记为UH 。

1个单位净雨是指单位时段内单位净雨深。

单位时段长可以任取，例如2h 、3h 、6h ，等。

而单位净雨深通常取为10mm 。

而实际发生的净雨，常常不是1个时段，也不是1个单位，应用于分析单位线时，有一些假定。

这些假定可归纳为以下两点：(1) 如果单位时段内净雨深不是一个单位，而是n 个，它所形成的出流过程线，总历时与UH 相同，流量则是UH 的n 倍。

(2) 如果净雨历时不是一个时段，而是m 个，则各个时段净雨所形成的出流过程之间互不干扰，出流过程的流量过程等于m 个流量过程之和。

由以上假定，净雨d r 、出流d Q 与UH 的纵坐标q 之间的关系如下：∑=+-=mi i t i d t d q r Q 11,, (2-1)式中：m i ,3,2,1 =，为净雨时段数。

d Q 和q 的单位为s /m 3，d r 则用单位净雨深的n 倍来表示。

如果UH 已知，根据上式，可由净雨转换为出流，计算十分简便。

关键是如何求得UH 。

可以根据流域的实测水文资料，分析出净雨及直接径流过程后，依据上式推求出UH ，为式(2-1)的逆过程。

3.1.2 单位线的推求推求UH 是使用次洪时段净雨深及相隔为计算时段长的直接径流时序过程。

前者由次洪降雨量经过扣损后得到，后者由径流过程线分割地下水后得到。

这里需要补充说明一下具体问题：(1) 由扣损方案求得的次洪净雨深，常不等于过程线分割得到的实测值，为了不把扣损的误差带入汇流计算，需要将计算值改正，或谓平差。

在平差前应分析误差的来源，作出较为合理的修正，以不改变原来的雨型为原则。

(2) 计算时段长t ∆的确定，主要考虑峰形的控制，一般取涨洪历时的1/3～1/4，常与流域大小成正比对于多时段净雨而言，传统的单位线分析方法有以下一些： (1) 分析法由 ∑=+-=mi i t i d t d q r Q 11,,，得到4)-(3 3)-(3 2)-(3 13,22,31,3,12,21,2,11,1,q r q r q r Q q r q r Q q r Q d d d d d d d d d ++=+==因此，上式组成的方程组为一个多元线性代数方程组，求解该代数方程组可以得到1q 、2q 的数值。

最简单的解法是逐一消去法。

由上面的方程组可以看出，由式(3-2)，已知1,d Q 和1,d r ，解出1q ：1,1,1d d r Q q =(3-5)1q 已知，将其带入式(3-3)，可得到1,12,2,2d d d r q r Q q -=(3-6)如此递推下去，得到1,21,,d mi i t i d t d t r q r Q q ∑=+--=(3-7)计算结果见表3-1和图3-1所示。

直接代数法对于降雨与径流实测资料没有误差，流域汇流符合线性时不变系统时，能得出正确的唯一解。

但实际情况是：提供分析UH 的实测资料存在着观测与分析误差，流域汇流为非线性系统，因此直接分析解法不但不能得出唯一解，由于误差累积，其解常很不合理。

如分析得到的t q ~呈锯齿形，如表3-1和图3-1的退水段，有的甚至出现负值，无法继续计算下去。

所以很少有人使用。

图3-1 分析法得到的单位线 表3-1 单位线分析法结果(2) 试错法这个方法是假设单位线，目估对比推流的与实测的t Q d ~。

当两者最接近时，所假设的UH 即为所求。

初始的UH ，可用其它洪水已分析得来的成果，或用斜线分割法的结果，也可任意假定。

试错法应用比较广泛，有的用科林法试错，有的凭经验试错。

但主要确定是单位线过程的初始假定比较困难，试错过程有时也会出现不合理现象，对其过程进行修正也不易做得完好。

(3) 系统识别方法UH 既然是线性系统的单位响应，进一步可以应用线性系统鉴别的方法推求UH 的最优解，如有约束的最小二乘法和回归法等。

(4) 各种方法的特点如上所述，推求单位线的方法主要有分析法、试错法和系统识别法。

试错法又可分为目估试错法和科伦试错法，后者是一种迭代性质的试错法。

分析法当降雨为１个时段时能取得很好的效果，但当降雨时段数大于１个时段，分析法推求的结果可能出现锯齿型，甚至出现负值，主要原因是误差的累积。

目估试错法是通过人工目估，逐步试错，使计算的流量过程与实测的流量过程吻合，避免了误差的累积，但任意性大，吻合程度缺乏客观标准，并且要求调试者具有相当的经验，费时费力。

科伦试错法是首先拟定初始单位线，然后按初始单位线计算出除最大降雨时段外的其它时段降雨产生的流量过程，并从实测流量过程中将其减去，差值即当成最大降雨时段产生的流量过程，据此推求新的单位线，将新单位线作为初始单位线，重复上述步骤，直至新旧单位线之间的差值达到给定的误差要求。

优点是当初始单位线拟定后，不必目估试错，能自动逐步修正，适合计算机编程。

缺点是计算结果及迭代的收敛性与初始单位线的拟定有关，推求的结果不一定是最佳结果。

另外当降雨时段较多时，迭代难以继续下去。

因此，科伦试错法仅当降雨较集中在最大时段或降雨时段数较小时，效果才较好。

3.1.3 单位线的综合为求得流域的单位线预报方案，需分析多次洪水。

多数流域，各次洪水所得到的UH 会有差别。

这时，首先要检查原始资料的观测误差，及根据原始资料计算用于分析UH 的t r d ~和t Q d ~过程中的操作误差，作出可能的改正，然后对UH 的变化根据UH 原理上存在的问题进行分析及处理。

如果各次洪水的UH 变化不大，可求出平均UH 。

平均UH 的绘制须注意，平均纵标值不宜取同时流量的平均值。

应先根据各个UH ，计算出平均峰值及峰现时间，确定峰点位置。

然后根据各个UH 的外形，初绘光滑的平均UH ，最后修正并校核总量为单位雨深。

3.1.4 单位线时段转换UH 是有一定长度的，同一次洪水，如单位时段长度不同，实际雨强不等，UH 不相同。

如原来UH 时段长为T ，现推求T 2的UH ，根据线性假定，可将UH滞后T h ，与原UH 相加，将该过程线的纵坐标除以2即得T 2的UH 。

该UH 的峰值应等于上述两个UH 的交点，比原来UH 峰值低并滞后，这是由于历时增长，雨强降低所致。

因此，对一个给定的流域综合UH 方案，或将不同地区的UH 方案综合，需将不同时段的UH 换算为同一时段。

UH 是作为一个经验方法提出来的，但方法简易，使用精度不错，生产上一直沿用至今。

系统概念引入后，建立了UH 的理论，明确了方法的物理实质，这对于推求UH 及正确的应用都有益。

UH 是个黑箱模型，并和流域上实际的水力状态没有关系，使用时必须有实测水文资料，这是它的应用受到限制的主要原因。

3.2 纳须单位线(Nash)纳须模型是现行概念性流域汇流模型中得到比较广泛应用的一种，该模型结构简单，包含的参数较少，且具有较好的适应性。

本文介绍纳须模型的结构及其参数率定方法。

3.2.1 纳须瞬时单位线1945年克拉克(C. O. Clark)首先提出瞬时单位线的概念。

所谓瞬时单位线，就是流域上均匀分布的、历时趋于无限小、强度趋于无穷大、但净雨总量为1个单位的净雨所形成的流域出口断面过程线。

通常用)(t u 表示。

1957年，纳须(Nash)把流域看作是一连串的n 个相同的“线性水库”，如图3-2所示。

可以推导出一个单位的瞬时入流进入水库系统后，其对应的出流即瞬时单位线的数学方程式为ktn kt n k t u --Γ=e )()(1)(1 (3-8)式中：Γ为伽马函数，当n 为整数时，其值为)!1(-n ；n 为相当于水库个数；k 为一个线性水库的蓄泄系数。

图3-2 纳须模型示意图3.2.2 纳须时段单位线在实际应用中，需要将瞬时单位线转换成时段单位线，一般用)(t S 曲线。

按照)(t S 曲线的定义，)(t S 等于瞬时单位线的积分，即 ⎰=tt t u t S 0d )( )(，对该式进行积分，可以很方便地导出)(t S 曲线，再利用线性叠加原理，)()(),(t t S t S t t u ∆--=∆，从而得到时段单位线。

即为∑∑=-=-∆---∆--=∆n i i n n i i n kt k tkti n k t t i n t t u 11])()!(1)()!(1e [e ),( (3-9)式(3-9)为当n 为自然数时，计算步长为t ∆时的纳须时段单位线的计算公式。

3.2.3 纳须单位线参数n 、k 的确定如何确定参数n 和k 是纳须模型应用中的重要问题之一。

纵观目前所有的确定该模型的方法，按依据的资料分，则可归纳为3类：一是依据降雨和径流一一对应资料的方法，如矩法、累积量法、最优化方法等；二是依据流域地形和地貌资料的方法，如经验公式法等；三是依据流域出口断面流量资料的方法。

本文着重介绍应用较为广泛的矩法。

根据矩法，可以求出参数：)2()2(2)1()1(][I Q I Q N N M M n --=(3-10))1()1()2()2(IQI Q MMN N K --=(3-11)式中：)1(I M 、)1(Q M 分别为入流量(净雨量)及出流量的一阶原点矩；)2(I N 、)2(Q N 分别为入流量和出流量的二阶中心矩。

入流量和出流量的一阶原点矩的计算公式分别为2)()()()(d )( d )( 11110)1(tt I mt I t I tt I tt I tt t I Mni i ni ii ni i ni ii I∆⋅===∑∑∑∑⎰⎰====∞∞(3-12) 2)()()()(d )( d )( 11110)1(tt Q mt Q t Q tt Q tt Q tt t Q Mni ini iini ini iiQ∆⋅===∑∑∑∑⎰⎰====∞∞(3-13)式中：)(t I 、)(t I i 分别为t 时刻的净雨量和净雨量的时段平均值；)(t Q 、)(t Q i 分别为t 时刻的出流量和出流量的时段平均值。

12 ,32 ,,7 ,5 ,3 ,1--=n n m i 。

同理，可以计算出净雨量和出流量的二阶原点矩为2112)2()2()()(t t I mt I Mni i ni ii I∆⋅=∑∑== (3-14) 2112)2()2()()(t t Q mt Q M ni ini iiQ ∆⋅=∑∑== (3-15) 由于入流量和出流量的二阶中心矩可用原点矩来表示，即2)1()2()2(][I I I M M N -= (3-16)2)1()2()2(][Q Q Q M M N -= (3-17)在推求某一流域纳须时段单位线时，首先选择几场有代表性的洪水资料，根据每场次洪水的相应入流和出流过程，分别求出它们的单位线参数n 和k ，然后把n 和k 平均(如果相差较大，可以分成几组)概化出流域的单位线参数，便可用纳须时段单位线计算公式计算出流域时段单位线。