大学自动控制原理2.4典型环节传递函数
合集下载
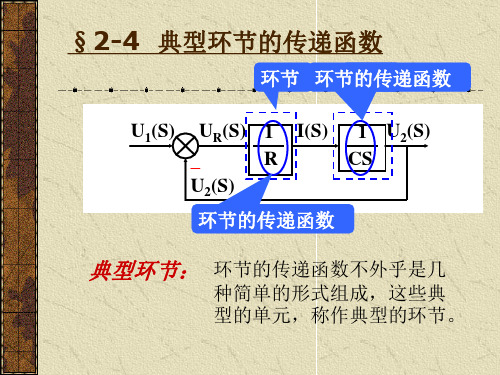
典型环节的传递函数

1 xo t xi t dt T
•传递函数为:
1 G s X i s Ts
Xo s
典型环节的传递函数
3、微分环节(纯微分环节) 凡输出量与输入量的微分成正比,称为微分环节, 又称为理想微分环节 •动力学方程为:
xo t T
•传递函数为:
dxi t dt
典型环节的传递函数
8、延时环节 延时环节是输出滞后输入时间 但不失真地反映 输入的环节,又称为时滞环节。 •动力学方程为:
xo t xi t s Xi s
e s
•拉普拉斯变换:
F s L f t f t e dt 0
Ts
G s
Xo s Xi s
典型环节的传递函数
4、惯性环节(一阶积分环节) 又称一阶惯性环节,是一个相位滞后环节。 •动力学方程为:
T
dxo t dt
xo t xi t
Xo s
•传递函数为:
1 G s X i s Ts 1
典型环节的传递函数
1、比例环节 凡输出量与输入量成正比,输出不失真也不延迟 而按比例地反映输入的环节,称为比例环节又叫 放大环节、无惯性环节、零阶环节 •动力学方程为:
xo t Kxi t
•传递函数为:
G s
Xo s Xi s
K
典型环节的传递函数
2、积分环节(纯积分环节) 凡输出量与输入量的积分成正比,称为积分环节, 又称为理想积分环节 •动力学方程为:
st
s a i
•拉普拉斯反变换:
1 a i st f t L F s 2 i a i F s e ds
第2章_控制系统的动态数学模型_2.4传递函数以及典型环节的传递函数

X o ( s) 1 G( s) Fi ( s ) Ms 2 Ds K
【例】R-L-C无源电路网络的传递函数
已知系统的微分方程为:
d2 d LC 2 uc (t ) RC uc (t ) uc (t ) ur (t ) dt dt
所有初始条件均为零时,其拉氏变换为:
LCs 2U c (s) RCsU c (s) U c (s) U r (s)
n
m n bm K =K * (-Zi ) / ( p j ) an i 1 j 1
为传递函数的增益
b0 K a0
*
为根轨迹增益
Ti和 i 为时间常数
零、极点分布图:
G ( s) b0 (s z1 )(s z2 )(s zm ) M (s) a0 (s p1 )(s p2 )(s pn ) D(s)
r (t ) 1(t )
零状态响应分别为: c1 (t ) 1 2et 3e2t
c2 (t ) 1 0.5et 0.5e2t
各个模态在两个系统输出响应中所占的比重不同,
取决于零点相对于极点的距离。
j
z2
z1
0
(5)关于传递函数的几点说明
传递函数是一种以系统参数表示的线性定常系统输 入量与输出量之间的关系式。传递函数的概念通常只 适用于线性定常系统。 传递函数是复数自变量s的复变函数。传递函数中 的各项系数和相应微分方程中的各项系数对应相等, 完全取决于系统结构参数。
D(s)=0 称为系统的特征方程,其根称为系统的 特征根。特征方程决定着系统的动态特性。
D(s) 中s 的最高阶次等于系统的阶次。
将传递函数的分子和分母多项式进行因式分解可得
【例】R-L-C无源电路网络的传递函数
已知系统的微分方程为:
d2 d LC 2 uc (t ) RC uc (t ) uc (t ) ur (t ) dt dt
所有初始条件均为零时,其拉氏变换为:
LCs 2U c (s) RCsU c (s) U c (s) U r (s)
n
m n bm K =K * (-Zi ) / ( p j ) an i 1 j 1
为传递函数的增益
b0 K a0
*
为根轨迹增益
Ti和 i 为时间常数
零、极点分布图:
G ( s) b0 (s z1 )(s z2 )(s zm ) M (s) a0 (s p1 )(s p2 )(s pn ) D(s)
r (t ) 1(t )
零状态响应分别为: c1 (t ) 1 2et 3e2t
c2 (t ) 1 0.5et 0.5e2t
各个模态在两个系统输出响应中所占的比重不同,
取决于零点相对于极点的距离。
j
z2
z1
0
(5)关于传递函数的几点说明
传递函数是一种以系统参数表示的线性定常系统输 入量与输出量之间的关系式。传递函数的概念通常只 适用于线性定常系统。 传递函数是复数自变量s的复变函数。传递函数中 的各项系数和相应微分方程中的各项系数对应相等, 完全取决于系统结构参数。
D(s)=0 称为系统的特征方程,其根称为系统的 特征根。特征方程决定着系统的动态特性。
D(s) 中s 的最高阶次等于系统的阶次。
将传递函数的分子和分母多项式进行因式分解可得
自动控制理论_哈尔滨工业大学_2 第2章线性系统的数学模型_(2.4.1) 典型环节的传递函数PPT

0
t
积分环节在单位阶跃输入下的响应
例:积分器
i2
C
ui R
_
i1
uo
+i1 i2Fra bibliotek1 Rui
(t)
C
d dt
u0
(t )
uo
(t)
1 RC
ui (t)dt
G(s) Uo (s) 1 1 Ui (s) RC s
二、几种典型环节的数学模型
4.微分环节
c(t) d r(t)
斜率1/T
0τ
t
例: • 汽车加速、火箭升空; ——作用力和输出速度
• 加热系统; ——加热量和温度变化
• 励磁回路; ——输入电压和励磁电流
惯性大小用τ来量度。 ——τ越大,接近目标值越慢 ,惯性越大;τ越小,接近 目标值越快,惯性越小。
几乎任何物理系统都包含 大大小小的惯性。
二、几种典型环节的数学模型
滞后环节
二、几种典型环节的数学模型
1.比例环节
y(t) Ku(t)
G(s) Y(s) K U (s)
K——称为比例系数或放大系数,也称为环节的增益,有量纲。
输出量无失真、无滞后、成比例地复现输入。
• 无弹性变形的杠杆;
——作用力和输出力
• 忽略非线性和时间迟后的运算放大器;
——比例放大器的输入电压和输出电压
τ=RC—时间常数
当 r(t) 1(t) 时, R(s) 1
s
Y(s) s 1 1 s 1 s s 1
t
y(t) e
t=0时,输出幅值为1;
t→∞时,指数衰减至0。
二、几种典型环节的数学模型
《自控原理》典型环节的传递函数
3.结构图: 结构图: 结构图 R(S)
1 T2S2+2ξTS +1
C(S)
七、二阶微分环节
d2r(t) dr(t) 2 + r(t) =c(t) 1.微分方程: 微分方程: 微分方程 τ + 2ξτ 2 dt dt
τ:环节的时间常数;ξ:阻尼比。
2.传递函数: 传递函数: 传递函数
G ( s ) = τ S + 2ξτS + 1
C(S)
三、微分环节
1.微分方程: 微分方程: 微分方程 2.特点: 特点: 特点 c(t) = dr(t) dt
输出对输入信号在时间上的微分, 输出对输入信号在时间上的微分, 即输出量与输入量的变化率成正比。 即输出量与输入量的变化率成正比。
3.传递函数: 传递函数: 传递函数
G(S)= S
R(S) C(S)
4.结构图: 结构图: 结构图 R(S)
1 TS+1
C(S)
五、一阶微分环节
dr(t) 1.微分方程: c(t)=τ dt + r(t) 微分方程: 微分方程 τ :一阶微分环节的时间常数 2.特点: 特点: 特点 3.传递函数: 传递函数: 传递函数 输入延迟地反应输出量的变化规律。 输入延迟地反应输出量的变化规律。
1 G(S)= 4、惯性环节: 、惯性环节: TS+1 5、一阶微分环节: G(S)= τS+1 、一阶微分环节: ω2n 6、二阶振荡环节: G(S)= 2 、二阶振荡环节: S +2 ξωnS+ω2n ω 7、二阶微分环节: G ( s ) = τ 2 S 2 + 2ξτS + 1 、二阶微分环节: τ G(S)=e-τs 8、延迟环节: 、延迟环节:
1 T2S2+2ξTS +1
C(S)
七、二阶微分环节
d2r(t) dr(t) 2 + r(t) =c(t) 1.微分方程: 微分方程: 微分方程 τ + 2ξτ 2 dt dt
τ:环节的时间常数;ξ:阻尼比。
2.传递函数: 传递函数: 传递函数
G ( s ) = τ S + 2ξτS + 1
C(S)
三、微分环节
1.微分方程: 微分方程: 微分方程 2.特点: 特点: 特点 c(t) = dr(t) dt
输出对输入信号在时间上的微分, 输出对输入信号在时间上的微分, 即输出量与输入量的变化率成正比。 即输出量与输入量的变化率成正比。
3.传递函数: 传递函数: 传递函数
G(S)= S
R(S) C(S)
4.结构图: 结构图: 结构图 R(S)
1 TS+1
C(S)
五、一阶微分环节
dr(t) 1.微分方程: c(t)=τ dt + r(t) 微分方程: 微分方程 τ :一阶微分环节的时间常数 2.特点: 特点: 特点 3.传递函数: 传递函数: 传递函数 输入延迟地反应输出量的变化规律。 输入延迟地反应输出量的变化规律。
1 G(S)= 4、惯性环节: 、惯性环节: TS+1 5、一阶微分环节: G(S)= τS+1 、一阶微分环节: ω2n 6、二阶振荡环节: G(S)= 2 、二阶振荡环节: S +2 ξωnS+ω2n ω 7、二阶微分环节: G ( s ) = τ 2 S 2 + 2ξτS + 1 、二阶微分环节: τ G(S)=e-τs 8、延迟环节: 、延迟环节:
典型环节的传递函数

P18 P28
2.4 典型环节的数学模型P22
思考题:
如何从该框图求得输出 与输入 之间的关系?
2.4 典型环节的数学模型P22
系统是由典型环节组成 常见的几种典型环节 比例、微分、积分、惯性、振荡、滞后 讨论内容
时域特征:微分方程,阶跃响应 复域(s域)特征:传递函数,零极点分布
实例:
测速发电机输出电压与输入角度间的传递函数即
为微分环节。P28 图2-4-9
[实例]
①
R1
理想微分环节
ui
①
C
+
uo
U o ( s) R1Cs Ts U i ( s)
R1
比例微分环节
ui
C R0
+
uo
Uo (s) R1 (1 R0Cs) K(Ts 1) Ui (s) R0
P28
3.阶跃响应及零极点分布
n2 C (s) 2 G(s) 2 R ( s ) s 2n s n
五、 振荡环节(Oscillating Element)
0
c(t)
P28
0 1 1
n
Im jn 1 2
0
单位阶跃响应曲线 [分析]:
p28图222244449999四微分环节derivativeelementp26实例tscsrsusuio????111001????????????tskrcsrrsusuior1iuour0cccc理想微分环节r1iuoucccc比例微分环节带有惯性的微分环节rtuituocrcsrcssusuio????1csrrrzrzszszsxsy112122121???????????111212112?????????????????ktstskcsrrrrcsrrsxsysgcrtrrrk1212??????式中
2-4 典型环节及其传递函数

1
气阻的数学表达式为 ∆p = R∆q ∆p 式中, 是气体压力降 ; ( N/m 2 ) ∆q ( N ⋅ s) 是气体重量流量 ; R 是气阻值。 因而它的传递函数为 ∆P( s ) G( s ) = =R ∆Q ( s ) (3)喷嘴一挡板机构 喷嘴一挡板机构由恒节流孔 1,背压室 2,喷嘴 3,和挡板 4 组成,如图 2-18 所示。 ∆h 它的作用是把输入挡板的微小位移 转换成相应 的气压信号输出。在忽略背压室气容影响时,可把喷嘴 1 2 4 一挡板机构看作一个比例环节,即 3 D ∆p D = k 1 ∆h 式中, 是喷嘴背压的变化; ∆p D ∆h 是挡板开度变化量; 是比例系数。 k1 d (4)放大器 h 在自动控制系统中用得最多的是运算放大 器,它是一个具有高放大倍数直接耦合式放大器。 1 − 恒节流孔 2 − 背压室 运算放大器一般由集成电路构成,其符号如图 2- 3 − 喷嘴 4 − 挡板 19 所示。 图 2-17 喷嘴挡板机构结构示意图 图中三角形尖端代表输出端,输出电压为 u 0 (t ) 它有两个输入端,一个是同相输入端 b 用 “十”表示,一个是反相输入端 a 用“一”表示。当 放大器工作在放大区而不是饱和区时,输出电压 与同相输入端电压 和反相输入 u 0 (t ) u i (t ) u ( t ) 端电压 之间的电压差成正比。即 i1 a u 0 (t ) = k [u i2 (t ) − u i1 ( t )] + 也可写成 b ∆u 0 (t ) = k∆u i (t ) U i1 因而其传递函数为 Ui2 U0 ∆U 0 ( s ) G( s ) = =k 图 2-19 运算放大器符号图 ∆U i ( s ) 式中, 为开环放大倍数,这个数值很高,可达到 。所以集成运算放大器工作在 k 10 6 ~ 10 7 无反馈状态时输入电阻很高。它有以下两个主要特点: ①由于开环输入电阻很高,运算放大器两个输入端的电流接近于零。 ②由于开环放大倍数很高,所以 b 端和 C 端电位接近相等,即 。 u i2 ≈ ui1 运算放大器本身虽属放大环节,但可用它来组成其他各种基本环节。
气阻的数学表达式为 ∆p = R∆q ∆p 式中, 是气体压力降 ; ( N/m 2 ) ∆q ( N ⋅ s) 是气体重量流量 ; R 是气阻值。 因而它的传递函数为 ∆P( s ) G( s ) = =R ∆Q ( s ) (3)喷嘴一挡板机构 喷嘴一挡板机构由恒节流孔 1,背压室 2,喷嘴 3,和挡板 4 组成,如图 2-18 所示。 ∆h 它的作用是把输入挡板的微小位移 转换成相应 的气压信号输出。在忽略背压室气容影响时,可把喷嘴 1 2 4 一挡板机构看作一个比例环节,即 3 D ∆p D = k 1 ∆h 式中, 是喷嘴背压的变化; ∆p D ∆h 是挡板开度变化量; 是比例系数。 k1 d (4)放大器 h 在自动控制系统中用得最多的是运算放大 器,它是一个具有高放大倍数直接耦合式放大器。 1 − 恒节流孔 2 − 背压室 运算放大器一般由集成电路构成,其符号如图 2- 3 − 喷嘴 4 − 挡板 19 所示。 图 2-17 喷嘴挡板机构结构示意图 图中三角形尖端代表输出端,输出电压为 u 0 (t ) 它有两个输入端,一个是同相输入端 b 用 “十”表示,一个是反相输入端 a 用“一”表示。当 放大器工作在放大区而不是饱和区时,输出电压 与同相输入端电压 和反相输入 u 0 (t ) u i (t ) u ( t ) 端电压 之间的电压差成正比。即 i1 a u 0 (t ) = k [u i2 (t ) − u i1 ( t )] + 也可写成 b ∆u 0 (t ) = k∆u i (t ) U i1 因而其传递函数为 Ui2 U0 ∆U 0 ( s ) G( s ) = =k 图 2-19 运算放大器符号图 ∆U i ( s ) 式中, 为开环放大倍数,这个数值很高,可达到 。所以集成运算放大器工作在 k 10 6 ~ 10 7 无反馈状态时输入电阻很高。它有以下两个主要特点: ①由于开环输入电阻很高,运算放大器两个输入端的电流接近于零。 ②由于开环放大倍数很高,所以 b 端和 C 端电位接近相等,即 。 u i2 ≈ ui1 运算放大器本身虽属放大环节,但可用它来组成其他各种基本环节。
自动控制原理课件:2_4典型环节
• 电枢回路电压平衡方程
• 电磁转距方程 • 电动机轴上的转距平衡方程
1)确定输入量、输出量 2)确定动态联系
Ua θc
ua
=
Raia
+ La
dia dt
+ eb
eb = Kbωm
(2)
J
dωm dt
=
Mm
−ML
−
fωm
ua
(1)
Eb Eb
ML
(3) Mm
1
Ia
LaS + Ra
1
ωm
JS + f
电磁力矩 M m = Cmia
Ua eb
La
f1 Mm ML
J1
ωmθm 1/i θc
nω
M2
J2 、f2
原理:直流电动机的工作实质是将输入的
电能转换为机械能,也就是由输入的电枢电压Ua(t) 在电枢回路中产生电枢电流ia (t),再由电流ia (t)与激磁磁通相互作用产生电磁转距Mm(t), 从而拖动负载运动。因此,直流电动机的运动方 程可由以下三部分组成。
(4)
Ia Cm
Mm
角速度 ωm = dθm dt
(5)
θm
ωm
S
输出轴转角方程
θm
θc = θm i (6)
1 i
θc
4、传递函数 联结各框图得系统方快图(P39:图表-48)
用结构变换或Mason公式求出传递函数
三、求取系统传递函数的一般方法
步骤: * 1.首先确定出系统的输出信号(被控量等)和输入
信号(如给定值、干扰等)。 * 2.把系统分成若干个典型环节,求出各环节的
传递函数。用信号线把这些方框连接起来,得 到系统的动态结构图。 * 3.对动态结构图进行变换,得到传递函数。
• 电磁转距方程 • 电动机轴上的转距平衡方程
1)确定输入量、输出量 2)确定动态联系
Ua θc
ua
=
Raia
+ La
dia dt
+ eb
eb = Kbωm
(2)
J
dωm dt
=
Mm
−ML
−
fωm
ua
(1)
Eb Eb
ML
(3) Mm
1
Ia
LaS + Ra
1
ωm
JS + f
电磁力矩 M m = Cmia
Ua eb
La
f1 Mm ML
J1
ωmθm 1/i θc
nω
M2
J2 、f2
原理:直流电动机的工作实质是将输入的
电能转换为机械能,也就是由输入的电枢电压Ua(t) 在电枢回路中产生电枢电流ia (t),再由电流ia (t)与激磁磁通相互作用产生电磁转距Mm(t), 从而拖动负载运动。因此,直流电动机的运动方 程可由以下三部分组成。
(4)
Ia Cm
Mm
角速度 ωm = dθm dt
(5)
θm
ωm
S
输出轴转角方程
θm
θc = θm i (6)
1 i
θc
4、传递函数 联结各框图得系统方快图(P39:图表-48)
用结构变换或Mason公式求出传递函数
三、求取系统传递函数的一般方法
步骤: * 1.首先确定出系统的输出信号(被控量等)和输入
信号(如给定值、干扰等)。 * 2.把系统分成若干个典型环节,求出各环节的
传递函数。用信号线把这些方框连接起来,得 到系统的动态结构图。 * 3.对动态结构图进行变换,得到传递函数。
自动控制原理--典型环节及其传递函数
hc t hd (t )
l
v
2.3 控制系统的复数域数学模型
4.典型元部件的传递函数
(1)电位计
(1)比例环节
(2)电桥式误差角检测器
(2)微分环节
(3)自整角机
(3)积分环节
(4)测速发电机(交流,直流) (4)惯性环节
(5)电枢控制式直流电动机 (5)振荡环节
(6)两相异步电动机
(6)一阶复合微分环节
特点: 输出量能准确复现输入量,但须延迟一固定的时 间间隔。
在线性控制系统中,系统含有典型环节的情况,反映了系 统的结构和性能。
时滞环节
对于时滞时间很小的时滞环节,常把它展开成泰勒级数,并 略去高次项,得:
W
(
s)
1
s
2
s
2
1
3
s3
2! 3!
1
1s
时滞环节在一定条件下可近似为惯性环节
实例
带钢厚度检测环节
(6)
复习拉普拉斯变换有关内容(13)
用L变换方法解线性常微分方程
0 初条件 n>m
: 特征根(极点) : 相对于 的模态
2.3 控制系统的复数域数学模型
3.传递函数的零点和极点对输出的影响
极点决定模态; 零点影响曲线形状。
4 传递函数的局限性
例 已知某系统在0初条件下的阶跃响应为:
c(t) 1 2 et 1 e4t 33
试求:(1) 系统的传递函数; (2) 系统的增益; (3) 系统的特征根; (4) 画出对应的零极点图; (5) 求系统的单位脉冲响应; (6) 求系统微分方程;
解.(1)
(2) (3) (4) 如图所示 (5)
积分环节实例:
l
v
2.3 控制系统的复数域数学模型
4.典型元部件的传递函数
(1)电位计
(1)比例环节
(2)电桥式误差角检测器
(2)微分环节
(3)自整角机
(3)积分环节
(4)测速发电机(交流,直流) (4)惯性环节
(5)电枢控制式直流电动机 (5)振荡环节
(6)两相异步电动机
(6)一阶复合微分环节
特点: 输出量能准确复现输入量,但须延迟一固定的时 间间隔。
在线性控制系统中,系统含有典型环节的情况,反映了系 统的结构和性能。
时滞环节
对于时滞时间很小的时滞环节,常把它展开成泰勒级数,并 略去高次项,得:
W
(
s)
1
s
2
s
2
1
3
s3
2! 3!
1
1s
时滞环节在一定条件下可近似为惯性环节
实例
带钢厚度检测环节
(6)
复习拉普拉斯变换有关内容(13)
用L变换方法解线性常微分方程
0 初条件 n>m
: 特征根(极点) : 相对于 的模态
2.3 控制系统的复数域数学模型
3.传递函数的零点和极点对输出的影响
极点决定模态; 零点影响曲线形状。
4 传递函数的局限性
例 已知某系统在0初条件下的阶跃响应为:
c(t) 1 2 et 1 e4t 33
试求:(1) 系统的传递函数; (2) 系统的增益; (3) 系统的特征根; (4) 画出对应的零极点图; (5) 求系统的单位脉冲响应; (6) 求系统微分方程;
解.(1)
(2) (3) (4) 如图所示 (5)
积分环节实例:
大学自动控制原理_2.4典型环节传递函数
U ( s ) = LsI ( s ) + I ( s ) R + 1 I ( s ) i cs LT,得: 1 U 0 ( s ) = I ( s ) cs U o (s) 1 ∴ G(s) = = 2 U i ( s ) LCs + RCs + 1 R C ∴ ω n = 1 LC ξ = 2 L
U1 ( s ) 1 1 ∴ G (s) = = = (设RC = T ) U 0 ( s ) RCs + 1 Ts + 1
例2、弹簧阻尼系统
k
xi (t)
xo(t)
x i (t ) — 输入位移 x o (t ) — 输出位移 k — 弹性刚度 c — 粘性阻尼系数
c
dxo (t ) 解: k [ xi (t ) − xo (t )] = c dt
解:ω = θ&(t ) = Ke(t )
∴θ (t ) = K ∫ e(t )dt
∴ G ( s ) = Θ( s ) E ( s ) = K s
设
则
T=1
K
G ( s ) = 1 Ts
振荡环节(二阶振荡环节) §2.4.5 振荡环节(二阶振荡环节)
& T &&o (t ) + 2ξTxo (t ) + xo (t ) = xi (t ) x
相似原理
R
xi (t )
k
ui
i
C
uo
c
xo (t )
对于上述两图知是电系统与机械系统两种装置。 对于上述两图知是电系统与机械系统两种装置。
对于这两种机构求其传递函数均为
1 G( s) = Ts + 1
控制工程基础:2.4 传递函数以及典型环节的传递函数
G(s)= 1 Ts 1
•2.4.3.振荡环节(二阶)
G(s)=
1
或
2
T 2s2 2 Ts 1
s2 2s 2
(0< <1)
•2.4.4.积分环节
G(s)= k s
•2.4.5.理想微分环节 •2.4.6.近似微分环节
G(s)=ks
G(s)= kTs Ts+1
• 2.4.7.延迟环节 G(s)= e -τs
N(s) – 分母多项式,又称特征多项式,它决定着系统 响应的基本特点和动态本质。
一般情况下,要求n≥m
G(s) C(s) b0sm b1s m1 bm1s bm M (s) R(s) a0s n a1s n1 an1s an N (s)
m
(s+zi )
K*
i 1 n
于是,由定义得系统传递函数为:
G(s)
C(s) R(s)
b0 s m a0 s n
b1s m1 a1s n1
bm1s bm an1s an
M (s) N(s)
M (s) b0 s m b1s m1 bm1s bm M(s) – 分子多项式
N (s) a0 s n a1s n1 an1s an
2.4 传递函数以及典型环节的传递函数
2.4 传递函数以及典型环节的传递函数
微分方程是在时域中描述系统动态性能的数学 模型,在给定输入量和初始条件下求解微分方 程可以得到系统的输出响应。系统结构和参数 变化时分析较麻烦。
传递函数是在用拉氏变换求解线性常微分方 程的过程中引申出来的概念。
用拉氏变化法求解微分方程时,可以得到控 制系统在复数域的数学模型-传递函数。
传递函数的局限性
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xo (t) xi (t ) τ为延迟时间 G(s) L[x0(t)] L[xi (t )]
L[xi (t)] L[xi (t)]
Xi (s)es es X i (s)
强调:
1、一个元件和一个环节不是等价的。 一个元件可能划分为几个环节,也可能几 个元件构成一个环节。
2、不要把表示系统结构情况的物理框图 与分析系统的传递函数的框图混淆。
3、环节的传递函数也不是固定不变的, 这取决于选取的输入及输出量是什么。 当输入、输出量不同时,传递函数不同。
相似原理
xi (t)
R
k
ui i
C
uo
c
xo (t)
对于上述两图知是电系统与机械系统两种装置。
对于这两种机构求其传递函数均为
G(s) 1 Ts 1
两者物理模型不同,但数学模型相同, 功能相同,对于二者的“异构同功”称其 为相似系统。
例1. 无源滤波电路
ui u
o
C为电容 R为电阻
解:
ui
(t
)
i
(t
)
R
1 C
i(t
)dt
1
uo (t) C i(t)dt
LT得:
Ui
(t)
I
(s)R
1 Cs
I
(s)
Uo
(t)
1 Cs
I
(s)
G(s) U1(s) 1 1 (设RC T ) U0(s) RCs 1 Ts 1
例2、弹簧阻尼系统
油缸的力平衡方程式:
A( p2 p1) kxo
通过节流阀的流量:
q
A(xi xo )
p2 R
p1
得:
(xi xo )
k A2R
xo
G(s)
XX((o ss)) i
s
s
k
A2 R
令T A2R k
G(s) Ts Ts 1
此系统为包含有惯性环节及微分环节的系统。
当|Ts|<<1时,G(s)=Ts, 才近似为理想的微分环节。
动力学方程为: xo (t) Kxi (t)
G(s) Xo (s) Xi (s) K
§2.4.2 惯性环节:(一阶惯性环节)
动力学方程为 : Txo (t) xo (t) Kxi (t)
G(s) K Ts 1
K为惯性环节的增益或放大系数;T为时间常数
理想的一阶惯性环节 G(s) 1 Ts 1
即 xo (t) Txi (t)
G(s) Xo (s) X (s) Ts i
T为微分环节的时间常数
1、理想的微分环节 G(s) Ts 2、实际的微分环节 G(s) Ts
Ts 1
3、微分环节对系统的控制作用
例1、 电压下图为一直流发电机原理
图。激磁电压ui恒定,磁通不变。此时 电枢u0与转速 成正比(θ为转子转 角),即输入量为θ,输出量为u0。
(1)预见输入(使输入提前)
比例环节 R(s)
r(t) t
1
X o (s)
xo (t)
1
o 45
t
比例+微分
R(s)
r(t) t
1 Ts
Xo (s)
xo (t)
21
o
t
t1 t 2
(2)增加阻尼
KP
K s(Ts 1)
G(s)
KPK
1
Ts 2 s K P K
K
K P (Td s 1)
§2.4 典型环节的传递函数
§2.4.1 比例环节 §2.4.2 惯性环节(一阶惯性环节) §2.4.3 微分环节 §2.4.4 积分环节 §2.4.5 振荡环节(二阶振荡环节) §2.4.6 延时环节(迟延环节)
§2.4.1 比例环节
凡输出量与输入量成正比,输出不失真 也不延迟,而按比例地反映输入的环节, 称为比例环节。
相似系统:能用形式相同的数学模型来 描述的物理系统。
s(Ts 1)
G(s) 2
Ts
2
K K(T s 1)
P
d
(1 K p KTd)s K P
K
(3)强化噪声
§2.4.4 积分环节
积分环节是输出正比于输入对时间的积分 的环节。
即:
x(t) o
1 T
x(t)dt i
拉氏变换得
:
X(o s)
1 Ts
X(i s)G(s)
1 Ts
T为积分环节的时间常数
例题:
G(s) (s) E(s) K s
设
T
1 K
则 G(s) 1 Ts
§2.4.5 振荡环节(二阶振荡环节)
T 2xo (t) 2Txo (t) xo (t) xi (t)
G(s)
1
T s2 2 2Ts 1
— 阻尼比(0 1)
T — 振荡环节的时间常数
n — 1 T
n
n代入G(s)得
G(s)
s2
n2 2ns
n2
注意:
1)0≤ξ<1时,二阶系统为振荡环节。 2) ξ≥1时,二阶环节不是振荡环节,
而是两个一阶惯性环节的组合。 所以二阶环节不一定是振荡环节。
例:无源R-C-L网络
L
R
ui
i
C
uo
ui (t) — 输入电压 L —电感 R —电阻 uo (t) — 输出电压 i(t) —电流 C —电容
k
xi(t) xi (t) —
xo (t) — 输出位移
xo(t) k —
c
c — 粘性阻尼系数
解:k[ xi
(t)
xo
(t
)]
c
dxo (t dt
)
LT得:G(s)
X o (s) X i (s)
c
1 s 1
k
1 (设 c 1) Ts 1 k
§2.4.3 微分环节
微分环节具有输出正比于输入的微分
解:因为磁通不变,既ui恒定
uo T d dt (T为常数)
G(s)
U
o(s)
i
(s)
Ts
直流发电机作为测速发电机时
可以认为是一个微分环节
例: 液压阻尼器的原理图,图中A为活 塞右边面积;k为弹簧刚度;R为节流 阀液阻;p1 、p2分别为油缸左、右腔 单位面积上的压力。
xi—活塞位移 x0—油缸位移
解:
di(t)
1
u (t) L i
dt
i(t)R C i(t)dt
u o
(t
)
1 C
i(t)dt
LT,得:U U
i (s)LsI (s)
0
(
s)
1 cs
I
(
s)
I
(s)
R
1 cs
I
(
s
)
G(s) Uo (s)
1
Ui (s) LCs 2 RCs 1
n 1 LC
R C
2LΒιβλιοθήκη §2.4.6 延时环节(迟延环节)
当 A盘作恒速转动,并靠摩擦力带动
B盘以角速度ω转动时,因 B盘和I 轴
间以滑动键联接,故B盘滑动就会改变 偏心量e;当时e=0,A盘转动而 B盘不 转;e增大, B盘角速度ω正比的增大, 设K为比例常数,B盘转角为θ(t)。 输入— e 输出—θ(t)
解: (t) Ke(t)
(t) K e(t)dt
L[xi (t)] L[xi (t)]
Xi (s)es es X i (s)
强调:
1、一个元件和一个环节不是等价的。 一个元件可能划分为几个环节,也可能几 个元件构成一个环节。
2、不要把表示系统结构情况的物理框图 与分析系统的传递函数的框图混淆。
3、环节的传递函数也不是固定不变的, 这取决于选取的输入及输出量是什么。 当输入、输出量不同时,传递函数不同。
相似原理
xi (t)
R
k
ui i
C
uo
c
xo (t)
对于上述两图知是电系统与机械系统两种装置。
对于这两种机构求其传递函数均为
G(s) 1 Ts 1
两者物理模型不同,但数学模型相同, 功能相同,对于二者的“异构同功”称其 为相似系统。
例1. 无源滤波电路
ui u
o
C为电容 R为电阻
解:
ui
(t
)
i
(t
)
R
1 C
i(t
)dt
1
uo (t) C i(t)dt
LT得:
Ui
(t)
I
(s)R
1 Cs
I
(s)
Uo
(t)
1 Cs
I
(s)
G(s) U1(s) 1 1 (设RC T ) U0(s) RCs 1 Ts 1
例2、弹簧阻尼系统
油缸的力平衡方程式:
A( p2 p1) kxo
通过节流阀的流量:
q
A(xi xo )
p2 R
p1
得:
(xi xo )
k A2R
xo
G(s)
XX((o ss)) i
s
s
k
A2 R
令T A2R k
G(s) Ts Ts 1
此系统为包含有惯性环节及微分环节的系统。
当|Ts|<<1时,G(s)=Ts, 才近似为理想的微分环节。
动力学方程为: xo (t) Kxi (t)
G(s) Xo (s) Xi (s) K
§2.4.2 惯性环节:(一阶惯性环节)
动力学方程为 : Txo (t) xo (t) Kxi (t)
G(s) K Ts 1
K为惯性环节的增益或放大系数;T为时间常数
理想的一阶惯性环节 G(s) 1 Ts 1
即 xo (t) Txi (t)
G(s) Xo (s) X (s) Ts i
T为微分环节的时间常数
1、理想的微分环节 G(s) Ts 2、实际的微分环节 G(s) Ts
Ts 1
3、微分环节对系统的控制作用
例1、 电压下图为一直流发电机原理
图。激磁电压ui恒定,磁通不变。此时 电枢u0与转速 成正比(θ为转子转 角),即输入量为θ,输出量为u0。
(1)预见输入(使输入提前)
比例环节 R(s)
r(t) t
1
X o (s)
xo (t)
1
o 45
t
比例+微分
R(s)
r(t) t
1 Ts
Xo (s)
xo (t)
21
o
t
t1 t 2
(2)增加阻尼
KP
K s(Ts 1)
G(s)
KPK
1
Ts 2 s K P K
K
K P (Td s 1)
§2.4 典型环节的传递函数
§2.4.1 比例环节 §2.4.2 惯性环节(一阶惯性环节) §2.4.3 微分环节 §2.4.4 积分环节 §2.4.5 振荡环节(二阶振荡环节) §2.4.6 延时环节(迟延环节)
§2.4.1 比例环节
凡输出量与输入量成正比,输出不失真 也不延迟,而按比例地反映输入的环节, 称为比例环节。
相似系统:能用形式相同的数学模型来 描述的物理系统。
s(Ts 1)
G(s) 2
Ts
2
K K(T s 1)
P
d
(1 K p KTd)s K P
K
(3)强化噪声
§2.4.4 积分环节
积分环节是输出正比于输入对时间的积分 的环节。
即:
x(t) o
1 T
x(t)dt i
拉氏变换得
:
X(o s)
1 Ts
X(i s)G(s)
1 Ts
T为积分环节的时间常数
例题:
G(s) (s) E(s) K s
设
T
1 K
则 G(s) 1 Ts
§2.4.5 振荡环节(二阶振荡环节)
T 2xo (t) 2Txo (t) xo (t) xi (t)
G(s)
1
T s2 2 2Ts 1
— 阻尼比(0 1)
T — 振荡环节的时间常数
n — 1 T
n
n代入G(s)得
G(s)
s2
n2 2ns
n2
注意:
1)0≤ξ<1时,二阶系统为振荡环节。 2) ξ≥1时,二阶环节不是振荡环节,
而是两个一阶惯性环节的组合。 所以二阶环节不一定是振荡环节。
例:无源R-C-L网络
L
R
ui
i
C
uo
ui (t) — 输入电压 L —电感 R —电阻 uo (t) — 输出电压 i(t) —电流 C —电容
k
xi(t) xi (t) —
xo (t) — 输出位移
xo(t) k —
c
c — 粘性阻尼系数
解:k[ xi
(t)
xo
(t
)]
c
dxo (t dt
)
LT得:G(s)
X o (s) X i (s)
c
1 s 1
k
1 (设 c 1) Ts 1 k
§2.4.3 微分环节
微分环节具有输出正比于输入的微分
解:因为磁通不变,既ui恒定
uo T d dt (T为常数)
G(s)
U
o(s)
i
(s)
Ts
直流发电机作为测速发电机时
可以认为是一个微分环节
例: 液压阻尼器的原理图,图中A为活 塞右边面积;k为弹簧刚度;R为节流 阀液阻;p1 、p2分别为油缸左、右腔 单位面积上的压力。
xi—活塞位移 x0—油缸位移
解:
di(t)
1
u (t) L i
dt
i(t)R C i(t)dt
u o
(t
)
1 C
i(t)dt
LT,得:U U
i (s)LsI (s)
0
(
s)
1 cs
I
(
s)
I
(s)
R
1 cs
I
(
s
)
G(s) Uo (s)
1
Ui (s) LCs 2 RCs 1
n 1 LC
R C
2LΒιβλιοθήκη §2.4.6 延时环节(迟延环节)
当 A盘作恒速转动,并靠摩擦力带动
B盘以角速度ω转动时,因 B盘和I 轴
间以滑动键联接,故B盘滑动就会改变 偏心量e;当时e=0,A盘转动而 B盘不 转;e增大, B盘角速度ω正比的增大, 设K为比例常数,B盘转角为θ(t)。 输入— e 输出—θ(t)
解: (t) Ke(t)
(t) K e(t)dt
