量 第十九章 4(薛定谔方程 一维方势阱 隧道效应 线性谐振子)2009
4线性谐振子与势垒贯穿

U r r r0处U r 有极小值 0 r r0
2U r 令k r 2 r 0 1 3U r g 2 r 3 r
0
1 1 2 3 U r U r0 k r r0 g r r0 1 2 3
线性谐振子 n=10时的几率密度分布
表明: 当n很大时, 量 迅速振荡,此时其平均值和经典振子
的概率密度已经接近,说明在n很大时即能量很高时, 量子振子的行为可以用经典振子来代替。
1 n x 例:设谐振子的初态为 x,0 A n 0 2
求(a)求归一化常数A;(b) x, t ? 解:(a)
1 2
1 2
(1)、(2)式改写为:
d 2 2 k1 0, 2 dx 2 d k22 0, dx2
x 0, x a 3
0 x a 4
x 0 :1 Aeik x Aeik x
E
1 En n , n 0,1,2,9 2
1 讨论: En n , n 0,1,2, 2
1、量子力学中一维线性谐振子的能量是不连续的,即量子化的。 2、能级的间隔等距,即
U(x)
n=3
En En1 En
/2
舍去!
应有限
方程(4)的渐进解为:
e
2 / 2
设方程(4)的一般解为: e
2
2 / 2
H ( )
2
6
2
代 入
d dH d H 2 2 H 2 H e 2 2 d d d
21.7 一维势阱 势垒 隧道效应

STM的发明者 宾尼、罗雷尔和电 子显微镜的发明者 卢斯卡分享了1986 年诺贝尔物理奖。
宾尼
罗雷尔
U0
电子云重叠 U0 U0 E
样 品
d
针 尖
扫描隧道显微镜(STM)装置示意图
用STM得到的神经细胞象
液体中观察原子图象
在电解液中得到的硫酸根离子吸附在铜 单晶表面的STM图象。
“扫描隧道绘画 ” 一氧化碳“分子人”
8 n1 x n2 y n3 z ( x, y, z ) sin sin sin l1l2 l3 l1 l2 l3
三维势阱中粒子的能量:
n12 2 2 n2 2 2 2 n32 2 2 E 2 2 2 2ml1 2ml2 2ml3
处在超晶格的一维量子线和两维量子阱中的电子 就属于一维和两维势阱中的粒子,而处在金属内的电 子可看作三维势阱中的粒子。
i En t
)e
i En t
( px En t )
C 2e
( px En t )
n ( x, t ) 是由两个沿相反方向传播的平面波叠加而
③粒子在阱中的分布 经典力学的结果:均匀分布 P ( x ) 1/ a a a P ( x)dx P ( x) dx P ( x)a 1
(4) 解方程、定常数 在 0<x<a 区域,定态薛定谔方程为
令
d x 2mE 2 x 0 2 dx 2mE 2 k 2 d 2 x 2 k x 0 2 dx
2
比较谐振动方程 特解为
d2x 2 x0 2 dt
( x ) C sin(kx )
2 2 2
薛定谔方程的应用
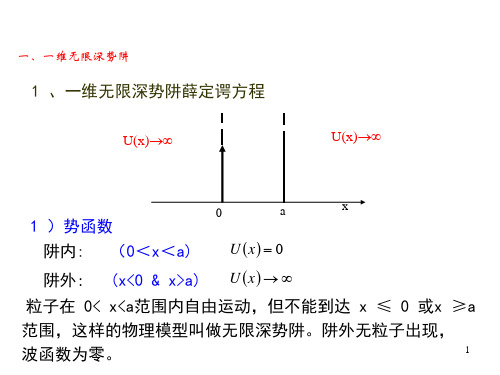
n 1,2,3...0 x a
待定系数是由边值条件和归一化条件所决定,与机械波中完 全由初始条件决定所不同,这就体现了物质波是概率波的特点。
5
2 、方程解的物理意义
nx
2 sin n x
aa
n 1,2,3...
1)处在势阱中的微观粒子,其德布罗意波只能是驻波。
这是因为在阱壁处(即 x=0,x=a处)其Ψ(x)=0 ,只能是 波节,因此物质波在阱内运动要能够稳定下来,其在阱壁两端 来回反射,必定形成德布罗意驻波。
2) 最低能量 (零点能) ——波动性
22
E1 2ma2 0
9
n 不能取 0 ,如 n=0 ,则意味着Ψ( x )= 0 ,即在方 势阱中到处找不到粒子,这显然是没有意义的。
nx
2 sin n x
aa
n 1,2,3...
n = 1 时,称基态能级(零点能)。基态能不为零,是经典
物理不能解释的。
3) 能级间距
E
En1
En
(2n 1)
2 2
2ma 2
(2n 1)E1
可看出,能级间距与粒子质量和阱宽的平方成反比。
对于微观粒子,若限制在原子尺度内运动时,ћ2~ma2,即阱宽 很小时,则能量的量子化是很显著的,因此必须考虑粒子的量子 性;
但即使是微观粒子,若其在自由空间运动 (相当于阱宽无穷
大) ,其能级间距就非常小,则可认为能量的变化是连续的;
一、一维无限深势阱
1 、一维无限深势阱薛定谔方程
U(x)
U(x)
1 )势函数
0
a
x
阱内: (0<x<a) U x 0
阱外: (x<0 & x>a) U x
定态薛定谔方程的解法一维无限深势阱与线性谐振子
2 d U 0 E , x 0, x a 2 2 d x 2
当势壁无限高是,不可能 在势阱外发现能量有限的 粒子,故阱外波函数为0
2. 引入参数简化方程,得到含待定系数的解;
令
2E k
2 势阱内定态薛定谔方程为: x k x 0
x
量子力学中把在势 1 2 U x kx 场 中运 2 动的微观粒子称为 线性振子 ,其势能 曲线为抛物线
讨论谐振子的意义:
(1)许多物理体系的 势能曲线可以近似看 作抛物线,双原子分 子的势能曲线在稳定 平衡点a附近的势能曲 线。 (2)复杂的振动可以 分解为相互独立的谐振 动动;
(3)处理线性谐振子的方法适用于:坐标表象、 粒子表象和电磁场量子化。
线性谐振子的哈密顿量
d 当, p i 时, dx
p2 1 H 2 x 2 2 2
线性谐振子的哈密哈密顿算符
2 d 2 1 2 2 x H 2 2 dx 2
故,定态薛定谔方程为
2 d 2 1 2 2 - 2 dx2 2 x x E x
2
1. 单调性;
2. 有限性;
在有限的空间范围内发现粒子的概率有限
3. 连续性;
V0
x, t
2
d 有限值
定态薛定谔方程包含 x, t 对坐标的二阶导数, 要求 x, t 及其对坐标的一阶导数连续。
1.5.2 一维无限深势阱 设质量为 的粒子在势场中运动
0,0 x a (势阱内) U x (1.5.1) , x 0, x a(时间外)
19.7波函数薛定谔方程一维势阱隧道效应贺泽东共23页

A和B是待定常数
U(x)=0
• 阱外: (x)0
经典力学
量子力学
不考虑物质的波粒二象性 经典质点有运动轨道概念
牛顿力学方程
根据初始条件可求出经典质点的
运动状态
针对物质的波粒二象性 微观粒子无运动轨道概念 是否存在一个
量子力学方程
根据某种条件可求出微观粒子的
运动状态 波函数
量子力学中的
算符
基本算符 算符是表示对某一函数进行某种数学运算的
符号。在量子力学中,一切力学量都可用算符
E h
经典的沿x方向 传播平面单色波
h
p
y(x,t)
A e i
2π
( t
x
)
沿 X方向匀 的自由粒子的波函数为
速直线运动
Ψ(x,t)
ei2π(vtx)
0
i(Etpx)
i p x Ψ(x,t) 0e h
0
待定 常数
0e h
i Et
eh
相当于x处波函数的复振幅 反映波函数随时间的变化
沿 X方向匀 的自由粒子的波函数为 速直线运动
了解
含时薛定 谔方程
定态 定态薛定谔方程
定态波函数
三 一维势阱问题
1.势能函数
U(x)0 (0xa) U(x)( x0, xa)
2.哈密顿量 由 H ˆ 2 2 U(r,t)
2m
得: H ˆ 2m 2 dd2x2U(x)
3.定态薛定谔方程
H ˆ (x)E (x)
U(x)=0
x
0
a
定态薛定谔方程 H ˆ (x)E (x)
i(Etpx)
Ψ(x,t) 0e h
三维 沿 方向匀 的自由粒子的波函数为 速直线运动
定态薛定谔方程的解法 一维无限深势阱与线性谐振子PPT文档共35页

谢谢!
51、 天 下 之 事 常成 于困约 ,而败 于奢靡 。——陆 游 52、 生 命 不 等 于是呼 吸,生 命是活 动。——卢 梭
53、 伟 大 的 事 业,需 要决心 ,能力 ,组织 和责任 感。 ——易 卜 生 54、 唯 书 籍 不 朽。——乔 特
定态薛定谔方程的解法 一维无限深势 阱与线性谐振子
1、战鼓一响,法律无声。——英国 2、任何法律的根本;不,不成文法本 身就是 讲道理 ……法 律,也 ----即 明示道 理。— —爱·科 克
3、法律是最保险的头盔。——爱·科 克 4、一个国家如果纲纪不正,其国风一 定颓败 。—— 塞内加 5、法律不能使人人平等,但是在法律 面前人 人是平 等的。 ——波 洛克
55、 为 中 华
一维谐振子问题
考虑一维谐振子的基态:
= E0
1 2
U (x) 1 2 x2
2
x2
1 ——谐振子的特征长度
x 1,经典允许区;
按照经典理论,
x 1,经典禁区.
按照量子力学中波函数的统计诠释,基态粒子处于经
典禁区中的概率为:
1
球坐标系下的体积元的表达式:
d r 2 sin dddr
r到r+dr的球壳的体积:
dV
0
2
0
d
sin
d
r
2dr
在r到r+dr的球壳内找到粒子的概率:
0
2
0
(r,
,
)
2
d
sin
d
r
2dr
例3:求处于一维无限深方势阱中的粒子的位置、动量 和动能的平均值。
2
由图可以看出,量子数n较小时,粒子位置的概率 密度分布与经典结论明显不同。随着量子数n的增 大, 概率密度的平均分布将越来越接近于经典结论。
例1:一个电子被束缚在一维无限深势阱内,势阱宽度 为1.011010 m。求当电子处于基态时对阱壁的平均 冲力。 解: 要求平均冲力,先要求平均冲力算符。 设电子质量为me、速度为vx、动量为px 、势阱宽度为a。 平均冲力等于单位时间内的冲量。 动量定理:在运动过程中,作用于质点的合力在一段 时间内的冲量等于质点动量的增量。
能量的分立现象在微观领域是普遍存在的!
② 一维谐振子的能谱是等间距的,即相邻两能级的 能量差是固定的;
一维无限深势阱薛定谔方程求解
一维无限深势阱薛定谔方程求解一维无限深势阱是量子力学中最经典的问题之一,其求解对于理解基本的量子力学原理以及波函数的性质具有重要的意义。
薛定谔方程是描述量子力学体系中粒子的行为的基本方程,通过求解薛定谔方程,我们可以获得系统的波函数及其相应的能级。
让我们来考虑一个无限深势阱,这个系统可以简单地用一个势能函数来描述。
在这个系统中,粒子只能在一个有限的空间区域内运动,而且势能在这个区域内是常数为零的。
首先,我们需要写出薛定谔方程。
对于一维情况,薛定谔方程可以写成:-ħ²/2m * d²ψ(x)/dx²+ V(x)ψ(x) = Eψ(x)。
其中,ψ(x)是系统的波函数,V(x)是势能函数,E是波函数对应的能量。
对于无限深势阱,势能函数在阱内为零,在阱外为无穷大。
因此,V(x)在阱外的值可以视为一个很大的正数。
接下来,我们需要考虑边界条件。
在无限深势阱中,粒子是被约束在一个有限空间内的。
因此,在边界处,粒子的波函数必须为零。
对于一个无限深势阱,边界条件可以写为ψ(0)=ψ(a)=0,其中,a是阱的宽度。
现在,让我们尝试求解薛定谔方程。
由于系统的势能在阱内为零,薛定谔方程可以简化为:-d²ψ(x)/dx² = k²ψ(x),其中,k=√(2mE/ħ²)。
这是一个常微分方程,我们可以通过分离变量和积分来求解。
假设ψ(x)可以分解为两个函数的乘积:ψ(x) = X(x)Y(y)。
将这个假设代入方程中,并整理得:1/X(x) * d²X(x)/dx² = -1/Y(y) * dY(y)/dy = -k²。
我们可以分别对X(x)和Y(y)进行求解,然后将两个解再组合起来得到系统的波函数。
针对常微分方程1/X(x) * d²X(x)/dx² = -k²,我们可以得到其解为X(x) = Asin(kx) + Bcos(kx),其中,A和B是常数。
大学物理-薛定谔方程
1.势能
若选线性谐振子平衡位置为坐标原点和势能
零点, 则一维线性谐振子的势能可以表示为:
U( x) 1 kx2 1 m 2 x2
2
2
m — 粒子的质量 k — 谐振子劲度系数
谐振子的角频率 k
m
2. 谐振子的定态薛定谔方程
由
d2
d x2
2m 2
[E
U
(
x)]
0
和 U(x) 1 m2x2
2
“有限”要求 D = 0,
2 C ek2x
E
(E U ,是衰减解)
U (x)
U= U0
U= 0
x
Ⅰ区 0 Ⅱ区
按经典力学……粒子不可能在 Ⅱ 区出现! 按量子力学……粒子仍有可能在Ⅱ 区出现!
若势能曲线 如图所示:
U
( x) U= U0
有一个有限 E 宽度的“势垒”。 U= 0
U= 0 x
n 所以有 o Asin a x,
n e Acos a x,
n 2,4,6, n 1,3,5,
为了求出 A,我们用波函数的归一化条件,例如
1
a / 2
a / 2 o
2
d
x
A2
a
/
2
s
in2
(
n
x)d
x
a
A2
a / 2
a
2
可得
A 2 a
于是对每一个 n 值,波函数的空间部分为
2 n
on
称为定态薛定谔方程。
对势能函数 U 与时间t 无关的定态问题, 只须解定态薛定谔方程(2)式,再乘上(1)式
即可得总波函数 (x, t )。
例.一维自由运动微观粒子的波函数。 电子枪
量子力学 一维无限深方势阱,线性谐振子,势垒贯穿
(7)
由此得到,
Asin a 0,
B cos a 0
(8)
第二章 波函数和薛定谔方程 2.6、 一维无限深方势阱
A 和 B 不能同时为零,否则 y 处处为零。因此,
A 0, B 0, cos a 0 sin a 0
(9) (10)
由此可求得:
n a , 2
(2n 1) 2 h2 En En1 En , 8ma 2
a)、 En µ n 2 ,当 n ® ¥时,
DEn 1 n®¥ ~ ¾ ¾¾ ®0 En n
正如对应原理所示大量子数极限下量子理论将逐渐 逼近经典理论。
第二章 波函数和薛定谔方程 2.6、 一维无限深方势阱
b)、 DEn µ
第二章 波函数和薛定谔方程 2.6、 一维无限深方势阱
一维无限深势阱的能量本征函数一维无限深势阱中粒子位置几率密度分布
第二章 波函数和薛定谔方程 2.7、 线性谐振子
2.7.1、谐振子模型
2.7、 线性谐振子 2.7.1、谐振子模型 经典力学中,当质量为 m 的粒子受到弹性力 F kx 作 用,其运动方程为,
考察上式解的渐进行为,当
很大时, 与 相比可
以忽略,方程(4)可以近似表示为:
d 2 2 0 2 d
(5)
第二章 波函数和薛定谔方程 2.7、 线性谐振子
2.7.2、 线性谐振子的能量本征值问题
不难证明,
时, ~ e
2
/2
,
~ e
第二章 波函数和薛定谔方程
第二章 波函数和薛定谔方程
第三部分、一维无限深方势阱,线性谐振子,势垒贯穿
第二章 波函数和薛定谔方程 引言
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一维无限深方势阱
, x 0. x a U (x ) 0, 0 x a
特点:
U m 0
粒子在势阱内势能为零 受力为零 在阱内自由运动 在阱外势能为无穷大
E
a
在阱壁上受极大的斥力 不能到阱 外
若是经典粒子,粒子如何运动?
E 可取任意值,且各处出现的 概率一样
薛定谔方程和波函数:
•令上述关系作用于波函数
i Px x
2 2 2 Px 2 x 替换关系
Ψ ( x, t )
•得到自由粒子满足的薛定谔方程
2 2 Ψ ( x, t ) i Ψ ( x, t ) t 2m x 2
自由粒子一维含时薛定谔方程
(二)、势场中粒子的薛定谔方程
d 2 2mE 2 0 2 dx
2mE 令k 2
2
方程变为
•通解
( x) A coskx B sinkx
式中 A 和 B 是待定常数
d 2 k 2 0, 2 dx
•通解
( x) A coskx B sinkx
式中 A 和 B 是待定常数
此解需满足标准化条件:即在 x = 0和 x = a 是连续的. 由于在边界外 ,ψ = 0 ,所以有
微分
•写出非相对论自由粒子能量动量关系式
2 P E= x
i E t
i Px x
2 2 2 Px 2 x 替换关系
2m
•写出非相对论自由粒子能量动量关系式
2 Px E= 2m
i E t
•将替换关系代入写成
2 2 i t 2m x 2
0 0, a 0,
x 0 处 (0) 0
解的形式为
A 0
Bsin ka 0
( x) B sin kx
x a 处 ( a) 0
B不能再为零了 只能sin ka 等于零 n k , n 1,2,3, (k 0) a
说明 (1)薛定谔方程是一个复数偏微分方程;
其解波函数 Ψ r , t 是一个复函数。 (2)薛定谔方程的解满足态叠加原理
ˆ Ψ r , t i Ψ r , t H t
说明
(1)薛定谔方程是一个复数偏微分方程; 其解波函数 Ψ r , t 是一个复函数。
19-7 薛定谔方程及应用简例
经典力学(质点) 特点 运动情况 状态描述 粒子性 有轨道 量子力学(微观粒子) 波粒二象性 无轨道 波函数Ψ
坐标 r 和动量 P
牛顿方程
薛定谔方程
运动方程
2 dp d r m 2 dt dt
?
一. 薛定谔方程
薛定谔方程是非相对论微观粒子的基本方程 ----量子力学基本假设 地位同经典物理的牛顿定律 薛定谔 Erwin Schrodinger 奥地利人 1887-1961 创立量子力学的波动理论 获1933年诺贝尔物理学奖
能量可能值
π 2 2 2 En n (n 1,2,3,) 2 2ma
nx n B sin a
每个可能的值叫能量本征值(能级) 能量本征函数
为求出 B 的值,利用波函数的归一化条件
n
( x) dx
2
x
n 0
a
2
dx 1,
为求出 B 的值,利用波函数的归一化条件
1 e2 氢原子中的电子…… U r 4 0 r
当粒子在
U U (r ) 势场中运动时
则哈密顿量
2 2 ˆ H U (r ) 不显含时间 2m
采用分离变量法
将波函数写成
Ψ (r , t ) (r ) f (t )
将波函数写成
Ψ (r , t ) (r ) f (t )
i E t
i Px x
2 2 2 Px 2 x 替换关系
2 2 U ( x, t )] Ψ ( x, t ) i Ψ ( x, t ) [ t 2m x 2
势场中的一维含时薛定谔方程 2.三维势场中粒子的薛定谔方程 2 2 2 2 2 2 2 2 U ( x, t ) U (r , t ) x 2 x y z 2 2 2 2 2 拉普拉斯算符 2 2 x y z
( 0 x a) U(x) 势函数: U→∞ U (x ( x 0 x a)
U ( x) 0
2
U→∞
d U ( x) ( x) E ( x) 2 2m dx
2
E
U=0
0 a
x
定态薛定谔方程: 阱外:
2 d2 ( x) E ( x) ( x 0 x a) 2 2m dx
(一)、自由粒子薛定谔方程的引进
1. 自由粒子满足的方程
质量为m的自由粒子, 在非相对论下能量和动量的关系: 自由粒子的波函数: Ψ ( x, t ) Ψ e 0
2 px E Ek 2m i
( Et - Px x )
应该是薛定谔方程的解 薛定谔给出自由粒子波函数满足的微分方程是
2 2 Ψ ( x, t ) i Ψ ( x , t ) t 2m x 2
将波函数代入可以验证该方程
2. 写薛定谔方程的简单途径
自由粒子波函数
i ( Et - Px x ) Ψ ( x, t ) Ψ 0e
注意到
Ψ ( x,t ) i EΨ ( x,t ) t Ψ ( x,t ) i PxΨ ( x,t ) x 2Ψ ( x,t ) Px2 2 Ψ ( x,t ) 2 x 写薛定谔方程的基本过程:
物理上的主要任务是解方程(2) 2 2 ˆ ˆ (r ) E (r ) H U (r ) H
2m
2 2 定态薛定谔方程: U (r ) (r ) E (r ) 2m
讨论:
2 2 U ( r ) ( r ) E ( r ) 2m
令=E
上式 左边是 t 的函数 右边是 r 的函数 且两变量相互独立
两边必须等于同 一个常量时才成 立
得
df ( t ) 1 1 ˆ i H ( r ) dt f ( t ) ( r )
令=E
df ( t ) 得到两个独立的方程: i Ef ( t ) (1) dt ˆ ( r ) E ( r ) (2) H df ( t ) i iEt E 具有能量的量纲 Edt f t Ce f (t ) 代表粒子的能量
或写成
E E (r )
i
Et 则粒子的波函数:Ψ E (r , t ) E (r ) f (t ) E (r ) e
Ψ ( r , t ) ( r )e
i Et
Et 则粒子的波函数:Ψ E (r , t ) E (r ) f (t ) E (r ) e
阱内:
2 d2 ( x) E ( x) 2m dx 2
( 0 x a)
分区求通解:
1)阱外
2 d2 ( x) E ( x) 2 2m dx
根据波函数有限的条件
阱外
2)阱内
( x) 0
x a, x 0
2 d2 ( x) E ( x) 2 2m dx
2 2 ˆ H U (r ) 2m
ˆ Ψ (r , t) i Ψ (r , t ) H 代入薛定谔方程 t df ( t ) ˆ (r ) f (t ) 得 i (r ) H dt (r ) f (t ) 左右两边同除
得
df ( t ) 1 1 ˆ i H ( r ) dt f ( t ) ( r )
2 2 U (r , t )] Ψ (r, t) i Ψ (r , t ) [ t 2m
2 2 ˆ 引入哈密顿算符: H U r , t 2m
薛定谔方程普遍形式
ˆ Ψ r , t i Ψ r , t H t
(2)它的解满足态的叠加原理 因为薛定谔方程是线性偏微分方程。
若 Ψ ( r , t ) 和 Ψ ( r , t )是薛定谔方程的解, 1 2 则 c1Ψ(r , t ) c2Ψ (r , t ) 也是薛定谔方程的解。 1 2
(3)它并非推导所得,最初是假设,后来通过实验 检验了它的正确性,地位相当“牛顿定律”。
(4)它是非相对论形式的方程。
ˆ Ψ r , t i Ψ r , t H t
(三)、定态薛定谔方程
2 2 ˆ H U r , t 2m (不含时的薛定谔方程)
微观粒子的势能函数 U 与时间 t 无关的问题------定态问题。 例如: 自由运动的粒子…………U = 0
或写成
i Et Ψ ( r , t ) ( r )e
i
4.定态:能量取确定值的状态
又指粒子在空间的概率密度不随时间变化的状态
即
2 Ψ ( r , t ) E ( r )e
i Et
2
2 E ( r ) 与时间无关
二.定态薛定谔方程的 应用
一维无限深势阱中运 动的粒子
1.一维势场U(x,t) 中的粒子
Px2 U ( x, t ) •粒子总能量 E 2m 2 2 U ( x, t ) •替换后关系式 i 2 t 2m x
• 令其作用于波函数 Ψ ( x, t ) •得到一维势场中粒子满足的薛定谔方程
