知识讲解_正切函数的性质和图象_基础
正切函数图象性质PPT课件

所以:tan1670<tan1730
(2)因为 tan(-11/4)=tan(- 3/4) tan(-13/5)=tan(-3/5)
又有:-3/2< - 3/4< -3/5< -/2
tan(- 3/4)< tan(-3/5) 即 tan(-11/4) tan(-13/5)
练习3 1) tan15190
T π |(taxn
图象关于原点对称 5.单调性:在(π 2kπ ,π 2kπ,k)Z内都是增
6.对称中心: (k2π,0),kZ
二、正切函数的性质:
y
1
x
-3/2 - -/2
0 /2
3/2
-1
性质 定义域
答案
{x|x k + /2, k z}
tan14930
2) tan7 /8
tan1/6
小 结:
1.画正切函数的图象 2.正切函数的性质
正切线平移 观察正切函数图象
定值 周 奇 单
义 域
域
期 性
偶 性
调 性
3.数学思想:类比法、换元法、数形结合等
谢谢!
1
o1
-/2 -/4
o /4 /2
x
-1
y=tanx,x (-/2, /2)
由正切函数的周期性,把图象向左、向右扩展,得到 正切函数的图象,称为正切曲线
y
1
x
-3/2 - -/2
0 /2
3/2
-1
y=tanx
二.正切函数的性质
1.定义域:{ x|xπ 2k πk ,Z }
2.值 域: yR
3.周期性: 周期为
正切函数图象性质PPT课件
21-22版:1.4.3 正切函数的性质与图象(步步高)

3.函数 f(x)=|tan 2x|是 A.周期为 π 的奇函数 C.周期为2π的奇函数
B.周期为 π 的偶函数
√D.周期为π2的偶函数
解析 f(-x)=|tan(-2x)|=|tan 2x|=f(x), 故 f(x)为偶函数,T=π2.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
为 T=|ωπ|.
(3)正切函数在-π2+kπ,π2+kπ(k∈Z)上单调递增,不能写成闭区间,正切函数无单 调减区间.
4 课时对点练
PART FOUR
一、选择题
1.函数 y=tanx+π5,x∈R 且 x≠130π+kπ,k∈Z 的一个对称中心是
A.(0,0)
B.π5,0
√C.45π,0
D.(π,0)
A.0°<A<30°
√B.30°<A<45°
C.45°<A<60°
D.60°<A<90°
解析 33<23<1,即 tan 30°<tan A<tan 45°. 由正切函数随锐角的增大而增大, 得30°<A<45°,故选B.
12345
4.函数 y=4tan3x+π6的最小正周期为____π3____. 解析 T=|ωπ|=π3.
√A.2π4+12kπ,8π+12kπ,k∈Z
B.-π8+12kπ,2π4+12kπ,k∈Z
C.2π4+kπ,π8+kπ,k∈Z
D.2π4+kπ,8π+kπ,k∈Z
解析 因为 f(x)=tan2x+π4,所以 f(x)≥ 3化为 tan2x+π4≥ 3, 即π3+kπ≤2x+π4<π2+kπ,k∈Z;解得2π4+12kπ≤x<π8+12kπ,k∈Z, 故使 f(x)≥ 3成立的 x 的集合是2π4+12kπ,8π+12kπ,k∈Z.
讲义21:正切函数的图像与性质
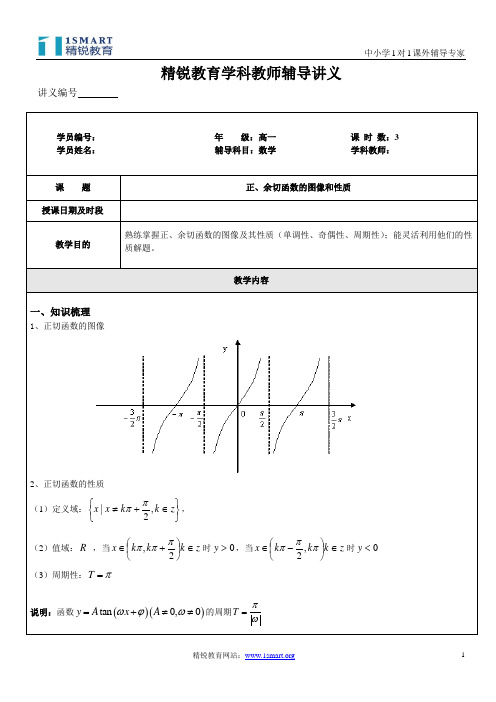
精锐教育学科教师辅导讲义讲义编号_学员编号: 年 级:高一 课 时 数:3 学员姓名: 辅导科目:数学 学科教师:课 题 正、余切函数的图像和性质授课日期及时段教学目的熟练掌握正、余切函数的图像及其性质(单调性、奇偶性、周期性);能灵活利用他们的性质解题。
教学内容一、知识梳理1、正切函数的图像2、正切函数的性质 (1)定义域:⎭⎬⎫⎩⎨⎧∈+≠z k k x x ,2|ππ, (2)值域:R ,当z k k k x ∈⎪⎭⎫⎝⎛+∈2,πππ时0>y ,当z k k k x ∈⎪⎭⎫⎝⎛-∈πππ,2时0<y(3)周期性:π=T说明:函数()()tan 0,0y A x A ωϕω=+≠≠的周期T πω=求三角函数式的最小正周期时,要尽可能地化为只含一个三角函数,且三角函数的次数为1的形式,否则很容易出现错误。
(4)奇偶性:()x x tan tan -=-奇函数,对称中心是,02k π⎛⎫⎪⎝⎭()k Z ∈ 特别提醒:正(余)切型函数的对称中心有两类:一类是图像与x 轴的交点,另一类是渐近线与x 轴的交点,但无对称轴,这是与正弦、余弦函数的不同之处。
(5)单调性:在开区间z k k k ∈⎪⎭⎫⎝⎛+-2,2ππππ内,函数单调递增。
但要注意在整个定义域上不具有单调性。
余切函数的图像和性质:二、例题解析例1 函数y =x tan log 21的定义域是( )A {x |0<x ≤4π) B {x |2k π<x ≤2k π+4π,k ∈Z }C {x |k π<x ≤k π+4π,k ∈Z }D {x |k π-2π<x ≤k π+4π,k ∈Z }巩固训练1、函数1tan y x =-的定义域是_______2、函数)1(cot log 2-x 的定义域是________2、函数tan 2()tan xf x x=的定义域为( ) A .{|x x R ∈ 且,4k x k Z π⎫≠∈⎬⎭B .{|x x R ∈ 且,2x k k Z ππ⎫≠+∈⎬⎭C .{|x x R ∈ 且,4x k k Z ππ⎫≠+∈⎬⎭D .{|x x R ∈ 且,4k x k k Z ππ⎫≠-∈⎬⎭4、函数tan()4y x π=-的定义域是( )A .|,4x x x R π⎧⎫≠∈⎨⎬⎩⎭ B .|,4x x x R π⎧⎫≠-∈⎨⎬⎩⎭C .|,,4x x k k R x R ππ⎧⎫≠+∈∈⎨⎬⎩⎭ D .3|,,4x x k k Z x R ππ⎧⎫≠+∈∈⎨⎬⎩⎭例2 函数tan()(0)6y ax a π=+≠的周期为( ).A .2a π B .2aπ C .a π D .a π 例3 比较大小:(1)125tan 与137tan ; (2)⎪⎭⎫ ⎝⎛-34tan π与⎪⎭⎫⎝⎛-511tan π。
正切函数的图象及性质

答:利用单位圆中的三角函数线先
在一个周期内作图,再由一个周期延伸 到整个定义域上,得出函数图象,观察 图象获取函数的性质。
教学过程设计
(二)、新 课 导 入
首先我们一起分析一下正切函数 y=tanx是否为周期函数? 因为
f ( x ) tan ( x ) tan x f ( x )
x | x k , k Z 2
全体实数集R
T
奇函数
在
, k k ,k Z 2 2
是增函数。
教学过程设计
(五)、例题讲解,巩固新知 例1:求下列函数 的定义域 。
y ta n ( x
设计说明
4
)
例2:不通过求值,判断下
教法分析
学法分析
过程分析
4.教学重、难点
(1)重点:正切函数的图象及其主要性质。 (2)难点:正切函数性质的理解和应用。
二、教 法 分 析
(一)教学方法
(二)教学手段
教材分析 (一)在教学方法上
教法分析
采用类比教学法,启发引导教学法,教授教学法等 诸多方法,引导学生自主学习,探究学习。教学过 程中以教师为主导,学生为主体,充分重视数形结合 的作用。
全体实数集 R
tan ( x ) tan ( x )
正切函数是奇函数,
且图象关于原点对称。 正切函数在开区间 k
, k , k Z 2 2
正切函数的周期为
内是增函数。
例1 求函数 y
tan( x
4 ,
4
) 的定义域。
高中数学第一册(下)第四章第十节:
高中数学 第一章 三角函数 1.4.3 正切函数的性质与图象讲义3 新人教A版必修4

知识点2 正切函数的图象 观察图形,回答下列问题:
问题1:画正切曲线的关键点和关键线分别是什么? 问题2:正切曲线是轴对称图形吗?是中心对称图形吗?
【总结提升】
1.正切函数图象的两种作法
(1)几何法:利用单位圆中的正切线作图,该方法较为精确,但画图时
较烦琐. (2)三点两线法:“三点”是指(-
lo g 1 x lo g 1 4,
2
2
tanx 1,
所以0<x< 或3 ≤x≤4.
所以所求定2 义域4 为(0, )∪[ 3, 4].
2
4
2在【.解[(变析0,换】π条由]件ta上、n的改x≠图变0象问,.法x∈),[将0本,题π]函,数解改得为x“≠0y , st且ainnxxx≠”试且 画x≠出π此. 函数
4
2
,xk∈kZ,
28
所以所求直线方程为x= k , k∈Z.
28
2.(变换条件)将本例函数改为“ y
么?
t a n x 1,
tan tan (x
x 1
”,其定义域又是什
)
6
【解析】根据题意,得
ta
n
(
x
) 6
0,
4
解得 x
2
(3)解形如tan x>a的不等式的步骤
【变式训练】函数 y 2log1x tanx 的定义域是______.
2
【解析】x应满足 2 lo g 1 x 0,
2
ta n x 0,
所以 0kxx4, k所2(以k0Z<), x<
高一数学正切函数的图像与性质课件

90 167 173 180
0 0
0
tan167 tan173
说明:比较两个正切值大小,关键是把相 应的角 化到y=tanx的同一单调区间内,再 利用y=tanx的单调递增性解决。
例题分析
例 2. 求函数y tan( x
3 3
A
0
3
X
y tan x x 利用正切线画出函数 , , 的图像: 2 2 把单位圆右半圆分成8等份。 作法: (1) 等分: 3 3 (2) 作正切线 , , , , , 8 8 4 8 8 4 (3) 平移 (4) 连线
90 167 173 180
0 0 0
4
0
5
2 tan tan 4 5 11 13 tan( ) tan( ). 4 5
例题分析
例1、比较下列每组数的大小。
(1)tan167 与 tan173
解:
0 0 0
o
o
13π 11π tan() 与 tan() (2) 4 5
补充练习
1. 已知
a tan1, b tan 2, c tan 3, 则( c )
B.c<b<a C .b<c<a D. b<a<c
A.a<b<c
2.求y (tan x)2 4 tan x 1 的值域; -5,+
3. 已知 是三角形的一个内角,且有 tan 1, 则的取值范围是 ( c )
解: (1)
11 (2) tan( ) tan , tan( 13 ) tan 2 4 4 5 5 2 又y tan x在 0, 0 , 是增函数 2 4 5 2
正切函数图像与性质
温故知新
回顾1:我们在学习正弦、余弦函数的图象时学习 过哪些作图方法? 几何描点作图法: 作正弦函数y=sinx的图象 作余弦函数y=cosx的图象 平移变换作图法: 作正弦、余弦函数的简图 五点作图法: 问题1:我们选择哪种方法作正切函数的图象? 几何描点作图法
正切函数的图象和性质 一、引入 如何几何描点法作正弦函数图象呢?
栏目 导引
知识回顾:任意角的正切线
y
T
y
x
o
(1,0)
A
x
正切线AT
o x(1,0) A
T
x
y
y
T
x
x
(1,0)
o
A
T
x
o
(1,0)
A
x
第一章
三角函数
作法如下:
作直角坐标
系,并在直角 坐标系y轴左侧 作单位圆。
y
找横坐标
(把x轴上 2 到 到这一 段分成8等份)
1
2
3 8 4 8
11 tan( ) tan , 4 4 2
2 4
13 2 tan( ) tan 5 5
又y tan x在(
2 tan tan 4 5
11 13 tan( ) tan( ). 4 5
5
2 2 ,
2
)是增函数
k , k , k z 2 2
2
k x
4
2ຫໍສະໝຸດ k , k z 函数y tan(x )的单调递增区间是: k , k , k z 4 4 4
正切函数的图像和性质
正切函数与三角函数图像的变换一、知识梳理1、正切函数2、三角函数的图像变换sin()(0,0)y A x A ωϕω=+>>(1)x ϕ对函数图像的影响在于轴上的平移量,称为平移变换; (2)x ω对函数图像的影响在于轴上的伸缩量,称为周期变换; (3)A y 对函数图像的影响在于轴上的伸缩量,称为振幅变换。
三角函数的图像变换有两种变换过程,一是先平移后伸缩,而是先伸缩后平移,注意会前后平移量的变化,第一种过程平移量是||ϕ,第二种过程平移量是||ϕω,主要是深刻理解变换过程均是针对的x 。
3、一般的我们把sin sin()(0,0)y x y A x A ωϕω==+>>变换到的过程可以叙述为:函数sin()(0,0)y A x A ωϕω=+>>的图像可以看作是先把sin y x =的图像上所有的点向左(ϕ>0)或向右(ϕ>1)平移|ϕ|个单位,再把所得各点的横坐标缩短(w>1)或伸长(0<w<1)到原来的ω1倍(纵坐标不变),再把所得各点的纵坐标伸长(A>1)或缩短(0<A<1)到原来的A 倍,(横坐标不变)。
即:平移变换→周期变换→振幅变换。
二、例题讲解1、 正切函数的图像和性质例1、求下列函数的定义域:()1()f x =; ()2 ()tan 1f x x =+例2、探讨函数()2tan(2)3f x x π=-的定义域、周期性及单调区间。
变式训练1:1函数tan cos y x x = 的部分图象是2、 函数1()tan()23f x x π=+的周期为_________3、函数()lg(1tan )f x x =-的定义域为____________2、三角函数图像的基本变换例3、把y =sin x 的图象向左平移3π个单位,得到函数____________的图象;再把所得图象上的所有点的横坐标伸长到原来的2倍,而纵坐标保持不变,得到函数____________的图象.例4、将正弦曲线如何变换可以得到到函数)32sin(2π+=x y 的图像,请写出变换过程,并画出一个周期的闭区间的函数简图。
正切函数的图象和性质
f ( x ) tan(x ) tan x f ( x)
所以 y=tanx 是周期函数, 是它的一个周期
类似正弦曲线的作法,我们先作正切函数在一 个周期上的图象。
y tan x, x (
, ) 的图象 2 2
y
利用正切线画图
3
2
4
6
1
A
2
课堂作业
课本P80 习题 4.10 1. 3.
所以函数
y tan(x ) 4
的定义域是
{x | x
4
k , k Z }
四:小 结
(1)图象:
y
3 2
2
0
2
3 2
x
(2)性质: 1. 定义域: 2. 值 域: 3. 周期性: 4. 奇偶性: 5. 单调性:
x x
k , k Z 正切函数的值域是实数集R 正切函数是周期函数,周期是 奇函数, 它的图象关于原点 对称. ( k , k ), k Z 增函数 2 2
4.10 正切函数的图象和性质
y
3 2
2
0
2
3 2
x
卢氏县第一高级中学
知识回顾:
1. 什么是正切线?y
P
O
T
A
x
2. 什么是周期函数?
f ( x) f ( x T )
3. 如何利用单位圆中的正弦线作出
正弦函数图象?
一:用正切线作正切函数的图象
首先我们一起分析一下正切函数y=tanx 是否为 周期函数? 因为
正切函数的性质与图象
§1.4.3正切函数的性质与图象编著:王西田 审核:高一数学组 【学习目标 】1、掌握正切函数的图象和性质.2、能正确应用正切函数的图象和性质解决有关问题.3、重点:正切函数的图象及其主要性质。
难点:利用正切线画出函数y=tanx (2π-<x<2π+)的图象,对直线x= 2π±是y=tanx 的两条渐近线的理解。
关键:对正切曲线特点的理解。
【知识探究】1、正切函数t a n y x =的定义域为____________;正切函数t a n y x = 的最小正周期为____________;tan()y x ωϕ=+的最小正周期为_____________.2、正切函数tan y x =为___________函数.(填:奇或偶)3、正切函数tan y x =在每一个开区间__________内为增函数.4、正切函数tan y x =的值域为_____________.5、利用正切线画出正切函数y=tanx (2π-<x<2π)的图像根据正切函数的周期性,只要把上述图像向左、右扩展,就可以得到正切函数的图像,我们把它叫做正切曲线。
【例题分析】例1、根据正切函数图象,写出满足下列条件的x 的范围①tan 0x >②tan 0x =③tan 0x <④tan x >例2、与函数tan(2)4y x π=+的图象不相交的一条直线是( ).A .2x π= B .2y π= C .8x π= D .8y π=例3、函数tan()3y x π=+的定义域( ).A .|,6x R x k k Z ππ⎧⎫∈≠+∈⎨⎬⎩⎭B .|,6x R x k k Z ππ⎧⎫∈≠-∈⎨⎬⎩⎭C .|2,6x R x k k Z ππ⎧⎫∈≠+∈⎨⎬⎩⎭D .|2,6x R x k k Z ππ⎧⎫∈≠-∈⎨⎬⎩⎭例4、函数4tan(3)4y x π=+的周期是().A .23π B .2πC .3πD .6π【基础训练】A1 1、tan (,)2y x x k k Z ππ=≠+∈在定义域上的单调性为().A .在整个定义域上为增函数B .在整个定义域上为减函数C .在每一个开区间(,)()22k k k Z ππππ-++∈上为增函数D .在每一个开区间(2,2)()22k k k Z ππππ-++∈上为增函数2、下列各式正确的是( ). A .1317tan()tan()45ππ-<- B .1317tan()tan()45ππ->-C .1317tan()tan()45ππ-=-D .大小关系不确定A2 3、若tan 0x ≤,则( ). A .22,2k x k k Zπππ-<<∈ B .2(21),2k x k k Zπππ+≤<+∈C .,2k x k k Zπππ-<≤∈ D .,2k x k k Zπππ-≤≤∈ B1 4、函数tan 2()tan x f x x=的定义域为( ).A .{|x x R ∈ 且,4k x k Z π⎫≠∈⎬⎭B .{|x x R ∈ 且,2x k k Z ππ⎫≠+∈⎬⎭C .{|x x R ∈且,4x k k Z ππ⎫≠+∈⎬⎭D .{|x x R ∈且,4k x k k Z ππ⎫≠-∈⎬⎭B2 5、函数y = ). A .|22,2x k x k k ππππ⎧⎫≤<+∈⎨⎬⎩⎭B .|22,2x k x k k ππππ⎧⎫<≤+∈⎨⎬⎩⎭{}C.|22,|2,2x k x k k x x k k Z ππππππ⎧⎫≤<+∈⋃=+∈⎨⎬⎩⎭ D .|222x k x k πππ⎧≤<+⎨⎩且}2,x k k Zππ≠+∈C1 6、直线y a =(a 为常数)与正切曲线tan (y x ωω=为常数,且0)ω>相交的两相邻点间的距离为( ). A .π B .2πω C .πωD .与a 值有关7、函数tan()4y x π=-的定义域是().A .|,4x x x R π⎧⎫≠∈⎨⎬⎩⎭B .|,4x x x R π⎧⎫≠-∈⎨⎬⎩⎭C .|,,4x x k k R x R ππ⎧⎫≠+∈∈⎨⎬⎩⎭D .3|,,4x x k k Z x R ππ⎧⎫≠+∈∈⎨⎬⎩⎭C2 8、函数tan()(0)6y ax a π=+≠的周期为( ).A .2aπ B .2aπ C .aπ D .aπ9、下列函数不等式中正确的是( ).A .43tan tan 77ππ> B .23tan tan 55ππ<C . 1315tan()tan()78ππ-<-D .1312tan()tan()45ππ-<-D1 10、在下列函数中,同时满足:①在0,2π⎛⎫⎪⎝⎭上递增;②以2π为周期;③是奇函数的是( ).A .tan y x =B .cos y x =C .tan 2x y = D .tan y x =-【能力拓展】D2 1、求函数tan ||y x =的定义域与值域,并作图象.2、求函数tan()26xy π=-的单调区间.【感悟反思】熟练掌握正切函数性质,同时要注意数形结合,借助单位圆或正切函数的图象对问题,直观迅速作业解答.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正切函数的性质与图象
【学习目标】
1.能画出tan y x =的图象,并能借助图象理解tan y x =在,22ππ⎛⎫
- ⎪⎝
⎭上的性质; 2.会利用正切函数的单调性比较函数值大小; 3.理解正切函数的对称性. 【要点梳理】
要点一:正切函数的图象 正切函数R x x
y ∈=tan ,且()z k k x ∈+≠
ππ
2
的图象,称“正切曲线”
(1)复习单位圆中的正切线: A T=tan α (2)利用正切线画函数y= tanx ,x ∈)2
,2(π
π-
的图象
步骤是:①作直角坐标系,并在x=2π
-的左侧作单位圆 ②把单位圆的右半圆分成8份,(每份8
π
).分别在单位圆中作出
正切线;
③把横坐标从2π-到2
π
也分成8份
④把正切线的端点移到对应的位置; ⑤把上面的点连成光滑的曲线.
由于tan (x+π)=tanx , y=tanx 是周期为π的周期函数只把y=tanx , x ∈)2
,2(π
π-的图象左、右移动k π个单位(k ∈z )就得到y=tanx (x ∈R 且x ≠k π+2
π
)的图象.
要点二:正切函数的性质 1.定义域:⎭
⎬⎫
⎩
⎨⎧∈+≠z k k x x ,2|ππ
, 2.值域:R
由正切函数的图象可知,当()2
x k k z π
π<
+∈且无限接近于2
k π
π+时,tan x 无限增大,记作tan x →+∞
(tan x 趋向于正无穷大);当()2
x k k z π
π>-
+∈,tan x 无限减小,记作tan x →-∞(tan x 趋向于负无穷
大).也可以从单位圆上的正切线来考虑.因此tan x 可以取任何实数值,但没有最大值和最小值.称直线
,2
x k k z π
π=+
∈为正切函数的渐进线.
3.周期性:正切函数是周期函数,最小正周期是π 4.奇偶性:正切函数是奇函数,即()x x tan tan -=-. 要点诠释:
观察正切函数的图象还可得到:点,0()2k k z π⎛⎫
∈ ⎪⎝⎭
是函数tan ,y x x R =∈,且2x k ππ≠+的对称中心,正
切函数图象没有对称轴
5.单调性:在开区间z k k k ∈⎪⎭
⎫
⎝⎛++-ππππ2,2内,函数单调递增要点诠释:
正切函数在开区间z k k k ∈⎪⎭
⎫
⎝⎛++-
ππππ2,2内单调递增,不能说正切函数在整个定义域上是增函数.
要点三:正切函数型tan()(0,0)y A x A ωϕω=+≠>的性质 1.定义域:将“x ωϕ+”视为一个“整体”.令,2
x k k z π
ωϕπ+≠+∈解得x .
2. 值域:(),-∞+∞ 3.单调区间:(1)把“
x ωϕ+”视为一个“整体”
;(2)0(0)A A ><时,函数单调性与t a n (,)
2y x x k k z π
π=≠+∈的相同(反);(3)解不等式,得出x 范围. 要点诠释:
若0ω<,一般先用诱导公式化为0ω>,使x 的系数为正值,然后求单调区间. 4.奇偶性:当()2
k k z π
ϕ=
∈时为奇函数,否则,不具备奇偶性. 5.周期:最小正周期为||
T πω=
. 【典型例题】
类型一:正切函数的定义域 例1.求下列函数的定义域. (1)1
lg(tan )y x =;(2)y =
举一反三:
【变式1】(2016 宁夏期中)已知函数()tan()23
f x x π
π
=+
(1)求f (x )的最小正周期.
(2)求f (x )的定义域和单调区间.
(3)求方程()f x =
类型二:正切函数的图象 例2.函数1
tan 2
3y x π⎛⎫=-
⎪⎝⎭在一个周期内的图象是下图中的( )
【变式1】(2015秋 安徽舒城县期末)如图所示,函数3cos |tan |(02y x x x π=≤≤且)2
x π
≠的图象是( )
类型三:正切函数的周期性
例3.求下列函数的周期 (1)y=3tan(2x+3π) (2)y=7tan(3x -6
π
)
举一反三:
【变式1】判断下列函数是否是周期函数.若是周期函数,求其最小正周期. (1)2
tan y x =; (2)|tan |y x =; (3)tan ||y x =.
类型四:正切函数的单调性
例4.(2015秋 新疆阿勒泰市月考)已知函数()3tan(2)3
f x x π
=-.
(1)求f (x )的定义域与单调区间 (2)比较()2
f π与()8
f π
-
的大小.
举一反三:
【变式1】求函数1
tan 2
4y x π⎛⎫=-+ ⎪⎝⎭的单调区间.
【变式2】求函数|tan(2-)|3
y x =π
的单调增区间.。
