高二文科数学定时训练16
2024届成都七中高二零诊模拟考试试卷(全科)24届高二文科数学零诊模拟考试试卷答案
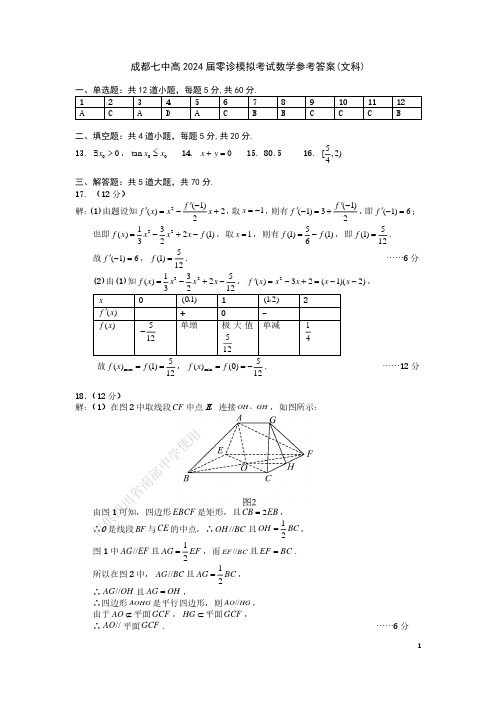
1成都七中高2024届零诊模拟考试数学参考答案(文科)二、填空题:共4道小题,每题5分,共20分.13. 00x ∃>,00tan x x ≤ 14. 0x y += 15. 80.5 16. 5[,2)4三、解答题:共5道大题,共70分. 17. (12分)解:(1)由题设知2(1)()22f f x x x '−'=−+,取1x =−,则有(1)(1)32f f '−'−=+,即(1)6f '−=; 也即3213()2(1)32f x x x x f =−+−,取1x =,则有5(1)(1)6f f =−,即5(1)12f =.故(1)6f '−=,5(1)12f =. ……6分(2)由(1)知32135()2f x x x x =−+−,2()32(1)(2)f x x x x x '=−+=−−,故max ()(1)12f x f ==,min ()(0)12f x f ==−. ……12分CF 中点H ,连接OH GH 、,如图所示:EBCF 是矩形,且2CB EB =,的中点,∴//OH BC 且12OH BC =,12EF ,而//EF BC 且EF BC =.BC 且12AG BC =,,是平行四边形,则//AO HG , HG ⊂平面GCF ,学使用四川省南部中学使用仅供2224t tt−=+,解得2,1()3t t==或舍去.故t的取值为23. ……12分21.(12分)解:(1)由()xf x e ax=−知()xf x e a'=−,1)当a e≤时,且有[1,)x∈+∞,()0f x'≥,()f x单增,故无极值;2)当a e>时,有(1,ln)x a∈,()0f x'<,()f x单减,而(ln,)x a∈+∞,()0f x'>,()f x单增,故()(ln)lnf x f a a a a==−极小值,()f x无极大值.综上,当a e≤时,()f x无极值;当a e>时,()f x极小值为lna a a−,()f x无极大值. ……4分(2)由(1)可知()1xf x e'=−,即有1111lntt t tλλ+>+−−,整理可令得(1)(1)()ln01tF t ttλλ+−=−>+, ……6分而22221(1)(1)(1)()(1)(1)t tF tt t t tλλλλ+−−'=−=++,……7分 1)当1λ≥时,且(1,)t∈+∞,有22(1)()0(1)tF tt tλ−'≥>+,()F t单增,()(1)0F t F>=,满足题设;……9分 2)当01λ<<时,且21(1,)tλ∈,有()0F t'<,()F t单减,()(1)0F t F<=,不满足题设;……11分综上,λ的取值范围为[1,)+∞. ……12分22.(10分)解:(1)由2sin2cosaρθθ=+,得22sin2cosaρρθρθ=+,故曲线的直角坐标方程为,即222()(1)1x a y a−+−=+;由sin()4πρθ−=,得sin cos2ρθρθ−=,故直线的直角坐标方程为. ……4分(2)点P的直角坐标为(2,0)−,在直线上,而直线的标准参数方程为(t为参数),将其代入,整理可得.由题设知222(3)4(44)2(1)0a a a∆=+−+=−>,解得.又,.当1,1a a>−≠且时,有12,0t t>,则1212||||||||3)PM PN t t t t a+=+=+=+=解得2a=;当1a≤−时,有12t t≤,则1212||||||||||1|PM PN t t t t a+=+=−==−=,解得4a=−.故a的值为2或-4. ……10分C2222x y y ax+=+l2y x=+ll22xy⎧=−⎪⎪⎨⎪=⎪⎩2222x y y ax+=+()2440t t a−+++=1a≠12t t+=1244t t a=+仅供四川省南部中学使用3。
高二文科数学一周一练0613

高二文科数学一周一练(6月13日)一、填空题:(每题8分,共24分)1.将参数方程222sin ()sin x y θθθ⎧=+⎪⎨=⎪⎩为参数化为普通方程为( ) A .2y x =- B .2y x =+C .2(23)y x x =-≤≤D .2(01)y x y =+≤≤2.化极坐标方程2cos 0ρθρ-=为直角坐标方程为( )A .201y y +==2x 或B .1x =C .201y +==2x 或xD .1y =3.点M的直角坐标是(1-,则点M 的极坐标为( )A .(2,)3π B .(2,)3π- C .2(2,)3π D .(2,2),()3k k Z ππ+∈ 二、填空题:(每题8分,共40分)4.直线cos sin 0x y αα+=的极坐标方程为____________________。
5.直线34()45x t t y t=+⎧⎨=-⎩为参数的斜率为______________________。
6.将参数方程222sin ()sin x y θθθ⎧=+⎪⎨=⎪⎩为参数化为普通方程为______________________。
7.已知曲线C 的参数方程是)(tan 4sec 3为参数θθθ⎩⎨⎧==y x ,则曲线C 的普通方程为 ________________ ;其左焦点直角坐标是 ;其右焦点极坐标可以表示为_____________________。
8.直线122()112x t t y t ⎧=-⎪⎪⎨⎪=-+⎪⎩为参数被圆224x y +=截得的弦长为______________。
三、解答题(共36分):9.(12分)求直线11:()5x t l t y =+⎧⎪⎨=-+⎪⎩为参数和直线2:0l x y --=的交点P 的坐标,及点P 与(1,5)Q -的距离。
10.(14分)在椭圆2211612x y +=上找一点,使这一点到直线2120x y --=的距离的最小值。
湖南省师大附中2016届高二第一次月考数学(文科)试题(含详细解答)

湖南省师大附中2016届高二第一次月考数学(文科)试题命题:高二文科数学备课组 审题:高二文科数学备课组一、选择题:本大题共10个小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设集合A ={1,2,3,5,7},B ={x ∈N |2<x ≤6},全集U A B =U ,则()U A B =I ð ( A ) A. {1,2,7} B. {1,7} C. {2,3,7} D. {2,7} 2.设a ,b ,c 为实数,则使a >b 成立的一个充分不必要条件是 ( D ) A. ac >bc B.a bc c> C. a +c >b +c D. ac 2>bc 2 3..函数f (x )=1ln (x +1)+( B )A.[-3,0)∪(0,3]B.(-1,0)∪(0,3]C. [-3,3]D. (-1,3]4.师大附中高二年级开展“我的未来不是梦”演讲比赛,七位评委为某参赛选手给出的分数(满分:100分)如右茎叶图所示, 去掉一个最高分和一个最低分后,则余下5个分数的方差是( A )A. 1.6B. 8C.D.5.已知tan (π-α)=2,则2s i n 2c o αα+=( D )A. 1B.35 C. 15- D. 35- 【解析】由已知,tan α=-2,则原式22222sin cos cos 2tan 13sin cos tan 15ααααααα++===-++,选D.6.在区间(0,1)上任取两个数x ,y ,则事件“43x y +<”发生的概率是 ( D )A.92B.95C. 94 【解析】图中阴影部分的面积除以正方形的面积为所求的概率所以122712339P =-⋅⋅=,选D.7.已知函数f (x )=(t 2-t +1)35t x +是幂函数,其图象关于y 轴对称,则实数t 的值为 ( C )A. -1B. 0C. 1D. 0或1 8.设等差数列{a n }的前n 项和为S n ,已知112a =,且123a a a +=,则S 40= ( C )A. 290B. 390C. 410D. 430 9.将函数sin(2)3y x π=+图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再将图象向右平移3π个单位,则所得图象的函数解析式是7 98 4 4 6 4 7 9 3 茎叶( D )A. f (x )=cos 4xB. f (x )=cos xC. f (x )=sin 4xD. f (x )=sin x10.已知向量a ,b 满足:|a |=1,b =1),则|a -b |的最大值是 ( B ) A. 4 B. 3 C. 2 D. 1二、填空题:本大题共5个小题,每小题5分,共25分.把各题答案的最简形式写在题中的横线上.11. 从某500件产品中随机抽取50件进行质检,利用随机数表法抽取样本时,先将这500件产品按001,002,…,500进行编号.如果从随机数表第8行第8列的数8开始,从左往右读数,则依次抽取的第4个个体的编号是_ 286 .(下面摘录了随机数表第7行至第9行各数)84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 7933 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54 【解析】第一个读数是859,舍去;第二个读数是169,取出;…. 依次抽取的前4个个体的编号分别是169,105,071,286.12. 一个底面是正三角形的三棱柱的正视图如图所示,则这个三棱柱13.若△ABC的面积为BC =3,C =60°,则AB14.已知x >0,y >0,且211x y+=,则x +2y 的最小值是 8 . 【解析】由已知,211x y +=,则2142(2)()442x y x y x y x y y x +=++=++≥+.当且仅当x =4,y =2时取等号,所以x +2y 的最小值是8.15. 函数221,0()(1),0axax x f x a e x ⎧+≥⎪=⎨-<⎪⎩在(,)-∞+∞上单调,则实数a 的取值范围是(,(1,2].-∞三、解答题:本大题共6个小题,共75分,解答应写出文字说明,证明过程或演算步骤.16.(本题满分12分)已知集合A ={x |x 2-4ax +3a 2<0},集合B ={x |x 2+6x +8≥0},其中a <0为常数.(Ⅰ)设条件p :x ∈A ;条件q :x ∈B ,若﹁p 是﹁q 的必要不充分条件,求a 的取值范围; (Ⅱ)设命题r :∃a <0,使A B =∅I ,试判断命题r 的真假. 【解】(Ⅰ)由x 2-4ax +3a 2<0,得(3)()0x a x a --<.因为a <0,则3a <x <a ,所以A =(3a ,a ). (2分)由x 2+6x +8≥0,得(x +4)( x +2)≥0,即x ≤-4或x ≥-2. 所以B =(-∞,-4]∪[-2,+∞). (4分)因为﹁p 是﹁q 的必要不充分条件,则q p ⌝⇒⌝,即p q ⇒,所以A 是B 的真子集. (6分)所以a ≤-4或-2≤3a <0,故a 的取值范围是2(,4][,0)3-∞--U . (8分)(Ⅱ)假设A B =∅I ,则342a a ≥-⎧⎨≤-⎩,即432a a ⎧≥-⎪⎨⎪≤-⎩,无解. (10分)所以对任意a <0,A B ≠∅I ,即﹁r 为真命题,故命题r 为假命题. (12分)17.(本题满分12分)已知函数f (x)=2cos x (3sin x +cos x )-1. (Ⅰ)求函数f (x )在区间[0,π2]上的最大值和最小值;(Ⅱ)若f (x 0)=65,x 0∈[π4,π2],求cos2x 0的值.【解】(Ⅰ)因为f (x )=23sin x cos x +2cos2x -1=3sin2x +cos2x =2sin(2x +π6). (3分) 当[0,]2x π∈时,72[,]666x πππ+∈,1sin(2)[,1]62x π+∈-.(5分)所以f (x )在区间[0,π2]上的最大值为2,最小值为-1. (6分)(Ⅱ)因为f (x 0)=2sin(2x 0+π6)=65,则sin(2 x 0+π6)=35. (7分)因为x 0∈[π4,π2],则2 x 0+π6∈[2π3,7π6].从而cos(2 x 0+π6)=45=-(2分)故cos2 x 0=cos[(2 x 0+π6)-π6]=cos(2 x 0+π6)cos π6+sin(2 x 0+π6)sin π6=3-4310.(12分)18.(本题满分12分)(2分)(6分)(Ⅱ)记从高一抽得的3个家长为a 、b 、c ,从高二抽得的1个家长为d ,从高三抽得的2个家长为e 、f ,则从6人中随机抽取3人的所有可能结果为:abc ,abd ,abe ,abf ,acd ,ace ,acf ,ade ,adf ,aef ,bcd ,bce ,bcf ,bde ,bdf ,bef ,cde ,cdf , cef ,def 共20种. (9分)抽取的3人中没有一人是高三学生家长的结果有:abc , abd , acd , bcd 共4种 故所求的概率为441205P =-=.(12分)19.(本题满分12分)如图,在长方体ABCD -A 1B 1C 1D 1中,BC =CC 1E 在棱AB 上. (Ⅰ)证明:B 1C ⊥C 1E ;(Ⅱ)若四棱锥E -B 1BCC 1的体积为43,求异面直线AA 1与C 1E 所成的角. 【解】(Ⅰ)连结BC 1,因为BC =CC 1,则 四边形BCC 1B 1为正方形,所以B 1C ⊥BC 1. ①(2分) 因为AB ⊥平面BCC 1B 1,则AB ⊥B 1C. ② (4分) 结合①②知,B 1C ⊥平面BC 1E ,所以B 1C ⊥C 1E. (6分) (Ⅱ)因为CC 1∥AA 1,则∠CC 1E 为所求的角. (7分)因为BC =CC 11111233E B BCC V BC CC BE BE -=⋅⋅⋅=. 由已知,2433BE =,则BE =2. (9分)在Rt △CBE 中,CE == (10分)在Rt △C 1CE 中,11tan CECC E CC ∠==CC 1E =60°. 故异面直线AA 1与C 1E 所成的角为60°. (12分)20. (本题满分13分)已知圆C :x 2+y 2-2x +4y -4=0.问在圆C 上是否存在两点A 、B 关于直线y =kx -1对称,且以AB 为直径的圆经过原点?若存在,写出直线AB 的方程;若不存在,说明理由.A B C D A 1 B 1 C 1D 1E。
高二数学午间小测16试题

智才艺州攀枝花市创界学校高二数
学午间小测〔16〕
函数的单调性:对于函数
()f x 的定义域I 内某个区间上自变量的任意两个值12,x x , ①假设当1
2x x <时,都有12()______()f x f x ,那么称()f x 在这个区间上是增函数; ②假设当12x x <时,都有12()______()f x f x ,那么称()f x 在这个区间上是减函数。
1、以下函数中,在区间(0,2)上为增函数的是〔〕
2、某几何体的正视图和侧视图均如图1所示,那么该几何体的俯视图不可能...
是 3、图2中的三个直角三角形是一个体积为20cm 3
的几何体的三视图,那么h =cm .
4、分别和两条异面直线都相交的两条直线,其位置关系是〔〕
〔A 〕平行〔B 〕相交〔C 〕异面〔D 〕相交或者异面 5、空间四边形ABCD 中,AB 、BC 、CD 的中点分别是P 、Q 、R ,且 PQ=2,QR=5,PR=3,那么异面直线AC 和BD 所成的角是〔〕
(A)30º(B)45º(C)60º(D)90º
6、假设直线a 不平行于平面,那么以下结论成立的是〔〕
(A)内的所有直线都与直线a 异面(B)内不存在与直线a 平行的直线 (C)a 内的直线都与直线a 相交(D)直线a 与平面有公一共点 单位:cm 俯视图
正视图 h
5 侧视图
6 A
B C
D P
Q R。
2020年高二文科数学上册限时训练

高二文科数学限时训练1 从点P(3,-2)发出的光线l 经直线m :20x y --=反射,若反射线恰经过点Q(5,1),则光线l 所在直线的方程是 .2. 过点A (4,8)且与点B (1,2)距离为3的直线方程为 3、已知不等式10)34()3(222++-<--i m m i m m m 成立的充要条件为 ___ _______ 4.定义在R 上的奇函数()f x 满足3()(),(1)12f x f x f =-+-=,则(1)(2)(3)(2008)f f f f ++++=L5.定义在),0(+∞上的函数)(x f 的导函数0)('<x f 恒成立,且1)4(=f ,若()1f x y +≤,则y x y x 2222+++的最小值是6.定义在R 上的函数()f x 对任意的x 都有(3)()3f x f x +≤+和(2)()2f x f x +≥+且(1)1f =,则(2008)f 的值为7、异面直线a ,b 成80°角,点P 是a ,b 外的一个定点,若过P 点有且仅有n 条直线与a ,b 所成的角相等且等于45°,则n =8.已知圆C 1:0276:07622222=--+=--+y y x C x y x 与圆相交于A ,B 两点,则线段AB 的中垂线方程为 9.如图,四条直线互相平行,且相邻两条平行线的距离均为h ,一直正方形的4个顶点分别在四条直线上,则正方形的面积为10、关于x 的不等式kx x x x ≥-++3922在]5,1[上恒成立,则实数a 的范围为11.已知点P 在直线,042上=+-y x 且到x 轴的距离是到y 轴的距离的32倍,则点P 的坐标是 12.已知函数)30(42)(2<<++=a ax ax x f ,若1-=+<a n m n m 且,则)(m f )(n f (>=<或或用)连接。
高中文科生学好数学的方法有哪些

高中文科生学好数学的方法有哪些高中文科生学好数学的方法有哪些高中数学对于文科生来说是个大难题,其实只要掌握恰当的高中数学学习方法,文科生一样可以学好高中数学。
那么高中文科生学好数学的方法有哪些呢?下面是小编整理的一些高中文科生学好数学的方法,供参考。
高中文科生学好数学的方法之吃透课本高中文科生想要提高数学成绩,首先要充分理解高中数学课本,学习高中数学的过程是活的,数学能力是随着知识的发生而同时形成的,所以要掌握高中数学课本中的每一个概念,每一条法则,从不同的角度来培养和提高高中数学水平,理解教材中的重点知识,弄清与前后知识的联系等,只有把握住教材,才能掌握学习的主动。
高中文科生学好数学的方法之自主学习学习是高中生自己的事,所以高中生应该主动学习,这样才能提升高中数学的学习质量。
在高中数学课前主动预习,数学课后自主复习,养成良好的高中数学学习习惯。
制定适合自己的高中数学学习方法,形成一个完整的知识体系,提高高中数学学习效率。
高中文科生学好数学的方法之练习高中文科生要想学好高中数学,平时的练习必不可少,但这并不意味着要进行题海战术,做练习也要讲究科学性。
在选择参考书方面可以听一下老师的意见,一般来说老师会根据自己的教学方式和进度给出一定的建议,在做做题时高中文科同学应注意总结出各类数学题目的解题方法并且掌握。
小编建议高中文科生要适当舍得放弃对于大部分数学基础不是很扎实的同学来说,放弃太难的高中数学题是一个比较明智的.选择。
一、对同学们的劝告进入了高二学年,已经适应了高中的学习和生活,在这个阶段是很关键也是很危险的,同学们很容易就散漫下来,对自己放松了,认为还有一两年才高考呢,现在不学高三学也来得及,有这种想法的同学就大错特错了,成绩是靠平时学习的积累,高二这年正是你继续打好基础的时间,这阶段学习是很关键的,我们不但不能对自己放松,更应该对自己加油,充电,为高三的复习打好铺垫,如果这个时候对自己放松是对自己的一种不负责任,而且想在高三这短短的一年时间里充电复习,这是完全不可行的,我们也是很理解学习的辛苦,偶尔的放松不是不行的,但是要切忌,千万不要对自己永久的放松。
高二数学综合训练题十六
高二数学综合训练题(十六) 2015/1/22 一、选择题(每小题5分,共50分)
1.从2 012名学生中选取50名学生参加数学竞赛,若采用下面的方法选取:先用简单随机 抽样从2 012人中剔除12人,剩下的2 000人再按系统抽样的方法抽取50人,则在2 012 人中,每人入选的概率 ( ) A.不全相等 B.均不相等 C.都相等,且为251 006 D.都相等,且为140 2.过点(1,3)P,且垂直于直线230xy的直线方程为( ) A.210xy B.250xy C.250xy D.270xy 3.甲、乙两人的各科成绩如茎叶图所示,则下列说法不正确的是( )
A.甲、乙两人的各科平均分相同 B.甲的中位数是83,乙的中位数是85 C.甲各科成绩比乙各科成绩稳定 D.甲的众数是89,乙的众数为87 4.从8名学生(其中男生6人,女生2人)中按性别用分层抽样的方法抽取4人参加接力比赛,若女生不排在最后一棒,则不同的安排方法数为 ( ) A.1440 B.960 C.720 D.360 5.甲、乙两人进行围棋比赛,比赛采取五局三胜制,无论哪一方先胜三局则比赛结束,假
定甲每局比赛获胜的概率均为23,则甲以3∶1的比分获胜的概率为( )
A.827 B.6481 C.49 D.89 6.若随机变量ξ~N(2,2),且(4)0.8P,则(02)P等于( ) A.0.6 B.0.4 C.0.3 D.0.2 7.执行如图所示的程序框图,若输入的p=0.8,则输出的n为( ) A. 4 B.5 C.6 D.3
8.若圆2244100xyxy上至少有三个不同点到直线 l:0axby的距离为22,则直线l的倾斜角的取值范围是( )
A.[,124] B.[5,1212] C.[,]63 D.[0,]2 9.设aR,则“1a”是“直线1:210laxy与直 第7题图 线2:(1)40lxay平行”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 10.已知2,2k,则k的值使得过点)2,0(A可以作2条直线与圆
高二文科生的数学学习方法
高二文科生的数学学习方法数学的学习有一个循序渐进的过程,妄想一步登天是不现实的。
熟记书本内容后将书后习题认真写好,有些同学可能认为书后习题太简单不值得做,这种想法是极不可取的,下面给大家提供一些高二文科生的数学学习方法,希望能够帮助大家,欢迎阅读!数学习题无非就是数学概念和数学思想的组合应用,弄清数学基本概念、基本定理、基本方法是判断题目类型、知识范围的前提,是正确把握解题方法的依据。
只有概念清楚,方法全面,遇到题目时,就能很快的得到解题方法,或者面对一个新的习题,就能联想到我们平时做过的习题的方法,到达迅速解答。
弄清基本定理是正确、快速解答习题的前提条件,特别是在立体几何等章节的复习中,对基本定理熟悉和灵活掌握能使习题解答条理清楚、逻辑推理严密。
反之,会使解题速度慢,逻辑、表达不清。
那么如何抓基础呢?复习数学时,要制定好计划,不但要有本学期大的规划,还要有每月、每周、每天的小计划,计划要与老师的复习计划吻合,不能相互冲突,如按照老师的复习进度,今天复习到什么知识点,就应该在今天之内掌握该知识点,加深对该知识点的理解,研究该知识点考查的不同侧面、不同角度。
在每天的复习计划里,要留有一定的时间看课本,看笔记,回顾过去知识点,思考老师当天讲了什么知识,归纳当天所学的知识。
可以说,每天的习题可以少做,但这些归纳、反思、回顾是必不可少的。
望你在制定计划时注意。
做习题是为了巩固知识、提高应变能力、思维能力、计算能力。
学数学要做一定量的习题,但学数学并不等于做题,在各种考试题中,有相当的习题是靠简单的知识点的堆积,利用公理化知识体系的演绎而就能解决的,这些习题是要通过做一定量的习题到达对解题方法的展移而实现的,但,随着高考的改革,高考已把考查的重点放在创造型、能力型的考查上。
因此要精做习题,注意知识的理解和灵活应用,当你做完一道习题后不访自问:此题考查了什么知识点?什么方法?我们从中得到了解题的什么方法?这一类习题中有什么解题的通性?实现问题的完全解决我应用了怎样的解题策略?只有这样才会培养自己的悟性与创造性,开发其创造力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二文科数学定时训练(16)
1.有一个容量为200的样本,其频率分布直方图如图所示,根据样本的频率分布直方图估计,
样本数据落在区间10,12内的频数为______
2.小波通过做游戏的方式来确定周末活动,他随机地往单位圆内
投掷一点,若此点到圆心的距离大于12,则周末去看电影;若
此点到圆心的距离小于14,则去打篮球;否则,在家看书,则
小波周末不在家看书的概率为
3.已知F是抛物线y2=x的焦点,A,B是该抛物线上的两点,
AF+BF=3
,则线段AB的中点到y轴的距离为________
4.函数()cosfxxx在[0,)内有______个零点
5. 观察下列式子:,232112 ,353121122 ,474131211222 ……,则可以猜
想: 2222011131211
6.设F1、F2是椭圆E:x2a2+y2b2=1(a>b>0)的左、右焦点,P为直线x=3a2上一点,△F1PF2是底
角为30°的等腰三角形,则E的离心率为___________
7.如图,设P是圆2225xy上的动点,点D是P在x轴上投影,M为PD上一点,且
4
||||5MDPD
.
(1)当P在圆上运动时,求点M的轨迹C的方程;
(2)求过点(3,0)且斜率为45的直线被C所截线段的长度.
8.设函数f(x)= ex-ax-2
(Ⅰ)求f(x)的单调区间
(Ⅱ)若a=1,k为整数,且当x>0时,(x-k) f´(x)+x+1>0,求k的最大值
