第2章-确知信号与随机信号分析基础
合集下载
第2章 确知信号与随机信号分析基础
P ( ) 与离散频谱
2
F n 的关系为
2
n
F n ( n 0 ) 期信号 ( 与离散谱 F n 相联系 ) 功率谱 F n 之间的关系 , 下进一步给出非 的关系 : P ( ) 与非周期信号频谱之间
2
上式实际上是给出了周 密度 P ( ) 与周期信号频谱 周期信号功率谱密度 P ( ) lim
习。这些基本内容是学习《信息论》与《通信原理》的 必备的数学知识，要求大家掌握。
2
第一部分：信号分析内容复习与总结
§1 周期信号和非周期信号的频谱
一、周期信号的付氏级数展开式
1、三角形式
n
f (t ) A0 其中 0
A n cos( n 0 t n ) , T 0 为信号的周期 ,
16
此定理的物理意义是
§3 信号的分类与特点
一、确定性信号与随机信号
确定性信号：可用确定的数学函数表示的信号， 且信号的取值是确定的。 随机信号：给定一个时间值时，信号的取值不确 定，只知其取某一数值的概率。 二、周期信号与非周期信号
满足x(t)=x(t+T0)，则称为周期信号，T0为周期， 不满足上述关系的信号称为非周期信号。
17
三、能量信号与功率信号 设信号为f(t)，它为电压或电流，则作用在1Ω电 阻上的功率为p(t)=f 2(t)。
1、能量信号
T 2
若 E lim
T
T 2
f ( t ) dt
2
f ( t ) dt
2
则称 f ( t )为能量信号
18
2、功率信号
第2章 确知信号分析
{
x1 ( t ) → y1 ( t ) x2 ( t ) → y 2 ( t )
⇒ [ x1 (t ) + x2 (t )] → [ y1 (t ) + y2 (t )]
（一个激励的存在并不影响另一个激励的响应） 一个激励的存在并不影响另一个激励的响应） 非线性系统： 非线性系统：凡是不满足叠加定理的系统
F (ω ) = T0 V n
F (ω )
：谱密度，即单位频率占有的振幅值，是相对值。 谱密度，即单位频率占有的振幅值，是相对值。
3）矩形脉冲的频谱函数；门函数的频谱函数 ）矩形脉冲的频谱函数；
τ τ A − <t< 2 2 f (t ) = τ τ 0 t < − , t > 2 2
2）时不变和时变系统 ） 时不变系统（恒参系统）：系统内的参数不随时间变化 时不变系统（恒参系统）：系统内的参数不随时间变化 ）：
{
y ( t ) = f [ x ( t )] y ( t −t 0 ) = f [ x ( t −t 0 )]; −∞ <t ,t 0 < ∞
时变系统（变参/随参系统）： 随参系统）： 时变系统（变参 随参系统 3）物理可实现和物理不可实现系统 ） 物理可实现系统： 物理可实现系统：系统的响应不可能在加上激励以前出现 物理不可实现系统： 物理不可实现系统：
F (ω) = F [ f (t )]
付氏正变换 付氏反变换
f (t ) = F −1 [ F (ω)]
或者记为： 或者记为： F (ω) ↔ f (t ) ， f (t ) ↔ F (ω)
2） (ω ) 与 Vn 、 Cn ） F
的关系
1 Vn = T0
第二章 随机信号分析
SCUT DT&P Labs
5
2.2 随机过程的一般表述
自相关函数 R (t1, t2), 衡量同一个过程的相关程度。 R(t1 , t 2 ) E[x (t1 ) x (t 2 )]
x1 x2 f 2 (x1 , x2 ; t1 , t 2 )dx1dx2
自协方差B (t1, t2), 衡量同一个过程的相关程度。
Ps () ＝
∞
-∞
R ( ) e -j d
∞
R ( ) ＝ (1/2) -∞ Ps () e j d (逆变换)
2001 Copyright
SCUT DT&P Labs
17
课堂练习
例2.4.1 x (t) sin(0 t + )，求x (t)的功率谱密度函数。 思路：首先证明x (t) 是平稳随机过程，然后对自相关函 数R ( ) 进行傅立叶变换，求得功率谱密度函数Ps () 。 其步骤为： 1，求数学期望 E[x (t)] ＝0，自相关函数R (t1, t2) ＝ 0.5 cos0 ，因此数学期望与时间无关，相关函数仅与时间 间隔有关，因此x (t) 是平稳随机过程。 2，对R ( ) 进行傅立叶变换，求得Ps ()
P ( ) E[ Ps ( )] lim x E FT ( ) T
2 T
2001 Copyright
SCUT DT&P Labs
16
可以证明：平稳随机过程的功率谱密度 等于该过程的自相关函数的富里叶变换。
P ( ) R( ) 表示富里叶变换 x
复习：富里叶变换。
2001 Copyright
《随机信号分析基础》第2章 课件_随机信号时域分析
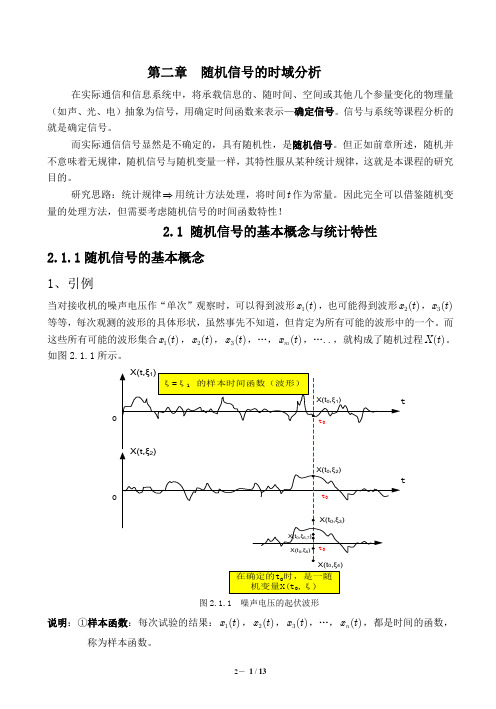
随机过程的一维统计特性具有普通随机变量的各种性质，区别在它们同时还是时间t 的函 数。“一维”只描述出随机过程在各个孤立时刻（任一时刻）的统计特性，没有反映各时刻之 间的内在联系 Þ 用“n 维”更为全面。 （2）二维分布
二维概率分布函数： X(t1)与 X(t2 ) ， FX (x1, x2;t1,t2 ) = FX (x1, x2 ) = P[X(t1) £ x1, X(t2 ) £ x2 ]
= E {X 2(t) - mX2 (t) - 2X(t)mX (t)} = E {X 2(t)} - mX2 (t)
【含义】 ① t2(t) ----随机信号在t 时刻取值相对于中心（均值）的偏离程度。 t(t)称为标准差。
② 若 X(t)为归一化阻抗下的电压或电流，则 E {X 2(t)}表示时刻t 上的瞬时总功率的统计平
若 n 阶偏导数存在，可有 n 维概率密度函数
fX (x1, x2,× × ×xn；t1,t2,× × ×tn )
=
¶FX (x1, x2,× × ×xn；t1,t2,× × ×tn ) ¶x1¶x2 × × × ¶xn
显然，n Þ 反映“内在联系”愈充分，也就越为完整地描述随机过程的全部统计特性。
2、定义 令随机试验的概率空间为 {W, F, P} ，若对于样本空间 W 中的任何一个样本点
xi Î W ，总有一个确知函数 xi = X(t, xi )，t Î T 与之对应，这样对于所有的 x Î W ，就可得 到一族关于t 的函数 X(t, x) ，称为随机信号。
族中的每一个函数称为该随机过程的样本函数。随机信号 X(t, x)常简记为 X(t)，对应的 样本函数简记为 x (t ) 。
2.1.3 随机过程的数字特征
第2章 确知信号
j 2nf 0 t
( 2.2 2)
( 2.2 3)
n
T0 / 2
T0 / 2
s( t )dt
复振幅：Cn Cn e j ，|Cn|—振幅，n—相位 Cn—双边频谱：负频率仅在数学上有意义，物理上并不存在。
2018/10/8
第16页
2.2 确知信号的频域性质
一、功率信号的频谱
周期性功率信号频谱的性质：物理上实信号的频谱和数学上的频谱函
T0 / 2
T0 / 2
s( t ) cos(2nf 0 t )dt j
1 T
T0 / 2
T0 / 2
s( t ) sin( 2nf 0 t )dt Re (C n ) j Im(C n )
而
T0 / 2
T0 / 2
s(t ) sin( 2nf0 t )dt 0 ，所以 Cn为实函数。
随机信号定义：是指其取值不确定、且不能事先确切预知
的信号。这种信号在任何时间的取值自然也是不可能用一个数学公
式准确计算出来的。然而，在一个长时间内观察，这种信号有一定的 统计规律，可以找到它的统计特性。通常，把这种信号看作是一个随 机过程。
2018/10/8
第2页
2.1 确知信号的类型
二、周期信号和非周期信号
Cn 1 T0 1 j 2nf 0 t s ( t ) e dt T0 / 2 T0
T0 / 2
j 2nf 0 t * s ( t ) e dt Cn T0 / 2
T0 / 2
( 2.2 5)
正频率部分和负频率部分间存在复数共轭关系，即： Cn的相位奇对称
2 2 bn (2) 实信号 s(t) 的各次谐波的振幅等于 an
确知信号分析基础精编版
jn1
2
2A
n1T
sin n1
2
A
T
sin n1
2
n1
A
T
Sa n1
2
2
清华大学出版社第2章 信号分析础式中 Sa(x) sin x / x 称为抽样函数。由此得周期矩形 信号f (t) 的傅里叶级数指数形式为
f
(t)
A
T
n
Sa
n1
2
e jn1t
据此画出 Fn 的双边频谱，如图2.9(b)所示。显然， 频谱的包络分布服从抽样函数分布规律，幅度呈
清华大学出版社
第2章 信号分析基础
幅度
图2.1 波形的二维描述
时间
清华大学出版社
第2章 信号分析基础
图2.2 波形的三维描述 清华大学出版社
第2章 信号分析基础
2．时限信号和非时限信号 信号一般都是独立时间变量的函数，按信号 的持续时间划分，可将其分为时限信号和非时限 信号。时限信号只在一定的时间范围内存在，而 非时限信号则不受时间限制，可在整个时间轴上 一直存在，分别如图2.3和图2.4所示。
4．周期信号和非周期信号 按信号是否具有重复性，将信号划分为周期 信号和非周期信号。一个连续信号 f (t) ，若对所有 t 均有
清华大学出版社
第2章 信号分析基础
f t f t nT ,n 0,1,2,...
则称 f (t)为连续周期信号，如图2.7所示。满足上式 的最小T值称为f (t)的周期。周期信号也可以表示 为
清华大学出版社
第2章 信号分析基础
5．能量信号和功率信号 按信号的能量特性划分，将信号分为能量信 号和功率信号。若将信号f (t)设为电压或电流，则 加载在单位电阻上产生的瞬时功率为 f (t) ，2 在一定 的时间区间内会消耗一定的能量。把该能量对时 间区间取平均，即得信号在此区间内的平均功率。 对时间区间取极限，则信号 f (t)的能量E和功率P 定义为
第2章 确知信号分析
例
求周期余弦信号 的自相关函数和功率谱 f t E cosω0t 求复指数信号 jω t f t E e 的自相关函数和功率谱
0
2.4 确知信号的频域特性
一、能量信号的能量和能量谱密度 二、无限非周期信号的平均功率和功率谱密度 三、周期信号的平均功率和功率谱密度
2 T
e
j0t
2 ( 0 )
1 cos 0t [e j0t e j0t ] [ ( 0 ) ( 0 )] 2 1 sin 0t [e j0t e j0t ] [ ( 0 ) ( 0 )] 2j j
f (t ) nf (0) (t ) jt
F ( x)dx
卷积性质：
f1 (t ) f 2 (t )
F1 () F2 ()
1 F1 ( ) F2 ( ) 2
f (t ) (t ) f (t )
f (t ) (t T ) f (t T )
平均功率P为
1 T /2 2 lim f (t )dt T T T / 2
能量信号：时间有限的信号，信号能量有 限，在全部时间内的平均功率为0。 功率信号：时间无限的信号，具有无限的 能量，但平均功率有限。
2.2 确知信号的频域分析
一、周期信号 二、付立叶变换 三、付氏变换的性质 四、常用信号的付氏变换
一、能量信号
能量信号的频谱密度 ——该信号的傅利叶变换
1 f (t ) 2Fra bibliotek
F ( )e jtd
F ( ) f (t )e jtdt F ( ) e j ( )
精品文档-随机信号分析基础(梁红玉)-第2章
一维概率分布函数为
FX(x; t)=P［X(t)≤x］ 一维概率密度函数为
（2-3）
fX
( x; t )
FX (x;t) x
（2-4）
第二章 随机信号的基本概念
与随机变量不同的是， 随机信号的一维概率分布或概率 密度函数不仅是状态x的函数， 也是时间t的函数。 图2-9给 出了一维概率密度函数示意图。
计算二元变换的雅可比行列式
g1 J = a
g2 a
g1 1
g2
=
cos 0t1+ cos 0t2 +
a a
cos cos
0t1 0t2
+ +
1
=
a
sin
1
0
t1
t2
第二章 随机信号的基本概念
1
a2
fX x1,x2;t1,t2
fA (a, )
J
2π
2
sin
0
t1
t2
exp
2
2
第二章 随机信号的基本概念
图2-5 脉冲信号发生器的典型波形
第二章 随机信号的基本概念
（3） 连续型随机信号(时间连续、 状态连续)。 例如随机正弦信号X(t)=acos(ωt+θ)， 式中a, ω, θ 部分或全部是随机变量。 图2-6示出了它在某个变量是随机 变量、 其他两个为常数时的典型波形。
y
mY
2
2 Y
2
第二章 随机信号的基本概念
在t=t1时刻， X(t1)是一个随机变量， 令 X1=X(t1)=Ycosω0t1， 根据一维随机变量函数的变换， 需求 出反函数及其导数：
Y X1 ,
cos 0t1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
G() F ( j) 2
还可证明, 功率谱密度 P( )与离散频谱 Fn 2的关系为
P() 2 Fn 2 ( n0 ) n
上式实际上是给出了周 期信号(与离散谱Fn相联系)功率谱
密度P()与周期信号频谱 Fn 之间的关系,下进一步给出非 周期信号功率谱密度 P()与非周期信号频谱之间 的关系 :
2 若对于所有的 ,都有R(0) R( ).
3 R( )是偶函数,满足 : R( ) R( ).
28
§7 自相关函数与功率谱和能量谱之间的关系
1 对于能量信号 :
R( ) G() 即能量信号的自相关函 数R( )与能量谱G()是一对付氏变换
2 对于功率信号 :
sin 0t
1 2j
e j0t e j0t
j[ ( 0 ) ( 0 )]
F ( j)
cos(0t)
( )
( )
0 0 0
sin(0t)
F ( j)
( )
( )
0 0 0
11
§2 付氏变换的性质 一、线性叠加性质
1、若为周期功率信号，设周期为T0，则
T0
R12( )
1 T0
2
f1(t) f2 (t
T0
)dt
2
25
2、若为非周期功率信号，则
T
R1 2 (
)
lim
T
1 T
2 T
f1 (t )
f2 (t
)dt
2
3、若为能量信号，则
R12( ) f1(t) f2 (t )dt
结论 : 矩形脉冲信号的带宽 f与信号的宽度 成反比 8
f (t) A
/ 2 0 / 2 t
9
数字信号频带宽度 f 估算
010110
f 1 T
T
数字信号带宽与码元宽度成反比
10
4. 正弦信号的付里叶变换
cos0t
1 2
e j0t
e j0t
[ ( 0 ) ( 0 )]
2A
0 0 0
A
13
0 0 0
三、时移特性
若 f (t) F ( j) 则 f (t t0 ) F ( j)e jt0
其物理意义是 ,时间域中的时移 , 在频域中反映在
原频谱函数F ( j)的基础上附加一个相移 函数e jt0
四、频移特性
若 f (t) F ( j) 则 f (t)e j0t F[ j( 0 )]
欢迎各位同学光临
《通信原理》课程
主讲教师：禹思敏
1
第2章 确知信号与随机信号分析基础
本章包括信号分析、概率论与随机过程三个方面的 内容。这些内容已在《信号与系统》、《高等数学》中 学过，本章对其中的部分内容作一个复习和总结，只给 出结论，并尽量通俗地理解其中的物理意义及背景，不 作证明。此外，还有一些内容将在具体的章节中进行复 习。这些基本内容是学习《信息论》与《通信原理》的 必备的数学知识，要求大家掌握。
T
2
则称f (t)为能量信号
18
2、功率信号
若E f 2 (t)dt
T
但S lim 1
2
f 2 (t)dt
T T T
2
则称f (t)为功率信号.
19
3、能量信号与功率的有关结论： （1）周期信号必定是功率信号，不可能是能量信号，
因为其能量必为无穷大，为什么？ （2）对于非周期信号，可能为功率信号，也可能为能
其物理意义是 ,时间域中的相移 , 对应频谱函数在频域中 的频移
14
五、调制定理
若f (t) F( j)
则f
(t) cos0t
1 2
F[
j(
0 )]
1 2
F[
j(
0 )]
f
(t) sin 0t
j 2
F[
j(
0 )]
j 2
F[
j(
0 )]
F ()
0
P() lim FT () 2
T T
上式中的FT ()为fT (t)的频谱,如后一页的图所示 .
23
f (t)
t
fT (t)
fT (t) FT ()
t
T /2
T /2
24
§6 互相关函数与自相关函数 一、互相关函数的定义：
设有两个信号f1(t)和f2 (t),则互相关函数R12( )定义为
满足x(t)=x(t+T0)，则称为周期信号，T0为周期， 不满足上述关系的信号称为非周期信号。
17
三、能量信号与功率信号
设信号为f(t)，它为电压或电流，则作用在1Ω电 阻上的功率为p(t)=f 2(t)。
1、能量信号
T
2
若E lim f 2 (t)dt f 2 (t)dt T
若 f1(t) F1( j) f2 (t) F2 ( j) 则 f1(t) f2 (t) F1( j) F2 ( j) 二、对称性
若 f (t) F( j) 则 F( jt) 2f () 或 F( jt) 2f ()
12
例题： 试利用对称性 求低通滤波器 的付氏变换。
f (t) A
/ 2 0 / 2 t
F (t) ASa t
2
2
0
F (t) 2A0Sa0t
比例特性, 两边
同时除以2
F (t)
A0
Sa0t
F () ASa
2
f () 2A
/ 2 0 / 2 f ()
量信号。如果其能量为有限值，则为能量信号， 如果其能量为无穷大，功率为有限值，则为功率 信号。一个信号或为能量信号，或为功率信号。
20
§4 Parseval定理（即能量守恒定理） 物理意义：能量守恒，时域能量等于频域能量， 即能量守恒不会变换后会发生改变。
一、对于能量信号f(t)，其频谱为F(jω)，则有
A sin( / 2) ASa
/ 2
2
F(
j)的零点满足如下关系
:
k , k
1,2,
2
从而得 : 2k , k 1,2,
注意到信号的大部分能 量集中在第一个主瓣内 ,
因此,得此信号的带宽为 2k f 1
R( ) P() 即功率信号的自相关函 数R( )与功率谱P()是一对付氏变换
29
第二部分 概率论与随机过程内容复习与总结
§1 随机事件与概率 一、事件与概率
1、随机事件：把某次试验中可能发生和不可能发生 的事件称为随机事件 A。如正弦波振荡器每次开机起 振的初相，二进制数字信号序列的某一位取值等等， 都属于随机事件。该事件出现的概率用P(A)表示，并
且有0 P(A) 1。若P(A)=1为必然事件，若P(A)=0
为不可能事件，等等。
30
§2 条件概率与统计独立 在事件A发生的条件下,事件B发生的概率用 P(B / A),
称为条件概率.按定义有 : P(B / A) P(AB) P( A)
在一般情况下, P(B / A) P(B),只有当A, B为统计独立时, P(B / A) P(B)才能成立.并且有P(AB) P(A)P(B).
则称f1(t)和f2 (t)完全相关.
3 互相关函数 R12( )满足 : R12( ) R21( ).
27
（二）自相关函数的性质
1 R(0)的性质(可直接从定义获得 ) :
对于功率信号, R(0)
lim
1
T /2
f
2 (t)dt S
T T T / 2
对于能量信号, R(0) f 2 (t)dt E
31
§3 概率的基本定理
1 事件之和的概率 : P( A B) P( A) P(B) P(AB)
当A与B互不相容时, P( AB) P() 0,有
P( A B) P( A) P(B) 2 事件之积的概率 :
P( AB) P( A)P(B / A) P(B)P( A / B) 当A与B相互独立时,有P(B / A) P(B), P( A / B) P( A)
1. 单位冲激函数 (t) E (t) E 或 (t) 1
物理意义 : 变化快的信号如很窄的 脉冲等,可近似用
数学模型 (t)来表示,上式说明这类随时间变 化很快
的信号的频谱很宽 .
(t)
F ( j)
(1)
1
0t
0
6
2 直流信号f (t) A
1 2 () A 2A ()
2
第一部分：信号分析内容复习与总结
§1 周期信号和非周期信号的频谱 一、周期信号的付氏级数展开式
1、三角形式
n
f (t) A0 An cos(n0t n )
n 1
其中0
2
T0
为基波频率 , T0为信号的周期 ,
而n0为n次谐波频率
3
2、指数形式
利用高等数学中的欧拉公式，可将三角形式的
(1)
f
F
(t)
( j)
1
2
F ( j)e jt
f (t)e jt dt
d
还可证明, 功率谱密度 P( )与离散频谱 Fn 2的关系为
P() 2 Fn 2 ( n0 ) n
上式实际上是给出了周 期信号(与离散谱Fn相联系)功率谱
密度P()与周期信号频谱 Fn 之间的关系,下进一步给出非 周期信号功率谱密度 P()与非周期信号频谱之间 的关系 :
2 若对于所有的 ,都有R(0) R( ).
3 R( )是偶函数,满足 : R( ) R( ).
28
§7 自相关函数与功率谱和能量谱之间的关系
1 对于能量信号 :
R( ) G() 即能量信号的自相关函 数R( )与能量谱G()是一对付氏变换
2 对于功率信号 :
sin 0t
1 2j
e j0t e j0t
j[ ( 0 ) ( 0 )]
F ( j)
cos(0t)
( )
( )
0 0 0
sin(0t)
F ( j)
( )
( )
0 0 0
11
§2 付氏变换的性质 一、线性叠加性质
1、若为周期功率信号，设周期为T0，则
T0
R12( )
1 T0
2
f1(t) f2 (t
T0
)dt
2
25
2、若为非周期功率信号，则
T
R1 2 (
)
lim
T
1 T
2 T
f1 (t )
f2 (t
)dt
2
3、若为能量信号，则
R12( ) f1(t) f2 (t )dt
结论 : 矩形脉冲信号的带宽 f与信号的宽度 成反比 8
f (t) A
/ 2 0 / 2 t
9
数字信号频带宽度 f 估算
010110
f 1 T
T
数字信号带宽与码元宽度成反比
10
4. 正弦信号的付里叶变换
cos0t
1 2
e j0t
e j0t
[ ( 0 ) ( 0 )]
2A
0 0 0
A
13
0 0 0
三、时移特性
若 f (t) F ( j) 则 f (t t0 ) F ( j)e jt0
其物理意义是 ,时间域中的时移 , 在频域中反映在
原频谱函数F ( j)的基础上附加一个相移 函数e jt0
四、频移特性
若 f (t) F ( j) 则 f (t)e j0t F[ j( 0 )]
欢迎各位同学光临
《通信原理》课程
主讲教师：禹思敏
1
第2章 确知信号与随机信号分析基础
本章包括信号分析、概率论与随机过程三个方面的 内容。这些内容已在《信号与系统》、《高等数学》中 学过，本章对其中的部分内容作一个复习和总结，只给 出结论，并尽量通俗地理解其中的物理意义及背景，不 作证明。此外，还有一些内容将在具体的章节中进行复 习。这些基本内容是学习《信息论》与《通信原理》的 必备的数学知识，要求大家掌握。
T
2
则称f (t)为能量信号
18
2、功率信号
若E f 2 (t)dt
T
但S lim 1
2
f 2 (t)dt
T T T
2
则称f (t)为功率信号.
19
3、能量信号与功率的有关结论： （1）周期信号必定是功率信号，不可能是能量信号，
因为其能量必为无穷大，为什么？ （2）对于非周期信号，可能为功率信号，也可能为能
其物理意义是 ,时间域中的相移 , 对应频谱函数在频域中 的频移
14
五、调制定理
若f (t) F( j)
则f
(t) cos0t
1 2
F[
j(
0 )]
1 2
F[
j(
0 )]
f
(t) sin 0t
j 2
F[
j(
0 )]
j 2
F[
j(
0 )]
F ()
0
P() lim FT () 2
T T
上式中的FT ()为fT (t)的频谱,如后一页的图所示 .
23
f (t)
t
fT (t)
fT (t) FT ()
t
T /2
T /2
24
§6 互相关函数与自相关函数 一、互相关函数的定义：
设有两个信号f1(t)和f2 (t),则互相关函数R12( )定义为
满足x(t)=x(t+T0)，则称为周期信号，T0为周期， 不满足上述关系的信号称为非周期信号。
17
三、能量信号与功率信号
设信号为f(t)，它为电压或电流，则作用在1Ω电 阻上的功率为p(t)=f 2(t)。
1、能量信号
T
2
若E lim f 2 (t)dt f 2 (t)dt T
若 f1(t) F1( j) f2 (t) F2 ( j) 则 f1(t) f2 (t) F1( j) F2 ( j) 二、对称性
若 f (t) F( j) 则 F( jt) 2f () 或 F( jt) 2f ()
12
例题： 试利用对称性 求低通滤波器 的付氏变换。
f (t) A
/ 2 0 / 2 t
F (t) ASa t
2
2
0
F (t) 2A0Sa0t
比例特性, 两边
同时除以2
F (t)
A0
Sa0t
F () ASa
2
f () 2A
/ 2 0 / 2 f ()
量信号。如果其能量为有限值，则为能量信号， 如果其能量为无穷大，功率为有限值，则为功率 信号。一个信号或为能量信号，或为功率信号。
20
§4 Parseval定理（即能量守恒定理） 物理意义：能量守恒，时域能量等于频域能量， 即能量守恒不会变换后会发生改变。
一、对于能量信号f(t)，其频谱为F(jω)，则有
A sin( / 2) ASa
/ 2
2
F(
j)的零点满足如下关系
:
k , k
1,2,
2
从而得 : 2k , k 1,2,
注意到信号的大部分能 量集中在第一个主瓣内 ,
因此,得此信号的带宽为 2k f 1
R( ) P() 即功率信号的自相关函 数R( )与功率谱P()是一对付氏变换
29
第二部分 概率论与随机过程内容复习与总结
§1 随机事件与概率 一、事件与概率
1、随机事件：把某次试验中可能发生和不可能发生 的事件称为随机事件 A。如正弦波振荡器每次开机起 振的初相，二进制数字信号序列的某一位取值等等， 都属于随机事件。该事件出现的概率用P(A)表示，并
且有0 P(A) 1。若P(A)=1为必然事件，若P(A)=0
为不可能事件，等等。
30
§2 条件概率与统计独立 在事件A发生的条件下,事件B发生的概率用 P(B / A),
称为条件概率.按定义有 : P(B / A) P(AB) P( A)
在一般情况下, P(B / A) P(B),只有当A, B为统计独立时, P(B / A) P(B)才能成立.并且有P(AB) P(A)P(B).
则称f1(t)和f2 (t)完全相关.
3 互相关函数 R12( )满足 : R12( ) R21( ).
27
（二）自相关函数的性质
1 R(0)的性质(可直接从定义获得 ) :
对于功率信号, R(0)
lim
1
T /2
f
2 (t)dt S
T T T / 2
对于能量信号, R(0) f 2 (t)dt E
31
§3 概率的基本定理
1 事件之和的概率 : P( A B) P( A) P(B) P(AB)
当A与B互不相容时, P( AB) P() 0,有
P( A B) P( A) P(B) 2 事件之积的概率 :
P( AB) P( A)P(B / A) P(B)P( A / B) 当A与B相互独立时,有P(B / A) P(B), P( A / B) P( A)
1. 单位冲激函数 (t) E (t) E 或 (t) 1
物理意义 : 变化快的信号如很窄的 脉冲等,可近似用
数学模型 (t)来表示,上式说明这类随时间变 化很快
的信号的频谱很宽 .
(t)
F ( j)
(1)
1
0t
0
6
2 直流信号f (t) A
1 2 () A 2A ()
2
第一部分：信号分析内容复习与总结
§1 周期信号和非周期信号的频谱 一、周期信号的付氏级数展开式
1、三角形式
n
f (t) A0 An cos(n0t n )
n 1
其中0
2
T0
为基波频率 , T0为信号的周期 ,
而n0为n次谐波频率
3
2、指数形式
利用高等数学中的欧拉公式，可将三角形式的
(1)
f
F
(t)
( j)
1
2
F ( j)e jt
f (t)e jt dt
d