从麦克斯韦速度分布函数直接推导高分子链末端距分布函数
大学物理(下册) 12.5麦克斯韦气体分子速率分布律
f (v) dN Ndv
f (v)
平衡态下,当气体分子间相互作
用忽略不计时,气体分子按速率
的分布规律:平衡态,分子间作 o 用忽略时,分布在 v v dv
v
内的分子数dN占总分子数N的比
率是:
dN f (v)dv 4π(
m0
)3
2
e
m0 v2 2kT
分子速率分布图
N /(Nv)
N :分子总数
S
o
v v v
v
N 为速率在 v v v 区间的分子数;
S N N
表示速率在 v v v
子数占总数的百分比;
区间的分
12.5.2 麦克斯韦气体分子速率分布律
速率分布函数:f (v) lim N 1 lim N 1 dN (1) v0 Nv N v0 v N dv
总之:三种统计速率各自对应不同的物理意义,拥 有不同的用途。他们都具有统计平均意义,反映的 是大量分子作热运动的统计规律性。
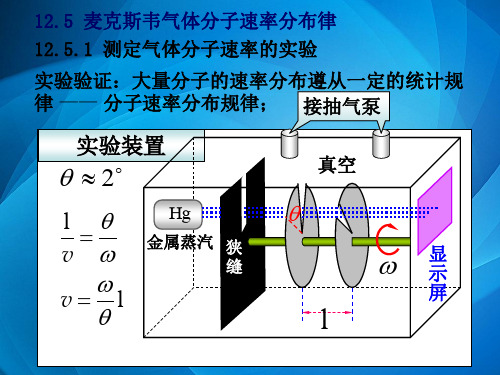
12.5 麦克斯韦气体分子速率分布律 12.5.1 测定气体分子速率的实验
实验验证:大量分子的速率分布遵从一定的统计规 律 —— 分子速率分布规律; 接抽气泵
实验装置
2
l v vl
ቤተ መጻሕፍቲ ባይዱ
Hg
金属蒸汽 狭 缝
真空
显 示
屏
l
实验验证:大量分子的速率分布遵从一定的规律,即 分子速率分布规律;
(6)
vrms
v2
3kT
m0
3RT M
(7)
4. 关于三种统计速率的讨论
vp v v2
麦克斯韦气体分子速率分布律知识
第十二章 气体动理论
16
物理学
第五版
本章目录
选择进入下一节:
12-4 理想气体分子的平均平动动能
与温度的关系
12-5 能量均分定理 理想气体内能
12-6 麦克斯韦气体分子速率分布律
*12-7 玻耳兹曼能量分布律 等温气压公式
12-8 气体分子平均碰撞次数和 平均自由程
第十二章 气体动理论
17
物理学
12-6 麦克斯韦气体分子速率分布律
第五版
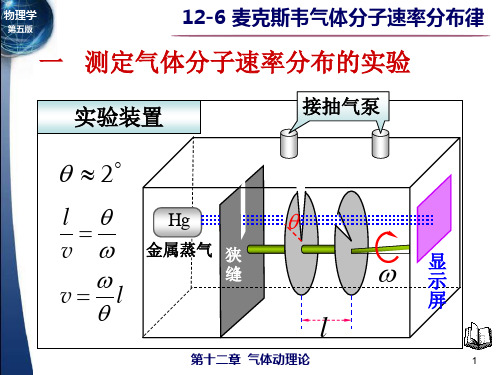
一 测定气体分子速率分布的实验
实验装置
接抽气泵
2
l v vl
Hg
金属蒸气 狭 缝
l
第十二章 气体动理论
显 示
屏
1
物理学
12-6 麦克斯韦气体分子速率分布律
第五版
分子速率分布图 N : 分子总数
N /(Nv)
N: v v v间的分子数.
S
o
v v v
第十二章 气体动理论
3
物理学
12-6 麦克斯韦气体分子速率分布律
第五版
第十二章 气体动理论
物理学
12-6 麦克斯韦气体分子速率分布律
第五版
f (v) 物理意义
表示在温度为 T 的平衡状态下,速
率在 v 附近单位速率区间 的分子数占总
数的百分比 .
f (v)dv 的物理意义:
表示速率在v v dv区间的分 子数占总分子数的百分比.
v
S N 表示速率在 v v v 区间
N 的分子数占总数的百分比 .
第十二章 气体动理论
2
物理学
12-6 麦克斯韦气体分子速率分布律
第五版
分布函数 f (v) lim N 1 lim N 1 dN v0 Nv N v0 v N dv
麦克斯韦速度分布函数的推导

麦克斯韦速度分布函数的推导:(由f05060699改正并完成)这里将讨论热平衡下的速度分布函数fM(v )=fM(v x ,v y ,v z ),即热平衡下速度空间内,在v 处单位体积元内的概率。
用下标M 来表示区分其它速度分布函数。
用g M (v x )dv x ,g M (v y )dv y ,g M (v z )dv z分别表示热平衡下分子代表点的速度分量在v x 到v x +dv x 、vy到v y +dv y 、v z 到v z +dv z 区间内的概率。
麦克斯韦假定:在热平衡状态下分子速度任一分量的分布应与其它分量的分布无关,即三个分量的分布是彼此独立的。
由独立事件概率公式知,气体分子在速度空间的代表点处于dv xdv ydv z内的概率等于它们速度分量分别处于dv x ,dv y ,dv z 区间内概率的乘积:fM(v x ,v y ,v z )dv xdv ydv z=g M(v x)dv xg M(v y )dv yg M(v z )dv z(1)f M (v x ,v y ,v z )=f M(v )=fM (v 2)=f M (v v v z y x 222++) (2)由(1)(2)有f M (v v v z y x 222++)=g M(v x )g M (v y )g M(v z )..................(3) 取上式的对数,得 ln f M (v v v z y x 222++)=ln g M(v x )+ln g M (v y )+ln g M(v z ).........(4) 就上式对v x ,v y ,v z 求偏导,并注意到v =v v v z y x 222++,有:)(1v fM.dvv dfM)(.v 1=v v g v g v ii Mi Mi d d )(.)(1.1(其中i=x,y,z),三个式子左边相同,又由三个分量的分布彼此独立知右边必为一常数D ,即v v g v g v ii MiMid d )(.)(1.1=D ,分离变量后积分得:ln g M (v i )=A-B v i 2,即g M (v i )=ciev i B-,c i=e A.由此按(3)式有fM(v x ,v y ,v z )=CeCev v v v BB z y x 2222)(-++-=,其中C=C i 3 (5)下面的任务是求出参量C 、B,它们由归一化条件决定.(注:这里我们假定C 、B 都是常量,其实C 是v 2的函数也可以满足(3)式或(4)式。
§2.4.4 从麦克斯韦速度分布导出速率分布

(二)在速度空间中的气体分子速率分布
我们知道,速度空间是能够同时表示分子的速度矢量 的大小和方向的直角坐标系。 在任一瞬时,一个气体分子在速度空间中与一个代表
点相对应,气体的N 个分子对应有N 个代表点。这样
就构成代表点在速度空间中的一种麦克斯韦速率分布表示了,在速度空间中,所有
dv
dNv
4N ( m )3/ 2 2k T
exp(
mv 2 ) v2 2kT
dv
dNv f (v)dv 4 ( m )3/2 exp( mv 2 ) v2dv
N
2kT
2kT
• 这就是麦克斯韦速率分布。
Nf (vx , vy , vz )dvxdvydvz dvxdvydvz
N ( m )3/2 exp( mv2 )
2kT
2kT
而
D(vx , vy , vz ) D(v)
将上二式代入到 dNv D(v) 4v2 dv
dNv
4N ( m )3/ 2 2k T
exp(
mv 2 ) v2 2kT
其速率介于v 到v + dv 范围内的分子的代表点都 落在以原点为球心,半径为v 的厚度为dv的一薄
层球壳中的概率,如图所示。
•根据分子混沌性假设,气体分子速度没有择优取 向,在各个方向上应该是等概率的,
•说明代表点的数密度D 是球 对称的,D 仅是离开原点的 距离v 的函数。 •设代表点的数密度为D(v)。 是D球(壳v)内与的球代表壳点体数积的d乘Nv 积应
dNv D(v) 4v2 dv
在速度空间中,在速度分量vx、vy、vz附 近的小立方体dvxdvydvz区间范围内的代表
点数就是麦克斯韦速度分布
Nf(vx、vy、vz) dvxdvydvz ,
7—5 麦克斯韦气体分子速率分布律

返回
1
南通大学
Nantong University
7-5 麦克斯韦气体分子速率分布律
一 麦克斯韦气体分子速率分布律
速率分布函数
N 1 N 1 dN f ( v) lim lim v0 Nv N v0 v N dv
f ( v)
dS
dN f ( v)dv dS N
第7章 气体动理论
返回
15
南通大学
Nantong University
7-5 麦克斯韦气体分子速率分布律
2 如图示两条 f ( v) ~ v 曲线分别表示氢 气和氧气在同一温度下的麦克斯韦速率分布 曲线, 从图上数据求出两气体最概然速率.
f ( v)
o
2 000
v / m s1
返回
第7章 气体动理论
第7章 气体动理论
返回
3
南通大学
Nantong University
7-5 麦克斯韦气体分子速率分布律
dN Nf ( v)dv 速率在v v dv 内分子数:
f ( v)
速率位于 v1 v2 区间的 分子数:
S
N
o
v1 v2
v
速率位于 v1 v2 区间的 分子数占总数的百分比:
南通大学
Nantong University
7-5 麦克斯韦气体分子速率分布律
麦克斯韦(James Clerk Max well 1831--1879)是继法拉第 之后集电磁学大成的伟大科学 家.他建立的电磁场理论,将 电学、磁学、光学统一起来, 是19世纪物理学发展的最光辉 的成果.在热力学与统计物理 学方面麦克斯韦也做出了重要 贡献,他是气体动理论的创始 人之一.他首次用统计规律得 出麦克斯韦速度分布律,从而 找到了由微观量求统计平均值 的更确切的途径.
麦克斯韦气体速率分布律推导

麦克斯韦气体速率分布律推导麦克斯韦-玻尔兹曼速率分布律描述了理想气体中分子速度的统计分布。
以下是该分布律的推导过程。
首先,考虑一个由大量相同分子组成的理想气体,这些分子在容器中随机、无序地运动。
由于分子间的碰撞非常频繁,我们可以假定每个分子的运动是相互独立的。
我们的目标是求出分子速率的分布函数。
1. 假设分子的运动是三维的随机运动,并且分子间无相互作用力。
2. 假设分子的运动是各向同性的,即在任何方向上运动的概率都是相等的。
3. 假设分子的运动是稳定的,即分子的速率分布不随时间改变。
4. 引入分子速度的微分元素d³v,表示速度在v到v+dv之间的分子数。
5. 引入微元体积元素dV和微元时间元素dt。
接下来,我们将使用微元分析法来推导速率分布律。
对于一个具有速率v的分子,在时间dt内,它将沿着速度方向移动的距离为v·dt。
因此,它所扫过的体积元素为dV = v²·cos²(θ)·sin(θ)·dv·dt,其中θ是速度方向与某一选定方向(通常是x轴)的夹角。
现在,考虑在dt时间内所有具有速率v的分子所扫过的体积总和,即所有可能的方向θ的贡献。
由于θ的取值范围是0到π,我们可以将上述体积元素乘以角度元素dθ(从0到π)并积分,以得到总的体积元素dV_total:dV_total = ∫(v²·cos²(θ)·sin(θ)·dv)·dθ·dt由于cos²(θ)·sin(θ)是关于θ的偶函数,而在0到π的范围内积分,它的积分结果为零。
为了解决这个问题,我们需要考虑在速度方向上的微小位移。
在速度方向上的微小位移为v·cos(θ)·dt,因此,在dt时间内,具有速率v的分子在速度方向上的微小体积元素为dV_v = v·cos(θ)·dv·dt。
麦克斯韦速率分布律的推导和验证
完美WORD 格式 编辑麦克斯韦速度分布律的推导与实验验证摘要:本文对麦克斯韦速度分布律的内容及其历史来历做了简略概述,重点是用初等方法推导了麦克斯韦速度分布律,同时简单地描述了一下它的实验验证。
关键词:速度分布函数,实验验证。
一. 内容1、麦克斯韦速度分布律的内容当气体处于平衡态时,气体分子的速度在v ~v dv +间隔内,及分子速度分量在x x x v ~v dv +,y y y v ~v dv +,z z z v ~v dv +间隔内的分子数dN(v)占总分子数N的比率为:2223()/22x y z d v m ()v v v N 2kTx y z m v v v kTN e d d d π-++=(), 其中m 为分子的质量,T 为气体温度,k 为波尔兹曼常数,222211()v 22x y z m v v v m ++=为气体分子平动能。
d v NN ()表示速度矢量的端点在速度体元d τ内的分子数占总分子数的比率,换言之,一个分子取得v ~v dv +间隔内速度的几率。
2、分子速度分布函数2223()/22m f ()2kTx y zm v v v kTe π-++=x y z dN(v)(v )=Ndv dv dvf (v )的物理意义是:分子速度在v 附近,单位时间间隔内的分子数占总分子数的比率。
3、速度分量分布函数2221/221/221/22m f ()2kTm f ()2kTm f ()2kTx y z mv kTmv kTmv kTee eπππ---===x x x y y y z z z dN(v )(v )=Ndv dN(v )(v )=Ndv dN(v )(v )=Ndv3、麦克斯韦速率分布律将以,,x y z v v v 为轴的笛氏坐标进行坐标变换,变为球坐标2,,,,sin {x y z v v v v v d d dv θϕθθϕ→→xyzdvdv dv 分子速度在v ~v dv +,~,~d d θθθϕϕϕ++内的分子数占总分子数的比率为23/222m ()sin 2kTmv kT e v d d dv θθϕπ-=dN(v)N 对θ,ϕ积分,得分子的速度在v ~v dv +内分子数占总分子数的比率为23/222m 4()2kTmv kT e v dv ππ-=dN(v)N 4、分子速率分布函数23/222m f v 4()2kTmv kT e v ππ-=dN(v)()=Ndv物理意义:分子速率在v 附近,单位速率间隔内的几率。
麦克斯韦分子速率分布定律的推导
麦克斯韦分子速率分布定律的推导麦克斯韦分子速率分布定律是分子运动理论中一个重要的概念,它用来描述分子或微粒在一定条件下的速率分布情况。
它表明,当以相同速率出射分子时,在不同瞬间可以得到不同的分子速度,而这些分子速度是具有特定分布函数的随机变化,这个分布函数就是麦克斯韦分子速率分布函数。
一般来说,微粒的运动属于无序性运动。
在实验中,出射的分子速度的分布状况不容易分析,只能藉助于实验结果推断出微粒速度的分布规律。
而麦克斯韦分子速率分布定律是1859年俄国物理学家麦克斯韦(Maxwell)推导出来的一个概念,他结合热力学原理和拉格朗日机械统计原理,以蒙特卡洛方法推导出了质点和分子在不同温度下的速率分布情况,结果发现分子速度都符合高斯分布,即可以用一个正态分布概率密度函数来对分子速度进行分析,而这就是麦克斯韦分子速率分布定律。
f(v) = 4πa^3v^2exp(-a^2v^2)其中f(v)是速度为v的粒子数,a是系统的温度模式,用a^3来表示。
其定义概括地表示出温室质点和分子在温度T下的速度分布情况。
而推导时最重要的一个步骤就是综合考虑热力学和机械统计原理,通过这两个原理,可以使得统计模型的概率守恒,即有能量的分配都是满足守恒定律的,从而可得到正态分布,即f(v)为高斯分布函数,最后积分得到麦克斯韦分子速率分布定律。
总的来说,麦克斯韦分子速率分布定律可以较为完整地描述出温室质点或分子在某一温度下的运动规律,统计是一种相对稳定的状态。
它在应用到能量或物质传输等实际场合中有重要作用,比如应用到气体流体动力学中。
历史上,麦克斯韦分子速率分布定律有很多改进版本,比如上面函数中的指数可以做出改变,也可以对新的分子进行同样的推导,从而求出其对应的概率分布函数。
因此,麦克斯韦分子速率分布定律仍然是理解物理世界中的质点运动、热力学和机械统计的重要工具,是实验物理学的理论基础。
【高聚物的结构与性能课件】4.从Maxwell速度分布函数直接推导高分子链末端距的径向分布函数
实现这种无规行走的几率:
Z! ⎛1⎞ ⎛1⎞ ⋅⎜ ⎟ ⋅⎜ ⎟ W ( Z , m) = Z +m Z −m ⎝2⎠ ⎝2⎠ ! ! 2 2
Z+ Z−
Z! ⎛1⎞ = ⋅⎜ ⎟ Z +m Z −m ⎝2⎠ ! ! 2 2
Z
几率密度函数—高斯函数
在 Z >> 1,m << Z 的假设条件下,作斯特林近似, 再将有关项作级数展开,略去高次项得:来自h0 = Nl2
2
h
2
:无规线团的均方末端距
h0 = N l
2 12
上述结果与维数无关,对于一维、二维、三 维甚至更高的维数都能成立
Flory: The effect of excluded volume
The configuration on the left represents the random coil in absence of volume exclusion, the chain being equivalent to a line in space.
2 2
三维空间的无规行走
在 三维空间无规行走过程中,每走一步b时,它在各坐 标轴上投影(bx,by,bz)为多少? 令b与x轴的夹角用ψ表示,则b在x轴上的投影
bx = b cosψ
bx = bcosψ
π
cosψ = ∫
0
bx = 0
2π b sinψ ⋅ bdψ =0 cosψ 2 4π b
三维空间的无规行走——每一步
设:一根链的空间有 ν ip根链相互穿透:
ν ip ∝ M
12
• 链段受到同一链上相隔较远的链段的排斥力被相 邻链上链段对它的排斥力所屏蔽 ——每根链呈无规线团形态
麦克斯韦速率分布函数
由此可得:
vpf(vp)=41/2e1 =常量。
这是一条双曲线 的方程。
用麦克斯韦速率分 布函数的约化形式来 求速率分布曲线出现 极大值的点的轨迹, 似乎更简便。
x=v/vp, dx/dv=1/vp. f(v)=F(x)dx/dv
=F(x)/vp =41/2x2 exp(x2)/vp.
f(vp)=F(1)/vp =41/2e1/vp.
四、随机事件 与概率
随机现象:有可 能出现多种结果的 现象。
随机事件:随机 现象的每一表现或 结果。
频率:某事件出 现次数对总次数的 比率。
概率:某事件频 率在总次数趋于无 限大时的极限。
不可能事件 的概率为零。
必然事件的 概率为一。
概率加法定理: 互不相容(互斥) 事件出现的概率的 和等于出现其中任 一事件的概率。
概率乘法定理: 互相独立事件同时 出现的概率等于各 事件单独出现时概 率的积。
五、麦克斯韦速 率分布曲线出现 极大值的点的轨
迹
f(v)=41/2[m/(2kT)]3/2 exp[mv2/(2kT)]v2.
将vp=(2kT/m)1/2代入f(v) 可得:
f(vp)=41/2[m/(2kT)]3/2 exp[mvp2/(2kT)]vp2 =41/2exp[vp2-2]vp-3+2 =41/2e1vp-1.
麦克斯韦速 率分布函数
及其 约化形式
一、麦克斯韦 速率分布函数
f(v)=4[m/(2kT)]3/2 exp[mv2/(2kT)]v2 =4-1/2[m/(2kT)]3/2 exp[mv2/(2kT)]v2.
f(v)称为麦克斯 韦速率分布函数, 式中的T 为气体的 热力学温度,m为 气体分子质量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)
由此得出
基金项目 :2004 年中国科学技术大学教学研究项目 ( YL5268) ; 作者简介 :朱平平 ,女 ,安徽无为人 ,中国科学技术大学高分子科学与工程系副教授 ,主要从事高分子溶液 、共混高 聚物性能等方面的研究 ,近年来同时开展了高分子物理的教学研究工作 。
E-mail :zhupp @ustc. edu. cn
(3)
式得到麦克斯韦速度分布函
数 : f ( v) =
m
2πkT
3P2
exp
-
mv2 2 kT
,如果考虑到速度分布的各向同性 ,麦克斯韦速度分布函数又可表
示为 :
f ( v)
=
4π
m
2πk T
3P2
exp
-
mv2 2 kT
·v2
(4)
式中 4πv2 为速度空间中半径为 v 的球壳面积 。
显然 , f ( vx ) 、f ( vy ) 、f ( vz ) 的独立性是麦克斯韦推导气体速度分布函数中最重要 、最基础的一
1P2
,β′2 =
3 2 ne
l2e
,这样 (5) 式可表示为 :
W ( h)
=
4π
3 2πne
le2
3P2
exp
-
3 h2 2 ne le2
·h2
(6)
这里 , ne 和 le 分别代表主链上可划分出来的最小独立运动单元的数目和长度 , ne 略小于 n , n 表 示主链上单键的数目 。这是因为 ,高分子链主链上的单键虽然能够发生不同程度的内旋转 ,但是单
参考文献 :
[ 1 ] 何平笙 ,朱平平 ,杨海洋. 高分子通报 ,2001 ,5 :74~79. [ 2 ] 马德柱 ,何平笙 ,徐种德 ,等. 高聚物的结构与性能 ,第二版 ,北京 :科学出版社 ,1995. [ 3 ] 何曼君 ,陈维孝 ,董西侠. 高分子物理 ,修订版 ,上海 :复旦大学出版社 ,1990. [ 4 ] Flory P J . Principle of Polymer Chemistry. New York :Cornell University Press ,1953. [ 5 ] 赵凯华 ,罗薇茵. 热学. 北京 :高等教育出版社 ,1998. [ 6 ] PJ 弗洛里著 ,吴大诚 ,高玉书 ,许元泽 ,等译. 链状分子的统计力学 ,成都 :四川科学技术出版社 ,1991. [ 7 ] 宗祥福 ,翁渝民. 材料物理基础 ,上海 :复旦大学出版社 ,2001. [ 8 ] 冯端 ,师昌绪 ,刘治国. 材料科学导论 ,北京 :化学工业出版社 ,2002. [ 9 ] 钱人元. 高分子通报 ,2000 ,2 :1~9.
第 6 期
高 分 子 通 报
·93 ·
直时的长度的 。但是注意到 W ( Lmax) 要比 W ( h2 ) 小一个数量级约为 exp (3 ne / 2) 的因子 ,对于聚 乙烯 ,当 n = 103 , ne = 102 时 ,这因子的数值就已达到约 1062 ,可见 , W ( Lmax ) 极小 ,对于实际的链长 度 ,这个不足之处完全可以忽略 ,因此 , (6) 式是描述柔性高分子链末端距分布的很好的近似公式 。
键旋转时互相牵制 ,一个键转动 ,带动相邻键以及靠得较近的一段链节的一起运动 ,这样每个键不
可能成为一个独立运动单元 ,但是只要主链足够长 、且具有一定的柔性 ,则总可以把若干个键组成
的一段链看作一个独立运动单元 ,称它为“链段”,链段之间按“无规行走”方式运动 。对于聚乙烯 ,
ne = nP10 , ne 仍是一个很大的数 。由于每个链段的运动类似于单个小分子的运动 ,因此又被称为
y , z) 表示 ,且仅取决于速度的量值 ,与它在空间的方向无关 ,即 :
f ( vx , vy , vz ) = f ( vx ) f ( vy ) f ( vz ) = f ( v2 ) = f ( v2x + v2y + v2z )
(1)
满足 (1) 式的唯一函数应具有如下形式 :
f ( vi ) α = e- β2 v2i ( i = x , y , z)
Deducing the Chain Displacement Length Distribution Function for Macromolecules Directly from Maxwell Velocity Distribution Function
ZHU Ping-ping , YANG Hai-yang , HE Ping- sheng
(3)
上式中的参数 α、β由如下的归一化条件决定 :
∫∝ 4πv2
·α3
e - β2 v2
dv
0
= α3
π β2
3P2
=1
∫ 1
2
m
∝
4πv4
0
·α3 e - β2 v2
dv
=
1 2
m
·4πα3
·3
π 8
1 β2
3P2
=ε=
3 2
kT
这里ε是分子的平均动能 。将得出的 α=
m
2πkT
1P2
,β2
=
m 代回 2 kT
对于小分子 ,个别分子的运动服从经典的动力学规律 ,然而大量分子的运动则服从一定的统计 规律 (用高斯函数描述) ,且分子整体的总动能或平均速度在定温下保持不变 。对于高分子 ,由于链 段的微布朗运动 ,我们并不知道任何一个实际高分子链在每一时刻的形状 、尺寸 ,但是其末端距的 分布总也遵循着一定的统计规律 (也用高斯函数描述) ,并且均方末端距与分子量的一次方成正比 , 与高分子具体的化学结构无关 。在“高聚物的结构与性能”教学中 ,阐明高分子链末端距分布与小 分子运动速度分布之间的这种相关性 ,对学生加深理解高分子链结构 、分子运动的特点以及产生于 这些特点的独特物理性能 (如 :橡胶的高弹性) 无疑是很有帮助的 。
( Department of Polymer Science and Engineering , University of Science and Technology of China , Hefei 230026 , China)
Abstract :Based on the correlation between the chain displacement length distribution for macromolecules and the velocity distribution for small molecules ,the radial distribution function of the chain displacement vectors could be directly deduced from the Maxwell velocity distribution function. The motion law for macromolecules and small molecules were discussed from the standpoint of quantitative change and qualitative change.
量 hx 、hy 、hz 分布的独立性假定推广到三维空间 ,很是繁琐 。实际上 ,在数学上求解末端距 h 与求
解小分子运动速度 v 一样 ,都采用向量运算 ,同时对于大量小分子的集合体 ,麦克斯韦认为速度三
个分量的分布也是彼此独立的 ,那么 ,就可以从熟知的麦克斯韦速度分布函数直接推导出高分子链
末端距的径向分布函数 。
Key words : Chain displacement length distribution for macromolecules ; Maxwell velocity distribution ; Segment ; Conformation statistics
© 1995-2005 Tsinghua Tongfang Optical Disc Co., Ltd. All rights reserved.
气体中 ,每个分子的速率 (用 v 表示) 时刻在变 ,完全受概率所支配 ,麦克斯韦假定[5] :在热平衡
态下 ,速度三个分量 vx 、vy 、vz 的分布是彼此独立的 。此外 ,对于宏观上静止的气体来说 ,速度的分
布应是各向同性的 ,这就是说 ,在速度空间中 , vx 、vy 、vz 的分布需要用同一形式的函数 f ( vi ) ( i = x ,
微布朗运动 。
根据 (6) 式 ,当 h > Lmax ( Lmax = ne le ,为链的最大伸直长度) 时 W ( h) 并不趋于零[7 ,8] ,由此可知
(6) 式存在一些误差 。一个正确的 W ( h) 在 h > Lmax 时应为零 ,因为末端距是不可能超过链完全伸
© 1995-2005 Tsinghua Tongfang Optical Disc Co., Ltd. All rights reserved.
© 1995-2005 Tsinghua Tongfang Optical Disc Co., Ltd. All rights reserved.
·92 ·
高 分 子 通 报
2004 年 12 月
f ( v) = f ( vx , vy , vz ) = α e 3 - β2 ( v2x + v2y + v2z ) = α3 e- β2 v2
函数形式 ,从而可以根据麦克斯韦速度分布函数直接写出高分子链末端距的径向分布函数 :
W ( h) = 4πα′3 e - β′2 h2 ·h2
(5)
再根据下列的归一化条件 :
∫∝ W ( h) d h = 1 0
