尺规作图三等分任意角
千古谜题--伽罗瓦的解答.
求方程根的问题！
（1）三等分任意角:设已知某角的角度为 3，得cos(3 ) a
则 cos(3 ) 4cos 3 3cos a 令 cos x
即问题转化为解方程： 4 x3 3 x a（, a为已知数）
（2）倍立方
x3 2
x3 2
（3）化圆为方
x2
x
花拉子米
早在古巴比伦时代,人们已经 掌握了解一次、二次方程的方法：
公元９世纪
“代数学”algebra） 这个词来源于花拉 子米所著的一本书
系统研究二次方程的一般解法并给出了求根公式
悲观派 乐天派
1494年,意大利数学家 帕西奥利
根本不可能
意大利波伦大学 教授费罗
x3 + mx n
数学史上称三次方程的求根公式为：
“卡尔达诺”公式
• 一位颇受欢迎的医生
• 哲学家和数学家， • 占星术家
塔尔塔利亚
卡尔达诺
撰写代数著作《大术》
1545年卡尔达诺出版《大术》一书，将三次方程解 的解法公诸于众，从而使自己在数学界声名鹊起。
ax2 + bx + c 0(a 0)
a( x + b )2 + 4ac b2 0
群的概念：
设G是一个集合，集合内的元素之间可以定义一个二元运算﹡
如果G满足如下的四条性质：
（1）（封闭性）集合中任意两个元素的积仍属于该集合
（2）（结合性）运算满足结合律，即 (a b) c a (b c)
e （3）（存在单位元）集合中存在单位元 ，对集合中任意元素 a
满足 ea ae a
用x 系数三分之一的三次方加上方程常数一半的平方；求这整个算
三大尺规作图问题
引人入胜的千古难题——三大尺规作图问题尺规作图是我们熟知的内容。
尺规作图对作图的工具——直尺和圆规的作用有所限制。
直尺和圆规所能作的基本图形只有：过两点画一条直线、作圆、作两条直线的交点、作两圆的交点、作一条直线与一个圆的交点。
公元前五世纪的希腊数学家，已经习惯于用不带刻度的直尺和圆规（以下简称尺规）来作图了。
在他们看来，直线和圆是可以信赖的最基本的图形，而直尺和圆规是这两种图形的具体体现，因而只有用尺规作出的图形才是可信的。
于是他们热衷于在尺规限制下探讨几何作图问题。
数学家们总是对用简单的工具解决困难的问题备加赞赏，自然对用尺规去画各种图形饶有兴趣。
尺规作图是对人类智慧的挑战，是培养人的思维与操作能力的有效手段。
所谓三大几何作图难题就是在这种背景下产生的。
传说大约在公元前400年，古希腊的雅典流行疫病，为了消除灾难，人们向太阳神阿波罗求助，阿波罗提出要求，说必须将他神殿前的立方体祭坛的体积扩大1倍，否则疫病会继续流行。
起初，人们并没有认识到满足这一要求会有多大困难，但经过多次努力还不能办到时，才感到事态的严重。
人们百思不得其解，不得不求教于当时最伟大的学者柏拉图，柏拉图经过慎重的思考，也感到无能为力。
这就是古希腊三大几何问题之一的倍立方体问题。
用数学语言表达就是：已知一个立方体，求作一个立方体，使它的体积是已知立方体的两倍。
任意给定一个角，仅用直尺和圆规作它的角平分线是很容易的，这就是说，二等分任意角是很容易做到的。
于是，人们自然想到，任意给定一个角，仅用直尺和圆规将它三等分，想必也不会有多大困难。
但是，尽管费了很大的气力，却没能把看来容易的事做成。
于是，第二个尺规作图难题——三等分任意角问题产生了。
正方形是一种美丽的直线形，圆是一种既简单又优美的曲线图形，它们都有面积，能不能用直尺和圆规作一个正方形，使它的面积等于一个给定的圆的面积？这就是尺规作图三大难题的第三个问题——化圆为方问题。
古希腊三大几何问题既引人入胜，又十分困难。
尺规三大作图问题
尺规三大作图问题尺规作图是我们熟知的内容。
尺规作图对作图的工具——直尺和圆规的作用有所限制。
直尺和圆规所能的基本图形只有：过两点画一条直线、作圆、作两条直线的交点、圆点、作一条直线与一个圆的交点。
公元前五世纪的希腊数学家，已经习惯于用不带刻度的直尺和圆规（以下简称尺规）来作图了。
在他们看来，直线和圆是可以信赖的最基本的图形，而直尺和圆规是这两种图形的具体体现，因而只有用尺规作出的图形才是可信的。
于是他们热衷于在尺规限制下探讨几何作图问题。
数学家们总是对用简单的工具解决困难的问题备加赞赏，自然对用尺规去画各种图形饶有兴趣。
尺规作图是对人类智慧的挑战，是培养人的思维与操作能力的有效手段。
所谓三大几何作图难题就是在这种背景下产生的。
传说大约在公元前400年，古希腊的雅典流行疫病，为了消除灾难，人们向太阳神阿波罗求助，阿波罗提出要求，说必须将他神殿前的立方体祭坛的体积扩大1倍，否则疫病会继续流行。
起初，人们并没有认识到满足这一要求会有多大困难，但经过多次努力还不能办到时，才感到事态的严重。
人们百思不得其解，不得不求教于当时最伟大的学者柏拉图，柏拉图经过慎重的思考，也感到无能为力。
这就是古希腊三大几何问题之一的倍立方体问题。
用数学语言表达就是：已知一个立方体，求作一个立方体，使它的体积是已知立方体的两倍。
任意给定一个角，仅用直尺和圆规作它的角平分线是很容易的，这就是说，二等分任意角是很容易做到的。
于是，人们自然想到，任意给定一个角，仅用直尺和圆规将它三等分，想必也不会有多大困难。
但是，尽管费了很大的气力，却没能把看来容易的事做成。
于是，第二个尺规作图难题——三等分任意角问题产生了。
正方形是一种美丽的直线形，圆是一种既简单又优美的曲线图形，它们都有面积，能不能用直尺和圆规作一个正方形，使它的面积等于一个给定的圆的面积？这就是尺规作图三大难题的第三个问题——化圆为方问题。
另类做法：总述：人们用尺规解几何三大作图题屡遭失败之后，一方面是从反面怀疑它是否可作；另一方面就很自然地考虑，假如跳出尺规作图的框框，也就是不限用尺规，而是借助于另外一些曲线，或者借助于尺规以外的一些工具，是不是可解决这些问题呢？人们发现，一旦跳出了尺规作图的框框，问题的解决将是轻而易举的.这方面的工作已经有许多人做过，而且取得了不少成就，下面的词条内容就择要介绍一二.三等分任意角★作法一三等分角问题尼科梅德斯(Nicomedes，公元前250年左右)方法对于已知锐角∠O，在角的一边上取任意点B，作OB的垂线，交∠O的另一边于点A.以O为定点，BA为定直线，2OA为定长，作出蚌线的右支C.从点A作BA的垂线，和蚌线C相交于点S，那么∠BOS=1/3∠BOA★作法二帕斯卡(Pascal，B.1623—1662)的方法对于∠AOB，在其一边上取任意长OA做半径，以点O为圆心作一圆(图12).延长AO，和圆O交于点C.以圆O为定圆，以C为定点，以定圆O的半径为定长，作一蚶线蚶线和角的另一边OB相交于点E.连结CE，过点O作OS∥CE，那么∠BOS=1/3∠BOA★作法三帕普斯(Pappus，约公元320年)方法对于∠AOB，在它的两边上截取OA=OB.连结AB并三等分，设两分点分别为C和D.以点C为中心，点A、D分别为顶点，作离心率e=√2的双曲线.以点O为圆心，OB为半径作弧，交双曲线于点S.则∠BOS=1/3∠BOA★作法四玫瑰线方法交∠AOB的两边于点A和B，分别以O和A为圆心，a为半径画弧，两弧交于点S，则有∠BOS=1/3∠BOA立方倍积★作法一倍立方问题倍立方问题柏拉图(Plato，公元前427—347年)的方法：作两条互相垂直的直线，两直线交于点O，在一条直线上截取OA=a，在另一条直线上截取OB=2a，这里a为已知立方体的棱长.在这两条直线上分别取点C、D，使∠ACD=∠BDC=90°(这只要移动两根直角尺，使一个角尺的边缘通过点A，另一个角尺的边缘通过点B，并使两直角尺的另一边重合，直角顶点分别在两直线上，这时两直角尺的直角顶点即为点C、D).线段OC之长即为所求立方体的一边。
利用渐开线三等分任意角的方法和证明
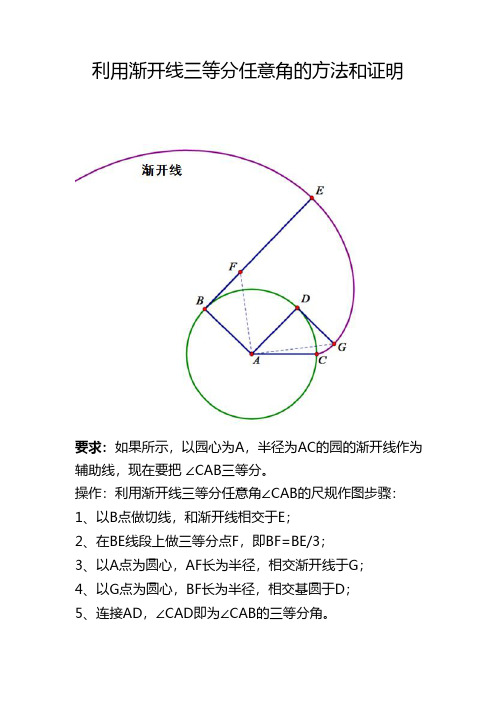
利用渐开线三等分任意角的方法和证明
要求：如果所示，以园心为A，半径为AC的园的渐开线作为辅助线，现在要把∠CAB三等分。
操作：利用渐开线三等分任意角∠CAB的尺规作图步骤：
1、以B点做切线，和渐开线相交于E；
2、在BE线段上做三等分点F，即BF=BE/3；
3、以A点为圆心，AF长为半径，相交渐开线于G；
4、以G点为圆心，BF长为半径，相交基圆于D；
5、连接AD，∠CAD即为∠CAB的三等分角。
证明：
1、先证明△BAF与△DAG全等
根据作图，BE是垂直于AB的圆上点B的切线，所
以∠FBA是直角，BF2=FA2-AB2，DG是垂直于AD的圆上点D的切线，所以∠ADG是直角，DG2=GA2-AD2,其中，AB=AD为园A的半径，且AF=AG，所
以BF=DG，△BAF与△DAG全等。
2、根据渐开线的性质，直线BE的长度=园弧BDC的长度，直线DG的长度 =园弧DC的长度，又因为DG=BF=BE/ 3，所以园弧DC的长度=园弧BDC的长度/3，因
此，∠CAD即为∠CAB的三等分角
总结：
伽罗瓦所证明的是，在不使用任何辅助线或用到除尺规外其他工具的前提下，不能在有限次操作内，使用尺规作图法三等分任意角，也就是说这三个限制只要有一个不成立，那么不能三等分任意角就不成立。
实际上只要引入渐开线，在有限次操作内，使用尺规作图法N等分任意角都是可行的，而且这种方法也同样可以解决化圆为方的问题。
这样，通过引入渐开线就一举解决的三大几何作图问题中的两个“不可能”的难题，并且渐开线在物理上是很容易得到的，它的本质是绕基圆展开的线，或者说大家常用的卷尺，就是渐开线所对应的物理实物。
角的三等分(尺规作图)
１ ． 以图 １中的 Ａ Ｏ为轴 ， 将 已三 等 分一 角 的 ＡＡ Ｏ Ｃ向
ＡＡ Ｏ Ｂ方 向旋转任意角度 Ｏ ｔ （ １ ８ ０ 。＞ Ｏ ｔ ＞０ 。 ） ， 连接 Ｂ Ｃ ， 即形
数 学 学 习与 研 究 ２ ０ １ ６ ． ２ ３
任意角被 三等分． Ｏ Ｆ 、 Ｏ Ｇ 为任意角的三等分线．
４ ． 证 明图 ２ 、 图 ３中的 ，点与 Ｆ 点、 Ｇ点与 Ｇ 点在 线段
． ．
Ａ Ｂ上分别为 同一 个 点 ， 从 而 逆推 证 明在平 面 图二 中 ， 用 尺
●
， ●
规作 图方法 三等分任意角的正确结论．
因图 ３ ＡＡ Ｂ Ｃ中， Ａ Ｃ、 Ａ Ｂ 的 长 度 及 Ｄ、 Ｅ两 点 在 Ａ Ｃ上 的
位置与图 ２ ＡＡ Ｂ Ｃ中的对应 部分相等 （ 旋 转后未发生 变化 ） ，
个三角形 中 Ｅ Ｆ ， Ｂ Ｃ、 ＤＧ ／ Ｂ Ｃ、 Ｅ Ｆ ｔ 力Ｂ Ｃ、 Ｄ Ｇ ｔ ／ Ｂ Ｃ ．
７ ． 连接 Ｏ Ｆ 、 Ｏ Ｇ， 所 得 ＬＡ Ｏ Ｆ（ １ ）＝ Ｆ Ｏ Ｇ （ ２ ）＝
Ａ Ｆ＝Ａ Ｆ ， Ｆ点与 Ｆ 点在 Ａ Ｂ上为 同一个点 ， 同理 ， Ａ Ｇ＝ Ａ Ｇ ， Ｇ点与 Ｇ 点在 Ａ Ｂ上为同一个点．
－Ｇ ／ Ｏ Ｂ（ ／ ＿ ３ ） ． Ｏ Ｇ、 Ｏ Ｆ为任意 ＬＡ Ｏ Ｂ三等分线 ， 任意 角被三
解 题 技 巧 与 方 法
◎ 栾鹤 臣
（ 黑 龙 江省 朗 乡林 区基 层 法 院 ， 黑龙 江
铁力
１ ５ ２ ５ １ ９ ）
【 摘 要】 用已 被 三等分 一角 的三角 形， 通 过平 行投 影 与
求解 的任 意角所在 的三角形重合 ， 三等分任 意角．
尺规作图不能问题
尺规作图不能问题就是不可能用尺规作图完成的作图问题。
这其中最著名的是被称为几何三大问题的古典难题：■三等分角问题：三等分一个任意角；■倍立方问题：作一个立方体，使它的体积是已知立方体的体积的两倍；■化圆为方问题：作一个正方形，使它的面积等于已知圆的面积。
在2400年前的古希腊已提出这些问题，直至1837年，法国数学家万芝尔才首先证明“三等分角”和“倍立方”为尺规作图不能问题。
1882年德国数学家林德曼证明π是超越数后，“化圆为方”也被证明为尺规作图不能问题。
【尺规作图不能问题的另类做法】[编辑本段]■总述人们用尺规解几何三大作图题屡遭失败之后，一方面是从反面怀疑它是否可作；另一方面就很自然地考虑，假如跳出尺规作图的框框，也就是不限用尺规，而是借助于另外一些曲线，或者借助于尺规以外的一些工具，是不是可解决这些问题呢？人们发现，一旦跳出了尺规作图的框框，问题的解决将是轻而易举的.这方面的工作已经有许多人做过，而且取得了不少成就，下面的词条内容就择要介绍一二.■关于三等分一任意角问题★作法一尼科梅德斯(Nicomedes，公元前250年左右)方法对于已知锐角∠O，在角的一边上取任意点B，作OB的垂线，交∠O的另一边于点A.以O为定点，BA为定直线，2OA为定长，作出蚌线的右支C.从点A作BA的垂线，和蚌线C相交于点S，那么∠BOS=1/3∠BOA★作法二帕斯卡(Pascal，B.1623—1662)的方法，对于∠AOB，在其一边上取任意长OA做半径，以点O为圆心作一圆(图12).延长AO，和圆O交于点C.以圆O为定圆，以C为定点，以定圆O的半径为定长，作一蚶线蚶线和角的另一边OB相交于点E.连结CE，过点O作OS∥CE，那么∠BOS=1/3∠BOA★作法三帕普斯(Pappus，约公元320年)方法，对于∠AOB，在它的两边上截取OA=OB.连结AB 并三等分，设两分点分别为C和D.以点C为中心，点A、D分别为顶点，作离心率e=√2的双曲线.以点O为圆心，OB为半径作弧，交双曲线于点S.则∠BOS=1/3∠BOA★作法四玫瑰线方法：交∠AOB的两边于点A和B，分别以O和A为圆心，a为半径画弧，两弧交于点S，则有∠BOS=1/3∠BOA■关于立方倍积问题★作法一柏拉图(Plato，公元前427—347年)的方法：作两条互相垂直的直线，两直线交于点O，在一条直线上截取OA=a，在另一条直线上截取OB=2a，这里a为已知立方体的棱长.在这两条直线上分别取点C、D，使∠ACD=∠BDC=90°(这只要移动两根直角尺，使一个角尺的边缘通过点A，另一个角尺的边缘通过点B，并使两直角尺的另一边重合，直角顶点分别在两直线上，这时两直角尺的直角顶点即为点C、D).线段OC之长即为所求立方体的一边.★作法二门纳马斯(Menaechmus，约公元前375—325年)方法：从a∶x=x∶y=y∶2a可得y2=2ax，x2=ay.所以，在直角坐标平面上画出上述两个二次方程所对应的两条抛物线(图16).这两条抛物线交于O、A两点，那么点A在x轴上的投影到原点的距离，就是所求的立方体的棱长.★作法三阿波罗尼(Apollonius de Perge，约公元前260—200年)方法：作一矩形ABCD，这里AB=a、AD=2a.以此矩形对角线交点G为圆心，以适当长度为半径作圆，与AB、AD之延长线分别交于E、F，使E、C、F三点共线，则AB∶DF=DF∶BE=BE∶AD，线段DF之长即为所求立方体的棱长.■化圆为方问题★作法：对于已知圆O，作出它在第一象限的圆积线①l.连结这一圆积线的两个端点B、F，过点B引BF的垂线BG，交x轴于G.在OA上取一点H，使HA=1/2GO.以H为圆心，HG 为半径画弧，交y轴于点K.则以OK为一边的正方形，即为所求作的与圆O等积的正方形．【尺规作图不能问题的积极意义】[编辑本段]我们可以看出，几何三大问题如果不限制作图工具，便很容易解决.从历史上看，好些数学结果是为解决三大问题而得出的副产品，特别是开创了对圆锥曲线的研究，发现了一批著名的曲线，等等.不仅如此，三大问题还和近代的方程论、群论等数学分支发生了关系.【尺规作图不能问题的相关趣事】[编辑本段]阿纳克萨戈勒斯是古希腊著名学者,在天文学中,他曾因解释日,月食的成因而闻名遐迩,并且认识到月球自身并不发光.正是他出色的研究成果给他带来了不幸, 在他大约50岁的时候,横祸从天而降,蒙受了冤狱之苦.灾难的起因是他认为太阳是一块炽热的石头.由于当时的宗教早已一口咬定太阳是神灵,而这位学者却无视宗教的权威,说太阳是一块石头,因而被投入监狱.尽管被囚禁的时间并不太长,可是,在被囚禁的日子里冤屈,苦闷,无聊实在让人度日如年.在阴暗,潮湿的牢房里,阿纳克萨戈勒斯看不到外面的朝霞暮霭,每天只有不长时间,阳光能穿过牢房那狭小的方形窗户进入室内.每当阳光进入囚室,在墙壁上撒下一片光亮时,总会引起作为学者的他的种种联想.有一天,他在凝视圆圆的太阳赏赐给他的方形的光亮时,他那习惯于思索的头脑突发奇想:能不能(仅用直尺和圆规)作一个正方形,使其面积与一个已知圆的面积恰好相等呢就这样,一道世界名题——"化圆为方"问题诞生了,它与"立方倍积"问题,"三等分任意角"问题一起被后人称作古希腊几何作图三大难题. 阿纳克萨戈勒斯想到化圆为方问题之后非常兴奋,因为他身边没有书籍,没有笔,很难研究别的问题,而这个问题却不同,只要用草棍在地上画就行了,草棍在牢房里有的是.他在进入高墙之前做梦也没有想到,在他最痛苦的时候,是数学排除了他的几分烦恼.不过,他一生也未能解决他提出的这个问题。
关于三等分任意角尺规作图的方法步骤(作者：张爱献)
关于三等分任意角尺规作图的方法步骤
作者：张爱献
（铁铁道部四局三处，1990年于山西沁水）
已知一任意角∠SOT用尺规作图法三等分该角的作图方法步骤
1、作角∠SOT。
2、以O为圆心以任意长为半径画弧，交∠SOT的两边于A、B两点得弧AB。
3、以A、B为圆心以大于1/2AB长为半径画弧交于一点，以O为起点过交点作射线，交弧AB于C点（简称作AB的平分线得C点）。
4、连AC并过C点作射线AC，在射线AC上截取AD=2AC。
5、将AD线段三等分（利用平行线截得成比例线段定理），得AH=1/3AD。
6、过H点作AD的垂线交弧AB于E点。
7、以A点为圆心，以AE长为半径画弧交AD线段于I点。
8、将HI线段九等分（利用平行线截得成比例线段定理），得HK=5/9HI。
9、过K点作AB线段的垂线交弧AB于F点。
10、以AF长为定长三等分弧AB，得三等分点F点和Y点。
11、以O点为起点过F点、Y点作射线，并去掉所有多余的辅助作图线。
说明：
1、作图中的第4条和第7条将线段三等分和9等分利用三角形中平行线截得成比例例线段定理进行等分，不再详细讲解等分步骤。
2、对于90度以下的锐角来说：因H点和I点近似重合，也可近似以E点作为等分点进行等分，（视分割精度要求而定）。
作者简介:张爱献（1964—）男河南省民权县高级工程师
4。
角三等分
角三等分和平前言一百多年来，国内外数学界一致认为用尺规（尺指的是不带刻度的直尺，规指的是圆规，简称为尺规）作图将一任意角三等分已被证明了这是一个“作图不能问题”的结论是完全正确的。
其实这个结论肯定是错误的，我就能，肯定能推翻这个错误的结论。
下面我用角三等分和剖析角三等分及解两种不同的解题方法中的一种方法即角三等分来证明用尺规作图可将一任意角三等分，並对大小各不相等的角进行角三等分尺规作图达2470多次，装订成册24本，验证了这个理论是完全正确的。
让角三等分无解的结论彻底破灭，也为角的其他等分的解决打下基础，角三等分也是角尺规等分法中的一部分。
由于本人水平有限，如有错误和缺欠，恳请给以指正。
2011-4-3 和平一角三等分∠α为任意一个角，用尺规作图将∠α三等分。
以∠α角顶点o为圆心，以任意长为半径画圆为A圆（图中只画圆的一部分），见图3-1，A 圆交∠α两边分别是A点和B点，在A圆上作∠AOB=∠BOC=∠AOD=∠α=1/3∠DOC,设∠OCD=∠β,2∠β+3∠α=180°.如果3∠α大于或等于180°时，先将∠α缩小偶数倍的角再扩大3倍的角小于180°为止。
连接CD交OA线上G点，作∠AOB角平分线OH,∠AOH=∠HOB=1/2∠AOB=1/2∠α，连接BD交OH 线上H1点，连接BG並延长交OD线上P点，连接AP交CD线上F点，连接BF交OH线上b2点，连接GH1、Gb2、H1A、AD、AB、BC,求证：∠H1Gb2=1/3×1/2∠α=1/3∠GOH1=1/3×1/2∠AOB。
在△OGH1中，分别作OG和GH1边的垂直平分线交于O2点，连接O2O, 以O2点为圆心，以O2O为半径经过O、G、H1三点的圆为B圆（图中只画圆的一部分）,GD=GB,ABGD为菱形，H1A=H1G=H1B，证明省略，B圆也经过B点，∠H1GB=∠H1BG=∠GBD=1/2∠α，∠DH1G=∠H1GB+∠H1BG=∠α=∠GOB,∠DH1G=∠GOB, ∠GOB+∠GH1B=180°，O、G、H1、B四点共圆，又∵O、G、H1三点可确定一个圆均在B圆上，∴B点也在B圆上。
尺规三等分任意角画法和证明
〈〈用直尺和圆规把一个任意角分成三个相等的小角的画法和证明〉〉（1）在图[1]中，圆心角AOB，圆心是O，边OA=OB是半径，弧AB。
（2）在AB弧上任意截取一段AC弧，再任意截取一段BD弧，令BD弧=2AC 弧，剩余一段CD弧；剩余CD弧=AB弧-AC弧-BD弧=AB弧-3AC弧，（BD弧=2AC弧），请看图[1]。
（3）连C点和D点，CD线段为剩余弧CD的弦；因为剩余弧CD很短与CD 弦重合成一段线段，所以，我们只要把CD弦三等分，剩余弧CD也就被三等分了，请看图[1]。
（4）大家知道CD弦是一段线段，我们用“平行线等分线段定理”把CD弦等分成三段：CH=HK=KD，因为，剩余弧CD很短与CD弦重合成一段线段，所以，CD弧也被同时三等分为：CH弧=HK弧=KD弧，请看图[1]，H点和K点便是CD 弦上的两个三等分点同时也是剩余弧CD上的两个三等分点，所以，剩余弧CD=3CH 弧（CH弧=HK弧=KD弧），请看图[1]。
（5）因为，AB弧=AC弧+BD弧+CD弧=3AC弧+3CH弧（BD弧=2AC弧，剩余弧CD=3CH弧），所以，AB弧=3（AC弧+CH弧）=3AH弧，请看图[1]。
所以，1/3AB弧=AH弧，请看图[1]，所以，H点是AB弧上的一个三等分点，请看图[1]。
（6）以H点为原点、以HA弧长为标准长在BH弧上截取一段弧HM，截点为M，则M点和H点便是AB弧上的两个三等分点，所以，AH弧=HM弧=MB弧=1/3AB弧，请看图[1]。
（7）连OH和OM，OH和OM把圆心角AOB分成三个小圆心角：小圆心角AOH、小圆心角HOM和小圆心角MOB，请看图[1]。
（8）在圆心角AOB中，依据圆心角、弧、弦的关系定理：因为：小圆心角AOH对应AH弧，小圆心角HOM对应HM弧，小圆心角MOB对应MB弧，AH弧=HM弧=MB弧=1/3AB弧，所以：小圆心角AOH=小圆心角HOM=小圆心角MOB=1/3圆心角AOB（依据圆心角、弧、弦的关系定理，等弧对等角），请看图[1]，所以，任意角AOB被尺规三等分了。
优质文档尺规作图三等分随便率性角和结构正十七边形
[优质文档]尺规作图三等分随便率性角和结构正十七边形尺规作图三等分任意和构造正十七边形饶剑明摘要:将角的等分问题转化为线段的等分问题，从而实现尺规作图的任意等分任意角。
对线段的任意等分是很容易做到的，就是根据平行线间线段对应成比例。
只要将角的等分转换成线段的段分问题就自然解决了，我们知道，角和线的关系在圆中可以实现，在一个圆中等角对应的弦长相等。
从而实现角的三等分和正十七边形的尺规作法。
关键词:三等分角平分线圆弧正十七边形一、任意角的三等分,，作角的平分线。
半径为的圆弧，所对的弦长为设角为,,a2,Ma,2sin 14,角所对的弦长 4,Ma,2sin 28,角所对的弦长为 3,Ma,2sin。
3642MMM,, 2313342,sin,,,MMM,,由于当很小时有，即有。
231332,,4,sin()sin()sin()当取不同值时，和的近似值如下: ,346381111可以看出利用会比更为精确，但在操作上会更为方便。
从数据上可以看出，锐角用4222,1就足够用了，在操作上也得到同样的结果。
但角度大于是就最好使用了。
由于尺规作42图本身在操作上就存在误差，所以这样的误差是允许的。
利用几何画板完全按尺规作图的步42MM,骤可以看到当角为锐角时有，即两个点完全重合。
2133操作步骤如下:1. 对角平分 ,1,2. 取上作图时角所对的弦长2AB3. 对线段AB三等分24.取线段AB的长线段AC 34. 以线段AB为半径，在圆弧等分 AB这样就对弧进行了三等分，标记三等分点，然后与顶点O连接就对角三等分了。
,除去多余的痕迹用这样的方法可以对任意角任意等分。
当角为锐角就一次性完成了操作。
,4,asin()当角是钝角是，就要用四分角去作图了，且从理论上要比稍微少一点，尤其,38是当接近平角时。
当角大于,时，就平分其补角然后反向延长。
,,24MM当一次实现不了的时候可以在和之间取值，每次折中而逼近，一般最多在两到1233三个循环操作能完成。
如何证明尺规作图三等分一个角是不可能问题
如何证明尺规作图三等分一个角是不可能问题？
1）.先说明尺规作图可能问题：
一个作图题中的所作的未知量，若能由若干已知量经过有限次的有理运算及开平方算出时，这个作图题便能由尺规作出。
2）.定理：
一个一元三次方程若它没有有理根，则长度等于它的任何实数根的线段是不能用尺规作出的。
3）.证明尺规作图三等分任意角是不可能的：
如图：设已知角为3a ,平分后的每一个角为a ,作单位圆交角于A、B、C
过B作BD⊥OA于D，过C作CE⊥OA于E ，
令OD＝m ,OE=x ,则m=cos(3a) ,x=cosa ,代入三角恒等式中：
cos(3a)= 4*(cosa)^3 - 3*cosa 得：4x^3 -3x -m = 0
由于在一般的情况下4x^3 -3x -m = 0 不是都有有理根(艾森斯坦因判别法)
所以根据上面的定理，任意三等分角用尺规作出是不可能的。
林浩南。
三大作图难题解决
即
AC a
AC 2 a
以上就是中学几何中一些基本的作图问题，下面借助解析几何的 理论将其 化。 6.3 数域与扩域 大家都知道有理数的加、减、乘、除四则运算的结果还是有理数，
换句话说，设 F 是至少包括一个不等于 O 的数的集合，如果在集合 各能进行加、减、乘、除四种运算，即对 F 中任意两个无素 a 与 b， 它们的和、差、积、商 (a b, a b, a b, , b 0) 均在 F 中，则段 F 是 一个数域。 有理数域克服了自然数系的缺陷，相对来说是比较完美的，它对 四则运算是封闭的等等， 在古代数学的数学家看来与有理数对应的点 充满了数轴， 因此当发现在数轴上存在不与任何有理数对应的一些点 时，在当时人们的心理上引起了极大的震惊，这个发现就是古希腊人 （正如我们在 6.2 节中的⑥用 a 的伟大成就之一，它就是 a 的发现， 。后来又发现数轴上还存在许多点也不对应于任何有理数， 作出 a ） 因此，必须发明一些就的数，使之与这样的点对应；又因为这些数不 能是有理数，所以地它们称为无理数，这就是有理数的扩张. 我们还从尺规作图上来讲一步分析 . 每一个尺规作图都不外乎由 以下几步之一组成： ① 用一条线边接两点； ② 求两条直线的交点； ③ 以一点为心，作定长的圆； ④ 求一个圆与一条直线的交点或切点； ⑤ 求两贺的交点或切点； 下面用解析几何的知识对上面几条作进一步的分析。假设在平面 上取好了直角坐标系，用 ( x, y ) 表示平面上的点，则有直线：
即它的系数是由 F 中的数作成的有理式 没有两条 F 中的数为系数的直线：
A1 x B1 y c1 0 A2 x B2 y c 2 0
联立方程，可待交点坐标：
x B1c1 C 2 B2 C A A2 C1 ,y 2 1 B2 A1 A2 B1 B2 A1 A2 B1
角的三等分（尺规作图）
角的三等分（尺规作图）
栾鹤臣
【期刊名称】《数学学习与研究：教研版》
【年(卷),期】2016(000)023
【摘要】用已被三等分一角的三角形,通过平行投影与求解的任意角所在的三角形重合,三等分任意角.
【总页数】1页(P139-139)
【作者】栾鹤臣
【作者单位】黑龙江省朗乡林区基层法院,黑龙江铁力152519
【正文语种】中文
【中图分类】G633.63
【相关文献】
1.尺规作图三等分一个给定的任意角
2.三等分角（近似）尺规作图法
3.尺规作图三等分任意角(0°≤α≤180°)
4.关于角三等分尺规作图的研究
5.解决两千三百年前古希腊几何学家提出的世界著名三大尺规作图难题之一——尺规作图三等分任意角
因版权原因，仅展示原文概要，查看原文内容请购买。
用尺规作图解决任意角的三等分
用尺规作图解决任意角的三等分引言：通常来说，尺规作图的方法是不能三等分任意角的。
如果继续使用原有的尺规作图的方法，我也不能解决这个几何问题。
原因在于传统的尺规作图停留在二维的范围，而我现在要用的方法是在三维的参考系中使用直尺、圆规、铅笔、作图纸解决三等分任意角。
首先，介绍所需的工具，本方法中所使用的圆规不是以铅笔画圆，而是以刀“划圆”。
至于直尺和铅笔就是传统的工具（没有刻度）。
至于白纸，我将利用它实现二维到三维的转换。
方法介绍：下面利用图解的方法来阐述我的思路。
1、首先我们在纸面上任意画一个∠AOB2、我们以顶点O3、利用另一张白纸啮合在步骤2得到的圆上并利用铅笔在白纸上标记弧A ’B ’(X,Y)的位置。
4、展开被标记的白纸，连接XY 得到直线XY ，再利用尺规作图（方法见下图）三等分此直线。
方法简述：作XY 垂线XC;和平行线QP; 在QP 上作三个等圆如图（三直径相加不等于XY ）； 如图连接即可三等分XY （简单相似三角形即可证明）X Y C Q P C J5、将白纸贴回圆O（XY对准弧A’B’）即可三等分弧A’B’6、利用等弧对应的圆心角相等的原理，简单可证三等分了∠AOB。
总结：也许大家会争议步骤3（同理的步骤5），在同指导教员（刘俊红教员）讨论时，我们也意识这一点也许会存在争议，利用了纸面的可重塑性到底算不算尺规作图？我们思考了很久，如果从单从操作的角度来讲，的确借助了“捷径”，但是如果从理论来讲，利用这种方法可以在三维的坐标系（不需要它的坐标刻度）中只借助直线方程和圆的方程（也就是圆规和直尺）就可以三等分任意角，大致思路是利用我们可以精确三等分直角和特殊角的原理（见下图），在弧面中三等分弧（本质来说是与前述方法一致的，但在弧面中三等分弧的方法是利用中垂线的方法）。
在三维坐标系中平分是在理论上不需要借助其它工具的，但是如果没有其他工具的帮助的话会有很大的误差，所以我利用白纸为辅助的工具，增加它的精度。
解决不可能的问题---尺规作图三等分任意角
解决不可能的问题---尺规作图三等分任意⾓
介绍
三等分⾓是古希腊三⼤⼏何问题之⼀。
三等分⾓是古希腊⼏何尺规作图当中的名题，和化圆为⽅、倍⽴⽅问题被并列为古代数学的三⼤难题之⼀，⽽如今数学上已证实了这个问题⽆解。
该问题的完整叙述为：在只⽤圆规及⼀把没有刻度的直尺将⼀个给定⾓三等分。
在尺规作图（尺规作图是指⽤没有刻度的直尺和圆规作图）的前提下，此题⽆解。
若将条件放宽，例如允许使⽤有刻度的直尺，或者可以配合其他曲线使⽤，可以将⼀给定⾓分为三等分。
题⽬：
已知：∠ABC
求作：HB,IB平分∠ABC
众所周知，尺规作图⽆解
但在运⽤弧长转换时会有⼀些解法
基本思路：
构造3个等边三⾓形得弦相等，再得圆弧相等，最后得圆周⾓相等
solve:
1.画任意⾓∠ABC
2. 以任意长为半径，B为圆⼼作弧 交AB,BC为EF
3.作垂直平分线求线段EF中点 G
4.以EG为半径分别以E,F,G作弧交于I，H两点连BI,BH
5.∠ABH,∠HIB,∠IBC即为所求。
尺规作图
三等分任意角★作法一三等分角问题尼科梅德斯(Nicomedes，公元前250年左右)方法对于已知锐角∠O，在角的一边上取任意点B，作OB的垂线，交∠O的另一边于点A.以O为定点，BA为定直线，2OA为定长，作出蚌线的右支C.从点A作BA的垂线，和蚌线C相交于点S，那么∠BOS=1/3∠BOA★作法二帕斯卡(Pascal，B.1623-1662)的方法对于∠AOB，在其一边上取任意长OA做半径，以点O为圆心作一圆(图12).延长AO，和圆O交于点C.以圆O为定圆，以C为定点，以定圆O的半径为定长，作一蚶线和角的另一边OB相交于点E.连结CE，过点O作OS∥CE，那么∠BOS=1/3∠BOA★作法三帕普斯(Pappus，约公元320年)方法对于∠AOB，在它的两边上截取OA=OB.连结AB并三等分，设两分点分别为C和D.以点C为中心，点A、D分别为顶点，作离心率e=√2的双曲线.以点O为圆心，OB为半径作弧，交双曲线于点S.则∠BOS=1/3∠BOA★作法四玫瑰线方法交∠AOB的两边于点A和B，分别以O和A为圆心，a为半径画弧，两弧交于点S，则有∠BOS=1/3∠BOA折叠立方倍积★作法一倍立方问题柏拉图(Plato，公元前427-347年)的方法:作两条互相垂直的直线，两直线交于点O，在一条直线上截取OA=a，在另一条直线上截取OB=2a，这里a为已知立方体的棱长.在这两条直线上分别取点C、D，使∠ACD=∠BDC=90°(这只要移动两根直角尺，使一个角尺的边缘通过点A，另一个角尺的边缘通过点B，并使两直角尺的另一边重合，直角顶点分别在两直线上，这时两直角尺的直角顶点即为点C、D).线段OC之长即为所求立方体的一边。
★作法二门纳马斯(Menaechmus，约公元前375-325年)方法:从a∶x=x∶y=y∶2a可得y2=2ax，x2=ay.所以，在直角坐标平面上画出上述两个二次方程所对应的两条抛物线(图16).这两条抛物线交于O、A两点，那么点A在x轴上的投影到原点的距离，就是所求的立方体的棱长。
关于三等分任意角的方法探究
三等分任意角的方法探究西工大附中孙开锋三等分任意角的方法探究摘要：三等分角是古希腊几何三大作图问题之一，本文关键词：只准用直角和圆规，你能将一个任意的角进行两等分吗？这可太简单了，几千前的数学家们就会做。
纸上任意画一个角，以其顶点O为圆心，任意选一个长度为半径画弧，找出弧与角的两边的交点，分别命名为A和B。
然后分别以A点和B点为圆心，以同一个半径画弧，这个半径要大于A、B之间距离的一半。
找出两段弧的相交点C，用直尺把O和C连接起来，那么直线OC就将角AOB平分成了两部分。
用同样的方法，我们可以把一个角任意分成4等分、8等分、16等分……，也就是说，只要你有耐心，可以把任意一个角等分为2的任意次方。
但是，如果只用直尺和圆规，并且，这直尺还不能有刻度，你能将任意一个角三等分吗？早在公元前5世纪，古希腊的巧辩学派就提出了在只用直尺画直线、圆规画弧的限定下，将任意给定的角三等分的命题。
很多伟大的数学家如阿基米德、笛卡儿、牛顿等都试图拿起直尺和圆规挑战自己的智力，但终于都以失败告终。
直至公元1837年，法国数学家闻脱兹尔宣布：“只准使用直尺与圆规，想三等分一个任意角是不可能的！”, 才暂时了结了这宗长达几千年的数学悬案。
但是，如果没有几何作图法的限制，任意角三等分问题当然可以解决，不妨举几个例子以共享。
一、利用工具三等分任意角如图1所示，叫做“三等分仪”吧 ，CE=EG=DG,ME ⊥CD,弧ED 是以G 为圆心的半圆，故ME 与半圆G 相切于点E.具体操作：将该仪器置于 ∠AOB 的内部，使得点C 落在OA 上，ME 经过点O,半圆G 与OB 相切于点F,则OE,OG 为∠AOB 的三等分线。
数理证明：分别连接OG,GF,故GF ⊥OB,而EG ⊥OE,所以易证：△GOE ≌△GOF;同理可证△GOE ≌△COE;故可得到：∠COE=∠GOE=∠FOG.所以，OE 、OG 为∠AOB 的三等分线。
二、中考中的三等分角题目：（广东佛山市）三等分一任意角是数学史上一个著名的问题，用尺规不可能“三等分一任意角”。
部分特殊角和任意角简易角三等分尺规作图
部分特殊角和任意角简易角三等分尺规作图上次我用尺规作图已将120°角三等分了，下面我用一本180例简易大小各不相等的角三等分尺规作图中的部分特殊角和任意角三等分尺规作图来验证角三等分确实有解。
一. 用尺规作图将30°角三等分（一）以O点为圆心，以任意长为半径画弧，在弧上任取一点为D,连接OD,在弧上作OD=DE,连接OE,∠EOD=60°,作∠COE=∠EOA=∠AOH=∠HOB=∠BOD=∠DOK=15°,∠AOB=∠α=30°,将∠α=30°角三等分。
连接CK交OA线上G点，连接BG並延长交OC线上P点，连接AP交CK线上F点，连接BC交OH线上H1点，连接BF交OH线上b2点，连接GH1、Gb2、AH1、 AB、AC,ABGC为菱形，H1G=AH1=H1B,则∠H1BG=∠H1GB=1/2∠α=15°,∠H1Gb2=∠a1Ga2=∠a2Ga3=∠a3Ga4=1/3×1/2∠α=5°，证明省略，∠AOm=∠mON=∠NOB=1/3∠α=1/3∠AOB=∠a1Ga3=10°,即将30°角三等分。
该图和编号就是一本180例简易大小各不相等的角三等分尺规作图中的一张图和编号。
图号和页号是3-1-15 , 15。
应该注意的是如果∠α大于或等于60°时，必须将大于或等于60°的角缩小偶数倍的角小于60°后才能进行角三等分。
如果60°≤∠α＜120°时，∠α缩小两倍，如果120°≤∠α＜240°时，∠α缩小四倍。
值得注意的是角的所在区域相同，角的尺规作图方式也应相同。
∠α缩小偶数倍的角已被分成三等分的角扩大同样偶数倍后的角才是∠α被分成三等分的角，∠α是否需要缩小和缩小多少偶数倍可用圆的半径来确定。
一. 用尺规作图将60°角三等分（二）以O点为圆心，以任意长为半径画弧，在弧上任取一点为A,连接OA ,在弧上作AB=OA,连接OB, ∠AOB=∠A1OA4=60°=∠α,∠α应该缩小两倍方可以进行角三等分。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
尺规作图三等分任意角（0°<α≤180°）黑龙江省巴彦县兴隆镇第二中学谭忠仁邮编：151801电话：150****5590目录关于三等分角的由来 (1)三等分任意角（0°<α≤180°） (2)已知：∠AOB (2)求作：∠AOB的两条三等分射线OC、OD (2)作法： (2)证明： (2)关于三等分角的由来众所周知，三等分角是著名的几何作图三大问题之一（另外两个问题是化圆为方、倍立方体），近两千年来，几十代人为这三大问题绞尽脑汁，希腊人的巧思、阿拉伯人的学识、文艺复兴时期大师们的睿智都曾倾注于此，却均以失败告终。
1837年范兹尔首先证明三等分角与倍立方体不能有限次使用尺规作出。
1895年，克莱因给出三大问题有限次使用尺规作图不可能的简单而清晰的证明，阿基米德在几何学上的造诣是很深的，从他的著作里可以看到他对三等分角问题的研究，他先采用在直尺上标注一个点的方法，然后把一个角三等分，显然，这一方法取消了直尺上无刻度的限制，此外，喜庇亚斯借助割圆曲线、尼克曼得斯借助于蚌线、巴普士借助于双曲线、帕斯卡借助于蚶线，解决了三等分角的问题，但所有这些曲线都不能仅用尺规来完成。
综上所述，尺规作图三等分任意角尚无先例，本人自1971年参加工作后，任初中数学教师，由于专业的需要、兴趣及其爱好，使我涉猎了大量数学方面的资料和相关知识，下决心研究三等分角问题，历尽40年时间，苦心钻研，现终得一法，并且给出了科学、严谨的证明，借此恳请数学专家和导师予以审核、验证，并提出宝贵意见。
注：本文所举资料，请详见《陕西中学数学》1991年第二期谭忠仁2011年5月10日三等分任意角（0°<α≤180°）已知：∠AOB求作：∠AOB的两条三等分射线OC、OD作法：1、以O为圆心，以任意长为半径作⊙O，交射线OA于A，交射线OB于B；2、连结AB，引直径EE1，并且使EE1⊥AB，垂足为H；3、连结BE，以B为圆心，以BE的长为半径画弧，交AB于F；4、连结EF并延长，交⊙O于G1，交BE1的延长线于T；5、以T为圆心，以TB的长为半径画弧，交⊙O于C1，连结TC1，交⊙O 于G；6、在⌒AB上截取⌒BC2，使⌒BC2=2⌒E1G；7、连结BC2，作BC2的垂直平分线T1D2，垂足为H2，交TB于T1，，连结T1 C2；8、作射线TP，在射线TP上依次截取TP1= P1P2= P2P3，连结T1P3，作T2P1∥T1P3，交TT1于T2；9、以T2为圆心，以T2B的长为半径画弧，交⊙O于C，连结T2C，交⊙O 于G2；10、连结BC，作BC的垂直平分线T2D，交⊙O于G3、D，垂足为H3，（T2D 必经过圆心O、必经过等腰三角形T2BC的顶角的顶点T2）；11、作射线OC，则射线OC、OD即为所求作的∠AOB的两条三等分射线。
证明：作BC3⊥TE，交⊙O于G3，垂足为H1、BC3与EE1交于N，与T2D交于N1，延长ET，交DT2的延长线于M，连结BC1，作BC1的垂直平分线TD1（TD1必经过圆心O，必经过等腰三角形TBC1的顶角的顶点T），作OH4⊥TB，H4为垂足，作OH5⊥T2C，H5为垂足，作OH6⊥TC1，H6为垂足。
1、由TC1=TB，可知△TC1B是等腰三角形，又由D2T1是C2B的垂直平分线，可知T1C2=T1B，△T1C2B也是等腰三角形，这两个等腰三角形顶角的顶点T和T1是线段TT1的两个端点，底角的顶点C1和C2是⌒C1C2的两个端点，且腰TC1和T1C2相交于⊙O内。
因此，当我们在线段TT1上任意取一点，以这点为圆心，以这点到B点的距离为半径画弧，必与⌒C1C2相交（因受两个底角的顶点C1和C2的局限），将交点分别与TT1上所取的那个任意一点连结、与B点连结，就可以作出（如同等腰三角形TC1B、等腰三角形T2CB、等腰三角形T1C2B）又一个等腰三角形，显然，TT1上有多少个点，就可以做出多少个这样的等腰三角形，就有多少个等腰三角形底角的顶点在⌒C1C2上。
反之，当我们在⌒C1C2上任意取一点，将这点与B点连结，作连线的垂直平分线，必与TT1相交（因受TD1和T1D2的局限），就可以得到（如同T、T2、T1）又一个交点，显然⌒C1C2上有多少个点，就有多少条连线，就有多少条垂直平分线，就有多少个与TT1相交的交点。
因此，TT1上点的个数、上述等腰三角形底角的顶点在⌒C1C2上的个数、⌒C1C2上点的个数、上述垂直平分线与TT1相交的交点个数，四个量相互制约，故TT1上点的个数与⌒C1C2上点的个数必相等。
为叙述方便起见，不妨设线段TT1上有n个点，则⌒C1C2上也有n个点与之相对应。
下面，我们用反证法证明这个命题：假设⌒C1C2点的个数不是n点，则会出现两种可能：1、⌒C1C2大于n点，2、⌒C1C2小于n点。
当⌒C1C2大于n点时，这些点与B点的连线大于n条，这些连线的垂直平分线也大于n条，这些垂直平分线与线段TT1的交点也大于n点，这与TT1上点的个数是点相矛盾（这里提请注意：因TD 1、T 2D 、T 1D 2等所有的垂直平分线都经过圆心O ，都交于圆心O ，故垂直平分线与TT 1的交点和交点根本不能再重合）。
当⌒C 1C 2小于n 点时，因TT 1上有n 个点，就有对应的n 个等腰三角形，就有相对应的n 个等腰三角形底角的顶点在⌒C 1C 2上，这与⌒C 1C 2小于n 点，显然也是矛盾的（这里提请注意：因TC 1、T 2C 、T 1C 2等所有等腰三角形的左腰都两两相交于⊙O 内，故所有等腰三角形左侧底角的顶点与顶点也根本不能重合）。
因此，假设不成立，⌒C 1C 2上点的个数既不能大于n 点，也不能小于n 点，只能等于n 点。
因为线段TT 1上点的个数是n 个点，⌒C 1C 2上点的个数也是n 个点，所以，线段TT 1上的点与⌒C 1C 2上的点一一对应，又因T 和C 1是对应点，T 2和C 是对应点，所以TT 2对应⌒C 1C ，TT 2上的点与⌒C 1C 上的点一一对应。
2、T 2P 1∥T 1P 3 =>TP 1=P 1P2=P 2P 3 因TT 1上有n 个点，可知TT 2上有13n个点，又因TT 2上点的个数与⌒C 1C 上点的个数一一对应，故⌒C 1C 上点的个数也是13n ，加之⌒C 1C 2上点的个数已推出为n ，所以有⌒C 1C ⌒C 1C 2=13nn=13，即⌒C 1C =13⌒C 1C 2；易知：⌒CC 2=23⌒C 1C 2。
T 2B=T 2C T 2D ⊥BCTB=TC 1 TD 1⊥BC 1=> TT 2TT 1=13 => TT 2=13TT 1OH 5=OH 6=>CG 2=C 1G=>⌒CG 2=⌒C 1G=>⌒CG +⌒GG 2=⌒C 1C +⌒CG =>⌒GG 2=⌒C 1C⌒C 1C =13⌒C 1C 2=>⌒CC 2=2⌒GG 23、 ⌒BC 2=2⌒E 1G⌒CC 2=2⌒GG 2=>⌒DB =⌒E 1G 2∠CT 2D 12（⌒CD −⌒G 2G 3)∠BT 2D 12（⌒DB −⌒G 3E 1)∠CT 2D=∠BT 2D⌒CD =⌒DB4、 BE=BF BH 1⊥EFOE ⊥AB=>⌒AE =⌒EB =>⌒AE =12⌒AB∠EH 1N=∠BHN=90°∠ENH 1=∠BNH =>⌒E 1G 1=14⌒AB⌒=12⌒m = m = =>∠ABC 3=∠EBC 3=>⌒AC 3=⌒C 3E =>⌒AC 3=12⌒AE=>⌒AC 3=14⌒AB=>∠NEH 1=∠NBH=>∠E 1EG 1=∠C 3BA=>⌒E 1G 1=⌒AC 3=>⌒BE =2⌒E 1G 1 ⌒DB =2⌒G 3E 15、∠MH 1B=∠MH 3B=90° ∠MN 1H 1=∠BN 1H 3=>12（⌒ED -⌒G 1G 3）=12⌒C 3C=>⌒ED =⌒G 1G 3+⌒C 3C ⌒ED =2⌒G 1G 36、⌒CD =⌒C 3D -⌒C 3C ⌒C 3D =⌒C 3E +⌒ED=>⌒AC =⌒CD =⌒DB=>∠AOC=∠COD=∠DOB =>⌒BE -⌒DB =2⌒E 1G 1-2⌒G 3E 1=2（⌒E 1G 1-⌒G 3E 1）=2⌒G 1G 3=>⌒ED =2⌒G 1G 3 =>∠M=∠N 1BH3=>∠M=∠C 3BC∠M 12（⌒ED -⌒G 1G 3）∠C 3BC 12⌒C 3C=>⌒ED =2⌒C 3C m = m= =>⌒CD =⌒C 3E +⌒ED -⌒C 3C ⌒ED =2⌒C 3C=>⌒CD =⌒C 3E +⌒C 3C⌒AC =⌒AC 3+⌒C 3C⌒AC 3=⌒C 3E => ⌒AC =⌒CD⌒CD =⌒DB。