1.5.2科学记数法课件
1.5.2 科学记数法

回顾
0.1¹=0.1 0.1²=0.01 0.1³=0.001 ... 10¹=10 10²=100 10³=1000 ... 观察上面的数据,你有什么发现?
0.1 0.0...01
n
n个0
10 10...0
n
n个0
光速约为300 000 000 m/s
世界人口约7 000 000 000人
准确数
4、中国的陆地面积约为9 600 000 km²,领水面积约为 370 000 km²,用科学计数法表示上述两个数字
与实际接近的数
近似数
判断下列哪些数是准确数,哪些是近似数? (1)班上男女生人数; 准确数 准确数 (2)教室里窗户个数; (3)同学们用的数学课本的厚度; 近似数 (4)圆周率。 近似数
7 5
4
2、数学医院:下列用科学记数法表示的数错在哪里? (1)25×10²; (2)0.36×10²; (3)23000=2.3×10³; (4)63000=6.3×10³
1.5.3 近似数
3、全国各地著名企业家聚首湖北共签约项目投资总额 为909 260 000 000 元,用科学计数法表示_______
1000 000 10
—
6
57 000 000 5.7 10
7
123 000 000 000 —1.231011
应用
1、用科学记数法写出下列各数: 10 000, 800 000, 56 000 000, -7 400 000
2、下列用科学记数法写出的数,原来分别是什么数?
110 ,7.04 10 , -3.96 10
300 000 000=3×100 000 000=3×108
1.5.2科学记数法

1.5.2科学记数法教学目标知识与技能:①利用10的乘方,进行科学记数,会用科学记数法表示大于10的数。
②体会科学记数法的好处,化繁为简的方法。
过程与方法:用科学记数法表示绝对值较大的数,体会科学记数法的优越性,增强对较大数的数感。
情感态度与价值观:①通过对科学记数法的意义及必要性的了解,感知数学来源于生活,并为生活服务。
②培养学生热爱数学,热爱生活的乐观态度。
教学重点用科学记数法表示绝对值大于10的数。
教学难点探究科学记数法表示绝对值大于10的数的方法。
教学建议:这一节课,从科学记数法到近似数的应用,不是简单地告诉学生结论和方法,然后进行大量的重复性练习,而是在教师的指导下,让学生自己去思索、判断,自己得出结论,从而达到培养学生观察、归纳、概括能力的目的。
教学过程一.情景引入情景一:神十飞船在太空中大约飞行 10 080 000千米。
情景二:第六次人口普查时,中国人口约为1339724852人。
情景三:太阳的半径约为696 000 000米。
情景四:光的速度约为300 000 000米/秒【教师说明】像这样较大的数据,书写和阅读都有一定困难,那么有没有这样一种表示方法,使得这些大数易写,易读,易于计算呢?同学们可以想一想,102=100;103=1000;104=10000。
那么100000= 105; 10000000=107那么1后面11个0应该写成1011.这样记数就方便多了。
【板书】1.5有理数的乘方第二课时交流讨论300000=3⨯10000=3⨯1052600000=2.6⨯1000000=2.6⨯10657600000=5.7610000000⨯=5.76⨯107观察上面等式右边表示大数的式子,它们的形式都有什么特点?【教师说明】像上述三个等式最右边表示形式那样,把一个数表示成a×10n的形式(其中1≤a<10,n是整数),既简单明了,又便于阅读和进行计算,这种记数法,习惯上叫科学记数法。
人教版七年级上册1.科学记数法课件

④-510 000
(2)已知下列用科学记数法表示的数,写出本来的数.
①2.01×104 ②6.070×105
③6×105
④104
(3)用科学记数法表示下列各小题中的量: ①银河系中的恒星约有160 000 000 000颗; ②地球离太阳大约有一亿五千万千米.
思考:等号左边整数的位数与右边10的指数有 什么关系?用科学记数法表示一个n 位整数,其中
10的指数是 n-1.
2.下列各数是否是用科学记数法表示的?
2 400 000 0.24107 × 2 400 000 2.4106
3 100 000 31105 ×
3 100 000 3.1106
整数数位只有一位
例如:90 000 = 9×10 000 = 9×104
读作:9乘10的4次方(幂)
696 000 = 6.96×100 000 = 6.96×105
300 000 000 = 3×100 000 000 = 3×108
7 000 000 000= 7×1 000 000 000 =7×109
书写简短,便于读数.
?
探析建构
用简单方法表示大数
696 000 km 300 000 00m/s
6.96×105 千米 3×107 米
你知道 102,103,104 分别等于多少吗?
10n 的意义和规律是什么?
10的乘方有如下的特点: 102 100 103 1 000 104 10 000 …
一般地,10的n次幂等于10···0(在1的后 面有n个0),所以就可以用10的乘方表示一 些大数.
2.下列用科学记数法写出的数,本来分别是什 么数?
1×107 =10 000 000 4×103 =4 000 8.5×106 =8 500 000 7.04×105 =704 000
1.5.2科学计数法

第周星期第课时年月日一.创设情境,提出问题.在阅读科普读物时,会遇到太阳的半径,光的速度,目前世界人口,到2013年底我国城镇失业人数等学生1:世界人口约 7 000 000 000 人。
学生2:光在空气中的速度约为300 000 000米/秒;学生3:太阳半径约 696 000 千米.学生4:2013年,我国城镇失业人数约为9260 000 人通过刚才几位同学的反馈,你发现了什么?(学生沉思)我发现这些数据都比较大,书写和读时都比较麻烦。
教师伺机点拨:同学们的观察都是正确的,那么有没有一种比较简单的方法来表示这些比较大的数呢?(学生沉思)1.小组合作,探讨交流刚才,同学们都已做了努力的思考,想必都有所发现。
你把你发现告诉其他同学吗?大家可以先在小组内说一说,看谁的方法好?学生小组合作,交流讨论。
教师巡视,了解情况,伺机点拨.2.择优反馈,提升理论小组交流结束,我们来比较一下,哪个小组的方法好?学生1:对于较大的数,我们认为可以用数字与记数单位百.千.万.亿等合写的方法来表示比较简单。
例如:7 000 000 000可以写作70亿。
学生2:我在查找资料时发现,有的数可以用一个数乘以10的几次方的形式来表示。
例如:7 000 000 000可以写作7×109。
这就是我们今天学习的科学计数法二、知识讲解(难点突破)问题1.请把下列数写成10n的形式101 = 102 = 103 = 104 = 105 =根据上面的问题,你有什么发现?总结: 1.n是几后面就有几个零2.n比运算结果的数位少1反之,1000…… 0=10n 1000…… 0=10nn个0 ( n+1)个0例如:1000…… 0=1077个0问题2. 把下列各数写成10的幂的形式:100 ,10000,100000000,即写成10()(学生动手完成后教师公布答案并解析)问题 3.你能把300 32000 3455000000也用上面的方法表示出来吗?根据上面的知识我们把300 看成3个100即:300=3×100=3×102同理32000=3.2×10000=3×104345000000=3.45×100000000=3.45×108问题:345000000是否也可以写成34.5×10000000==3.45×107或者0.345×1000000000=0.345×109的形式呢?可以,但是当我们把3.45×108 3.45×107 0.345×109放在一起时不易看出他们是同一个数,因此在比较数据大小时就显得不容易了,为了避免麻烦便规定10n前面的数必须是一个大于等于1且小于10的数。
七年级数学上册《科学记数法》课件

在生活中我们还会遇到一些比较大的数.例如:
(1)第六次人口普查时,中国人口约为1370000000人. (2)光的速度约为300000000米/秒. (3)地球上煤的储量估计15万亿吨以上.
像这样较大的数据,书写和阅读都有一定困难,那么有 没有这样一种表示方法,使得这些大数易写,易读呢?
讲授新课
交流研讨
交流内容:研讨一、研讨二 研讨要求:
1.组长组织先统一答案,再互教; 2.将错题订正,再向组长回述; 3.收集易错点,总结解题思路和方法。 时间:10分钟
拓展提升
课堂小结
1.用科学计数法表示较大的数应注意以下两点: 1≤a<10 指数n=小数点移动的次数
2.灵活运用科学计数法,看清题意,注意解题技 巧,总结解题规律.
回顾有理数的乘方,计算:
101=10 103= 106= … 10n=
102= 104= 1010=
600= 32000= 696000= 345000000=
小技巧:10的指数=小数点移动的次数
600= 6×102 32000= 3.2×10 4 696000= 6.96×10 5 345000000= 3.45×10 8 小技巧:10的指数=小数点移动的次数
像上面这样,把一个大于10的数表示成a×10n的形式 (其中a是大于或等于1且小于10,n是正整数)。这 种记数方法叫做科学记数法。
对于小于-10的数也可以类似科学记数法表示. 例如:
-567000000=
例: 用科学记数法表示下列各数: 1000 000
57 000 000ቤተ መጻሕፍቲ ባይዱ
-123 000 000 000
七年级数学上册
第一章 有理数
1.5.2 《科学记数法》
1.5.2科学记数法
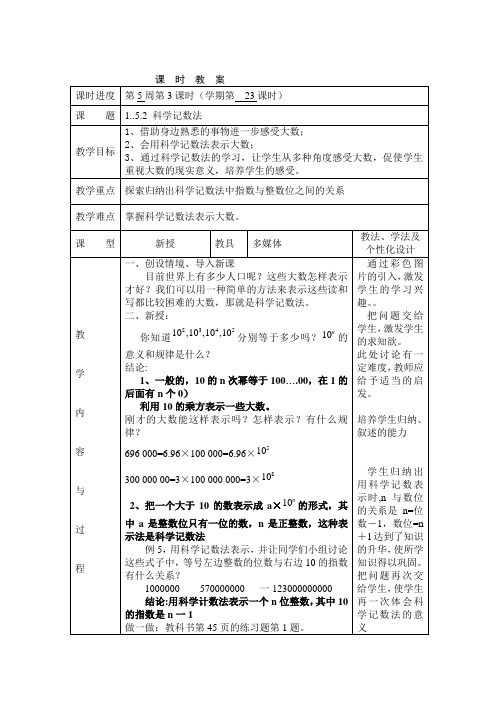
结论:用科学计数法表示一个n位整数,其中10的指数是n一1。
课
后
反
思
通过具体的数,学生归纳出用科学记数表示时,n与数位的关系是n=位数-1,数位=n+1达到了知识的升华,使所学知识得以巩固。
课时教案
课时进度
第5周第3课时(学期第23课时)
课题
1..5.2科学记数法
教学目标
1、借助身边熟悉的事物进一步感受大数;
2、会用科学记数法表示大数;
3、通过科学记数法的学习,让学生从多种角度感受大数,促使学生重视大数的现实意义,培养学生的感受。
教学重点
探索归纳出科学记数法中指数与整数位之间的关系
教学难点
掌握科学记数法表示大数。
课型
新授
教具
多媒体
教法、学法及
个性化设计
教
学
内
容
与
过
程
一、创设情境、导入新课
目前世界上有多少人口呢?这些大数怎样表示才好?我们可以用一种简单的方法来表示这些读和写都比较困难的大数,那就是科学记数法。
二、新结论:
1、一般的,10的n次幂等于100….00,在1的后面有n个0)
把问题再次交给学生,使学生再一次体会科学记数法的意义
发挥学生的主观能动性,借助集体的力量巩固新知。
板
书
设
计
1..5.2科学记数法
1、一般的,10的n次幂等于100….00,在1的后面有n个0)
利用10的乘方表示一些大数。
2、把一个大于10的数表示成a× 的形式,其中a是整数位只有一位的数,n是正整数,这种表示法是科学记数法
做一做:教科书第45页练习第2题、3题
1.5.2 科学记数法
1.5 有理数的乘方
活动2
教材导学
科学记数法 对于较大的数,我们读、写都有一定困难,那么可以用怎样 的方法来表示这些大数,使它易读、易记、易判断大小还便 于计算呢?为此我们先探究 10 的正整数幂的规律.
10 , 101=______ 1000 , 103=________ 100000 , 105=__________ 10000000000 1010=________________ .
解:5.11×10 ×71%=3.6281×10 (平方千米).
答:海洋的面积是 3.6281×108 平方千米.
8 8
[归纳总结] 1 亿=108,1 万=104,1 千=103,这类问题先根据 题意进行计算,然后再将计算结果表示成科学记数法.
3 ,结果是________ 1000 ; 10 ,指数是______ (1)103 的底数是______ 10 ,指数是______ 3 -1000 ; (2)-103 的底数是______ ,结果是________ -10 ,指数是______ 3 -1000 . (3)(-10)3 的底数是______ ,结果是________
1.5 有理数的乘方
新 知 梳 理 知识点 科学记数法
n a × 10 定义:把一个大于 10 的数表示成__________的形式(其中 a
1 且小于______ 10 ,n 是________) 正整数 ,这样的方 大于或等于______
法叫做科学记数法.
[点拨] 科学记数法中,a值是将小数点放在原数最高位后面 得到的数,n值比原整数位数小1.
1.5 有理数的乘方
重难互动探究
探究问题一 例1 用科学记数法表示绝对值较大的数
用科学记数法表示下列各数:
1.5.2科学计数法
点击进入相应模块
据宁波市统计局公布的第六次人口普查数据, 1. 据宁波市统计局公布的第六次人口普查数据, 本市常住人口760.57万人,其中760.57万人用 本市常住人口760.57万人,其中760.57万人用 760.57万人 760.57 科学记数法表示为( 科学记数法表示为( 7× (A)7.605 7×105人 7× (C)7.605 7×107人 ) 7× (B)7.605 7×106 人 57× (D)0.760 57×107人
点击进入相应模块
点击进入相应模块
根据全国第六次人口普查统计, 2. 根据全国第六次人口普查统计,湖州 市常住人口约为2 000人 近似数2 市常住人口约为2 890 000人,近似数2 890 000用科学记数法表示为( 000用科学记数法表示为 用科学记数法表示为( (A)2.89×104 2.89× (C)2.89×106 2.89× )
点击进入相应模块
5.( 5.(1)用科学记数法表示下列各数: 用科学记数法表示下列各数: 000; 3 240,50 600,468 000; (2)下列用科学记数法表示的数,原来各 下列用科学记数法表示的数, 是什么数? 是什么数? ,6.2× ,8.005× 3×105,6.2×103,8.005×104.
3 ×103 4
)
(B)10.3×107 10.3× (D)3.75×104 3.75×
点击进入相应模块
2.(2011·德州中考)温家宝总理强调, 十二五”期间, 2.(2011·德州中考)温家宝总理强调,“十二五”期间, 德州中考 将新建保障性住房36 000套 将新建保障性住房36 000 000套,用于解决中低收入和新参 加工作的大学生住房的需求. 加工作的大学生住房的需求.把36 000 000 用科学记数法表 示应是( 示应是( ) (B)3.6×106 3.6× (D)0.36×108 0.36×
13新人教版1.5.2 科学计数法
18
2.下列用科学计数法记出的数,原来 分别是什么数。
(1) (2) (3) (4) (5) 1×107= 10000000 4000 4×103= 8.5×106= 8500000 7.04×105= 704000 -3.96×104= -39600
§1.5.2 科学计数法
数学+
数学+
1
1、计算:
102 103 104 105 106 107 108
观察上述计算,你发现了什么规律:
一般地,10的n次幂,是在1的 后面写 n 个 0。
2
月球的质量约为734万万亿吨。
734 0000 0000 0000 0000
请 写 出 这 个 数 据
3
11 0000 0000
19
1×106
5.7×107
⑴1 000 000=____. ⑵ 57 000 000=___
⑶ 12 300 000=____. ⑹ 200.001=___ 7
1.23×10 2.00001×102
⑷ -30 060=___.
-3.006×104
⑸ 15 400 000=
1.54×107
.
用科学计数法表示一个数的整数 部分有n位数时,10的指数是___ __ n _- .1 用科学计数法可以直观地表示 一个数的整数部分的位数.
21
一个人每天呼入和呼出大约 20000升空气,那么一年共呼入和 呼出的空气大约有多少升? 20000×365=7 300 000= 7.3×106
P45
22
归纳总结: 让学生说出这一节课学 习的主要内容和注意点。
原创1:1.5.2科学记数法
解:因为1 年=365 天=365×24×60 分,
所以一年心跳次数约为:
365×24×60×70= 36 792 000 =3.679 2×107(次);
因为心跳达到1亿次需要的时间是:
108÷( 3.6792×107 ) ≈2.7(年),
所以一个正常人一生心跳次数能达到1亿次.
第一章 有理数1.5.2 来自学记数法初中数学·精品课件
课件说明
• 本节课学习用科学记数法表示较大的数,指数n与
整数位数间的关系.
• 学习目标:
理解科学记数法的意义,学会用科学记数法表示
较大的数.
• 学习重点:
理解科学记数法的意义,并会对科学记数法表示的
数进行简单的运算.
快速记忆游戏
• 下面有几组数据,你能过目不忘吗?一闪而过之后,
5
不是
应用与提高
3.下列用科学记数法表示的数,原数是什么?
3.2 10
4
=32 000
6 103 =6 000
3.25 107 =32 500 000
练一练,你一定行
1
用科学记数法写出下列各数:
10 000, 800 000, 56 000 000, 7 400 000.
7
6
4
5
=5.6×10
你能记住多少,请大家一起来试一试,看谁记得多!
• 中国国土面积有9 600 000平方公里;
• 中国人口约有1 300 000 000人;
• 银河系的直径为925 000 000 000 000 000公里.
光的速度约为30 0000 000米/秒;
太阳的半径约为69 600 000 000米;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1×107 ;
4×103 ;
8.5×106 ;
7.04×106; 3.96×104
你知道吗?
一个指甲缝里有近5万个细菌, 在1克指甲污垢里竟藏着近30亿个细菌, 请用科学记数法表示以上两个数。
解:5万=50 000=5×104 30亿=3 000 000 000=3×109
连接中考
1、地球半径约为150 000 000 000米可用科学记 数法表示为_____
2、上半年,全国财政收入10954.99亿元,可用 科学记数法表示为_____
本节课你有什么收获?
1.遇到较大的数时可用科学记数法来表示.
一般形式: a×10n( 1≤a<10,n为正整数)
2.用科学记数法表示大数有什么好处?
3.用科学记数法a×10n表示大数关键要注意两点: (1)1≤a<10. (2)当大数是大于10的整数时,n为整数位数减去1.
1010= 10 000 000 000 10 =
n
; ;
1000 · · ·0(n个0)
把下列各数写成10的幂的形式 1000 , 100 000 , 10 000 000 000 ,
利用前面知识,你能把一个较大的数表示 成整数段是一位数的数乘以10n的形式吗?
10 100=1×_____,
1000 3000=3×______=____ 10000 25000=2.5×______=______
4
5 4
32 000=3.2×10 32 000=3.2×10
2、 用科学记数法写出下列各数
10 000,800 000,56 000 000,7 400 000 解:10000=104 800000=8×105 56000000=5.6×107 7400000=7.4×106
3、下列用科学记数法写出的数,原来分别是什么数
ቤተ መጻሕፍቲ ባይዱ
2
归纳
为了记数方便和表示形式规范,我们作 如下规定: 把一个较大的数写成a×10n (1≤a< 10,n为正整数)的形式,这种记数的方法 叫科学记数法.
把一个大于10的数写成a×10n的形式,其中 1≤a<10, n是正整数,这种记数的方法称为科 学记数法
用科学记数法表示下列各数: 例题: (1)1 000 000;(2)57 000 000; (3)123 000 000 000 解(1)1000000= 106 (2)57000000= 5.7 × 10 000 000= 5.7 × 107 (3)123 000 000 000 =1.23 × 100 000 000 000 =1.23 × 1011
第五次人口普查时,中国人口约为1300 000 000人。
太阳的半径约为:696 000 000米
光的传播速度大约是300,000,000米/秒.
102 =
3 100 ; 10 = 1 000 ;
104= 10 000 ; 105= 100 000 ; 以10为底的幂的0的个数与指数有何关系? 相等
观察与思考:
1、上面的式子中,等号左边整数的位数与右边10的指数有 什么关系? 2、用科学记数法表示一个m位整数,其中10的指数是m-1 。
关键:①a的确定1≤a<10 ;②n的确定n=m-1
即n=m-1
第五次人口普查时,中国人口约为1300 000 000人。
1 300 000 000人 = 1.3×1000000000 人 =1.3 ×109人
太阳的半径约为:696 000 000米 8 10 =6.96 × 米
人类观测的宇宙深度大约是: 15,000,000,000光年.
光的传播速度大约是300,000,000米/秒.
巩固练习:
1、请你辨析下列用科学记数法表示 的数是否正确。 32 000=0.32×10
5
32 000=32×10
