华师大九年级下第27章《圆》章末测试(1)含答案解析
【期末复习】华东师大版九年级数学下册《第27章圆》单元评估检测试卷(含答案)

期末专题复习:华师大版九年级数学上册第27章圆单元评估检测试卷一、单选题(共10题;共30分)1.如图,⊙O为△ABC的外接圆,∠BAC=55°,则∠OBC 的度数为()A. 25°B. 35°C. 55°D. 70°2.已知圆O的半径是3,A,B,C 三点在圆O上,∠ACB=60°,则弧AB的长是()A. 2πB. πC. πD. π3.如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠OCB的度数为()A. 40°B. 50°C. 65°D. 75°4.某圆锥的母线长为6cm,其底面圆半径为3cm,则它的侧面积为()A. 18πcm2B. 18cm2C. 36πcm2D. 36cm25.如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于点C,若∠AOB=120°,则大圆半径R与小圆半径r之间满足()A. B. R=3r C. R=2r D.6.如图,在⊙O中,若C是BD的中点,则图中与∠BAC相等的角有()A.1个B.2个C.3个D.4个7.如图,是⊙的弦,点在圆上,已知,则()A. B. C. D.8.如图,两圆相交于A,B两点,小圆经过大圆的圆心O,点C、D分别在两圆上,若∠ADB=110°,则∠ACB 的度数为()A. 35°B. 40°C. 50°D. 80°9.如图,在⊙O中,∠AOB的度数为m,C是上一点,D,E是上不同的两点(不与A,B两点重合),则∠D +∠E的度数为( )A. mB. 180°-C. 90°+m2D. m210.如图,从⊙O外一点P引圆的两条切线PA、PB,切点分别是A、B,如果∠APB=60°,线段PA=10,那么弦AB的长是()A. 10B. 12C. 5D. 10二、填空题(共10题;共30分)11.已知如图,在⊙O中,弦AB的长为8,圆心O到AB的距离为3.若点P是AB上的一动点,则OP的取值范围是________.12.某体育馆的圆弧形屋顶如图所示,最高点C到弦AB的距离是20m,圆弧形屋顶的跨度AB是80m,则该圆弧所在圆的半径为________m.13.如图,AB是⊙O的直径,点C为⊙O上一点,∠AOC=50°,则∠ABC= ________.14.如图,AB是半圆的直径,∠BAC=20°,D是的中点,则∠DAC的度数是________.15.若用半径为12,圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥底面圆的半径的长________.16.如图,AB、AC与⊙O相切于点B、C,∠A=50゜,P为⊙O上异于B、C的一个动点,则∠BPC的度数为________ 。
第27章 圆数学九年级下册-单元测试卷-华师大版(含答案)

第27章圆数学九年级下册-单元测试卷-华师大版(含答案)一、单选题(共15题,共计45分)1、如图,正方形ABCD内接于,点P在上,则的度数为()A. B. C. D.2、如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=10,AE=2,则弦CD的长是()A.4B.6C.8D.103、如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为()A.4B.3C.2D.4、已知⊙O的半径为5cm,点P是⊙O外一点,则OP的长可能是()A.3cmB.4cmC.5cmD.6cm5、如图,在Rt△ABC中,BC 2,∠BAC 30°,斜边AB的两个端点分别在相互垂直的射线OM,ON上滑动,下列结论:①若C,O两点关于AB对称,则OA ;②C,O两点距离的最大值为4;③若AB平分CO,则AB⊥CO;④斜边AB的中点D运动路径的长为. 其中正确的是()A.①②B.①②③C.①③④D.①②④6、已知在△ABC中,∠BAC=90°,M是边BC的中点,BC的延长线上的点N满足AM⊥AN.△ABC的内切圆与边AB,AC的切点分别为E,F,延长EF分别与AN,BC的延长线交于P、Q,则=()A.1B.0.5C.2D.1.57、如图,在△ABC中,AB=6, AC=12,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P、Q,则线段PQ长度的最小值是()A.6B.12C.D.68、如图,如果直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长是()A.2B.8C.2D.29、如图,已知圆周角,则圆心角=()A.130°B.115°C.100°D.50°10、如图,已知圆锥的母线长为6,圆锥的高与母线所夹的角为θ,且sinθ= ,则该圆锥的侧面积是()A.24B.24πC.16πD.12π11、一块圆形宣传标志牌如图所示,点A,B,C在⊙O上,CD垂直平分AB于点D,现测得AB=8dm,DC=2dm,则圆形标志牌的半径为()A.6dmB.5dmC.4dmD.3dm12、如图,是⊙O的直径,的平分线交⊙O于点,连接,,给出下列四个结论:①;②是等腰直角三角形;③;④.其中正确的结论是()A.①②③B.①②④C.①③④D.①②③④13、已知正方形内接于半径为20,圆心角为90°的扇形(即正方形的各顶点都在扇形边或弧上),则正方形的边长是()A. B. C. 或 D. 或14、如图所示,AB为⊙O的直径,点C在⊙O上,且OC⊥AB,过点C的弦CD与线段OB相交于点E,满足∠AEC=65°,连接AD,则∠BAD等于()A.20°B.25°C.30°D.32.5°15、如图,CD是⊙O的直径,弦AB⊥CD于点G,直线EF与⊙O相切于点D,则下列结论中不一定正确的是()A.AG=BGB.AB∥EFC.AD∥BCD.∠ABC=∠ADC二、填空题(共10题,共计30分)16、如图,在ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则的长为________.17、小红随机地在如图所示的边长为6的正三角形及其内部区域投针,则针扎到其内切圆阴影区域的概率为________.18、如图,在Rt△ABC中,∠C=90°,∠B=70°,△ABC的内切圆⊙O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为________.19、如图,在半径为13的⊙O中,OC垂直弦AB于点B,交⊙O于点C,AB=24,则CD的长是________.20、如图,点D为∠BAC边AC上一点,点O为边AB上一点,AD=DO.以O为圆心,OD长为半径作半圆,交AC于另一点E,交AB于点F、G,连接EF.若∠BAC=22°,则∠EFG=________°.21、在矩形ABCD中,AB=5,AD=12,将矩形ABCD沿直线l向右翻滚两次至如图所示位置,则点B所经过的路线长是________ (结果不取近似值).22、如图,AB是⊙O的直径,弦BC=4cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A的方向运动,设运动时间为t(s)(0≤t<6),连接EF,当△BEF是直角三角形时,t的值为________.23、如图,正六边形ABCDEF内接于,若,则的半径为________.24、如图,在扇形AOC中,B是弧AC上一点,且AB、BC分别是⊙O的内接正方形、正五边形的边.若OA=1,则弧AC长为________.25、如图,⊙O的直径为10,弦AB长为8,点P在AB上运动,则OP的最小值是________三、解答题(共5题,共计25分)26、圆锥的底面半径为3cm,侧面展开图是圆心角为120º的扇形,求圆锥的全面积。
(易错题)华师大九年级数学下《第27章圆》单元测试卷(学生用)

【易错题解析】华师大版九年级数学下册第27章圆单元测试卷一、单选题(共10题;共32分)1.已知⊙O的半径是10cm,是120°,那么弦AB的弦心距是()A. 5cmB. cmC. cmD. cm2.如图,△ABC为⊙O的内接三角形,∠AOB=100°,则∠ACB的度数为()A. 100°B. 130°C. 150°D. 160°3.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么线段OE的长为()A.6 B.5 C.4 D.34.如图,圆内接四边形ABCD是由四个全等的等腰梯形组成,AD是⊙O的直径,则∠BEC的度数为()A. 15°B. 30°C. 45°D. 60°5.已知圆锥底面圆的半径为6cm,高为8cm,则圆锥的侧面积为()A. 48cm2B. 48πcm2C. 60πcm2D. 120πcm26.如图,正五边形ABCDE内接于⊙O,若⊙O的半径为5,则的长度为()A. πB. 2πC. 5πD. 10π7.如图,已知⊙O的半径等于1cm,AB是直径,C,D是⊙O上的两点,且==,则四边形ABCD的周长等于()A. 4cmB. 5cmC. 6cmD. 7cm8.如图,CD是⊙O的直径,已知∠1=30°,则∠2=()A. 30°B. 45°C. 60°D. 70°9.如图,AB是的直径,,∠COD=34 ,则∠AE0的度数是()A. 51B. 56C. 68D. 7810.(2017·衢州)运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8。
则图中阴影部分的面积是()A. B. C. D.二、填空题(共10题;共30分)11.半径为6cm的圆中,垂直平分半径OA的弦长为________cm.12.同圆中,已知弧AB所对的圆心角是100°,则弧AB所对的圆周角是________.13.如图,点A,B,C,D分别在⊙O上,,若∠AOB=40°,则∠ADC的大小是________度.14.已知弦AB把圆周分成1:5的两部分,则弦AB所对的圆心角的度数为________.15.若⊙O的半径为4cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系是________.16.若正六边形的边长为2,则它的半径是________.17.如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若∠C=22.5°,AB=6cm,则阴影部分面积为________.18.如图,△ABC是⊙O的内接正三角形,⊙O的半径为2,则图中阴影部的面积是________.19.如图,两个同心圆,大圆半径为5cm,小圆的半径为3cm,若大圆的弦AB与小圆相交,则弦AB的取值范围是________ .20.如图,线段AB为⊙O的直径,点C在AB的延长线上,AB=4,BC=2,点P是⊙O上一动点,连接CP,以CP为斜边在PC的上方作Rt△PCD,且使∠DCP=60°,连接OD,则OD长的最大值为________.三、解答题(共7题;共58分)21.如图,已知AB是⊙O的弦,C是的中点,AB=8,AC= ,求⊙O半径的长.22.如图,Rt△ABC中∠C=90°,点O是AB边上一点,以OA为半径作⊙O,与边AC交于点D,连接BD,若∠DBC=∠A,求证:BD是⊙O的切线.23.如图,一拱桥所在弧所对的圆心角为120°(即∠AOB=120°),半径为5 m,一艘6 m宽的船装载一集装箱,已知箱顶宽3.2 m,离水面AB高2 m,问此船能过桥洞吗?请说明理由.24.如图,AB是半圆的直径,0是圆心,C是半圆上一点,D是弧AC的中点,0D交弦AC于E,连接BE.若AC=8,DE=2,求BE的长度.25.如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD 的延长线于点C,连接AD并延长,交BE于点E.(1)求证:AB=BE;(2)若PA=2,cosB=,求⊙O半径的长.26.如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD 与AB的延长线交于点E.(1)求证:直线CD为⊙O的切线;(2)当AB=2BE,且CE=时,求AD的长.27.(2017•滨州)如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC.(Ⅰ)求证:直线DM是⊙O的切线;(Ⅱ)求证:DE2=DF•DA.答案解析部分一、单选题1.【答案】A2.【答案】B3.【答案】D.4.【答案】B5.【答案】C6.【答案】B7.【答案】B8.【答案】C9.【答案】A10.【答案】A二、填空题11.【答案】12.【答案】50°13.【答案】2014.【答案】60°15.【答案】相离16.【答案】217.【答案】π﹣918.【答案】19.【答案】8<AB≤1020.【答案】2 +1三、解答题21.【答案】解:连接OC交AB于D,连接OA,由垂径定理得OD垂直平分AB,设⊙O的半径为r,在△ACD中,CD2+AD2=AC2,CD=2,在△OAD中,OA2=OD2+AD2,r2=(r-2)2+16,解得r=5,∴☉O的半径为5.22.【答案】证明:如图,连接OD.∵OA=OD,∴∠A=∠ADO.∵∠C=90°,∴∠CBD+∠CDB=90°又∵∠CBD=∠A,∴∠ADO+∠CDB=90°,∴∠ODB=180°﹣(∠ADO+∠CDB)=90°.∴直线BD与⊙O相切.23.【答案】解:如图所示,连接OE,过点O作OH⊥EF于点H,∵∠AOB=120°OA=5m,∴∠OAB=30°,OK=2.5m,则OH=2.5+2=4.5m,∵OE=5m,∴在Rt△OEH中,EH= ,∴EF=2EH= ,∴此船能过桥洞.24.【答案】解:如图,连接BCD是弧AC的中点OD垂直平分ACEA=EC=设OD=OA=x,则OE=x-2,即,解得x=5AB=2OA=10答:BE的长度为25.【答案】(1)证明:连接OD,∵PD切⊙O于点D,∴OD⊥PD,∵BE⊥PC,∴OD∥BE,∴ADO=∠E,∵OA=OD,∴∠OAD=∠ADO,∴∠OAD=∠E,∴AB=BE;(2)解:由(1)知,OD∥BE,∴∠POD=∠B,∴cos∠POD=cosB=,在Rt△POD中,cos∠POD==,∵OD=OA,PO=PA+OA=2+OA,∴=,∴OA=3,∴⊙O半径=3.26.【答案】(1)证明:连接OC,∵AC平分∠DAB,∴∠1=∠2,∵又AO=CO,∴∠3=∠2,∴∠1=∠3,∴OC∥AD,∵又CD⊥AD,∴CD⊥OC,∴CD为⊙O的切线;(2)解:∵直径AB=2BE,∴OE=2OC,在Rt△EOC中,设CO=x,即OE=2x,由勾股定理得:CE=x,又∵CE=,∴x=1即OC=1,∵OC∥AD(已证)∴△EOC∽△EAD,∴,即,∴AD=27.【答案】解:(Ⅰ)如图所示,连接OD,∵点E是△ABC的内心,∴∠BAD=∠CAD,∴= ,∴OD⊥BC,又∵∠BDM=∠DAC,∠DAC=∠DBC,∴∠BDM=∠DBC,∴BC∥DM,∴OD⊥DM,∴直线DM是⊙O的切线;(Ⅱ)如图所示,连接BE,∵点E是△ABC的内心,∴∠BAE=∠CAE=∠CBD,∠ABE=∠CBE,∴∠BAE+∠ABE=∠CBD+∠CBE,即∠BED=∠EBD,∴DB=DE,∵∠DBF=∠DAB,∠BDF=∠ADB,∴△DBF∽△DAB,∴= ,即DB2=DF•DA,∴DE2=DF•DA.。
华师大版九年级下册数学第27章 圆含答案(有答案)
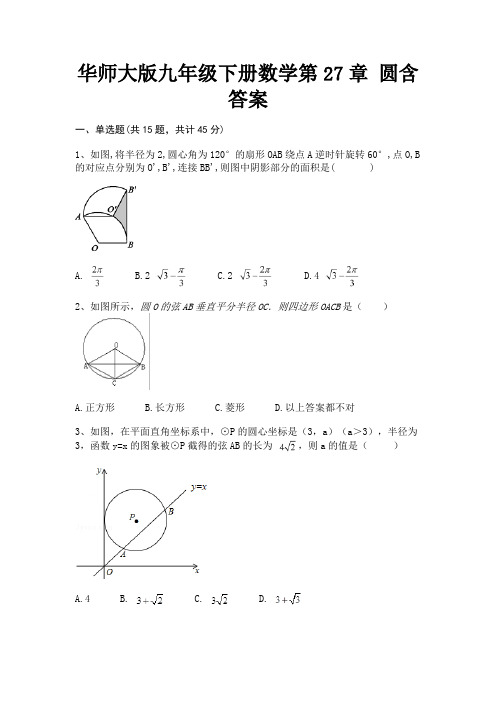
华师大版九年级下册数学第27章圆含答案一、单选题(共15题,共计45分)1、如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B 的对应点分别为O',B',连接BB',则图中阴影部分的面积是( )A. B.2 C.2 D.42、如图所示,圆O的弦AB垂直平分半径OC.则四边形OACB是()A.正方形B.长方形C.菱形D.以上答案都不对3、如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是()A.4B.C.D.4、如图,正方形ABCD内接于,直径,则阴影部分的面积占圆面积的()A. B. C. D.5、如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是()A.25°B.30°C.40°D.50°6、如图,在平面直角坐标系中,⊙P的圆心坐标是(3+ ,3),半径为3,函数y=x的图象被⊙P截得的弦AB,AB=()A.4B.2C.3D.47、如图,在△ABC中,以BC为直径的⊙O,又AB的延长线于点D,交AC于点E,连接OD,OE。
若∠A=40°,则∠DOE的度数为()A.140°B.100°C.50D.80°8、如图,E是△ABC的内心,若∠BEC=130°,则∠A的度数是()A.60°B.80°C.50°D.75°9、把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则的度数是()A.120°B.135°C.150°D.165°10、如图是切线,点A为切点,交于点C,点D在上,连接,若,则的度数为()A. B. C. D.11、如图,是的外接圆,它的半径为3,若,则劣弧的长为A. B. C. D.12、如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连结AC交⊙O于D,∠C=38°.点E在AB右侧的半圆上运动(不与A、B重合),则∠AED的大小是()A.19°B.38°C.52°D.76°13、如图,半径为1cm的在边长为9πcm,12πcm,15πcm的三角形外沿三边滚动(没有滑动)一周,则圆P所扫过的面积为()cm2A.73πB.75πC.76πD.77π14、如图,Rt△ABC中,∠C=90°,AB=5,AC=3,D点从BC的中点到C点运动,点E在AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径R的取值范围为()A. ≤R≤B. ≤R≤C.≤R≤2 D.1≤R≤15、如图,在纸上剪一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径r=1,扇形的半径为R,扇形的圆心角等于90°,则R的值是()A.R=2B.R=3C.R=4D.R=5二、填空题(共10题,共计30分)16、一个圆锥的左视图是一个正三角形,则这个圆锥的侧面展开图的圆心角等于________.17、如图,∠AOB=45°,点M,N在边OB上,OM=x,ON=x+4,点P是边OA上的点,且△PMN是等腰三角形.在x>2的条件下,(1)当x=________时,符合条件的点P只有一个;(2)当x=________时,符合条件的点P恰好有三个.(两个小题都只写出一个数即可)18、半径为3cm的⊙O中有长为的弦AB,则弦AB所对的圆周角为________19、如图,要拧开一个边长为a=12mm的六角形螺帽,扳手张开的开口b至少要________ mm.20、如图,为了美化校园,学校在一块靠墙角的空地上建造了一个扇形花圃,其圆心角AOB=120°,半径为6m,则扇形的弧长是________m.(结果保留π)21、如图,在⊙O中,AC是弦,AD是切线,CB⊥AD于B,CB与⊙O相交于点E,连接AE,若AE平分∠BAC,BE=1,则CE=________.22、在半径为R的圆中有一条长度为R的弦,则该弦所对的圆周角的度数是________.23、数学家刘徽首创割圆术,用圆内接正多边形的面积去无限逼近圆面积并以此求出圆周率.如图,正六边形的边长为2,现随机向该图形内掷一枚小针,则针尖落在阴影区域的概率为________.24、如图,△ABC中,AB=AC=5cm,BC=8cm,以A为圆心,3cm•长为半径的圆与直线BC的位置关系是________.25、到原点的距离等于4的点是________ .三、解答题(共5题,共计25分)26、已知:如图,四边形ABCD是⊙O的内接矩形,AB=4,BC=3,点E是劣弧上的一点,连接AE,DE.过点C作⊙O的切线交线段AE的延长线于点F,若∠CDE=30°,求CF的长.27、如图,AB为半圆直径,O为圆心,C为半圆上一点,E是弧AC上的一点,且OE⊥AC交弦AC于点D.若AC=8cm,DE=2cm,求OD的长.28、如图,为圆的直径,弦于点,,,求圆的半径.29、如图,AB、CD是⊙O的直径,弦CE∥AB,弧CE的度数为40°,求∠AOC 的度数.30、如图,在平行四边形ABCD中,以A为圆心,AB的长为半径的圆恰好与CD 相切于点C,交AD于点E,延长BA与⊙A相交于点F.若弧EF的长为,求图中阴影部分的面积.参考答案一、单选题(共15题,共计45分)1、C2、C3、B4、D5、C6、D7、B8、B9、C10、B11、C13、A14、B15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、30、。
难点详解华东师大版九年级数学下册第27章 圆专项测评试题(含答案解析)

华东师大版九年级数学下册第27章圆专项测评考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图,正六边形螺帽的边长是4cm,那么这个正六边形半径R和扳手的开口a的值分别是()A.2,B.4,C.4,D.42、如图,在矩形ABCD中,点E在CD边上,连接AE,将ADE沿AE翻折,使点D落在BC边的点F 处,连接AF,在AF上取点O,以O为圆心,线段OF的长为半径作⊙O,⊙O与AB,AE分别相切于点G,H,连接FG,GH.则下列结论错误的是()A .2BAE DAE ∠=∠B .四边形EFGH 是菱形C .3AD CE = D .GH AO ⊥3、如图是一个含有3个正方形的相框,其中∠BCD =∠DEF =90°,AB =2,CD =3,EF =5,将它镶嵌在一个圆形的金属框上,使A ,G , H 三点刚好在金属框上,则该金属框的半径是( )A B C .D 4、如图,A 、B 、C 、D 为一个正多边形的顶点,O 为正多边形的中心,若18ADB ∠=︒,则这个正多边形的边数为( )A .10B .11C .12D .135、如图,O 的半径为6,将劣弧沿弦AB 翻折,恰好经过圆心O ,点C 为优弧AB 上的一个动点,则ABC 面积的最大值是( )A .B .C .D .6、如图,△ABC 外接于⊙O ,∠A =30°,BC =3,则⊙O 的半径长为( )A .3BCD .7、如图,在Rt △ABC 中,90BAC ∠=︒,6AB AC ==,点D 、E 分别是AB 、AC 的中点.将△ADE 绕点A 顺时针旋转60°,射线BD 与射线CE 交于点P ,在这个旋转过程中有下列结论:①△AEC ≌△ADB ;②CP 存在最大值为3+BP 存在最小值为3;④点P 运动的路径长为2π.其中,正确的( )A .①②③B .①②④C .①③④D .②③④8、如图,在矩形ABCD 中,AB =1,AD =2,以A 为圆心,AD 为半径作弧交BC 于点D ˊ,则图中阴影部分的面积为( )A .πB .2πC .3πD .4π 9、如图,DC 是⊙O 的直径,弦AB ⊥CD 于M ,则下列结论不一定成立的是( )A .AM =BMB .CM =DMC .AC BC =D .AD BD =10、如图,AB 是⊙O 的直径,点C 是⊙O 上一点,若∠BAC =30°,BC =2,则AB 的长为( )A .4B .6C .8D .10第Ⅱ卷(非选择题 70分)二、填空题(10小题,每小题3分,共计30分)1、如图,半径为2的扇形AOB 的圆心角为120°,点C 是弧AB 的中点,点D 、E 是半径OA 、OB 上的动点,且满足∠DCE =60°,则图中阴影部分面积等于___________.2、如图,在四边形ABCD 中,AB =BC =BD .若∠ABC =112°,则∠ADC =_____°.3、已知60°的圆心角所对的弧长l 是3.14厘米,则它所在圆的周长是______厘米.4、如图,已知ABC ,外心为O ,18BC =,60BAC ∠=︒,分别以AB ,AC 为腰向形外作等腰直角三角形ABD △与ACE ,连接BE ,CD 交于点P ,则OP 的最小值是______.5、到点A 的距离等于8厘米的点的轨迹是__.6、已知圆弧所在圆的半径为36cm .所对的圆心角为60°,则该弧的长度为______cm .7、已知Rt ABC 中,90ACB ∠=︒,6cm AC =,8cm BC =,以C 为圆心,4.8cm 长度为半径画圆,则直线AB 与O 的位置关系是__________.8、如图,等边ABC 边长为4,点D 、E 、F 分别是AB 、BC 、AC 的中点,分别以D 、E 、F 为圆心,DE 长为半径画弧,围成一个曲边三角形,则曲边三角形的周长为______.9、如图,在平行四边形ABCD 中,7AB =,3AD =,120A ︒∠=,以点B 为圆心,BC 为半径的圆弧交AB 于点E ,连接DE ,则图中黑色阴影部分的面积为________.(结果保留π)10、如图,在Rt ABC 中,90ACB ∠=︒,30B ∠=︒,2AB =,以点A 为圆心,AC 的长为半径画弧,以点B 为圆心,BC 的长为半径画弧,两弧分别交AB 于点D 、F ,则图中阴影部分的面积是_________.三、解答题(5小题,每小题8分,共计40分)1、如图,△ABC 内接于⊙O ,AB 为⊙O 的直径,AB =5,AC =3.(1)求tanA 的值;(2)若D 为AB 的中点,连接CD 、BD ,求弦CD 的长.2、如图,AB 是O 的直径,PA ,PC 是O 的切线,A ,C 是切点,连接AC ,PO ,交点为D .(1)求证:BAC OPC ∠=∠;(2)延长PO 交O 于点E ,连接BE ,CE .若30BEC ∠=︒,8PA =,求AB 的长.3、如图,已知P 是⊙O 外一点.用直尺和圆规作图.(1)过点P 作一条直线l ,使l 与⊙O 相切;(2)在⊙O 上作一点Q ,使∠OQP =60°.(要求:保留作图痕迹,不写作法)4、如图,在Rt △ABC 中,∠B =90°,∠BAC 的平分线AD 交BC 于点D ,点E 在AC 上,以AE 为直径的⊙O 经过点D .(1)求证:①BC 是⊙O 的切线;②2CD CE CA =⋅;(2)若点F 是劣弧AD 的中点,且CE =3,试求阴影部分的面积.5、一个扇形的圆心角60︒,半径为12cm ,求它的面积.(保留)π-参考答案-一、单选题1、B【解析】【分析】根据正六边形的内角度数可得出∠BAD =30°,OAB ∆为等边三角形,得BC =2AB ,再通过解直角三角形即可得出12a 的值,进而可求出a 的值,此题得解.【详解】解:如图,∵正六边形的任一内角为120°,∴∠ABD =180°-120°=60°,60OAB OBA ∠=∠=︒∴∠BAD =30°,OAB ∆为等边三角形,∵4AB =∴2,4BD OB OA ===∴AD =∴2a =⨯=∴这个正六边形半径R 和扳手的开口a 的值分别是4,故选:B .【点睛】本题考查了正多边形以及勾股定理,牢记正多边形的内角度数是解题的关键.2、C【解析】【分析】由折叠可得∠DAE =∠FAE ,∠D =∠AFE =90°,EF =ED ,再根据切线长定理得到AG =AH ,∠GAF =∠HAF ,进而求出∠GAF =∠HAF =∠DAE =30°,据此对A 作出判断;接下来延长EF 与AB 交于点N ,得到EF 是⊙O 的切线,∆ANE 是等边三角形,证明四边形EFGH 是平行四边形,再结合HE =EF 可对B 作出判断;在Rt ∆EFC 中,∠C =90°,∠FEC =60°,则EF =2CE ,再结合AD 对C 作出判断;由AG =AH ,∠GAF =∠HAF ,得出GH ⊥AO ,不难判断D .【详解】解:由折叠可得∠DAE =∠FAE ,∠D =∠AFE =90°,EF =ED .∵AB 和AE 都是⊙O 的切线,点G 、H 分别是切点,∴AG =AH ,∠GAF =∠HAF ,∴∠GAF =∠HAF =∠DAE =30°,∴∠BAE =2∠DAE ,故A 正确,不符合题意;延长EF 与AB 交于点N ,如图:∵OF⊥EF,OF是⊙O的半径,∴EF是⊙O的切线,∴HE=EF,NF=NG,∴△ANE是等边三角形,∴FG//HE,FG=HE,∠AEF=60°,∴四边形EFGH是平行四边形,∠FEC=60°,又∵HE=EF,∴四边形EFGH是菱形,故B正确,不符合题意;∵AG=AH,∠GAF=∠HAF,∴GH⊥AO,故D正确,不符合题意;在Rt△EFC中,∠C=90°,∠FEC=60°,∴∠EFC=30°,∴EF=2CE,∴DE=2CE.∵在Rt△ADE中,∠AED=60°,∴AD,∴AD ,故C 错误,符合题意.故选C .【点睛】本题是一道几何综合题,考查了切线长定理及推论,切线的判定,菱形的定义,含30 的直角三角形的性质,等边三角形的判定和性质,翻折变换等,正确理解翻折变换及添加辅助线是解决本题的关键.3、A【解析】【分析】如图,记过A ,G , H 三点的圆为,Q 则Q 是HG ,AG 的垂直平分线的交点,,QH QG QA 记,PM EF 的交点为,N ,HG PM 的交点为,M 延长AB 交QM 于,P PM 为HG 的垂直平分线,结合正方形的性质可得:,AP PM 再设,PQ x 利用勾股定理建立方程,再解方程即可得到答案.【详解】 解:如图,记过A ,G , H 三点的圆为,Q 则Q 是HG ,AG 的垂直平分线的交点,,QH QG QA 记,PM EF 的交点为,N ,HG PM 的交点为,M 延长AB 交QM 于,P PM 为HG 的垂直平分线,结合正方形的性质可得:,AP PM四边形HGFE 为正方形,则,HG EF ∥,,QM HG QM EF设,PQ x 而AB =2,CD =3,EF =5,结合正方形的性质可得:5,NQ x而222,HM MQ HQ 115,5,5510,222HM HG EF MN EF MQ x x 222510,4HQ x 又222,AQ PQ AP 而51523,22AP 22215,2AQ x222522510,44x x 解得:5,2x 25225250510.4442AQ 故选A【点睛】本题考查的是正方形的性质,三角形外接圆圆心的确定,圆的基本性质,勾股定理的应用,二次根式的化简,确定过A ,G , H 三点的圆的圆心是解本题的关键.4、A【解析】【分析】作正多边形的外接圆,连接 AO ,BO ,根据圆周角定理得到∠AOB =36°,根据中心角的定义即可求解.【详解】解:如图,作正多边形的外接圆,连接AO,BO,∴∠AOB=2∠ADB=36°,∴这个正多边形的边数为36036=10.故选:A.【点睛】此题主要考查正多边形的性质,解题的关键是熟知圆周角定理.5、C【解析】【分析】如图,过点C作CT⊥AB于点T,过点O作OH⊥AB于点H,交⊙O于点K,连接AO、AK,解直角三角形求出AB,求出CT的最大值,可得结论.【详解】解:如图,过点C作CT⊥AB于点T,过点O作OH⊥AB于点H,交⊙O于点K,连接AO、AK,由题意可得AB垂直平分线段OK,∴AO =AK ,OH =HK =3,∵OA =OK ,∴OA =OK =AK ,∴∠OAK =∠AOK =60°,∴AH =OA ×sin ∵OH ⊥AB ,∴AH =BH ,∴AB =2AH∵OC +OH ⩾CT ,∴CT ⩽6+3=9,∴CT 的最大值为9,∴△ABC 的面积的最大值为192⨯故选:C.【点睛】本题考查垂径定理、三角函数、三角形的面积、垂线段最短等知识,解题的关键是求出CT 的最大值,属于中考常考题型.6、A【解析】【分析】分析:连接OA 、OB ,根据圆周角定理,易知∠AOB=60°;因此△ABO 是等边三角形,即可求出⊙O 的半径.【详解】解:连接BO ,并延长交⊙O 于D ,连结DC ,∵∠A =30°,∴∠D =∠A =30°,∵BD 为直径,∴∠BCD =90°,在Rt△BCD 中,BC =3,∠D =30°,∴BD =2BC =6,∴OB =3.故选A .【点睛】本题考查了圆周角性质,利用同弧所对圆周角性质与直径所对圆周角性质,30°角所对直角三角形性质,掌握圆周角性质,利用同弧所对圆周角性质与直径所对圆周角性质,30°角所对直角三角形性质是解题的关键.7、B【解析】【分析】根据90BAC ∠=︒,6AB AC ==,点D 、E 分别是AB 、AC 的中点.得出∠DAE =90°,AD =AE =16=32⨯,可证∠DAB =∠EAC ,再证△DAB ≌△EAC (SAS ),可判断①△AEC ≌△ADB 正确;作以点A 为圆心,AE 为半径的圆,当CP 为⊙A 的切线时,CP 最大,根据△AEC ≌△ADB ,得出∠DBA=∠ECA ,可证∠P =∠BAC =90°,CP 为⊙A 的切线,证明四边形DAEP 为正方形,得出PE =AE =3,在Rt △AEC 中,CE=CP存在最大值为3+AEC ≌△ADB ,得出BD =CE=Rt △BPC 中,BP 最小3==可判断③BP 存在最小值为3不正确;取BC 中点为O ,连结AO ,OP ,AB =AC =6,∠BAC =90°,BP =CO =AO=1122BC ==⨯,当AE ⊥CP 时,CP 与以点A 为圆心,AE 为半径的圆相切,此时sin∠ACE =3162AE AC ==,可求∠ACE =30°,根据圆周角定理得出∠AOP =2∠ACE =60°,当AD ⊥BP′时,BP′与以点A 为圆心,AE 为半径的圆相切,此时sin∠ABD =3162AD AB ==,可得∠ABD =30°根据圆周角定理得出∠AOP′=2∠ABD =60°,点P 在以点O 为圆心,OA 长为半径,的圆上运动轨迹为PAP ',L PAP '12032180ππ⨯==可判断④点P 运动的路径长为2π正确即可. 【详解】解:∵90BAC ∠=︒,6AB AC ==,点D 、E 分别是AB 、AC 的中点.∴∠DAE =90°,AD =AE =16=32⨯, ∴∠DAB +∠BAE =90°,∠BAE +∠EAC =90°,∴∠DAB =∠EAC ,在△DAB 和△EAC 中,AD AE DAB EAC AB AC =⎧⎪∠=∠⎨⎪=⎩, ∴△DAB ≌△EAC (SAS ),故①△AEC ≌△ADB 正确;作以点A为圆心,AE为半径的圆,当CP为⊙A的切线时,CP最大,∵△AEC≌△ADB,∴∠DBA=∠EC A,∴∠PBA+∠P=∠ECP+∠BAC,∴∠P=∠BAC=90°,∵CP为⊙A的切线,∴AE⊥CP,∴∠DPE=∠PEA=∠DAE=90°,∴四边形DAEP为矩形,∵AD=AE,∴四边形DAEP为正方形,∴PE=AE=3,在Rt△AEC中,CE===,∴CP最大=PE+EC=3+故②CP存在最大值为3+∵△AEC ≌△ADB ,∴BD =CE =在Rt △BPC 中,BP 最小3=,BP 最短=BD -PD =,故③BP 存在最小值为3不正确;取BC 中点为O ,连结AO ,OP ,∵AB =AC =6,∠BAC=90°,∴BP =CO =AO =1122BC =⨯=, 当AE ⊥CP 时,CP 与以点A 为圆心,AE 为半径的圆相切,此时sin∠ACE =3162AE AC ==, ∴∠ACE =30°,∴∠AOP =2∠ACE =60°, 当AD ⊥BP′时,BP′与以点A 为圆心,AE 为半径的圆相切,此时sin∠ABD =3162AD AB ==, ∴∠ABD =30°,∴∠AOP′=2∠ABD =60°,∴点P在以点O为圆心,OA长为半径,的圆上运动轨迹为PAP',∵∠POP=∠POA+∠AOP′=60°+60°=120°,∴L PAP'12032180ππ⨯==.故④点P运动的路径长为2π正确;正确的是①②④.故选B.【点睛】本题考查图形旋转性质,线段中点定义,三角形全等判定与性质,圆的切线,正方形判定与性质,勾股定理,锐角三角函数,弧长公式,本题难度大,利用辅助线最长准确图形是解题关键.8、C【解析】【分析】证明∠DAD′=∠AD′B=30°,再利用扇形的面积公式求解即可.【详解】解:∵四边形ABCD是矩形,∴∠B=90°,AD∥CB,∵AB=1,AD′=AD=2,∴AD′=2AB,∴∠AD′B=30°,∴∠DAD′=∠AD′B=30°,∴S阴=2302360π⨯=3π,故选:C.【点睛】本题考查扇形的面积,矩形的性质等知识,解题的关键是证明∠AD′B=30°.9、B【解析】【分析】根据垂径定理“垂直于弦的直径平分这条弦,并且平分弦所对的两条弧”进行判断即可得.【详解】解:∵弦AB⊥CD,CD过圆心O,∴AM=BM,AC BC=,AD BD=,即选项A、C、D选项说法正确,不符合题意,当根据已知条件得CM和DM不一定相等,故选B.【点睛】本题考查了垂径定理,解题的关键是掌握垂径定理.10、A【解析】【分析】根据直径所对的圆角为直角,可得90C ∠=︒ ,再由直角三角形中,30°角所对的直角边等于斜边的一半,即可求解.【详解】解:∵AB 是⊙O 的直径,∴90C ∠=︒ ,∵∠BAC =30°,BC =2,∴24AB BC ==.故选:A【点睛】本题主要考查了直径所对的圆角,直角三角形的性质,熟练掌握直径所对的圆角为直角;直角三角形中,30°角所对的直角边等于斜边的一半是解题的关键.二、填空题1、43π【解析】【分析】如图,连接,,OC AC 过C 作CF OA ⊥于,F AOC △是等边三角形,求解3,CF证明,60,AC OC DAC ACO 再证明,ACD OCE ASA ≌ 可得AOC AOB S S S 阴影扇形,再计算即可得到答案.【详解】解:如图,连接,,OC AC 过C 作CF OA ⊥于,FC 是AB 的中点,120,AOB ∠=︒ 160,2AOC BOC AOB ,AO COAOC ∴是等边三角形, ,60,AC OC OAC ACO 60,DACEOC ,2,CFAO AO CO 11,2AF OF AO 2222213,CF OC OF60,DCE,DCE OCD ACO OCD,ACD OCE ∴∠=∠ 而60,,DAC EOC AC OC ,ACD OCE ASA ≌ ,DOC OEC AOC DCEO S S S S 四边形 AOC AOB S S S 阴影扇形212021423336023故答案为:43π【点睛】 本题考查的是全等三角形的判定与性质,等边三角形的判定与性质,扇形面积的计算,掌握“利用转化的思想求解阴影部分的面积”是解本题的关键.2、124【解析】【分析】根据题意,,,A D C 在以B 为圆心半径为AB 的圆上,设E 是优弧AC 上任意一点,则四边形ADCE 是B 的内接四边形,进而根据圆内接四边形对角互补,圆周角定理求得E ∠,即可求得ADC ∠.【详解】解:如图,AB =BC =BD∴,,A D C 在以B 为圆心半径为AB 的圆上,设E 是优弧AC 上任意一点,则四边形ADCE 是B 的内接四边形180E ADC ∴∠+∠=︒又∠ABC =112°,56E ∴∠=︒18056124ADC ∴∠=︒-︒=︒故答案为:124【点睛】本题考查了圆内接四边形对角互补,圆周角定理,转为圆内接四边形求解是解题的关键. 3、18.84【解析】【分析】先根据弧长公式求得πr ,然后再运用圆的周长公式解答即可.【详解】解:设圆弧所在圆的半径为r 厘米, 则60 3.14180r π⨯=, 解得9.42r π=,则它所在圆的周长为229.4218.84r π=⨯=(厘米),故答案为:18.84.【点睛】本题主要考查了弧长公式、圆的周长公式等知识点,牢记弧长公式是解答本题的关键.4、9-【解析】【分析】由ABD △与ACE 是等腰直角三角形,得到90BAD CAE ∠=∠=︒,DAC BAE ∠=∠,根据全等三角形的性质得到ADC ABE ∠=∠,求得在以BC 为直径的圆上,由ABC 的外心为O ,60BAC ∠=︒,得到120BOC ∠=︒,如图,当PO BC ⊥时,OP 的值最小,解直角三角形即可得到结论.【详解】 解:ABD 与ACE 是等腰直角三角形,90BAD CAE ∴∠=∠=︒,DAC BAE ∴∠=∠,在DAC △与BAE 中,AD AB DAC BAE AC AE =⎧⎪∠=∠⎨⎪=⎩, DAC ∴≌()BAE SAS ,ADC ABE ∴∠=∠,90PDB PBD ∴∠+∠=︒,90DPB ∴∠=︒,P ∴在以BC 为直径的圆上, ABC 的外心为O ,60BAC ∠=︒,120BOC ∴∠=︒,如图,当PO BC ⊥时,OP 的值最小,18BC =,9BH CH ∴==,12OH OB =BH ∴==OH ∴=9PH =,9OP ∴=-则OP 的最小值是9-故答案为:9-【点睛】本题考查了三角形的外接圆与外心,全等三角形的判定和性质,等腰直角三角形的性质,正确的作出辅助线是解题的关键.5、以点A 为圆心,8厘米长为半径的圆【解析】【分析】由题意直接根据圆的定义进行分析即可解答.【详解】到点A 的距离等于8厘米的点的轨迹是:以点A 为圆心,2厘米长为半径的圆.故答案为:以点A 为圆心,8厘米长为半径的圆.【点睛】本题主要考查了圆的定义,正确理解定义是关键,注意掌握圆的定义是在同一平面内到定点的距离等于定长的点的集合.6、12π【解析】【分析】根据弧长公式直接计算即可.【详解】∵圆的半径为36cm.所对的圆心角为60°,∴弧的长度为:6036 180180n rππ⨯⨯==12π,故答案为:12π.【点睛】本题考查了弧长的计算,熟练掌握弧长公式及其使用条件是解题的关键.7、相切【解析】【分析】过点C作CD⊥AB于D,在Rt△ABC中,根据勾股定理AB10=cm,利用面积得出CD·AB=AC·BC,即10CD=6×8,求出CD=4.8cm,根据CD=r=4.8cm,得出直线AB与O的位置关系是相切.【详解】解:过点C作CD⊥AB于D,在Rt△ABC中,根据勾股定理AB10=cm,∴S△ABC=12CD·AB=12AC·BC,即10CD=6×8,解得CD=4.8cm,∴CD=r=4.8cm,∴直线AB与O的位置关系是相切.故答案为:相切.【点睛】本题考查勾股定理,直角三角形面积,圆的切判定,掌握勾股定理,直角三角形面积,圆的切判定是解题关键.8、2π【解析】【分析】证明△DEF是等边三角形,求出圆心角的度数,利用弧长公式计算即可.【详解】解:连接EF、DF、DE,∵等边ABC边长为4,点D、E、F分别是AB、BC、AC的中点,∴DEF是等边三角形,边长为2,∴∠EDF=60°,弧EF的长度为60221803ππ⨯=,同理可求弧DF、DE的长度为23π,则曲边三角形的周长为2323ππ⨯=;故答案为:2π.【点睛】本题考查了等边三角形的性质与判定和弧长计算,中位线的性质,解题关键是熟记弧长公式,正确求出圆心角和半径.932π 【解析】【分析】过点C 作CH AB ⊥于点H ,根据正弦定义解得CH 的长,再由扇形面积公式、三角形的面积公式解题即可.【详解】解:过点C 作CH AB ⊥于点H ,在平行四边形ABCD 中,120A ∠=︒18012060B ∴∠=︒-︒=︒=sin sin 603CH BC B AD ∴⋅=⨯︒=平行四边形ABCD 的面积为:7AB CH ⨯=图中黑色阴影部分的面积为:()2216016037323602360BC AE CH ππ⋅⨯⋅⋅-=⨯-=32π,32π. 【点睛】 本题考查平行四边形的性质、扇形面积等知识,是基础考点,掌握相关知识是解题关键.10、512π-【解析】【分析】根据直角三角形30度角的性质及勾股定理求出AC 、BC ,∠A =60°,利用扇形面积公式求出阴影面积.【详解】解:在Rt ABC 中,90ACB ∠=︒,30B ∠=︒,2AB =,∴AC =1,BC ==A =60°,∴图中阴影部分的面积=ABC CAD CBE S S S+-扇形扇形=2601113602π⨯⨯=512π故答案为:512π 【点睛】此题考查了直角三角形30度角的性质,勾股定理,扇形面积的计算公式,直角三角形面积公式,熟记各知识点并综合应用是解题的关键.三、解答题1、 (1)4 tan3A=【解析】【分析】(1)根据直径所对的圆周角是90°可判断∠ACB=90º,再根据勾股定理求得BC的长度,从而可求得tanA的值;(2)过点B作BE⊥CD于E,根据相等的弧对应圆周角相等可得∠ACD=∠BCD=45º,从而可得Rt△BCE 为直角三角形,求得BE的值,再根据同弧所对的圆周角相等可得∠A=∠D,利用(1)中所求正切值即可求得DE的值,从而求得CD的值.(1)解:∵AB为⊙O的直径,∴∠ACB=90º,∵AB=5,AC=3,∴BC=4,∴4 tan3A=.(2)解:过点B作BE⊥CD于E,∵D 为AB 的中点,∴ AD BD =,∴ ∠ACD =∠BCD =45º,∵BC =4,在Rt △BCE 中,BE CE ==∵∠A=∠D , ∴4tan tan 3D A ==, 在Rt △BDE 中,tan 3BE DE D ===∴CD =CE +DE. 【点睛】本题考查圆周角定理,三角函数的应用,勾股定理等.(1)中能根据直径所对的圆周角是90°得出∠ACB =90º是解题关键;(2)中正确构造辅助线,构造直角三角形是解题关键.2、 (1)证明见解析【解析】【分析】(1)如图,连接,OC 先证明90,,,OAP BAC CAP PA PC APO CPO 再证明,OP AC 可得90,CAP APO 从而可得结论; (2)如图,先求解 30,BAC ∠=︒ 结合,AC OP 求解60,AOP 再利用tan AOP ∠建立方程求解即可.(1)证明:如图,连接,OC,PC PA 为O 的切线,90,,,OAP BAC CAP PA PC APO CPO,OC OA =,OP AC90,CAP APO.BAC APO CPO(2)解:如图,30,BEC30,BAC 而,AC OP60,AOP90,8,OAP PAtan tan 603,PAAOP AO 883,33AO 1632.3AB AO【点睛】本题考查的是圆的的切线的性质,切线长定理的应用,圆周角定理的应用,锐角三角函数的应用,熟练的运用切线长定理解题是解本题的关键.3、 (1)见解析(2)见解析【解析】【分析】(1)连接OP ,作线段PO 的垂直平分线MN ,MN 交PO 于点B ,以B 为圆心,OB 的长为半径作弧,交O 于点A ,过点,P A 作直线l ,则l 即为所求;(2)构造四点共圆,作120PDO ∠=︒,步骤如下,连接OP ,作OP 垂直平分线MN 与OP 交于点B ,分别以,B O 为圆心,OB 的长为半径作弧,两弧交于点C ,连接PC ,交MN 于点D ,则30CPO ∠=︒,连接OD ,则120PDO ∠=︒,作PDO △的外心,即作PD 的垂直平分线与MN 交于点E ,以EB 为半径作E ,交O 于点Q ,连接,OQ PQ ,则60OQP ∠=︒,点Q 即为所求.(1)连接OP ,作线段PO 的垂直平分线MN ,MN 交PO 于点B ,以B 为圆心,OB 的长为半径作弧,交O 于点A ,过点,P A 作直线l ,则l 即为所求;理由:,,P O A 三点共圆,PO 是直径,则PAO ∠是直角,即OA l ⊥,则l 为所求作的切线(2)如图,连接OP ,作OP 垂直平分线MN 与OP 交于点B ,分别以,B O 为圆心,OB 的长为半径作弧,两弧交于点C ,连接PC ,交MN 于点D ,则30CPO ∠=︒,连接OD ,则120PDO ∠=︒,作PDO △的外心,即作PD 的垂直平分线与MN 交于点E ,以EB 为半径作E ,交O 于点Q ,连接,OQ PQ ,则60OQP ∠=︒,点Q 即为所求,理由是:PQOD 是E 的内接四边形,120PDO ∠=︒,则60OQP ∠=︒【点睛】本题考查了尺规作图,作圆的切线,作圆周角,四点共圆,作特殊角,掌握基本作图是解题的关键.4、(1)①见解析;②见解析;(2)32π. 【解析】【分析】(1)①连接OD ,由角平分线的性质解得DAB DAO ∠=∠,再根据内错角相等,两直线平行,证明//DO AB ,继而由两直线平行,同旁内角互补证明90ODB ∠=︒即可解题; ②连接DE ,由弦切角定理得到CDE DAC ∠=∠,再证明CDE CAD ,由相似三角形对应边成比例解题; (2)证明,OFD OFA 是等边三角形,四边形DOAF 是菱形,=DFO S S 阴影扇形,结合扇形面积公式解题.【详解】解:(1)①连接OD , AD 是∠BAC 的平分线DAB DAO ∴∠=∠OD OA =DAO ODA ∴∠=∠DAB ODA ∴∠=∠//DO AB ∴180B ODB ∴∠+∠=︒90B ∠=︒90ODB ∴∠=︒OD BC ∴⊥BC ∴是⊙O 的切线;②连接DE,BC是⊙O的切线,CDO∴∠=︒90∵是直径AE∴∠=︒90ADE∴∠=∠CDE ODA=OD OA∴∠=∠ODA DAC∴∠=∠CDE DAC∠∠C C=∴CDE CADCD CE∴=AC CD2CD CE CA∴=⋅(2)连接DE、OD、DF、OF,设圆的半径为R ,点F 是劣弧AD 的中点,∴OF 是DA 中垂线∴DF =AF ,FDA FAD ∴∠=∠//DO ABODA DAF ∴∠=∠ODA DAO FDA FAD ∴∠=∠=∠=∠AF DF OA OD ∴===,OFD OFA ∴是等边三角形,四边形DOAF 是菱形,60ODF DOF FOA ∴∠=∠=∠=︒=DFO S S ∴阴影扇形60,90DOC ODC ∠=︒∠=︒30C ∴∠=︒11()22OD OC OE EC ∴==+ ,3OE OD CE ==3CE OE R ∴===26033===3602DFO S S ππ⋅∴阴影扇形.【点睛】本题考查圆的综合题,涉及切线的判定与性质、平行四边形的性质、等边三角形的判定与性质、相似三角形的判定与性质、扇形面积等知识,综合性较强,有难度,掌握相关知识是解题关键. 5、224cm π.【解析】【分析】将6012n r ==,代入2360n r S π=,求解即可. 【详解】 解:由题意知扇形面积为:()222601224360360n r S cm πππ⋅=== ∴扇形的面积为:224cm π.【点睛】本题考查了扇形的面积.解题的关键在于熟练使用扇形的面积公式.。
精品试题华东师大版九年级数学下册第27章 圆达标测试试题(含答案及详细解析)

华东师大版九年级数学下册第27章圆达标测试考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图,BE是O的直径,点A和点D是O上的两点,过点A作O的切线交BE延长线于点C,若36∠=︒,则CADE∠的度数是()A.18°B.28°C.36°D.45°2、如图,O的半径为6,将劣弧沿弦AB翻折,恰好经过圆心O,点C为优弧AB上的一个动点,则ABC面积的最大值是()A .B .C .D .3、如图,ABC 中,90ABC ∠=︒,2AB =,4AC =,点O 为BC 的中点,以O 为圆心,OB 长为半径作半圆,交AC 于点D ,则图中阴影部分的面积是( )A 2πB .32C .2πD 4、如图,AB 为O 的直径,弦CD AB ⊥于E ,已知16CD =,6OE =,则O 的直径为( )A .10B .18C .26D .205、如图,在矩形ABCD 中,6AB =,8AD =,点O 在对角线BD 上,以OB 为半径作O 交BC 于点E ,连接DE ;若DE 是O 的切线,此时O 的半径为( )A .716B .2110C .2116D .35166、如图,在33⨯的网格中,A ,B 均为格点,以点A 为圆心,AB 的长为半径作弧,图中的点C 是该弧与格线的交点,则tan BAC ∠的值是( )A .12BCD .237、如图,AB 为⊙O 的切线,切点为A ,连接AO 、BO ,BO 与⊙O 交于点C ,延长BO 与⊙O 交于点D ,连接AD .若∠ABO =36°,则∠ADC 的度数为( )A .54°B .36°C .32°D .27°8、如图,在Rt ABC 中,90C ∠=︒,10cm AB =,若以点C 为圆心,CB 的长为半径的圆恰好经过AB 的中点D ,则AC 的长等于( )A.5cm B.6cm C.D.9、如图,在O中,如果AB=2AC,则下列关于弦AB与弦AC之间关系正确的是()A.AB=AC B.AB= 2AC C.AB>2AC D.AB< 2ACOA ,则点A在()10、已知⊙O的半径为4,5A.⊙O内B.⊙O上C.⊙O外D.无法确定第Ⅱ卷(非选择题 70分)二、填空题(10小题,每小题3分,共计30分)1、如图,从一块直径为2cm的圆形铁皮上剪出一圆心角为90°的扇形,则此扇形的面积为______cm2.2、如图,在⊙O 中,AB 是⊙O 的内接正六边形的一边,BC 是⊙O 的内接正十边形的一边,则∠ABC =______°.3、已知60°的圆心角所对的弧长l 是3.14厘米,则它所在圆的周长是______厘米.4、如图,AB 为⊙O 的弦,∠AOB =90°,AB =a ,则OA =______,O 点到AB 的距离=______.5、如图,已知圆周角∠ACB =128°,则圆心角∠AOB =__________.6、如图,把O 分成相等的六段弧,依次连接各分点得到正六边形ABCDEF ,如果O 的周长为12π,那么该正六边形的边长是______.7、在圆内接四边形ABCD 中,40D B ∠-∠=︒,则D ∠的度数为______.8、如图,AB 、CD 为一个正多边形的两条边,O 为该正多边形的中心,若∠ADB =12°,则该正多边形的边数为 _____.9、如图,AB 是半圆O 的直径,点C ,D 在半圆上,若∠D =120°,则∠B 的度数是 _____.10、在Rt ABC ∆中,90C ∠=︒,2AC =,4AB =,如果以点A 为圆心,AC 为半径作A ,那么斜边AB 的中点D 在A ______.(填“内”、“上”或者“外”)三、解答题(5小题,每小题8分,共计40分)1、如图,ABC 与O 交于D ,F 两点,AB 是直径,∥OD BC .(1)证明:CD DE =;(2)若13,52AD CE==,求OA的长度.2、如图,在平面直角坐标系中,△ABC的三个顶点A、B、C的坐标分别为(0,3)、(2,1)、(4,1).(1)以原点O为位似中心,在第一象限画出△ABC的位似图形△ABC,使△A1B1C1与△ABC的相似比为2:1;(2)借助网格,在图中画出△ABC的外接圆P,并写出圆心P的坐标;(3)将△ABC绕(2)中的点P将△ABC绕点P顺时针旋转90°,则点A运动的路线长是.3、如图,在Rt△ABC中,∠B=90°,∠BAC的平分线AD交BC于点D,点E在AC上,以AE为直径的⊙O经过点D.(1)求证:①BC是⊙O的切线;②2CD CE CA=⋅;(2)若点F是劣弧AD的中点,且CE=3,试求阴影部分的面积.4、如图,在平面直角坐标系中,ABC顶点的横、纵坐标都是整数.若将ABC以某点为旋转中心,顺时针旋转90°得到DEF,其中A、B、C分别和D、E、F对应.(1)请通过画图找出旋转中心M,点M的坐标为______.(2)直接写出点A经过的路径长为______.5、如图,等边△ABC内接于⊙O,P是AB上任一点(点P与点A、B重合),连接AP、BP,过点C作CM∥BP交PA的延长线于点M.(1)求∠APC和∠BPC的度数;(2)求证:△ACM≌△BCP;(3)若PA=1,PB=2,求四边形PBCM的面积;(4)在(3)的条件下,求AB的长度.-参考答案-一、单选题1、A【解析】连接OA ,根据同弧所对的圆周角相等可得ABE ADE ∠=∠,根据圆周角定理可得272AOE ADE ∠=∠=︒,根据切线的性质以及直角三角形的两锐角互余即可求得C ∠的度数.【详解】解:如图,连接OAAE AE =,36ADE ∠=︒∴ABE ADE ∠=∠∴272AOE ADE ∠=∠=︒ AC 是O 的切线90CAO ∴∠=︒90907218C AOE ∴∠=︒-∠=︒-︒=︒故选A【点睛】本题考查了切线的性质,圆周角定理,求得AOE ∠的度数是解题的关键.2、C【解析】如图,过点C作CT⊥AB于点T,过点O作OH⊥AB于点H,交⊙O于点K,连接AO、AK,解直角三角形求出AB,求出CT的最大值,可得结论.【详解】解:如图,过点C作CT⊥AB于点T,过点O作OH⊥AB于点H,交⊙O于点K,连接AO、AK,由题意可得AB垂直平分线段OK,∴AO=AK,OH=HK=3,∵OA=OK,∴OA=OK=AK,∴∠OAK=∠AOK=60°,∴AH=OA×sin∵OH⊥AB,∴AH=BH,∴AB=2AH∵OC+OH⩾CT,∴CT⩽6+3=9,∴CT的最大值为9,∴△ABC 的面积的最大值为192⨯故选:C.【点睛】本题考查垂径定理、三角函数、三角形的面积、垂线段最短等知识,解题的关键是求出CT 的最大值,属于中考常考题型.3、A【解析】【分析】连接OD ,BD ,作OH ⊥CD 交CD 于点H ,首先根据勾股定理求出BC 的长度,然后利用等面积法求出BD 的长度,进而得到OBD ∆是等边三角形,60BOD ∠=︒,然后根据30°角直角三角形的性质求出OH 的长度,最后根据ACB COD ODB S S S S ∆∆=--形阴影扇进行计算即可.【详解】解:如图所示,连接OD ,BD ,作OH ⊥CD 交CD 于点H∵2AB =,4AC =,90ABC ∠=︒∴在Rt ABC ∆中,BC∵点O 为BC 的中点,以O 为圆心,OB 长为半径作半圆∴BC 是圆的直径,∴90CDB ∠=︒∴1122ABC S AB BC AC BD ∆==,即112422BD ⨯⨯=⨯⨯解得:BD =又∵12OB OC OD BC ====∴OB OD BD ==∴OBD ∆是等边三角形∴60BOD ∠=︒∴1302C CDO BOD ∠=∠=∠=︒∵OH ⊥CD∴12OH OC ==,3CD =∴2601123223602ACB COD ODB S S S S ππ∆∆⨯=--=⨯⨯-=形阴扇影. 故选:A .【点睛】本题考查了30°角直角三角形的性质,等边三角形的性质和判定,扇形面积,勾股定理等知识,正确添加辅助线,熟练掌握和灵活运用相关知识是解题的关键.4、D【解析】【分析】连接OC ,由垂径定理及勾股定理即可求得圆的半径,从而可得直径的长.【详解】连接OC ,∵AB 为O 的直径,弦CD AB ⊥于E , ∴182CE CD ==,∴10OC ,∴O 的直径220AB OC ==,故选:D .【点睛】本题考查了垂径定理及勾股定理,连接OC 得到直角三角形是关键.5、D【解析】【分析】设O 半径为r ,如解图,过点O 作OF BE ⊥,根据等腰三角形性质BF EF =,根据四边形ABCD 为矩形,得出∠C =90°=∠OFB ,∠OBF =∠DBC ,可证BOF BDC ∽.得出BF BO BC BD=,根据勾股定理10BD ,代入数据810BF BO =,得出4455BF EF OB r ===,根据勾股定理在Rt DCE 中,222EC CD DE +=,即2225688r DE ⎛⎫- ⎪⎝⎭+=,根据DE 为O 的切线,利用勾股定理()222222618850E E r r O D r ⎛⎫+=++=⎭-- ⎪⎝,解方程即可. 【详解】解:设O 半径为r ,如解图,过点O 作OF BE ⊥,∵OB =OE ,∴BF EF =,∵四边形ABCD 为矩形,∴∠C =90°=∠OFB ,∠OBF =∠DBC ,∴BOF BDC ∽. ∴BF BO BC BD=, ∵6,8AB AD ==,∴10BD ==, ∴810BF BO =, ∴4455BF EF OB r ===, ∴885EC r =-. 在Rt DCE 中,222EC CD DE +=,即2225688r DE ⎛⎫- ⎪⎝⎭+=, 又∵DE 为O 的切线,∴OE DE ⊥, ∴()222222618850E E r r O D r ⎛⎫+=++=⎭-- ⎪⎝, 解得3516r =或0(不合题意舍去). 故选D .【点睛】本题考查矩形性质,等腰三角形性质,圆的切线,勾股定理,一元二次方程,掌握矩形性质,等腰三角形性质,圆的切线性质,勾股定理,一元二次方程,矩形性质,等腰三角形性质,圆的半径相等,勾股定理,一元二次方程,是解题关键.6、B【解析】【分析】利用CD AB ∥,得到∠BAC =∠DCA ,根据同圆的半径相等,AC =AB =3,再利用勾股定理求解,CD 可得tan ∠ACD =AD CD =. 【详解】解:如图, ∵CD AB ∥,∴∠BAC =∠DCA .∵同圆的半径相等, ∴AC =AB =3,而2,AD =225,CD AC AD在Rt △ACD 中,tan ∠ACD =AD CD∴tan ∠BAC =tan ∠ACD . 故选B .【点睛】 本题主要考查了解直角三角形的应用,利用图形的性质进行角的等量代换是解本题的关键.7、D【解析】【分析】由切线的性质得出∠OAB =90°,由直角三角形的性质得出∠AOB =90°-∠ABO =54°,由等腰三角形的性质得出∠ADC =∠OAD ,再由三角形的外角性质即可得出答案.【详解】解:∵AB 为⊙O 的切线,∴∠OAB =90°,∵∠ABO =36°,∴∠AOB =90°﹣∠ABO =54°,∵OA =OD ,∴∠ADC =∠OAD ,∵∠AOB =∠ADC +∠OAD ,∴∠ADC =12∠AOB =27°;故选:D .本题考查了切线的性质、直角三角形的性质、等腰三角形的性质以及三角形的外角性质;熟练掌握切线的性质和等腰三角形的性质是解题的关键.8、D【解析】【分析】连接CD ,由直角三角形斜边中线定理可得CD =BD ,然后可得△CDB 是等边三角形,则有BD =BC =5cm ,进而根据勾股定理可求解.【详解】解:连接CD ,如图所示:∵点D 是AB 的中点,90C ∠=︒,10cm AB =, ∴15cm 2CD BD AB ===, ∵CD BC =,∴5cm CD BD BC ===,在Rt△ACB 中,由勾股定理可得AC =;故选D .本题主要考查圆的基本性质、直角三角形斜边中线定理及勾股定理,熟练掌握圆的基本性质、直角三角形斜边中线定理及勾股定理是解题的关键.9、D【解析】【分析】取AB 的中点D ,连接AD ,BD ,则AB =2BD =2AD 根据圆心角、弧、弦关系定理的推论得到AD BD AC ==,又在ABD ∆中,根据三角形三边关系定理得出AD BD AB +>,即可得到2AB AC <.【详解】如图,取弧AB 的中点D ,连接AD ,BD ,则AB =2BD =2AD∵AB =2AC∴BD =AD =ACAD BD AC ∴==.在ABD ∆中,AD BD AB +>,AC AC AB ∴+>,即2AB AC <.故选:D .【点睛】本题主要考查了圆心角、弧、弦的关系及三角形三边关系定理,准确作出辅助线,得出==是解题的关键.AD BD AC10、C【解析】【分析】根据⊙O的半径r=4,且点A到圆心O的距离d=5知d>r,据此可得答案.【详解】解:∵⊙O的半径r=4,且点A到圆心O的距离d=5,∴d>r,∴点A在⊙O外,故选:C.【点睛】本题主要考查点与圆的位置关系,点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:①点P在圆外⇔d>r;②点P在圆上⇔d=r;③点P在圆内⇔d<r.二、填空题π1、2【解析】【分析】连接AC,根据圆周角定理得出AC为圆的直径,解直角三角形求出AB,根据扇形面积公式进行求解即可.【详解】解:如图,连接AC,∵从一块直径为2cm 的圆形铁皮上剪出一个圆心角为90°的扇形,即∠ABC =90°,∴AC 为直径,即AC =2cm ,AB =BC (扇形的半径相等),∵在Rt ABC 中,22222AB BC AC +==,∴AB =BC ∴阴影部分的面积是()29023602ππ= (cm 2).故答案为:2π. 【点睛】 本题考查了圆周角定理和扇形的面积计算,熟记扇形的面积公式是解题的关键.2、132°【解析】【分析】连接AO 、BO 、CO ,根据AB 是⊙O 的内接正六边形的一边,可得360606AOB ︒∠==︒ ,AO BO = ,从而得到∠ABO =60°,再由BC 是⊙O 的内接正十边形的一边,可得3603610BOC ︒︒∠== ,BO =CO ,从而得到72CBO ∠=︒,即可求解.【详解】解:如图,连接AO 、BO 、CO ,∵AB 是⊙O 的内接正六边形的一边, ∴360606AOB ︒∠==︒ ,AO BO = , ∴()118060602ABO ∠=︒-︒=︒ , ∵BC 是⊙O 的内接正十边形的一边, ∴3603610BOC ︒︒∠== ,BO =CO , ∴()118036722CBO ∠=︒-︒=︒, ∴∠ABC =∠ABO + ∠CBO =60°+72°=132°.故答案为:132°【点睛】本题主要考查了圆的内接多边形的性质,等腰三角形的性质,熟练掌握圆的内接多边形的性质,等腰三角形的性质是解题的关键.3、18.84【解析】【分析】先根据弧长公式求得πr ,然后再运用圆的周长公式解答即可.【详解】解:设圆弧所在圆的半径为r 厘米,则60 3.14180r π⨯=, 解得9.42r π=,则它所在圆的周长为229.4218.84r π=⨯=(厘米),故答案为:18.84.【点睛】本题主要考查了弧长公式、圆的周长公式等知识点,牢记弧长公式是解答本题的关键.4、 12a 【解析】【分析】过O 作OC 垂直于弦AB ,利用垂径定理得到C 为AB 的中点,然后由OA =OB ,且∠AOB 为直角,得到三角形OAB 为等腰直角三角形,由斜边AB 的长,利用勾股定理求出直角边OA 的长即可;再由C 为AB 的中点,由AB 的长求出AC 的长,在直角三角形OAC 中,由OA 及AC 的长,利用勾股定理即可求出OC 的长,即为O 点到AB 的距离.【详解】解:过O 作OC ⊥AB ,则有C 为AB 的中点,∵OA =OB ,∠AOB =90°,AB =a ,∴根据勾股定理得: OA 2+OB 2=AB ,∴OA ,在Rt△AOC中,OA,AC=12AB=12a,根据勾股定理得:OC 12 a.;1 2 a【点睛】此题考查了垂径定理,等腰直角三角形的性质,以及勾股定理,在圆中遇到弦,常常过圆心作弦的垂线,根据近垂径定理由垂直得中点,进而由弦长的一半,圆的半径及弦心距构造直角三角形,利用勾股定理来解决问题.5、104°##104度【解析】【分析】在优弧AB上取一点D,连接AD、BD,由圆内接四边形的性质求出∠ADB=52°,根据圆周角定理即可得出结论.【详解】解:在优弧AB上取一点D,连接AD、BD,如图所示:∵∠ACB=128°,∴∠ADB=180°-∠ACB=52°,∴∠AOB=2∠ADB=104°.故答案为:104°.【点睛】本题考查了圆周角定理.在同圆或等圆中,同弧和等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.6、6【解析】【分析】如图,连接OA、OB、OC、OD、OE、OF,证明△AOB、△BOC、△DOC、△EOD、△EOF、△AOF都是等边三角形,再求出圆的半径即可.【详解】解:如图,连接OA、OB、OC、OD、OE、OF.∵正六边形ABCDEF,∴AB=BC=CD=DE=EF=FA,∠AOB=∠BOC=∠COD=∠DOE=∠EOF=∠FOA=60°,∴△AOB、△BOC、△DOC、△EOD、△EOF、△AOF都是等边三角形,∵O的周长为12π,∴O的半径为1262ππ=,正六边形的边长是6;【点睛】本题考查正多边形与圆的关系、等边三角形的判定和性质等知识,明确正六边形的边长和半径相等是解题的关键.7、110°##110度【解析】【分析】根据圆内接四边形对角互补,得∠D +∠B =180°,结合已知求解即可.【详解】∵圆内接四边形对角互补,∴∠D +∠B =180°,∵40D B ∠-∠=︒∴∠D =110°,故答案为:110°.【点睛】本题考查了圆内接四边形互补的性质,熟练掌握并运用性质是解题的关键.8、15##十五【解析】【分析】根据圆周角定理可得正多边形的边AB 所对的圆心角∠AOB =24°,再根据正多边形的一条边所对的圆心角的度数与边数之间的关系可得答案.【详解】解:如图,设正多边形的外接圆为⊙O ,连接OA ,OB ,∵∠ADB =12°,∴∠AOB =2∠ADB =24°,而360°÷24°=15,∴这个正多边形为正十五边形,故答案为:15.【点睛】本题考查正多边形与圆,圆周角,掌握圆周角定理是解决问题的关键,理解正多边形的边数与相应的圆心角之间的关系是解决问题的前提.9、60︒【解析】【分析】根据圆内接四边形的性质,对角之和等于180︒即可求解.【详解】解:根据圆内接四边形的性质,对角之和等于180︒,∴∠+∠=︒,D B180∴∠=︒-︒=︒,B18012060故答案为:60︒.【点睛】本题考查了圆周角定理,解题的关键是掌握圆周角定理.10、上【解析】【分析】AD AC结合点与圆心的距离等于圆的半径,则点在圆上,从而可得答先利用中点的含义求解2,案.【详解】解:如图,90C ∠=︒,2AC =,4AB =,D 为AB 的中点,12,2ADAB ACD ∴在A 上, 故答案为:上【点睛】本题考查的是点与圆的位置关系的判断,掌握“点与圆的位置关系的判断方法”是解本题的关键.三、解答题1、 (1)见解析(2)16920【解析】【分析】(1)根据平行线的性质可得C ADO ∠=∠,根据圆内接四边形的一个外角等于其内对角可得CED DAO ∠=∠,又半径相等可得DAO ADO ∠=∠,等量代换可得C CED ∠=∠,根据等角对等边即可求证;(2)根据平行线分线段成比例可得132AD DC ==,根据根据(1)的结论可得CAB CED △∽△,列出比例式,代入数值即可求得AB 的长,进而求得OA 的长.(1)证明:∥OD BCC ADO∴∠=∠四边形ADEB是O的内接四边形∴CED DAO∠=∠OD OA=DAO ADO∴∠=∠C CED∴∠=∠∴CD DE=(2)OD BC∥AD AODC OB∴=OA OB=,13,52AD CE==132AD DC∴==,C C CED CAB ∠=∠∠=∠CAB CED∴∽CE CACD AB∴=即513 132AB=解得16910AB=1169 220OA AB ∴==【点睛】本题考查了等边对等角证明边相等,圆内接四边形,平行线分线段成比例,相似三角形的性质与判定,掌握以上知识是解题的关键.2、 (1)见解析(2)图见解析,圆心P 的坐标是(3,4)【解析】【分析】(1)根据题意可得()()()1110,6,4,2,8,2A B C ,再顺次连接,即可求解;(2)根据题意可得分别作出BC ,AC 边的垂直平分线,交于点P ,即可求解;(3)连接AP ,可得AP =,再利用弧长公式计算,即可求解.(1)解:根据题意得:()()()1110,6,4,2,8,2A B C , 根据题意画出图形,如下图所示:111A B C △即为所求;(2)解:根据题意分别作出BC ,AB 边的垂直平分线,交于点P ,再以P 为圆心,BP 长为半径作圆,则P 即为所求,如图所示,∵点()()()0,3,2,1,4,1A B C ,∴点P 的横坐标为3,∵点P 在AB 的垂直平分线上,且AB 是边长为2的正方形的对角线,∴点P 位于边长为3的正方形的对角线上,∴点P 的纵坐标为4,∴圆心P 的坐标是(3,4);(3)解:连接AP ,则AP =,∵将△ABC 绕(2)中的点P 将△ABC 绕点P 顺时针旋转90°,∴点A =. 【点睛】本题主要考查了画位似图形,三角形的外接圆,求弧长,熟练掌握位似图形的性质,三角形的外接圆的性质,弧长公式是解题的关键.3、(1)①见解析;②见解析;(2)32π. 【解析】(1)①连接OD ,由角平分线的性质解得DAB DAO ∠=∠,再根据内错角相等,两直线平行,证明//DO AB ,继而由两直线平行,同旁内角互补证明90ODB ∠=︒即可解题;②连接DE ,由弦切角定理得到CDE DAC ∠=∠,再证明CDE CAD ,由相似三角形对应边成比例解题; (2)证明,OFD OFA 是等边三角形,四边形DOAF 是菱形,=DFO S S 阴影扇形,结合扇形面积公式解题.【详解】解:(1)①连接OD , AD 是∠BAC 的平分线DAB DAO ∴∠=∠OD OA =DAO ODA ∴∠=∠DAB ODA ∴∠=∠//DO AB ∴180B ODB ∴∠+∠=︒90B ∠=︒90ODB ∴∠=︒OD BC ∴⊥BC ∴是⊙O 的切线;BC是⊙O的切线,∴∠=︒90CDO∵是直径AEADE∴∠=︒90∴∠=∠CDE ODA=OD OA∴∠=∠ODA DAC∴∠=∠CDE DAC∠∠=C C∴CDE CADCD CE∴=AC CD2∴=⋅CD CE CA(2)连接DE、OD、DF、OF,设圆的半径为R,点F 是劣弧AD 的中点,∴OF 是DA 中垂线∴DF =AF ,FDA FAD ∴∠=∠//DO ABODA DAF ∴∠=∠ODA DAO FDA FAD ∴∠=∠=∠=∠AF DF OA OD ∴===,OFD OFA ∴是等边三角形,四边形DOAF 是菱形,60ODF DOF FOA ∴∠=∠=∠=︒=DFO S S ∴阴影扇形60,90DOC ODC ∠=︒∠=︒30C ∴∠=︒11()22OD OC OE EC ∴==+ ,3OE OD CE ==3CE OE R ∴===26033===3602DFO S S ππ⋅∴阴影扇形. 【点睛】本题考查圆的综合题,涉及切线的判定与性质、平行四边形的性质、等边三角形的判定与性质、相似三角形的判定与性质、扇形面积等知识,综合性较强,有难度,掌握相关知识是解题关键.4、 (1)(1,1)-(2)32π【解析】【分析】(1)根据对应点连线段的垂直平分线的交点即为旋转中心,可得结论.(2)根据A 经过的路径长为以M 为圆心,3为半径的圆周长的14即可求解. (1)解:连接,AD BE ,分别作,AD BE 的垂直平分线交点M 即为所求,如下图:(1,1)M ∴-,故答案是:(1,1)-;(2)解:由题意及下图,知点A 经过的路径长为以M 为圆心,3为半径的圆周长的14,∴点A 经过的路径长为:13242r ππ⨯=, 故答案是:32π.【点睛】 本题考查坐标与图形变化-旋转,解题的关键是理解旋转中心是对应点连线段的垂直平分线的交点.5、 (1)∠APC =60°,∠BPC =60°(2)见解析【解析】【分析】(1)根据等边三角形的性质得到∠ABC =∠BAC =∠ACB =60°,根据圆周角定理即可得到∠APC =∠ABC =60°,∠BPC =∠BAC =60°;(2)根据平行线的性质得到∠BPM +∠M =180°,∠PCM =∠BPC ,求得∠M =∠BPC =60°,根据圆周角定理得到∠PAC +∠PCB =180°,根据全等三角形的判定定理即可得到结论;(3)作PH ⊥CM 于H ,根据全等三角形的性质得到CM =CP ,AM =BP ,根据直角三角形的性质得到PH ,根据三角形的面积公式即可得到结论;(4)过点B 作BQ ⊥AP ,交AP 的延长线于点Q ,过点A 作AN ⊥BC 于点N ,连接OB ,求得∠PBQ =30°,得到PQ ,根据勾股定理得到BQ 和AN ,根据弧长公式即可得到结论.(1)解:∵△ABC 是等边三角形,∴∠ABC =∠BAC =∠ACB =60°,∵BC BC =,AC AC =,∴∠APC =∠ABC =60°,∠BPC =∠BAC =60°;(2)证明:∵CM ∥BP ,∴∠BPM +∠M =180°,∠PCM =∠BPC ,∵∠BPC =∠BAC =60°,∴∠PCM =∠BPC =60°,∴∠M =180°-∠BPM =180°-(∠APC +∠BPC )=180°-120°=60°,∴∠M =∠BPC =60°,又∵A 、P 、B 、C 四点共圆,∴∠PAC +∠PCB =180°,∵∠MAC +∠PAC =180°,∴∠MAC =∠PBC ,∵AC =BC ,在△ACM 和△BCP 中,M BPC MAC PBC AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ACM ≌△BCP (AAS );(3)解:∵CM ∥BP ,∴四边形PBCM 为梯形,作PH ⊥CM 于H ,∵△ACM ≌△BCP ,∴CM =CP ,AM =BP ,又∠M =60°,∴△PCM 为等边三角形,∴CM =CP =PM =PA +AM =PA +PB =1+2=3,在Rt △PMH 中,∠MPH =30°,∴PH ,∴S 四边形PBCM =12(PB +CM )×PH =12(2+3; (4) 解:过点B 作BQ ⊥AP ,交AP 的延长线于点Q ,过点A 作AN ⊥BC 于点N ,连接OB ,∵∠APC =∠BPC =60°,∴∠BPQ =60°,∴∠PBQ =30°,∴PQ =12PB =1,在Rt △BPQ 中,BQ在Rt △AQB 中,AB =∵△ABC为等边三角形,∴AN经过圆心O,∴BN=12 AB∴AN=在Rt△BON中,设BO=x,则ON−x,2x)2=x2,解得:x,∵∠BOA=∠BCA=120°,∴AB的长度为1203180π=【点睛】本题考查了三角形的外接圆与外心,全等三角形的判定和性质,解直角三角形,等边三角形的判定和性质,平行线的性质,正确的作出辅助线是解题的关键.。
【期末复习】华东师大版九年级数学下册《第27章圆》单元评估检测试卷(有答案)
期末专题复习:华师大版九年级数学上册第27章圆单元评估检测试卷一、单选题(共10题;共30分)1.如图,⊙O为△ABC的外接圆,∠BAC=55°,则∠OBC 的度数为()A. 25°B. 35°C. 55°D. 70°2.已知圆O的半径是3,A,B,C 三点在圆O上,∠ACB=60°,则弧AB的长是()A. 2πB. πC. 32π D. 12π3.如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠OCB的度数为()A. 40°B. 50°C. 65°D. 75°4.某圆锥的母线长为6cm,其底面圆半径为3cm,则它的侧面积为()A. 18πcm2B. 18cm2C. 36πcm2D. 36cm25.如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于点C,若∠AOB=120°,则大圆半径R与小圆半径r之间满足()A. R=3rB. R=3rC. R=2rD. R=22r6.如图,在⊙O中,若C是BD的中点,则图中与∠BAC相等的角有()A.1个B.2个C.3个D.4个7.如图,AB是⊙O的弦,点C在圆上,已知∠AOB=100°,则∠C=()A. 40°B. 50°C. 60°D. 80°8.如图,两圆相交于A,B两点,小圆经过大圆的圆心O,点C、D分别在两圆上,若∠ADB=110°,则∠ACB 的度数为()A. 35°B. 40°C. 50°D. 80°9.如图,在⊙O中,∠AOB的度数为m,C是上一点,D,E是上不同的两点(不与A,B两点重合),则∠D +∠E的度数为( )C. 90°+m2D. m2A. mB. 180°-m210.如图,从⊙O外一点P引圆的两条切线PA、PB,切点分别是A、B,如果∠APB=60°,线段PA=10,那么弦AB的长是()A. 10B. 12C. 53D. 103二、填空题(共10题;共30分)11.已知如图,在⊙O中,弦AB的长为8,圆心O到AB的距离为3.若点P是AB上的一动点,则OP的取值范围是________.12.某体育馆的圆弧形屋顶如图所示,最高点C到弦AB的距离是20m,圆弧形屋顶的跨度AB是80m,则该圆弧所在圆的半径为________m.13.如图,AB是⊙O的直径,点C为⊙O上一点,∠AOC=50°,则∠ABC= ________.14.如图,AB是半圆的直径,∠BAC=20°,D是AC的中点,则∠DAC的度数是________.15.若用半径为12,圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥底面圆的半径的长________.16.如图,AB、AC与⊙O相切于点B、C,∠A=50゜,P为⊙O上异于B、C的一个动点,则∠BPC的度数为________ 。
达标测试华东师大版九年级数学下册第27章 圆同步测评练习题(含详解)
华东师大版九年级数学下册第27章 圆同步测评考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图,点C 是以点O 为圆心,AB 为直径的半圆上的动点(点C 不与点A ,B 重合),4AB =.设弦AC 的长为x ,ABC ∆的面积为y ,则下列图象中,能表示y 与x 的函数关系的图象大致是( )A .B .C .D .2、如图,Rt ABC △中,90C ∠=︒,O 是AB 边上一点,O 与AC 、BC 都相切,若3BC =,4AC =,则O 的半径为( )A .1B .2C .52 D .1273、如图,CD 是ABC 的高,按以下步骤作图:(1)分别以点A 和点B 为圆心,大于12AB 的长为半径作弧,两弧相交于G 、H 两点. (2)作直线GH 交AB 于点E .(3)在直线GH 上截取EF AE =.(4)以点F 为圆心,AF 长为半径画圆交CD 于点P .则下列说法错误的是( )A .AE BE =B .GH CD ∥C .AB =D .45APB ∠=︒4、如图,P 为正六边形ABCDEF 边上一动点,点P 从点D 出发,沿六边形的边以1cm/s 的速度按逆时针方向运动,运动到点C 停止.设点P 的运动时间为()s x ,以点P 、C 、D 为顶点的三角形的面积是()2cm y ,则下列图像能大致反映y 与x 的函数关系的是( )A .B .C .D .5、如图,PA ,PB 是⊙O 的切线,A ,B 为切点,PA =4,则PB 的长度为()A .3B .4C .5D .66、如图,AB 是O 的直径,CD 是O 的弦.50CAB ∠=,则∠D =()度A .30B .40C .50D .607、如图,点A 、B 、C 在O 上,50∠=°ACB ,则OAB ∠的度数是()A .100°B .50°C .40°D .25°8、如图,在⊙O 中,C 、D 为⊙O 上两点,AB 是⊙O 的直径,已知∠AOC=130°,则∠BDC 的度数为( )A .65°B .50°C .30°D .25°9、已知正五边形的边长为1,则该正五边形的对角线长度为( ).A B C D 10、如图,正六边形螺帽的边长是4cm ,那么这个正六边形半径R 和扳手的开口a 的值分别是( )A .2,B .4,C .4,D .4第Ⅱ卷(非选择题 70分)二、填空题(10小题,每小题3分,共计30分)1、如图,AB 为O 的直径,点C ,D ,E 在O 上,且AD CD =,若64E ∠=︒,则ABC ∠的度数为__________︒.2、AC是⊙O的直径,弦BD⊥AC于点E,连接BC,过点O作OF⊥BC于点F,若BD=12cm,OE=5 2cm,则OF=________cm.3、如图,点A,B,C在⊙O上,四边形OABC是平行四边形,若对角线AC=AC的长为_____.4、在⊙O中,圆心角∠AOC=120°,则⊙O内接四边形ABCD的内角∠ABC=_____.5、如图,在Rt△ABC中,∠CAB=90°,AB=AC,点D为斜边BC上一点,且BD=3CD,将△ABD沿直线AD翻折,点B的对应点为B′,则sin∠CB′D=______.6、如图,过⊙O 外一点P ,作射线PA ,PB 分别切⊙O 于点A ,B ,50P ∠=︒,点C 在劣弧AB 上,过点C 作⊙O 的切线分别与PA ,PB 交于点D ,E .则DOE ∠=______度.7、圆锥的底面直径是80cm ,母线长90cm .它的侧面展开图的圆心角和圆锥的全面积依次是______.8、如图,在四边形ABCD 中,AB =BC =BD .若∠ABC =112°,则∠ADC =_____°.9、如图,把O 分成相等的六段弧,依次连接各分点得到正六边形ABCDEF ,如果O 的周长为12π,那么该正六边形的边长是______.10、已知:矩形ABCD 的长8AB =,宽6AD =,按如图放置在直线AP 上,然后不滑动地转动,当它转动一周时(A A '→,B B '→),顶点A 所经过的路线的长等于______.三、解答题(5小题,每小题8分,共计40分)1、已知四边形 ABCD 是菱形, 4AB =, 点 E 在射线 CB 上, 点 F 在射线 CD 上,且 EAF BAD ∠=∠.(1)如图, 如果 90BAD ∠=, 求证: AE AF = ;(2)如图, 当点 E 在 CB 的延长线上时, 如果 60ABC ∠=, 设 ,AF DF x y AE==, 试建立 y 与 x 的函数关系式,并写出 x 的取值范围(3)联结 ,2AC BE =, 当 AEC △ 是等腰三角形时,请直接写出 DF 的长.2、在平面直角坐标系xOy 中,⊙O 的半径为1,对于直线l 和线段AB ,给出如下定义:若将线段AB 关于直线l 对称,可以得到⊙O 的弦A ´B ´(A ´,B ´分别为A ,B 的对应点),则称线段AB 是⊙O 的关于直线l 对称的“关联线段”.例如:在图1中,线段AB 是⊙O 的关于直线l 对称的“关联线段”.(1)如图2,11,2233,,,,A B A B A B 的横、纵坐标都是整数.①在线段11,2233,A B A B A B 中,⊙O 的关于直线y =x +2对称的“关联线段”是_______;②若线段11,2233,A B A B A B 中,存在⊙O 的关于直线y =-x +m 对称的“关联线段”,则 m = ;(2)已知直线+(0y x b b =>)交x 轴于点C ,在△ABC 中,AC =3,AB =1,若线段AB 是⊙O 的关于直线+(0y x b b =>)对称的“关联线段”,直接写出b 的最大值和最小值,以及相应的BC 长.3、如图1,ABC中,AC=BC=4,∠ACB=90°,过点C任作一条直线CD,将线段BC沿直线CD翻折得线段CE,直线AE交直线CD于点F.直线BE交直线CD于G点.(1)小智同学通过思考推得当点E在AB上方时,∠AEB的角度是不变的,请按小智的思路帮助小智完成以下推理过程:∵AC=BC=EC,∴A、B、E三点在以C为圆心以AC为半径的圆上,∴∠AEB=∠ACB,(填写数量关系)∴∠AEB=°.(2)如图2,连接BF,求证A、B、F、C四点共圆;(3)线段AE最大值为,若取BC的中点M,则线段MF的最小值为.4、如图,在平面直角坐标系中,△ABC的三个顶点A、B、C的坐标分别为(0,3)、(2,1)、(4,1).(1)以原点O为位似中心,在第一象限画出△ABC的位似图形△ABC,使△A1B1C1与△ABC的相似比为2:1;(2)借助网格,在图中画出△ABC的外接圆P,并写出圆心P的坐标;(3)将△ABC 绕(2)中的点P 将△ABC 绕点P 顺时针旋转90°,则点A 运动的路线长是 .5、下面是小亮设计的“过圆上一点作已知圆的切线”的尺规作图过程.已知:点A 在O 上.求作:直线PA 和O 相切.作法:如图,①连接AO ;②以A 为圆心,AO 长为半径作弧,与O 的一个交点为B ;③连接BO ;④以B 为圆心,BO 长为半径作圆;⑤作B 的直径OP ;⑥作直线PA .所以直线PA 就是所求作的O 的切线.根据小亮设计的尺规作图过程,(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)完成下面的证明:证明:在O 中,连接BA .∵OA OB =,AO AB =,∴OB AB =.∴点A 在B 上.∵OP 是B 的直径,∴90OAP ∠=︒(______)(填推理的依据).∴OA AP ⊥.又∵点A 在O 上,∴PA 是O 的切线(______)(填推理的依据).-参考答案-一、单选题1、B【解析】【分析】由AB 为圆的直径,得到∠C =90°,在Rt △ABC 中,由勾股定理得到BC =而列出△ABC 面积的表达式即可求解.【详解】解:∵AB 为圆的直径,∴∠C =90°,4AB =,AC x =,由勾股定理可知:∴BC ==∴1122∆=⋅=⋅ABC S BC AC x 此函数不是二次函数,也不是一次函数,∴排除选项A 和选项C ,AB 为定值,当OC AB ⊥时,ABC ∆面积最大,此时AC =即x =y 最大,故排除D ,选B .故选:B .【点睛】本题考查了动点问题的函数图象,根据题意列出函数表达式是解决问题的关键.2、D【解析】【分析】作OD ⊥AC 于D ,OE ⊥BC 于E ,如图,设⊙O 的半径为r ,根据切线的性质得OD =OE =r ,易得四边形ODCE 为正方形,则CD =OD =r ,再证明△ADO ∽△ACB ,然后利用相似比得到443r r -=,再根据比例的性质求出r 即可.【详解】解:作OD ⊥AC 于D ,OE ⊥BC 于E ,如图,设⊙O 的半径为r ,∵⊙O 与AC 、BC 都相切,∴OD =OE =r ,而∠C =90°,∴四边形ODCE 为正方形,∴CD =OD =r ,∵OD∥BC,∴△ADO∽△ACB,∴AF OF AC BC=∵AF=AC-r,BC=3,AC=4,代入可得,443r r -=∴r=127.故选:D.【点睛】本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了相似三角形的判定与性质.3、C【解析】【分析】连接AF、BF,由作法可知,FE垂直平分AB,再根据EF AE=可得∠AFE=45°,进而得出∠AFB=90°,根据等腰直角三角形和圆周角定理可判断哪个结论正确.【详解】解:连接AF、BF,由作法可知,FE垂直平分AB,∴AE BE=,故A正确;∵CD是ABC的高,∴GH CD∥,故B正确;∵EF AE=,AE BE=,∴2AB EF =,故C 错误;∵EF AE =,∴∠AFE =45°,同理可得∠BFE =45°,∴∠AFB =90°,1452APB AFB ∠=∠=︒,故D 正确; 故选:C .【点睛】本题考查了作垂直平分线和圆周角定理,解题关键是明确作图步骤,熟练运用垂直平分线的性质和圆周角定理进行推理证明.4、A【解析】【分析】设正六边形ABCDEF 的边长为1,当P 在DE 上时,过P 作PH CD ⊥于,H 而120,,CDP PD x 求解此时的函数解析式,当P 在EF 上时,延长,CD FE 交于点,M 过P 作PQ CD ⊥于,Q 并求解此时的函数解析式,当P 在AF 上时,连接,,AC CF 并求解此时的函数解析式,由正六边形的对称性可得:P 在AB 上的图象与P 在EF 上的图象是对称的,P 在BC 上的图象与P 在DE 上的图象是对称的,从而可得答案.【详解】解:设正六边形ABCDEF 的边长为1,当P 在DE 上时,过P 作PH CD ⊥于,H 而120,,CDP PD x60,PDH 3sin 60,2PH PD x11331,2224y CD PH x x 当P 在EF 上时,延长,CD FE 交于点,M 过P 作PQ CD ⊥于,Q同理:120,CDEFED 60,EDM DEM则DEM △为等边三角形, 60,1,,EMD EM ED PMPE EM PE ED x 3sin 60,2PQ PM x 11331,2224y CD PQ x x 当P 在AF 上时,连接,,AC CF由正六边形的性质可得:120,,ABCBAF AFE BA BC 118012030,1203090,2BAC CAF 由正六边形的对称性可得:160,2AFC AFE 而1,AF =tan 603,AC AF 11313,222y CD AC 由正六边形的对称性可得:P 在AB 上的图象与P 在EF 上的图象是对称的,P 在BC 上的图象与P 在DE 上的图象是对称的,所以符合题意的是A ,故选A【点睛】本题考查的是动点问题的函数图象,锐角三角函数的应用,正多边形的性质,清晰的分类讨论是解本题的关键.5、B【解析】【分析】由切线的性质可推出OA AP ⊥,OB BP ⊥.再根据直角三角形全等的判定条件“HL ”,即可证明OAP OBP ≅,即得出4PB PA ==.【详解】∵PA ,PB 是⊙O 的切线,A ,B 为切点,∴OA AP ⊥,OB BP ⊥,∴在Rt OAP △和Rt OBP 中,OA OB OP OP =⎧⎨=⎩, ∴()OAP OBP HL ≅,∴4PB PA ==.故选:B【点睛】本题考查切线的性质,三角形全等的判定和性质.熟练掌握切线的性质是解答本题的关键.6、B【解析】【分析】由AB 是⊙O 的直径,推出∠ACB =90°,再由∠CAB =50°,求出∠B =40°,根据圆周角定理推出∠D =40°.【详解】解:∵AB 是⊙O 的直径,∴∠ACB =90°,∵∠CAB =50°,∴∠B =40°,∴∠D =40°.故选:B .【点睛】本题主要考查圆周角定理,余角的性质,关键在于推出∠A 的度数,正确的运用圆周角定理.7、C【解析】【分析】先根据圆周角定理求出∠AOB的度数,再由等腰三角形的性质即可得出结论.【详解】∵∠ACB=50°,∴∠AOB=100°,∵OA=OB,∴∠OAB=∠OBA= 40°,故选:C.【点睛】本题考查的是圆周角定理,即在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.8、D【解析】【分析】先求出∠BOC的度数,再根据同弧所对的圆周角等于圆心角的一半求出答案.【详解】解:∵∠AOC=130°,AB是⊙O的直径,∴∠BOC=180°-∠AOC=50°,∠BOC=25°,∴∠BDC=12故选:D.【点睛】此题考查了圆周角定理:同弧所对的圆周角等于圆心角的一半,熟记定理是解题的关键.9、C【解析】【分析】如图,五边形ABCDE 为正五边形, 证明,AB BCAE CD ,AF BF BG CG 1,AB AG 再证明,ABF ACB ∽可得:,ABBF AC CB设AF =x ,则AC =1+x ,再解方程即可. 【详解】解:如图,五边形ABCDE 为正五边形,∴五边形的每个内角均为108°,,AB BC AE CD∴∠BAG =∠ABF =∠ACB =∠CBD = 36°,∴∠BGF =∠BFG =72°,72,ABGAGB ,,,AF BF BG GC BG BF ,AF BF BG CG 1,ABAG ,,BAC FAB ABF ACB,ABF ACB ∽,ABBF AC CB设AF =x ,则AC =1+x , 1,11x x210,x x ∴+-=解得:12x x ==经检验:x =15151.22AC故选C【点睛】本题考查的是正多边形的性质,等腰三角形的判定与性质,相似三角形的判定与性质,证明ABF ACB ∽△△是解本题的关键.10、B【解析】【分析】根据正六边形的内角度数可得出∠BAD =30°,OAB ∆为等边三角形,得BC =2AB ,再通过解直角三角形即可得出12a 的值,进而可求出a 的值,此题得解.【详解】解:如图,∵正六边形的任一内角为120°,∴∠ABD =180°-120°=60°,60OAB OBA ∠=∠=︒∴∠BAD =30°,OAB ∆为等边三角形,∵4AB =∴2,4BD OB OA ===∴AD =∴2a =⨯=∴这个正六边形半径R 和扳手的开口a 的值分别是4,故选:B .【点睛】本题考查了正多边形以及勾股定理,牢记正多边形的内角度数是解题的关键.二、填空题1、52【解析】【分析】如图,连接OD ,BD .利用圆周角定理求出∠DOB ,再求出∠OBD =26°,可得结论.【详解】解:如图,连接OD ,BD .∵AD CD =,∴∠ABD=∠CBD,∵∠DOB=2∠DEB=128°,∴∠OBD=∠ODB=26°,∴∠ABC=2∠OBD=52°,故答案为:52.【点睛】本题考查圆周角定理,等腰三角形的性质,三角形内角和定理等知识,解题的关键是掌握圆周角定理.2【解析】【分析】根据题意分两种情况并综合利用垂径定理和勾股定理以及圆的基本性质进行分析即可求解.【详解】解:如图,连接BO∵AC是⊙O的直径,弦BD⊥AC于点E,BD=12cm,∴162BE ED BD cm ===,∵OE =52cm ,BD ⊥AC ,∴132BO CO AO ===cm ,∴9CE CO CE cm =+=,BC =,∵OF ⊥BC ,∴12CF BF BC ==,∴OF ,如图,∵OE =52cm ,BD ⊥AC , 132BO CO AO cm ===,∴4,EC CO OE cm BC =-==,∵OF ⊥BC ,∴12BF CF BC ==,∴OF =.【点睛】 本题考查圆的综合问题,熟练掌握并利用垂径定理和勾股定理以及圆的基本性质进行分析是解题的关键.注意未作图题一般情况下要进行分类作图讨论.3、4π3【解析】【分析】连接OB ,交AC 于点D ,根据有一组邻边相等的平行四边形是菱形,可得四边形OABC 为菱形,根据菱形的性质可得:OB AC ⊥,OA AB =,AD DC =,根据等边三角形的判定得出OAB 为等边三角形,由此得出120AOC ∠=︒,在直角三角形中利用勾股定理即可确定圆的半径,然后代入弧长公式求解即可.【详解】解:如图所示,连接OB ,交AC 于点D ,∵四边形OABC 为平行四边形,OA OC =,∴四边形OABC 为菱形,∴OB AC ⊥,OA AB =,12AD DC AC === ∵OA OB AB ==,∴OAB 为等边三角形,∴60AOB ∠=︒,∴120AOC ∠=︒,在Rt OAD 中,设AO r =,则12OD r =, ∴222AD OD AO +=,即22212r r ⎛⎫+= ⎪⎝⎭, 解得:2r =或2r =-(舍去),∴AC 的长为:120241803ππ⨯⨯=, 故答案为:43π. 【点睛】题目主要考查菱形的判定和性质,等边三角形的判定和性质,勾股定理,弧长公式等,熟练掌握各个定理和公式是解题关键.4、120°##120度【解析】【分析】先根据圆周角定理求出∠D ,然后根据圆内接四边形的性质求解即可.【详解】解:∵∠AOC =120°∴∠D =12∠AOC =60°∵⊙O 内接四边形ABCD∴∠ABC =180°-∠D =120°.故答案是120°.【点睛】本题主要考查了圆周角定理、圆内接四边形的性质等知识点,掌握圆内接四边形的性质是解答本题的关键.5【解析】【分析】先证明A、B′、C、D四点共圆,推出∠CB′D=∠CAD,过点D作DE⊥AC于点E,利用平行线分线段成比例定理得到AE=3CE,由勾股定理得到AD,再由正弦函数即可求解.【详解】解:∵∠CAB=90°,AB=AC,∴∠ACB=∠B=45°,由折叠的性质得∠AB′D=∠B=45°,∴∠AB′D=∠ACD=45°,∴A、B′、C、D四点共圆,∴∠CB′D=∠CAD,过点D作DE⊥AC于点E,∵∠CAB=90°,∴DE∥AB,∵BD =3CD ,∴AE =3CE ,∵∠ACB =45°,∴△DEC 是等腰直角三角形,∴DE =CE ,设DE =CE =a ,则AE =3CE =3a ,在Rt △ADE 中,AD =,∴sin ∠CB ′D = sin ∠CAD =DE AD ==. 【点睛】 本题考查了圆内接四边形的知识,正弦函数,折叠的性质以及勾股定理,解答本题的关键是明确题意,找出所求问题需要的条件.6、65【解析】【分析】连接OA ,OC ,OB ,根据四边形内角和可得130AOB ∠=︒,依据切线的性质及角平分线的判定定理可得DO 平分ADC ∠,EO 平分BEC ∠,再由各角之间的数量关系可得AOD COD ∠=∠,COE BOE ∠=∠,根据等量代换可得12DOE AOB ∠=∠,代入求解即可.【详解】解:如图所示:连接OA ,OC ,OB ,∵PA 、PB 、DE 与圆相切于点A 、B 、E ,∴OA PA ⊥,OB PB ⊥,OC DE ⊥,∵50P ∠=︒,∴180130AOB P ∠=︒-∠=︒,∵OA OB OC ==,∴DO 平分ADC ∠,EO 平分BEC ∠,∴ADO CDO ∠=∠,CEO BEO ∠=∠,∴AOD COD ∠=∠,COE BOE ∠=∠, ∴11165222DOE COD COE AOC BOC AOB ∠=∠+∠=∠+∠=∠=︒,故答案为:65.【点睛】题目主要考查圆的切线的性质,角平分线的判定和性质,四边形内角和等,理解题意,作出相应辅助线,综合运用这些知识点是解题关键.7、160°,52002cm π【解析】【分析】由题意知,圆锥的展开图扇形的r 半径为90cm ,弧长l 为18022π80π2r π=⨯=.代入扇形弧长公式π180n r l =求解圆心角;代入扇形面积公式2π360n r S =侧求出圆锥侧面积,然后加上底面面积即可求出全面积.【详解】解:圆锥的展开图扇形的r 半径为90cm ,弧长l 为18022π80π2r π=⨯= ∵π180n r l = ∴9080π180n π⨯=解得160n =︒ ∵2π360n r S =侧 ∴22160π903600360S cm π⨯⨯==侧 22803600ππ52002S cm π⎛⎫=+⨯= ⎪⎝⎭全 故答案为:160°,25200cm π.【点睛】本题考查了扇形的圆心角与面积.解题的关键在于运用扇形的弧长与面积公式进行求解.难点在于求出公式中的未知量.8、124【解析】【分析】根据题意,,,A D C 在以B 为圆心半径为AB 的圆上,设E 是优弧AC 上任意一点,则四边形ADCE 是B 的内接四边形,进而根据圆内接四边形对角互补,圆周角定理求得E ∠,即可求得ADC ∠.【详解】解:如图,AB=BC=BDA D C在以B为圆心半径为AB的圆上,∴,,设E是优弧AC上任意一点,则四边形ADCE是B的内接四边形180∴∠+∠=︒E ADC又∠ABC=112°,E∴∠=︒56∴∠=︒-︒=︒ADC18056124故答案为:124【点睛】本题考查了圆内接四边形对角互补,圆周角定理,转为圆内接四边形求解是解题的关键.9、6【解析】【分析】如图,连接OA、OB、OC、OD、OE、OF,证明△AOB、△BOC、△DOC、△EOD、△EOF、△AOF都是等边三角形,再求出圆的半径即可.【详解】解:如图,连接OA、OB、OC、OD、OE、OF.∵正六边形ABCDEF,∴AB=BC=CD=DE=EF=FA,∠AOB=∠BOC=∠COD=∠DOE=∠EOF=∠FOA=60°,∴△AOB、△BOC、△DOC、△EOD、△EOF、△AOF都是等边三角形,∵O的周长为12π,∴O的半径为1262ππ=,正六边形的边长是6;【点睛】本题考查正多边形与圆的关系、等边三角形的判定和性质等知识,明确正六边形的边长和半径相等是解题的关键.10、12π【解析】【分析】点A走过的路线是三段弧线的和,即求出三个扇形的弧长之和.【详解】解:第一段是以AB为半径,弧长为:9028360π⨯⨯=4π;第二段是以AC,弧长为:90210360π⨯⨯=5π;第三段是以BC 为半径,弧长为:9026360π⨯⨯=3π; 所以顶点A 所经过的路线的长等于4π+5π+3π=12π.故答案为12π.【点睛】本题主要考查了弧长公式,根据题意确定扇形的半径是解答本题的关键.三、解答题1、 (1)证明过程详见解答; (2)4(04)4x y x -=<< (3)85DF =或167 【解析】【分析】(1)先证明四边形ABCD 是正方形,再证明ABE ADF ∆≅∆,从而命题得证;(2)在AD 上截取DG DF =,先证明DGF ∆是正三角形,再证明ABE AGF ∆∆∽,进一步求得结果;(3)当AE AC =时,作AH CE ⊥于H ,以F 为圆心,DF 为半径画弧交AD 于G ,作FN AD ⊥于N ,证明ABH FND ∆∆∽,AGF ABE ∠=∠,可推出12DG DF =,再证明ABE AGF ∆∆∽,可推出442DG GF -=,从而求得DF ,当6AC CE ==时,作AH CE ⊥于H ,以F 为圆心,DF 为半径画弧交AD 于G ,作FN AD ⊥于N ,作BM AC ⊥于M ,先根据1122ABC S AC BM BC AH ∆=⋅=⋅求得AH ,进而求得BH ,根据ABH FGN ∆∆∽,ABE AFF ∆∆∽,14DG GF =和412DG GF +=,从而求得DF ,根据三角形三边关系否定AE CE =,从而确定DF 的结果.(1) 解:证明:四边形ABCD 是菱形,90BAD ∠=︒,∴菱形ABCD 是正方形,90BAE ABC ADF ∴∠=∠=∠=︒,AD AB =,BAE DAF ∠=∠,()ABE ADF ASA ∴∆≅∆,AE AF ∴=;(2)解:如图1,在AD 上截取DG DF =,四边形ABCD 是菱形,60ADF ABC ∴∠=∠=︒,6AD AB ==,DGF ∴∆是正三角形,60DFG ∴∠=︒,GF DF DG x ===,120AGF ABE ∴∠=∠=︒,4AG x =-,BAE DAF ∠=∠,ABE AGF ∴∆∆∽, ∴AF AG AE AB=, 4(04)4x y x -∴=<<; (3)如图2,当AE AC =时,作AH CE ⊥于H ,以F 为圆心,DF 为半径画弧交AD 于G ,作FN AD ⊥于N ,11(42)322CH CE ∴==⨯+=,90FND AHB ∠=∠=︒,D FGD ∠=∠,2DG DN =, 431BH BC CH ∴=-=-=,四边形ABCD 是菱形,D ABC ∴∠=∠,ABH FND ∴∆∆∽,AGF ABE ∠=∠, ∴14DN BH DF AB ==, ∴12DG GF =①, BAE DAF ∠=∠,ABE AGF ∴∆∆∽, ∴AG GF AB BE=, ∴442DG GF -=②, 由①②得,85GF =,5如图3,当6AC CE ==时,作AH CE ⊥于H ,以F 为圆心,DF 为半径画弧交AD 于G ,作FN AD ⊥于N , 作BM AC ⊥于M ,132CM AC ∴==,BM ∴= 由1122ABC S AC BM BC AH ∆=⋅=⋅得,4AH =⋅,AH ∴12BH ∴, 由第一种情形知:ABH FGN ∆∆∽,ABE AFF ∆∆∽, ∴18GN BH FG AB ==,12AG AB GF BE ==, ∴14DG GF =①,412DG GF +=②, 由①②得,7167DF ∴=, AB BE AE +>,BC BE AE ∴+>,即CE AE >, 综上所述:85DF =或167. 【点睛】本题考查了菱形性质,正方形的判定和性质,相似三角形的判定和性质,面积法等知识,解题的关键是作辅助线,构造相似三角形.2、(1)① A 1B 1;②2或3;(2)b BC b BC =【解析】【分析】(1)①根据题意作出图象即可解答;②根据“关联线段”的定义,可确定线段A 2B 2存在“关联线段”,再分情况解答即可;(2)设与AB 对应的“关联线段”是A ’B ’,由题意可知:当点A ’(1,0)时,b 最大,当点A ’(-1,0)时,b 最小;然后分别画出图形求解即可;【详解】解:(1)①作出各点关于直线y =x +2的对称点,如图所示,只有A 1B 1符合题意;故答案为:A1B1;②由于直线A1B1与直线y=-x+m垂直,故A1B1不是⊙O的关于直线y=-x+m对称的“关联线段”;由于线段A3B3O的最大弦长直径=2,故A3B3也不是⊙O的关于直线y=-x+m对称的“关联线段”;A B A2B2是⊙O的关于直线y=x+2对称的“关联线段”;直线A2B2的解析式是y=-x+5,且22当A2B2是⊙O的关于直线y=-x+m对称的“关联线段”,且对应两个端点分别是(0,1)与(1,0)时,m=3,当A2B2是⊙O的关于直线y=-x+m对称的“关联线段”,且对应两个端点分别是(0,-1)与(-1,0)时,m=2,故答案为:2或3.(2)设与AB对应的“关联线段”是A’B’,由题意可知:当点A’(1,0)时,b最大,当点A’(-1,0)时,b最小;当点A’(1,0)时,如图,连接OB’,CB’,作B’M⊥x轴于点M,∴CA’=CA=3,∴点C坐标为(4,0),代入直线+=,得by b∵A’B’=OA’=OB’=1,∴△OA’B’是等边三角形,,'B M=,∴OM=12在直角三角形CB’M中,CB'=BC=当点A’(-1,0)时,如图,连接OB’,CB’,作B’M⊥x轴于点M,∴CA’=CA=3,∴点C坐标为(2,0),代入直线+y b=,得b∵A’B’=OA’=OB’=1,∴△OA’B’是等边三角形,∴OM=1,'B M=,2在直角三角形CB’M中,CB'=BC=综上,b BC b BC【点睛】本题是新定义综合题,主要考查了一次函数图象上点的坐标特点、圆的有关知识、等边三角形的判定和性质、勾股定理、轴对称的性质等知识,正确理解新定义的含义、灵活应用数形结合思想是解题的关键.,45;3、 (1)12(2)见解析;(3)8,2【解析】【分析】(1)根据同弧所对的圆周角等于圆心角的一半解答;(2)由题意知,CD垂直平分BE,连接BF,则BF=EF,求得∠EBF=∠AEB=45°,利用外角的性质得到∠AFB=∠EBF+∠AEB=90°,即可得到结论;(3)当点A、C、E在一条直线上时,线段AE最大,最大值为4+4=8,当MF⊥BC时线段MF最小,根据BC的中点M,得到CF=BF,设BG=FG=x,则x,CG x,由勾股定理得222+=,求出28CG BG BCx=-222MF=.BM MF BF+=,即可求出2(1)解:∵AC=BC=EC,∴A、B、E三点在以C为圆心以AC为半径的圆上,∠ACB,∴∠AEB=12∴∠AEB=45°.,45;故答案为:12(2)解:由题意知,CD垂直平分BE,连接BF,则BF=EF,∴∠EBF=∠AEB=45°.∴∠AFB=∠EBF+∠AEB=90°.∵∠ACB=90°,∴A、B、F、C在以AB为直径的圆上,即A、B、F、C四点共圆;(3)解:当点A、C、E在一条直线上时,线段AE最大,最大值为4+4=8,当MF⊥BC时线段MF最小,∵BC的中点M,∴CF=BF,设BG=FG=x ,则,CG +1)x ,∵222CG BG BC +=,∴2221)4x x ⎡⎤+=⎣⎦,得28x =-∵222BM MF BF +=,∴2222)MF +=,得2MF =,故答案为:8,2 ..【点睛】此题考查了圆周角定理,四点共圆的判定及性质,线段垂直平分线的性质,勾股定理,等腰直角三角形的性质,熟记各知识点并熟练应用解决问题是解题的关键.4、 (1)见解析(2)图见解析,圆心P 的坐标是(3,4)【解析】【分析】(1)根据题意可得()()()1110,6,4,2,8,2A B C ,再顺次连接,即可求解;(2)根据题意可得分别作出BC ,AC 边的垂直平分线,交于点P ,即可求解;(3)连接AP ,可得AP =,再利用弧长公式计算,即可求解.(1)解:根据题意得:()()()1110,6,4,2,8,2A B C , 根据题意画出图形,如下图所示:111A B C △即为所求;(2)解:根据题意分别作出BC ,AB 边的垂直平分线,交于点P ,再以P 为圆心,BP 长为半径作圆,则P 即为所求,如图所示,∵点()()()0,3,2,1,4,1A B C ,∴点P 的横坐标为3,∵点P 在AB 的垂直平分线上,且AB 是边长为2的正方形的对角线,∴点P 位于边长为3的正方形的对角线上,∴点P 的纵坐标为4,∴圆心P 的坐标是(3,4);(3)解:连接AP ,则AP =,∵将△ABC 绕(2)中的点P 将△ABC 绕点P 顺时针旋转90°,∴点A =. 【点睛】 本题主要考查了画位似图形,三角形的外接圆,求弧长,熟练掌握位似图形的性质,三角形的外接圆的性质,弧长公式是解题的关键.5、 (1)见解析(2)直径所对的圆周角是直角;经过半径的外端,并且垂直于这条半径的直线是圆的切线【解析】【分析】(1)根据题意作出图形即可;(2)根据圆周角定理得到∠OAP =90°,根据切线的判定定理即可得到结论.(1)解:补全的图形如图所示;(2)证明:在O 中,连接BA .∵OA OB =,AO AB =,∴OB AB =.∴点A 在B 上.∵OP 是B 的直径,∴90OAP ∠=︒(直径所对的圆周角是直角)(填推理的依据).∴OA AP ⊥.又∵点A 在O 上,∴PA 是O 的切线(经过半径的外端,并且垂直于这条半径的直线是圆的切线)(填推理的依据). 故答案为:直径所对的圆周角是直角;经过半径的外端,并且垂直于这条半径的直线是圆的切线【点睛】本题考查了作图,切线的判定,圆周角定理,正确的作出图形是解题的关键.。
精品试题华东师大版九年级数学下册第27章 圆同步测试试题(含详细解析)
华东师大版九年级数学下册第27章 圆同步测试考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图,在△ABC 中,∠A =30°,∠C =45°,BC =2,则AB 的长度为( )A .4π B .2π C .π D .2π2、如图,AB 是O 的直径,弦CD AB ⊥,垂足为E ,若61CD BE ==,,则AE =( )A .5B .8C .9D .103、扇形的半径扩大为原来的3倍,圆心角缩小为原来的19,那么扇形的面积( ) A .不变B .面积扩大为原来的3倍C .面积扩大为原来的9倍D .面积缩小为原来的134、如图,AB 为⊙O 的直径,C 、D 为⊙O 上两点,∠CDB =30°,BC =4.5,则AB 的长度为( )A .6B .3C .9D .125、如图,O 的半径为6,将劣弧沿弦AB 翻折,恰好经过圆心O ,点C 为优弧AB 上的一个动点,则ABC 面积的最大值是( )A .B .C .D .6、如图,O 是ABC ∆的外接圆,40OCB ∠=︒,则A ∠的度数是( )A .40︒B .80︒C .50︒D .45︒7、若120︒的圆心角所对的弧长是2π,则此弧所在圆的半径为( ) A .1B .2C .3D .48、如图,在Rt ABC 中,90C ∠=︒,10cm AB =,若以点C 为圆心,CB 的长为半径的圆恰好经过AB 的中点D ,则AC 的长等于( )A .5cmB .6cmC .D .9、筒车是我国古代发明的一种水利灌溉工具,如图1,筒车盛水桶的运行轨道是以轴心O 为圆心的圆,如图2,已知圆心O 在水面上方,且O 被水面截得弦AB 长为4米,O 半径长为3米.若点C 为运行轨道的最低点,则点C 到弦AB 所在直线的距离是( )A .1米B .2米C .(3米D .(3+米10、如图,PA ,PB 是⊙O 的切线,A ,B 为切点,PA =4,则PB 的长度为( )A .3B .4C .5D .6第Ⅱ卷(非选择题 70分)二、填空题(10小题,每小题3分,共计30分)1、如图,直线AB 与x 轴、y 轴分别相交于A 、B 两点,点A (-3,0),点 B (0,圆心P 的坐标为(1,0),圆P 与y 轴相切与点O .若将圆P 沿x 轴向左移动,当圆P 与该直线相交时,令圆心P 的横坐标为m ,则m 的取值范围是________.2、在圆内接四边形ABCD 中,40D B ∠-∠=︒,则D ∠的度数为______.3、圆锥的底面直径是80cm ,母线长90cm .它的侧面展开图的圆心角和圆锥的全面积依次是______.4、如图,一次函数1y x =+的图象与x 轴交于点A ,与y 轴交于点B ,作ABO 的外接圆C ,则图中阴影部分的面积为______.(结果保留π)5、若O 的半径为5cm ,点A 到圆心O 的距离为4cm ,那么点A 与O 的位置关系是__.6、如图,从一块直径为2cm 的圆形铁皮上剪出一圆心角为90°的扇形,则此扇形的面积为______cm 2.7、已知圆弧所在圆的半径为36cm .所对的圆心角为60°,则该弧的长度为______cm .8、如图,将半径为10cm 的圆形纸片沿一条弦AB 折叠,折叠后弧AB 的中点C 与圆心O 重叠,则弦AB 的长度为________cm .9、如图,在平行四边形ABCD 中,7AB =,3AD =,120A ︒∠=,以点B 为圆心,BC 为半径的圆弧交AB 于点E ,连接DE ,则图中黑色阴影部分的面积为________.(结果保留π)10、在△ABC 中,已知∠ABC =90°,∠BAC =30°,BC =1,如图所示,将△ABC 绕点A 按逆时针方向旋转90°后得到△AB ′C ′.则图中阴影部分的面积为_____.三、解答题(5小题,每小题8分,共计40分)1、一个扇形的圆心角60︒,半径为12cm,求它的面积.(保留)π2、如图,在88⨯的网格纸中,点O和点A都是格点,以O为圆心,OA为半径作圆.请仅用无刻度的直尺完成以下画图:(不写画法,保留作图痕迹.)(1)在图①中画⊙O的一个内接正八边形ABCDEFGH;(2)在图②中画⊙O的一个内接正六边形ABCDEF.3、如图,在△ABC中,AC=BC,AB=12,tan∠A=13.(1)尺规作图:以AC为直径作⊙O,与AB交于点D(不写作法,保留作图痕迹);(2)求⊙O的半径长度.4、定义: 有一边是另一边的 倍的三角形叫做优美三角形, 这两边的夹角叫做优美角. 如图1, 在优美三角形ABC 中, A ∠是优美角, AC AB D <,是AB 上一点,2ACD ABC AC ∠∠==,.(1)写出ACAB=____________; (2)求DB 的值;(3)如图2, CAB ∠的角平分线交CD 于点F , 交BC 于点E , 连结DE . ①求证: DBE 是优美三角形:②如图3,连结BF 交DE 于点G , 直接写出sin ABF ∠的最大值.5、已知如图,等腰△ABC 中,AB=AC ,∠BAC=α(α>90︒),F 为BC 中点,D 为BC 延长线上一点,以点A 为中心,将线段AD 逆时针旋转α得到线段AE ,连接CE ,DE .(1)补全图形并比较∠BAD 和∠CAE 的大小; (2)用等式表示CE ,CD ,BF 之间的关系,并证明;(3)过F 作AC 的垂线,并延长交DE 于点H ,求EH 和DH 之间的数量关系,并证明.-参考答案-一、单选题 1、C 【解析】 【分析】由题意知260BOC A ∠=∠=︒,290AOB C ∠=∠=︒,BOC 为等边三角形,2OB BC ==,180n rAB π=可得弧长的值. 【详解】解:如图连接OA 、OB 、OC∵30A ∠=︒,45C ∠=︒∴260BOC A ∠=∠=︒,290AOB C ∠=∠=︒ ∴BOC 为等边三角形 ∴2OB BC ==90π2π180180n r AB π⨯⨯=== 故选C . 【点睛】本题考查了圆周角,弧长等知识.解题的关键在于找出弧长所对的圆心角以及半径. 2、C【解析】 【分析】连接CO ,根据垂径定理可得3CE ED ==,设O 的半径为r ,则OB OC r ==,进而勾股定理列出方程求得半径,进而求得AE 【详解】解:如图,连接CO ,∵AB 是O 的直径,弦CD AB ⊥,6CD = ∴3CE =设O 的半径为r ,则OB OC r ==在Rt COE △中,222OC OE CE =+,1OE OB OE r =-=- 即()22213r r =-+ 解得=5r 即10AB =9AE AB BE ∴=-=故选C 【点睛】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.3、A 【解析】 【分析】设原来扇形的半径为r ,圆心角为n ,则变化后的扇形的半径为3r ,圆心角为19n ,利用扇形的面积公式即可计算得出它们的面积,从而进行比较即可得答案. 【详解】设原来扇形的半径为r ,圆心角为n ,∴原来扇形的面积为2360n r π,∵扇形的半径扩大为原来的3倍,圆心角缩小为原来的19,∴变化后的扇形的半径为3r ,圆心角为19n ,∴变化后的扇形的面积为221(3)9360360n r n r ππ=, ∴扇形的面积不变. 故选:A . 【点睛】本题考查了扇形面积,熟练掌握并灵活运用扇形面积公式是解题关键. 4、C 【解析】 【分析】连接AC ,由圆周角定理得90ACB ∠=︒,30CAB CDB ∠=∠=︒,再由含30角的直角三角形的性质求解即可.【详解】解:如图,连接AC.AB为O的直径,∴∠=︒,ACB90BC=,∠=∠=︒, 4.5CAB CDB30∴==,AB BC29故选:C.【点睛】本题考查了圆周角定理、含30角的直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.5、C【解析】【分析】如图,过点C作CT⊥AB于点T,过点O作OH⊥AB于点H,交⊙O于点K,连接AO、AK,解直角三角形求出AB,求出CT的最大值,可得结论.【详解】解:如图,过点C作CT⊥AB于点T,过点O作OH⊥AB于点H,交⊙O于点K,连接AO、AK,由题意可得AB 垂直平分线段OK ,∴AO =AK ,OH =HK =3,∵OA =OK ,∴OA =OK =AK ,∴∠OAK =∠AOK =60°,∴AH =OA ×sin ∵OH ⊥AB ,∴AH =BH ,∴AB =2AH∵OC +OH ⩾CT ,∴CT ⩽6+3=9,∴CT 的最大值为9,∴△ABC 的面积的最大值为192⨯故选:C.【点睛】本题考查垂径定理、三角函数、三角形的面积、垂线段最短等知识,解题的关键是求出CT 的最大值,属于中考常考题型.6、C【解析】【分析】在等腰三角形OCB中,求得两个底角∠OBC、∠OCB的度数,然后根据三角形的内角和求得∠COB=100°;最后由圆周角定理求得∠A的度数并作出选择.【详解】解:在OCB∆中,OB OC=,OBC OCB∴∠=∠;40OCB∠=︒,180COB OBC OCB∠=︒-∠-∠,100COB∴∠=︒;又12A COB ∠=∠,50A∴∠=︒,故选:C.【点睛】本题考查了圆周角定理,等腰三角形的性质,三角形的内角和定理,熟练掌握圆周角定理是解题的关键.7、C【解析】【分析】先设半径为r,再根据弧长公式建立方程,解出r即可【详解】设半径为r,则周长为2πr,120°所对应的弧长为120222π3603r r ππ︒⨯==︒ 解得r =3故选C【点睛】 本题考查弧长计算,牢记弧长公式是本题关键.8、D【解析】【分析】连接CD ,由直角三角形斜边中线定理可得CD =BD ,然后可得△CDB 是等边三角形,则有BD =BC =5cm ,进而根据勾股定理可求解.【详解】解:连接CD ,如图所示:∵点D 是AB 的中点,90C ∠=︒,10cm AB =, ∴15cm 2CD BD AB ===, ∵CD BC =,∴5cm CD BD BC ===,在Rt△ACB中,由勾股定理可得AC=;故选D.【点睛】本题主要考查圆的基本性质、直角三角形斜边中线定理及勾股定理,熟练掌握圆的基本性质、直角三角形斜边中线定理及勾股定理是解题的关键.9、C【解析】【分析】连接OC交AB于点E.利用垂径定理以及勾股定理求出OE,可得结论.【详解】解:连接OC交AB于点E.由题意OC⊥AB,AB=2(米),∴AE=BE=12在Rt△AEO中,OE,∴CE=OC-OE=(3(米),故选:C.【点睛】本题考查垂径定理的应用,勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.10、B【解析】【分析】由切线的性质可推出OA AP ⊥,OB BP ⊥.再根据直角三角形全等的判定条件“HL ”,即可证明OAP OBP ≅,即得出4PB PA ==.【详解】∵PA ,PB 是⊙O 的切线,A ,B 为切点,∴OA AP ⊥,OB BP ⊥,∴在Rt OAP △和Rt OBP 中,OA OB OP OP =⎧⎨=⎩, ∴()OAP OBP HL ≅,∴4PB PA ==.故选:B【点睛】本题考查切线的性质,三角形全等的判定和性质.熟练掌握切线的性质是解答本题的关键.二、填空题1、51m -<<-【解析】【分析】当⊙P 在直线AB 下方与直线AB 相切时,可求得此时m 的值;当⊙P 在直线AB 上方与直线AB 相切时,可求得此时m 的值,从而可确定符合题意的m 的取值范围.【详解】∵圆心P 的坐标为(1,0),⊙P 与y 轴相切与点O∴⊙P 的半径为1∵点A (-3,0),点 B (0∴OA =3,OB =∴tan OB BAO OA ∠==∴∠BAO =30°当⊙P 在直线AB 下方与直线AB 相切时,如图,设切点为C ,连接PC则PC ⊥AB ,且PC =1∴AP =2PC =2∴OP =OA −AP =3−2=1∴P 点坐标为(−1,0)即m =−1当⊙P 在直线AB 上方与直线AB 相切时,如图,设切点为C ,连接PD则PD ⊥AB ,且PD =1∴AP =2PD =2∴OP =OA +AP =3+2=5∴P 点坐标为(−5,0)即m =−5∴⊙P 沿x 轴向左移动,当⊙P 与直线AB 相交时,m 的取值范围为51m -<<-故答案为:51m -<<-【点睛】本题考查了直线与圆相交的位置关系,切线的性质定理等知识,这里通过讨论直线与圆相切的情况来解决直线与圆相交的情况,体现了转化思想,注意相切有两种情况,不要出现遗漏的情况. 2、110°##110度【解析】【分析】根据圆内接四边形对角互补,得∠D +∠B =180°,结合已知求解即可.【详解】∵圆内接四边形对角互补,∴∠D +∠B =180°,∵40D B ∠-∠=︒∴∠D =110°,故答案为:110°.【点睛】本题考查了圆内接四边形互补的性质,熟练掌握并运用性质是解题的关键.3、160°,52002cm π【解析】【分析】由题意知,圆锥的展开图扇形的r 半径为90cm ,弧长l 为18022π80π2r π=⨯=.代入扇形弧长公式π180n r l =求解圆心角;代入扇形面积公式2π360n r S =侧求出圆锥侧面积,然后加上底面面积即可求出全面积.【详解】解:圆锥的展开图扇形的r 半径为90cm ,弧长l 为18022π80π2r π=⨯= ∵π180n r l = ∴9080π180n π⨯=解得160n =︒ ∵2π360n r S =侧 ∴22160π903600360S cm π⨯⨯==侧 22803600ππ52002S cm π⎛⎫=+⨯= ⎪⎝⎭全 故答案为:160°,25200cm π.【点睛】本题考查了扇形的圆心角与面积.解题的关键在于运用扇形的弧长与面积公式进行求解.难点在于求出公式中的未知量.4、3π【解析】【分析】先求出A 、B 、C 坐标,再证明三角形BOC 是等边三角形,最后根据扇形面积公式计算即可.【详解】过C 作CD ⊥OA 于D∵一次函数1y =+的图象与x 轴交于点A ,与y 轴交于点B , ∴当0x =时,1y =,B 点坐标为(0,1)当0y =时,y =A 点坐标为∴2,1AB OB OA ===,∵作ABO 的外接圆C ,∴线段AB 中点C 的坐标为1)2,112OC BC AB OB ==== ∴三角形BOC 是等边三角形∴120ACO ∠=︒∵C 的坐标为1)2∴12CD =∴2120111360223AOCACO S S Sππ︒=-=⨯⨯-=︒扇形故答案为:3π【点睛】本题主要考查了一次函数的综合运用,求扇形面积.用已知点的坐标表示相应的线段是解题的关键. 5、点A 在圆内 【解析】 【分析】比较点到圆心的距离d 与半径r 的大小关系;当d r 时,点在圆外;当d r =时,点在圆上;当d r<时,点在圆内;求值后进行判断即可. 【详解】 解:O 的半径为5cm r =,点A 到圆心O 的距离为=4cm dd r ∴<∴点A 与O 的位置关系是:点A 在圆内故答案为:点A 在圆内. 【点睛】本题考查了点与圆的位置关系.解题的关键在于比较点到圆心的距离d 与半径r 的大小关系. 6、2π 【解析】【分析】连接AC ,根据圆周角定理得出AC 为圆的直径,解直角三角形求出AB ,根据扇形面积公式进行求解即可. 【详解】解:如图,连接AC ,∵从一块直径为2cm 的圆形铁皮上剪出一个圆心角为90°的扇形,即∠ABC =90°, ∴AC 为直径,即AC =2cm ,AB =BC (扇形的半径相等), ∵在Rt ABC 中,22222AB BC AC +==,∴AB =BC∴阴影部分的面积是()29023602ππ=(cm 2).故答案为:2π. 【点睛】本题考查了圆周角定理和扇形的面积计算,熟记扇形的面积公式是解题的关键. 7、12π 【解析】 【分析】根据弧长公式直接计算即可. 【详解】∵圆的半径为36cm.所对的圆心角为60°,∴弧的长度为:6036 180180n rππ⨯⨯==12π,故答案为:12π.【点睛】本题考查了弧长的计算,熟练掌握弧长公式及其使用条件是解题的关键.8、【解析】【分析】连接OC交AB于点D,再连接OA.根据轴对称的性质确定OC AB⊥,OD=CD;再根据垂径定理确定AD=BD;再根据勾股定理求出AD的长度,进而即可求出AB的长度.【详解】解:如下图所示,连接OC交AB于点D,再连接OA.∵折叠后弧AB的中点C与圆心O重叠,∴OC AB⊥,OD=CD.∴AD=BD.∵圆形纸片的半径为10cm,∴OA=OC=10cm.∴OD=5cm.∴AD =.∴BD =.∴AB AD BD =+=.故答案为: 【点睛】本题考查轴对称的性质,垂径定理,勾股定理,综合应用这些知识点是解题关键.932π 【解析】 【分析】过点C 作CH AB ⊥于点H ,根据正弦定义解得CH 的长,再由扇形面积公式、三角形的面积公式解题即可. 【详解】解:过点C 作CH AB ⊥于点H ,在平行四边形ABCD 中,120A ∠=︒ 18012060B ∴∠=︒-︒=︒=sin sin 603CH BC B AD ∴⋅=⨯︒=平行四边形ABCD 的面积为:7AB CH ⨯=图中黑色阴影部分的面积为:()2216016037323602360BC AE CH ππ⋅⨯⋅⋅-=⨯-=32π,32π. 【点睛】本题考查平行四边形的性质、扇形面积等知识,是基础考点,掌握相关知识是解题关键.10、2π【解析】 【分析】利用勾股定理求出AC 及AB 的长,根据阴影面积等于AB C CAC DAB S S S ''''--扇形扇形求出答案.【详解】解:由旋转得,AB AB AC AC ''==,90CAC '∠=︒,B AC ''∠=∠BAC =30°, ∵∠ABC =90°,∠BAC =30°,BC =1,∴AC =2BC =2,AB 60CAB '∠=︒,∴阴影部分的面积=AB C CAC DAB S S S''''--扇形扇形2260902113603602ππ⨯⨯=--⨯=2π故答案为:2π.【点睛】此题考查了求不规则图形的面积,正确掌握勾股定理、30度角直角三角形的性质、扇形面积计算公式及分析出阴影面积的构成特点是解题的关键. 三、解答题 1、224cm π. 【解析】 【分析】将6012n r ==,代入2360n r S π=,求解即可.【详解】解:由题意知扇形面积为:()222601224360360n r S cm πππ⋅=== ∴扇形的面积为:224cm π. 【点睛】本题考查了扇形的面积.解题的关键在于熟练使用扇形的面积公式. 2、 (1)见解析 (2)见解析 【解析】 【分析】(1)在图①中画⊙O的一个内接正八边形ABCDEFGH即可;(2)在图②中画⊙O的一个内接正六边形ABCDEF即可.(1)解:如图,正八边形ABCDEFGH即为所求:(2)解:如图,正六边形ABCDEF即为所求:【点睛】本题考查了作图-应用与设计作图、正多边形和圆,解决本题的关键是准确画图.3、 (1)见解析【解析】【分析】(1)分别以点A,C为圆心,大于12AC长为半径画弧交于两点,连接这两点交AC于点O,以O为圆心,OA为半径作圆交AB于点D;(2)连接CD,根据AC是⊙O的直径,可得∠ADC=90°,由tan∠A=13,可得CD=2,再运用勾股定理可得AC=(1)如图所示,⊙O即为所作的圆:(2)连接CD,如图,∵AC 是圆O 的直径∴90ADC ∠=︒,即CD AB ⊥ ∵BC =AC ∴1112622AD AB ==⨯= ∵tan∠A =13∴13CD AD = ∴123CD AD ==在Rt △ACD 中,222AD CD AC +=∴AC∴⊙O 的半径=12⨯【点睛】本题考查了线段中点和圆的作图,圆的性质,,等腰三角形性质,勾股定理等知识,熟练掌握圆的性质是解题关键.4、(1;(2)2DB =;(3)①见解析;②sin ABF ∠【解析】 【分析】(1)根据定义直接可得AC AB =(2)根据证明ACD ABC △∽△,可得2AC AD AB =⋅,又AC AB =AD ,进而求得BD 的长;(3)过点E 作EQ CD ∥,交于BF 于点P ,连接DP ,证明四边形DPEF 是平行四边形,进而求得DG =,进而判断D 在以D 为半径的半圆上运动,从而求得ABF ∠的最大值,即可求得sin ABF ∠的最大值. 【详解】(1)在优美三角形ABC 中, A ∠是优美角, AC AB <,∴AC AB=(2)如图,2ACD ABC AC ∠∠==,,A A ∠=∠ACD ABC ∴△∽△∴AC ADAB AC=即2AC AD AB =⋅4AD AB ∴⋅=又AC AB =AC AB ∴=1AB ∴== 41AD AB∴== )112BD AB AD ∴=--= 2BD ∴=(3)如图2,设点E 到,AC AB 的距离分别为12,h hAE 是CAB ∠的角平分线12h h ∴=11212ACEAEB AC h S AC S AB AB h ⋅∴===⋅△△ 设A 点到BC 的距离为h , 则1212AEC ABECE h S CE S BE BE h ⋅==⋅△△CE AC BE AB ∴=又51,1,2AB AD BD===AD BD ∴=CE AD EB BD∴= BC BE BD AB ∴= 又B B ∠=∠BED BCA ∴∽△△BED BCA ∴∠=∠ED AC ∴∥ED DBAC AB∴= 即ED AC DB AB == ∴DBE 是优美三角形:②如图,过点E 作EQ CD ∥,交于BF 于点P ,连接DP ,AC ED ∥,1,2AD BD ==,CE ADEB DB ∴==EQ CD ∥FP CE PB EB ∴== FP AD PB DB∴= FB AB PB DP ∴= 又ABF DBP ∠=∠BPD BFA ∴∽BDP BAF ∴∠=∠DP AE ∴∥∴四边形DPEF 是平行四边形EG DG ∴=ED AC DB AB ==2DB =1DE AD ∴==12ED DE ∴== DG ∴在以D为半径的半圆上运动,如图,ABF ∴∠最大时,DBG ∠最大,此时BG 是D 的切线,则sin ABF ∠也最大,2sin sin 2DG ABF DBG DB∴∠=∠===∴sin ABF ∠【点睛】本题考查了新定义,相似三角形的,切线的性质,求一个角的正弦,正弦的增减性,最后一问中求得点G 是DE 的中点是解题的关键.5、 (1)补全图形见解析,BAD CAE ∠=∠;(2)2CE CD BF -=;(3)EH DH =,理由见解析.【解析】【分析】(1)根据题意补全图形即可,再根据旋转的性质可知BAC DAE ∠=∠,即BAC CAD DAE CAD ∠+∠=∠+∠,即得出BAD CAE ∠=∠;(2)由旋转可知AD AE =,即可利用“SAS ”证明BAD CAE ≅△△,得出BD CE =.再由点F 为BC 中点,即可得出2CE CD BF -=.(3)连接AF ,作AN DE ⊥,由等腰三角形“三线合一”可知90AFD ∠=︒,12FAB FAC α∠=∠=.即得出180AFD AND ∠+∠=︒,说明A 、F 、D 、N 四点共圆.再根据圆周角定理可知AFN ADN ∠=∠.再次利用等腰三角形“三线合一”的性质可知EN DN =,1902AFN ADN α∠=∠=︒-.即得出90AFN FAC ∠+∠=︒.再由90AFH FAC ∠+∠=︒,即可说明 点H 与点N 重合,即得出结论EH DH =.(1)如图,即为补全的图形,根据题意可知BAC DAE α∠=∠=,∴BAC CAD DAE CAD ∠+∠=∠+∠,即BAD CAE ∠=∠.(2)由旋转可知AD AE =,∴在BAD 和CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩, ∴()BAD CAE SAS ≅,∴BD CE =.∵BD BC CD =+,∴CE BC CD =+.∵点F 为BC 中点,∴2BC BF =,∴2CE BF CD =+,即2CE CD BF -=.(3)如图,连接AF ,作AN DE ⊥,∵AB=AC ,F 为BC 中点,∴90AFD ∠=︒,12FAB FAC α∠=∠=. 根据作图可知90AND ∠=︒,∴180AFD AND ∠+∠=︒,∴A 、F 、D 、N 四点共圆,∴AFN ADN ∠=∠.∵AD AE =,AN DE ⊥,∴EN DN =,11(180)9022AFN ADN DAE α∠=∠=︒-∠=︒-. ∴11909022AFN FAC αα∠+∠=︒-+=︒. ∵90AFH FAC ∠+∠=︒,且点H 在线段DE 上,∴点H 与点N 重合,∴EH DH =.【点睛】本题考查旋转的性质,全等三角形的判定和性质,等腰三角形的性质,四点共圆,圆周角定理等知识,较难.利用数形结合的思想是解答本题的关键.。
第27章 圆数学九年级下册-单元测试卷-华师大版(含答案)
第27章圆数学九年级下册-单元测试卷-华师大版(含答案)一、单选题(共15题,共计45分)1、若⊙O的半径为5,点P到圆心的距离为d,当点P在圆上时,则有()A.d<5B.d>5C.d = 5D.d =2、如图,圆锥的表面展开图由一个扇形和一个圆组成,已知圆的面积为100π,扇形的圆心角为120°,则这个扇形的面积为()A.300πB.150πC.200πD.600π3、如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时处于弧AB上,此时∠AOE=56°,则α的度数是()A.52°B.60°C.72°D.76°4、如图,⊙O的直径AB与弦CD的延长线交于点E,若DE=OB,∠AOC=84°,则∠E等于()A.42°B.28°C.21°D.20°5、如图,在△ABC中,AB=AC=10,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=∠A,tan∠CBF=,则CF的长为()A. B. C. D.6、AB为⊙O的直径,点C、D在⊙O上.若∠ABD=42°,则∠BCD的度数是()A.122°B.128°C.132°D.138°7、如图,已知四边形ABCD内接于⊙O,连结BD,∠BAD=105°,∠DBC=75°.若⊙O的半径为3,则弧BC的长是( )A. B.π C. D.8、如图,在矩形ABCD中,AB=3,AD=4,若以点A为圆心,以4为半径作⊙A,则下列各点中在⊙A外的是()A.点AB.点BC.点CD.点D9、如图,AB是半圆的直径,点D是弧AC的中点,∠ABC=500,则∠DAB等于()A.55°B.60°C.65°D.70°10、如图,PA、PB是⊙O的切线,切点是A、B,已知∠P=60°,0A=3,那么∠AOB所对弧的长度为( ).A.5πB.4πC.3πD.2π11、如图,一个半径为r(r<1)的圆形纸片在边长为10的正六边形内任意运动,则在该六边形内,这个圆形纸片不能接触到的部分的面积是()A.πr 2B.C. r 2D. r 212、一个正五边形和一个正六边形按如图方式摆放,它们都有一边在直线上,且有一个公共顶点,则的度数是A. B. C. D.13、已知中,,,,点P为边AB的中点,以点C 为圆心,长度r为半径画圆,使得点A,P在⊙C内,点B在⊙C外,则半径r的取值范围是()A. B. C. D.14、如图,AB是半圆O直径,半径OC⊥AB,连接AC,∠CAB的平分线AD分别交OC于点E,交于点D,连接CD、OD,以下三个结论:①AC∥OD;②AC=2CD;③线段CD是CE 与CO的比例中项,其中所有正确结论的序号是()A.①②B.②③C.①③D.①②③15、如图,已知是的外接圆,连接,若,则的度数为()A. B. C. D.二、填空题(共10题,共计30分)16、如图,在⊙O中,半径OC与弦AN垂直于点D,且AB=16,OC=10,则CD的长是________.17、已知⊙O的面积为36π,若PO=7,则点P在⊙O________.18、若圆锥的底面半径为3cm,母线长为5cm,则这个圆锥的全面积为________cm2.(结果保留π)19、如图,在平面直角坐标系xoy中,四边形OABC是矩形,点A、C分别在x轴、y轴的正半轴上,点B的坐标为(1,2),若点P是第一象限内的一点,且∠OPC=45°,则线段AP最长时的P点坐标为________.20、如图,AB是⊙O直径,CD⊥AB,∠CDB=30°,CD=2 ,则S阴影=________.21、如图,正五边形ABCDE内接于⊙O,若⊙O的半径为5,则弧AB的长为________.22、如图,BD是⊙O的切线,B为切点,连接DO与⊙O交于点C,AB为⊙O的直径,连接CA,若∠D=30°,⊙O的半径为4,则图中阴影部分的面积为________.23、如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连结AC,BD.若图中阴影部分的面积是,OA=2,则OC的长为________.24、如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二十七章圆章末测试(一)总分120分120分钟农安县合隆中学徐亚惠一.选择题(共8小题,每题3分)1.如图,在⊙O中,OD⊥BC,∠BOD=60°,则∠CAD的度数等于()A.15° B.20°C.25°D.30°2.从下列直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是()A.B.C.D.3.两圆的半径分别为2cm,3cm,圆心距为2cm,则这两个圆的位置关系是()A.外切B.相交C.内切D.内含4.如图,当半径分别是5和r的两圆⊙O1和⊙O2外切时,它们的圆心距O1O2=8,则⊙O2的半径r为()A.12 B.8 C.5 D.35.圆锥体的底面半径为2,侧面积为8π,则其侧面展开图的圆心角为()A.90° B.120°C.150°D.180°6.已知圆锥的底面半径为4cm,母线长为5cm,则这个圆锥的侧面积是()A.20πcm2B.20cm2C.40πcm2D.40cm27.如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为()A.B.C.D.8.如图,某同学用一扇形纸板为一个玩偶制作一个圆锥形帽子,已知扇形半径OA=13cm,扇形的弧长为10πcm,那么这个圆锥形帽子的高是()cm.(不考虑接缝)A.5 B.12 C.13 D.14二.填空题(共6小题,每题3分)9.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长l为_________cm.10.如图,在一张正方形纸片上剪下一个半径为r的圆形和一个半径为R的扇形,使之恰好围成图中所示的圆锥,则R与r之间的关系是_________.11.已知⊙O1与⊙2外切,圆心距为7cm,若⊙O1的半径为4cm,则⊙O2的半径是_________cm.12.如图,⊙A与⊙B外切于⊙O的圆心O,⊙O的半径为1,则阴影部分的面积是_________.13.如图,已知A、B、C三点都在⊙O上,∠AOB=60°,∠ACB=_________.14.如图,△ABC是⊙O的内接三角形,如果∠AOC=100°,那么∠B=_________度.三.解答题(共10小题)15.(6分)如图,在半径为5cm的⊙O中,直径AB与弦CD相交于点P,∠CAB=50°,∠APD=80°.(1)求∠ABD的大小;(2)求弦BD的长.16(6分).如图,已知⊙O的直径AB与弦CD相交于点E,AB⊥CD,⊙O的切线BF与弦AD的延长线相交于点F.(1)求证:CD∥BF;(2)若⊙O的半径为5,cos∠BCD=0.8,求线段AD与BF的长.17.(6分)如图,平面直角坐标系中,以点C(2,)为圆心,以2为半径的圆与x轴交于A,B两点.(1)求A,B两点的坐标;(2)若二次函数y=x2+bx+c的图象经过点A,B,试确定此二次函数的解析式.18.(8分)如图,AB是⊙O的直径,弦CD交AB于点E,OF⊥AC于点F,(1)请探索OF和BC的关系并说明理由;(2)若∠D=30°,BC=1时,求圆中阴影部分的面积.(结果保留π)19(8分).如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,AO=1.(1)求∠C的大小;(2)求阴影部分的面积.20.(8分)已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.(1)求证:△ACB∽△CDB;(2)若⊙O的半径为1,∠BCP=30°,求图中阴影部分的面积.21.(8分)如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点恰好为BC的中点D,过点D作⊙O 的切线交AC于点E.(1)求证:DE⊥AC;(2)若AB=3DE,求tan∠ACB的值.22(8分).如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D点,连接CD.(1)求证:∠A=∠BCD;(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.23(10分).如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.(1)求证:BC是⊙O的切线;(2)若⊙O的半径为,OP=1,求BC的长.24.(10分)如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,OC=2.(1)求OE和CD的长;(2)求图中阴影部分的面积.第二十七章圆章末测试(一)参考答案与试题解析一.选择题(共8小题)1.如图,在⊙O中,OD⊥BC,∠BOD=60°,则∠CAD的度数等于()A.15°B.20°C.25°D.30°考点:圆周角定理;垂径定理.专题:计算题.分析:由在⊙O中,OD⊥BC,根据垂径定理的即可求得:=,然后利用圆周角定理求解即可求得答案.解答:解:∵在⊙O中,OD⊥BC,∴=,∴∠CAD=∠BOD=×60°=30°.故选:D.点评:此题考查了圆周角定理以及垂径定理.此题难度不大,注意掌握数形结合思想的应用.2.从下列直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是()A. B.C.D.考点:圆周角定理.分析:根据圆周角定理(直径所对的圆周角是直角)求解,即可求得答案.解答:解:∵直径所对的圆周角等于直角,∴从下列直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是B.故选:B.点评:此题考查了圆周角定理.此题比较简单,注意掌握数形结合思想的应用.3.两圆的半径分别为2cm,3cm,圆心距为2cm,则这两个圆的位置关系是()A.外切B.相交C.内切D.内含考点:圆与圆的位置关系.分析:由两个圆的半径分别是3cm和2cm,圆心距为2cm,根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系即可得出两圆位置关系.解答:解:∵两个圆的半径分别是3cm和2cm,圆心距为2cm,又∵3+2=5,3﹣2=1,1<2<5,∴这两个圆的位置关系是相交.故选:B.点评:此题考查了圆与圆的位置关系.注意掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系是解此题的关键.4.如图,当半径分别是5和r的两圆⊙O1和⊙O2外切时,它们的圆心距O1O2=8,则⊙O2的半径r为()A.12 B.8 C.5 D. 3考点:圆与圆的位置关系.分析:根据两圆外切时,圆心距=两圆半径的和求解.解答:解:根据两圆外切,圆心距等于两圆半径之和,得该圆的半径是8﹣5=3.故选:D.点评:本题考查了圆与圆的位置关系,注意:两圆外切,圆心距等于两圆半径之和.5.圆锥体的底面半径为2,侧面积为8π,则其侧面展开图的圆心角为()A.90°B.120°C.150°D.180°考点:圆锥的计算.专题:计算题.分析:设圆锥的侧面展开图的圆心角为n°,母线长为R,先根据锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式得到•2π•2•R=8π,解得R=4,然后根据弧长公式得到=2•2π,再解关于n的方程即可.解答:解:设圆锥的侧面展开图的圆心角为n°,母线长为R,根据题意得•2π•2•R=8π,解得R=4,所以=2•2π,解得n=180,即圆锥的侧面展开图的圆心角为180°.故选:D.点评:本题考查了圆锥的计算:锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.6.已知圆锥的底面半径为4cm,母线长为5cm,则这个圆锥的侧面积是()A.20πcm2B.20cm2C.40πcm2D.40cm2考点:圆锥的计算.专题:计算题.分析:圆锥的侧面积=底面周长×母线长÷2,把相应数值代入即可求解.解答:解:圆锥的侧面积=2π×4×5÷2=20π.故选:A.点评:本题考查了圆锥的计算,解题的关键是弄清圆锥的侧面积的计算方法,特别是圆锥的底面周长等于圆锥的侧面扇形的弧长.7.如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为()A.B.C.D.考点:正多边形和圆.专题:压轴题.分析:由于六边形ABCDEF是正六边形,所以∠AOB=60°,故△OAB是等边三角形,OA=OB=AB=2,设点G为AB与⊙O的切点,连接OG,则OG⊥AB,OG=OA•sin60°,再根据S阴影=S△OAB﹣S扇形OMN,进而可得出结论.解答:解:∵六边形ABCDEF是正六边形,∴∠AOB=60°,∴△OAB是等边三角形,OA=OB=AB=2,设点G为AB与⊙O的切点,连接OG,则OG⊥AB,∴OG=OA•sin60°=2×=,∴S阴影=S△OAB﹣S扇形OMN=×2×﹣=﹣.故选A.点评:本题考查的是正多边形和圆,根据正六边形的性质求出△OAB是等边三角形是解答此题的关键.8.如图,某同学用一扇形纸板为一个玩偶制作一个圆锥形帽子,已知扇形半径OA=13cm,扇形的弧长为10πcm,那么这个圆锥形帽子的高是()cm.(不考虑接缝)A. 5 B.12 C.13 D.14考点:圆锥的计算.专题:几何图形问题.分析:首先求得圆锥的底面半径,然后利用勾股定理求得圆锥的高即可.解答:解:先求底面圆的半径,即2πr=10π,r=5cm,∵扇形的半径13cm,∴圆锥的高==12cm.故选:B.点评:此题主要考查圆锥的侧面展开图和勾股定理的应用,牢记有关公式是解答本题的关键,难度不大.二.填空题(共6小题)9.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长l为6cm.考点:圆锥的计算.分析:易得圆锥的底面周长,也就是侧面展开图的弧长,进而利用弧长公式即可求得圆锥的母线长.解答:解:圆锥的底面周长=2π×2=4πcm,设圆锥的母线长为R,则:=4π,解得R=6.故答案为:6.点评:本题考查了圆锥的计算,用到的知识点为:圆锥的侧面展开图的弧长等于底面周长;弧长公式为:.10.如图,在一张正方形纸片上剪下一个半径为r的圆形和一个半径为R的扇形,使之恰好围成图中所示的圆锥,则R与r之间的关系是R=4r.考点:圆锥的计算.专题:几何图形问题.分析:利用圆锥的底面周长等于侧面展开图的扇形弧长,根据弧长公式计算.解答:解:扇形的弧长是:=,圆的半径为r,则底面圆的周长是2πr,圆锥的底面周长等于侧面展开图的扇形弧长则得到:=2πr,∴=2r,即:R=4r,r与R之间的关系是R=4r.故答案为:R=4r.点评:本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.11.已知⊙O1与⊙2外切,圆心距为7cm,若⊙O1的半径为4cm,则⊙O2的半径是3cm.考点:圆与圆的位置关系.分析:根据两圆外切时,圆心距=两圆半径的和求解.解答:解:根据两圆外切,圆心距等于两圆半径之和,得该圆的半径是7﹣4=3cm.故答案为:3.点评:本题考查了圆与圆的位置关系,注意:两圆外切,圆心距等于两圆半径之和.12.如图,⊙A与⊙B外切于⊙O的圆心O,⊙O的半径为1,则阴影部分的面积是﹣.考点:圆与圆的位置关系;扇形面积的计算.专题:压轴题.分析:阴影部分的面积等于⊙O的面积减去4个弓形ODF的面积即可.解答:解:如图,连接DF、DB、FB、OB,∵⊙O的半径为1,∴OB=BD=BF=1,∴DF=,∴S弓形ODF=S扇形BDF﹣S△BDF=﹣××=﹣,∴S阴影部分=S⊙O﹣4S弓形ODF=π﹣4×(﹣)=﹣.故答案为:.点评:本题考查了圆与圆的位置关系,解题的关键是明确不规则的阴影部分的面积如何转化为规则的几何图形的面积.13.如图,已知A、B、C三点都在⊙O上,∠AOB=60°,∠ACB=30°.考点:圆周角定理.分析:由∠ACB是⊙O的圆周角,∠AOB是圆心角,且∠AOB=60°,根据圆周角定理,即可求得圆周角∠ACB的度数.解答:解:如图,∵∠AOB=60°,∴∠ACB=∠AOB=30°.故答案是:30°.点评:此题考查了圆周角定理.此题比较简单,注意掌握数形结合思想的应用.14.如图,△ABC是⊙O的内接三角形,如果∠AOC=100°,那么∠B=50度.考点:圆周角定理.专题:计算题.分析:直接根据圆周角定理求解.解答:解:∠B=∠AOC=×100°=50°.故答案为:50.点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.三.解答题(共10小题)15.如图,在半径为5cm的⊙O中,直径AB与弦CD相交于点P,∠CAB=50°,∠APD=80°.(1)求∠ABD的大小;(2)求弦BD的长.考点:圆周角定理;垂径定理.分析:(1)先根据三角形外角的性质求出∠C的度数,由圆周角定理即可得出结论;(2)过点O作O E⊥BD于点E,由垂径定理可知BD=2BE,再根据直角三角形的性质可求出BE的长,进而得出结论.解答:解:(1)∵∠APD是△APC的外角,∠CAB=50°,∠APD=80°,∴∠C=80°﹣50°=30°,∴∠ABD=∠C=30°;(2)过点O作OE⊥BD于点E,则BD=2BE,∵∠ABD=30°,OB=5cm,∴BE=OB•cos30°=5×=cm,∴BD=2BE=5cm.点评:本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等是解答此题的关键.16.如图,已知⊙O的直径AB与弦CD相交于点E,AB⊥CD,⊙O的切线BF与弦AD的延长线相交于点F.(1)求证:CD∥BF;(2)若⊙O的半径为5,cos∠BCD=0.8,求线段AD与BF的长.考点:圆周角定理;解直角三角形.分析:(1)由BF是圆O的切线,AB是圆O的直径,可得BF⊥AB,又由AB⊥CD,即可证得CD∥BF;(2)由圆周角定理可证得∠BAD=∠BCD,然后利用三角函数的性质求得答案.解答:(1)证明:∵BF是圆O的切线,AB是圆O的直径,∴BF⊥AB.∵CD⊥AB,∴CD∥BF;(2)解:∵AB是圆O的直径,∴∠ADB=90°,∵∠BAD=∠BCD,∴cos∠BAD=cos∠BCD=0.8,在Rt△ABD中,AB=10,cos∠BAD=,∴AD=AB•cos∠BAD=10×0.8=8,在Rt△ABF中,AB=10,cos∠BAF=,∴,.点评:此题考查了圆周角定理、切线的性质以及三角函数等知识.此题难度适中,注意掌握数形结合思想的应用.17.如图,平面直角坐标系中,以点C(2,)为圆心,以2为半径的圆与x轴交于A,B两点.(1)求A,B两点的坐标;(2)若二次函数y=x2+bx+c的图象经过点A,B,试确定此二次函数的解析式.考点:垂径定理;待定系数法求二次函数解析式;勾股定理.专题:计算题.分析:(1)连接AC,过点C作CM⊥x轴于点M,根据垂径定理得MA=MB;由C点坐标得到OM=2,CM=,再根据勾股定理可计算出AM,可计算出OA、OB,然后写出A,B两点的坐标;(2)利用待定系数法求二次函数的解析式.解答:解:(1)过点C作CM⊥x轴于点M,则MA=MB,连结AC,如图∵点C的坐标为(2,),∴OM=2,CM=,在Rt△ACM中,CA=2,∴AM==1,∴OA=OM﹣AM=1,OB=OM+BM=3,∴A点坐标为(1,0),B点坐标为(3,0);(2)将A(1,0),B(3,0)代入y=x2+bx+c得,解得.所以二次函数的解析式为y=x2﹣4x+3.点评:本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了勾股定理和待定系数法求二次函数的解析式.18.如图,AB是⊙O的直径,弦CD交AB于点E,OF⊥AC于点F,(1)请探索OF和BC的关系并说明理由;(2)若∠D=30°,BC=1时,求圆中阴影部分的面积.(结果保留π)考点:垂径定理;三角形中位线定理;圆周角定理;扇形面积的计算.分析:(1)先根据垂径定理得出AF=CF,再根据AO=BO得出OF是△ABC的中位线,由三角形的中位线定理即可得出结论;(2)连接OC,由(1)知OF=,再根据直角三角形的性质得出AB及AC的长,根据扇形的面积公式求出扇形AOC的度数,根据S阴影=S扇形AOC﹣S△AOC即可得出结论.解答:解:(1)OF∥BC,OF=BC.理由:由垂径定理得AF=CF.∵AO=BO,∴OF是△ABC的中位线.∴OF∥BC,OF=BC.(2)连接OC.由(1)知OF=.∵AB是⊙O的直径,∴∠ACB=90°.∵∠D=30°,∴∠A=30°.∴AB=2BC=2.∴AC=.∴S△AOC=×AC×OF=.∵∠AOC=120°,OA=1,∴S扇形AOC==.∴S阴影=S扇形AOC﹣S△AOC=﹣.点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.19.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,AO=1.(1)求∠C的大小;(2)求阴影部分的面积.考点:垂径定理;圆心角、弧、弦的关系;扇形面积的计算.分析:(1)根据垂径定理可得=,∠C=∠AOD,然后在Rt△COE中可求出∠C的度数.(2)连接OB,根据(1)可求出∠AOB=120°,在Rt△AOF中,求出AF,OF,然后根据S阴影=S扇形OAB﹣S△OAB,即可得出答案.解答:解:(1)∵CD是圆O的直径,CD⊥AB,∴=,∴∠C=∠AOD,∵∠AOD=∠COE,∴∠C=∠COE,∵AO⊥BC,∴∠C=30°.(2)连接OB,由(1)知,∠C=30°,∴∠AOD=60°,∴∠AOB=120°,在Rt△AOF中,AO=1,∠AOF=60°,∴AF=,OF=,∴AB=,∴S阴影=S扇形OADB﹣S△OAB=﹣××=π﹣.点评:本题考查了垂径定理及扇形的面积计算,解答本题的关键是利用解直角三角形的知识求出∠C、∠AOB的度数,难度一般.20.已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.(1)求证:△ACB∽△CDB;(2)若⊙O的半径为1,∠BCP=30°,求图中阴影部分的面积.考点:切线的性质;扇形面积的计算;相似三角形的判定与性质.专题:几何综合题.分析:(1)由CP是⊙O的切线,得出∠BCD=∠BAC,AB是直径,得出∠ACB=90°,所以∠ACB=∠CDB=90°,得出结论△ACB∽△CDB;(2)求出△OCB是正三角形,阴影部分的面积=S扇形OCB﹣S△OCB=π﹣.解答:(1)证明:如图,连接OC,∵直线CP是⊙O的切线,∴∠BCD+∠OCB=90°,∵AB是直径,∴∠ACB=90°,∴∠ACO+∠OCB=90°∴∠BCD=∠ACO,又∵∠BAC=∠ACO,∴∠BCD=∠BAC,又∵BD⊥CP∴∠CDB=90°,∴∠ACB=∠CDB=90°∴△ACB∽△CDB;(2)解:如图,连接OC,∵直线CP是⊙O的切线,∠BCP=30°,∴∠COB=2∠BCP=60°,∴△OCB是正三角形,∵⊙O的半径为1,∴S△OCB=,S扇形OCB==π,故阴影部分的面积=S扇形OCB﹣S△OCB=π﹣.点评:本题主要考查了切线的性质及扇形面积,三角形的面积,解题的关键是利用弦切角找角的关系.21.如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点恰好为BC的中点D,过点D作⊙O的切线交AC于点E.(1)求证:DE⊥AC;(2)若AB=3DE,求tan∠ACB的值.考点:切线的性质.专题:几何综合题.分析:(1)连接OD,可以证得DE⊥OD,然后证明OD∥AC即可证明DE⊥AC;(2)利用△DAE∽△CDE,求出DE与CE的比值即可.解答:(1)证明:连接OD,∵D是BC的中点,OA=OB,∴OD是△ABC的中位线,∴OD∥AC,∵DE是⊙O的切线,∴OD⊥DE,∴DE⊥AC;(2)解:连接AD,∵AB是⊙O的直径,∴∠ADB=90°,∵DE⊥AC,∴∠ADC=∠DEC=∠AED=90°,∴∠ADE=∠DCE在△ADE和△CDE中,∴△CDE∽△DAE,∴,设tan∠ACB=x,CE=a,则DE=ax,AC=3ax,AE=3ax﹣a,∴,整理得:x2﹣3x+1=0,解得:x=,∴tan∠ACB=或.点评:本题主要考查了切线的性质的综合应用,解答本题的关键在于如何利用三角形相似求出线段DE与CE的比值.22.如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D点,连接CD.(1)求证:∠A=∠BCD;(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.考点:切线的判定.专题:几何综合题.分析:(1)根据圆周角定理可得∠ADC=90°,再根据直角三角形的性质可得∠A+∠DCA=90°,再由∠DCB+∠ACD=90°,可得∠DCB=∠A;(2)当MC=MD时,直线DM与⊙O相切,连接DO,根据等等边对等角可得∠1=∠2,∠4=∠3,再根据∠ACB=90°可得∠1+∠3=90°,进而证得直线DM与⊙O相切.解答:(1)证明:∵AC为直径,∴∠ADC=90°,∴∠A+∠DCA=90°,∵∠ACB=90°,∴∠DCB+∠ACD=90°,∴∠DCB=∠A;(2)当MC=MD(或点M是BC的中点)时,直线DM与⊙O相切;解:连接DO,∵DO=CO,∴∠1=∠2,∵DM=CM,∴∠4=∠3,∵∠2+∠4=90°,∴∠1+∠3=90°,∴直线DM与⊙O相切,故当MC=MD(或点M是BC的中点)时,直线DM与⊙O相切.点评:此题主要考查了切线的判定,以及圆周角定理,关键是掌握切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.23如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.(1)求证:BC是⊙O的切线;(2)若⊙O的半径为,OP=1,求BC的长.考点:切线的判定.专题:几何图形问题.分析:(1)由垂直定义得∠A+∠APO=90°,根据等腰三角形的性质由CP=CB得∠CBP=∠CPB,根据对顶角相等得∠CPB=∠APO,所以∠APO=∠CBP,而∠A=∠OBA,所以∠OBC=∠CBP+∠OBA=∠APO+∠A=90°,然后根据切线的判定定理得到BC是⊙O的切线;(2)设BC=x,则PC=x,在Rt△OBC中,根据勾股定理得到()2+x2=(x+1)2,然后解方程即可.解答:(1)证明:连接OB,如图,∵OP⊥OA,∴∠AOP=90°,∴∠A+∠APO=90°,∵CP=CB,∴∠CBP=∠CPB,而∠CPB=∠APO,∴∠APO=∠CBP,∵OA=OB,∴∠A=∠OBA,∴∠OBC=∠CBP+∠OBA=∠APO+∠A=90°,∴OB⊥BC,∴BC是⊙O的切线;(2)解:设BC=x,则PC=x,在Rt△OBC中,OB=,OC=CP+OP=x+1,∵OB2+BC2=OC2,∴()2+x2=(x+1)2,解得x=2,即BC的长为2.点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了勾股定理.24.如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,OC=2.(1)求OE和CD的长;(2)求图中阴影部分的面积.考点:扇形面积的计算;垂径定理.分析:(1)在△OCE中,利用三角函数即可求得CE,OE的长,再根据垂径定理即可求得CD的长;(2)根据半圆的面积减去△ABC的面积,即可求解.解答:解:(1)在△OCE中,∵∠CEO=90°,∠EOC=60°,OC=2,∴OE=OC=1,∴CE=OC=,∵OA⊥CD,∴CE=DE,∴CD=;(2)∵S△ABC=AB•EC=×4×=2,∴.点评:本题主要考查了垂径定理以及三角函数,一些不规则的图形的面积可以转化为规则图形的面积的和或差求解.。
