结晶学第八讲—14种布拉菲格子
14种布拉菲格子
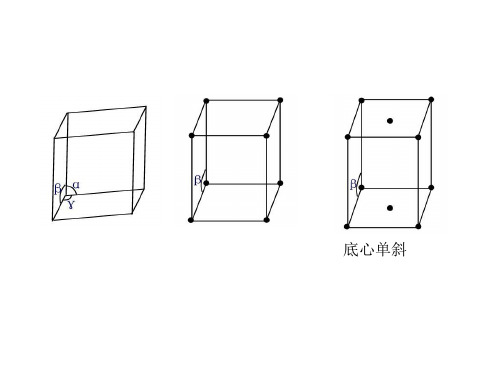
简单正交
底心正交
体心正交
面心正交
简单六方
三方菱面体
简单四方
体心四方
简单立方
体心立方
面心立方
为什么没有面心四方?
•
1、有时候读书是一种巧妙地避开思考 的方法 。20.1 2.1020. 12.10Thursday, December 10, 2020
•
2、阅读一切好书如同和过去最杰出的 人谈话 。00:3 7:2900: 37:2900 :3712/ 10/2020 12:37:29 AM
•
3、越是没有本领的就越加自命不凡。 20.12.1 000:37: 2900:3 7Dec-20 10-Dec-20
•
4、越是无能的人,越喜欢挑剔别人的 错儿。 00:37:2 900:37: 2900:3 7Thursday, December 10, 2020
•
5、知人者智,自知者明。胜人者有力 ,自胜 者强。 20.12.1 020.12. 1000:3 7:2900: 37:29D ecembe r 10, 2020
• 13、无论才能知识多么卓著,如果缺乏热情,则无异 纸上画饼充饥,无补于事。Thursday, December 10, 202
010-Dec-2020.12.10
• 14、我只是自己不放过自己而已,现在我不会再逼自 己眷恋了。20.12.1000:37:2910 December 202000:37
2020 12:37:29 AM00:37:292020/12/10
• 11、自己要先看得起自己,别人才会看得起你。12/10/
谢 谢 大 家 2020 12:37 AM12/10/2020 12:37 AM20.12.1020.12.10
布拉菲点阵——精选推荐

关于奥古斯特·布拉菲及布拉菲点阵浅析奥古斯特·布拉菲(August Bravais,1811—1863),法国物理学家,于1845年推导出了三维晶体原子排列的所有14种点阵结构,首次将群的概念应用到物理学,为固体物理学做出了重大贡献。
这是非常有意义的结论,为了纪念他,后人称这14种点阵为布拉菲点阵。
除此之外,布拉菲还对磁性、极光、气象、植物地理学、天文学和水文学等方面进行过研究。
图1 奥古斯特·布拉菲在几何学以及晶体学中,布拉菲晶格(又译布拉菲点阵)是为了纪念奥古斯特·布拉维在固态物理学的贡献命名的。
法国晶体学家布拉菲(A.Bravais)于1850年用数学群论的方法推导出空间点阵只能有十四种: 简单三斜、简单单斜、底心单斜、简单正交、底心正交、体心正交、面心正交、简单六方、简单菱方、简单四方、体心四方、简单立方、体心立方、面心立方。
根据其对称特点,它们分别属于七个晶系。
空间点阵到底有多少种排列形式?按照“每个阵点的周围环境相同”的要求,在这样一个限定条件下,法国晶体学家布拉菲(A. Bravais)曾在1848年首先用数学方法证明,空间点阵只有14种类型。
这14种空间点阵以后就被称为布拉菲点阵。
空间点阵是一个三维空间的无限图形,为了研究方便,可以在空间点阵中取一个具有代表性的基本小单元,这个基本小单元通常是一个平行六面体,整个点阵可以看作是由这样一个平行六面体在空间堆砌而成,我们称此平行六面体为单胞。
当要研究某一类型的空间点阵时,只需选取其中一个单胞来研究即可。
在同一空间点阵中,可以选取多种不同形状和大小的平行六面体作为单胞,如下图所示:其选取方式有,1.固体物理选法:在固体物理学中,一般选取空间点阵中体积最小的平行六面体作为单胞,这样的单胞只能反映其空间点阵的周期性,但不能反映其对称性。
如面心立方点阵的固体物理单胞并不反映面心立方的特征。
2.晶体学选法:由于固体物理单胞只能反映晶体结构的周期性,不能反映其对称性,所以在晶体学中,规定了选取单胞要满足以下几点原则:①要能充分反映整个空间点阵的周期性和对称性;②在满足①的基础上,单胞要具有尽可能多的直角;③在满足①、②的基础上,所选取单胞的体积要最小。
晶体学基础知识点及思维导图

HOMEWORKS知识点晶体结构Crystal structure 点阵结构Lattice晶胞Unit cells晶系Crystal systems布拉菲格子The Bravais lattices点群point group空间群space group关系Relationships/思维导图Mind mapping具体中文解释粒子抽象成点,形成了点阵结构,而这些点连接起来就形成了晶格,可以说点阵和晶格具有同一性,但区别于点阵具有唯一性,晶格不具有。
同样我们需要区别“lattice ”的意义 它在这应该准确的代表点阵结构而不是单单的点阵,点阵结构是具体的客观存在的而点阵是人为抽象出来的,相比于点阵对应的点阵点,点阵结构对应的就是结构基元。
晶胞堆砌成了点阵结构,晶胞又具有晶胞参数和晶胞内容两方面,也就是说可以这么表示晶胞=点阵格子+结构基元。
根据晶胞的晶胞参数我们可以把晶体的结构从宏观上分为七个方面,也就是七大晶系.七大晶系结合晶胞类型产生了14种Bravais晶格点群表示的是晶体中所包含所有点对称操作的(旋转、反应、反演)的集合。
(晶体的宏观性质不变)。
点群描述了分子结构和晶体的宏观对称性(后来老师讲点群只是对于结构基元里的原子的对称排布,我个人后来查阅思考了一下,这是局限的,点群所描述的对称性正是可以描述宏观的晶格以及肉眼可见的晶体的对称性,所以它才被引为宏观对称性。
)微观对称元素:点阵、滑移面、旋转轴(无数阶次)而晶体的宏观对称元素和微观对称元素在内的全部对称元素的一种组合就构成晶体的一种微观对称类型也就是空间群,它反应的是内部微观结构的对称性(结构基元内部原子)或者是微观的晶胞堆积方式的不同。
晶体的宏观对称性就是晶体微观对称性的宏观表现。
晶系与对称的关系:七种晶系从宏观的对称操作来看,有旋转、反射、反演,这些构成的是32种点群。
而晶系必须符合平移操作(晶体对称定律的要求),结合平移我们限定了它有14种Bravais 格子。
固体物理学-晶格结构的分类

注:四方也不可能有底心(或面心),假如有,则破坏了“点
阵点最少”的原则,还可画出只有一个点阵点的格子。
Solid State Physics
三角和六角晶系的关系
(1)围绕z 轴旋转一周,三角晶系晶体的横轴可以重合三次,六角晶系的横轴则重合六次
(2)三角晶系有两种格子,其中一种和六方格子相同(注意对称轴不同)
另外一种则为三角晶胞(菱面三角晶胞),通常也采用六角晶胞来进行描述,
称为R心六角晶胞
(3)六角格子中,部分属于六角晶系,部分属于三角晶系
Solid State Physics
“底心四方”
“面心四方”
Solid State Physics
单斜(P)
单斜(C)
晶胞类型: a b c
三斜(P)
固体物理
Solid State Physics
1.7 晶格结构的分类
Solid State Physics
晶胞的选取
晶格对称性
基矢的模=晶轴上的周期(晶格常数)
晶胞的基矢方向=晶轴方向
十四种布喇菲格子
格点分布特点
晶胞基矢的特征
七大晶系
റ
、、
റ
റ 为布喇菲原胞三个矢,
റ
՜
՜
、、 分别为 与 ՜
晶胞类型:a b c
90
90
90
在这些型式中,其对称性由高到低的排列顺序为:
立方﹥六方﹥三方﹥四方﹥正交﹥单斜﹥三斜
Solid State Physics
立方
a
a
a
三方
六方
四方
c
a
a a
晶体结构知识

晶体结构
1.拉伐格子
布拉伐格子指的是多个点在空间格子的排列组合,任何晶体的宏观对称型都可以归结为其原子分布所对应的布拉伐格子的对称性。
三维空间的布拉伐格子总共有十四种,详见下表
2.晶系与布拉伐格子及空间点群的关系
晶系布拉伐格子所属点群
三斜晶系简单三斜C1, C i
单斜晶系简单单斜底心单斜C2 C s C2h
正交晶系简单正交底心正交体心正交面心正交D2 C2v D2h
三角晶系三角C3 C3i D3 C3v D3d
四方晶系简单四方体心四方C4 C4h D4 C4v D4h S4 D2d 六角晶系六角C6 C6h D6 C3v D6h C3h D2h 立方晶系简单立方体心立方面心立方T T h T d O O h
3.单质的晶体结构
单质的晶体结构
名称英文名称代号晶格类型晶系金属铜结构 metallic copper structure A1型面心立方晶格立方晶系
金属钠结构 metallic sodium structure A2型体心立方晶格立方晶系
金属镁结构 metallic magnesium structure A3型六方密排晶格六方晶系
金刚石结构 diamond structure A4型立方晶系
石墨结构graphite structure A9型六方晶系4.化合物的晶体结构。
称作布拉菲晶格

參考資料
• .tw/~wangzen/3.htm • /zhtw/%E6%99%B6%E4%BD%93%E7%BB%93%E6%9E %84 • /wiki/%E7%BB%B4%E6%A0%BC %E7%BA%B3%E8%B5%9B%E5%85%B9%E5%8E%9F%E8%83%9E • Introduction to Solid State Physics 8/e 原著:Kittel • /wiki/%E6%99%B6%E6%A0%BC
批注本地保存成功开通会员云端永久保存去开通
固態物理 第一章-晶體結構
指導老師: 陳美利 學生: 光電三甲 499L0104 石崇甫 499L0903 楊鎮嘉
目錄
1. 2. 3. 4. 5. 6. 7. 8. 9. 晶體結構………………………………..3 晶體結構特性…………………………..4 晶系……………………………………..5 維格納-賽茲原胞……………………..6 晶胞的構造……………………………..7 二維晶格類型…………………………..8 布拉菲晶格……………………………10 三維晶格類型…………………………11 立方晶系………………………………12
2
晶體結構
• 晶體結構是指晶體的周期性結構。固體材料可以分為晶體, 准晶體和非晶體三大類,其中,晶體內部原子的排列具有 周期性,外部具有規則外形。 • Hauy最早提出晶體的規則外形是因為晶體內部原子分子 呈規則排列,比如鑽石所具有的完美外形和優良光學性質 就可以歸結為其內部原子的規則排列。20世紀初期,勞厄 發明X射線繞射法,從此人們可以使用X射線來研究晶體 內部的原子排列,其研究結果進而證實了Hauy的判斷。 • 對於晶體結構的研究是研究固體材料的宏觀性質及各種微 觀過程的基礎。專門研究分子結晶結構的科學稱為晶體學, 經常應用在化學、生物化學與分子生物學。
对称性和布拉维格子的分类
群论作为数学的分支,是处理有一定对称性 的物理体系的有力工具,可以简化复杂的计算, 也可以预言物理过程的发展趋势,还可以对体 系的许多性质作出定性的了解。 群及其表示理论是物理系研究生的一门重要 基础课,对于本科生不作要求。因此,我们不 打算在这里讲过多的群论的知识。只是简单介 绍一下,让大家对群的概念有一个认识。 一、群的知识简介 1. 群的定义 ts)或操 作的集合,常用符号 G 来表示。
Ai Aj Ak , i j or i j
2). 群中一定包含一个不变元素(单位元素) E E G, EAi Ai E Ai 3). 存在逆元素 Ai G, Ai1 Ai Ai1 Ai1 Ai E
4). 满足组合定则
( Ai Aj ) Ak Ai ( Aj Ak )
因为B 和A 完全等价,所有旋转同样可以绕B 进行. 由此可设想绕B 转角,这将使A 格点转到 A的 位臵。同样 A处原来也必定有一个格点
显然n=1,相当于不动操作(元素)E, n=2,3,4,6的转轴分别称为二度、三度、四度、 六度转轴
晶体的对称性定律的证明
B
A
如图,A为格点,B为离A最近 a a 的格点之一,则与 AB 平行的 格点之间的距离一定是 AB a B A 的整数倍。 如果绕A转角,晶格保持不变(对称操作).则该 操作将使B格点转到B’ 位臵,则由于转动对称操作 不改变格子,在 B’ 处必定原来就有一个格点。
在晶体的几何对称性的研究中,每一个能 使晶体复原的对称操作,都满足上述群中的 元素的要求,由这些元素(或操作)所构成的 群叫对称性群(symmetry group),包括点群 (point group)和空间群(space group)
1830年,赫塞耳(Johann Friedrich Christian Hessel)首先导出了32种点群,由32种点群出发, 可以对布拉维点阵进行分类,这正是1850年布 拉维所作的工作,他证明了只有7个晶系。(点 群不含平移对称操作,因为平移导致任何格点 都要动,而点群必须至少有一个格点不动) 熊夫利(Schoenflies1891)和费奥多罗夫 (Fedorove 1892) 为了研究复式晶格(几套简单 格子的平移)的分类,考虑了平移对称操作, 提出了空间群的概念,并证明只有230种独立 的空间群。 1850年布拉维由此证明只有14种 三维布拉维点阵
晶体学基础第二章-晶体的对称分类与布拉菲点阵
2.晶系(crystal system):7个晶系
三斜晶系:只有 1 或 1
单斜晶系:2 和 m 均不多于一个 正交晶系(斜方晶系):2 和 m 的总数不少于3个
三方晶系:唯一的一个高次轴是 3 或 3 四方晶系:唯一的一个高次轴是 4 或 4 六方晶系:唯一的一个高次轴是 6 或 6
立方晶系(等轴晶系):有4个 3
32种点群描述的晶体对称性对应的只有14种布拉菲点阵分为7个晶系沿晶体的对称轴或对称面的法向在一般情况下它们构成斜坐标系三个晶轴之间的夹角二晶体的14种布拉菲点阵布拉菲格子
2.4 晶体的对称分类与布拉菲点阵
一、晶体的对称分类
按晶体的对称性特征晶体分类
1.晶族(crystal category):3个晶族 低级晶族:无高次轴 中级晶族:只有一个高次轴 高级晶族:高次轴多于一个
3.晶类: 属于同一点群的晶体。32个晶类。
二、晶体的14种布拉菲点阵(布拉菲格子)
—— 32种点群描述的晶体对称性 —— 对应的只有14种布拉菲点阵 —— 分为7个晶系
—— 单胞的三个基矢
沿晶体的对称轴或对称面
的法向,在一般情况下,它们构成斜坐标系
三个晶轴之间的夹角
7大晶系的形成
固体物理第一章 7-8
p 1, p 2 k h k hkl n n
'
d h1h2 h 3 d hkl
d h1h2 h 3 d hkl / 2
结晶学中的衍射级数都是偶数
立方晶系(001)面
( h1h2 h3 ) 1 {( h k l )( h k l )( h k l )} p
14种布拉伐原胞
1) 简单三斜
2) 简单单斜 3) 底心单斜
4) 简单正交
5) 底心正交 6) 体心正交 7) 面心正交
a1 a2 a3
a1 a2 a3
8) 三角
900 1200
a1 a2 a3
9) 简单四方(四角) 10) 体心四方(四角)
2 * * b3 (i j ) a b a
则
* * K h h1b1 h2 b2 h3b3 (h2 h3 )a (h3 h1 )b (h1 h2 )c *
与 K h pK hkl
比较得到
可见p是(h2+h3)、(h3+h1)、(h1+h2)的公因数,是一 个整数。同样可以得到 p K hkl Kh 2
则两者平行,有
K h pK hkl
2 * * b1 ( j k ) b c a
2 * * b2 (k i ) c a a
对于体心立方元素晶体
* 2 1 a i (b1 b2 b3 ) a 2 * 2 1 b j (b1 b2 b3 ) a 2 * 2 1 c k (b1 b2 b3 ) a 2
chap结晶学及矿物学 (25)
二十四、十四种空间格子(布拉维格子)
七个晶系---七套晶体常数—七种平行六面体形状。
每种形状有四种类型,那么就有7×4=28种空间格子?
但在这28种中,某些类型的格子彼此重复并可转换,还有一些不符合某晶系的对称特点而不能在该晶系中存
在,因此,只有14种空间格子,也叫14种布拉维格子。
(A.Bravais于1848年最先推导出来的)
例1:四方底心格子=四方原始格子
所以,在14种布拉维格子中,四方底心格子不需要保留。
例2:立方底心格子不符合等轴晶系对称。
所以,在14种布拉维格子中,立方底心格子不存在。
那么请思考:立方底心格子符合什么晶系的对称?
还应指出的是:对于三、六方晶系的四轴定向也可转换成三轴定向,变为菱面体格子。
现在对于三、六方晶系都用四轴定向。
四轴定向的格子形状为菱形柱。
另外,六方原始格子为六方柱的顶底面加心,不要误认为六方底心格子。
十四种空间格子见表7-1。
四轴定向格
子三轴定向格子两种格子的转换
表7-1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复习:
点对称操作、7种晶系、32种点群
点对称操作
1 (E, L1) 2 (C2, L2) 3 (C3, L3) 4 (C4, L4) 6 (C6, L6)
旋转轴, n
360o/n (n = 1,2,3,4,6)
1 (i, C) 2 (σ, P), m
+, + _, +
3 (S65, Li3)
y
系
y
x
x
没有4次真旋转轴!
432 (43, 3L44L36L2)
z
立
方
晶 系
y
y
x
x
有4次轴!
x
z y
X
y
X
m3 (2/m3, 3L24L33PC) x
m3m (4/m32/m,3L44L36L29PC)
z
立
方
晶 系
y
y
x
x
有4次轴!
y
432 (43, 3L44L36L2) x
23 (3L24L3)
4
[2,2]
centrosymmetric
8
[4]+ enantiomorphic polar 4
cyclic cyclic 2×cyclic dihedral dihedral 2×dihedral Cyclic
x
3、4、2次轴
23 (3L24L3)
立 方
{3[111]}{3[111]} = {2[010]}
X
z
晶
y
系
X
y
x
x
没有4次轴!
32 (L33L2)
y
x
m3 (2/m3, 3L24L33PC)
立
z
方
X
晶
y
系
X
y
x
x
没有4次轴!
X
y
没有4次轴! 左右手问题
X
x
43m (3Li44L36P)
立
z
方 晶
种 (L2PC) (3L23PC) (L44P)
(L66P)
(3Li44L36P)
点 群
4/mmm 6/mmm 3(Li3)
(L44L25PC) (L66L27PC)
432
(3L44L36L2)
及
y
其
422
622
3m
m3m
点
x
(L44L2)
(L66L2)
(Li33L23P) (3L44L36L29PC)
推导32种点群的熊夫利斯方案 熊夫利斯符号
五种循环群 Cn (5 种) Cnh = Cn × {E, σh} (5 种) Cnv = Cn × {E, σv} (4 种, C1v = C1h) Dn = Cn × {E, C2[100] } (4 种) Dnh = Cnh × {E, d} (4 种)
100
101
001
面、方向、轴
110
111
z
011
010 y
111
y
101
x
110
100
x
45o, 54o44’ ,109o28’
35o16’ , 70o32’, 60o
110
111
010
011
111 110
100
一般点及其操作
110
101
111
001
011
010 y
z
111 101
110
y
x
100
L44L2)
4 (Li4)
42m (Li42L22P)
四
方
晶 系
4 (L4)
4/m
(L4PC)
4mm
(L44P)
4/mmm
(L44L25PC)
422 (42, L44L2)
4 42m (Li4)
(Li42L22P)
一般形,可直观地反映(尤其是同一晶系)各点群的差别
110
111
010
011
111 110
立方 4、4、2或2
沿<100>
3或3沿<111>
2或2沿<110>
1(L1) 2(L2) 222(3L2) 4(L4)
6(L6)
3(L3)
23(3L24L3)
1(C) m(P) mm2 4/m
(L22P) (L4PC)
6/m
(L6PC)
3m
(L33P)
m3
(3L24L33PC)
32 2/m mmm 4mm 6mm 32(L33L2) 43m
[ ]+ enantiomorphic polar 1
trivial
[2,1+]
centrosymmetric
2
cyclic
[2,2]+ enantiomorphic polar 2
[]
polar
2
[2,2+]
centrosymmetric
4
[2,2]+
enantiomorphic
4
[2]
polar
S6 (C3i)
D3 C3v D3d C6
C3h
C6h D6 C6v D3h D6h T Td Th O Oh
1
2 m 2/m 222 mm2 mmm 4
4/m 422 4mm 2m or m2 4/mmm
3
32 or 321 or 312 3m or 3m1 or 31m
m or m1 or 1m 6
1 twofold axis of rotation or 1 mirror plane
3
13
2
Monoclinic
Orthorhombic
3 twofold axes of rotation or 1 twofold axis of rotation and two mirror planes.
3
从旋转点群推导32种点群 点群的熊夫利斯符号
11种纯旋转群:
1234 6
C1 C2 C3 C4 C6 循环点群
222 32 422 622
D2 D3 D4 D6 二面体点群
11种中心对称点群:
23 432
TO 立方点群
1 2/m 3 4/m 6/m mmm 3m 4/mmm 6/mmm m3 m3m
trigonal-pyramidal
rhombohedral
trigonal-trapezoidal ditrigonal-pyramidal ditrigonal-scalahedral hexagonal-pyramidal
trigonal-dipyramidal
hexagonal-dipyramidal hexagonal-trapezoidal dihபைடு நூலகம்xagonal-pyramidal ditrigonal-dipyramidal dihexagonal-dipyramidal
对
4 (Li4)
6 (Li6)
称
操
42m 62m
y
作
(Li42L22P) (Li63L23P)
x
按晶系推到点群举例
正
交
y
y
y
晶
系
x
x
x
222
(3L2)
mm2
(L22P)
mmm
(3L23PC)
按晶系推到点群举例
四
方
晶
系
4 (L4)
4/m
(L4PC)
4mm
(L44P)
4/mmm
(L44L25PC)
422 (42,
(C41, C42, C43, C44 )
6 (C6, L6)
(C61, C62, C63, C64 , C65, C66 )
n = 1n (iCn), Sn = σCn !!!
1 (i, C)
2 (σ, P), m (σh, σv, σd)
3 (S65, Li3)
S6, S62(C3), S63(i), S64(C32), S65, S66(E)
非真旋转 Sn (3 种,n =2, 4, 6) Dnd = S2n × {E, C2[100] } (n =2, 3 共2种)
立方点群(无主轴)5 种: T, Th, Td, O, Oh
crystal family crystal system triclinic
monoclinic orthorhombic
59
4
Orthorhombic
Tetragonal
1 fourfold axis of rotation
7
68
2
Tetragonal
Hexagonal
Trigonal Hexagonal
1 threefold axis of rotation 1 sixfold axis of rotation
7 5
S2 C2h S6 C4h C6h D2h D3d D4h
D6h
Th Oh
10种新子群:
1 2/m 3 4/m 6/m mmm 3m 4/mmm 6/mmm m3 m3m
m
4 6 mm2 3m 4mm 42m 6mm 62m
43m
C1h
S4 C3h C2v C3v C4v D2d C6v D3h
Td
tetragonal
trigonal hexagonal
hexagonal
cubic
point group / crystal class
