函数的凸性
函数凹凸的定义

02 函数凹凸的几何意义
凹函数的几何意义
凹函数图像呈下凹状,即对于函数图 像上的任意两点A和B,如果A、B两 点连线的中点始终位于A、B连线的下 方,则该函数为凹函数。
在几何意义上,凹函数具有一个明显 的特征,即函数图像上任意两点的连 线的斜率始终小于或等于该点处的函 数导数。
凸函数的几何意义
通过分析函数的凹凸性,我们可以确定函数的拐点,从而更好地理解函数 的性质,为求解最优化问题提供指导。
在求解无约束最优化问题时,可以利用函数凹凸性选择合适的算法,如梯 度下降法、牛顿法等,以提高求解效率。
在经济学中的应用
函数凹凸性在经济学中也有 广泛应用,它可以帮助我们 理解经济现象和预测经济行
为。
函数凹凸的定义
目录
• 函数凹凸的基本概念 • 函数凹凸的几何意义 • 函数凹凸的判定方法 • 函数凹凸的应用 • 函数凹凸的反例 • 函数凹凸的扩展知识
01 函数凹凸的基本概念
凹函数
01
凹函数是指函数图形在任意两点 之间总是位于这两点连线的下方, 即对于定义域内的任意x1和x2, 都有 f((x1+x2)/2)≥f(x1)+f(x2)/2。
03
在计算机科学中,函数凹凸性可以帮助我们设计更有效的算法和数据 结构,如动态规划、图算法等。
04
在生物学中,函数凹凸性可以帮助我们理解生物系统的复杂性和行为, 如生态学、生物化学反应等。
05 函数凹凸的反例
凹函数的反例
总结词
凹函数的反例是指函数图像呈现下凹形状的反例。
详细描述
凹函数的反例通常是指那些在一定区间内,函数值随着自变量的增加而减少的函数。例如,二次函数 $f(x) = x^2$在区间$(-infty, 0)$内是一个凹函数的反例,因为在这个区间内,函数值随着$x$的增加 而减少。
求导与函数的凹凸性

求导与函数的凹凸性在微积分中,求导是一个重要的概念,它能够帮助我们研究函数的性质和特点。
而函数的凹凸性则是求导的一个应用,通过求导我们可以判断一个函数在某一区间内是凹函数还是凸函数,进而对函数的性质有更深入的认识。
一、求导的基本概念求导是微积分的基础概念之一,它表示函数在某一点的变化率。
一个函数在某一点处的导数,可以理解为该函数在该点处的斜率。
求导的基本公式是:\[f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}\]二、凹凸函数的定义凹凸函数是指函数在其定义域上的曲线形状,具有凹形或凸形的特点。
凹函数指曲线上的任意两点的割线位于曲线的下方或与曲线重合,而凸函数则相反。
凹函数的导数递增,凸函数的导数递减。
在求导的过程中,我们可以通过函数的一、二阶导数来判断函数的凹凸性。
三、求导与凹凸性的关系对于一个函数而言,通过求导可以得到其一阶导数和二阶导数。
一阶导数可以帮助我们判断函数的递增区间和递减区间,而二阶导数则能够帮助我们判断函数的凹凸性。
1. 一阶导数与凹凸性的关系对于一个函数而言,如果在某一区间内它的一阶导数恒大于0,则该函数在该区间内是递增的;如果一阶导数恒小于0,则函数在该区间内是递减的。
当一阶导数从正值逐渐减小到负值时,函数的凹凸性发生改变。
当一阶导数从正值变为负值时,函数的凹凸性由凸转为凹;当一阶导数从负值变为正值时,函数的凹凸性由凹转为凸。
2. 二阶导数与凹凸性的关系对于一个函数而言,如果在某一区间内它的二阶导数恒大于0,则该函数在该区间内是凹的;如果二阶导数恒小于0,则函数在该区间内是凸的。
当二阶导数从正值逐渐减小到负值时,函数的凹凸性发生改变。
当二阶导数从正值变为负值时,函数的凹凸性由凹转为凸;当二阶导数从负值变为正值时,函数的凹凸性由凸转为凹。
综上所述,通过求导我们可以得到函数的一阶导数和二阶导数,进而判断函数的递增区间、递减区间以及凹凸性的改变。
函数的凹凸性ppt课件

一、曲线的凹凸性与拐点
1
一、曲线的凹凸性与拐点
如图,观察抛物线 y x2 , y x ,它们
在区间[0,1]上都是单调增加的,但弯曲的方向
不一样。
y
这说明,在研究函数的图形时,
仅知道他们的单调性是不够的, 1
还需要考察曲线的弯曲方向及 扭转弯曲方向的点。
o1
x
2
二、凹凸与拐点的定义 y
② f (x1 x2 ) f (x1 ) f (x2 ) ;
③ f (x1 ) f (x2 ) 0; x1 x2
④ f ( x1 x2 ) f (x1 ) f (x2 ) .
2
2
当 f (x) lg x 时,上述结论中正确结论的序号
是
.
9
10
【详解】
对于①②可以用 f (x) lg x
y log2 x 在 0 x 1内为凸函数。所以答案为 B。
点评:只要能作出这四个初等函数的草图,马上根据函数 的凹凸性可直接作结论.
8
典例 2.(05 北京理工科 13).对于函数 f (x) 定义域中
任意的 x1 , x2 (x1 x2 ) ,有如下结论:
① f (x1 x2 ) f (x1 ) f (x2 ) ;
的研究函数的一个概念,是用来研究函数图象的变化趋 势的。
【高考联接】在高考中常借助函数的凹凸性来考查基
本初等函数的图象及性质,这一知识点常渗透在与函数 的图象与性质的选择填空题中。经常与高中所学的函数、 三角、不等式知识相结合。此类问题的常规处理思路有 数形结合法、导数分析法、增量分析法、估猜法等。
y (1)x a
• (0,1)
y ax (a 1)
16
函数的凹凸性

yloagxa
3、幂函数
yx y
y x2
1
(是常)数
yx y x
(1,1)
o1
x
y 1 x
6、双曲函数
由 ex, ex 构成.
ycosxh
双曲 si正 n xh ex 弦 ex
2 y 1ex
D:(, ), 奇函数.
(2) 如果x 0,1 时 f (x) 1,试求实数a的范围。
解析:(1)对任意的
x, 1
x 2
R,
a
0
,
f (x ) 1
f (x ) 2
2
f
(
x 1
x 2
)
=
2
ax2 1
x 1
ax2 2
x 2
2a(
x 1
2
x 2
)2
x 1
2
x 2
A
o
x
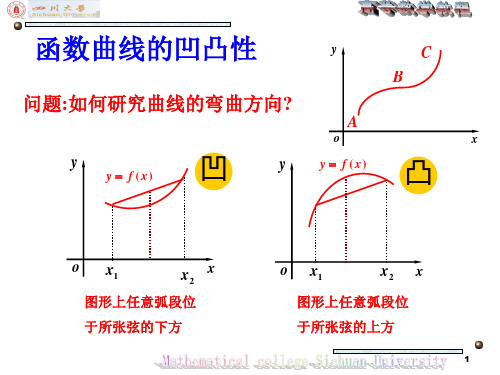
问题: 如何用准确的数学语言描述曲线的凹凸性?
y
yf(x)
y yf(x)
o x1
x2 x
图形上任意弧段(的中点)
位于所张弦的下方。
o x1
x2 x
图形上任意弧段(的中点)
位于所张弦的上方。
二、曲线的凹凸性与拐点
y
C
问题:如何研究曲线的弯曲方向?
B
y
yf(x) f(x1) f(x2)
2
解析:答案为 B。要使 f ( x1 x2 ) f (x1 ) f (x2 ) 恒成
2
2
立,由函数值的定义及函数图象即需要函数在 0 x 1
《函数的凹凸性》课件

凸函数的性质
凸函数图像呈上凸状,即对于函数图像上的任意两点A(x1, y1)和B(x2, y2),当x1 < x2时,y1 < y2。
凸函数的导数在定义域内小于0,即f''(x) < 0。
凸函数具有局部最大值,即对于任意x0属于定义域,存在一个邻域使得 该邻域内所有点的函数值都小于或等于f(x0)。
在物理学中,凹凸性可以用于描述物 体的弹性、光学性质等。
在经济学中,凹凸性可以用于描述商 品的需求和供给关系,以及价格和产 量的变化关系。
在计算机科学中,凹凸性可以用于图 像处理、机器学习等领域。
02
函数的凹凸性判定
判定方法一:二阶导数法
总结词
举例说明
二阶导数法是判断函数凹凸性的常用 方法之一,通过计算函数的二阶导数 并分析其符号来判断函数的凹凸性。
05
实际应用案例
金融领域的应用
金融数据分析
函数的凹凸性在金融数据分析中有着广泛的应用,如股票价格、收益率等金融时间序列数 据的分析,通过识别数据的凹凸性,可以预测未来的价格走势和风险评估。
投资组合优化
在投资组合优化中,凹凸性可用于确定最优投资组合,通过最小化投资组合的风险或最大 化预期收益,实现资产的有效配置。
判定方法三:几何意义法
总结词
几何意义法是通过观察函数图像 ቤተ መጻሕፍቲ ባይዱ几何形状来判断函数的凹凸性
。
详细描述
如果一个函数的图像是一条向下 凸出的弧形线,则该函数是凹的 ;如果图像是一条向上凸起的弧
形线,则函数是凸的。
举例说明
以函数$f(x) = x^4 - x^2$为例 ,通过绘制该函数的图像可以观 察到,该函数在$x < 0$时图像 向下凸出,因此函数$f(x) = x^4
函数的凹凸性,极值
y
y f (x) B
y y f (x)
B
A
oa
bx
f ( x) 递增 y 0
A oa
f ( x) 递减
bx y 0
4
四、曲线凹凸的判定
定理2 如果 f ( x) 在 [a,b] 上连续,在 (a,b) 内具有
二阶导数 ,若在 (a,b)内 (1) f ( x) 0,则 f ( x) 在 [a,b] 上的图形是凹的; (2) f ( x) 0,则 f ( x) 在 [a,b] 上的图形是凸的.
f (x1)
f
(
x2
)
2
f
(
x1
2
x2)
1 2!
(
x2
2
x1
)
2
[
f
(1)
f (2 )]
当 f (x) 0时,
f
( x1) 2
f
(x2 )
f (x1 x2 ),
2
说明 (1) 成立; (2)
7
例2 判别曲线 y 1 的凹凸性. x
解 函数的定义域为 ( , 0) U (0, ) .
故 f (t) et 所对应的曲线在 ( , ) 内是凹的 . x, y ( , ) , 由曲线凹性的定义, 有
1
(e x
e
y
)
e
x y 2
,
(x y) .
2
9
y
y x3
O
在 (, 0)上 , y x3是凸的,
此时 y 0 .
在 (0, )上 ,
x
y x3 是凹的,
此时 y 0 .
f ( x) 0 ( x x0 )
14
函数的凹凸性与拐点
得证.
15
不等式证明的方法:
1、拉格朗日中定理;
2、函数的单调性、极值; 3、函数的凹凸性;
16
作业:
P 3 134
17
爱是什么? 一个精灵坐在碧绿的枝叶间沉思。 风儿若有若无。 一只鸟儿飞过来,停在枝上,望着远处将要成熟的稻田。 精灵取出一束黄澄澄的稻谷问道:“你爱这稻谷吗?” “爱。” “为什么?” “它驱赶我的饥饿。” 鸟儿啄完稻谷,轻轻梳理着光润的羽毛。 “现在你爱这稻谷吗?”精灵又取出一束黄澄澄的稻谷。 鸟儿抬头望着远处的一湾泉水回答:“现在我爱那一湾泉水,我有点渴了。” 精灵摘下一片树叶,里面盛了一汪泉水。 鸟儿喝完泉水,准备振翅飞去。 “请再回答我一个问题,”精灵伸出指尖,鸟儿停在上面。 “你要去做什么更重要的事吗?我这里又稻谷也有泉水。” “我要去那片开着风信子的山谷,去看那朵风信子。” “为什么?它能驱赶你的饥饿?” “不能。” “它能滋润你的干渴?” “不能。”爱是什么? 一个精灵坐在碧绿的枝叶间沉思。 风儿若有若无。 一只鸟儿飞过来,停在枝上,望着远处将要成熟的稻田。 精灵取出一束黄澄澄的稻谷问道:“你爱这稻谷吗?” “爱。” “为什么?” “它驱赶我的饥饿。” 鸟儿啄完稻谷,轻轻梳理着光润的羽毛。 “现在你爱这稻谷吗?”精灵又取出一束黄澄澄的稻谷。 鸟儿抬头望着远处的一湾泉水回答:“现在我爱那一湾泉水,我有点渴了。” 精灵摘下一片树叶,里面盛了一汪泉水。 鸟儿喝完泉水,准备振翅飞去。 “请再回答我一个问题,”精灵伸出指尖,鸟儿停在上面。 “你要去做什么更重要的事吗?我这里又稻谷也有泉水。” “我要去那片开着风信子的山谷,去看那朵风信子。” “为什么?它能驱赶你的饥饿?” “不能。” “它能滋润你的干渴?” “不能。”
《函数凹凸性》课件
在函数图像上,凸函数表现为图像位于其连接直线的上方。
凹凸函数的几何意义
凹函数的几何意义
在凹函数的图像上,任意两点之间的线段都位于这两点之间函数的曲线下方。这 表明,对于凹函数,中点的函数值总是大于或等于两端点连线上中点的函数值。
凸函数的几何意义
在凸函数的图像上,任意两点之间的线段都位于这两点之间函数的曲线上方。这 表明,对于凸函数,中点的函数值总是小于或等于两端点连线上中点的函数值。
几何意义
在函数图像上,凹函数表现为图像位于其连接直线的下方。
凸函数的定义
凸函数
对于函数$f(x)$,如果在区间$I$上,对于任意$x_1, x_2$( $x_1 < x_2$)都有$f(x_1) + f(x_2) < 2f[(x_1 + x_2)/2]$, 则称$f(x)$在区间$I$上是凸函数。Βιβλιοθήκη 4凹凸性在优化问题中的应用
利用凹凸性求解优化问题
01
确定函数的凹凸性
首先需要判断函数的凹凸性,可以通过求二阶导数或观察函数图像来进
行判断。
02 03
利用凹凸性寻找极值点
在确定了函数的凹凸性之后,可以利用凹凸性寻找函数的极值点。在凹 函数中,极值点出现在二阶导数为0的点;在凸函数中,极值点出现在 边界点或一阶导数为0的点。
有$f(x_1) + f(x_2) < 2fleft(frac{x_1 + x_2}{2}right)$,则称$f(x)$在区间$I$上是凸函数。
二次导数法
总结词
通过判断一阶导数的正负来判断函数 凹凸性的常用方法
详细描述
如果函数$f(x)$的二阶导数$f''(x) > 0$,则函数$f(x)$为凹函数;如果二 阶导数$f''(x) < 0$,则函数$f(x)$为 凸函数。这种方法适用于一阶导数容 易计算或形式较为简单的函数。
函数凹凸性
2) 根据拐点的定义, 可得拐点的判别法如下:
若曲线
或不存在,
但 f (x) 在 x0 两侧异号, 则点(x0 , f (x0 )) 是曲线
的一个拐点.
求拐点的步骤见教材P162.
机动 目录 上页 下页 返回 结束
例4. 求曲线
的上(下)凸区间及拐点.
解: 1) 求 y
y 12x3 12x2,
36x(x 32)
机动 目录 上页 下页 返回 结束
(2) 若恒有
则称
图形是上凸的; 或称f (x)为I上的上凸函数。
弦在弧的下方;切线在曲线的上方。
下凸也称为凸,上凸也称为凹。 y
o
x1 x1 x2 x2 x
2
机动 目录 上页 下页 返回 结束
等价定义:
定义1´:设函数 在区间 I 上连续 ,
(1) 若恒有
则称
f (1) f (0) f ( ) (0 1)
机动 目录 上页 下页 返回 结束
作业
P168 1(3,6);2 ; 3; 5(1,3) 6(3,4);7(2)
第七节 目录 上页 下页 返回 结束
例如, 双曲线
L PN
o
x
有渐近线
x y0
y
ab
但抛物线
无渐近线 .
ox
机动 目录 上页 下页 返回 结束
1. 水平与铅直渐近线
若
则曲线
有水平渐近线 y b.
(或x )
若
则曲线
有垂直渐近线 x x0 .
(或x x0 )
例1. 求曲线
的渐近线 .
解: lim ( 1 2) 2
2
x x 1
证明:
令
函数的凸凹性及其应用
函数的凸凹性及其应用定义:函数的凸凹性 定义:如果函数()f x 对其定义域中任意的1x ,2x 都有[])()(21)2(2121x f x f x x f +≤+成立,则称)(x f 是下凸(凸)函数(如图1所示),当且仅当21x x =时等号成立.如果函数()f x 对其定义域中任意的1x ,2x 都有[])()(21)2(2121x f x f x x f +≥+成立,则称)(x f 是上凸(凹)函数(如图2所示),当且仅当21x x =时等号成立.定理1 (Jensen 不等式)若函数()f x 在区间I 是上凸函数,则有不等式:)()()()(22112211n n n n x f q x f q x f q x q x q x q f +++≥+++ ;若函数()f x 在区间I 是下凸函数,则有不等式:)()()()(22112211n n n n x f q x f q x f q x q x q x q f +++≤+++ ,其中n i q I x i i,,2,1,0, =>∈;121=+++n q q q .定理2 若)(x f 是下凸函数,则其对应定义域中的任意n 个点n x x x ,,21恒有:[])()()(1)(2121n n x f x f x f nn x x x f +++≤+++ ;类似地,对于上凸函数有:[])()()(1)(2121n n x f x f x f nn x x x f +++≥+++ ,当且仅当n x x x === 21时等号成立.定理3:设函数)(x f 在开区间I 上存在二阶导数:(1)若对任意I x ∈,有0)(>''x f ,则)(x f 在I 上为下凸函数; (2)若对任意I x ∈,有0)(<''x f ,则)(x f 在I 上为上凸函数.下面对于一些常用的的函数的凹凸性作一个探讨.(1)对数函数:)10(log ≠>=a a x y a 且若10<<a ,则为下凸函数;若1>a,则为上凸函数. (2)指数函数)1,0(≠>=a a a y x且为下凸函数.(3)三角函数sin (0,)(,23cos (,)(,2222tan (,0)(022y x x x y x x x y x x x πππππππππ=∈∈=∈-∈=∈-∈,是上凸函数;)是下凸函数;,是上凸函数;)是下凸函数;,是上凸函数;,)是下凸函数.(4)二次函数:)0(2≠++=a c bx ax y若0>a ,则为下凸函数;若0<a ,则为上凸函数.(5)反比例函数:)0(≠=k xky当0>k 时: 若)0,(-∞∈x ,则为上凸函数;若),0(+∞∈x ,则为下凸函数. 当0<k 时: 若)0,(-∞∈x ,则为下凸函数;若),0(+∞∈x ,则为上凸函数.(6)双勾函数:)0,0(>>+=b a xbax y当)0,(-∞∈x 时,为上凸函数;当),0(+∞∈x 时,为下凸函数.T1 设()y f x =是(),a b 上的严格凸函数,则对于(),a b 内的任意n 个点12,,,n x x x ,都有()()()()12121n n x x x f f x f x f x n n+++⎛⎫≤+++ ⎪⎝⎭ ,当且仅当12n x x x === 时等号成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有关函数的凸性问题
柴全水
(新绛中学 山西 043100)
在高中数学的函数部分,我们在研究函数性质时,除了研究学习函数的单调性、奇偶性、周期性等这些性质外,特别还要注意到函数的凸性性质,下面我从三方面来谈函数的凸性问题(图象、代数定义、导数)
一. 首先从图象上直观认识函数的凸性问题
①图为上凸增函数 ②图为上凸减函数 ③图为下凸增函数 ④图为下凸减函数 二. 代数定义上凸、下凸函数
y =f(x)在区间I 上连续任取x 1 , x 2∈I . 且λ>0 (λ∈R ), 若f ( )>(或<)
恒成立,则f(x)在区间I 上为上凸(或下凸)函数 。
函数上凸、下凸性质可推广为Jensen (琴森)不等式
设f(x)在区间I 上是下凸函数,则对任意x i ∈I 及p i >0(i =1,2…n )
有 , 其中等号当且仅当x 1=x 2=…=x n 时成立。
若f(x)在区间I 上是上凸函数,则不等号反向。
例1:(2005年鄂,理6)在y=2x ,y=log 2x ,y=x 2,y=cos2x ,这四个函数中,当0<x 1 <x 2 <1时,使f ( ) > 恒成立的函数个数是( ) A 、0 B 、1
C 、2
D 、3
解析:B 做四个函数图象,观察在(0,1)上的凹凸性,最后发现只有y=log 2x 函数满足条件,故选B 。
例2:如图,f i (x) (i = 1, 2, 3, 4 ) 是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的 x 1和x 2,任意λ∈(0,1),f [λx 1 + (1—λ) x 2]< λf (x 1) + (1—λ)f (x 2 ) 恒成立”的只有( )
A 、f 1(x)
B 、f 2 (x)
C 、 f 3 (x)
D 、f 4 (x)
x +λx
1+λ
1 2 f (x )+λf (x )1+λ
1 2 ① ② ③ ④
x +x 2f (x )+
f (x )21 2 1
2
解析:A 。
由题意可知函数应该是下凸曲线,故选A 。
例3:(2005年高考全国卷I 试题)
(1)设函数f(x) = xlog 2x + (1—x) log 2 (1—x ) (0 < x < 1) ,求f(x)的最小值;
(2)设正数p 1,p 2,p 3,…,p 2 满足p 1 +p 2 +p 3+…+p 2 = 1,证明p 1log 2p 1 +p 2log 2p 2 +p 3log 2p 3 +…+ p 2 log 2p 2 ≥—n 。
解:(1)构造函数g (x) =x log 2x ,x ∈(0,1),g '' (x) = >0,由Jensen 不等式得g( )≤ [ g(x) + g(1—x)] ,
g(x) +g(1—x ) ≥2g ( )=—1,即x log 2x + (1—x) log 2 (1—x)≥—1, 所以当x = 时,f(x)取得最小值—1。
(2)直接利用Jensen 不等式可知
即:p 1log 2p 1 +p 2log 2p 2 +p 3log 2p 3 +…+p 2 log 2p 2 ≥—n 。
三.利用导数来判断函数的上凸、下凸
若f '(x)为减函数,则原函数为上凸曲线。
若[f '(x)]'存在,即f ''(x)<0.上凸。
同理f '(x)为增函数,则下凸。
若f ''(x)>0.则下凸。
下面举例说明函数凸性在函数作图中的应用: 例如:作y =ax 3+bx 2+cx +d (a >0)的图像
∵y ' =3ax 2+2bx +c 为二次函数,导函数有3种情况:①在x 轴上方,②与x 轴1个交点,③与x 轴
有两个交点。
①对应的原函数:x ∈R f '(x)>0 原函数为增函数,但在(-∞,- )上f ' (x)为减函数,故原函数在(—∞,— )为上凸增,在(- ,+∞ ) f ' (x)为增函数,则原函数在(- , +∞ )为下凸增。
b
3a b 3a
n n n 1
xln 2x +1—x 2
12
12
1
2
n
n
b 3a
—
b
3a
— x
x 1 2 ① ② ③
b 3a
b 3a
n b
3a
—
图象为①,同理②③对应图分别(大致)为②③。
知道了三次函数的图象,那么依次类推,四次函数、五次…不难做出大致图象的。
练习:f '(x)是f(x)的导函数,f ' (x) 的图象如右图所示,则f(x)的图象只可能是下图中的( )
b 3a
—
b 3a
—
b 3a
— x 1
x 2
① ②
③。
