2016新课标三维人教B版数学选修4-1 1.3 圆幂定理与圆内接四边形
北师大版数学高二圆内接四边形的性质与判定定理 选修4-1

高中数学圆内接四边形的性质与判定定理教案选修4-1 几何证明是培养学生逻辑推理能力的最好载体,迄今为止还没有其他课程能够代替几何的这种地位,几何证明过程包含着大量的直观、想象、探究和发现的因素,这对培养学生的创新意识也非常有利.本讲主要证明一些反映圆与直线关系的重要定理,提高学生几何直观能力和综合运用几何方法解决问题的能力.研究近几年的新课标高考试卷,不难发现,高考对本部分内容的考查大多集中在与圆相关的性质定理和相似三角形等知识上,难度不大,一根据新课程改革考纲的要求,这一讲我们计划安排4 课时复习,具体安排如下:第一节:圆周角定理一课时.这节课的重点是帮助学生复习圆周角定理,会用圆周角定理,并会借助圆周角定理证明角相等,三角形相似等问题.第二节:圆内接四边形的性质与判定定理一课时.这节课的重点是帮助学生复习圆内接四边形的性质与判定定理,会灵活运用定理、证明四点共圆问题及解决角相等的问题.第三节:圆的切线的性质及判定定理、弦切角的性质一课时.这节课主要帮助学生通过复习圆的切线的性质及判定定理、弦切角的性质,熟练掌握判定切线的方法.已知圆的切线时,第一要考虑过切点和圆心连线成直角,第二应考虑弦切角定理,第三涉及线段成比例或线段的积时要考虑切割线定理.第四节:与圆有关的比例线段一课时.这节课主要帮助学生复习相交弦定理、切割线定理、割线定理、切线长定理,会结合三角形及其相似等知识来证明线段相等或等比例线段问题.复习时,我们主要是通过知识梳理→开心自测→金题精讲→知能演练→课堂小结→能力锤炼等几个环节进行的.由于湖北高考数学试题选考几何证明专题,从近几年新课标高考试题中不难看出,以圆为载体的证明题或计算题出现的频率较高,所以我们认为:对直线与圆的位置关系复习是重中之重,而圆内接四边形的性质与判定定理是该讲的核内知识,它起到了承前启后的作用,它之前有圆周角定理,它之后还有圆的切线的性质及判定定理、弦切角的性质、相交弦定理、切割线定理、切线长定理等.另外,认真落实教材所讲的知识,重视教材中的例题和习题,深研教材,发掘教材中的内涵是提高几何专题复习效率的一种有效途径.第二节《圆内接四边形的性质与判定定理》说课稿一、说教材(一)教材分析圆内接四边形的性质与判定定理是选修4-1第二讲的核心内容,也是新课标高考试题中的常见考点.以圆为载体的相关问题是新高考命题的潜规则,这是因为:1.根据四点共圆这个条件,可以构造出直角三角形,容易设置高考题.2.四点共圆时,可充分利用外角等于它的内对角、对角互补、相交弦、切割线、割线定理等证明等式.所以应高度重视对这一节教材中的三个定理和一个推论的复习,关键是要让学生懂得定理的应用.(二)教学目标知识目标1.了解圆内接多边形和多边形外接圆的概念;掌握圆内接四边形的概念及其性质定理;2.掌握圆内接四边形判定定理及其推论;熟练运用圆内接四边形的性质与判定定理进行计算和证明.能力目标1.通过对圆内接四边形的概念及其性质定理的复习,培养学生应用定理解决问题的能力;2.通过复习圆内接四边形判定定理及其推论,促使学生会用定理判定四点共圆;3.通过定理的应用,培养学生逻辑推理能力.情感目标1.开心自测引入复习,激发学生观察、分析、探求的学习激情,强化学生参与意识及主体作用.2.通过证明方法的探求,培养学生勤于思考的习惯,并促进学生辩证思维的能力和严谨的治学精神和态度,渗透教学内容中普遍存在的相互联系、相互转化的观点.(三)教学重难点1.重点圆内接四边形的性质与判定定理.2.难点定理的灵活应用.二、说教法在课堂教学过程中,要充分调动学生学习的主动性.通过学生自己动手操作、探索,获得对知识的深刻理解,这符合中学生好动厌静的心理特点,能更好地吸引学生的注意力.要把课堂还给学生,多注意倾听,理顺学生思维过程,引导学生合作探究.借助学生的嘴来说,借助学生的脑来想.自己要注意选用示范性强、有一定梯度的2—3道例题进行重点分析、讲评,要善于把自己对于问题的理解转化为学生的理解,而不是直接强加给学生.要培养学生自己“找路”的能力,在学生迷路时及时给予点拨,让学生在主动参与学习的过程中真正的理解.针对本节课的复习目标,主要以下面几个环节进行:知识梳理→开心自测→金题精讲→知能演练→课堂小结→能力锤炼.三、说学法因为这节课的内容学生在初中已经接触过,内容也比较熟悉,但是定理如何灵活地在解题中运用还有一些欠缺,遇到题目时往往无从下手,所以在复习过程中要善于引导学生运用目标分析意识来解决问题.这节课以解决问题为主线展开,主要采用“探究式学习法”,引导学生发挥主观能动性,主动探索新知.四、说教学过程知识梳理圆内接四边形的性质定理:定理1 圆内接四边形的对角互补.定理2 圆内接四边形的外角等于它的内角的对角圆内接四边形的判定定理:如果一个四边形的对角互补,那么这个四边形的四个顶点共圆.推论: 如果四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆.设计意图:通过梳理知识,使学生明确本节所复习的内容,熟练掌握本节的三个定理和一个推论.开心自测1.如图1,⊙O的内接四边形BCED,延长ED,CB交于点A,若BD⊥AE,AB=4,BC=2,AD=3,则DE=_______;CE=__________.2.如图2,AD、BE是△ABC的两条高,求证:∠CED=∠ABC.1.选题立意:设计开心自测题,主要体现课堂中的自主学习,目的是激发学生的学习兴趣.其中第1题的立意是:考查圆内接四边形性质定理及割线定理的灵活运用.第2题的立意是:考查灵活运用圆内接四边形性质定理证明角相等问题.2.处理过程:让学生独立完成这两道自测题,并分成两组,每一组推荐一名同学说出解题思路和答案.金题精讲例1 (2011·课标全国卷)如图3,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于方程x2-14x+mn=0的两个根.(1)证明:C,B,D,E四点共圆;(2)若∠A=90°,且m=4,n=6,求C,B,D,E所在圆的半径.1.选题立意:本题考查三角形相似、四点共圆的基本知识与方法,考查推理论证能力及运算求解能力.2.处理过程:第(1)小题是证明四点共圆问题,那么要证四点共圆,我们有那些方法呢?通过提问让学生在大脑中搜索相关知识,寻找最佳解题方案.这样问题可以转化为证明Rt△ADE与Rt△ABC相似,从而利用本节的推论来证明四点共圆.第(2)小题是计算问题,关键是引导学生如何确定圆心的位置.根据圆的性质可知,圆心即为该圆弦的中垂线的交点,问题就转化为在矩形AFHG中求圆的半径了.3.老师点评:证明四点共圆主要是利用圆内接四边形的判定定理或其推论.解题时,关键是寻找四边形的对角互补或其一外角与它的内角的对角相等.金题精讲例2(2011·辽宁卷)如图4,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.(1)证明:CD∥AB;(2)延长CD到F,延长DC到G,使得EF=EG,证明A,B,G,F四点共圆.1.选题立意:本题考查平面几何的证明问题,主要涉及两条直线平行以及四点共圆的判定.2.处理过程:第(1)小题如何利用已知条件来证明CD∥AB?让学生去“找路”,证平行问题主要是运用平行线的判定定理.本题中A、B、C、D四点共圆这个条件的正确运用是证明该问题的关键.第(2)小题是证明四点共圆问题,引导学生作出辅助线,连接AF、BG得四边形ABGF,如何运用四点共圆的判定定理呢?此时,把问题交给学生去探究.要证∠AFD+∠ABC=180°,即证∠FAB=∠GBA.3.老师点评:灵活运用圆内接四边形性质与判定定理是解题的关键.例3 (2009年·宁夏)如图5,已知△ABC的两条角平分线AD和CE相交于H,∠B=60°,F在AC上,且AE=AF.(1)证明:B,D,H,E四点共圆;(2)证明:CE平分∠DEF.1.选题立意:本题考查四点共圆的判定方法及利用四点共圆的性质证明角相等问题.2.处理过程:第(1)小题只要证明四边形BDHE的内对角互补即可,但该小题的的难点恰在于如何证明内对角互补.这时可以分组讨论,充分调动学生的学习积极性,只要学生能想的就让学生想,学生能说的让学生说,学生能做的让学生做.第(2)小题实际上是证明角相等问题,请一个学生用分析法来寻求证明思路.当学生“找路”有困难时,及时正确引导,同时注意引导方式.3.老师点评:解答平面几何问题时不仅要用到几何定理,而且还要用到各种不同的推理形式,推理策略,有时还要使用“添加辅助线”之类的技巧性较高的方法.在几何学习中,除了运用逻辑推理外,还要应用观察、比较、类比、直觉、猜想、归纳、概括等合情推理.知能演练如图6,已知△ABC中,AB=AC,D是△ABC外接圆劣弧AC⌒上的点(不与A,C重合),延长BD到E.(1)求证:AD的延长线平分∠CDE;(2)若∠BAC=30°,△ABC中BC边上的高为2+ 3 ,求△ABC外接圆的面积.设计意图:检验所学习的知识,从而熟练掌握本节的重点,形成相应的数学能力.能力锤炼:1. 如图7,在Rt △ABC 中,∠BCA=90°,以BC 为直径的⊙O 交AB 于E 点,D 为AC 的中点,连结BD 交⊙O 于F 点.求证:BC BE = CFEF .2. 如图8,AB 为⊙O 的弦,CD 切⊙O 于P,AC ⊥CD 于C,BD ⊥DC 于D,PQ ⊥AB 于Q,求证:PQ 2=AC ·BD.3. 如图9,已知AP 是⊙O 的切线,P 为切点,AC 是⊙O 的割线,与⊙O 交于B,C 两点,圆心O 在∠PAC 的内部,点M 是BC 的中点. (1)证明:A,P,O,M 四点共圆; (2)求∠OAM+∠APM 的大小.4.如图10,已知四边形ABCD 内接于圆,延长AB 和DC 相交于E,EG 平分∠E,且与BC 、AD 分别相交于F 、G.求证:∠CFG=∠DGF.5.如图11,已知PA 、PB 是圆O 的切线,A 、B 分别是切点,C 为圆O 上不与A 、B 重合的另一点,课堂小结 1.本节课我们复习了圆内接四边形的性质与判定定理.2.通过开心自测、金题精讲和知能演练,使我们初步掌握了如何灵活运用圆内接四边形的性质与判定定理解决问题.3.这节课我们运用了数形结合、转化与化归等数学思想方法.设计意图:课堂小结使学生深切体会到本节课的主要内容和思想方法,从而实现对圆内接四边形的性质与判定定理认识的再次深化.能力锤炼能力锤炼题见表下面.设计意图:课后检测,巩固本节知识点,深化相应的数学能力.若∠ACB=120°,求∠APB的大小.。
人教B版高中数学-选修4-1教学案-第一章-圆 幂 定 理 (Word)

_1.3圆幂定理与圆内接四边形1.3.1圆幂定理[对应学生用书P25][读教材·填要点]1.相交弦定理圆内的两条相交弦,被交点分成的两条线段长的积相等.2.切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.3.圆幂定理已知⊙(O,r),通过一定点P,作⊙O的任一条割线交圆于A,B两点,则PA·PB为定值,设定值为k,则:(1)当点P在圆外时,k=PO2-r2,(2)当点P在圆内时,k=r2-OP2,(3)当点P在⊙O上时,k=0.[小问题·大思维]1.从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积有什么关系?提示:相等.2.从圆外一点引圆的切线,则这一点、两个切点及圆心四点是否共圆?若共圆,圆的直径是什么?提示:四点共圆.且圆心为圆外一点与原圆心连线的中点,直径为圆外一点到原圆心的距离.[对应学生用书P26][例1] 如图,AB 、CD 是半径为a 的圆O 的两条弦,它们相交于AB 的中点P ,PD =23a ,∠OAP =30°,求CP 的长.[思路点拨] 本题考查相交弦定理及垂径定理、勾股定理的综合应用.解决本题需要先在Rt △OAP 中,求得AP 的长,然后利用相交弦定理求解.[精解详析] ∵P 为AB 的中点, ∴由垂径定理得OP ⊥AB .在Rt △OAP 中,BP =AP =a cos30°=32a . 由相交弦定理,得BP ·AP =CP ·DP , 即⎝⎛⎭⎫32a 2=CP ·23a ,解之得CP =98a .在实际应用中,若圆中有两条相交弦,要想到利用相交弦定理.特别地,如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项.1.如图,已知AB 和AC 是圆的两条弦,过点B 作圆的切线与AC 的延长线相交于点D .过点C 作BD 的平行线与圆相交于点E ,与AB 相交于点F ,AF =3,FB =1,EF =32,则线段CD 的长为________.解析:因为AF =3,EF =32,FB =1,所以CF =AF ·FB EF =3×132=2,因为EC ∥BD ,所以△ACF ∽△ADB ,所以AF AB =CF BD =AC AD =AD -CD AD =34,所以BD =CF ·AB AF =2×43=83,且AD =4CD ,又因为BD 是圆的切线,所以BD 2=CD ·AD =4CD 2, 所以CD =43.答案:43[例2] 自圆O 外一点P 引圆的一条切线PA ,切点为A ,M 为PA 的中点,过点M 引圆的割线交圆于B ,C 两点,且∠BMP =100°,∠BPC =40°.求∠MPB 的大小.[思路点拨] 本题考查切割线定理,由定理得出△BMP ∽△PMC 而后转化角相等进行求解.[精解详析] 因为MA 为圆O 的切线, 所以MA 2=MB ·MC . 又M 为PA 的中点, 所以MP 2=MB ·MC . 因为∠BMP =∠PMC , 所以△BMP ∽△PMC , 于是∠MPB =∠MCP .在△MCP 中,由∠MPB +∠MCP +∠BPC +∠BMP =180°,得∠MPB =20°.相交弦定理、切割线定理涉及与圆有关的比例线段问题,利用相交弦定理能做到知三求一,利用切割线定理能做到知二求一.。
选修4-1 直线与圆的位置关系——.圆的内接四边形
一 定理的探究
A
1.定义:如果多边形的所有顶点都 在一个圆上,那么这个多边形叫做圆内 接多边形,这个圆叫做多边形的外接圆.
O B C
D
A F
A
B O
O B C
C
·
D
E
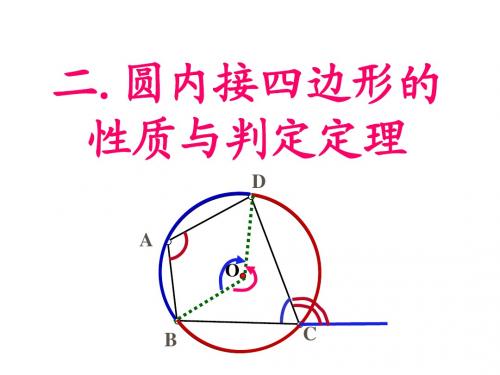
二.圆内接四边形的性质与判定定理
圆内接多边形-----所有顶点都在一个圆上的多边形.
思考: 这个圆称多边形的外接圆. 任意三角形都有外接圆.那么 任意正方形有外接圆吗?为什么?
性质定理1
圆内接四边形的对角互补
如果一个四边形的对角互补,那么它的四个顶点共圆.
性质定理2
圆内接边形的外角等于它的内角的对角。
如果四边形的一个外角等于它的内角的对角, 那么它的四个顶点共圆.
性质定理的逆命题成立吗?
假设:四边形ABCD中,∠B+∠D=180°
求证:A,B,C,D在同一圆周上(简称四点共圆).
任意矩形有外接圆吗?
等腰梯形呢?
一般地, 任意四边形都有外接圆吗?
A D A D A D A D
O B C B C
B
C B C
如果一个四边形内接于圆,那么它有何特征? 1 1 如图(1)连接OA,OC.则∠B= . ∠D=
360 1 B D 360 0 180 0 2
B
C
D E
例1:如图⊙O1与⊙O2都经过A、B两点.经过点 A的直线CD与⊙O1交于点C,与⊙O2交于点D.经 过点B的直线EF与⊙O1交于点E,与⊙O2交于点F. 求证:CE∥DF. 分析:只要证明同旁内角互补即可!
证明:连接AB. 并利用圆内接四边形的性质定理. ∵四边形ABEC是⊙O1的内接四边形,∴ ∠BAD=∠E. 又∵四边形ABFD是⊙O2的内接四边形, ∴ ∠BAD+∠F=180º . ∴ ∠E+∠F=180º . ∴ CE//DF.
最新人教版高二数学选修4-1(B版)电子课本课件【全册】

0002页 0004页 0006页 0059页 0163页 0201页 0203页 0205页 0239页 0264页 0303页
第一章 相似三角形定理与圆幂定理 1.1 相似三角
1.1.3 平行截割定理
1.2 圆周角与弦切角
1.2.1 圆的切线
最新人教版高二数学选修4-1(B版) 电子课本课件【全册】
1.2.3 弦切角定理
1.3.2 圆内接四边形的性质与判定
阅读与欣赏
欧几里得
第二章 圆柱、圆锥与圆锥曲线 2.1 平行投影与圆
2.2 用内切球探索圆锥曲线的性质
2.2.1 球的
2.2.3 圆锥面及其内切球
本章小结
ห้องสมุดไป่ตู้
附录 部分中英文词汇对照表
第一章 相似三角形定理与圆 幂定理 1.1 相似三角形 1.1.1 相似三角形判定定理
《1.3.2圆内接四边形的性质与判定》课件1-优质公开课-人教B版选修4-1精品

的四个顶点共圆;
④如果两个三角形有公共边,公共边所对的角相等且在公共边的 同侧,那么这两个三角形的四个顶点共圆.
试一试:判断下列各命题是否正确. (1)任意三角形都有一个外接圆,但可能不止一个; (2)矩形有唯一的外接圆; (3)菱形有外接圆;
(4)正多边形有外接圆.
提示 (1)错误,任意三角形有唯一的外接圆;(2)正确,因为矩
证明:连接AB. 因为四边形ABEM是⊙O的内接四边形, 所以∠ABF=∠M.
又因为四边形ABFN是⊙O1内接四边形,所以
∠ABF +∠N=180°.
所以EF//FN.
例2 如图,四边形ABCD内接于⊙O,过A作⊙O的切 线交CB的延长线于P,已知∠EAD=∠PCA. 求证:DA2=CD×BP.
证明:因为EP是⊙O的切线,所以 所以∠EAD=∠DCA, ∠PAB=∠PCA. 又因为∠EAD = ∠PCA ,所以 ∠DCA =∠PAB=∠PCA, 所以AD=AB. 又因为圆内接四边形ABCD,所以 ∠PBA=∠D, 所以△DCA与△BAP相似,因此 DA DC . BP BA
A,B,C,D四点共圆.
方法技巧
综合运用圆内接四边形的性质定理与判定定理解决 问题
【示例1】 已知CF是△ABC的AB边上的高,FP⊥BC,FQ⊥AC.
求证:A、B、P、Q四点共圆. [思维启迪] 首先,连接PQ,要证A、B、P、Q四点共圆,只
要利用判定定理或推论即可.而由题目中的垂直条件易得 Q 、 F、P、C四点共圆,再考虑利用圆内接四边形的性质.
三角形一定存在外接圆,并且三角形的外接圆的圆心(即外心)
是三条边的垂直平分线的交点;圆内接梯形一定是等腰梯形 等. (4)要注意圆内接四边形的性质定理和判定定理的综合应用.
人教版高中数学选修4-1《2.2 圆内接四边形的性质与定理》

圆的内接四边形的性质定理1的推导:
连接OA、OC
C D
α
1 B 2
3600
1 D 2
β
O A B
1 B D 360 0 180 0 2 A C 1800
2、圆的内接四边形的性质定理1:
文字语言:圆的内接四边形对角互补 符号语言:若四边形ABCD内接于圆O,则有
A D
A D E O C B
O B C
圆内接四边形
圆内接五边形
思考:
1.任意三角形都有外接圆,那么任意正 方形都有外接圆吗?为什么?
2.任意矩形都有外接圆吗?为什么? 3.等腰梯形呢? 4.任意四边形都有外接圆吗?
如下四边形都内接于圆
A
D
A
D
A
D
A D
O B C
O B C
B
O C
B
O C
这些四边形有什么共同特征?
这与“三角形的外角大于任一不相邻的内角”矛盾
故点D不可能在圆内
4、圆的内接四边形的判定定理:
文字语言:如果一个四边形对角互补,那么这个四边 形的四个顶点共圆
符号语言:在四边形ABCD中,如果则有A C 1800 或( B D 1800 ),那么A、B、C、 D四点共圆
图形语言:
FQ AC .
求证:A、B、P、Q四点共圆
C
P Q A F B
练习1、如图,AD、BE是 ABC 的两条高.
求证: CED ABC
C E D
A
B
练习2、求证:对角线互相垂直的四边形中,各 边中点在同一个圆周上。
B F E A H D G C
练习3、如图四边形ABCD内接于圆,延长AB和
高中数学 1.3.1 圆内接四边形课件 北师大版选修4-1
∵DE∥AC, ∴∠E=∠ACB. ∵∠ACB=∠ADB, ∴∠ADB=∠E.
在△ABD 与△CDE 中, ∵∠ADB=∠E, ∠BAD=∠DCE, ∴△ABD∽△CDE. AB AD ∴ = . CD CE 故 AB· CE=AD· CD.
圆内接四边形的判定
如图 1-3-6,在△ABC 中,E,D,F 分别为 AB,BC,AC 的中点,且 AP⊥BC 于 P. 求证:E、D、P、F 四点共圆.
如图 1-3-7, D, E 分别为△ABC 的边 AB, AC 上的点, 且不与△ABC 的顶点重合.已知 AE 的长为 m, AC 的长为 n, AD,AB 的长是关于 x 的方程 x2-14x+mn=0 的两个根, (1)证明:C,B,D,E 四点共圆; (2)若∠A=90° ,且 m=4,n=6,求 C,B,D,E 所在 圆的半径.
图 1-3-6
【思路探究】 证明本题可先连接 PF, 构造四边形 EDPF 的外角∠FPC,证明∠FPC=∠C,再证明∠FPC=∠FED 即 可得出结论.
【自主解答】 连接 PF, ∵AP⊥BC,F 为 AC 的中点, 1 ∴PF= AC. 2 1 ∵FC=2AC, ∴PF=FC, ∴∠FPC=∠C.
图 1-3-7
【证明】
(1)如图,连接 DE,在△ADE 和△ACB 中,
AD· AB=mn=AE· AC, AD AE 即 = .又∠DAE=∠CAB,从而△ADE∽△ACB. AC AB 因此∠ADE=∠ACB.所以 C,B,D,E 四点共圆.
(2)m=4, n=6 时, 方程 x2-14x+mn=0 的两根为 x1=2, x2=12,故 AD=2,AB=12. 如图,取 CE 的中点 G,DB 的中点 F,分别过 G,F 作 AC,AB 的垂线,两垂线相交于 H 点,连接 DH.因为 C,B, D,E 四点共圆,所以 C,B,D,E 四点所在圆的圆心为 H, 半径为 DH. 由于∠A=90° , 故 GH∥AB,HF∥AC. 1 从而 HF=AG=5,DF= 2(12-2)=5. 故 C,B,D,E 四点所在圆的半径为 5 2.
高中数学新人教版B版精品教案《人教版B高中数学选修4-1:几何证明选讲 1.3.2 圆内接四边形的性质与判定》9
圆的内接四边形的性质与判定教学设计一、教材分析《圆内接四边形的性质与判定定理》是人教B版选修4-1几何证明选讲的内容,几何证明是培养学生逻辑推理能力和综合运用数学知识和思想方法解决几何问题的最好载体,几何证明的过程包含着大量的直观想象,探究和发现问题的因素,对培养学生的创新意识和发散思维有很大的帮助;本节课通过对圆内接四边形的性质和判定定理的进一步学习,使学生能灵活运用定理证明四点共圆问题和有关角的问题.二、学情分析本节课的内容是在学生初中对平面几何知识有了一定的了解和进一步学习了圆周角定理的基础上进行的,学生有一定的基础,但是学生对综合运用数学知识和思想方法解决问题的能力比较欠缺,有待于进一步的培养.三、教学目标知识与技能:了解圆内接多边形的概念;理解并掌握圆内接四边形的性质定理和判定定理及推论,能够用性质定理和判定定理解决相关的几何问题.过程与方法:学习并掌握圆内接四边形的性质与判定定理的推导过程,应用性质定理和判定定理解决相关的几何问题,使学生领会“分类讨论”和“反证法”这两种数学思想在几何证明中的作用,培养学生的逆向思维、发散思维和严谨的逻辑思维.情感态度与价值观:培养学生的逆向思维、逻辑推理能力和综合运用数学知识和思想方法解决问题的能力,提高学生学习数学的积极性.四、教学重点与难点重点:掌握圆内接四边形的性质与判定定理的证明过程.难点:综合运用数学知识和思想方法解决圆内接四边形的相关问题.五、教学过程(一)复习回顾问题一:我们前面学过的圆周角定理、推论1、推论2及推论3的内容什么?圆周角定理:圆周角的度数等于它所对弧的度数的一半.推论1:直径(或半圆)所对的圆周角是直角.推论2:同弧或等弧所对的圆周角相等.推论3:等于直角的圆周角所对的弦是圆的直径.设计意图:通过对圆周角定理相关知识的复习,激发学生的求知欲;对后面利用圆周角定理的知识证明圆内接四边形的性质做好铺垫.(二)新知探究1.基本概念如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.设计意图:让学生了解圆内接多边形的概念.2.创设研究情境探究一:如右图,四边形ABCD叫做⊙O的内接四边形,而⊙O叫做四边形A BCD的外接圆.试讨论四边形ABCD具有什么样的性质?并证明你的结论.设计意图:通过图形使学生直观的感受圆内接四边形,并能通过小组讨论来探究圆内接四边形的性质;培养学生解决问题的能力及合作意识.让学生自己上去证明得到的结论,培养学生对数学的兴趣和学好数学的信心.性质定理:圆内接四边形的对角互补;并且任何一个外角都等于它的内对角.(证明过程由学生完成)3.性质定理的应用(典例剖析)思考:圆内接平行四边形、菱形、梯形分别是什么图形?(由学生课后证明)设计意图:通过思考、例1的设置使学生能进一步掌握圆内接四边形的性质定理,并能灵活运用性质定理解决与圆内接四边形性质有关的数学问题.4.圆内接四边形判定定理的探究探究二:我们知道,任意三角形都有外接圆.那么,任意正方形有外接圆吗?为什么?任意矩形是否有外接圆?一般地,任意四边形都有外接圆吗?设计意图:让学生理解正方形、长方形都有外接圆(因为它们的对角线交点到四个顶点的距离相等),而对于一般地四边形是否有外接圆学生比较模糊,这时通过坐标法的思想使学生明白一般地四边形不一定有外接圆,进一步引导学生考虑圆内接四边形性质定理的逆命题.结论:平面内,若OA=OB=OC=OD ,则A 、B 、C 、D 四点共圆. 性质定理的逆命题:如果一个四边形的对角互补,那么它的四个顶点共圆.已知:四边形ABCD 中,∠B+∠D=180° 求证:A,B,C,D 在同一圆周上(简称四点共圆).分析:不共线的三点确定一个圆,不妨设经过A 、B 、C 三点可以做一个圆O,如果能由条件得出圆O 过点D ,那么就证明了上述命题..//..,.,1212121DF CE F O E O EF B D O C O CD A B A O O 求证:交于点,与圆于点交与圆的直线经过点交于点与圆交于点与圆的直线经过点两点都经过与圆:如图,圆例DFCE F E F BAD O ADFB EBAD O ABEC AB //.180.180.21∴=∠+∠∴=∠+∠∴∠=∠∴︒︒的内接四边形,是圆四边形又的内接四边形,是圆四边形证明:连接显然,点D 与圆有且只有三种位置关系: (1) 点D 在圆外. (2) 点D 在圆内. (3) 点D 在圆上.设计意图:引导学生将文字语言叙述的命题转化成数学符号语言和图形语言进行证明,通过分析让学生自己证明,使学生理解反证法和穷举法的思想;通过两种不同的证明过程来培养学生严谨的逻辑思维和发散思维.判定定理:如果一个四边形的对角互补,那么它的四个顶点共圆.(证明过程学生完成) 推论:如果四边形的一个外角等于它的内对角,那么它的四个顶点共圆. 5.判定定理的应用(典例剖析)例2:如果两个三角形有一条公共边,这条边所对的角相等,并且在公共边的同侧,那么这两个三角形有公共的外接圆...180...90,90,...90,.四点共圆、、、即又四点共圆、、、,中,在四边形证明:连接Q P B A QPB A QPC A QFC A QFA A QFA QFC AB CF QPC QFC C P F Q FPC FQC AC FQ BC FP QFPC PQ ∴=∠+∠∠=∠∴∠=∠∴=∠+∠=∠+∠∴⊥∠=∠∴∴=∠=∠∴⊥⊥︒︒︒︒ ....180,.180...有公共的外接圆和即四点共圆、、、,只有一个圆,即圆、、过不共线的三点四点共圆、、、又四点共圆,、、、的两侧在与使,上取点的弧,在圆的外接圆证明:作有公共的外接圆与求证:同侧,在,已知:如右图,ABD ABC D C B A O B E A D B E A AEB ADB ADBACB AEB ACB C B E A AB C E E AB O O ABC ABD ABC D C AB D C ∆∆∴∴︒=∠+∠∴∠=∠︒=∠+∠∴∆∆∆∠=∠∠∠ ..,四点共圆、、、求证:边上的高,的是如图,变式训练:Q P B A AC FQ BC FP AB ABC CF ⊥⊥∆设计意图:进一步培养学生将文字语言叙述的命题转化为数学符号语言和图形语言的能力;巩固圆内接四边形的性质定理和判定定理.6.课堂小结问题二:通过这节课的学习,你获得了什么?设计意图:通过提问培养学生的问题意识,检验这节课学生在知识和思想方法上的掌握情况,以便课后有针对性的进行辅导.知识方面:1、圆内接四边形性质定理:圆内接四边形的对角互补;并且任何一个外角都等于它的内对角.2、四点共圆的条件(1)圆内接四边形判定定理:如果一个四边形的对角互补,那么它的四个顶点共圆.(2)推论:如果四边形的一个外角等于它的内对角,那么它的四个顶点共圆(3)结论:平面内,若OA=OB=OC=OD,则A、B、C、D四点共圆.(4)结论:如果两个三角形有一条公共边,这条边所对的角相等,并且在公共边的同侧,那么这两个三角形有公共的外接圆.思想方法:(1)反证法(正难则反)(2)穷举法7.课后反思。
1.3.1-圆幂定理-课件-(人教B版选修4-1)
第8页,共29页。
课堂讲练互动
课后智能提升
知识点三 圆幂定理 圆幂定理:已知⊙O(O,r),通过一定点P,作⊙O的任一条割 线交圆于A、B两点,则当点P在圆外时,k=PO2-r2; 当点P在圆内时,k=r2-PO2; 当点P在圆上时,k=0. 其中k叫点P对⊙O的“幂”.
(3)解:对于五边形 MEAFN 的五条边,从是否相等考虑,有: MN=AE=AF,EM=FN. 证明如下: 先证明 AE=AF,不妨假设正方形 ABCD 边长为 1,易证四边形 OMCN 是正方形,则 MO=NO=MC=R=2- 2, MN= OM2+ON2= 2R=2 2-2. 而 BM=DN=1-MC=1-(2- 2)= 2-1,BC 切⊙O 于 M, ∴BM2=BE·BA,即( 2-1)2=BE·1, ∴BE=3-2 2.同理 DF=3-2 2. ∴AE=AF=1-BE=2 2-2.
第27页,共29页。
课堂讲练互动
课后智能提升
知识框图
第28页,共29页。
课堂讲练互动
课后智能提升
单击此处进入 课后智能提升
第29页,共29页。
课堂讲练互动
课后智能提升
分析:由于PO既不是⊙O的切线,也不是割线,故需将PO延 长交⊙O于D,构成了圆的一条割线,而OD又恰好是⊙O的半 径,于是运用切割线定理的推论,问题得解.
第7页,共29页。
课堂讲练互动
课后智能提升
解:将 PO 延长交⊙O 于 D,根据割线定理, 可得 PA·PB=PC·PD. 设半径为 r,则 6×(6+8)=(10.9-r)(10.9+r), 所以 r=5.9 (cm).
∴BDDA=196.
答案:196
人教B版高中数学选修4-1习题课件:1.3.1 圆幂定理
解析:∵PA2=PB·PC=4×9=36, ∴PA=6.
答案:B
-7-
1.3.1 圆幂定理
M Z Z 目标导航 UBIAODAOHANG
知识梳理
HISHI SHULI
重难聚焦
HONGNAN JVJIAO
D S 典例透析 IANLI TOUXI
随堂演练
UITANGYANLIAN
-9-
1.3.1 圆幂定理
M Z Z 目标导航 UBIAODAOHANG
知识梳理
HISHI SHULI
重难聚焦
HONGNAN JVJIAO
D S 典例透析 IANLI TOUXI
随堂演练
UITANGYANLIAN
2.垂径定理、射影定理、相交弦定理、切割线定理之间的关系 剖析如图,PA,PB为☉O的两条切线,A,B为切点,PCD为过圆心O的 割线,连接AB,交PD于点E,则有下列结论: (1)PA2=PB2=PC·PD=PE·PO; (2)AE2=BE2=DE·CE=OE·PE; (3)若AC平分∠BAP,则C为△PAB的内心; (4)OA2=OC2=OE·OP=OD2; (5)������������ = ������������ , ������������ = ������������,PD⊥AB; (6)∠AOP=∠BOP,∠APD=∠BPD.
图形语言
作 用 证明线段成比例或求线段的长
归纳总结 垂直于弦的直径平分这条弦,且弦的一半是直径被弦 分成的两条线段的比例中项.
-4-
1.3.1 圆幂定理
M Z Z 目标导航 UBIAODAOHANG
知识梳理
HISHI SHULI
重难聚焦
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
_1.3圆幂定理与圆内接四边形1.3.1圆幂定理[对应学生用书P25][读教材·填要点]1.相交弦定理圆内的两条相交弦,被交点分成的两条线段长的积相等.2.切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.3.圆幂定理已知⊙(O,r),通过一定点P,作⊙O的任一条割线交圆于A,B两点,则P A·PB为定值,设定值为k,则:(1)当点P在圆外时,k=PO2-r2,(2)当点P在圆内时,k=r2-OP2,(3)当点P在⊙O上时,k=0.[小问题·大思维]1.从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积有什么关系?提示:相等.2.从圆外一点引圆的切线,则这一点、两个切点及圆心四点是否共圆?若共圆,圆的直径是什么?提示:四点共圆.且圆心为圆外一点与原圆心连线的中点,直径为圆外一点到原圆心的距离.[对应学生用书P26][例1] 如图,AB 、CD 是半径为a 的圆O 的两条弦,它们相交于AB 的中点P ,PD =23a ,∠OAP =30°,求CP 的长.[思路点拨] 本题考查相交弦定理及垂径定理、勾股定理的综合应用.解决本题需要先在Rt △OAP 中,求得AP 的长,然后利用相交弦定理求解.[精解详析] ∵P 为AB 的中点, ∴由垂径定理得OP ⊥AB .在Rt △OAP 中,BP =AP =a cos30°=32a . 由相交弦定理,得BP ·AP =CP ·DP , 即⎝⎛⎭⎫32a 2=CP ·23a ,解之得CP =98a .在实际应用中,若圆中有两条相交弦,要想到利用相交弦定理.特别地,如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项.1.如图,已知AB 和AC 是圆的两条弦,过点B 作圆的切线与AC 的延长线相交于点D .过点C 作BD 的平行线与圆相交于点E ,与AB 相交于点F ,AF =3,FB =1,EF =32,则线段CD 的长为________.解析:因为AF =3,EF =32,FB =1,所以CF =AF ·FB EF =3×132=2,因为EC ∥BD ,所以△ACF ∽△ADB , 所以AF AB =CF BD =AC AD =AD -CD AD =34,所以BD =CF ·AB AF =2×43=83,且AD =4CD ,又因为BD 是圆的切线,所以BD 2=CD ·AD =4CD 2, 所以CD =43.答案:43[例2] 自圆O 外一点P 引圆的一条切线P A ,切点为A ,M 为P A 的中点,过点M 引圆的割线交圆于B ,C 两点,且∠BMP =100°,∠BPC =40°.求∠MPB 的大小.[思路点拨] 本题考查切割线定理,由定理得出△BMP ∽△PMC 而后转化角相等进行求解.[精解详析] 因为MA 为圆O 的切线, 所以MA 2=MB ·MC . 又M 为P A 的中点, 所以MP 2=MB ·MC . 因为∠BMP =∠PMC , 所以△BMP ∽△PMC , 于是∠MPB =∠MCP .在△MCP 中,由∠MPB +∠MCP +∠BPC +∠BMP =180°,得∠MPB =20°.相交弦定理、切割线定理涉及与圆有关的比例线段问题,利用相交弦定理能做到知三求一,利用切割线定理能做到知二求一.2.(北京高考)如图,AB 为圆O 的直径,P A 为圆O 的切线,PB 与圆O 相交于D .若P A =3,PD ∶DB =9∶16,则PD =________;AB =________.解析:设PD =9t ,DB =16t ,则PB =25t ,根据切割线定理得32=9t ×25t ,解得t =15,所以PD =95,PB =5.在直角三角形APB 中,根据勾股定理得AB =4.答案:95 4[例3] 如图所示,已知P A 与⊙O 相切,A 为切点,PBC 为割线,弦CD ∥AP ,AD 、BC 相交于E 点,F 为CE 上一点,且DE 2=EF ·EC .(1)求证:∠P =∠EDF ; (2)求证:CE ·EB =EF ·EP ;(3)若CE ∶BE =3∶2,DE =6,EF =4,求P A 的长.[思路点拨] 本题考查切割线定理、相交弦定理.以及相似三角形的判定与性质的综合应用.解答本题需要分清各个定理的适用条件,并会合理利用.[精解详析] (1)证明:∵DE 2=EF ·EC , ∴DE ∶CE =EF ∶ED .∵∠DEF 是公共角,∴△DEF ∽△CED . ∴∠EDF =∠C .∵CD ∥AP ,∴∠C =∠P . ∴∠P =∠EDF .(2)证明:∵∠P =∠EDF ,∠DEF =∠PEA , ∴△DEF ∽△PEA . ∴DE ∶PE =EF ∶EA . 即EF ·EP =DE ·EA . ∵弦AD 、BC 相交于点E , ∴DE ·EA =CE ·EB . ∴CE ·EB =EF ·EP .(3)∵DE 2=EF ·EC ,DE =6,EF =4, ∴EC =9.∵CE ∶BE =3∶2,∴BE =6. ∵CE ·EB =EF ·EP , ∴9×6=4×EP . 解得:EP =272.∴PB =PE -BE =152,PC =PE +EC =452.由切割线定理得:P A 2=PB ·PC , ∴P A 2=152×452.∴P A =1523.相交弦定理、切割线定理是最重要的定理,在与圆有关的问题中经常用到,这是因为这三个定理可得到的线段的比例或线段的长,而圆周角定理、弦切角定理得到的是角的关系,这两者的结合,往往能综合讨论与圆有关的相似三角形问题.因此,在实际应用中,见到圆的两条相交弦要想到相交弦定理;见到切线和割线要想到切割线定理.3.如图所示,过点P的直线与⊙O相交于A,B两点.若P A=1,AB=2,PO=3,则⊙O的半径等于________.解析:设⊙O的半径为r(r>0),∵P A=1,AB=2,∴PB=P A+AB=3.延长PO交⊙O于点C,则PC=PO+r=3+r.设PO交⊙O于点D,则PD=3-r.由圆的割线定理知,P A·PB=PD·PC,∴1×3=(3-r)(3+r),∴9-r2=3,∴r= 6.答案:6[对应学生用书P27]一、选择题1.如右图,⊙O的直径CD与弦AB交于P点,若AP=4,BP=6,CP=3,则⊙O半径为()A.5.5B.5C.6 D.6.5解析:由相交弦定理知AP·PB=CP·PD,∵AP=4,BP=6,CP=3,∴PD =AP ·BP CP =4×63=8.∴CD =3+8=11,∴⊙O 的半径为5.5. 答案:A2.如图,P 是圆O 外一点,过P 引圆O 的两条割线PB ,PD ,P A =AB = 5,CD =3,则PC 等于( )A .2或-5B .2C .3D .10解析:设PC =x ,由割线定理知P A ·PB =PC ·PD .即5×2 5=x (x +3),解得x =2或x =-5(舍去).故选B.答案:B3.如图,AD 、AE 和BC 分别切⊙O 于D ,E ,F ,如果AD =20,则△ABC 的周长为( )A .20B .30C .40D .35解析:∵AD ,AE ,BC 分别为圆O 的切线. ∴AE =AD =20,BF =BD ,CF =CE .∴△ABC 的周长为AB +AC +BC =AB +AC +BF +CF =(AB +BD )+(AC +CE )=AD +AE =40.答案:C4.如图,△ABC 中,∠C =90°,⊙O 的直径CE 在BC 上,且与AB 相切于D 点,若CO ∶OB =1∶3,AD =2,则BE 等于( )A. 3 B .2 2 C .2D .1解析:连接OD ,则OD ⊥BD , ∴Rt △BOD ∽Rt △BAC .∴OD AC =BD BC. 设⊙O 的半径为a ,∵OC ∶OB =1∶3,OE =OC , ∴BE =EC =2a .由题知AD 、AC 均为⊙O 的切线,AD =2,∴AC =2.∴a 2=BD4a,∴BD =2a 2. 又BD 2=BE ·BC ,∴BD 2=2a ·4a =8a 2. ∴4a 4=8a 2,∴a = 2. ∴BE =2a =2 2. 答案:B 二、填空题5.(重庆高考)过圆外一点P 作圆的切线P A (A 为切点),再作割线PBC 分别交圆于B ,C .若P A =6,AC =8,BC =9,则AB =________.解析:如图所示,由切割线定理得P A 2=PB ·PC =PB ·(PB +BC ),即62=PB ·(PB +9),解得PB =3(负值舍去).由弦切角定理知∠P AB =∠PCA ,又∠APB =∠CP A ,故△APB ∽△CP A ,则AB CA =AP CP ,即AB 8=63+9,解得AB =4.答案:46.如图,已知圆中两条弦AB 与CD 相交于点F ,E 是AB 延长线上一点,且DF =CF =2,AF ∶FB ∶BE =4∶2∶1.若CE 与圆相切,则线段CE 的长为____________.解析:设BE =x ,则FB =2x ,AF =4x ,由相交弦定理得DF ·FC =AF ·FB ,即2=8x 2,解得x =12,EA =72,再由切割线定理得CE 2=EB ·EA =12×72=74,所以CE =72.答案:727.如图,⊙O 的弦ED 、CB 的延长线交于点A .若BD ⊥AE ,AB=4,BC =2,AD =3,则DE =________;CE =________.解析:由切割线定理知, AB ·AC =AD ·AE .即4×6=3×(3+DE ),解得DE =5.∵BD ⊥AE ,且E 、D 、B 、C 四点共圆,∴∠C =90°. 在直角三角形ACE 中,AC =6,AE =8, ∴CE =64-36=27. 答案:5 278.(重庆高考)如图,在△ABC 中,∠C =90°,∠A =60°,AB =20,过C 作△ABC 的外接圆的切线CD ,BD ⊥CD ,BD 与外接圆交于点E ,则DE 的长为________.解析:由题意得BC =AB ·sin 60°=10 3. 由弦切角定理知∠BCD =∠A =60°, 所以CD =53,BD =15,由切割线定理知,CD 2=DE ·BD ,则DE =5. 答案:5 三、解答题9.如图,PT 切⊙O 于T ,P AB ,PDC 是圆O 的两条割线,P A =3,PD =4,PT =6,AD =2,求弦CD 的长和弦BC 的长.解:由已知可得PT 2=P A ·PB , 且PT =6,P A =3,∴PB =12. 同理可得PC =9,∴CD =5. ∵PD ·PC =P A ·PB ,∴PD PB =P A PC ,∴△PDA ∽△PBC , ∴AD BC =PD PB ⇒412=2BC,∴BC =6. 10.如图,⊙O 的半径OB 垂直于直径AC ,M 为AO 上一点,BM 的延长线交⊙O 于N ,过N 点的切线交CA 的延长线于P .(1)求证:PM 2=P A ·PC ;(2)若⊙O 的半径为2 3,OA = 3OM ,求MN 的长.解:(1)证明:连接ON ,则ON ⊥PN ,且△OBN 为等腰三角形,则∠OBN =∠ONB ,∵∠PMN =∠OMB =90°-∠OBN , ∠PNM =90°-∠ONB , ∴∠PMN =∠PNM , ∴PM =PN .由条件,根据切割线定理,有PN 2=P A ·PC , 所以PM 2=P A ·PC .(2)依题意得OM =2,在Rt △BOM 中, BM =OB 2+OM 2=4.延长BO 交⊙O 于点D ,连接DN . 由条件易知△BOM ∽△BND , 于是BO BN =BM BD,即2 3BN =44 3,得BN =6. 所以MN =BN -BM =6-4=2.11.如下图,已知⊙O 1和⊙O 2相交于A 、B 两点,过点A 作⊙O 1的切线,交⊙O 2于点C ,过点B 作两圆的割线分别交⊙O 1,⊙O 2于点D 、E ,DE 与AC 相交于点P .(1)求证:P A ·PE =PC ·PD ;(2)当AD 与⊙O 2相切,且P A =6,PC =2,PD =12时,求AD 的长. 解:(1)证明:连接AB ,CE , ∵CA 切⊙O 1于点A , ∴∠1=∠D .又∵∠1=∠E ,∴∠D =∠E .又∵∠2=∠3, ∴△APD ∽△CPE . ∴P A PC =PDPE. 即P A ·PE =PC ·PD .(2)∵P A =6,PC =2,PD =12. ∴6×PE =2×12,∴PE =4. 由相交弦定理,得PE ·PB =P A ·PC . ∴4PB =6×2,∴PB =3. ∴BD =PD -PB =12-3=9, DE =PD +PE =16. ∵DA 切⊙O 2于点A ,∴DA 2=DB ·DE ,即AD 2=9×16,∴AD =12.1.3.2 圆内接四边形的性质与判定[对应学生用书P29][读教材·填要点]1.圆内接四边形的性质定理圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角.2.圆内接四边形的判定(1)定理:如果一个四边形的一组对角互补,那么这个四边形内接于圆.(2)符号语言表述:在四边形ABCD中,如果∠B+∠D=180°或∠A+∠C=180°,那么四边形ABCD内接于圆.[小问题·大思维]1.所有的三角形都有外接圆吗?所有的四边形是否都有外接圆?提示:所有的三角形都有外接圆,但四边形并不一定有外接圆.2.如果一个平行四边形有外接圆,它是矩形吗?提示:因为平行四边形的对角相等,圆内接四边形的对角和为180°,所以该平行四边形一定是矩形.[对应学生用书P29][例1]如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C 两点,圆心O在∠P AC的内部,点M是BC的中点.(1)证明:A,P,O,M四点共圆;(2)求∠OAM+∠APM的大小.[思路点拨]本题考查四点共圆的判定及性质的应用问题,解答(1)可利用圆内接四边形的判定定理证明。
