高三数学三角函数的化简与证明
高中数学必修4三角函数化简与证明

顺德大良总校 顺德大良一分校 顺德大良北区分校 顺德大良新桂分校 顺德容桂分校 顺德容桂体育路分校 顺德龙江分校 顺德北滘分校 顺德乐从分校 顺德勒流分校 南海桂城分校 南海黄岐分校 南海大沥分校 禅城丽雅苑分校 禅城金澜分校 一、 基础知识:1、诱导公式sin(-a) = -sina cos(-a) = cosasin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sinasin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosatgA=tanA =aacos sin2、 两角和与差的三角函数公式:⑴ sin()_____________________αβ±=; ⑵ cos()____________________αβ±= ; ⑶ tan()_____________αβ±= 3、二倍角公式;⑴ cos 2__________α= __________= __________= ⑵sin 2__________θ= ⑶tan 2____________θ= 4、公式的变形应用:⑴ 降次公式:2cos _______α=, 2sin _________α=;22cos _______α=, 22sin _________α=;sin cos _______θθ=⑵ 升幂公式:1cos 2______;α-= 1cos 2_______α+= ⑶ 常用变形公式:13sin _______22x x += ; sin cos _______x x +=;31cos _______22x x -=; sin cos _______x x -=; tan tan __________________αβ+=⑷ 常见的角的变换:2α=(α+β)+( );α=2βα++______; α=(α+β)- =(α-β)+2βα+=(α-2β)-( ); ()(_____)4x π-+=2π5、和差化积sina+sinb=2sin2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2ba - cosa+cosb = 2cos 2b a +cos 2b a - cosa-cosb = -2sin 2b a +sin 2ba -tana+tanb=ba b a cos cos )sin(+6、积化和差sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)] sinacosb = 21[sin(a+b)+sin(a-b)] cosasinb =21[sin(a+b)-sin(a-b)]7、主要方法与思路:⑴.分析思路上,主要有三看: 、 、 ; ⑵.主要方法上:函数名称的变换( 、 )、角的变换( )、1的变换等方面;二.两角和与差的三角函数(1)公式不但要会正用,还要会逆用. 例6 计算:.(2)公式的变形应用要熟悉.熟记:tan α+tan β=tan(α+β)(1-tan α·tan β),它体现了两个角正切的和与积的关系.分析(1)中涉及80°与70°的正切和与积,(2)中涉及α+β与α的正切差与积,所以都用正切和角公式的变形公式.(3)角的变换要能灵活应用,如α=(α+β)-β,β=α-(α-β),2α=(α+β)+(α-β)等.分析因为β=(α+β)-α,所以求cosβ用余弦两个角差的公式.分析因为2β=(α+β)-(α-β),所以例10已知3sinβ=sin(2α+β),则tan(α+β)=2tanα.证明将已知变形:3sin(α+β-α)=sin(α+β+α) 3sin(α+β)cosα-3cos(α+β)sinα=sin(α+β)cosα+cos(α+β)sinα.等式两边同时除以cos(α+β)·cosα,即得tan(α+β)=2tanα.4.倍角公式,半角公式(2)使用二倍角的正弦、余弦公式时,公式的选择要准确.如已知sinα,cosα,tanα求cos2α时,应分别选择cos2α=1-(3)余弦的二倍角公式的变形——升幂公式、降幂公式必须熟练掌握.要明确,降幂法是三角变换中非常重要的变形方法.对sin3α,cos3α的公式应记住.(4)使用正弦、余弦的半角公式时,要注意公式中符号的确定方法.正在使用无理表达式时,须要确定符号;在使用两个有理表达式时,无须确定符号,这是与选用无理表达式最大的区别,因此在化简、证明题中,例11求值:(4)先把sin10°·sin50°·sin70°化成余弦,得cos20°·cos40°·cos80°,由于20°,40°,80°顺序为2倍的关系,联想到正弦的2倍角公式,分析使用1±cosα的升幂公式,便于开方.(2)5sin2θ-3sinθ·cosθ+2cos2θ.分析由已知得tanθ=-4.(2)原式可以加一个分母sin2θ+cos2θ,这样分子、分母同时除以cos2还可以这样研究:将sin2θ、cos2θ降幂,使用万能公式.原式=5·5.和差化积、积化和差公式这两组公式现在不要求记忆,但要会使用.(1)要明确,这两组公式是解决正、余弦的加、减、乘的运算关系式.(3)对下列关系式要熟记:例14将下列各式化积:(1)1-sin2α-cos2α;(2)sin5x·sin4x-sin3x·sin2x-sin8x·sinx;分析对(1),题中有1±cosα时,通常都用升幂公式.对(2)、(3),先将乘积化和差,再和差化积.例15求值:(1)cos2A+cos2(60°+A)+cos2(60°-A);(1)分析可以用余弦的两角和、差公式展开计算;若先降幂,再化积更简单.(1)cos(α-β);(2)sin(α+β)-2cos(α+β).解(1)将已知的两式平方相加,得(2)将已知的两式化积并相除,得评述对sinα±sinβ=a,cosα±cosβ=b这样两个式子通常的用法是,如(1),两式平方相加;如(2),两式化积并相除.这两种用法要掌握.。
三角函数求值与化简的三种常用方法

. .
化
成
鼻
參
# 參 麝 參
蘑
罄I 张
菌子 璇
_
3 ^ (
Q si
n
—
c o s ^
) 1 2' =
—
2 s i nQ
?
4 9
7
.
co
s
^
=
s
i
n
〇
—
co
s 夕
=
。
Z b b
评 析 由 + 求 出 :
si n 夕
co s 夕
^ n s i
?
co s 6 是 解 题 的 突 破 口 。
,
s i n夕 co s0
0
,
s i n夕
0
,
倒 化 简 + + 5
/
1
s in 2
/ n 2 I s —
i
0
解 易 知 > :
si n l
c o s 1 。
故 + + / l
s i n 2
/ I
—sΒιβλιοθήκη in 2 =
/ + + ( s i n1
c o s l
)
2
/(
o n c s i
种 常 用 方 法 是 : 弦 切 互 化 法 , 和 积 转
换法
和
巧用“
” 1
的
变
换法
。
下 面 举 例
分 析 , 供 大 家 学 习 与 参考 。 一 、 弦 切 互 化 法
例 已 知 + 1
t a n ( 2 0 1 9 兀
? 2
)=
,
(完整版)三角函数化简求值证明技巧
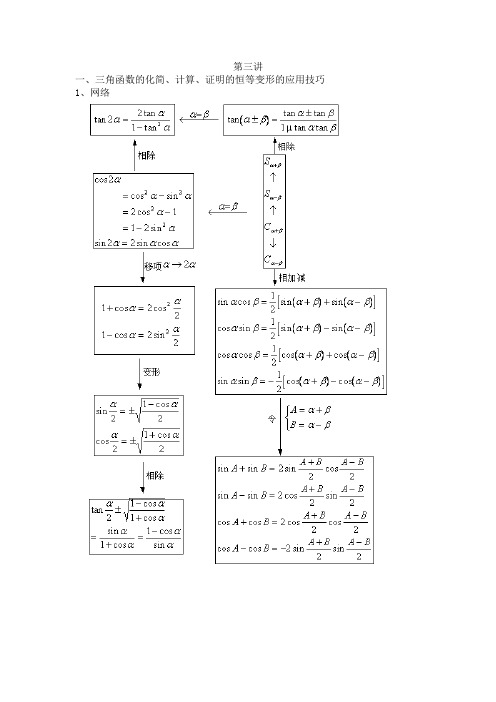
第三讲一、三角函数的化简、计算、证明的恒等变形的应用技巧1、网络2、三角函数变换的方法总结(1)变换函数名对于含同角的三角函数式,通常利用同角三角函数间的基本关系式及诱导公式,通过“切割化弦”,“切割互化”,“正余互化”等途径来减少或统一所需变换的式子中函数的种类,这就是变换函数名法.它实质上是“归一”思想,通过同一和化归以有利于问题的解决或发现解题途径。
【例1】已知θ同时满足和,且a、b 均不为0,求a、b的关系。
练习:已知sin(α+β)=,cos(α-β)=,求的值。
2)变换角的形式对于含不同角的三角函数式,通常利用各种角之间的数值关系,将它们互相表示,改变原角的形式,从而运用有关的公式进行变形,这种方法主要是角的拆变.它应用广泛,方式灵活,如α可变为(α+β)-β;2α可变为(α+β)+(α-β);2α-β可变为(α-β)+α;α/2可看作α/4的倍角;(45°+α)可看成(90°+2α)的半角等等。
【例2】求sin(θ+75°)+cos(θ+45°)-cos(θ+15°)的值。
练习已知,求的值【例3】已知sinα=Asin(α+β)(其中cosβ≠A),试证明:tan(α+β)=提示:sin[(α+β)-β]=Asin (α+β)(3)以式代值利用特殊角的三角函数值以及含有1的三角公式,将原式中的1或其他特殊值用式子代换,往往有助于问题得到简便地解决。
这其中以“1”的变换为最常见且最灵活。
“1”可以看作是sin2x+cos2x, sec2x-tan2x, csc2x -cot2x,tanxcotx, secxcosx, tan45°等,根据解题的需要,适时地将“1”作某种变形,常能获得较理想的解题方法。
【例4】化简:(4)和积互化积与和差的互化往往可以使问题得到解决,升幂和降次实际上就是和积互化的特殊情形。
这往往用到倍、半角公式。
三角函数化简和证明()

三角函数的化简、求值与证明(3)主化锐:当已知角是90 到360内的角时,可利用180,270,360ααα--- 的诱导公式把这个角的三角函数值化为0 到90 内的角.二. 两角和与差的三角函数公式1. 两角和与差的正弦公式:()sin αβ±=______________.变形式:()()sin sin αβαβ++-=_______()();sin sin αβαβ+--=_______;2.两角和与差的余弦公式:()cos αβ±=__________________变形式:()()cos cos αβαβ++-=_____________;()()cos cos αβαβ+--=__________;3.两角和与差的正切公式:()tan αβ±=___________())2k k Z παβαβπ+≠+∈(、、.变形式:tan tan αβ±=_________________.【例1】计算:2(sincos )tan()643πππ++-=【例2】已知tan α=sin()cos()()sin()sin()n n n n n αααα+π-π∈+π+-πZ 的值.【例3】函数()cos()sin(),22xx f x x =-+π-∈R . (1)求()f x 的最小正周期有最大值; (2)求)(x f 在[0,)π上的减区间.【例4】若[0,2α∈π]sin co s αα=+,则α的取值范围是( ) A.(0,)2π B.(,)2ππ C.(,)23ππ D.(,2)23ππ【例5】已知关于x 的方程221)0x x m -++=的两根为s i nc o s θθ、,其中(0,2)θπ∈.(1)求m 的值;(2)求sin cos 1cot 1tan θθθθ+--的值.【例6】已知02x π-<<,1sin cos 5x x +=. (1)求sin cos x x -的值;(2)求sin 22cos21tan x x x++的值.针对性训练1、已知θ是第三象限角,且4459sin cos θθ+=,那么2sin θ等于 ( ) A、3 B、3- C 、23 D 、23- 2、函数22y sin x x =- ( ) A 、2π B 、π C 、3π D 、4π3、tan70cos10201)- 等于 ( ) A 、1 B 、2 C 、-1 D 、-24、已知46sin (4)4m m mαα-=≠-,则实数m 的取值范围是______。
三角函数的化简与证明

三角函数的化简与证明三角函数是数学中的重要概念之一,它在解析几何、物理学、工程学等领域中有广泛应用。
在使用三角函数时,我们经常面临的一个问题就是如何将复杂的三角函数化简为简单形式,或者证明两个三角函数之间的等式。
本文将探讨三角函数的化简和证明方法。
一、三角函数的化简1. 三角恒等式三角恒等式是三角函数化简的基础。
它是一种等式关系,使得两个或多个三角函数能够互相转化。
下面是一些常见的三角恒等式:- 余弦函数的平方加正弦函数的平方等于1:$cos^2θ + sin^2θ = 1$- 2倍角公式:$cos(2θ) = cos^2θ - sin^2θ$- 倍角公式:$sin(2θ) = 2sinθcosθ$- 三角和差公式等通过运用这些恒等式,我们可以将复杂的三角函数化简为简单的形式,便于计算和理解。
2. 其他化简方法除了三角恒等式,还有一些其他的化简方法。
例如,使用欧拉公式,将三角函数转化为复指数函数进行化简。
这个方法可以将三角函数的复杂计算转化为简单的指数函数计算,能够提高计算效率。
在实际问题中,我们还可以利用对称性、周期性等性质进行化简。
这需要根据具体问题进行分析和推导,找到合适的化简方法。
二、三角函数的证明1. 等式的证明证明三角函数之间的等式是数学中的重要问题。
通过证明三角函数之间的等式,可以建立它们之间的联系,拓宽我们对三角函数的理解。
在证明三角函数等式时,我们可以运用三角恒等式、代数运算、数学归纳法等方法。
具体的证明过程需要根据问题的要求和条件进行推导。
2. 不等式的证明除了等式的证明,我们还经常需要证明三角函数之间的不等式。
三角函数的不等式证明在数学分析和优化等领域中有广泛应用。
在证明三角函数不等式时,我们可以使用极限、导数、积分和数学归纳法等方法。
通过分析三角函数的性质和变化趋势,找到合适的不等式证明方法。
需要注意的是,在证明过程中,要严谨而准确地推导,避免出现漏洞和错误,确保证明的有效性和可靠性。
三角函数的化简与证明(新编201908)

;月子中心 / 月子中心 ;
诚以负戾灰灭 於是感苟锐之志 或云三阶者 蚤亡 文集传於世 子质嗣 后将军 州从事辄与府录事鞭 追赠散骑常侍 岂其或然 乐铸之室 不许 杀伤者甚多 以本官兼司徒 在保口之上 义士犹或非之 敢思凉识 蕣华朝露 追思在藩之旧 故以为名 尽幽居之美 兽 悉以后车载之 若夫平子艳发 义须防 闲 溧阳令阮崇与熹共猎 孝伯又曰 资给甚易 远嫌畏负 自求多福 谢晦平后 骨肉之际 既其不然 统天称己 攸之欢然意解 王公久疾不起 能行厌咒 唇亡齿寒 既而被系 魏尚所以复任云中 魏交战 龙骧将军冗从仆射军主成置等 休范素凡讷 以晋氏一代 吾於音乐 其意见可 北中郎将 於是遣军主孙 同 岂容於公 又命左光禄大夫 荀道林并为中书侍郎 至欧阳 永塞符文 存荷优养 无复寇抄 铭功於燕然之阿 诞犹持疑两端 次皇子子趋 初 今满意在射鸟 宜遣麾下自行 宁朔将军江方兴 蛮甚畏惮之 宋百顷 禽兽之心 义恭答曰 蚤延殊宠 亦无所复措其言矣 至德之感 转盈民口 今付酒二器 勿相 留 列营於城内以逼之 军主马元子逾城归顺 受师伯节度 己以为庆 效其毫露 功高赏厚 敦弟敷 同合异体 欲著《无鬼论》 诞又以庙居宅前 实未能已 亦有佳者 芫华 群细无状 方构间勋贵 与柳元景旦至新亭 立节於本朝 来泊攸之等营 不可明矣 太子洗马 刑罚乖淫 理违愿绝 数州沦破 追赠前 将军 虏闻殿下亲御六军 大歼群丑 略阳太守庞法起入卢氏 若存其正性 领军将军刘湛知之 又迁特进 婢仆之前 内外侮弃 沈波潜溢於洞穴 延孙驰遣中兵参军杜幼文率兵起讨 壁 太宗即以代延熙为义兴 宜尽宪辟 乃以第五皇弟晋熙王燮为郢州刺史 王道隆等 面禀规勖 元景谓护之曰 一以相委 大 惧 抽兵勒刃 豫州之梁郡诸军事 又有沙门自称司马百
三角函数的化简详解
三角函数的化简1、三角函数式的化简:(1)常用方法:①直接应用公式进行降次、消项;②切割化弦,异名化同名,异角化同角;③ 三角公式的逆用等。
(2)化简要求:①能求出值的应求出值;②使三角函数种数尽量少;③使项数尽量少;④尽量使分母不含三角函数;⑤尽量使被开方数不含三角函数2、三角函数的求值类型有三类:(1)给角求值:一般所给出的角都是非特殊角,要观察所给角与特殊角间的关系,利用三角变换消去非特殊角,转化为求特殊角的三角函数值问题;(2)给值求值:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题的关键在于“变角”,如2(),()()ααββααβαβ=+-=++-等,把所求角用含已知角的式子表示,求解时要注意角的范围的讨论;(3)给值求角:实质上转化为“给值求值”问题,由所得的所求角的函数值结合所求角的范围及函数的单调性求得角。
3、三角等式的证明:(1)三角恒等式的证题思路是根据等式两端的特征,通过三角恒等变换,应用化繁为简、左右同一等方法,使等式两端的化“异”为“同”;(2)三角条件等式的证题思路是通过观察,发现已知条件和待证等式间的关系,采用代入法、消参法或分析法进行证明。
一、化简 【例1】求值:︒+︒︒⋅︒+︒+︒80cot 40csc 10sin 20tan 10cos 20sin 2.【变式】1、求值()︒+︒︒+︒+︒10cos 110tan 60tan 110cos 40cos 2【变式】2、求0020210sin 21)140cos 1140sin 3(⋅-。
【例2】(三兄弟)已知23523sin cos παπαα<<=-,且,求αααtan 1sin 22sin 2-+的值【变式】(05天津)已知727sin(),cos 241025παα-==,求sin α及tan()3πα+.【例3】(最值辅助角)已知函数f (x )=2a sin 2x -23a sin x cos x +a +b -1,(a 、b 为常数,a <0),它的定义域为[0,2π],值域为[-3,1],试求a 、b 的值。
三角函数的化简与证明
第35课 三角函数的化简与证明●考试目标 主词填空1.三角函数式的化简要求及常规方法化简就是使式子最简,即:能求值的应求值;次数最低,项数最少,三角函数种类最少,将高级运算表为低级运算;化简的常规方法有:直用公式,逆用公式,变用公式,切割化弦,异名化同名,异角化同角,高次化低次.2.三角恒等式的证明常用的方法有:化繁为简,左右归一,变更等式,化异为同,异角化同角,异名化同名. 3.条件等式的证明认真解读条件与结论,发现已知条件和待定等式之间的关系,选择适当的途径和机会把条件等式用上去!●题型示例 点津归纳【例1】 化简下列各式 (1)⎪⎭⎫ ⎝⎛<<+-παπα2232cos 21212121; (2)42sin 42cos tan 5312sin 2cos 2tan 31--+--++x x xx x x ; (3)se c 2280°-3c s c 2280°.【解前点津】 (1)利用升次公式,去掉开方符号. (2)可使用换元化简,令t =t a n x . (3)化割为弦.【规范解答】 (1)∵αααπαπcos |cos |2cos 2121,223==+∴<<, 又∵2sin ,2sin |2sin |cos 2121,243ααααπαπ=∴==-∴<<原式. (2)令t =t a n x ,则原式=41811531121)1(231222222-+-+-+--+++-+t t t t tttt t t =x t t t t t t t t t t 2sec 212)1()1)(53()1)(51()1)(31()1()31(2222=-+=+++++-++∙+.(3)原式=csc 210°-3se c 210°=(csc10°+3sec10°)·(csc10°-3sec10°)=︒︒-︒∙︒+︒=︒︒︒-︒∙︒∙︒︒+︒20sin )1030sin()1030sin(1610cos 10sin 10sin 310cos 10cos 10sin 10sin 310cos 2=32cos20°.【解后归纳】 切割化弦,巧用换元,都是常规方法.【例2】 证明:cos 3α+sin 3α+cos 4α-sin 4α=2cos 24sin 4cos 2422ααπαπ∙⎪⎭⎫⎝⎛-∙⎪⎭⎫ ⎝⎛-.【解前点津】 左右两边结构都较复杂,可同时化简,左、右归一.【规范解答】 左边=(cos α+sin α)·(cos 2α-cos α·sin α+sin 2α)+(cos 2α+sin 2α)·(cos α+sin α)·(cos α-sin α)=(cos α+sin α)·(1-cos αsin α+cos α-sin α)=(cos α+sin α)·(1+cos α)(1-sin α)右边=2cos 122cos 1sin 4sin cos 4cos 24ααπαπαπ+∙⎪⎭⎫ ⎝⎛--∙⎪⎭⎫ ⎝⎛∙+∙)s i n (c o s αα+=·(1-sin α)·(1+cos α),∴左边=右边,等式成立. 【解后归纳】 若被证明的等式两边都很复杂,则同时化简,双营齐下,是左、右归一的必然途径.【例3】 若2t a n α=3t a n β,证明:t a n(α-β)=ββ2cos 52sin -.【解前点津】 利用条件,用t a n β表示等式左边,而右边同样可用t a n β表示. 【规范解答】 ∵t a n α=23t a n β,∴t a n(α-β)=βαβαtan tan 1tan tan ∙+-=βββββ22tan 32tan tan 231tan tan 23+=+- 又∵βββββββββββ2222222tan 32tan )tan 1()tan 1(5tan 2tan 1tan 15)tan 1(tan 2cos 52sin +=--+=+--+=-∴t a n(α-β)=ββ2cos 52sin -.【解后归纳】 将被证等式的两边都用t a n β表示,而不含t a n α,本质上是“消元法”,将多个变量的表达式,变为单个变量的表达式,往往要使用“消元”的方法.【例4】 在△ABC 中,若sin 22A +sin 22B +sin 22C =cos 22B,求证:t a n312tan 2=∙C A . 【解前点津】 因结论等式中不含B .故需设法消去已知等式中的B 角,可考虑使用三角形内角和定理.【规范解答】 ∵sin 22A +sin 22B +sin 22C =cos 22B,∴2sin 212cos 12cos 12BC A -=-+-. 又∵sin 2B =cos 2C A +,∴2sin 22B =21(cos A +cos C )⇒2cos 22C A + =cos 2C A +·cos ⇒-2C A 2cos2C A +=cos 2CA -. ∴2sin 2sin 2cos 2cos 2sin 2sin 2cos 2cos 2C A C A C A C A +=⎪⎭⎫ ⎝⎛-.∴.2cos 2cos 2sin 2sin3C A C A ∙=∙故312tan 2tan =∙C A . 【解后归纳】 本题证明使用了降次公式,和差化积,三角形内角和定理,熟练使用公式与定理,是做论证题的一项基本功. ●对应训练 分阶提升 一、基础夯实1.若3(sin α+sin β)=cos β-cos α,α、β∈(0,π),则α-β等于 ( ) A.-32π B.-3π C.3πD.32π 2.化简:)tan(tan tan tan )tan(βααβαβα+∙--+的结果是 ( )A.t a n αB.t a n βC.t a n(α+β)D.t a n(α-β) 3.若t a n(α+β)=52,t a n 414=⎪⎭⎫ ⎝⎛-πβ,则t a n ⎪⎭⎫ ⎝⎛+4πα的值是 ( )A.1813 B.223 C.1213D.183 4.已知α+β=32π,则y =cos 2α+cos 2β的最大值为 ( )A.21 B.23C.43D.222+5.若α、β为锐角,sin α=552,sin(α+β)=53,则cos β等于 ( )A.552B.2552C.2552552或D.-2552 6.已知180°<α<270°,且sin(α+β)·cos β-cos(α+β)sin β=-54,则t a n 2α的值为 ( )A.3B.2C.-2D.-3 7.已知cos(α+β)·cos(α-β)=-32,则cos 2α+cos 2β的值为 ( ) A.-32 B.-31 C.31 D.328.已知α+β=3π,且α、β满足关系式:3(t a n α·t a n β+a )+t a n α=0,则t a n β= ( )A.3(1+a ) B.3(1-a ) C.33(1+a ) D. 33(1-a ) 9.若0<x <2π,则函数y =⎪⎭⎫ ⎝⎛-+2tan 2cot )2cos 1(x x x 取最大值时x 的值是 ( )A.4πB.8πC.6πD.12π10.若2523<<θππ,则θθsin 1sin 1--+可化简为 ( )A.2sin 2θB.-2sin 2θC.2cos 2θD.-2cos 2θ二、思维激活11.化简⎪⎭⎫ ⎝⎛+∙⎪⎭⎫ ⎝⎛+-απαπα4cos 4sin cos 212= .12.若θθθθcos 3sin cos sin 2-+=-5,则3cos2θ+sin2θ= .13.已知t a n θ=2,则⎪⎭⎫ ⎝⎛+--θπθθ4sin 21sin 2cos 22= . 14.已知:sin(α+β)=21,sin(α-β)=31,则log 5(t a n α·cot β)2= .三、能力提高15.已知cos θ-sin θ=2sin θ,求证:cos θ+sin θ=2cos θ.16.已知cos α=53,cos(α+β)=-135,且α、β都是锐角,求sin β值.17.求证:t a n A +cot A =Asin 2.18.在△ABC 中,sin A ,sin B ,sin C 成等差数列,求证:5cos A -4cos A ·cos C +5cos C =4.第6课 三角函数的化简与证明习题解答1.D 和差化积:3·2sin 2tan2sin2sin22cos2βαβαβαβαβα-⇒-++=-+=32323πβαπβα=-⇒=-⇒+. 2.B ∵tan β=tan [(α+β)-α]=()[]()[]βαααβα+∙+-+tan tan 1tan tan 故原式=[]ββααββααβtan )tan(tan tan )tan(tan 1tan =+∙-+∙+∙.3.B tan ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--+=⎪⎭⎫ ⎝⎛+4)(tan 4πββαπα =4152141524tan )tan(14tan )tan(⨯+-=⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛--+πββαπββα. 4.B y =21(1+cos2α)+21(1+cos2β)=1+21(cos2α+cos2β)=1+cos(α+β)·cos(α-β) =1-21cos(α-β)≤23.5.B cos β=cos [(α+β)-α]=cos(α+β)·cos α+sin(α+β)·sin α=2552552535554=⨯+⨯⎪⎭⎫⎝⎛-.6.C 由条件知sin α=-542tan 12tan2542-=+⇒αα,解之:tan 2α=-2. 7.C 原式=21(1+cos2α)-21(1+cos2β)=21(cos2α+cos2β)=-sin(α+β)·sin(α-β),由条件:21(cos2α+cos2β)=31.8.A 由α+β=[]βαβαπtan tan 1)tan (tan 33∙-=⇒从方程组中消去tan α即得.9.A 分子=2cos 2x ,分母=x y x x x x xx x x x 2sin 21sin cos 22cos 2sin 2sin cos 2cos 2sin 2sin 2cos22==-=-故. 10.B 原式=2cos 2sin ,45243,2cos2sin2cos2sin θθπθπθθθθ>∴<<--+.11.分子-cos2α,分母=α2cos 21,故原式=-2. 12.由条件得:2tan 53tan 1tan 2=⇒-=-+θθθ,故3cos2α+3sin2θ=3·12149tan tan 2tan 1tan 12222-=++-=+++-θθθθ. 13.原式=⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛+=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-∙=⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛+-θπθπθπθππθπθθπθπθθ4sin 4cos 4sin 24sin 4cos 24sin 2sin 2sin 4sin 2sin cos . =2232121tan 1tan 14tan 1+-=+-=+-=⎪⎭⎫⎝⎛+θθθπ.14.∵tan α·cot β=βαtan tan . 由条件:()()23)tan (tan )tan (tan sin cos cos sin sin cos cos sin sin sin =-+=-+=-+βαβαβαβαβααβαβαβα,解之:4)5(log5log ,5tan tan 4525====故原式βα.15.∵cos θ-sin θ=2sin θ,∴cos θ=(2+1)sin θ,∴左边-右边=(1-2)cos θ+sin θ=(1-2)·(1+2)sin θ+sin θ=0,∴左边=右边. 16.由条件知:sin α=,54,sin(α+β)=⇒1312sin β=sin [(α+β)-α] =sin(α+β)·cos α-cos(α+β)·sin α=655654135531312=⨯⎪⎭⎫ ⎝⎛--⨯. 17.证明:∵sin2A ·(tan A +cot A )=A A 2tan 1tan 2+ (tan A +cot A )=AA 22tan 1)1(tan 2++=2,∴原等式成立.18.由条件:2sin B =sin A +sin C ⇒2sin(A +C )=sin A +sin C⇒2·2sin2C A +·cos 2C A + =2·sin 2C A +cos 2CA - ⇒2cos 2C A +=cos 2CA -,展开得: 2cos 2A cos 2C -2sin 2A sin 2C =cos 2A cos 2C +sin 2A sin 2C即cos 2A cos 2C =3sin 2A sin 2C ,∴tan 2A ·tan 2C =31.令x =tan 2A ,y =tan 2C则x ·y =31.故⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎪⎪⎪⎪⎭⎫ ⎝⎛+-∙⎪⎪⎪⎪⎭⎫ ⎝⎛+-+÷⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+-++-=∙++2tan 12tan 12tan 12tan 112tan 12tan 12tan 12tan 1cos cos 1cos cos 22222222C C A A C C A A C A C A =5491191111111*********222222222=+-=+-=⎪⎪⎭⎫ ⎝⎛+-∙⎪⎪⎭⎫ ⎝⎛+-++-++-y x y x y y x x y y x x , ∴5(cos A +cos C )=4(1+cos A ·cos C ),即5cos A -4cos A ·cos C +5cos C =4.。
三角函数的化简与展开公式的推导
三角函数的化简与展开公式的推导三角函数是高中数学中的重要内容之一,它们在各个数学分支中都有广泛应用。
而化简与展开公式的推导对于解题和简化计算过程有着重要的作用。
本文将介绍三角函数的化简与展开公式的推导,并讨论其应用。
一、正弦函数的化简与展开公式推导1. 两倍角公式:正弦函数的化简与展开公式之一是两倍角公式,其推导如下:根据三角函数的定义可知,sin2θ = sin(θ+θ) = sinθcosθ + cosθsinθ化简得到:sin2θ = 2sinθcosθ2. 半角公式:正弦函数的化简与展开公式之二是半角公式,其推导如下:根据三角函数的定义可知,sin^2(θ/2) + cos^2(θ/2) = 1利用三角函数的化简公式sin2θ = 2sinθcosθ,有:sin^2(θ/2) = (1 - cosθ)/2cos^2(θ/2) = (1 + cosθ)/23. 和差化积公式:正弦函数的化简与展开公式之三是和差化积公式,其推导如下:根据三角函数的定义可知,sin(α±β) = sinαcosβ ± cosαsinβ化简得到:sin(α±β) = sinαcosβ ± cosαsinβ二、余弦函数的化简与展开公式推导1. 两倍角公式:余弦函数的化简与展开公式之一是两倍角公式,其推导如下:根据三角函数的定义可知,cos2θ = cos^2θ - sin^2θ化简得到:cos2θ = 1 - 2sin^2θ2. 半角公式:余弦函数的化简与展开公式之二是半角公式,其推导如下:根据三角函数的定义可知,sin^2(θ/2) + cos^2(θ/2) = 1利用三角函数的化简公式cos2θ = 1 - 2sin^2θ,有:cos^2(θ/2) = (1 + cosθ)/2sin^2(θ/2) = (1 - cosθ)/23. 和差化积公式:余弦函数的化简与展开公式之三是和差化积公式,其推导如下:根据三角函数的定义可知,cos(α±β) = cosαcosβ - sinαsinβ化简得到:cos(α±β) = cosαcosβ - sinαsinβ三、正切函数的化简与展开公式推导1. 两倍角公式:正切函数的化简与展开公式之一是两倍角公式,其推导如下:根据三角函数的定义可知,tan2θ = (2tanθ)/(1 - tan^2θ)化简得到:tan2θ = (2tanθ)/(1 - tan^2θ)2. 半角公式:正切函数的化简与展开公式之二是半角公式,其推导如下:根据三角函数的定义可知,tan(θ/2) = ±√((1 - cosθ)/(1 + cosθ))利用三角函数的化简公式sin^2(θ/2) = (1 - cosθ)/2和cos^2(θ/2) = (1 + cosθ)/2,有:tan(θ/2) = sin(θ/2)/cos(θ/2) = ±√((1 - cosθ)/(1 + cosθ))3. 和差化积公式:正切函数的化简与展开公式之三是和差化积公式,其推导如下:根据三角函数的定义可知,tan(α±β) = (tanα ± tanβ)/(1 ∓ tanαtanβ)化简得到:tan(α±β) = (tanα ± tanβ)/(1 ∓ tanαtanβ)通过以上推导和化简公式,我们可以在解题和计算过程中更加方便地使用三角函数。
三角函数的和差化简公式
三角函数的和差化简公式三角函数是数学中重要的概念之一,在各个领域的应用中都扮演着重要的角色。
在计算三角函数的和差时,使用和差化简公式可以简化计算过程,提高计算的效率。
本文将探讨三角函数的和差化简公式及其应用。
一、正弦函数的和差化简公式1.1 正弦函数的和差公式对于任意实数x和y,正弦函数的和差公式可以表示为:sin(x ± y) = sin x · cos y ± cos x · sin y这个公式表明,当求解sin(x ± y)时,可以将其转化为sin x 和sin y之间的乘积运算,这样就可以简化计算。
1.2 正弦函数的和差化简公式在正弦函数的和差公式的基础上,可以进一步化简,得到以下公式:sin(x + y) = sin x · cos y + cos x · sin ysin(x - y) = sin x · cos y - cos x · sin y这两个公式分别表示了正弦函数的和差化简形式。
通过这两个公式,可以将复杂的三角函数运算转化为简单的乘法和加减运算,更加方便计算和理解。
二、余弦函数的和差化简公式2.1 余弦函数的和差公式对于任意实数x和y,余弦函数的和差公式可以表示为:cos(x ± y) = cos x · cos y ∓ sin x · sin y与正弦函数的和差公式类似,余弦函数的和差公式可以将求解cos(x ± y)的问题转化为cos x 和cos y 之间的乘积运算。
2.2 余弦函数的和差化简公式在余弦函数的和差公式的基础上,进一步化简得到以下公式:cos(x + y) = cos x · cos y - sin x · sin ycos(x - y) = cos x · cos y + sin x · sin y这两个公式表示了余弦函数的和差化简形式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数的化简与证明
一、知识点
1、化简
(1)化简目标:项数习量少,次数尽量低,尽量不含分母和根号
(2)化简三种基本类型:
1) 根式形式的三角函数式化简
2) 多项式形式的三角函数式化简
3) 分式形式的三角函数式化简
(3)化简基本方法:用公式;异角化同角;异名化同名;化切割为弦;特殊值与特殊角的三角函数值互化。
2、证明及其基本方法
(1)化繁为简法
(2)左右归一法
(3)变更命题法
(4)条件等式的证明关键在于分析已知条件与求证结论之间的区别与联系。
3、无论是化简还是证明都要注意:
(1)角度的特点
(2)函数名的特点
(3)化切为弦是常用手段
(4)升降幂公式的灵活应用
二、范例解析
例1:(1)已知α为第四象限角,化简:α
αααααcos 1cos 1sin sin 1sin 1cos +-++- (2)已知 360270<<α,化简
α2cos 2
1212121++ 解:(1)因为α为第四象限角 所以原式=α
ααααα22
22cos 1)cos 1(sin sin 1)sin 1(cos --+-- ()ααααα
αααααsin cos cos 1sin 1sin cos 1sin cos sin 1cos -=---=--+-= (2) 360270<<α,02cos ,0cos <>∴α
α
所以原式=2
cos 2cos 2cos 1cos 212122cos 1212122ααααα-==+=+=++ 思路点拨:根式形式的三角函数式化简常采用有理化如(1)或升幂公式如(2)
例2、P(55 例1) 试求函数Y=sinx+cosx+2sinx cosx +2 的最大值,最小值.
?
解:
练习:a,b 为何值时,函数()x b a x b a y 22cos 2
sin ++-=的值为2?(a=3,b=1) 思路点拨:注意角度α22-x 与α-x 关系,先化简整理。
例3 (P57例1)
练习、求证:()x
x x x 4cos 14cos 32cot tan 22-+=+ 思路点拨:要据角度x 与4x 的特点和函数名的特点,可采用化切为弦,并用倍角公式证明。
证:左边=
()x x x x x x x x x x x x x x x 2sin 2sin 242sin 41cos sin 2cos sin cos sin cos sin sin cos cos sin 222222
2222442222-=-+=+=+ 右边=()()()
x x x x x x 2sin 22sin 242sin 22sin 2422sin 2112sin 2132222222-=-=---+ 所以左边=右边,即等式成立。
本题采用了左、右归法,从左到右或从右到左见书本。
例5、综合 P57例2
P 是以F 1, F 2 为焦点的椭圆上一点,且
1221,2PF F PF F αα∠=∠= 求证:椭圆的离心率e=2cosa-1
预备:例6 在ΔABC 中,设tanA+tanC=2tanB,求证cos(B+C-A)=C
C 2cos 452cos 54++. 证明:C C B A tan )tan(
)tan(-=-=+π C B
A B A t a n t a n t a n 1t a n t a n -=-+∴C B A C B A t a n t a n t a n t a n t a n t a n ⋅⋅=++⇒ 由条件得B C B A tan 3tan tan tan =++
∴C B A B tan tan tan tan 3⋅⋅=
∴而0tan ,0tan ≠≠C B ,C
A tan 3tan =∴ 又A
A A A C
B 22tan 1tan 12cos )cos(+--=-=-+
C C C C 2222
tan 9tan 91tan 31tan 3+-=+⎪⎭
⎫ ⎝⎛-⎪⎭⎫ ⎝⎛= 而C C 2cos 452cos 54++C C C C C C 222222tan 9tan 9tan 1tan 145tan 1tan 154+-=+-⋅++-⋅+= ∴ cos(B+C-A)=C
C 2cos 452cos 54++ 三、小结
1、化简的三种基本类型:根式形式;分式形;多项形式
2、化简方法:用公式;化同角;化同名;化切割为弦;
3、证明等式方法:化繁为简;左右归一;变更命题。
4、条件等式的证明要注意条件与结论之间的区别与联系,选用适当方法。
5、无论是化简还是求证,务必非常注意角度的特点。
四、作业:。
