第13讲+拉伸和压缩(二)
第二章 轴向拉伸和压缩
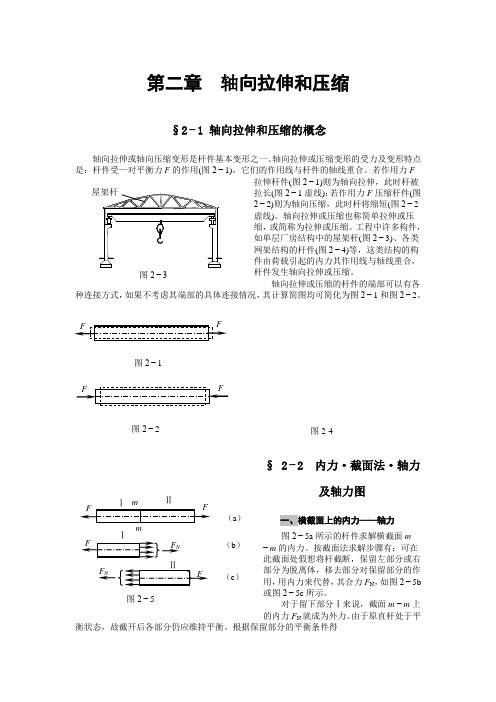
第二章 轴向拉伸和压缩§2−1 轴向拉伸和压缩的概念F(图2−1)则为轴向拉伸,此时杆被2−1虚线);若作用力F 压缩杆件(图(图2−2工程中许多构件,(图2−3)、各类(图2−4)等,这类结构的构2−1和图2−2。
§ 2−2 内力·截面法·轴力及轴力图一、横截面上的内力——轴力图2−5a 所示的杆件求解横截面m−m 的内力。
按截面法求解步骤有:可在此截面处假想将杆截断,保留左部分或右部分为脱离体,移去部分对保留部分的作用,用内力来代替,其合力F N ,如图2−5b 或图2−5c 所示。
对于留下部分Ⅰ来说,截面m −m 上的内力F N 就成为外力。
由于原直杆处于平衡状态,故截开后各部分仍应维持平衡。
根据保留部分的平衡条件得 mF N F N(a )(b ) (c )图2−5Ⅱ图2−1图2−2图2-4F F F F Fx==-=∑N N ,0,0 (2−1)式中,F N 为杆件任一截面m −m 上的内力,其作用线也与杆的轴线重合,即垂直于横截面并通过其形心,故称这种内力为轴力,用符号F N 表示。
若取部分Ⅱ为脱离体,则由作用与反作用原理可知,部分Ⅱ截开面上的轴力与前述部分上的轴力数值相等而方向相反(图2−5b,c)。
同样也可以从脱离体的平衡条件来确定。
二、轴力图当杆受多个轴向外力作用时,如图2−7a ,求轴力时须分段进行,因为AB 段的轴力与BC 段的轴力不相同。
要求AB 段杆内某截面m −m 的轴力,则假想用一平面沿m −m 处将杆截开,设取左段为脱离体(图2−7b),以F N Ⅰ代表该截面上的轴力。
于是,根据平衡条件∑F x =0,有 F F -=ⅠN负号表示的方向与所设的方向相反,即为压力。
要求B C 段杆内某截面n-n 的轴力,则在n −n 处将杆截开,仍取左段为脱离体(图2−7c ),以F N Ⅱ代表该截面上的轴力。
于是,根据平衡条件∑F x =0,有 02N Ⅱ=+-F F F由此得F F =N Ⅱ在多个力作用时,由于各段杆轴力的大小及正负号各异,所以为了形象地表明各截面轴力的变化情况,通常将其绘成“轴力图”(图2−7d)。
(完整版)13.DMA讲解

(5)经过仪器的自动处理,得到储能模量E’、损耗 模量E”、力学损耗tgδ
形变模式
包括拉伸、压缩、剪切、 弯曲(三点、单悬臂、双悬臂梁弯曲)等
有些仪器中还有杆、棒的扭转模式。
Options: Single Cantilever 3 Point Bending Dual Cantilever Tension Shear Compression
损耗模量 黏性性質
E’ – Storage Modulus
E’
储存模量
彈性性質
复数模量与力学损耗
力学损耗
E
E*
E tg E
E
称力学损耗角正切
力学损耗影响因素
分子结构
链段运动阻碍大
损耗大
空间位阻
次价力作用
(侧基体积大、数量多) (氢键、极性基团存在)
链段运动阻碍小
损耗小
外界条件
温度和外力作用频率
样品要求——形状、尺寸随测量系统变化, 要求均匀、平整、无气泡、尺寸精确;
测量扫描模式的选择
(1)温度扫描模式——在固定频率下,测量 动态模量及力学损耗随温度的变化。
T
(2)频率扫描模式——在恒温下,测量动
态模量与力学损耗随频率的变化。
(3)蠕变-回复扫描模式——在恒温下瞬时对试
样施加一恒定应力,测量试样应变随时间的变化 (蠕变曲线);在某一时刻取消应力,测量应变随时 间的变化(蠕变回复曲线);
振簧仪原理图
当改变振动频率与试样的自然频率相 同时,引起试样的共振
试率样称自为由共振端振簧振频仪幅率共将f振r 出曲线现极大值时的频
强迫非共振法
医学图像处理第十三讲 1-6节习题

例题10:简洁说明如下两种灰度变换函数会对图像产生什 么效果。(简答题,中等)
考点:对灰度变换函数及其作用于图像之后的效果的理解
答案:左图的变换函数会提高原始图像的对比度,进行变 换时,原始图像中灰度级低于 m 的像素会变暗,灰度级高 于m的像素会变亮,灰度级比m低得多或高得多的像素灰度 被压缩在较窄的范围内,接近黑色或白色。右图是左图的 极端情况,此变换函数将图像二值化为黑白图像,即灰度 值低于m的像素置为黑色,灰度级高于m的像素置为白色。
2019年1月8日12时16分
例题5:人眼视网膜上的感光细胞中, 比较敏感。 (填空题,容易) 考点:人眼视觉感知(锥状体、杆状体) 答案:锥状细胞 例题6:图像数字化包括 和 参数分别决定了图像的空间分辨率和 容易) 考点:采样与量化的概念 答案: 采样 、 量化 、灰度级分辨率
对颜色信息
两个过程,其 (填空题,
图像的增强处理,如平滑和锐化。例如可以通过低通滤波
器滤掉图像中的高频噪声,或通过高通滤波提取图像的边 缘并进行高频强调增强等等。
例题16:下列滤波器中属于带通滤波的是 容易)
。(选择题,
考点:各种滤波器的图像表示 答案:(b)
例题17:技术人员在检查一类由电子显微镜生成的代表性 图像的过程中发现如下问题: 1) 不感兴趣的明亮的孤立点; 2) 边缘不清晰; 3) 图像对比度不够; 4) 希望图像的平均灰 度值为指定值K,以便进行某种测量。试提出一种数字图像 增强处理方案,使技术人员能够按步骤纠正这些问题。( 解 答题,较难) 考点:包括空间域和频域的图像增强技术的综合应用 答案:技术人员可依次进行如下步骤: 1)对图像进行中值滤波; 2)进行高频强调滤波; 3)进行直方图均衡化; 4)计算图像的平均灰度K0,使所有像素灰度值加上K-K0。
第13章《分子热运动》教案 (公开课)2022年人教版

第十三章内能第1节分子热运动【教学目标】1.知识与技能1). 知道物质是由分子、原子构成的,一切物质的分子都在不停地做无规那么运动。
2).能识别并能用分子热运动的观点解释扩散现象。
3). 知道分子之间存在相互作用力。
2.过程与方法1〕.通过观察实验及列举生活中的事例认识到一切物质的分子都在不停地做无规那么的运动。
2).通过实验验证使学生知道物体温度越高,分子热运动越剧烈。
3).利用弹簧的弹力类比分子间的相互作用力,使学生了解分子间既存在斥力又存在引力。
3.情感、态度、价值观用实验和多媒体教学素材激发学生对大千世界的兴趣。
使学生了解,可以通过直接感知的现象,认识无法直接感知的事实。
【教学重点】分子热运动【教学难点】1〕.从宏观出发,通过直接感知的现象推测出无法感知的事实。
2〕.用分子热运动观点解释有关现象。
【教学准备】盛有二氧化氮的广口瓶、空广口瓶、玻璃板、烧杯、红墨水、水、胶头滴管、两个铅柱和钩码、弹簧和橡胶球、多媒体课件等。
【教学过程】这酒香是如何进入宾客鼻子里的呢?【板书课题】§13-1 分子热运动〔设计意图:以故事导入,调动学生的积极性,激发学生的学习兴趣和求知欲望。
〕学生讨论交流二、探究新知:(一)、物质的构成[建立情境]:原来这与我们肉眼看不见的组成物质的微观粒子有关,现代研究发现:常见的物质是由极其微小的粒子---分子、原子构成的。
请看图片。
〔教师出示图片〕【板书】:常见的物质是由分子、原子构成的。
[课件展示]:如果把分子设想成球形,它的直径大约只有百亿分之几米,人们通常用10-10m为单位来量度。
1cm3的空气中大约有 2.7×1019个分子,现在大型计算机每秒100亿次,如果人数数的速度也到达每秒100亿次,要想数完需要80多年。
学生观察、体会:常见物质是由极其微小的粒子---分子、原子构成的。
学生体会:分子体积特别小;一个物体中,分子的数目是巨大的。
×肉眼光学显微镜×电子显微镜√〔二〕、分子热运动1、扩散现象〔1〕、定义:[提出问题]:那么组成物体的这些数目众多的分子,你认为它们是运动还是静止的呢?[过渡]同学们对此提出了不同的观点,接下来我们通过实验验证分子是否在运动。
无机非金属材料测试方法教学设计 (2)

无机非金属材料测试方法教学设计背景无机非金属材料的研究和生产已成为当今世界重要的产业之一。
随着科学技术的发展,无机非金属材料性能的测试方法也得到了不断的完善和创新。
因此,对于学习无机非金属材料相关专业的学生而言,熟练掌握基本的测试方法是必不可少的。
教学目标•熟练掌握无机非金属材料所有性能测试方法;•理解测试过程中需要注意的相关安全问题;•掌握无机非金属材料性能测试结果的分析方法。
教学内容1.无机非金属材料压缩试验方法 1.1 压缩强度测试 1.2 破坏应变测试1.3 应力-应变曲线绘制 1.4 压缩模量测定方法2.无机非金属材料拉伸试验方法 2.1 极限拉伸强度测试 2.2 屈服强度测试 2.3 断裂应变测试 2.4 断裂延伸率测试3.无机非金属材料硬度测试方法 3.1 布氏硬度测试 3.2 洛氏硬度测试3.3 维氏硬度测试4.无机非金属材料造粒和碎裂检测方法 4.1 阴影法检测 4.2 静态显微镜检测 4.3 动态显微镜检测 4.4 残留粉尘分析法5.无机非金属材料表面测试方法 5.1 扫描电子显微镜检测 5.2 红外光谱测试 5.3 X射线衍射测试教学方法1.课堂教学法:通过讲解理论知识,向学生介绍测试方法的基本知识;2.实验教学法:通过实验,引导学生感性认识测试方法的过程和结果;3.讨论教学法:通过分析讨论实际案例,教授测试方法应用的实践技巧。
教学资源1.实验室:提供实验室测试设备、无机非金属材料样品和实验环境;2.教材:选用《材料测试与分析》(第二版)等相关教材,结合实际情况,进行案例分析和课堂讲解;3.多媒体教学资源:结合多媒体教学设备,进行PPT、演示视频等教学。
评估方法1.实验报告:让学生通过实验,根据测试结果撰写实验报告,评分占比20%;2.课堂考试:考试题目涵盖本学期所学的基本理论知识,占比30%;3.讨论与分析:结合案例分析,进行课堂讨论与分析,评分占比50%。
教学进度第一周•课程介绍和安排;•无机非金属材料压缩试验方法讲解。
资料:13 第13讲第三章第二节工程质量主要试验与检测方法(二)

⒉单桩动测试验采用各种动测方法求得单桩承载力及检验桩的质量是一种简便经济的方法。
在采用各种动测法时,应遵循下列原则:应做足够数量的动静对比试验,以检验方法本身的准确程度(误差在一定范围内),并确定相应的计算参数或修正系数。
试验本身可重复,系非破损试验,方法简便快捷。
⑴高应变动测高应变动测是指采用锤冲击桩顶,使桩周土产生塑性变形,实测桩顶附近所受力和速度随时间变化的规律,通过应力波理论分析得到桩土体系的有关参数。
适用于检测基桩的竖向抗压承载力和桩身完整性。
监测预制桩打入时的桩身应力和锤击能量传递比,为沉桩工艺参数及桩长选择提供依据。
检测数量:在地质条件相近、桩型和施工条件相同时,不宜少于总桩数5%,且不应少于5根。
对于一柱一桩的建筑物、构筑物,应全部进行完整性检测;对于非一柱一桩的建筑物、构筑物,当工程地质条件复杂或对桩基施工质量有疑问时,应增加试桩数量。
⑵低应变动测低应变动测主要采用弹性波反射法,对各类混凝土桩进行质量普查,检查桩身是否有断桩、夹泥、离析、缩颈等缺陷存在。
确定缺陷位置,对桩身完整性作出分类判别。
检测数量。
采用随机采样的方式抽检。
①柱下三桩或三桩以下的承台抽检桩数不少于一根。
②对设计等级为甲级,或地质条件复杂,成桩质量可靠性低的灌注桩,动测桩数不应少于总桩数的30%,且不得少于20根。
其他桩基工程的抽检数量不应少于总桩数的20%且不得少于10根。
③对于端承型大直径灌注桩,在以上抽检范围内,应采用钻芯、声波透射进行检测,抽检数量不应低于受检总桩数的10%。
动测结果不合格的桩比例过高时(占抽检总数5%以上),宜以相同的百分比进行扩大抽检,设计单位认为需要时,可扩大到普检。
对同一工程中同一批桩中有疑义的桩,宜采用多种方法同时进行检测,并进行综合分析。
低应变动测桩身质量评定等级分为四类:①无缺陷的完整桩;②有轻度缺陷,但基本不影响原设计桩身结构强度的桩;③有明显缺陷,影响原设计桩身结构强度的桩(可部分利用或降级使用);④有严重缺陷的桩(废桩)。
第十三章动荷载(讲稿)材料力学教案(顾志荣)
第十三章动荷载(讲稿)材料力学教案(顾志荣)第十五章动荷载一、教学目标和教学内容1、教学目标通过本章学习,唤起学生对动荷载问题的注意。
让学生知道动荷载问题的两个方面,目前应当掌握在较简单的工程问题中,动荷载引起杆件的应力、应变和位移的计算。
对于材料在动荷载下的力学行为,以后根据工作的需要再进一步补充学习。
让学生掌握动荷载问题的基本知识,如杆件作等加速运动时的应力计算,作等速旋转圆盘的应力分析,简单的自由落体冲击和水平冲击,以及循环应力问题的有关概念。
能够深刻认识动荷系数概念,并能够熟练地进行杆件作等加速运动时的应力计算,作等速旋转圆盘的应力分析,完成简单的自由落体冲击和水平冲击的计算。
2、教学内容介绍杆件作等加速运动拉伸、压缩及弯曲时的应力计算。
介绍等角速度旋转的动荷应力计算。
讲解简单冲击时,能量守恒的基本方程,分别导出自由落体冲击和水平冲击时的动荷系数公式,及杆件经受冲击时的应力计算公式。
二、重点难点重点:建立三类动荷载概念。
掌握杆件作等加速运动时的应力计算。
作等速旋转圆盘的应力分析。
简单的自由落体冲击和水平冲击问题的计算难点:对动静法和动荷系数的理解。
对于动荷载问题与静荷载问题的联系与区别。
1在简单冲击问题中,被冲击杆件冲击点的相应静荷位移的理解和计算,特别是水平冲击时的静荷位移的理解和计算。
三、教学方式采用启发式教学,通过提问,引导学生思考,让学生回答问题。
四、建议学时3学时五、实施学时六、讲课提纲(一)概念(动荷载的概念)1、静荷载:作用在构件上的荷载由零开始,逐渐(平缓、慢慢)地增长到最终值,以致在加载过程中,构件各点的加速度很小,可以不计;荷载加到最终值保持不变或变动的不显著的荷载,称之为静荷载。
2、动荷载:如果构件本身处于加速度运动状态(高层、超高层建筑施工时起吊重物;这些建筑物中运行的电梯―惯性力问题);或者静止的构件承受处于运动状态的物体作用(落锤打桩,锤头猛烈冲击砼桩顶―冲击问题);地震波引起建筑物晃动(构件在振动状态下工作―振动问题);机械零件在周期性变化的荷载下工作(交变应力疲劳问题),则构件受到荷载就是动荷载。
拉伸与压缩试题
拉伸与压缩试题————————————————————————————————作者:————————————————————————————————日期:第二章 拉伸与压缩一、是非题2-1 、当作用于杆件两端的一对外力等值反向共线时则杆件产生轴向拉伸或压缩变形。
( ) 2-2 、关于轴力有下列几种说法: 1、轴力是作用于杆件轴线上的载荷( ) 2、轴力是轴向拉伸或压缩时杆件横截面上分布内力系的合力( )3、轴力的大小与杆件的横截面面积有关( )4、轴力的大小与杆件的材料无关( )2-3、 同一材料制成的阶梯杆及其受力如图2-1CD 段的横截面面积为ABC 和DE 段均为2A 分别用和表示截面上的轴力和正应力则有1、轴力321N N N F F F >> 。
( )2、正应力1σ>2σ>3σ。
( )2-4、 轴力越大,杆件越容易拉断,因此轴力的大小可以用来判断杆件的强度。
( )2-5 、一轴向拉伸的钢杆材料弹性模量E =200GP a,比例极限p σ=200MP a ,今测得其轴向线应变ε=0.0015,则由胡克定律得其应力εσE ==300MP a 。
( ) 2-6 、关于材料的弹性模量E,有下列几种说法:1、E 的量纲与应力的量纲相同。
( )2、E 表示弹性变形能力的大小。
( )3、各种牌号钢材的E 值相差不大。
( )4、橡皮的E 比钢材的E值要大。
( )5、从某材料制成的轴向拉伸试样,测的应力和相应的应变,即可求的其εσ=E 。
( ) 2-7 、关于横向变形系数(泊松比)μ,有下列几种说法:1、为杆件轴向拉、压时,横向应变ε'与纵向应变ε之比的绝对值。
( )2、 μ值越大,其横向变形能力越差。
( )3、各种材料的μ值都满足:0<μ≤0.5。
( )2-8、 受轴向拉、压的等直杆,若其总伸长为零,则有1、杆内各处的应变必为零。
( )2、杆内各点的位移必为零。
( )3、杆内各点的正应力必为零。
人教版七年级数学上册同步讲义 第十三讲 归纳猜想——找规律
第十三讲归纳猜想——找规律13.1数字排列规律题【例1】一群整数朋友按照一定的规律排成一排,可排在□位置的数跑掉了,请帮它们把跑掉的朋友找回来.(1)5,8,11,14,□,20;(2)1,3,7,15,31,□;(3)1,1,2,3,5,8,□,21【答案】(1)17,(2)63,(3)13【练习1.1】下面数列后两位应该填上什么数字呢?2 3 5 8 12 17 ______ _______ ;3 6 10 15 21 ______【答案】23,30;28.【例2】观察下列一组数的排列:1、2、3、4、1、2、3、4、1、2、…,那么第2015个数是__________.【答案】3.【练习2.1】观察下列一组数的排列:1、2、3、4、3、2、1、2、3、4、3、2、1、…聪明的你猜猜第210个数是_________.【答案】2.【练习2.2】有一串数,它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个数是________.【答案】34.13.2几何图形变化规律题【例3】观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球__________个.【答案】602.【练习3.1】现有黑色三角形“▲”和“△”共200个,按照一定规律排列如下:▲▲△△▲△▲▲△△▲△▲▲……则黑色三角形有个,白色三角形有个.【答案】101,99.【练习3.2】观察下列图形排列规律(其中△是三角形,□是正方形,○是圆),□○△□□○△□○△□□○△□┅┅,若第一个图形是正方形,则第2008个图形是___________(填图形名称).【答案】圆.【例4】如图,在图1中,互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,……,则在第6个图形中,互不重叠的三角形共有____________个.【答案】19【练习4.1】“◆”代表甲种植物,“★”代表乙种植物,为美化环境,采用如图所示方案种植. 按此规律第六个图案中应种植乙种植物_________ 株.【答案】49.【练习4.2】已知一个面积为S的等边三角形,现将其各边n(n 为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如上图所示).(1)当n = 5时,共向外作出了个小等边三角形(2)当n = k时,共向外作出了个小等边三角形(用含k的式子表示).……n=3n=4n=5【答案】9,3(k-2).13.3数、式计算规律题【例5】观察下列顺序排列的等式:9×0+1=19×1+2=119×2+3=219×3+4=319×4+5=41……猜想:第10个等式应为.【答案】9×9+10=91.【例5.1】已知下列等式:①13=12;②13+23=32;③13+23+33=62;④13+23+33+43=102;由此规律知,第⑤个等式是.【答案】13+23+33+43+53=152.【例5.2】观察下面的几个算式:1+2+1=4, 1+2+3+2+1=9, 1+2+3+4+3+2+1=16, 1+2+3+4+5+4+3+2+1=25,…根据你所发现的规律,请你直接写出下面式子的结果: 1+2+3+…+99+100+99+…+3+2+1=__________.【答案】10000【例5.3】已知:22222233445422,33,44,55,338815152415+=⨯+=⨯+=⨯+=⨯ =+⨯=+b a aba b 则符合前面式子的规律,,若 (21010)【答案】109.【例6】观察:11111()37437⨯=-11111()7114711⨯=- 11111()111541115⨯=- ……计算:1111111111++++37711111515171721⨯⨯⨯⨯⨯.【答案】114.【例6.1】观察:11111() 35235⨯=-,11111() 57257⨯=-11111() 79279⨯=-…………计算:11111111 2446681820⨯+⨯+⨯++⨯=。
轴向拉伸与压缩的名词解释
轴向拉伸与压缩的名词解释引言:轴向拉伸与压缩是物理学领域中常见的概念,用于描述物体在力的作用下的变形情况。
本文将对轴向拉伸与压缩进行详细的解释与探讨。
一、轴向拉伸轴向拉伸是指物体在受到拉力作用下沿着其长度方向发生的变形现象。
当外力作用于物体的两端,并朝外拉伸时,物体会在轴向上发生拉伸。
拉伸的大小可以通过物体的伸长率来衡量,伸长率定义为单位长度的伸长与初始长度之比。
轴向拉伸现象广泛应用于工程领域,例如建筑中的钢筋,拉伸试验中的拉力传感器等。
钢筋在混凝土中起到增强材料的作用,能够抵抗建筑物的拉力。
而拉力传感器则是一种能够测量外力大小的传感器,利用了材料的拉伸特性。
二、轴向压缩轴向压缩是指物体在受到压力作用下沿着其长度方向发生的变形现象。
当外力作用于物体的两端,并朝内压缩时,物体会在轴向上发生压缩。
压缩的大小可以通过物体的压缩率来衡量,压缩率定义为单位长度的压缩与初始长度之比。
轴向压缩现象同样广泛应用于工程领域。
例如,桥梁中的墩柱、压缩试验中的压力传感器等。
墩柱是承受桥梁重力和交通荷载的重要结构部件,压缩试验中的压力传感器则是能够测量外力大小的传感器,利用了材料的压缩特性。
三、轴向拉伸与压缩的应用轴向拉伸与压缩的应用十分丰富,不仅在工程领域中有广泛应用,在其他领域中也有其独特的应用价值。
1. 材料科学:轴向拉伸与压缩是材料性能研究的重要手段。
通过对材料在拉伸和压缩条件下的变形进行测试,可以获得材料的各种力学性能参数,例如抗拉强度、抗压强度等。
这对材料的设计和应用具有重要的指导意义。
2. 生物医学:轴向拉伸与压缩在生物医学研究中具有重要的作用。
例如,在骨骼生物力学研究中,可以通过对骨骼的拉伸和压缩测试,了解骨骼力学特性并分析疾病的发生机制。
3. 电子工程:轴向拉伸与压缩的特性也可以应用于电子工程领域。
例如,电子产品中常使用弹性材料来保护内部电路。
这些材料可以在外力作用下发生轴向拉伸或压缩,起到减缓冲击力的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A B
A B
ACC 50 22 15 2 840mm2
s max
C C
N A
38000 560 10 6
67.86MPa
南京航空航天大学
剪应力互等定律
第七章 拉伸和压缩 南京航空航天大学
第一次 7.1 7.2 7.5 7.6 第二次 第三次 第四次 第五次 7.23 7.25
7.7 7.8 7.9
7.11 7.13 7.16
7.17 7.20 7.21
张明
江西九江长江大桥
南京航空航天大学 要点回顾
•应力的概念 •拉压杆横截面上的应力 •应力集中的概念 •许用应力与安全系数
南京航空航天大学
变形与应变
变形体与刚体 变形的定义及特点
构件内任意两点间的位置发生了变化 变形在弹性体内是连续的
变形与刚性位移的区别 对变形的定量描述-应变
两种基本变形-长度变化及角度变化 应变定义:线应变;剪应变(角应变)
南京航空航天大学
y
M’
M
应变的定义
g
Dx+Ds
Dx
由于拉伸和压缩的许用 应力相同,而AD段的截 面面积是BC段的两倍, 所以,BC段比AD段危 险。 BC段的应力为 取 b 9.5 mm N 20000 s s 则 h 13.3 mm A bh 20000 2 b 9.45 mm bh 1.4b
s
南京航空航天大学
例7.5
有一三角架图,其斜杆 由二根80×80×7等边角 钢组成,横杆由两根10 号槽钢组成,材料均为 A3钢,许用应力 [s]=120MPa。试求许可 载荷[P]。
南京航空航天大学
例7.5解
由节点A的平衡,可得
Y 0
P N1 2P sin 30 X 0
N2 N1 cos 30 1.732P
拉压杆件轴向伸长计算公式
N s A
Dl l
n
s E
Nl Dl EA
N i li Dl i 1 Ei Ai
南京航空航天大学
例7.7
图示阶梯状钢直杆,AB段和BC段的横截面面 积为AAB=ABC=500mm2,CD段的横截面面积为 AAB=ABC=500mm2。已知钢的弹性模量 E=200GPa。试求杆的纵向变形DL。
南京航空航天大学
例补1续解
这时
s = P/A= [s]/ cos226.57 =125MPa
a=60 时
s = [t]/ cos60 sin60 =115.5MPa<125MPa
所以
Pmax= 125×106×4×10-4=50000N=50kN
南京航空航天大学
例补2
已知P =38kN,问零件内最大拉应力 发生在哪个截面上?并求其值。
南京航空航天大学
§7.2 拉压杆的强度计算
破坏的概念及形式
塑性材料-大的塑性变形(屈服) 脆性材料-断裂 交变载荷-疲劳破坏 高温下的破坏-蠕变及应力松驰 破坏应力与许用应力(容许应力) 安全系数及其确定
强度计算准则
实例
南京航空航天大学
许用应力的定义
破坏应力s0除以一个大于1的系数n,即称为许用 应力,用[s]表示
南京航空航天大学
题7.12
一杆受轴向拉伸,某斜截面上的应力为 sa=50MPa,ta=-20MPa。试利用应力圆求该杆 横截面上的应力。
南京航空航天大学
§7.4 拉(压)杆的变形与位移
位移与应变 应变的定义-线(正)应变与角(剪)应变 应力与应变的关系-虎克定律 横向应变-横向变形系数(泊松比) 拉压杆件轴向伸长计算公式
泊松比n有时也使用m表示
南京航空航天大学
几种常用材料的E和n的约值
材料名称 E(GPa)
n
0.24~0.28
0.25~0.30 0.23~0.27 0.31~0.42 0.33
碳钢
合金钢 灰铸铁 铜及其合金 铝合金
196~216
186~206 78.5~157 72.6~128 70
南京航空航天大学
原始尺寸原理
AB ? AC ?
d2
A
南京航空航天大学
应力与应变的关系-虎克定律
拉压杆的应力与应变成正比,比例系数称为弹 性模量,用 E 表示
s E
•由于应变是无量纲的量,因而弹性模量与 应力具有相同的量纲
南京航空航天大学
关于弹性模量
弹性模量是材料常数,与受力状态无关,但 与温度等环境因素有关 弹性模量的数值通常很大,所以用GPa作为 单位,而不用MPa。 1GPa=109Pa =109N/m2
常用材料中,钢材的弹性模量最大,达 210GPa。当合金含量不大时,各种合金钢 的弹性模量也接近200~210GPa。
南京航空航天大学
横向变形
杆件在发生轴向变形(称纵向变形)的同时, 横向也会发生变形。 轴向伸长时,横向会发生收缩变形;轴长缩 短时,横向会发生伸长变形。 实验证明:当轴向应变为时,则横向应变为 -n。其中,n为材料常数,无量纲,其值在 0.2~0.5之间。 材料常数n称为泊松比。
取sa为横坐标, ta为纵坐标,则上式即是 一圆的方程,称为应力圆(也称莫尔圆)
南京航空航天大学
应力圆
t
s0 s0 2 s a t a 2 2
2
2
s
南京航空航天大学
应力状态的概念
描述一点的应力随空间方位而变化的现象 一点的应力通常不能仅使用某一个特殊面上 的应力来完整描述,因为应力的实质是张量 而不是标量或矢量 通过对应力状态的分析,发现可以使用三个 特殊的应力(主应力)及其方位(主方向)来完整 描述应力状态,从而可避开复杂的数学概念
2
s 0 1 cos 2a s a s 0 1 cos 2a 2 2 s sin 2a t s 0 sin 2a 0 a 2 2
南京航空航天大学
应力圆
s0 s0 2 s a t a 2 2
2 2
P P 30000 4 s 2 2 A d1 / 4 0.01729
127.8 MPa s
安全
南京航空航天大学
例7.3解
套筒处d2=,30mm, D2=40mm
P P 30000 4 s 2 2 2 2 A D2 d 2 / 4 0.04 0.03
x 0
Ds m Dx
南京航空航天大学
正应变与剪应变
Ds m Dx
平均应变
Ds lim Dx 0 Dx
线应变 正应变
g ?
角应变
直角的角度变化!
剪应变
南京航空航天大学
支架
AB、AC杆有无剪应变?有无 线应变?如何计算?
d1
a
a A” A’
AA d 2 d1 cos tan a cos a
2
s max s 0 s s t max t 45
2
南京航空航天大学
例补1
斜截面m-n由两部分胶合而成。胶合面 上 [s]=100MPa,[t]=50MPa。设由胶合 面的强度控制杆件的拉力。为使P最大, a应为多少?当A=4cm2,a60,确定 许可载荷P。
P
m
a
n
P
南京航空航天大学
54.6 MPa s
安全
南京航空航天大学
一横截面为矩形的钢制阶梯状直杆, 受力及各段长度如图。AD段和DB段 的横截面面积为BC段的两倍。矩形 截面的高度和宽度的比h/b=1.4,材 料的容许应力[s]=160MPa。试选择 各段和横截面尺寸h和b。
例7.4
南京航空航天大学
例7.4解
s
s
0
n
南京航空航天大学
安全系数的确定
材料特性
塑性材料-小 脆性材料-大
不定因素大-大 动载荷-大 静载荷-小 结构破坏对整体影响大-大 结构破坏造成严重后果-大 结构仅是功能性的-小
载荷特性
结构特性
寿命要求、经济性等、美学因素等
南京航空航天大学
强度计算的三种不同目的
南京航空航天大学
例7.6
图(a)所示为从拉杆内 取出的一个微小的正 六面体(单元体)及其 应力状态,求图示 30°斜截面上的应力, 并求该单元体中的最 大剪应力及其作用面。
南京航空航天大学
例7.6解
给定斜面上的应力可用 应力圆求得,也可用公 式直接计算。
s a s 0 cos a t a s 0 cos a sin a
s max s
s
0
n
强度设计 强度校核 确定许可载荷
南京航空航天大学
某张紧器工作时可能出现的最大张 力P=30kN,套筒和拉杆的材料均 为A3钢,[s]=160MPa。试校核其 强度。应力集中不考虑。
例7.3
南京航空航天大学
例7.3解
拉杆M20处的最小外径d1=17.29mm
例补1解
P
m
a
n
P
横截面上的应力 s = N/A = P/A 按强度条件 s cos2a[s] s cosa sina[t]
